diff options
Diffstat (limited to 'ml')
| -rw-r--r-- | ml/ADCharts.cc | 233 | ||||
| -rw-r--r-- | ml/ADCharts.h | 23 | ||||
| -rw-r--r-- | ml/Config.cc | 114 | ||||
| -rw-r--r-- | ml/Config.h | 51 | ||||
| -rw-r--r-- | ml/Dimension.cc | 173 | ||||
| -rw-r--r-- | ml/Dimension.h | 94 | ||||
| -rw-r--r-- | ml/Host.cc | 255 | ||||
| -rw-r--r-- | ml/Host.h | 100 | ||||
| -rw-r--r-- | ml/KMeans.cc | 43 | ||||
| -rw-r--r-- | ml/KMeans.h | 41 | ||||
| -rw-r--r-- | ml/Query.h | 57 | ||||
| -rw-r--r-- | ml/README.md | 310 | ||||
| -rw-r--r-- | ml/SamplesBuffer.cc | 150 | ||||
| -rw-r--r-- | ml/SamplesBuffer.h | 146 | ||||
| -rw-r--r-- | ml/SamplesBufferTests.cc | 146 | ||||
| -rw-r--r-- | ml/ml-dummy.c | 50 | ||||
| -rw-r--r-- | ml/ml-private.h | 26 | ||||
| -rw-r--r-- | ml/ml.cc | 165 | ||||
| -rw-r--r-- | ml/ml.h | 50 | ||||
| -rw-r--r-- | ml/notebooks/README.md | 5 | ||||
| -rw-r--r-- | ml/notebooks/netdata_anomaly_detection_deepdive.ipynb | 1712 |
21 files changed, 3944 insertions, 0 deletions
diff --git a/ml/ADCharts.cc b/ml/ADCharts.cc new file mode 100644 index 0000000..00c593c --- /dev/null +++ b/ml/ADCharts.cc @@ -0,0 +1,233 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#include "ADCharts.h" +#include "Config.h" + +void ml::updateDimensionsChart(RRDHOST *RH, + collected_number NumTrainedDimensions, + collected_number NumNormalDimensions, + collected_number NumAnomalousDimensions) { + static thread_local RRDSET *RS = nullptr; + static thread_local RRDDIM *NumTotalDimensionsRD = nullptr; + static thread_local RRDDIM *NumTrainedDimensionsRD = nullptr; + static thread_local RRDDIM *NumNormalDimensionsRD = nullptr; + static thread_local RRDDIM *NumAnomalousDimensionsRD = nullptr; + + if (!RS) { + std::stringstream IdSS, NameSS; + + IdSS << "dimensions_on_" << localhost->machine_guid; + NameSS << "dimensions_on_" << localhost->hostname; + + RS = rrdset_create( + RH, + "anomaly_detection", // type + IdSS.str().c_str(), // id + NameSS.str().c_str(), // name + "dimensions", // family + "anomaly_detection.dimensions", // ctx + "Anomaly detection dimensions", // title + "dimensions", // units + "netdata", // plugin + "ml", // module + 39183, // priority + RH->rrd_update_every, // update_every + RRDSET_TYPE_LINE // chart_type + ); + rrdset_flag_set(RS, RRDSET_FLAG_ANOMALY_DETECTION); + + NumTotalDimensionsRD = rrddim_add(RS, "total", NULL, + 1, 1, RRD_ALGORITHM_ABSOLUTE); + NumTrainedDimensionsRD = rrddim_add(RS, "trained", NULL, + 1, 1, RRD_ALGORITHM_ABSOLUTE); + NumNormalDimensionsRD = rrddim_add(RS, "normal", NULL, + 1, 1, RRD_ALGORITHM_ABSOLUTE); + NumAnomalousDimensionsRD = rrddim_add(RS, "anomalous", NULL, + 1, 1, RRD_ALGORITHM_ABSOLUTE); + } + + rrddim_set_by_pointer(RS, NumTotalDimensionsRD, NumNormalDimensions + NumAnomalousDimensions); + rrddim_set_by_pointer(RS, NumTrainedDimensionsRD, NumTrainedDimensions); + rrddim_set_by_pointer(RS, NumNormalDimensionsRD, NumNormalDimensions); + rrddim_set_by_pointer(RS, NumAnomalousDimensionsRD, NumAnomalousDimensions); + + rrdset_done(RS); +} + +void ml::updateHostAndDetectionRateCharts(RRDHOST *RH, collected_number AnomalyRate) { + static thread_local RRDSET *HostRateRS = nullptr; + static thread_local RRDDIM *AnomalyRateRD = nullptr; + + if (!HostRateRS) { + std::stringstream IdSS, NameSS; + + IdSS << "anomaly_rate_on_" << localhost->machine_guid; + NameSS << "anomaly_rate_on_" << localhost->hostname; + + HostRateRS = rrdset_create( + RH, + "anomaly_detection", // type + IdSS.str().c_str(), // id + NameSS.str().c_str(), // name + "anomaly_rate", // family + "anomaly_detection.anomaly_rate", // ctx + "Percentage of anomalous dimensions", // title + "percentage", // units + "netdata", // plugin + "ml", // module + 39184, // priority + RH->rrd_update_every, // update_every + RRDSET_TYPE_LINE // chart_type + ); + rrdset_flag_set(HostRateRS, RRDSET_FLAG_ANOMALY_DETECTION); + + AnomalyRateRD = rrddim_add(HostRateRS, "anomaly_rate", NULL, + 1, 100, RRD_ALGORITHM_ABSOLUTE); + } + + rrddim_set_by_pointer(HostRateRS, AnomalyRateRD, AnomalyRate); + rrdset_done(HostRateRS); + + static thread_local RRDSET *AnomalyDetectionRS = nullptr; + static thread_local RRDDIM *AboveThresholdRD = nullptr; + static thread_local RRDDIM *NewAnomalyEventRD = nullptr; + + if (!AnomalyDetectionRS) { + std::stringstream IdSS, NameSS; + + IdSS << "anomaly_detection_on_" << localhost->machine_guid; + NameSS << "anomaly_detection_on_" << localhost->hostname; + + AnomalyDetectionRS = rrdset_create( + RH, + "anomaly_detection", // type + IdSS.str().c_str(), // id + NameSS.str().c_str(), // name + "anomaly_detection", // family + "anomaly_detection.detector_events", // ctx + "Anomaly detection events", // title + "percentage", // units + "netdata", // plugin + "ml", // module + 39185, // priority + RH->rrd_update_every, // update_every + RRDSET_TYPE_LINE // chart_type + ); + rrdset_flag_set(AnomalyDetectionRS, RRDSET_FLAG_ANOMALY_DETECTION); + + AboveThresholdRD = rrddim_add(AnomalyDetectionRS, "above_threshold", NULL, + 1, 1, RRD_ALGORITHM_ABSOLUTE); + NewAnomalyEventRD = rrddim_add(AnomalyDetectionRS, "new_anomaly_event", NULL, + 1, 1, RRD_ALGORITHM_ABSOLUTE); + } + + /* + * Compute the values of the dimensions based on the host rate chart + */ + ONEWAYALLOC *OWA = onewayalloc_create(0); + time_t Now = now_realtime_sec(); + time_t Before = Now - RH->rrd_update_every; + time_t After = Before - Cfg.AnomalyDetectionQueryDuration; + RRDR_OPTIONS Options = static_cast<RRDR_OPTIONS>(0x00000000); + + RRDR *R = rrd2rrdr_legacy( + OWA, HostRateRS, + 1 /* points wanted */, + After, + Before, + Cfg.AnomalyDetectionGroupingMethod, + 0 /* resampling time */, + Options, "anomaly_rate", + NULL /* group options */, + 0, /* timeout */ + 0, /* tier */ + QUERY_SOURCE_ML + ); + if(R) { + assert(R->d == 1 && R->n == 1 && R->rows == 1); + + static thread_local bool PrevAboveThreshold = false; + bool AboveThreshold = R->v[0] >= Cfg.HostAnomalyRateThreshold; + bool NewAnomalyEvent = AboveThreshold && !PrevAboveThreshold; + PrevAboveThreshold = AboveThreshold; + + rrddim_set_by_pointer(AnomalyDetectionRS, AboveThresholdRD, AboveThreshold); + rrddim_set_by_pointer(AnomalyDetectionRS, NewAnomalyEventRD, NewAnomalyEvent); + rrdset_done(AnomalyDetectionRS); + + rrdr_free(OWA, R); + } + onewayalloc_destroy(OWA); +} + +void ml::updateDetectionChart(RRDHOST *RH) { + static thread_local RRDSET *RS = nullptr; + static thread_local RRDDIM *UserRD, *SystemRD = nullptr; + + if (!RS) { + std::stringstream IdSS, NameSS; + + IdSS << "prediction_stats_" << RH->machine_guid; + NameSS << "prediction_stats_for_" << RH->hostname; + + RS = rrdset_create_localhost( + "netdata", // type + IdSS.str().c_str(), // id + NameSS.str().c_str(), // name + "ml", // family + "netdata.prediction_stats", // ctx + "Prediction thread CPU usage", // title + "milliseconds/s", // units + "netdata", // plugin + "ml", // module + 136000, // priority + RH->rrd_update_every, // update_every + RRDSET_TYPE_STACKED // chart_type + ); + + UserRD = rrddim_add(RS, "user", NULL, 1, 1000, RRD_ALGORITHM_INCREMENTAL); + SystemRD = rrddim_add(RS, "system", NULL, 1, 1000, RRD_ALGORITHM_INCREMENTAL); + } + + struct rusage TRU; + getrusage(RUSAGE_THREAD, &TRU); + + rrddim_set_by_pointer(RS, UserRD, TRU.ru_utime.tv_sec * 1000000ULL + TRU.ru_utime.tv_usec); + rrddim_set_by_pointer(RS, SystemRD, TRU.ru_stime.tv_sec * 1000000ULL + TRU.ru_stime.tv_usec); + rrdset_done(RS); +} + +void ml::updateTrainingChart(RRDHOST *RH, struct rusage *TRU) { + static thread_local RRDSET *RS = nullptr; + static thread_local RRDDIM *UserRD = nullptr; + static thread_local RRDDIM *SystemRD = nullptr; + + if (!RS) { + std::stringstream IdSS, NameSS; + + IdSS << "training_stats_" << RH->machine_guid; + NameSS << "training_stats_for_" << RH->hostname; + + RS = rrdset_create_localhost( + "netdata", // type + IdSS.str().c_str(), // id + NameSS.str().c_str(), // name + "ml", // family + "netdata.training_stats", // ctx + "Training thread CPU usage", // title + "milliseconds/s", // units + "netdata", // plugin + "ml", // module + 136001, // priority + RH->rrd_update_every, // update_every + RRDSET_TYPE_STACKED // chart_type + ); + + UserRD = rrddim_add(RS, "user", NULL, 1, 1000, RRD_ALGORITHM_INCREMENTAL); + SystemRD = rrddim_add(RS, "system", NULL, 1, 1000, RRD_ALGORITHM_INCREMENTAL); + } + + rrddim_set_by_pointer(RS, UserRD, TRU->ru_utime.tv_sec * 1000000ULL + TRU->ru_utime.tv_usec); + rrddim_set_by_pointer(RS, SystemRD, TRU->ru_stime.tv_sec * 1000000ULL + TRU->ru_stime.tv_usec); + rrdset_done(RS); +} diff --git a/ml/ADCharts.h b/ml/ADCharts.h new file mode 100644 index 0000000..0be324f --- /dev/null +++ b/ml/ADCharts.h @@ -0,0 +1,23 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#ifndef ML_ADCHARTS_H +#define ML_ADCHARTS_H + +#include "ml-private.h" + +namespace ml { + +void updateDimensionsChart(RRDHOST *RH, + collected_number NumTrainedDimensions, + collected_number NumNormalDimensions, + collected_number NumAnomalousDimensions); + +void updateHostAndDetectionRateCharts(RRDHOST *RH, collected_number AnomalyRate); + +void updateDetectionChart(RRDHOST *RH); + +void updateTrainingChart(RRDHOST *RH, struct rusage *TRU); + +} // namespace ml + +#endif /* ML_ADCHARTS_H */ diff --git a/ml/Config.cc b/ml/Config.cc new file mode 100644 index 0000000..eedd8c2 --- /dev/null +++ b/ml/Config.cc @@ -0,0 +1,114 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#include "Config.h" +#include "ml-private.h" + +using namespace ml; + +/* + * Global configuration instance to be shared between training and + * prediction threads. + */ +Config ml::Cfg; + +template <typename T> +static T clamp(const T& Value, const T& Min, const T& Max) { + return std::max(Min, std::min(Value, Max)); +} + +/* + * Initialize global configuration variable. + */ +void Config::readMLConfig(void) { + const char *ConfigSectionML = CONFIG_SECTION_ML; + + bool EnableAnomalyDetection = config_get_boolean(ConfigSectionML, "enabled", true); + + /* + * Read values + */ + + unsigned MaxTrainSamples = config_get_number(ConfigSectionML, "maximum num samples to train", 4 * 3600); + unsigned MinTrainSamples = config_get_number(ConfigSectionML, "minimum num samples to train", 1 * 900); + unsigned TrainEvery = config_get_number(ConfigSectionML, "train every", 1 * 3600); + unsigned NumModelsToUse = config_get_number(ConfigSectionML, "number of models per dimension", 1 * 24); + + unsigned DiffN = config_get_number(ConfigSectionML, "num samples to diff", 1); + unsigned SmoothN = config_get_number(ConfigSectionML, "num samples to smooth", 3); + unsigned LagN = config_get_number(ConfigSectionML, "num samples to lag", 5); + + double RandomSamplingRatio = config_get_float(ConfigSectionML, "random sampling ratio", 1.0 / LagN); + unsigned MaxKMeansIters = config_get_number(ConfigSectionML, "maximum number of k-means iterations", 1000); + + double DimensionAnomalyScoreThreshold = config_get_float(ConfigSectionML, "dimension anomaly score threshold", 0.99); + + double HostAnomalyRateThreshold = config_get_float(ConfigSectionML, "host anomaly rate threshold", 1.0); + std::string AnomalyDetectionGroupingMethod = config_get(ConfigSectionML, "anomaly detection grouping method", "average"); + time_t AnomalyDetectionQueryDuration = config_get_number(ConfigSectionML, "anomaly detection grouping duration", 5 * 60); + + /* + * Clamp + */ + + MaxTrainSamples = clamp<unsigned>(MaxTrainSamples, 1 * 3600, 24 * 3600); + MinTrainSamples = clamp<unsigned>(MinTrainSamples, 1 * 900, 6 * 3600); + TrainEvery = clamp<unsigned>(TrainEvery, 1 * 3600, 6 * 3600); + NumModelsToUse = clamp<unsigned>(TrainEvery, 1, 7 * 24); + + DiffN = clamp(DiffN, 0u, 1u); + SmoothN = clamp(SmoothN, 0u, 5u); + LagN = clamp(LagN, 1u, 5u); + + RandomSamplingRatio = clamp(RandomSamplingRatio, 0.2, 1.0); + MaxKMeansIters = clamp(MaxKMeansIters, 500u, 1000u); + + DimensionAnomalyScoreThreshold = clamp(DimensionAnomalyScoreThreshold, 0.01, 5.00); + + HostAnomalyRateThreshold = clamp(HostAnomalyRateThreshold, 0.1, 10.0); + AnomalyDetectionQueryDuration = clamp<time_t>(AnomalyDetectionQueryDuration, 60, 15 * 60); + + /* + * Validate + */ + + if (MinTrainSamples >= MaxTrainSamples) { + error("invalid min/max train samples found (%u >= %u)", MinTrainSamples, MaxTrainSamples); + + MinTrainSamples = 1 * 3600; + MaxTrainSamples = 4 * 3600; + } + + /* + * Assign to config instance + */ + + Cfg.EnableAnomalyDetection = EnableAnomalyDetection; + + Cfg.MaxTrainSamples = MaxTrainSamples; + Cfg.MinTrainSamples = MinTrainSamples; + Cfg.TrainEvery = TrainEvery; + Cfg.NumModelsToUse = NumModelsToUse; + + Cfg.DiffN = DiffN; + Cfg.SmoothN = SmoothN; + Cfg.LagN = LagN; + + Cfg.RandomSamplingRatio = RandomSamplingRatio; + Cfg.MaxKMeansIters = MaxKMeansIters; + + Cfg.DimensionAnomalyScoreThreshold = DimensionAnomalyScoreThreshold; + + Cfg.HostAnomalyRateThreshold = HostAnomalyRateThreshold; + Cfg.AnomalyDetectionGroupingMethod = web_client_api_request_v1_data_group(AnomalyDetectionGroupingMethod.c_str(), RRDR_GROUPING_AVERAGE); + Cfg.AnomalyDetectionQueryDuration = AnomalyDetectionQueryDuration; + + Cfg.HostsToSkip = config_get(ConfigSectionML, "hosts to skip from training", "!*"); + Cfg.SP_HostsToSkip = simple_pattern_create(Cfg.HostsToSkip.c_str(), NULL, SIMPLE_PATTERN_EXACT); + + // Always exclude anomaly_detection charts from training. + Cfg.ChartsToSkip = "anomaly_detection.* "; + Cfg.ChartsToSkip += config_get(ConfigSectionML, "charts to skip from training", "netdata.*"); + Cfg.SP_ChartsToSkip = simple_pattern_create(ChartsToSkip.c_str(), NULL, SIMPLE_PATTERN_EXACT); + + Cfg.StreamADCharts = config_get_boolean(ConfigSectionML, "stream anomaly detection charts", true); +} diff --git a/ml/Config.h b/ml/Config.h new file mode 100644 index 0000000..d876d4a --- /dev/null +++ b/ml/Config.h @@ -0,0 +1,51 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#ifndef ML_CONFIG_H +#define ML_CONFIG_H + +#include "ml-private.h" + +namespace ml { + +class Config { +public: + bool EnableAnomalyDetection; + + unsigned MaxTrainSamples; + unsigned MinTrainSamples; + unsigned TrainEvery; + unsigned NumModelsToUse; + + unsigned DBEngineAnomalyRateEvery; + + unsigned DiffN; + unsigned SmoothN; + unsigned LagN; + + double RandomSamplingRatio; + unsigned MaxKMeansIters; + + double DimensionAnomalyScoreThreshold; + + double HostAnomalyRateThreshold; + RRDR_GROUPING AnomalyDetectionGroupingMethod; + time_t AnomalyDetectionQueryDuration; + + bool StreamADCharts; + + std::string HostsToSkip; + SIMPLE_PATTERN *SP_HostsToSkip; + + std::string ChartsToSkip; + SIMPLE_PATTERN *SP_ChartsToSkip; + + std::vector<uint32_t> RandomNums; + + void readMLConfig(); +}; + +extern Config Cfg; + +} // namespace ml + +#endif /* ML_CONFIG_H */ diff --git a/ml/Dimension.cc b/ml/Dimension.cc new file mode 100644 index 0000000..bf34abb --- /dev/null +++ b/ml/Dimension.cc @@ -0,0 +1,173 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#include "Config.h" +#include "Dimension.h" +#include "Query.h" + +using namespace ml; + +bool Dimension::isActive() const { + bool SetObsolete = rrdset_flag_check(RD->rrdset, RRDSET_FLAG_OBSOLETE); + bool DimObsolete = rrddim_flag_check(RD, RRDDIM_FLAG_OBSOLETE); + return !SetObsolete && !DimObsolete; +} + +std::pair<CalculatedNumber *, size_t> Dimension::getCalculatedNumbers() { + size_t MinN = Cfg.MinTrainSamples; + size_t MaxN = Cfg.MaxTrainSamples; + + // Figure out what our time window should be. + time_t BeforeT = now_realtime_sec() - 1; + time_t AfterT = BeforeT - (MaxN * updateEvery()); + + BeforeT -= (BeforeT % updateEvery()); + AfterT -= (AfterT % updateEvery()); + + BeforeT = std::min(BeforeT, latestTime()); + AfterT = std::max(AfterT, oldestTime()); + + if (AfterT >= BeforeT) + return { nullptr, 0 }; + + CalculatedNumber *CNs = new CalculatedNumber[MaxN * (Cfg.LagN + 1)](); + + // Start the query. + unsigned Idx = 0; + unsigned CollectedValues = 0; + unsigned TotalValues = 0; + + CalculatedNumber LastValue = std::numeric_limits<CalculatedNumber>::quiet_NaN(); + Query Q = Query(getRD()); + + Q.init(AfterT, BeforeT); + while (!Q.isFinished()) { + if (Idx == MaxN) + break; + + auto P = Q.nextMetric(); + CalculatedNumber Value = P.second; + + if (netdata_double_isnumber(Value)) { + CNs[Idx] = Value; + LastValue = CNs[Idx]; + CollectedValues++; + } else + CNs[Idx] = LastValue; + + Idx++; + } + TotalValues = Idx; + + if (CollectedValues < MinN) { + delete[] CNs; + return { nullptr, 0 }; + } + + // Find first non-NaN value. + for (Idx = 0; std::isnan(CNs[Idx]); Idx++, TotalValues--) { } + + // Overwrite NaN values. + if (Idx != 0) + memmove(CNs, &CNs[Idx], sizeof(CalculatedNumber) * TotalValues); + + return { CNs, TotalValues }; +} + +MLResult Dimension::trainModel() { + auto P = getCalculatedNumbers(); + CalculatedNumber *CNs = P.first; + unsigned N = P.second; + + if (!CNs) + return MLResult::MissingData; + + unsigned TargetNumSamples = Cfg.MaxTrainSamples * Cfg.RandomSamplingRatio; + double SamplingRatio = std::min(static_cast<double>(TargetNumSamples) / N, 1.0); + + SamplesBuffer SB = SamplesBuffer(CNs, N, 1, Cfg.DiffN, Cfg.SmoothN, Cfg.LagN, + SamplingRatio, Cfg.RandomNums); + std::vector<DSample> Samples = SB.preprocess(); + + KMeans KM; + KM.train(Samples, Cfg.MaxKMeansIters); + + { + std::lock_guard<std::mutex> Lock(Mutex); + Models[0] = KM; + } + + Trained = true; + ConstantModel = true; + + delete[] CNs; + return MLResult::Success; +} + +bool Dimension::shouldTrain(const TimePoint &TP) const { + if (ConstantModel) + return false; + + return (LastTrainedAt + Seconds(Cfg.TrainEvery * updateEvery())) < TP; +} + +bool Dimension::predict(CalculatedNumber Value, bool Exists) { + if (!Exists) { + CNs.clear(); + AnomalyBit = false; + return false; + } + + unsigned N = Cfg.DiffN + Cfg.SmoothN + Cfg.LagN; + if (CNs.size() < N) { + CNs.push_back(Value); + AnomalyBit = false; + return false; + } + + std::rotate(std::begin(CNs), std::begin(CNs) + 1, std::end(CNs)); + + if (CNs[N - 1] != Value) + ConstantModel = false; + + CNs[N - 1] = Value; + + if (!isTrained() || ConstantModel) { + AnomalyBit = false; + return false; + } + + CalculatedNumber *TmpCNs = new CalculatedNumber[N * (Cfg.LagN + 1)](); + std::memcpy(TmpCNs, CNs.data(), N * sizeof(CalculatedNumber)); + SamplesBuffer SB = SamplesBuffer(TmpCNs, N, 1, + Cfg.DiffN, Cfg.SmoothN, Cfg.LagN, + 1.0, Cfg.RandomNums); + const DSample Sample = SB.preprocess().back(); + delete[] TmpCNs; + + std::unique_lock<std::mutex> Lock(Mutex, std::defer_lock); + if (!Lock.try_lock()) { + AnomalyBit = false; + return false; + } + + for (const auto &KM : Models) { + double AnomalyScore = KM.anomalyScore(Sample); + if (AnomalyScore == std::numeric_limits<CalculatedNumber>::quiet_NaN()) { + AnomalyBit = false; + continue; + } + + if (AnomalyScore < (100 * Cfg.DimensionAnomalyScoreThreshold)) { + AnomalyBit = false; + return false; + } + } + + AnomalyBit = true; + return true; +} + +std::array<KMeans, 1> Dimension::getModels() { + std::unique_lock<std::mutex> Lock(Mutex); + return Models; +} diff --git a/ml/Dimension.h b/ml/Dimension.h new file mode 100644 index 0000000..3ec56e0 --- /dev/null +++ b/ml/Dimension.h @@ -0,0 +1,94 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#ifndef ML_DIMENSION_H +#define ML_DIMENSION_H + +#include "Query.h" +#include "Config.h" + +#include "ml-private.h" + +namespace ml { + +enum class MLResult { + Success = 0, + MissingData, + NaN, +}; + +static inline std::string getMLDimensionID(RRDDIM *RD) { + RRDSET *RS = RD->rrdset; + + std::stringstream SS; + SS << rrdset_context(RS) << "|" << rrdset_id(RS) << "|" << rrddim_name(RD); + return SS.str(); +} + +class Dimension { +public: + Dimension(RRDDIM *RD) : + RD(RD), + LastTrainedAt(Seconds(0)), + Trained(false), + ConstantModel(false), + AnomalyScore(0.0), + AnomalyBit(0) + { } + + RRDDIM *getRD() const { + return RD; + } + + unsigned updateEvery() const { + return RD->update_every; + } + + time_t latestTime() const { + return Query(RD).latestTime(); + } + + time_t oldestTime() const { + return Query(RD).oldestTime(); + } + + bool isTrained() const { + return Trained; + } + + bool isAnomalous() const { + return AnomalyBit; + } + + bool shouldTrain(const TimePoint &TP) const; + + bool isActive() const; + + MLResult trainModel(); + + bool predict(CalculatedNumber Value, bool Exists); + + std::pair<bool, double> detect(size_t WindowLength, bool Reset); + + std::array<KMeans, 1> getModels(); + +private: + std::pair<CalculatedNumber *, size_t> getCalculatedNumbers(); + +public: + RRDDIM *RD; + + TimePoint LastTrainedAt; + std::atomic<bool> Trained; + std::atomic<bool> ConstantModel; + + CalculatedNumber AnomalyScore; + std::atomic<bool> AnomalyBit; + + std::vector<CalculatedNumber> CNs; + std::array<KMeans, 1> Models; + std::mutex Mutex; +}; + +} // namespace ml + +#endif /* ML_DIMENSION_H */ diff --git a/ml/Host.cc b/ml/Host.cc new file mode 100644 index 0000000..4a57178 --- /dev/null +++ b/ml/Host.cc @@ -0,0 +1,255 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#include "Config.h" +#include "Host.h" +#include "ADCharts.h" + +#include "json/single_include/nlohmann/json.hpp" + +using namespace ml; + +void RrdHost::addDimension(Dimension *D) { + std::lock_guard<std::mutex> Lock(Mutex); + + DimensionsMap[D->getRD()] = D; + + // Default construct mutex for dimension + LocksMap[D]; +} + +void RrdHost::removeDimension(Dimension *D) { + // Remove the dimension from the hosts map. + { + std::lock_guard<std::mutex> Lock(Mutex); + DimensionsMap.erase(D->getRD()); + } + + // Delete the dimension by locking the mutex that protects it. + { + std::lock_guard<std::mutex> Lock(LocksMap[D]); + delete D; + } + + // Remove the lock entry for the deleted dimension. + { + std::lock_guard<std::mutex> Lock(Mutex); + LocksMap.erase(D); + } +} + +void RrdHost::getConfigAsJson(nlohmann::json &Json) const { + Json["version"] = 1; + + Json["enabled"] = Cfg.EnableAnomalyDetection; + + Json["min-train-samples"] = Cfg.MinTrainSamples; + Json["max-train-samples"] = Cfg.MaxTrainSamples; + Json["train-every"] = Cfg.TrainEvery; + + Json["diff-n"] = Cfg.DiffN; + Json["smooth-n"] = Cfg.SmoothN; + Json["lag-n"] = Cfg.LagN; + + Json["random-sampling-ratio"] = Cfg.RandomSamplingRatio; + Json["max-kmeans-iters"] = Cfg.MaxKMeansIters; + + Json["dimension-anomaly-score-threshold"] = Cfg.DimensionAnomalyScoreThreshold; + + Json["host-anomaly-rate-threshold"] = Cfg.HostAnomalyRateThreshold; + Json["anomaly-detection-grouping-method"] = group_method2string(Cfg.AnomalyDetectionGroupingMethod); + Json["anomaly-detection-query-duration"] = Cfg.AnomalyDetectionQueryDuration; + + Json["hosts-to-skip"] = Cfg.HostsToSkip; + Json["charts-to-skip"] = Cfg.ChartsToSkip; +} + +void TrainableHost::getModelsAsJson(nlohmann::json &Json) { + std::lock_guard<std::mutex> Lock(Mutex); + + for (auto &DP : DimensionsMap) { + Dimension *D = DP.second; + + nlohmann::json JsonArray = nlohmann::json::array(); + for (const KMeans &KM : D->getModels()) { + nlohmann::json J; + KM.toJson(J); + JsonArray.push_back(J); + } + Json[getMLDimensionID(D->getRD())] = JsonArray; + } + + return; +} + +std::pair<Dimension *, Duration<double>> +TrainableHost::findDimensionToTrain(const TimePoint &NowTP) { + std::lock_guard<std::mutex> Lock(Mutex); + + Duration<double> AllottedDuration = Duration<double>{Cfg.TrainEvery * updateEvery()} / (DimensionsMap.size() + 1); + + for (auto &DP : DimensionsMap) { + Dimension *D = DP.second; + + if (D->shouldTrain(NowTP)) { + LocksMap[D].lock(); + return { D, AllottedDuration }; + } + } + + return { nullptr, AllottedDuration }; +} + +void TrainableHost::trainDimension(Dimension *D, const TimePoint &NowTP) { + if (D == nullptr) + return; + + D->LastTrainedAt = NowTP + Seconds{D->updateEvery()}; + D->trainModel(); + + { + std::lock_guard<std::mutex> Lock(Mutex); + LocksMap[D].unlock(); + } +} + +void TrainableHost::train() { + Duration<double> MaxSleepFor = Seconds{10 * updateEvery()}; + + worker_register("MLTRAIN"); + worker_register_job_name(0, "dimensions"); + + worker_is_busy(0); + while (!netdata_exit) { + netdata_thread_testcancel(); + netdata_thread_disable_cancelability(); + + updateResourceUsage(); + + TimePoint NowTP = SteadyClock::now(); + + auto P = findDimensionToTrain(NowTP); + trainDimension(P.first, NowTP); + + netdata_thread_enable_cancelability(); + + Duration<double> AllottedDuration = P.second; + Duration<double> RealDuration = SteadyClock::now() - NowTP; + + Duration<double> SleepFor; + if (RealDuration >= AllottedDuration) + continue; + + worker_is_idle(); + SleepFor = std::min(AllottedDuration - RealDuration, MaxSleepFor); + TimePoint Now = SteadyClock::now(); + auto Until = Now + SleepFor; + while (Now < Until && !netdata_exit) { + std::this_thread::sleep_for(std::chrono::milliseconds(1000)); + Now = SteadyClock::now(); + } + worker_is_busy(0); + } +} + +#define WORKER_JOB_DETECT_DIMENSION 0 +#define WORKER_JOB_UPDATE_DETECTION_CHART 1 +#define WORKER_JOB_UPDATE_ANOMALY_RATES 2 +#define WORKER_JOB_UPDATE_CHARTS 3 + +#if WORKER_UTILIZATION_MAX_JOB_TYPES < 5 +#error WORKER_UTILIZATION_MAX_JOB_TYPES has to be at least 5 +#endif + +void DetectableHost::detectOnce() { + size_t NumAnomalousDimensions = 0; + size_t NumNormalDimensions = 0; + size_t NumTrainedDimensions = 0; + size_t NumActiveDimensions = 0; + + { + std::lock_guard<std::mutex> Lock(Mutex); + + for (auto &DP : DimensionsMap) { + worker_is_busy(WORKER_JOB_DETECT_DIMENSION); + + Dimension *D = DP.second; + + if (!D->isActive()) + continue; + + NumActiveDimensions++; + NumTrainedDimensions += D->isTrained(); + + bool IsAnomalous = D->isAnomalous(); + if (IsAnomalous) + NumAnomalousDimensions += 1; + } + + if (NumAnomalousDimensions) + HostAnomalyRate = static_cast<double>(NumAnomalousDimensions) / NumActiveDimensions; + else + HostAnomalyRate = 0.0; + + NumNormalDimensions = NumActiveDimensions - NumAnomalousDimensions; + } + + this->NumAnomalousDimensions = NumAnomalousDimensions; + this->NumNormalDimensions = NumNormalDimensions; + this->NumTrainedDimensions = NumTrainedDimensions; + this->NumActiveDimensions = NumActiveDimensions; + + worker_is_busy(WORKER_JOB_UPDATE_CHARTS); + updateDimensionsChart(getRH(), NumTrainedDimensions, NumNormalDimensions, NumAnomalousDimensions); + updateHostAndDetectionRateCharts(getRH(), HostAnomalyRate * 10000.0); + + struct rusage TRU; + getResourceUsage(&TRU); + updateTrainingChart(getRH(), &TRU); +} + +void DetectableHost::detect() { + worker_register("MLDETECT"); + worker_register_job_name(WORKER_JOB_DETECT_DIMENSION, "dimensions"); + worker_register_job_name(WORKER_JOB_UPDATE_DETECTION_CHART, "detection chart"); + worker_register_job_name(WORKER_JOB_UPDATE_ANOMALY_RATES, "anomaly rates"); + worker_register_job_name(WORKER_JOB_UPDATE_CHARTS, "charts"); + + std::this_thread::sleep_for(Seconds{10}); + + heartbeat_t HB; + heartbeat_init(&HB); + + while (!netdata_exit) { + netdata_thread_testcancel(); + worker_is_idle(); + heartbeat_next(&HB, updateEvery() * USEC_PER_SEC); + + netdata_thread_disable_cancelability(); + detectOnce(); + + worker_is_busy(WORKER_JOB_UPDATE_DETECTION_CHART); + updateDetectionChart(getRH()); + netdata_thread_enable_cancelability(); + } +} + +void DetectableHost::getDetectionInfoAsJson(nlohmann::json &Json) const { + Json["version"] = 1; + Json["anomalous-dimensions"] = NumAnomalousDimensions; + Json["normal-dimensions"] = NumNormalDimensions; + Json["total-dimensions"] = NumAnomalousDimensions + NumNormalDimensions; + Json["trained-dimensions"] = NumTrainedDimensions; +} + +void DetectableHost::startAnomalyDetectionThreads() { + TrainingThread = std::thread(&TrainableHost::train, this); + DetectionThread = std::thread(&DetectableHost::detect, this); +} + +void DetectableHost::stopAnomalyDetectionThreads() { + netdata_thread_cancel(TrainingThread.native_handle()); + netdata_thread_cancel(DetectionThread.native_handle()); + + TrainingThread.join(); + DetectionThread.join(); +} diff --git a/ml/Host.h b/ml/Host.h new file mode 100644 index 0000000..52a0cd0 --- /dev/null +++ b/ml/Host.h @@ -0,0 +1,100 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#ifndef ML_HOST_H +#define ML_HOST_H + +#include "Config.h" +#include "Dimension.h" + +#include "ml-private.h" +#include "json/single_include/nlohmann/json.hpp" + +namespace ml { + +class RrdHost { +public: + RrdHost(RRDHOST *RH) : RH(RH) {}; + + RRDHOST *getRH() { return RH; } + + unsigned updateEvery() { return RH->rrd_update_every; } + + std::string getUUID() { + char S[UUID_STR_LEN]; + uuid_unparse_lower(RH->host_uuid, S); + return S; + } + + void addDimension(Dimension *D); + void removeDimension(Dimension *D); + + void getConfigAsJson(nlohmann::json &Json) const; + + virtual ~RrdHost() {}; + +protected: + RRDHOST *RH; + + // Protect dimension and lock maps + std::mutex Mutex; + + std::unordered_map<RRDDIM *, Dimension *> DimensionsMap; + std::unordered_map<Dimension *, std::mutex> LocksMap; +}; + +class TrainableHost : public RrdHost { +public: + TrainableHost(RRDHOST *RH) : RrdHost(RH) {} + + void train(); + + void updateResourceUsage() { + std::lock_guard<std::mutex> Lock(ResourceUsageMutex); + getrusage(RUSAGE_THREAD, &ResourceUsage); + } + + void getResourceUsage(struct rusage *RU) { + std::lock_guard<std::mutex> Lock(ResourceUsageMutex); + memcpy(RU, &ResourceUsage, sizeof(struct rusage)); + } + + void getModelsAsJson(nlohmann::json &Json); + +private: + std::pair<Dimension *, Duration<double>> findDimensionToTrain(const TimePoint &NowTP); + void trainDimension(Dimension *D, const TimePoint &NowTP); + + struct rusage ResourceUsage{}; + std::mutex ResourceUsageMutex; +}; + +class DetectableHost : public TrainableHost { +public: + DetectableHost(RRDHOST *RH) : TrainableHost(RH) {} + + void startAnomalyDetectionThreads(); + void stopAnomalyDetectionThreads(); + + void getDetectionInfoAsJson(nlohmann::json &Json) const; + +private: + void detect(); + void detectOnce(); + +private: + std::thread TrainingThread; + std::thread DetectionThread; + + CalculatedNumber HostAnomalyRate{0.0}; + + size_t NumAnomalousDimensions{0}; + size_t NumNormalDimensions{0}; + size_t NumTrainedDimensions{0}; + size_t NumActiveDimensions{0}; +}; + +using Host = DetectableHost; + +} // namespace ml + +#endif /* ML_HOST_H */ diff --git a/ml/KMeans.cc b/ml/KMeans.cc new file mode 100644 index 0000000..edc2ef4 --- /dev/null +++ b/ml/KMeans.cc @@ -0,0 +1,43 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#include "KMeans.h" +#include <dlib/clustering.h> + +void KMeans::train(const std::vector<DSample> &Samples, size_t MaxIterations) { + MinDist = std::numeric_limits<CalculatedNumber>::max(); + MaxDist = std::numeric_limits<CalculatedNumber>::min(); + + ClusterCenters.clear(); + + dlib::pick_initial_centers(NumClusters, ClusterCenters, Samples); + dlib::find_clusters_using_kmeans(Samples, ClusterCenters, MaxIterations); + + for (const auto &S : Samples) { + CalculatedNumber MeanDist = 0.0; + + for (const auto &KMCenter : ClusterCenters) + MeanDist += dlib::length(KMCenter - S); + + MeanDist /= NumClusters; + + if (MeanDist < MinDist) + MinDist = MeanDist; + + if (MeanDist > MaxDist) + MaxDist = MeanDist; + } +} + +CalculatedNumber KMeans::anomalyScore(const DSample &Sample) const { + CalculatedNumber MeanDist = 0.0; + for (const auto &CC: ClusterCenters) + MeanDist += dlib::length(CC - Sample); + + MeanDist /= NumClusters; + + if (MaxDist == MinDist) + return 0.0; + + CalculatedNumber AnomalyScore = 100.0 * std::abs((MeanDist - MinDist) / (MaxDist - MinDist)); + return (AnomalyScore > 100.0) ? 100.0 : AnomalyScore; +} diff --git a/ml/KMeans.h b/ml/KMeans.h new file mode 100644 index 0000000..0398eeb --- /dev/null +++ b/ml/KMeans.h @@ -0,0 +1,41 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#ifndef KMEANS_H +#define KMEANS_H + +#include <atomic> +#include <vector> +#include <limits> +#include <mutex> + +#include "SamplesBuffer.h" +#include "json/single_include/nlohmann/json.hpp" + +class KMeans { +public: + KMeans(size_t NumClusters = 2) : NumClusters(NumClusters) { + MinDist = std::numeric_limits<CalculatedNumber>::max(); + MaxDist = std::numeric_limits<CalculatedNumber>::min(); + }; + + void train(const std::vector<DSample> &Samples, size_t MaxIterations); + CalculatedNumber anomalyScore(const DSample &Sample) const; + + void toJson(nlohmann::json &J) const { + J = nlohmann::json{ + {"CCs", ClusterCenters}, + {"MinDist", MinDist}, + {"MaxDist", MaxDist} + }; + } + +private: + size_t NumClusters; + + std::vector<DSample> ClusterCenters; + + CalculatedNumber MinDist; + CalculatedNumber MaxDist; +}; + +#endif /* KMEANS_H */ diff --git a/ml/Query.h b/ml/Query.h new file mode 100644 index 0000000..78d1170 --- /dev/null +++ b/ml/Query.h @@ -0,0 +1,57 @@ +#ifndef QUERY_H +#define QUERY_H + +#include "ml-private.h" + +namespace ml { + +class Query { +public: + Query(RRDDIM *RD) : RD(RD), Initialized(false) { + Ops = RD->tiers[0]->query_ops; + } + + time_t latestTime() { + return Ops->latest_time(RD->tiers[0]->db_metric_handle); + } + + time_t oldestTime() { + return Ops->oldest_time(RD->tiers[0]->db_metric_handle); + } + + void init(time_t AfterT, time_t BeforeT) { + Ops->init(RD->tiers[0]->db_metric_handle, &Handle, AfterT, BeforeT); + Initialized = true; + points_read = 0; + } + + bool isFinished() { + return Ops->is_finished(&Handle); + } + + ~Query() { + if (Initialized) { + Ops->finalize(&Handle); + global_statistics_ml_query_completed(points_read); + points_read = 0; + } + } + + std::pair<time_t, CalculatedNumber> nextMetric() { + points_read++; + STORAGE_POINT sp = Ops->next_metric(&Handle); + return { sp.start_time, sp.sum / sp.count }; + } + +private: + RRDDIM *RD; + bool Initialized; + size_t points_read; + + struct storage_engine_query_ops *Ops; + struct storage_engine_query_handle Handle; +}; + +} // namespace ml + +#endif /* QUERY_H */ diff --git a/ml/README.md b/ml/README.md new file mode 100644 index 0000000..f6fd923 --- /dev/null +++ b/ml/README.md @@ -0,0 +1,310 @@ +<!-- +title: Configure machine learning (ML) powered anomaly detection +custom_edit_url: https://github.com/netdata/netdata/edit/master/ml/README.md +description: This is an in-depth look at how Netdata uses ML to detect anomalies. +keywords: [machine learning, anomaly detection, Netdata ML] +--> +# Machine learning (ML) powered anomaly detection + +## Overview + +As of [`v1.32.0`](https://github.com/netdata/netdata/releases/tag/v1.32.0), Netdata comes with some ML powered [anomaly detection](https://en.wikipedia.org/wiki/Anomaly_detection) capabilities built into it and available to use out of the box, with zero configuration required (ML was enabled by default in `v1.35.0-29-nightly` in [this PR](https://github.com/netdata/netdata/pull/13158), previously it required a one line config change). + +🚧 **Note**: If you would like to get involved and help us with some feedback, email us at analytics-ml-team@netdata.cloud, comment on the [beta launch post](https://community.netdata.cloud/t/anomaly-advisor-beta-launch/2717) in the Netdata community, or come join us in the [🤖-ml-powered-monitoring](https://discord.gg/4eRSEUpJnc) channel of the Netdata discord. + +Once ML is enabled, Netdata will begin training a model for each dimension. By default this model is a [k-means clustering](https://en.wikipedia.org/wiki/K-means_clustering) model trained on the most recent 4 hours of data. Rather than just using the most recent value of each raw metric, the model works on a preprocessed ["feature vector"](#feature-vector) of recent smoothed and differenced values. This should enable the model to detect a wider range of potentially anomalous patterns in recent observations as opposed to just point anomalies like big spikes or drops. ([This infographic](https://user-images.githubusercontent.com/2178292/144414415-275a3477-5b47-43d6-8959-509eb48ebb20.png) shows some different types of anomalies.) + +The sections below will introduce some of the main concepts: +- anomaly bit +- anomaly score +- anomaly rate +- anomaly detector + +Additional explanations and details can be found in the [Glossary](#glossary) and [Notes](#notes) at the bottom of the page. + +### Anomaly Bit - (100 = Anomalous, 0 = Normal) + +Once each model is trained, Netdata will begin producing an ["anomaly score"](#anomaly-score) at each time step for each dimension. This ["anomaly score"](#anomaly-score) is essentially a distance measure to the trained cluster centers of the model (by default each model has k=2, so two cluster centers are learned). More anomalous looking data should be more distant to those cluster centers. If this ["anomaly score"](#anomaly-score) is sufficiently large, this is a sign that the recent raw values of the dimension could potentially be anomalous. By default, "sufficiently large" means that the distance is in the 99th percentile or above of all distances observed during training or, put another way, it has to be further away than the furthest 1% of the data used during training. Once this threshold is passed, the ["anomaly bit"](#anomaly-bit) corresponding to that dimension is set to 100 to flag it as anomalous, otherwise it would be left at 0 to signal normal data. + +What this means is that in addition to the raw value of each metric, Netdata now also stores an ["anomaly bit"](#anomaly-bit) that is either 100 (anomalous) or 0 (normal). Importantly, this is achieved without additional storage overhead due to how the anomaly bit has been implemented within the existing internal Netdata storage representation. + +This ["anomaly bit"](#anomaly-bit) is exposed via the `anomaly-bit` key that can be passed to the `options` param of the `/api/v1/data` REST API. + +For example, here are some recent raw dimension values for `system.ip` on our [london](http://london.my-netdata.io/) demo server: + +[`https://london.my-netdata.io/api/v1/data?chart=system.ip`](https://london.my-netdata.io/api/v1/data?chart=system.ip) + +``` +{ + "labels": ["time", "received", "sent"], + "data": + [ + [ 1638365672, 54.84098, -76.70201], + [ 1638365671, 124.4328, -309.7543], + [ 1638365670, 123.73152, -167.9056], + ... + ] +} +``` + +And if we add the `&options=anomaly-bit` params, we can see the "anomaly bit" value corresponding to each raw dimension value: + +[`https://london.my-netdata.io/api/v1/data?chart=system.ip&options=anomaly-bit`](https://london.my-netdata.io/api/v1/data?chart=system.ip&options=anomaly-bit) + +``` +{ + "labels": ["time", "received", "sent"], + "data": + [ + [ 1638365672, 0, 0], + [ 1638365671, 0, 0], + [ 1638365670, 0, 0], + ... + ] +} +``` +In this example, the dimensions "received" and "sent" didn't show any abnormal behavior, so the anomaly bit is zero. +Under normal circumstances, the anomaly bit will mostly be 0. However, there can be random fluctuations setting the anomaly to 100, although this very much depends on the nature of the dimension in question. + +### Anomaly Rate - average(anomaly bit) + +Once all models have been trained, we can think of the Netdata dashboard as essentially a big matrix or table of 0's and 100's. If we consider this "anomaly bit"-based representation of the state of the node, we can now think about how we might detect overall node level anomalies. The figure below illustrates the main ideas. + +``` + dimensions +time d1 d2 d3 d4 d5 NAR + 1 0 0 0 0 0 0% + 2 0 0 0 0 100 20% + 3 0 0 0 0 0 0% + 4 0 100 0 0 0 20% + 5 100 0 0 0 0 20% + 6 0 100 100 0 100 60% + 7 0 100 0 100 0 40% + 8 0 0 0 0 100 20% + 9 0 0 100 100 0 40% + 10 0 0 0 0 0 0% + +DAR 10% 30% 20% 20% 30% 22% NAR_t1-t10 + +DAR = Dimension Anomaly Rate +NAR = Node Anomaly Rate +NAR_t1-t10 = Node Anomaly Rate over t1 to t10 +``` + +To work out an ["anomaly rate"](#anomaly-rate), we can just average a row or a column in any direction. For example, if we were to just average along a row then this would be the ["node anomaly rate"](#node-anomaly-rate) (all dimensions) at time t. Likewise if we averaged a column then we would have the ["dimension anomaly rate"](#dimension-anomaly-rate) for each dimension over the time window t=1-10. Extending this idea, we can work out an overall ["anomaly rate"](#anomaly-rate) for the whole matrix or any subset of it we might be interested in. + +### Anomaly Detector - Node level anomaly events + +An ["anomaly detector"](#anomaly-detector) looks at all anomaly bits of a node. Netdata's anomaly detector produces an ["anomaly event"](#anomaly-event) when a the percentage of anomaly bits is high enough for a persistent amount of time. This anomaly event signals that there was sufficient evidence among all the anomaly bits that some strange behavior might have been detected in a more global sense across the node. + +Essentially if the ["Node Anomaly Rate"](#node-anomaly-rate) (NAR) passes a defined threshold and stays above that threshold for a persistent amount of time, a "Node [Anomaly Event](#anomaly-event)" will be triggered. + +These anomaly events are currently exposed via `/api/v1/anomaly_events` + +**Note**: Clicking the link below will likely return an empty list of `[]`. This is the response when no anomaly events exist in the specified range. The example response below is illustrative of what the response would be when one or more anomaly events exist within the range of `after` to `before`. + +https://london.my-netdata.io/api/v1/anomaly_events?after=1638365182000&before=1638365602000 + +If an event exists within the window, the result would be a list of start and end times. + +``` +[ + [ + 1638367788, + 1638367851 + ] +] +``` + +Information about each anomaly event can then be found at the `/api/v1/anomaly_event_info` endpoint (making sure to pass the `after` and `before` params): + +**Note**: If you click the below url you will get a `null` since no such anomaly event exists as the response is just an illustrative example taken from a node that did have such an anomaly event. + +https://london.my-netdata.io/api/v1/anomaly_event_info?after=1638367788&before=1638367851 + +``` +[ + [ + 0.66, + "netdata.response_time|max" + ], + [ + 0.63, + "netdata.response_time|average" + ], + [ + 0.54, + "netdata.requests|requests" + ], + ... +``` + +The query returns a list of dimension anomaly rates for all dimensions that were considered part of the detected anomaly event. + +**Note**: We plan to build additional anomaly detection and exploration features into both Netdata Agent and Netdata Cloud. The current endpoints are still under active development to power the upcoming features. + +## Configuration + +If you are running a netdata version after `v1.35.0-29-nightly` then ML will be enabled by default. + +To enable or disable anomaly detection: +1. Find and open the Netdata configuration file `netdata.conf`. +2. In the `[ml]` section, set `enabled = yes` to enable or `enabled = no` to disable. +3. Restart netdata (typically `sudo systemctl restart netdata`). + +**Note**: If you would like to learn more about configuring Netdata please see [the configuration guide](https://learn.netdata.cloud/guides/step-by-step/step-04). + +Below is a list of all the available configuration params and their default values. + +``` +[ml] + # enabled = yes + # maximum num samples to train = 14400 + # minimum num samples to train = 3600 + # train every = 3600 + # dbengine anomaly rate every = 30 + # num samples to diff = 1 + # num samples to smooth = 3 + # num samples to lag = 5 + # random sampling ratio = 0.2 + # maximum number of k-means iterations = 1000 + # dimension anomaly score threshold = 0.99 + # host anomaly rate threshold = 0.01000 + # minimum window size = 30.00000 + # maximum window size = 600.00000 + # idle window size = 30.00000 + # window minimum anomaly rate = 0.25000 + # anomaly event min dimension rate threshold = 0.05000 + # hosts to skip from training = !* + # charts to skip from training = netdata.* +``` + +### Configuration Examples + +If you would like to run ML on a parent instead of at the edge, some configuration options are illustrated below. + +This example assumes 3 child nodes [streaming](https://learn.netdata.cloud/docs/agent/streaming) to 1 parent node and illustrates the main ways you might want to configure running ML for the children on the parent, running ML on the children themselves, or even a mix of approaches. + +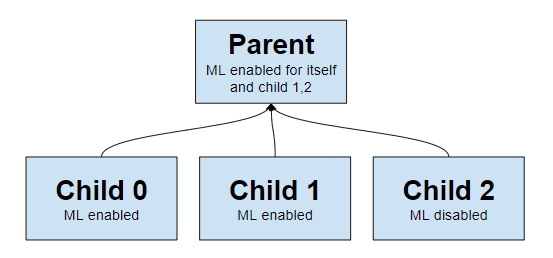 + +``` +# parent will run ML for itself and child 1,2, it will skip running ML for child 0. +# child 0 will run its own ML at the edge. +# child 1 will run its own ML at the edge, even though parent will also run ML for it, a bit wasteful potentially to run ML in both places but is possible (Netdata Cloud will essentially average any overlapping models). +# child 2 will not run ML at the edge, it will be run in the parent only. + +# parent-ml-enabled +# run ML on all hosts apart from child-ml-enabled +[ml] + enabled = yes + hosts to skip from training = child-0-ml-enabled + +# child-0-ml-enabled +# run ML on child-0-ml-enabled +[ml] + enabled = yes + +# child-1-ml-enabled +# run ML on child-1-ml-enabled +[ml] + enabled = yes + +# child-2-ml-disabled +# do not run ML on child-2-ml-disabled +[ml] + enabled = no +``` + +### Descriptions (min/max) + +- `enabled`: `yes` to enable, `no` to disable. +- `maximum num samples to train`: (`3600`/`86400`) This is the maximum amount of time you would like to train each model on. For example, the default of `14400` trains on the preceding 4 hours of data, assuming an `update every` of 1 second. +- `minimum num samples to train`: (`900`/`21600`) This is the minimum amount of data required to be able to train a model. For example, the default of `900` implies that once at least 15 minutes of data is available for training, a model is trained, otherwise it is skipped and checked again at the next training run. +- `train every`: (`1800`/`21600`) This is how often each model will be retrained. For example, the default of `3600` means that each model is retrained every hour. Note: The training of all models is spread out across the `train every` period for efficiency, so in reality, it means that each model will be trained in a staggered manner within each `train every` period. +- `dbengine anomaly rate every`: (`30`/`900`) This is how often netdata will aggregate all the anomaly bits into a single chart (`anomaly_detection.anomaly_rates`). The aggregation into a single chart allows enabling anomaly rate ranking over _all_ metrics with one API call as opposed to a call per chart. +- `num samples to diff`: (`0`/`1`) This is a `0` or `1` to determine if you want the model to operate on differences of the raw data or just the raw data. For example, the default of `1` means that we take differences of the raw values. Using differences is more general and works on dimensions that might naturally tend to have some trends or cycles in them that is normal behavior to which we don't want to be too sensitive. +- `num samples to smooth`: (`0`/`5`) This is a small integer that controls the amount of smoothing applied as part of the feature processing used by the model. For example, the default of `3` means that the rolling average of the last 3 values is used. Smoothing like this helps the model be a little more robust to spiky types of dimensions that naturally "jump" up or down as part of their normal behavior. +- `num samples to lag`: (`0`/`5`) This is a small integer that determines how many lagged values of the dimension to include in the feature vector. For example, the default of `5` means that in addition to the most recent (by default, differenced and smoothed) value of the dimension, the feature vector will also include the 5 previous values too. Using lagged values in our feature representation allows the model to work over strange patterns over recent values of a dimension as opposed to just focusing on if the most recent value itself is big or small enough to be anomalous. +- `random sampling ratio`: (`0.2`/`1.0`) This parameter determines how much of the available training data is randomly sampled when training a model. The default of `0.2` means that Netdata will train on a random 20% of training data. This parameter influences cost efficiency. At `0.2` the model is still reasonably trained while minimizing system overhead costs caused by the training. +- `maximum number of k-means iterations`: This is a parameter that can be passed to the model to limit the number of iterations in training the k-means model. Vast majority of cases can ignore and leave as default. +- `dimension anomaly score threshold`: (`0.01`/`5.00`) This is the threshold at which an individual dimension at a specific timestep is considered anomalous or not. For example, the default of `0.99` means that a dimension with an anomaly score of 99% or higher is flagged as anomalous. This is a normalized probability based on the training data, so the default of 99% means that anything that is as strange (based on distance measure) or more strange as the most strange 1% of data observed during training will be flagged as anomalous. If you wanted to make the anomaly detection on individual dimensions more sensitive you could try a value like `0.90` (90%) or to make it less sensitive you could try `1.5` (150%). +- `host anomaly rate threshold`: (`0.0`/`1.0`) This is the percentage of dimensions (based on all those enabled for anomaly detection) that need to be considered anomalous at specific timestep for the host itself to be considered anomalous. For example, the default value of `0.01` means that if more than 1% of dimensions are anomalous at the same time then the host itself is considered in an anomalous state. +- `minimum window size`: The Netdata "Anomaly Detector" logic works over a rolling window of data. This parameter defines the minimum length of window to consider. If over this window the host is in an anomalous state then an anomaly detection event will be triggered. For example, the default of `30` means that the detector will initially work over a rolling window of 30 seconds. Note: The length of this window will be dynamic once an anomaly event has been triggered such that it will expand as needed until either the max length of an anomaly event is hit or the host settles back into a normal state with sufficiently decreased host level anomaly states in the rolling window. Note: If you wanted to adjust the higher level anomaly detector behavior then this is one parameter you might adjust to see the impact of on anomaly detection events. +- `maximum window size`: This parameter defines the maximum length of window to consider. If an anomaly event reaches this size, it will be closed. This is to provide an upper bound on the length of an anomaly event and cost of the anomaly detector logic for that event. +- `window minimum anomaly rate`: (`0.0`/`1.0`) This parameter corresponds to a threshold on the percentage of time in the rolling window that the host was considered in an anomalous state. For example, the default of `0.25` means that if the host is in an anomalous state for 25% of more of the rolling window then and anomaly event will be triggered or extended if one is already active. Note: If you want to make the anomaly detector itself less sensitive, you can adjust this value to something like `0.75` which would mean the host needs to be much more consistently in an anomalous state to trigger an anomaly detection event. Likewise, a lower value like `0.1` would make the anomaly detector more sensitive. +- `anomaly event min dimension rate threshold`: (`0.0`/`1.0`) This is a parameter that helps filter out irrelevant dimensions from anomaly events. For example, the default of `0.05` means that only dimensions that were considered anomalous for at least 5% of the anomaly event itself will be included in that anomaly event. The idea here is to just include dimensions that were consistently anomalous as opposed to those that may have just randomly happened to be anomalous at the same time. +- `hosts to skip from training`: This parameter allows you to turn off anomaly detection for any child hosts on a parent host by defining those you would like to skip from training here. For example, a value like `dev-*` skips all hosts on a parent that begin with the "dev-" prefix. The default value of `!*` means "don't skip any". +- `charts to skip from training`: This parameter allows you to exclude certain charts from anomaly detection. By default, only netdata related charts are excluded. This is to avoid the scenario where accessing the netdata dashboard could itself tigger some anomalies if you don't access them regularly. If you want to include charts that are excluded by default, add them in small groups and then measure any impact on performance before adding additional ones. Example: If you want to include system, apps, and user charts:`!system.* !apps.* !user.* *`. + +## Charts + +Once enabled, the "Anomaly Detection" menu and charts will be available on the dashboard. + + + +In terms of anomaly detection, the most interesting charts would be the `anomaly_detection.dimensions` and `anomaly_detection.anomaly_rate` ones, which hold the `anomalous` and `anomaly_rate` dimensions that show the overall number of dimensions considered anomalous at any time and the corresponding anomaly rate. + +- `anomaly_detection.dimensions`: Total count of dimensions considered anomalous or normal. +- `anomaly_detection.dimensions`: Percentage of anomalous dimensions. +- `anomaly_detection.detector_window`: The length of the active window used by the detector. +- `anomaly_detection.detector_events`: Flags (0 or 1) to show when an anomaly event has been triggered by the detector. + +Below is an example of how these charts may look in the presence of an anomaly event. + +Initially we see a jump in `anomalous` dimensions: + +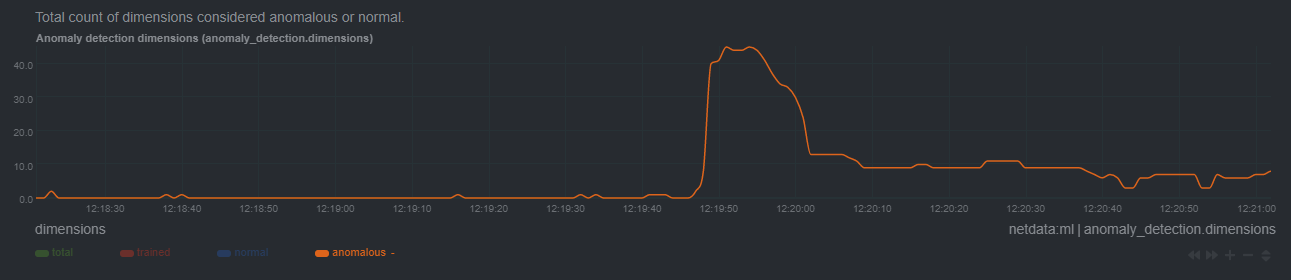 + +And a corresponding jump in the `anomaly_rate`: + +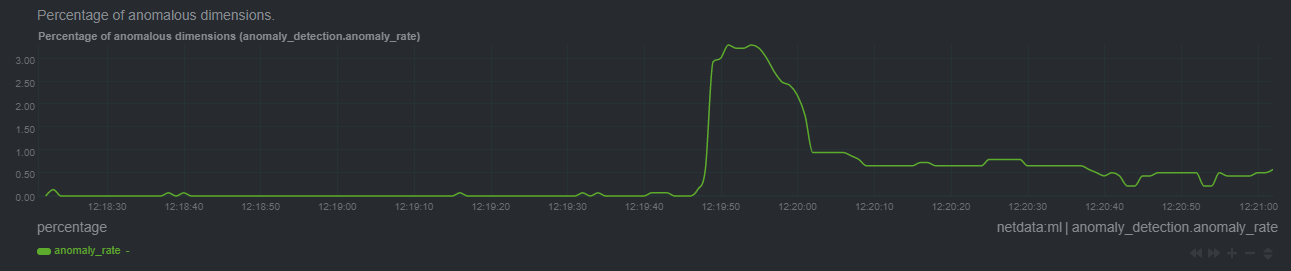 + +After a short while the rolling node anomaly rate goes `above_threshold`, and once it stays above threshold for long enough a `new_anomaly_event` is created: + +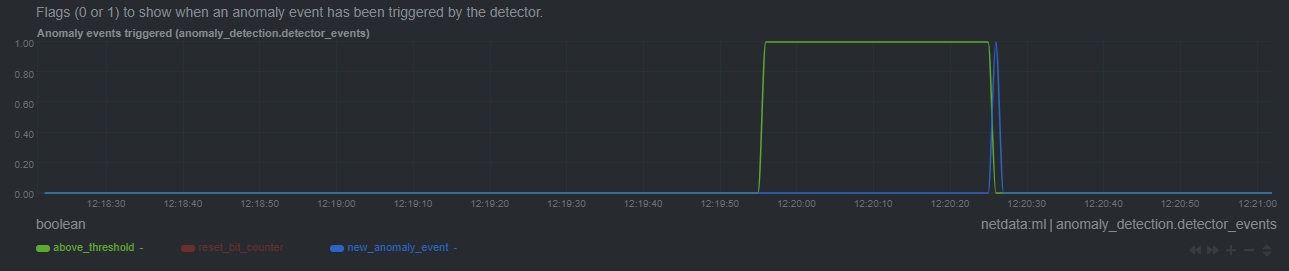 + +## Glossary + +#### _feature vector_ + +A [feature vector](https://en.wikipedia.org/wiki/Feature_(machine_learning)) is what the ML model is trained on and uses for prediction. The most simple feature vector would be just the latest raw dimension value itself [x]. By default Netdata will use a feature vector consisting of the 6 latest differences and smoothed values of the dimension so conceptually something like `[avg3(diff1(x-5)), avg3(diff1(x-4)), avg3(diff1(x-3)), avg3(diff1(x-2)), avg3(diff1(x-1)), avg3(diff1(x))]` which ends up being just 6 floating point numbers that try and represent the "shape" of recent data. + +#### _anomaly score_ + +At prediction time the anomaly score is just the distance of the most recent feature vector to the trained cluster centers of the model, which are themselves just feature vectors, albeit supposedly the best most representative feature vectors that could be "learned" from the training data. So if the most recent feature vector is very far away in terms of [euclidean distance](https://en.wikipedia.org/wiki/Euclidean_distance#:~:text=In%20mathematics%2C%20the%20Euclidean%20distance,being%20called%20the%20Pythagorean%20distance.) it's more likely that the recent data it represents consists of some strange pattern not commonly found in the training data. + +#### _anomaly bit_ + +If the anomaly score is greater than a specified threshold then the most recent feature vector, and hence most recent raw data, is considered anomalous. Since storing the raw anomaly score would essentially double amount of storage space Netdata would need, we instead efficiently store just the anomaly bit in the existing internal Netdata data representation without any additional storage overhead. + +#### _anomaly rate_ + +An anomaly rate is really just an average over one or more anomaly bits. An anomaly rate can be calculated over time for one or more dimensions or at a point in time across multiple dimensions, or some combination of the two. Its just an average of some collection of anomaly bits. + +#### _anomaly detector_ + +The is essentially business logic that just tries to process a collection of anomaly bits to determine if there is enough active anomaly bits to merit investigation or declaration of a node level anomaly event. + +#### _anomaly event_ + +Anomaly events are triggered by the anomaly detector and represent a window of time on the node with sufficiently elevated anomaly rates across all dimensions. + +#### _dimension anomaly rate_ + +The anomaly rate of a specific dimension over some window of time. + +#### _node anomaly rate_ + +The anomaly rate across all dimensions of a node. + +## Notes + +- We would love to hear any feedback relating to this functionality, please email us at analytics-ml-team@netdata.cloud or come join us in the [🤖-ml-powered-monitoring](https://discord.gg/4eRSEUpJnc) channel of the Netdata discord. +- We are working on additional UI/UX based features that build on these core components to make them as useful as possible out of the box. +- Although not yet a core focus of this work, users could leverage the `anomaly_detection` chart dimensions and/or `anomaly-bit` options in defining alarms based on ML driven anomaly detection models. +- [This presentation](https://docs.google.com/presentation/d/18zkCvU3nKP-Bw_nQZuXTEa4PIVM6wppH3VUnAauq-RU/edit?usp=sharing) walks through some of the main concepts covered above in a more informal way. +- After restart Netdata will wait until `minimum num samples to train` observations of data are available before starting training and prediction. +- Netdata uses [dlib](https://github.com/davisking/dlib) under the hood for its core ML features. +- You should benchmark Netdata resource usage before and after enabling ML. Typical overhead ranges from 1-2% additional CPU at most. +- The "anomaly bit" has been implemented to be a building block to underpin many more ML based use cases that we plan to deliver soon. +- At its core Netdata uses an approach and problem formulation very similar to the Netdata python [anomalies collector](https://learn.netdata.cloud/docs/agent/collectors/python.d.plugin/anomalies), just implemented in a much much more efficient and scalable way in the agent in c++. So if you would like to learn more about the approach and are familiar with Python that is a useful resource to explore, as is the corresponding [deep dive tutorial](https://nbviewer.org/github/netdata/community/blob/main/netdata-agent-api/netdata-pandas/anomalies_collector_deepdive.ipynb) where the default model used is PCA instead of K-Means but the overall approach and formulation is similar. diff --git a/ml/SamplesBuffer.cc b/ml/SamplesBuffer.cc new file mode 100644 index 0000000..d276c6e --- /dev/null +++ b/ml/SamplesBuffer.cc @@ -0,0 +1,150 @@ +// SPDX-License-Identifier: GPL-3.0-or-later +// +#include "SamplesBuffer.h" + +#include <fstream> +#include <sstream> +#include <string> + +void Sample::print(std::ostream &OS) const { + for (size_t Idx = 0; Idx != NumDims - 1; Idx++) + OS << CNs[Idx] << ", "; + + OS << CNs[NumDims - 1]; +} + +void SamplesBuffer::print(std::ostream &OS) const { + for (size_t Idx = Preprocessed ? (DiffN + (SmoothN - 1) + (LagN)) : 0; + Idx != NumSamples; Idx++) { + Sample S = Preprocessed ? getPreprocessedSample(Idx) : getSample(Idx); + OS << S << std::endl; + } +} + +std::vector<Sample> SamplesBuffer::getPreprocessedSamples() const { + std::vector<Sample> V; + + for (size_t Idx = Preprocessed ? (DiffN + (SmoothN - 1) + (LagN)) : 0; + Idx != NumSamples; Idx++) { + Sample S = Preprocessed ? getPreprocessedSample(Idx) : getSample(Idx); + V.push_back(S); + } + + return V; +} + +void SamplesBuffer::diffSamples() { + // Panda's DataFrame default behaviour is to subtract each element from + // itself. For us `DiffN = 0` means "disable diff-ing" when preprocessing + // the samples buffer. This deviation will make it easier for us to test + // the KMeans implementation. + if (DiffN == 0) + return; + + for (size_t Idx = 0; Idx != (NumSamples - DiffN); Idx++) { + size_t High = (NumSamples - 1) - Idx; + size_t Low = High - DiffN; + + Sample LHS = getSample(High); + Sample RHS = getSample(Low); + + LHS.diff(RHS); + } +} + +void SamplesBuffer::smoothSamples() { + // Holds the mean value of each window + CalculatedNumber *AccCNs = new CalculatedNumber[NumDimsPerSample](); + Sample Acc(AccCNs, NumDimsPerSample); + + // Used to avoid clobbering the accumulator when moving the window + CalculatedNumber *TmpCNs = new CalculatedNumber[NumDimsPerSample](); + Sample Tmp(TmpCNs, NumDimsPerSample); + + CalculatedNumber Factor = (CalculatedNumber) 1 / SmoothN; + + // Calculate the value of the 1st window + for (size_t Idx = 0; Idx != std::min(SmoothN, NumSamples); Idx++) { + Tmp.add(getSample(NumSamples - (Idx + 1))); + } + + Acc.add(Tmp); + Acc.scale(Factor); + + // Move the window and update the samples + for (size_t Idx = NumSamples; Idx != (DiffN + SmoothN - 1); Idx--) { + Sample S = getSample(Idx - 1); + + // Tmp <- Next window (if any) + if (Idx >= (SmoothN + 1)) { + Tmp.diff(S); + Tmp.add(getSample(Idx - (SmoothN + 1))); + } + + // S <- Acc + S.copy(Acc); + + // Acc <- Tmp + Acc.copy(Tmp); + Acc.scale(Factor); + } + + delete[] AccCNs; + delete[] TmpCNs; +} + +void SamplesBuffer::lagSamples() { + if (LagN == 0) + return; + + for (size_t Idx = NumSamples; Idx != LagN; Idx--) { + Sample PS = getPreprocessedSample(Idx - 1); + PS.lag(getSample(Idx - 1), LagN); + } +} + +std::vector<DSample> SamplesBuffer::preprocess() { + assert(Preprocessed == false); + + std::vector<DSample> DSamples; + size_t OutN = NumSamples; + + // Diff + if (DiffN >= OutN) + return DSamples; + OutN -= DiffN; + diffSamples(); + + // Smooth + if (SmoothN == 0 || SmoothN > OutN) + return DSamples; + OutN -= (SmoothN - 1); + smoothSamples(); + + // Lag + if (LagN >= OutN) + return DSamples; + OutN -= LagN; + lagSamples(); + + DSamples.reserve(OutN); + Preprocessed = true; + + uint32_t MaxMT = std::numeric_limits<uint32_t>::max(); + uint32_t CutOff = static_cast<double>(MaxMT) * SamplingRatio; + + for (size_t Idx = NumSamples - OutN; Idx != NumSamples; Idx++) { + if (RandNums[Idx] > CutOff) + continue; + + DSample DS; + DS.set_size(NumDimsPerSample * (LagN + 1)); + + const Sample PS = getPreprocessedSample(Idx); + PS.initDSample(DS); + + DSamples.push_back(DS); + } + + return DSamples; +} diff --git a/ml/SamplesBuffer.h b/ml/SamplesBuffer.h new file mode 100644 index 0000000..1c7215c --- /dev/null +++ b/ml/SamplesBuffer.h @@ -0,0 +1,146 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#ifndef SAMPLES_BUFFER_H +#define SAMPLES_BUFFER_H + +#include <iostream> +#include <vector> + +#include <cassert> +#include <cstdlib> +#include <cstring> + +#include <dlib/matrix.h> + +typedef double CalculatedNumber; +typedef dlib::matrix<CalculatedNumber, 0, 1> DSample; + +class Sample { +public: + Sample(CalculatedNumber *Buf, size_t N) : CNs(Buf), NumDims(N) {} + + void initDSample(DSample &DS) const { + for (size_t Idx = 0; Idx != NumDims; Idx++) { + DS(Idx) = std::abs(CNs[Idx]); + } + } + + void add(const Sample &RHS) const { + assert(NumDims == RHS.NumDims); + + for (size_t Idx = 0; Idx != NumDims; Idx++) + CNs[Idx] += RHS.CNs[Idx]; + }; + + void diff(const Sample &RHS) const { + assert(NumDims == RHS.NumDims); + + for (size_t Idx = 0; Idx != NumDims; Idx++) + CNs[Idx] -= RHS.CNs[Idx]; + }; + + void copy(const Sample &RHS) const { + assert(NumDims == RHS.NumDims); + + std::memcpy(CNs, RHS.CNs, NumDims * sizeof(CalculatedNumber)); + } + + void scale(CalculatedNumber Factor) { + for (size_t Idx = 0; Idx != NumDims; Idx++) + CNs[Idx] *= Factor; + } + + void lag(const Sample &S, size_t LagN) { + size_t N = S.NumDims; + + for (size_t Idx = 0; Idx != (LagN + 1); Idx++) { + Sample Src(S.CNs - (Idx * N), N); + Sample Dst(CNs + (Idx * N), N); + Dst.copy(Src); + } + } + + const CalculatedNumber *getCalculatedNumbers() const { + return CNs; + }; + + void print(std::ostream &OS) const; + +private: + CalculatedNumber *CNs; + size_t NumDims; +}; + +inline std::ostream& operator<<(std::ostream &OS, const Sample &S) { + S.print(OS); + return OS; +} + +class SamplesBuffer { +public: + SamplesBuffer(CalculatedNumber *CNs, + size_t NumSamples, size_t NumDimsPerSample, + size_t DiffN, size_t SmoothN, size_t LagN, + double SamplingRatio, std::vector<uint32_t> &RandNums) : + CNs(CNs), NumSamples(NumSamples), NumDimsPerSample(NumDimsPerSample), + DiffN(DiffN), SmoothN(SmoothN), LagN(LagN), + SamplingRatio(SamplingRatio), RandNums(RandNums), + BytesPerSample(NumDimsPerSample * sizeof(CalculatedNumber)), + Preprocessed(false) {}; + + std::vector<DSample> preprocess(); + std::vector<Sample> getPreprocessedSamples() const; + + size_t capacity() const { return NumSamples; } + void print(std::ostream &OS) const; + +private: + size_t getSampleOffset(size_t Index) const { + assert(Index < NumSamples); + return Index * NumDimsPerSample; + } + + size_t getPreprocessedSampleOffset(size_t Index) const { + assert(Index < NumSamples); + return getSampleOffset(Index) * (LagN + 1); + } + + void setSample(size_t Index, const Sample &S) const { + size_t Offset = getSampleOffset(Index); + std::memcpy(&CNs[Offset], S.getCalculatedNumbers(), BytesPerSample); + } + + const Sample getSample(size_t Index) const { + size_t Offset = getSampleOffset(Index); + return Sample(&CNs[Offset], NumDimsPerSample); + }; + + const Sample getPreprocessedSample(size_t Index) const { + size_t Offset = getPreprocessedSampleOffset(Index); + return Sample(&CNs[Offset], NumDimsPerSample * (LagN + 1)); + }; + + void diffSamples(); + void smoothSamples(); + void lagSamples(); + +private: + CalculatedNumber *CNs; + size_t NumSamples; + size_t NumDimsPerSample; + size_t DiffN; + size_t SmoothN; + size_t LagN; + double SamplingRatio; + std::vector<uint32_t> &RandNums; + + size_t BytesPerSample; + bool Preprocessed; +}; + +inline std::ostream& operator<<(std::ostream& OS, const SamplesBuffer &SB) { + SB.print(OS); + return OS; +} + +#endif /* SAMPLES_BUFFER_H */ diff --git a/ml/SamplesBufferTests.cc b/ml/SamplesBufferTests.cc new file mode 100644 index 0000000..5997a2a --- /dev/null +++ b/ml/SamplesBufferTests.cc @@ -0,0 +1,146 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#include "ml/ml-private.h" +#include <gtest/gtest.h> + +/* + * The SamplesBuffer class implements the functionality of the following python + * code: + * >> df = pd.DataFrame(data=samples) + * >> df = df.diff(diff_n).dropna() + * >> df = df.rolling(smooth_n).mean().dropna() + * >> df = pd.concat([df.shift(n) for n in range(lag_n + 1)], axis=1).dropna() + * + * Its correctness has been verified by automatically generating random + * data frames in Python and comparing them with the correspondent preprocessed + * SampleBuffers. + * + * The following tests are meant to catch unintended changes in the SamplesBuffer + * implementation. For development purposes, one should compare changes against + * the aforementioned python code. +*/ + +TEST(SamplesBufferTest, NS_8_NDPS_1_DN_1_SN_3_LN_1) { + size_t NumSamples = 8, NumDimsPerSample = 1; + size_t DiffN = 1, SmoothN = 3, LagN = 3; + + size_t N = NumSamples * NumDimsPerSample * (LagN + 1); + CalculatedNumber *CNs = new CalculatedNumber[N](); + + CNs[0] = 0.7568336679490107; + CNs[1] = 0.4814406581763254; + CNs[2] = 0.40073555156221874; + CNs[3] = 0.5973257298194408; + CNs[4] = 0.5334727814345868; + CNs[5] = 0.2632477193454843; + CNs[6] = 0.2684839023122384; + CNs[7] = 0.851332948637479; + + std::vector<uint32_t> RandNums(NumSamples, std::numeric_limits<uint32_t>::max()); + SamplesBuffer SB(CNs, NumSamples, NumDimsPerSample, DiffN, SmoothN, LagN, 1.0, RandNums); + SB.preprocess(); + + std::vector<Sample> Samples = SB.getPreprocessedSamples(); + EXPECT_EQ(Samples.size(), 2); + + Sample S0 = Samples[0]; + const CalculatedNumber *S0_CNs = S0.getCalculatedNumbers(); + Sample S1 = Samples[1]; + const CalculatedNumber *S1_CNs = S1.getCalculatedNumbers(); + + EXPECT_NEAR(S0_CNs[0], -0.109614, 0.001); + EXPECT_NEAR(S0_CNs[1], -0.0458293, 0.001); + EXPECT_NEAR(S0_CNs[2], 0.017344, 0.001); + EXPECT_NEAR(S0_CNs[3], -0.0531693, 0.001); + + EXPECT_NEAR(S1_CNs[0], 0.105953, 0.001); + EXPECT_NEAR(S1_CNs[1], -0.109614, 0.001); + EXPECT_NEAR(S1_CNs[2], -0.0458293, 0.001); + EXPECT_NEAR(S1_CNs[3], 0.017344, 0.001); + + delete[] CNs; +} + +TEST(SamplesBufferTest, NS_8_NDPS_1_DN_2_SN_3_LN_2) { + size_t NumSamples = 8, NumDimsPerSample = 1; + size_t DiffN = 2, SmoothN = 3, LagN = 2; + + size_t N = NumSamples * NumDimsPerSample * (LagN + 1); + CalculatedNumber *CNs = new CalculatedNumber[N](); + + CNs[0] = 0.20511885291342846; + CNs[1] = 0.13151717360306558; + CNs[2] = 0.6017085062423134; + CNs[3] = 0.46256882933941545; + CNs[4] = 0.7887758447877941; + CNs[5] = 0.9237989080034406; + CNs[6] = 0.15552559051428083; + CNs[7] = 0.6309750314597955; + + std::vector<uint32_t> RandNums(NumSamples, std::numeric_limits<uint32_t>::max()); + SamplesBuffer SB(CNs, NumSamples, NumDimsPerSample, DiffN, SmoothN, LagN, 1.0, RandNums); + SB.preprocess(); + + std::vector<Sample> Samples = SB.getPreprocessedSamples(); + EXPECT_EQ(Samples.size(), 2); + + Sample S0 = Samples[0]; + const CalculatedNumber *S0_CNs = S0.getCalculatedNumbers(); + Sample S1 = Samples[1]; + const CalculatedNumber *S1_CNs = S1.getCalculatedNumbers(); + + EXPECT_NEAR(S0_CNs[0], 0.005016, 0.001); + EXPECT_NEAR(S0_CNs[1], 0.326450, 0.001); + EXPECT_NEAR(S0_CNs[2], 0.304903, 0.001); + + EXPECT_NEAR(S1_CNs[0], -0.154948, 0.001); + EXPECT_NEAR(S1_CNs[1], 0.005016, 0.001); + EXPECT_NEAR(S1_CNs[2], 0.326450, 0.001); + + delete[] CNs; +} + +TEST(SamplesBufferTest, NS_8_NDPS_3_DN_2_SN_4_LN_1) { + size_t NumSamples = 8, NumDimsPerSample = 3; + size_t DiffN = 2, SmoothN = 4, LagN = 1; + + size_t N = NumSamples * NumDimsPerSample * (LagN + 1); + CalculatedNumber *CNs = new CalculatedNumber[N](); + + CNs[0] = 0.34310900399667765; CNs[1] = 0.14694315994488194; CNs[2] = 0.8246677800938796; + CNs[3] = 0.48249504592307835; CNs[4] = 0.23241087965531182; CNs[5] = 0.9595348555892567; + CNs[6] = 0.44281094035598334; CNs[7] = 0.5143142171362715; CNs[8] = 0.06391303014242555; + CNs[9] = 0.7460491027783901; CNs[10] = 0.43887217459032923; CNs[11] = 0.2814395025355999; + CNs[12] = 0.9231114281214198; CNs[13] = 0.326882401786898; CNs[14] = 0.26747939220376216; + CNs[15] = 0.7787571209969636; CNs[16] =0.5851700001235088; CNs[17] = 0.34410728945321567; + CNs[18] = 0.9394494507088997; CNs[19] =0.17567223681734334; CNs[20] = 0.42732886195446984; + CNs[21] = 0.9460522396152958; CNs[22] =0.23462747016780894; CNs[23] = 0.35983249900892145; + + std::vector<uint32_t> RandNums(NumSamples, std::numeric_limits<uint32_t>::max()); + SamplesBuffer SB(CNs, NumSamples, NumDimsPerSample, DiffN, SmoothN, LagN, 1.0, RandNums); + SB.preprocess(); + + std::vector<Sample> Samples = SB.getPreprocessedSamples(); + EXPECT_EQ(Samples.size(), 2); + + Sample S0 = Samples[0]; + const CalculatedNumber *S0_CNs = S0.getCalculatedNumbers(); + Sample S1 = Samples[1]; + const CalculatedNumber *S1_CNs = S1.getCalculatedNumbers(); + + EXPECT_NEAR(S0_CNs[0], 0.198225, 0.001); + EXPECT_NEAR(S0_CNs[1], 0.003529, 0.001); + EXPECT_NEAR(S0_CNs[2], -0.063003, 0.001); + EXPECT_NEAR(S0_CNs[3], 0.219066, 0.001); + EXPECT_NEAR(S0_CNs[4], 0.133175, 0.001); + EXPECT_NEAR(S0_CNs[5], -0.293154, 0.001); + + EXPECT_NEAR(S1_CNs[0], 0.174160, 0.001); + EXPECT_NEAR(S1_CNs[1], -0.135722, 0.001); + EXPECT_NEAR(S1_CNs[2], 0.110452, 0.001); + EXPECT_NEAR(S1_CNs[3], 0.198225, 0.001); + EXPECT_NEAR(S1_CNs[4], 0.003529, 0.001); + EXPECT_NEAR(S1_CNs[5], -0.063003, 0.001); + + delete[] CNs; +} diff --git a/ml/ml-dummy.c b/ml/ml-dummy.c new file mode 100644 index 0000000..492dfe2 --- /dev/null +++ b/ml/ml-dummy.c @@ -0,0 +1,50 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#include "ml.h" + +#if !defined(ENABLE_ML) + +bool ml_capable() { + return false; +} + +bool ml_enabled(RRDHOST *RH) { + (void) RH; + return false; +} + +void ml_init(void) {} + +void ml_new_host(RRDHOST *RH) { (void) RH; } + +void ml_delete_host(RRDHOST *RH) { (void) RH; } + +char *ml_get_host_info(RRDHOST *RH) { + (void) RH; + return NULL; +} + +char *ml_get_host_runtime_info(RRDHOST *RH) { + (void) RH; + return NULL; +} + +char *ml_get_host_models(RRDHOST *RH) { + (void) RH; + return NULL; +} + +void ml_new_dimension(RRDDIM *RD) { (void) RD; } + +void ml_delete_dimension(RRDDIM *RD) { (void) RD; } + +bool ml_is_anomalous(RRDDIM *RD, double Value, bool Exists) { + (void) RD; (void) Value; (void) Exists; + return false; +} + +bool ml_streaming_enabled() { + return false; +} + +#endif diff --git a/ml/ml-private.h b/ml/ml-private.h new file mode 100644 index 0000000..2bd72ac --- /dev/null +++ b/ml/ml-private.h @@ -0,0 +1,26 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#ifndef ML_PRIVATE_H +#define ML_PRIVATE_H + +#include "KMeans.h" +#include "ml/ml.h" + +#include <chrono> +#include <map> +#include <mutex> +#include <sstream> + +namespace ml { + +using SteadyClock = std::chrono::steady_clock; +using TimePoint = std::chrono::time_point<SteadyClock>; + +template<typename T> +using Duration = std::chrono::duration<T>; + +using Seconds = std::chrono::seconds; + +} // namespace ml + +#endif /* ML_PRIVATE_H */ diff --git a/ml/ml.cc b/ml/ml.cc new file mode 100644 index 0000000..1a7d6ae --- /dev/null +++ b/ml/ml.cc @@ -0,0 +1,165 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#include "Config.h" +#include "Dimension.h" +#include "Host.h" + +#include <random> + +using namespace ml; + +bool ml_capable() { + return true; +} + +bool ml_enabled(RRDHOST *RH) { + if (!Cfg.EnableAnomalyDetection) + return false; + + if (simple_pattern_matches(Cfg.SP_HostsToSkip, rrdhost_hostname(RH))) + return false; + + return true; +} + +/* + * Assumptions: + * 1) hosts outlive their sets, and sets outlive their dimensions, + * 2) dimensions always have a set that has a host. + */ + +void ml_init(void) { + // Read config values + Cfg.readMLConfig(); + + if (!Cfg.EnableAnomalyDetection) + return; + + // Generate random numbers to efficiently sample the features we need + // for KMeans clustering. + std::random_device RD; + std::mt19937 Gen(RD()); + + Cfg.RandomNums.reserve(Cfg.MaxTrainSamples); + for (size_t Idx = 0; Idx != Cfg.MaxTrainSamples; Idx++) + Cfg.RandomNums.push_back(Gen()); +} + +void ml_new_host(RRDHOST *RH) { + if (!ml_enabled(RH)) + return; + + Host *H = new Host(RH); + RH->ml_host = static_cast<ml_host_t>(H); + + H->startAnomalyDetectionThreads(); +} + +void ml_delete_host(RRDHOST *RH) { + Host *H = static_cast<Host *>(RH->ml_host); + if (!H) + return; + + H->stopAnomalyDetectionThreads(); + + delete H; + RH->ml_host = nullptr; +} + +void ml_new_dimension(RRDDIM *RD) { + RRDSET *RS = RD->rrdset; + + Host *H = static_cast<Host *>(RD->rrdset->rrdhost->ml_host); + if (!H) + return; + + if (static_cast<unsigned>(RD->update_every) != H->updateEvery()) + return; + + if (simple_pattern_matches(Cfg.SP_ChartsToSkip, rrdset_name(RS))) + return; + + Dimension *D = new Dimension(RD); + RD->ml_dimension = static_cast<ml_dimension_t>(D); + H->addDimension(D); +} + +void ml_delete_dimension(RRDDIM *RD) { + Dimension *D = static_cast<Dimension *>(RD->ml_dimension); + if (!D) + return; + + Host *H = static_cast<Host *>(RD->rrdset->rrdhost->ml_host); + if (!H) + delete D; + else + H->removeDimension(D); + + RD->ml_dimension = nullptr; +} + +char *ml_get_host_info(RRDHOST *RH) { + nlohmann::json ConfigJson; + + if (RH && RH->ml_host) { + Host *H = static_cast<Host *>(RH->ml_host); + H->getConfigAsJson(ConfigJson); + } else { + ConfigJson["enabled"] = false; + } + + return strdupz(ConfigJson.dump(2, '\t').c_str()); +} + +char *ml_get_host_runtime_info(RRDHOST *RH) { + nlohmann::json ConfigJson; + + if (RH && RH->ml_host) { + Host *H = static_cast<Host *>(RH->ml_host); + H->getDetectionInfoAsJson(ConfigJson); + } else { + return nullptr; + } + + return strdup(ConfigJson.dump(1, '\t').c_str()); +} + +char *ml_get_host_models(RRDHOST *RH) { + nlohmann::json ModelsJson; + + if (RH && RH->ml_host) { + Host *H = static_cast<Host *>(RH->ml_host); + H->getModelsAsJson(ModelsJson); + return strdup(ModelsJson.dump(2, '\t').c_str()); + } + + return nullptr; +} + +bool ml_is_anomalous(RRDDIM *RD, double Value, bool Exists) { + Dimension *D = static_cast<Dimension *>(RD->ml_dimension); + if (!D) + return false; + + return D->predict(Value, Exists); +} + +bool ml_streaming_enabled() { + return Cfg.StreamADCharts; +} + +#if defined(ENABLE_ML_TESTS) + +#include "gtest/gtest.h" + +int test_ml(int argc, char *argv[]) { + (void) argc; + (void) argv; + + ::testing::InitGoogleTest(&argc, argv); + return RUN_ALL_TESTS(); +} + +#endif // ENABLE_ML_TESTS + +#include "ml-private.h" @@ -0,0 +1,50 @@ +// SPDX-License-Identifier: GPL-3.0-or-later + +#ifndef NETDATA_ML_H +#define NETDATA_ML_H + +#ifdef __cplusplus +extern "C" { +#endif + +#include "daemon/common.h" +#include "web/api/queries/rrdr.h" + +// This is a DBEngine function redeclared here so that we can free +// the anomaly rate dimension, whenever its backing dimension is freed. +void rrddim_free(RRDSET *st, RRDDIM *rd); + +typedef void* ml_host_t; +typedef void* ml_dimension_t; + +bool ml_capable(); + +bool ml_enabled(RRDHOST *RH); + +void ml_init(void); + +void ml_new_host(RRDHOST *RH); +void ml_delete_host(RRDHOST *RH); + +char *ml_get_host_info(RRDHOST *RH); +char *ml_get_host_runtime_info(RRDHOST *RH); +char *ml_get_host_models(RRDHOST *RH); + +void ml_new_dimension(RRDDIM *RD); +void ml_delete_dimension(RRDDIM *RD); + +bool ml_is_anomalous(RRDDIM *RD, double value, bool exists); + +bool ml_streaming_enabled(); + +#define ML_ANOMALY_RATES_CHART_ID "anomaly_detection.anomaly_rates" + +#if defined(ENABLE_ML_TESTS) +int test_ml(int argc, char *argv[]); +#endif + +#ifdef __cplusplus +}; +#endif + +#endif /* NETDATA_ML_H */ diff --git a/ml/notebooks/README.md b/ml/notebooks/README.md new file mode 100644 index 0000000..5e9db6d --- /dev/null +++ b/ml/notebooks/README.md @@ -0,0 +1,5 @@ +## Machine Learning Notebooks + +This folder is a home for any documentation supporting machine learning related notebooks. + +- [Netdata anomaly detection deepdive](netdata_anomaly_detection_deepdive.ipynb): This is a starter notebook to help users understand how anomaly detection works in the Netdata agent and go a little deeper if they want.
\ No newline at end of file diff --git a/ml/notebooks/netdata_anomaly_detection_deepdive.ipynb b/ml/notebooks/netdata_anomaly_detection_deepdive.ipynb new file mode 100644 index 0000000..8d0c0c7 --- /dev/null +++ b/ml/notebooks/netdata_anomaly_detection_deepdive.ipynb @@ -0,0 +1,1712 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "metadata": { + "pycharm": { + "name": "#%% md\n" + } + }, + "source": [ + "## Netdata Anomaly Detection Deepdive" + ] + }, + { + "cell_type": "markdown", + "metadata": { + "pycharm": { + "name": "#%% md\n" + } + }, + "source": [ + "[](https://colab.research.google.com/github/netdata/netdata/blob/master/ml/notebooks/netdata_anomaly_detection_deepdive.ipynb)" + ] + }, + { + "cell_type": "markdown", + "metadata": { + "pycharm": { + "name": "#%% md\n" + } + }, + "source": [ + "This notebook will walk through a simplified python based implementation of the C & C++ code in [`netdata/netdata/ml/`](https://github.com/netdata/netdata/tree/master/ml) used to power the [anomaly detection capabilities](https://github.com/netdata/netdata/blob/master/ml/README.md) of the Netdata agent.\n", + "\n", + "The main goal here is to help interested users learn more about how the machine learning works under the hood. If you just want to get started by enabling ml on your agent you can check out these [simple configuration steps](https://learn.netdata.cloud/docs/agent/ml#configuration). \n", + "\n", + "🚧 **Note**: This functionality is still under active development and considered experimental. Changes might cause the feature to break. We dogfood it internally and among early adopters within the Netdata community to build the feature. If you would like to get involved and help us with some feedback, email us at analytics-ml-team@netdata.cloud or come join us in the [🤖-ml-powered-monitoring](https://discord.gg/4eRSEUpJnc) channel of the Netdata discord. Alternativley, if GitHub is more of your thing, feel free to create a [GitHub discussion](https://github.com/netdata/netdata/discussions?discussions_q=label%3Aarea%2Fml).\n", + "\n", + "In this notebook we will:\n", + "\n", + "1. [**Get raw data**](#get-raw-data): Pull some recent data from one of our demo agents.\n", + "2. [**Add some anomalous data**](#add-some-anomalous-data): Be evil and mess up the tail end of the data to make it obviously \"anomalous\".\n", + "3. [**Lets do some ML!**](#lets-do-some-ml): Implement an unsupervised clustering based approach to anomaly detection.\n", + "4. [**Lets visualize all this!**](#lets-visualize-all-this): Plot and explore all this visually.\n", + "5. [**So, how does it _actually_ work?**](#so-how-does-it-actually-work): Dig a little deeper on what's going on under the hood." + ] + }, + { + "cell_type": "markdown", + "metadata": { + "pycharm": { + "name": "#%% md\n" + } + }, + "source": [ + "### Imports & Helper Functions" + ] + }, + { + "cell_type": "markdown", + "metadata": { + "pycharm": { + "name": "#%% md\n" + } + }, + "source": [ + "Uncomment and run the next cell to install [netdata-pandas](https://github.com/netdata/netdata-pandas) which we will use to easily pull data from the [Netdata agent REST API](https://learn.netdata.cloud/docs/agent/web/api) into a nice clean [Pandas](https://pandas.pydata.org/) [DataFrame](https://pandas.pydata.org/docs/reference/api/pandas.DataFrame.html) where it will be easier to work with. \n", + "\n", + "Once you have [netdata-pandas](https://github.com/netdata/netdata-pandas) installed you can comment it back out and rerun the cell to clear the output." + ] + }, + { + "cell_type": "code", + "execution_count": 1, + "metadata": { + "id": "aL4gm-jUffEx", + "pycharm": { + "is_executing": true + } + }, + "outputs": [], + "source": [ + "# uncomment the line below (when running in google colab) to install the netdata-pandas library, comment it again when done.\n", + "#!pip install netdata-pandas" + ] + }, + { + "cell_type": "code", + "execution_count": 2, + "metadata": { + "id": "EMZBHjG4mOQh", + "pycharm": { + "is_executing": true + } + }, + "outputs": [], + "source": [ + "from datetime import datetime, timedelta\n", + "import itertools\n", + "import random\n", + "import pandas as pd\n", + "import numpy as np\n", + "import matplotlib.pyplot as plt\n", + "import seaborn as sns\n", + "import matplotlib.patches as mpatches\n", + "from sklearn.cluster import KMeans\n", + "from scipy.spatial.distance import cdist\n", + "from netdata_pandas.data import get_data\n", + "\n", + "# helper functions\n", + "\n", + "\n", + "def preprocess_df(df, lags_n, diffs_n, smooth_n):\n", + " \"\"\"Given a pandas dataframe preprocess it to take differences, add smoothing, lags and abs values. \n", + " \"\"\"\n", + " if diffs_n >= 1:\n", + " # take differences\n", + " df = df.diff(diffs_n).dropna()\n", + " if smooth_n >= 2:\n", + " # apply a rolling average to smooth out the data a bit\n", + " df = df.rolling(smooth_n).mean().dropna()\n", + " if lags_n >= 1:\n", + " # for each dimension add a new columns for each of lags_n lags of the differenced and smoothed values for that dimension\n", + " df_columns_new = [f'{col}_lag{n}' for n in range(lags_n+1) for col in df.columns]\n", + " df = pd.concat([df.shift(n) for n in range(lags_n + 1)], axis=1).dropna()\n", + " df.columns = df_columns_new\n", + " # sort columns to have lagged values next to each other for clarity when looking at the feature vectors\n", + " df = df.reindex(sorted(df.columns), axis=1)\n", + " \n", + " # take absolute values as last step\n", + " df = abs(df)\n", + " \n", + " return df\n", + "\n", + "\n", + "def add_shading_to_plot(ax, a, b, t, c='y', alpha=0.2):\n", + " \"\"\"Helper function to add shading to plot and add legend item.\n", + " \"\"\"\n", + " plt.axvspan(a, b, color=c, alpha=alpha, lw=0)\n", + " handles, labels = ax.get_legend_handles_labels()\n", + " patch = mpatches.Patch(color=c, label=t, alpha=alpha)\n", + " handles.append(patch) \n", + " plt.legend(handles=handles)\n", + "\n" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "### Inputs & Parameters" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "A full list of all the anomaly detection configuration parameters, and descriptions of each, can be found in the [configuration](https://github.com/netdata/netdata/blob/master/ml/README.md#configuration) section of the [ml readme](https://github.com/netdata/netdata/blob/master/ml/README.md).\n", + "\n", + "Below we will focus on some basic params to decide what data to pull and the main ml params of importance in understanding how it all works.\n", + "\n", + "#### training size/scheduling parameters:\n", + "- `train_every`: How often to train or retrain each model.\n", + "- `num_samples_to_train`: How much of the recent data to train on, for example 3600 would mean training on the last 1 hour of raw data. The default in the netdata agent currently is 14400, so last 4 hours.\n", + "\n", + "#### feature preprocessing related parameters:\n", + "- `num_samples_to_diff`: This is really just a 1 or 0 flag to turn on or off differencing in the feature preprocessing. It defaults to 1 (to take differences) and generally should be left alone.\n", + "- `num_samples_to_smooth`: The extent of smoothing (averaging) applied as part of feature preprocessing.\n", + "- `num_samples_to_lag`: The number of previous values to also include in our feature vector.\n", + "\n", + "#### anomaly score related parameters:\n", + "- `dimension_anomaly_score_threshold`: The threshold on the anomaly score, above which the data it considered anomalous and the [anomaly bit](https://github.com/netdata/netdata/blob/master/ml/README.md#anomaly-bit) is set to 1 (its actually set to 100 in reality but this just to make it behave more like a rate when aggregated in the netdata agent api). By default this is `0.99` which means anything with an anomaly score above 99% is considered anomalous. Decreasing this threshold makes the model more sensitive and will leave to more anomaly bits, increasing it does the opposite.\n", + "\n", + "#### model parameters:\n", + "- `n_clusters_per_dimension`: This is the number of clusters to fit for each model, by default it is set to 2 such that 2 cluster [centroids](https://en.wikipedia.org/wiki/Centroid) will be fit for each model.\n", + "- `max_iterations`: The maximum number of iterations the fitting of the clusters is allowed to take. In reality the clustering will converge a lot sooner than this.\n", + "\n", + "**Note**: There is much more detailed discussion of all there configuration parameters in the [\"Configuration\"](https://github.com/netdata/netdata/blob/master/ml/README.md#configuration) section of the ml readme." + ] + }, + { + "cell_type": "code", + "execution_count": 3, + "metadata": { + "id": "tBUVUpR3fohX" + }, + "outputs": [], + "source": [ + "# data params\n", + "hosts = ['london.my-netdata.io']\n", + "charts = ['system.cpu']\n", + "# if want to just focus on a subset of dims, in this case lets just pick one for simplicity\n", + "dims = ['system.cpu|user'] \n", + "last_n_hours = 2\n", + "# based on last_n_hours define the relevant 'before' and 'after' params for the netdata rest api on the agent\n", + "before = int(datetime.utcnow().timestamp())\n", + "after = int((datetime.utcnow() - timedelta(hours=last_n_hours)).timestamp())\n", + "\n", + "# ml params\n", + "train_every = 3600\n", + "num_samples_to_train = 3600\n", + "num_samples_to_diff = 1\n", + "num_samples_to_smooth = 3\n", + "num_samples_to_lag = 5\n", + "dimension_anomaly_score_threshold = 0.99\n", + "n_clusters_per_dimension = 2\n", + "max_iterations = 1000" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "### 1. Get raw data<a id=\"get-raw-data\"></a>" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "Next we will use the `get_data()` function from the [netdata-pandas](https://github.com/netdata/netdata-pandas) library to just pull down our raw data from the agent into a Pandas dataframe." + ] + }, + { + "cell_type": "code", + "execution_count": 4, + "metadata": { + "colab": { + "base_uri": "https://localhost:8080/", + "height": 660 + }, + "id": "Ypudrfu-fpje", + "outputId": "b25c7322-03b4-4475-c416-37c3abbe78a4" + }, + "outputs": [ + { + "name": "stdout", + "output_type": "stream", + "text": [ + "(7200, 1)\n", + "1647978087 1647985286\n" + ] + }, + { + "data": { + "text/html": [ + "<div>\n", + "<style scoped>\n", + " .dataframe tbody tr th:only-of-type {\n", + " vertical-align: middle;\n", + " }\n", + "\n", + " .dataframe tbody tr th {\n", + " vertical-align: top;\n", + " }\n", + "\n", + " .dataframe thead th {\n", + " text-align: right;\n", + " }\n", + "</style>\n", + "<table border=\"1\" class=\"dataframe\">\n", + " <thead>\n", + " <tr style=\"text-align: right;\">\n", + " <th></th>\n", + " <th>system.cpu|user</th>\n", + " </tr>\n", + " <tr>\n", + " <th>time_idx</th>\n", + " <th></th>\n", + " </tr>\n", + " </thead>\n", + " <tbody>\n", + " <tr>\n", + " <th>1647978087</th>\n", + " <td>1.503759</td>\n", + " </tr>\n", + " <tr>\n", + " <th>1647978088</th>\n", + " <td>0.252525</td>\n", + " </tr>\n", + " <tr>\n", + " <th>1647978089</th>\n", + " <td>0.755668</td>\n", + " </tr>\n", + " <tr>\n", + " <th>1647978090</th>\n", + " <td>0.503778</td>\n", + " </tr>\n", + " <tr>\n", + " <th>1647978091</th>\n", + " <td>0.501253</td>\n", + " </tr>\n", + " </tbody>\n", + "</table>\n", + "</div>" + ], + "text/plain": [ + " system.cpu|user\n", + "time_idx \n", + "1647978087 1.503759\n", + "1647978088 0.252525\n", + "1647978089 0.755668\n", + "1647978090 0.503778\n", + "1647978091 0.501253" + ] + }, + "metadata": {}, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAA5gAAAGECAYAAABTQ490AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAACFCUlEQVR4nO3dd5zbRN4G8Ge2J5teSYMU0gkJpFBCqKGGezl6P9odcAccnQt3oQcInePoNXQCoRNIL5CeTe99k9203U2yva/n/cNlZVu2JVuyJPv58uGTta0ykkYz8xuNJCGlBBEREREREVGsUqxOABERERERESUGBphERERERERkCAaYREREREREZAgGmERERERERGQIBphERERERERkCAaYREREREREZAgGmERERBSWECJXCNHd6nQQEZH9McAkIkpCnoChSghRLoTYL4SYKIRoZvI6JwohaoUQZZ7/1wkhnhVCtNSZ7tFmptNInm0eb3U6iIiI4oUBJhFR8vqTlLIZgCEAjgPwcBzW+byUsjmA9gBuAnAigAVCiOw4rJscQgiRZnUaiIgoOgwwiYiSnJRyP4BpcAeaAAAhxFghxHbPlcYNQoiLFb/tEkIM9fx9rRBCCiEGej7fIoT4QcM6q6WUywD8H4C2cAebEEL0EkLMFkIcFEIUCSE+F0K08vz2KYAjAfzsufL6kOf7bzxXYUuEEL970xINIcQIIUSOEKJUCHFACPGy5/spQoi7AqZdI4S4WLi9IoQo8My3VghxjBDiVgDXAnjIk96fPfN1FkJ8K4QoFELsFEL8U7HMxz3b85ln368VQvQRQjzsWX6eEOKcMOkfKISYIYQ45En/vxXLnSyEmORZ7gohxGDFfFIIcbTic8grr0KIG4UQ8wO+880vhLjAk2fKhBB7hBAPKKa7UAixSghRLIRYKIQ4VvFbrhDiX0KINQAqGGQSETkTA0wioiQnhOgK4HwA2xRfbwcwCkBLAE8A+EwI0cnz2zwAp3v+Pg3ADgCnKj7P07puKWUZgBmedQGAAPAsgM4A+gPoBuBxz7TXA9gNz5VXKeXznnl+A9AbQAcAKwB8rnX9Kv4L4L9SyhYAegH42vP9xwCu807kCc66AJgC4By4t78P3PvrCgAHpZTvetLyvCe9fxJCpAD4GcBqz/xnAbhHCHGuIg1/AvApgNYAVsId/Kd4pn8SwDtqCRdCNAcwE8BUuPff0QBmKSa5CMA3ANoA+ALAD0KIdJ37R4sPANzmuVJ9DIDZnvQdB+BDALfB3anwDoCfhBCZinmvBjAGQCspZb0JaSMiIpMxwCQiSl4/CCHKAOQBKADwmPcHKeU3Usq9UkqXlHISgK0ARnh+ngd3IAm4A8NnFZ91BZgee+EOeiCl3CalnCGlrJFSFgJ4WbFsVVLKD6WUZVLKGriD0cF67usMUAfgaCFEOylluZRysef7nwD0EUL09ny+HsAkKWWtZ57mAPoBEFLKjVLKfSGWPxxAeynlk1LKWinlDgDvAbhKMc0fUsppngDrG7iHE0+QUtYB+ApAd+9V3QAXAtgvpXzJc4W4TEq5RPH7cinlZM9yXgaQBfcQZaPVARgghGghpTwspVzh+f5WAO9IKZdIKRuklB8DqAlIw2tSyjwpZZUJ6SIiojhggElElLz+7LnKdDrcwVE77w9CiL8ohjIWw30lyvv7PACjPFc0U+G+yjdSuJ8y2hLAKp3p6ALgkGe9HYUQX3mGVpYC+EyZrkBCiFQhxATPcN5SALmen4LmEUKM8gxVLRdCrA+xyFvgvhK5SQixTAhxIeAe0gtgEoDrPFchr4b7KiOklLMBvA7gDQAFQoh3hRAtQiz/KACdvfvVs2//DaCjYpoDir+rABRJKRsUnwFA7YFM3eC+8hxKnvcPKaULQD7cVzqNdimACwDsEkLME0Kc5Pn+KAD3B2x7t4A05IGIiByNASYRUZKTUs4DMBHAiwAghDgK7qtqdwJoK6VsBWAd3MNXIaXcBqASwF0AfpdSlgLYD/cVqvme4EUT4X5y7WgAf3i+egaABDDIM0z1Ou96vckNWMQ1cA/9HA13cNvdu2iV7fzDM1S1mZRS9T5NKeVWKeXVcA+3fQ7AZNH4AKKP4b6n8iwAlVLKRYr5XpNSDgUwAO4A9cEQ6c0DsFNK2Urxf3Mp5QVq6dEpD0DPML938/7hCZK7wn31GHAfz6aKaY8Is5wK5bRCCL9ppZTLpJQXwb0Pf0DjMOM8AE8HbHtTKeWXytnDrJeIiByAASYREQHAqwDO9txbmA13Q78QAIQQN8F9BVNpHtwBqHc47NyAz2EJITKF+0FBPwA4DOAjz0/NAZQDKBFCdEFjoOZ1AP5BVHO4h1kehDvoeUbL+sOk6zohRHtPkFzs+doFAJ6A0gXgJXiuXnrmGS6EOMFzP2MFgGrvPCrpXQqgzPMwmyaeK7DHCCGGx5Juj18AdBJC3OPZv82FECcofh8qhLjE8/Cce+Deb94hwKsAXONJz3kIPyx5NYCBQoghQogseO6RBQAhRIZwP/ippWcobika98V7AG737CshhMgWQozx3DtKREQJggEmERHBc7/jJwAelVJugDuIWgR3gDQIwIKAWebBHdz9HuJzKA957vs86FnfcgAnSykrPL8/AeB4ACVwP0Dnu4D5nwUwzjPE8gHPMnYB2ANgAxoDpmidB2C9EKIc7gf+XBVwP+AncO+PzxTftYA7eDrsSctBAC94fvsA7vsRi4UQP3iGul4I9xN7dwIoAvA+3FdfdRNCvC2EeBvwPTDpbLgfErQf7vtmz1BM/iOAKz3pvB7AJZ4gEADu9sxXDPdV2h9CrVNKuQXuhw3N9KxjfsAk1wPI9QxZvt2zPEgpcwD8De7hxIfhfqjUjbo3moiIbE1IydEoREREWggh/gLgVinlKVanRQ8hxOMAjpZSXhdp2hDz5wI4XUqZa2CyiIgoAfEKJhERkQZCiKYA/gHgXavTQkREZFcMMImIiCLwvKeyEO4hw19YnBwrvIrGe1KJiIhC4hBZIiIiIiIiMkSalok8916UAWgAUC+lHGZmooiIiIiIiMh5NAWYHmdIKYtMSwkRERERERE5mp4AU7N27drJ7t27m7FoIiIiIiIistDy5cuLpJTt1X7TGmBKANOFEBLAO1LKoCfoCSFuBXArABx55JHIycmJNr1ERERERERkU0KIXaF+0/oU2VOklMcDOB/AHUKIUwMnkFK+K6UcJqUc1r69ajBLRERERERECUxTgCml3OP5twDA9wBGmJkoIiIiIiIicp6IAaYQIlsI0dz7N4BzAKwzO2FERERERETkLFruwewI4HshhHf6L6SUU01NFREREREROUpdXR3y8/NRXV1tdVLIIFlZWejatSvS09M1zxMxwJRS7gAwOJaEERERERFRYsvPz0fz5s3RvXt3eC5OkYNJKXHw4EHk5+ejR48emufT+pAfIiIiIiKikKqrq9G2bVsGlwlCCIG2bdvqviLNAJOIiIiIiAzB4DKxRHM8GWASERERERGRIRhgEhERERFR0ps4cSL27t1rdTLCmjhxIh5//HGrkxEWA0wiIiIiIkp6TggwzVZfXx/zMrS8poSIiIiIiEizJ35ejw17Sw1d5oDOLfDYnwaG/L2iogJXXHEF8vPz0dDQgEceeQRffvklfvjhBwDAjBkz8Oabb2Ly5Mm45ZZbkJOTAyEEbr75ZnTr1g05OTm49tpr0aRJEyxatAgbNmzAfffdh/LycrRr1w4TJ05Ep06dcPrpp+O4447DH3/8gYqKCnzyySd49tlnsXbtWlx55ZUYP358UNqWLVuGu+++GxUVFcjMzMSsWbPw7bff4vvvv0dJSQn27NmD6667Do899hhyc3Nx4YUXYt26dQCAF198EeXl5UFXLidOnIicnBy8/vrrAIALL7wQDzzwAEaNGhW0fffeey+2b9+OO+64A4WFhWjatCnee+899OvXDzfeeCOysrKwcuVKjBw5Ei+//HJMx4kBpo0crqhF6+wMq5NBREREROQ4U6dORefOnTFlyhQAQElJCR577DEUFhaiffv2+Oijj3DzzTdj1apV2LNnjy+AKy4uRqtWrfD666/jxRdfxLBhw1BXV4e77roLP/74I9q3b49JkybhP//5Dz788EMAQEZGBnJycvDf//4XF110EZYvX442bdqgV69euPfee9G2bVtfumpra3HllVdi0qRJGD58OEpLS9GkSRMAwNKlS7Fu3To0bdoUw4cPx5gxY9CuXbuY9oPa9gHArbfeirfffhu9e/fGkiVL8I9//AOzZ88G4H7FzMKFC5GamhrTugEGmLbx46o9uPurVfjhjpEY0q2V1ckhIiIiIopauCuNZhk0aBDuv/9+/Otf/8KFF16IUaNG4frrr8dnn32Gm266CYsWLcInn3yCsrIy7NixA3fddRfGjBmDc845J2hZmzdvxrp163D22WcDABoaGtCpUyff7//3f//nW+fAgQN9v/Xs2RN5eXl+AebmzZvRqVMnDB8+HADQokUL329nn322b9pLLrkE8+fPx5///OeY9kPPnj2Dtq+8vBwLFy7E5Zdf7puupqbG9/fll19uSHAJMMC0jUXbDwIANu4rZYBJRERERKRTnz59sGLFCvz6668YN24czjrrLPz1r3/Fn/70J2RlZeHyyy9HWloaWrdujdWrV2PatGl4++238fXXX/uuTHpJKTFw4EAsWrRIdV2ZmZkAgJSUFN/f3s967mMMfA2IEAJpaWlwuVy+70K9hzLUdGrb9+qrr6JVq1ZYtWqV6rKys7M1pzkSPuSHiIiIiIgcb+/evWjatCmuu+46PPjgg1ixYgU6d+6Mzp07Y/z48bjpppsAAEVFRXC5XLj00ksxfvx4rFixAgDQvHlzlJWVAQD69u2LwsJCX4BZV1eH9evXR5Wuvn37Yt++fVi2bBkAoKyszBeEzpgxA4cOHUJVVRV++OEHjBw5Eh07dkRBQQEOHjyImpoa/PLLL6rL7d69O1atWgWXy4W8vDwsXbo05Pa1aNECPXr0wDfffAPAHUCvXr06qu2JhFcwiYiIiIjI8dauXYsHH3wQKSkpSE9Px1tvvQUAuPbaa1FYWIj+/fsDAPbs2YObbrrJd/Xv2WefBQDceOONuP32230P+Zk8eTL++c9/oqSkBPX19bjnnnswcKD2ob8XXHAB3n//fXTu3BmTJk3CXXfdhaqqKjRp0gQzZ84EAIwYMQKXXnop8vPzcd1112HYsGEAgEcffRQjRoxAly5d0K9fP9Xljxw5Ej169MCAAQPQv39/HH/88WG37/PPP8ff//53jB8/HnV1dbjqqqswePBgXftYCyGlNHyhw4YNkzk5OYYvN5GN/XYNvlqWh2cvGYSrRxxpdXKIiIiIiHTZuHGjL4izkzvvvBPHHXccbrnlFquT4ifwKbBa58nNzY3ruzDVjqsQYrmUcpja9LyCSURERERECWno0KHIzs7GSy+9ZHVSkgYDTCIiIiIiSkjLly+3Ogkh3Xjjjbjxxht1zTNkyBB0797dlPQYhQGmTZgwUpmIiIiIKK6klEFPRiXjDBkyJK7ri+Z2Sj5FloiIiIiIYpaVlYWDBw9GFZSQ/UgpcfDgQWRlZemaj1cwbYIdPURERETkZF27dkV+fj4KCwutTgoZJCsrC127dtU1DwNMIiIiIiKKWXp6Onr06GF1MshiHCJLREREREREhmCASURERERERIZggElERERERESGYIBpE3zYFhEREREROR0DTJvhw2SJiIiIiMipGGDaDC9kEhERERGRUzHAtAm+B5OIiIiIiJyOASYREREREREZggEmERERERERGYIBJhERERERERmCAaZN8DUlRERERETkdAwwbYbP+iEiIiIiIqdigGkzvJBJREREREROxQDTJviaEiIiIiIicjoGmERERERERGQIBphERERERERkCAaYNsGnyBIRERERkdMxwLQZ3opJREREREROxQCTiIiIiIiIDMEAk4iIiIiIiAzBANNmeCsmERERERE5FQNMm+B7MImIiIiIyOkYYBIREREREZEhGGDaBF9TQkRERERETscA02Y4UpaIiIiIiJyKASYREREREREZggEmERERERERGYIBJhERERERERmCAabN8Fk/RERERETkVAwwbYLvwSQiIiIiIqdjgGkTfE0JERERERE5HQNMm+GFTCIiIiIicioGmERERERERGQIBphERERERERkCAaYREREREREZAjNAaYQIlUIsVII8YuZCSIiIiIiIiJn0nMF824AG81KCLnxYbJERERERORUmgJMIURXAGMAvG9ucoiIiIgomU1fvx+FZTVWJ8P2dhZVYOH2IquTYXvVdQ34dnk+JN8JGDdar2C+CuAhAK5QEwghbhVC5AghcgoLC41IW1JKlteU3DJxGT6cv9PqZBAREZGNVNU24NZPl+P6D5ZYnRTbO+PFubjmPe6nSJ6fuhn3f7Ma87YwPomXiAGmEOJCAAVSyuXhppNSviulHCalHNa+fXvDEkiJadamAjz5ywark0FEREQ20uC5ypR3qNLilFCiOFBWDQAoq663OCXJQ8sVzJEA/k8IkQvgKwBnCiE+MzVVRERERERE5DgRA0wp5cNSyq5Syu4ArgIwW0p5nekpIyIiIqKkxLvliJyL78EkIiIiIltIlmdRECWyND0TSynnAphrSkqIiIiIiIhMwKvi8cMrmERERERElJB4VTz+GGASEREREVFC4pXL+GOASURERERECY1XMuOHASYRERER2YrkZScix2KASURERES2IHiZiUzCPov4YYBJREREREQJiX0W8ccAk4iIiIhsgUNjiZyPASYZZuO+Ujz83Rq4XKwdiIiSxTvztuPXtfusTgYREdkEA0wyzF8/zsGXS/Owt6TK6qQQEVGcPPvbJvzj8xVWJ4MSBO/BJHI+BphERERERJSQOK4u/hhgkuF4/wQRERHFQjIsIHIsBphEREREZAuCz/wkgzFHxR8DTCIiIiIiIjIEA0yb4FAQIiIiIiJyOgaYNsOnpxERERERkVMxwLQZPiCHiIiIiMhYko3suGGAaRO8qZ2IiIjIjbEAkXMxwCTDcHgvEREREdmRYEM1bhhgEhERERERkSEYYJLhOKyFiIiIosGn6hM5HwNMm2CBSkRERERkDj7kJ34YYNpMIgwPT4RtICIiIiLn472X8ccAkwzHDiLj1DW4UF3XYHUyiIiI4opNCaL4q6lvQG29K+blMMC0GScHZ+wgMt417y1Gv0emWp0MIiIiIkpwfcdNxSnPzY55OQwwTdB97BT8+/u1uubhezBJzbLcw1YngYiIiMixeO+lPgVlNTEvgwGmSb5YstvqJFiGDywiIiKiaDAWILPwXsz4YYBJhuFVWCIiIiKyI17JjB8GmDaRCFf9EmEbiIiIiChx8Mpl/DHAtBmeA0RERERE5FQMMMkwHCJLREREhuCgKCLHYoBJREREREREhmCAaTOJcP9xImwDERERxR+bEETOxwDTJhJheCnvHyUiIiIiSm4MMMkwvHJJRERERJTcGGDaBF/xQURERERETscA02acPMzUyWknIiIi+2DHO5FzMcAkIiIiIiIiQzDAJMOxz5GIiIiI7IAD7OKPASYZhicwERERxULyiYFEjscA02bsVq6+MWcbuo+dgvoGV8RpbZZ0IiIiIkpybJ/GHwNMm7DrezBfn70NAFCrIcAkIiJ1+Ycr0X3sFMzZVGB1UoiIiEzFANMmEuFpafYMkYmIrLc6rwQA8M3yPItTQkREZC4GmDZjt1d9JELgS0RERM5it1uGiEg7BphkON6gT0RERER2YLNrN0mBASaFpefeUGG3y69ERDbB0SBE2vBMIXI+BpgUFhtFRERERESkFQNMm7Hr6FK7PuWWiMgJWIYSEVnDpk3rhMYAkzThlUwiIiIiIoqEAabNJMJtjAxFiYj8sZOOSB+eMWSUBGhaOw4DTNKEw7uIiGLHspSIiBIdA0wyDJtNRETh8UomUXh2fRYFEWnHAJMMx8qBiMgfr1wSEVGyYIBJRERkMl65JCKyFi+AxE/EAFMIkSWEWCqEWC2EWC+EeCIeCSPniseDikoq6zD86ZlYlVds/sqIiAzCK5lERPGVCA/QdBotVzBrAJwppRwMYAiA84QQJ5qaKrKNaHp74tFDtGTnQRSW1eD12dvMX1kY2wrKsXL3YUvTQETGq6ipx29r91mdDKKkJXm5KWZSSvy4ag9q611WJ8VSzErxFzHAlG7lno/pnv95qChYkvUQ1dQ3YPTL83DxmwutTgoRGWzcD+vw989XYN2eEkOXa4ehspW19eg+dgomLdttdVKIyERzNhfg7q9W4aUZm61Oii3wSmb8aLoHUwiRKoRYBaAAwAwp5RKVaW4VQuQIIXIKCwsNTiZZhSdjaFZfPSUi8+QfrgQAVNY2WJwS4xWW1QAA3piz3eKUkNIva/ZyRAwZqriyDgBQUFpjcUoo2WgKMKWUDVLKIQC6AhghhDhGZZp3pZTDpJTD2rdvb3AyySrRDSuwvoc+HrwFNxGRVrwHk0K584uVHBEDJEsTgizAobLxo+spslLKYgBzAJxnSmqIiIhshPeBEZFTsfhy42i8+NPyFNn2QohWnr+bADgbwCaT00U2o+++oeQ4k+1wLxURmcPoK412aujZKS1ERJR40jRM0wnAx0KIVLgD0q+llL+YmyxyNrZeiMjZ2IFERE7HK3dklYgBppRyDYDj4pCWpJYIPcosx4iI1NmpoWentBCFkgDNIrKJRGhjO42uezApefHkJKJkwofxEJHTse3mj51r8cMA0yYSKdOzQCOiRGFUcWanctFOaSEKxOHpxkugJmZMWPbFDwNMMoxIpCiZiIiIKAEke1zF5mn8McAkw8Tzcf7JXlgSUXwY1S6xUwPHTmkhIqLEwwCTNGFAR0TJiGUfETkd+5Qo3hhgkmHiOUSWhSURmcrgQsZO9/7YKS1EoTCfEjkXA0ybYEFKRJQE2DtGRGQJPkAqfhhgWqywrAa3fZqD8pp6APZ7NH40p6IEsGL3YVPvyWQRQYHW7SlBdV2D1cmwvfzDlThQWm11MpKXDQovu9+D+cqMLZi6bp/VybDM6rxi1De4rE5GSF/n5OH9P3aYtnx2uBM5HwNMi70+eyumrT+A39btB2Df3hW1YPGFaZtw2VsL8cacbVix+7AvNJ63uRCXvLkQHy/MjWsa442VoHXW5Bdj8/4y3+eC0mpc+L/5+Pd3ay1MlTOc8twcnPDMLKuTkXTsEtSVVNZh+voDVicjrP/O2orbP1sR9/X+b9ZWXP3uYgDAzqIK5OQeMnT5e4ursGBbUcTpLnpjAV6YttnQdRvpoclrMH7KRquTQaSb3S7iJLI0qxNA9hbuVHxjznYAQM6uwwCAozs0AwA8/au74vloYS5uHNkj7umixPd/ry8AAOROGAMAKPOMAFiVV2xVkojCskuH1J1frsAfWyMHOclg+vr9uPXT5fjjoTPQrU1TvDRji++3M16cC6CxjDHC6JfnobK2AbkTxmDIk9MxqEtLfHrLCarTrt9bath6iYjijVcwKaxY2kS7DlYalg47sssVCWpkkzY8JRDDA0OLy428Q43lcrKXYd+t2APAPbw+HiprG4fwF1fWMdAnooTFAJMME8+2ih0CCbtckSDL2+yUgBI1T6UookqWYfZl19tliJyM51X8MMAkTXhKElEyMa3Ms7gwTfarlkSUfFjsxR8DTHIkFhZERPrF833FTmHHDlQ+jISMYMe8TcmBAabNOLlSYbuFrGbmq3EouZhWnFlcTqYo1s8ym+yIpbgJkvxcZ56KPwaYZJh4tu1ZWJASr8oQacN7MIPZsfTgvWJkKGYnAM6+iOM0DDBtxq6VChsiRJSM7FomR4udMUTJg2c7WYUBJhkmnu0WFppERPqx7Axmxy4EXmkhI9gxb1sp0ToM7YwBJhElDFYdZLREa+inKGp9Xsy0LzaEyVBJfq4n+eZbggEmhWfTOs6mySKLsPIgsyRaQ5/3YAZj+UEJj+c6xRkDTNJGQ+GUaD39kbC8JkpcRl/ds0t5wXswye74NHAi52OAabBYC0bbBWk2S46XTZNFRBSW1WUXX1MSzI7hjO3aAuRszE4UZwwwDVZT79I1ve17k+1Y89qEzY9cUjKj49vlkqjVeV4ThWJkFnW5JD5fsgs19Q2a50mxe51DABJvaDYR6aOnXLcjBpgGmrpuP/o9MlXXPIFXPFmpaGOHvWSHNJCbmW3mR35chz7jfjNvBZQUjMqib8zZhsU7DgIAfl6zF//5fh3+N2ub5vlTbBZf7i+pRv7hyritb/3eElTX+TfcotklB0qrkXdIPd1l1XXYvL8siqXGR3FlLbYXlludDIqjVXnFVich4fywcg++XZ5vyrK3HihD33FT8fPqvaYsPx4YYBpo9qYDVifBNE4PfH9YuSdkY0ApJ/cQuo+dgoLSal3LH/vtGlz17qJok0c29vmS3VYngRyiuq4hKHjxMqoEfWHaZlz17mIAQGl1PQDgcGWt5vntNvTyxGdn4ZTn5sS8nAXbitB97BQcqgi9Lw5X1GLMa/PxwDerY17fCc/Mwqjn1dN9w4dLce6rvwMAFm4rwvJdh/x+/+/Mrb6/rbjfcMxr83HWS/Pivl6yzo7CCizcXmR1MvDyjC0448W5VifDEPdMWoX7DShL1KzfWwoAmLnRuXEFA0wD2a3iTmR69/Q9k1bhz28siDjdRwtzAQBLdh4KP2GAr5blYfEOffPY0dR1+/H4T+utTgYBeH7qJvywco/VySAd7f/jn5oRcRRLvGsJKSXu/molluU6v3wK5+152wEAa/eUhJymotYdkK/cXez3vdEh3grF8q95fwkufcu/8/GVmVt8f8/eVGDw2iPbU1wV93WS9fYW6+s4N8Nrs7ZiZ1GF1cmgOGCAaTHb34Opg9035WCYnm27i1cv9+2fLcdET5DtRE6/0q705tztuGfSKquTkbSi6TCsrLXfPTNlNfX4cdVe3PzRMquTEhfhysrAn+xQZ1WFuOKdzBKnFCdKXgwwDRRNZRVYGfIqqDasgIjITGZ1VpixVF3LTNAqxttZq2df8G0YlOj4yhd/3B3xwwCTNOFJaS3uf+uxoiZKTAkacxORRyKNFnQKBpgGiib/MtNHh3uNlHjln4xmVp5iTrUfdh1RomIb040dxPHHAJPIAVg0amNmHcL6KTkl2mFP1Oamb7t0HDC2vSnRMbDy55RzPhGeJ8EA01Cx51y7ZSq7pcfLDqliuU1EerHYMEd0z0AwPh1EduWQ2IoSBANM0sTJ9XAi9OAlwjY4HY8A2U00DUan9ODHk5W7hEV7MO4Tc3C3Okci3PbDAJPCsmsmt0Oq2FCzDx4LcgpmVXNpGXUTWF6w4U2Jivdg+nNK54VdRw/qwQDTZuwW0CVCJo+Glq12SkGVTMy9B5MHPJmwXeYsvJpLFExZbyVzdndqoO3MVLsxwDSQQ/OvJnZrXNsrNeZLtu0lInPYrRPTaOGqqsDf7FCt2SAJRGRTTi4fGGBSWInQGImmEeH8rSYiI9ghCKHI9FyhCJyU5T0R2UkitL0ZYBrI+dkhmJ4hsvEcgpCI+zocNnKtx0NAdsXyQZ+gK5nWJIOI4sRuo/AiSYTb0xhghvDYj+vw/h87rE6GbnUNLrhcxmTMmvqGmJdRVF6DWRsPaF5mXYMLl721EAu2FcW8bi1i2cb6BpeBKSEn0JtfXp6+GS9N3+z7XFvvclxFl+wS+daHeKhvcKHBoDpJi3CnV9CVSwOO7eq8Yt/fszYewNCnZijSEnm7WR6EZ0Q7JB7mbC5AQVm11cnw45R9l0waXBJ1OtqOdqt+auu1xxhJF2BKKTFjw4GIhfrHi3Zh/JSNmpc7e9MBQyrRwF6L12dvxU+r94adp6KmHvO3ugOy3v/5Dac8NzvmdHy/Mh99x01FXYM7PdsLK7CtoMz3u7LRHM71HyzFLR/noLquAQu3F6HvuKlYsuOg3zSb95cht6gCALD7UCVydh3Gte8vQW5RBVbnFWPa+v1B6zOiSp618QD6jpuKNfnFmudZm1+CfSVVAIBvlucbkAptEqE3yyqHK2qxdOch3fNNXeef73YdrETfcVPxTU6e5mW8Nnsb/jd7GwB3wdxn3G945lft5Uokuw5WYNP+0piW8dbc7fhuRfzystFKq+uwcLt5HVJWtf9/XbsPr8zYYvhyzQyYl+UewqGKWr/vjnl8Gk6eMEvzMhZtP6j6fUVNfdiOR+9mhTtc0RzLhduK8PhP60P+ftEbC3x/3/JxDg4GbH8i+XZ5Pt6Zt9309Sjru77jpuL7lfYvn276aBmueHuR1cnw8bZvflmzL6r5XS6Jhyav1tU+srN4jLBzuSRmhogvZm86gGd/24ibJy5D7//8pnmZdmv59Rn3Gx76do2maW0fYC7cXhRVgdZ97BSMVdkJXy3Lw98+ycGkZdobiZEs3FaEmyfm4CsDl+n14vQt+OeXK32fv8nJQ/exU/x6yu7/ejWu+2AJ9hS7A5+9JbH3ok1dt9/v8xXvLMLol3/HIz+sQ4NL+hrNSmqnrzdwbHBJX8NhSUBj/9xXf8fpL84F4N8AOP3FubjojQW47dPlquvTKtQJOndzIQBglaIHOpI/vT4fJz0bewBP8XP1e4txxTv6K/7bP/PPd1sPuDtYAs8Nrao9vclfLjWunDjthbk479U/YlrGc1M34b6vV6O4shbdx07Bp4t3GZS6+Pj7Z8txzXtLUFJZZ+hyjW6P6L1S9Y/PV+C/s7Yam4gAuw5W6moUdx87BfdOWgXA3fmZk+tfll/+9qKgc626zoUDpTWa17Foh3qAee+kVbj2/SXY66nnYuE9tloOyTXvL8HEhbkxrzMR3P/Najz726a4r3fGhgORJ7KB3IOVVifBx9u+mbelMKr5D1bU4uucfNw8cVlU80sp8eyvG7HlQFnkiRPExIW5+OsnOfhp9V7M3VyA7mOn+Lb/5ok5eGfejqiPhxGijae8vJ3ZkzVeXLF9gHnNe0uiLtDUAr59nuBrnwFBmJeRPZaRbuz92nP1JLeosSDb6rmyWFlTb1g6Qvl08S4sy1W/GqRWV/sqcoPTYXZfVKT0bi8sNzkF/jiKKrxwwcCm/cZUcLEeAt8VFpsezPzD7ob7l0t2W5wSfTZ7jm+twUPWbXqYDLc0RHkeyvcr9wBwd35ephKcbiswp2z0LreqzjnD/pIlD5mN+1E/q0c9FZXX4p3fd+Ca95ZYmo548nZ+FZTW+Dqil+86HNMyjWzrxhJPAdB9hd72AabRtAyj0cvqss/O7/dRpiyRKomSKmOvlpAx4hG8RbsG73maQKcB6WBGOR3NIm1cXcSk8apk6DMssNFt532RSPVlorNrp2Ega/K7M/aNWRySNTTRuy3JF2DauEJxunC71ugC2OxzNlI2SaRCg+KDRY+zsK5wGu0dOGa9AoB5huxMT7vF6iugZolX282ossDJRyHpAsxEZuhVWYMWZoerNqGC20QtQEldrJ0c3tljrTfYOZGc7HKVIxHerxYrb9lv9iGJZfEMVhvZ5NRJUsyIerFt6Za8AWYClVh2Pv3V0mZEeu28zRR/8RwmHv0QWe/8iVP2JAOjj5edb2mg2Bh5ZBOoiaKfw7bdjsdKLU3RFT3RbZxd67l4F7+x7gcn1xZJF2Amcu+tkYVcNIsKd+IaXQBbX3TFNwV2rMDsyOhXFPgvO9aKInHLHis57dywy5XMRKPnybDec5GxPhGZg4VL0gWYXolUxdulklSt2M14qpJy8TbZdkoeHCKbXBKtY8DuZWa0ydMynx3PPTumiahRdGdkopWbpF/SBZh6ejm1skuPtJFDEgy7B1O5TBOiTC3pjGatkeaJ9yG363ATJzFqD8a6HB5JY5kdMDl9iKxNqifNzExu4LJNvwczhhXYvSOAGtnxFLM6TXZtszitPHSypAswyTxhh8ga3UgzdGn6sYxKPoZVTMw8hjKrweCsHnhmqkZhXlPiySxOCN7YEG5k12AloSXYLrfqlE/m85gBJpnK9xRZzSeZtgmtfk1JvCVzIaVHuP0U81NkPf9Gmzec0khyRipJKycEU0pRD5HVMGNg3jZ630Rzddop5QIRadf4UL/klXQBpsPqWk28Pe12DELU6lsjK3UjlqW2CBvuSgojnsPUYx8iy9xFZIX439pA0XDafrPLbVKGMqydloitbnVO68zTTef2JV2A6ZVIjTxzMrX+/RN+iKw5NN2DacLK2VBxHrvsQ7u3RZxaRyZ85U6a2P38InIEw84je5yQ9khFcokYYAohugkh5gghNggh1gsh7jY7UTX1DahrcPl9V1FTb8iyzXjIj10YuU0zNxbonqeypiHoO7PafLEuN1J+YlvVmeoaXKipD86HgAGvKYl1iG0Cljl24vT9W13XgF/W7LU6GbYX6jhru2fW3EzCeqNRg0uiqla9LNbL7ue2HZNn2IMaEyxTx2t7Emy3RUXLFcx6APdLKQcAOBHAHUKIAWYmqu+4qTjjxbl+3w18bBp2FlX4PpdU1eHD+TtRXddYgDW4JIrKa8IuW3mPxLT1+/HsrxtRUFoddp7qugZc+tZCrMorBgAUltWgvKYeF72xAJv2l2rcKnUTF+b6ff55zV4cjLAN0ZJS4saPlmLWxgOorXdhT3EV3py7DS6XxNKdh7Bi92EUV9Zi5oYDYZdz1buLVb/foTg+aus+VFEXMY019a6QvxWWufdLSVUdqsNMF8mczQUY+Ng0zNygP4j2iibY2Ftchanr9muatrS6LmTlXFJZh+9W5Ps+v/f7Djzx83rd6UlEBytq0XfcVFPXUVbdmI+llPhy6W6/ckiN8rjHozEybf1+7C2uisOags3dXIBr3luMzxbvQn1D9OepV2FZTczBfW29C18s2Q2Xy72cg+U1fmkLd75FWnVxZS2W7zqMnNxDQb/9tnYf9pcE1y/VdQ24+t3FuOOLFb7vnvplA+78YiWWqSwnlGgeRKTWudbgkqiua8BHC3aipMo/f3+9LC9sh9zlby/UtN4pa/bh9k+X604vAHy0YGfY+kVJy7twdx2sREmlf31UqjivP1u8S1f6qusaUFJZh3pX6LVX1obeh6XVdRHLEK9F2w/iqncX+eXfgjJ3Hntlxha8PH2zxlQjaB+EkpN7COe+8rvm5QLAfV+vQv9Hg8vi6roGfLV0t22HlRaUVQelraq2wa/cdyprgkXjVlpb78Llby/E8l3ay8hAatmutLoOk5fnB/+gg/ccBIBKgzpWQjlcUYvaGNrAXmXVdfgmJ8+AFKmLGGBKKfdJKVd4/i4DsBFAF9NS5JF/OLhx9L2iUf2vyWvw5C8b0P/RqSgsq8HHC3Px3NRNGDZ+JgY9Ni3i8ncWVeC2T5fjnd934Nr3lwAAPl+yC/tK/Nf7y5q9eGPONizfdRiP/rgOuw5WYPjTM3HMY9OwOq8Yz/22KeQ63pm33deg0eqPrUUYOn4mnpvqv9zp6/fjH58vx7Lcw7qWp/Tjqr2Yu7kQt3ycg7u+XIGRE2bj+amb8e2KfFzxziJc8uZCDHlyBv76SU7U6wh02FOBSQBfLt0NwD/Izz9c6Tf9Xz5YGnJZw5+eicd+XIfBT0zHP79c6VlW5DT8vNr/qsDCbUUAgP1hOhZeilBJXxkiyFZ6/Kf1ePCb1b7Pl7y5ELd/thxf5+Rh0GPTwjYojn18Oka/PM/3WVnh3fv1Ktz39WpsKygDADz960Z8tCA35LKklDj75Xn4YeWeiGlWs25PCaau2xfVvNGQUuKjBTtVO4uKK2sxbPwMlXk0LNeg0E55Dk5dtx8Pf7cWL8/YEnae2z9bjp88+dDMhlX+4UpU1tbjtk+X4/9enx/TsqSUOOcV/fnmtk+XY+H2gxj3w7qgDjTlsrcVlEdcVm6Ru7x9748dEadVlgXec8PrnXnb8e/v12Ly8nyU19Rj6PiZeOqXDb7fj318Ovo/OhV/bC0MWt4TP6/Hic/MChkgDHlyBi59ayEue3uR3/f1DS78/fMVuPLdRUHzvDR9MxbtOIgpaxrPqz2eDgGzG7IrdhcHfffi9M0Y9Pg0PPHzBjygKLOW7DyEh75dg8d/Ct2BpVYnfb8yH+e8Ms/vuzu+WIGp67V1sAV64ufGYxWqzNf7kJ8ZG/07Uo99fLrv73E/rFOdf86mAox6fnbQKInL3l6IwU9OD5peeaoPeDR0u+TYx6fj7ID9FbTuzQUYOWE2/v75cizecQgb9rk7txduK8KIp2dh6rr9+O+srXht9rawy1FSS7OahyavweYDZUHf9/7Pr+j3yG/YXth4LlfXNSDvUCV+XKV+NX7Cb5sw9ru1mL2pwFfWa+1Uv+TNBfh0Ua6mabU6UFrt61TZWVSBEU/Pwvt/7ATgHhGTW1SBU56bjUGP+++rJTsO4o+thcg7VIkhT2jbj4Gmr9+P1Z4LF2q2HijDkCen40CEiyBaRVP1FJbVYOSE4DxvlPKaepzwzEws3Rk5aNxRVI5luYfx0OQ1eGvuds2dMkD4MPdfk9fggW9WY92eEs3LU5q54QBGPD0L73nyzasztzb+aEJ9f9xTM3CnonMyWg9/txYPTl7jlwe9F3IAd8fj2/O2q9Z9WtqEuu7BFEJ0B3AcgCUqv90qhMgRQuQUFhYGzWsEZcHpDQ6kBO78YgUe+2k93v3d3Qgp0zCcNvdgY2CztaAcReU1+M/363DDh/4Bzp1frMT/FOsNDHzDPTXu2d82YebG8FcDQ3lr7na/z7d+uhy/rg1fOUdqQN8zaZXv72nrG9NVVm3M8ONwQp1jpzw3x+/zwYrasMv5eJF/z7KWc/d+RYNJK2X+iNbEhbn4RtEr5s2zD01eg7Ka+ojp2hPiCpT3ikh1nfYerK0F5X7HX48L/zcft38We2Gm1eYDZXji5w24+6uVQb8t3XkIReXh80g8ecuagxrS9PB3awGYewXzlOfm4MYPlwGAIftpy4Ho8w0AFIe4QvL5kt0Y/fI8LNlxMOz8eZ4OqN+3FGle5/T1+zH65d/9Opa8HV2l1XUo95R3asHO01M2+v72li3bCyuwv7QaWw9EDoiVvMdZrbM0XDln9OtRtJSRMzccQF2De8ICRQPD27CINDIo0L2TVmOLzv1lJJdLote/fw0KRmJt6z3y4zrkHapCQan//li3J7aRTACQdyj8iIMnflqPPcVVvnPqNs/V4LWeRvGK3dF3PkerrkGius6FL5fs9n33t09yMOr5OSHn8eb98pp6bNznLusjlTHew7ZidzEe+dHY0TonPDMLp73gTu/uQ57yxtPRNP6XDTj9xbmq5+uV7y7G9R8sxY+r9qAiyitWt366HBe9sSDk7xMX5qK4sg7TI4wqM9ue4irsKzYmyA20bk8JDpTW4EUdV963F1bguamb8GZAOzla3jJPT8CqpHbumX212Ig84d3uKsV23/F5Y1vv17X7MOG3TXh+avCxUeuoDKQ5wBRCNAPwLYB7pJRBpamU8l0p5TAp5bD27dtrXWzUlPVEqEZM2PkDahrvlcbDYZYlZXAvSKQ8FMtQznCU6VcLcu02/MRu6bGD3zdr74iJZe85bdfX1bsTrByqZwQz9oMd77NYqmOIpRrvbjIz33h7THMPahv2qMcWz5UW5e0Ltnuom82Sk0j3WUkJ1LlcaHBJPPXLRv/fFDveLnVStMk4XGmfjjalP7aG7wxS7nfvszaMLuv1CtWGXLg9fAcYEN2raXSLKpMEz6MnqYFz606BKfWt/wYY9WwWM8uCaJccl+JJZR3KcsUbeJZHuZ81BZhCiHS4g8vPpZTfRbUmE9mu8WARZYa0Sd3po3OksKnssm/inQynNSLtcpy00FMGOWm77MKKMt5p54sdxTOIa3zvXOh1xv/p3zzZwwm1d1hGxi72h9oZkw5yFr96L8Y8oOUpsgLABwA2Silfjm111gvVaIh2P1rVCInUa2a3ssGsijZZGoGxFPZ2ywtOpXYM4tJ7HWfeLTIi38R63scyXNRpDaSYzvEYt9XoYbl2EZj//Dph45wWs8RlOwx9d7V985pdrmrbQfC5o3Pf2PXCrgo75knLYgsDD5yWK5gjAVwP4EwhxCrP/xcYloJoRZmzvDsv6oxpv3yoym4FpVlXMG22mZSsEigfxnNT4h3YRGpIhPs9bvvF6F2iIeFmNWYS4R3EBEMzv9/tPcYt1hRaNtvMQMDKuCfwPLPDEFmzmNFejjnWiCPN2UzntqRFXJ6U8/Ws3+kibWhwg8j6XaOWArvlab1P0zWTXVKiq1CL6eqGXbZYG7s2dtWuxll/9pvHafnGbvTuPi2TO+2YWNFZEW4XxXvIqqanW0eZJDtddY62zNa66Q7L9qSDnmMbmM/scuHRjOxpVZ43cp/qeoqsncS6742qaISwvvBTyxBWpymQ3dJD9uXEvOLAJIdk5BDZRBJtveu0oNDuQjaAhPJP9YmcdChsldYYGp2Jnv/tFOgbKeghPzY8jHZMU0KJMWs7N8CMttcvxh1mlx4TNf73l9jrzHOZVBIYcjzsfFA9Yjme9soJ5ojHezDV78GMaZEJL9RxMTJParvyF5/1+E9v/JnntAZVNMFF3DbRYfvSqUJlATve9xaNuDxENpp5Yn7IT8zPkQUQef/YKRsYmZaEiDXMfshPojLs5uCI6zG/FnPEFUyzlhvFgoPLTWt2VtyfIhvn9UXLFgWrTonUS+/dEjttkr5hVPbOQJFvw9CxLA0Tawl0/faZYmfHPqw8mpli7Agyb9G++Y08N0ItSm82tmuuD/2k2ND3YlrdQW73MiQejMrjRp4rRuQTM8sH9WVGt1A71b9eepOUEAGmrsaHd54olhEqM1tdGDqBWVcwKTKn7nqj023KezB9r0YgM2hp59m1KRju6q3aT1oaImblMy370O6dKJq2IVQdrnPTWJ/5C/twLEP2lX33t13LH6M5Pss79ECZ2dmh+lwJA9eXEAFmPAU94semmTZOz4/Rvg7Hl07W4u6zp0S8/6axEy72TBdxCQbsPiNPDTscTcuvnijWH+LCpmZRzaN/loB1SsMCyVDiEWAmSpmfIJthCaPrl5he+2RgOhKNmeeqHdrO0eYaxwaYygoknvVxYOVvpwamcp/Y7aqq8iGyVo9zt9u+0UvvNjt1e/Vsp5ZtjL3hGt1vTmPHIbLkZlZjQ9tQW/3ieR+qlsBc+v2trw2h3PdWXMEMXKPV/RBaObkc0XK+2fU4qJ17es7HeB23uOWPOOfDWB+WFypfWRFwRrtG5waYUv3vSHxD2pxc6gVQezy7riuYcdgXygo5gXZ93Bixyyy/MqKTE/KJw3ZpQtJ1z6JpqQgWMhCKYxoAI++liuJ+J4vPYaPX7z3ftb51K5b126lsiSUpoYIaIURCtcMSTeBxs+rBmuFEk6ZwyYn+dTvx60gzg7JtaOThsiTArKytR2VtvRWrbgzGop3fgPfwlFTWob7BhboGV5SpiJwG5fb9sbUQBaXVhqwrWi7FppZW1Rm2XO9J2OCSKK6s9f0LACVVdar7eHJOfsjlGXVylSi2saSyTrUi1VOA7DpYgZzcQ2GnkVLix1V7grY50noOltdoT4hiHuU2Vdc14P6vV6MoimWZQe3Ye9NbXFmLeoPOPd+yVb57fuomTfPuKa7Cou0HY0+DQTWS8CzrUEVtxGkXbi/C3uIqQ9YbTvh3G+r7Xis7dsiEfmCKtvlr69Xz/fq9pb6/V+cV61q3XlsOlIX9PdK2qB2Wg+U1mLu5IOQ83rrBv8xq3BdW3oMZ6rz1fr2vpAq/rNkb/IAT6f9vOPUNLhyuqMXqvGJsKwi//wNV1zWgoqZB1zxKP67cq/p9TV0DflmzL+rl6lVb70JptbtellKq1nvRHFUjR7HlFlVg+S53Pe9ySRz2tGW8xziaulpJT1oD85VZI6H0FLOhpi0sq8HvWwpjTks8g7pw9WtpdR1mbDgAILge0prGfSVVWLitSHe61Pax72qszh1kWoC5ZMdBuFwSv28pxLT1+1FT34AXpm1CVW0DBjw6DQMenYYnfl7vN4+U/hWAdwcr1da7Ija0lbqPnYLxv2xA/uFK7D5Y6ft+R2GF6vQFZTWYFyajRpMBH/5uDUa/PA8lVXVwuSQGPzkdD327Bv/8cmXY+fZobLityS9RSWdjQq//YClGPDMr5Pw/r1avAIykLJze+X2H6jRrVbYjkpkbD2B/STVu/2w5hjw5Aw9OXo0hT87ARwt2YvAT03HnFyv8pv/H58tRVuPfuXGowl3pfLl0NzYoGloAUF5Tj+5jp+Cytxbi5embNadr8BPTG/9+cjqGPx16/2tx8ZsLcdnbi8JOM3Xdftz91Sq8MWeb3/cPTV7j9/l/s7biT/+bj9yiCvzj8+UYOn4mVu4+HDENJZV1OOaxaXj8p/UYOn4mPluy25fPvl+5B9+uyMeL00Lvo1gCoMCyIfh3/8+Dn5iOu7/yP78k3I2lIU/OwNH/+Q3jflgbtJzVecU47YU52F8S3CGjJ/VzNxfgzbnbQ/5+3qu/o/vYKfht7T6c+eJcXP3eYgDAit2HUV3XgOW7Go/HoMemYeq6/Rj46FQsC1H2vfv7dkxdt1/1t+2F5egz7je/8g8AznxxrmoHzIZ9pRjz2nycPGF20G/P/rYRN3601Pf5mveW4OyX5/lNE2o/7T5YifzDlVidV6ypg7G23uXbD1rKwnHfr/M739+aux1f5+SFnP5AqXpjTUqJ12ZtRWGZ/++vzNiCwxqCbgCYueGAr8yTABbvOBiy7rjnq5VYtL3x9xs+XIovl+4Omu7PbyzA2yHy1K5DFeg+dgq6j52CtfklKKmqwynPzcbk5Y2daRLAbZ/maEr/9R8sgZQSMzc2Bm0HDOqkPOeV38P+HtiQ3RoQkEoJnP/fP/Dh/J2+7/7y4VKUVbvz1N1frcLXnk7EepfE3M0FGPLkDDz20zq/JT/2U2P7Q0vjeU9xle8YnffqHxGn1+rBgPLZa9GOg5BS4qRnZ+POL1Zi1yH/87eqrgH/9/p8POfpyNquaNN4y8vPFu/CWS+5y5fjnpqBi95YgNEv++//H1buwfUfLMHlby9EQVk1thWUobiyFsc8Ng3Lcg/hrJfmYX+EY7+jsAIfKI6H0kPfurcvt6gC+0oaz+Mnf94Qcp6g4Cbg89Kd7nLw4e/W4p9frsScTQXuc05Kz7nUOEN5TT1emLYJf/lwCY593F0vPzR5DYaOn4mbFGWZMp8VlFbjvzO3+u3TUPT2Q630lPFKLs8l8dNfnItL33LX86/O3OIXgK/KK8bQ8TPxw8o9qsstra7DB/N3YnthOQD9o9henbnF10EspQzqRJm6bj/entdY/uwsqsD7fzS25T5UrDuUX9aEbmsWldXgtVlbg+r5+gYX7p20Kmzb4op3FuEvHy5FQVm1L/1SStz+6XI89uM6vDV3O/I9dUjgbtlWUIai8uByfdKy3UFt0kjtED2Of2oGuo+dgu2F5Xh5+mZc42kDHCitxkWvL8Bvnvr8+5V7UFMfuYNnW0EZ+oz7DXmecuK8V//ANe+7y/E3525TrUOX5brrV2/7Y1nuITQohmd4yxaJ4PbbjsJyvzJYTVrEVEehvLoeV767GGPP74cJv7kT+MiFA/DGnO1IVZyNHy3IxWN/Guj7/MA3a/DtisYKcfyUDUHLfubXjZi4MBepKdrP6vfn78T7nh0xbkx/1Wn+/MYC3983fLhUdRopg38TIvKJ/OVSdyPnmvcW48c7RgJwF+qRhtmMVGngKVXW1mP6+uAgHNDXGF4dRWCnl0vDBaMPF4TPrKGc+Gxj8PbdCnfh+8TP7rwzLWD//Lo2uBH+yswtuHt0bzz8XXDAsXm/u9LJ2XUYOYpGv17xuLJ30NP4DWw4/6ToQKioqcdLM7YAcFdmXpv2l+G4I1uHXf6KvMMor6nHxIW5AIBHfliHRduL8Oa1QyOmbcmOg7jy3cX49u8nY+hR4dej5tr3l2Dh9oN49/rI6/IKPNbHPj4dV4/o5vv82eLdGP/nQXC5JCYuzMU1JxyJizzlwJjXghuQ4QNc/99u/GhZ2LRt8uSrv3/eGBDlH67EJW8uxLCjWvvltbKaetz+2XIAwJtztuGjm0YELe+ZX0NfLZ28PB+19S78vGYv7jjjaN/3O4oqQjZWNuwrVf3+nXnBnUMVtf6Vn/IqmXK3nPrCnJBpVOMt6wFgd0DjWslbE0xd7z7e/Tu18P320OQ1uGJYN5W5QluVV4yXPeeI0rwthXjkx3V4/ZrjIy4jZ9dhnHx0WwDufXDVu4v9flfmlx9W7cUPq/wbXmpl0aq8YqwKcXVx8Y7Gjoc/vT4fAzu3QP7hKjw0eTVyxp0NwN3QnrNZWy//H1uLMGlZHr5Y0hjonvKcvuMHxH5FYFtBmWqjdeO+Ujz5ywbcfEoPAMEdxo/8sM73t/dc/GXNPlx8XFfV9dz5RfjOXsDdmaK109cr1pFafcdN9f2tti+VncszNzbWdT0e/hWn922PuZ7jHS5QumfSKt/fIyfMRl2DxIc3DkN5TT0uj9CpqVz3zI0HcN2JR4acxlvfXHhsJwAI6ujV44p3FmHSrSf6OmK8ddzzlx2LhyavwX+vGoKLhnQBALw0fTM+WpDrm3dfSRW+8XS8KM+Hs1/5HR/dNByAu3z2ltFGOlBajYvfXIj/G9wZr119nO/7BduLMKp3e79pA9suGz1l8qLtB/Hn47oELfua9xZj3Z5SvDYrHasfOydiWrYcKMPD363FJzePwPq9pXh15laszivGoK6t8NqsrUHTvzrT/d3Fx3VBxxZZuOKdRSgsq8E1JxyJzLRUPPnLBjSfmYa1j58bcp3hzrMdRRV4ecYWtGqajilr9uGTW0YgMy0VU9buw/eeeurEnm1V591Z5M7fI56ehe//cTKe+mUDVuwujrgPAPh1uCg7C/71rbsMzp0wxvfdKzO24LXZ27DpqfOQlZ4adrkfL9oFIHIZ+O3yfL/O6BNULgYVlNagW5um7uWFWM7XOe56/te1+3Dbab18o+jyDlXh+amb8fPq0KMFGlwSq/OKg853b5ty8vJ8TF6e7xd3zdxY4NcBqcaUANPbK75DUTF4I/CaMEPTlMEloD4MZdN+90nWoPUmCI0i9dB5VQX0POkZcqAchiS0RKYR3PjhMixVXNFQLs1utzY49UEzifbsNKO3JjCIC5Xvft/qrsgXbS/SHGAqF7XQgCGkQGNnj9KUtfvw5C8b/IZ6HtR4pcrIYZSlVe4GVywdGXrVG1yOGilwNEEoRm6BEOHrFuWwynAkpKVlsLeuiSV/fhei88Fsyv3mHV2iFNspF/1BCdfJEUptjEPxY5l/rsbOBKW6BosybRQH9UBZcKftroPuQCNPcawCrxZ6y1krlHuC6nV7/Dv11crhwDZTpD20bo/7nK/QGLg/++tGLN91GEt2HvQFS1V1DarBpV+6PMkqrw5ej9Z1qy3P69Ef3SMLth4oxzFdWvp3WGo4fxfvOKQ5uNTrk8XuoLGytiFigKmVUVVwqA7wBs/3kTq7ClTOp6Bl6Uxs3O/BjGUMeKjvnMTI5C8NGC7nl8Fstp+cftwovEhntZ2Pv7fgLYlwb3C4TTBi88y65c/OT7+1312OZKRYOxaNflqr1fmdopMohy2e+S/SqhJln9pCDDtTbxkZaYhu0HNi9CbIQHELMEPtEz33VdmS3ldGyKhm081uVwz5YmrzefdwqEBFwFkNej1pjSV3xfKQBiftTzV2KyfMJkSctlnGpwFn1/zX+LT22JZjZCezABvVdpBoxyDeDwMzpfzSsUjfua18LZ7aQwxjTZPaugNKPKueQmxo2yROmxBpV5mxL00JMMMlM/BcDN+7HvxjpCemRmL1kwHNbNzYeYgsBYs1L0T1iG67tkhVxDsLx7Q+nm+qki2AtRvvE4GjYtGh86/HjB1qHO960an1cLSdbnbcXrPTpOs1SdG+BkNKzfPGUsdb8V53J7VJvIzMUlouvij3kd51W7l/LX8Ppt5hZ3YrwPQODfRdwTT5oHszrV3eM2WPVOhn5u6zyaExlCMDilgq5DgX3rF0kDmxIncqCfuUvVaKdQ+o3fLDfOxsWg6flnzjxPMrHkk2O0hUHVVg4nrsdJTN2LNG5YmYR4sYkww/cRwi605+8Luc4jtENqYXBocc5hvDQk3iTZJd0havykDt4cLxbpDEa1vDDYWNt0Ro9EU8bOFGWxhQPFuxD60uH8IFzEZ2Vug5J404DpHWZ5NiObyYroS4RVMWKmdR692PJc86MShxEi27N+4jU8y+ghnNeRLDuRXL9phRxygDWmV5btWpZkk9Gu43g+uCSPs1VAeDFZ3/cb8HM2iIbJh5nHDfnt4rCo33YBp/Fvg948dmvT/xOpRWD4EGtG9rrLtE7z414MHFERmx/GgOYSwNxxTPCqMpgK0YUmQWU04duxRAGhm5D+yw6TYoDnVTnocuaWyzKHBZZu8fO+SBeDKrERvTO5QD0uSUUTaBm2xEXaO2G/UuV/U2tZg6fWKYN/pZY2JkR5W2IbKxPCdC27xmtA3jF2B6/g2+STfyPHam97CbW7gpbrr2vuTbJkF6vN6GYHR7IZpkW9YxomG99sgN4cV79/nyTIT1hjt3DQmsTQpWtZY5NikqEkK4fRn3ERXxXZ2h61abP9r9J4QIecsKGcOO+9PsNKXoypDx20FWHwsz2rpO7DCLRO9xCrVfIw7AsiA/mBpgqjWYgq9gGtdo05L5rM6gvm0yIR1++8tmVzDjxQ7bqzkNMSY25BBZGxfCdrjCHEo0h8PGm6OJ0eeLXTq0Qonn4XLSLRVG857nUW2r30gcY3eWU65eOZUTRp0ZzUkdRqHSGntHUOglRNo9odOkocM8ioQbUaZY2Y4xIy7yLFlvUiKywWtKws6lcdnq93fGQ6SDFzw8Iz6S9R5MO9A+RDa2fWJV4arGyKtv8X9wjrbp7Pw+SbsIukJkTTJiZMBQNANSYQSnD+F2uVTyVCw71y4HJkHZcffqSpPpGxDl03mjn9UyrBO10TRENg7pcPgQWf1BoP5IPfLSrT5HzQyG/S5g+q5g2uMsj9cQWTXxPuZae3Gjfp9btEPEIEzPDYbeL6VjBxmx3miC73jnrVjW57Rgw8kPiZAS9mxtx1uM+8DwK+wBn02/B9OpreyoX6dhzurUFmuXXavzKRwmpUJB5T2VZlB75ocpy1cs2y41WOB5HdM9wgbtu0hvqIi0HjNyS/xfUxKw9fG+BzOWS9uq94MYsIxoqL7YVnnC++7BNGiFMYpXoOvYCl2HkKMB4psMf3Yp+aPQ+OLo8ML97tSnyBpdQOhdmhGbrOWct1OpEI+HbSlZWSRGc14o51DrrIvlPIn3PZiOrY6iTbdhjWXjdpwdj4EZbzOwihUjscKJPCQ33BTh5zZjaGwiDyu3fIhsuJ2rd8dbEVxE/RRZU+7BlIq/jV9+LOyWHq2iG4aqcTr9i9a03nBXqpx0HIwqzCMtJpYre06/B9NoTujgCfsAHr3XI0IsTHr+07t+vSLmP4vyZ+NrSvTPG1iPBd1mYv8s5pNs5UM8R0zZZXSWWQc56Gq7KWvRT2s64nF0oskD9Q2usEs0WqTySsvoPmUWc1L5lxavFW0vLAcA5BZV+H1/08RleO/6YWjZND1onuLKuqDv6lWOxvZC9zLN3u8b95Wqfh9uvd+t2KN9Yh3UGt/KRb8wbTNG9GiDPw/pYswKY/TRgp0Rp5m9qSDm9aidrFpO4NNfmKP6/ZYDZbrW/8gP67Box0Fd8+ghpcT6ve58uHFfKQZ2bhE0TUFZNb5fmY+Lj+sa9Nv6vSWa1rN05yGUVtVh9ICOEafdW1wV9vefVu/FnoBp7pu0CuU19Xj3L8Owt7gKJ0+YjbbZGVj48Jm+aTbuK8VHC3YiMy3V913g8dhbXIUjWmThk4W5qus+79XfwxbIgx6bhrtH9wYANETIKA9/t9b3d96hSox6fg6uHnEkAKCgrAbfLs9Hj/bZ+GzRrrDLCUVLxf3H1iIcqqhFdV0DjmiRpW3Bis3aX1Lt99Pq/Mb8kH84/HFUmr5+P3p1aOb7XF3XgPzDlejeNtt/1Z6dv62gXHU5+0qqMH9rEZplpWH5rsO4eWR3vDJzK3q1zw6atqSyzq+eqKlvwO6DlZo6IgpKa3x/b9jbWI5/vzIfw45qE3F+NSt3H8ahilrd8+06WIGN+7WXKz+v3oua+uBG0ccLc/HYT+vDzltb78Kni6PLj+FU1NSH/d1bT6/fq15ndh87BU3SU/Gv8/r6vrvt0xxcMKiT33Tv/L4dK3cXh1zPDyv3oEUTbc0YgeAGaV3YxmbscnIPm7p8s+RHKNNDCVXWRipbV+UV+/7OO1SJ0mr/tp/eRvUPq/Ziy4Fy/LR6L87WUIfpsSqvGBPDtGcWbivCz2v24dlLBgX9ZmRw4C5z1Y/T/K1FwW1PDWnREiuvyitGRlqKr0z6efVeDD2qNQD3ce4+dgqm3jMKzbPcZXVBWU3IZTW4JGZvOhB5pb4EBn+1fNch7fMDeHrKRhzTpSX6d2qh2r7rM+43XHq8f7vZ5ZL4dPEu1NQ1qC4ztuPaOHNgvvfasLcUR7TIghACG/Y11tk/r96L7m2z8crMLSHrorfmbdeWChMCKGFGj3OHngNk0ytewJXDumFSTl7E6R8+vx9uO60Xuo+dYnhaAmWkpqDW5EpFiybpqagKkVmj9eXfTsTV7y32++6WU3rgg/mRgzsKljthjKl5MkUAO54do/pbqPVeMOgI/Lp2v+9zz3bZ2BHQaeO15vFzkJ6Sgv6PTo2Yli6tmuDkXm3xzfJ8v+83PXUe+j0Sef7nLzsWD01e4/t826k98c7vO4Kme/DcvrjuxKMw+InpAICrhnfDV8say4grhnVFn47NMX7KxojrtAMjy5MrhnXF1zn5kSf0eOva4/H3z1eEnabfEc2xyRPMDOnWyq8hp8eo3u3wx9Yi3fMdd2SrsAFCNN669nicP6gT7pu0Ct+tDG5EPXReXzw/dbPvs7IM7NOxGbYc8A92A8+pcNTmV3Pjyd1x91m9cdxTMzQtN5KmGamorDW2vohkRI82WLpTX+PNCNHmtUjaZmfglSuH4C8fLjV82eSmpc035thOmLJmX9D3uRPcdaFa3Xdan/aYeNNw9Hj4V993r1w5GPdOWu033R1n9MIbc8I3qKfeMwrnvfqH6m8f3TgcN01cFnLegZ1bhOw0CfSXk47CJ4t2+bYLAK57fwnmbytCr/bZmHX/6b5t/eim4Tijbwff59wJYzD65Xl+HXMvXHYsHpy8Bpcc3wUvXzEEf/skBzM26AjOAIwZ1AlT1u7D3AdOx2M/rce8LYX46MbhyEhLwbXvL8HJvdpi4Xb9HeTZGamoUJRPlw/tirtH98Ypz7k77j+4YRhu+TjHb55I9dHFx3XB9yv3YNyY/r72wBd/OwHXvLfEN01aigi66OTd75Ec0SIL+0v9O1y//fvJuPSthX7fhWoH/vHQGRj1vHv7/npKD7wfop09onsbfH37SZraku2aZaCoXH+npRadW2Zhr6eDee3j56B5Vrpfmt645njc8UX49oSaXc9duFxKOUztN1OGyHp7q+w4PMQOwWU8Mbi0r2i6dgIbwqGCSwA4UFKtKbgEgD3FVUHBJQA89mP4KyRegae6WnDppezNVgaXgLvH3ynBpdH0BJcAUB7hKhIAX3AJIOrgEkDUDX6jg0sA+HHVXgDAYo0jBZRloJbgMJxY549WvINLK+0LuMpuJAeNLnMkLRcUrBbLNRWtwSUA1SBn/rboO04CR2osjGJZU9a6A/u1e7SNZNKqIqB8CmxL/Lx6b9A8keqj7z2dh+GugKqNaNQSXAIICi7dtGeOjxbkappuaa72TjqzgstAC7YF151mDDmP/0N+CIA5B9M29ySQLew1oKG2IcSwcNPYsFOK7MWOHZdqHF8aW7QBZt7H64R7hEldvB/QZFu+53g459kBsRwqnrPOxQAzkfA8JKIkYefijo2i6Jm553hUbIAHIarg0CH9aj5Gv34jPmJ4T6nNRXxKvgkbwQDTIqa8N8j4RZKJ2AYN5rhKlGdd3DnmCqbTT3CL9rNZu024n/JDDiQRfOicfnpFErfyIw6vTTJs+Ql+zBMNA8wEksjv0yH94tk+NOP9UERqvK8SsXNxZ+Ok2Z6Z9Rg7hBJbLK+cApyRP4xIYaz7SS/779XEF6lYNeMYMcC0CE84MpsTYz4GqpQI3O9vpGjYueOArKPlip4TAsRoBVaNyVJTyhB/k/0xwEwgrJhJKZ69lHrW5PihgzaR7HsxkRuTyczUK5jMMkmPeSA+lPvZqDqfx848ZrTLGGBaxYQThUNkScmIi4HxbsQnS68sxcABmURCsjEUJTP3G4+JM0kZXBMl66E0LFgzZCnmr8svULXpUXdCuWLFvmOAmUAckMeJOAzWIMm6F73b7YRKneyFWYbiTS0gjKbsNrLaDLUsu1fNLPOdhQGmRUx5DybPPlKwa3YIl0/tXsEFsnIf2/TwWi7eD7BQ474Hk0coGuaNxBGsIx0s+D2YzjiWJmZnW/Mr/2LYB8rl2PWIO6Gst+J0sUWAaf9DYzyHlI3kYPEs9LQGhk4LIMm+7FyE2jltdmfqEFnzFk02YIfOpUBqeS6mIaMxzKsmHnvMqLaIUzoVnIjvwaSweO6R09mxgUD24pgh1iyPo8KH/JAaLUGKHa8kRRsUBc4VWDfGUgrGJahMone9O6/dEp89aUqA6c1YWtsByVjom7HJriTcj0SUXCLdg2mHRmYy1mlGMbce44Gh+FLLcU4LR2IVS3noN69NT1871DmRREqhGdtgiyuYlbX12H2w0upkxFWDCbXozA0HDF9mMqutd5m+Dm/vpsuE/GDHRm6kNDnl4pQdcLiQMczajU4/OnsOV1m0ZqfvOQon2oZs0D2YBqQlHhpc0tCyWkpg0/7SmLa/rLoe+Ycb29xmBBeb9pf5/jaqvatMc7wY0TazW13tkkBJVZ3p6xFmbHhmp96y0w2v4vS+7TF3c6HhyydKJF1bN0G+ZY05Y/zngv54+teNmqadfPtJuOztRSanKD7SUgTqOXSAAozo0QZXDe+G+75ebXVSSOHCYzvhlzX7rE4GqcidMAbFlbUY8uSMoN/6d2qBjftKDVnPsKNaI2fXYdXf7j6rN/47a6sh6wk0un9HzNzovgjQu0Mz3HxKDzz83VoAwBl922PMsZ3xwDfu8uLJiwZi4oJc7CiqMCUtoYw8ui0WbDsY13VG0r55JgrLauKyriuHdcOknLy4rCvehAjfmXrV8G74apn+bd/13IXLpZTDVNdpZoBJRMmhZ/ts7CiMb2VoB6kpwpTRCEREySR3whgc+/g0lFbXW50U0/Xp2AxbDpRbnYwgdgwwyd7CBZi2GCJLRM5WU2f+cGI7stvQFyIip0qG4BKw5+0rREZjgElEFCW2E4iIiIj8McAkIooSe6KJiEgPuz7Mznmv2yA7Y4BJRDHjUFEiIiIiAhhgEhERERERkUEYYBJRzHj9koiIKDIORaVkwACTiIiIiCgOJLtkKQkwwCSimPEWTCIiIuey68OHyJkYYBJRzNgjS0REFBmHyFIyYIBJREREREREhmCASURERERERIZggElEMeM9mEREREQEaAgwhRAfCiEKhBDr4pEgIiIiIiIiciYtVzAnAjjP5HQQkYO5eAWTiIiitH5vidVJiJvNB8qsToKq/MNVVieBEkjEAFNK+TuAQ3FICxE5VFF5jdVJICIihxrz2nyrk5D0dhZVWJ0ESiCG3YMphLhVCJEjhMgxaplERERERETkHIYFmFLKd6WUw6SUw4xaJhERERE5x6l92mP2/adZnQwishCfIktEREREhpBSIkUIq5NBRBZigElEREREhmF8SZTctLym5EsAiwD0FULkCyFuMT9ZREREROREvIJJlNzSIk0gpbw6HgkhIiIiIiIiZ+MQWSIiIiIyTEoKr2ASJTMGmERERERkGIaXRMmNASYRERERGUJK3oNJlOwYYBIRERGRYRhfEiU3BphEREREZBgGmETJjQEmERERERlCQkLwLkyipMYAk4iIiIgMw4fIEiU3BphEREREZBjBMbJESY0BJhEREREZwv0UWatTQURWYoBJSemq4d2sTgIREVHCufHk7miSkWp1MojIQrYNMP9zQX9N01134pFY98S5WDD2THxwwzBMu+dUbH/mAmx7+nw0y0wDALxz/VB88dcTAAD9jmiOG046Sldatj19PrY/c4HfdxcMOiLsPO//ZVjY33c+e0HIad6+7nhd6dNr+zMX4KIhnUP+3q1NE9/fKx45Gzufde9Ppb+e0iPieu44o1fQdxufPA/3ju7j993m8ef5fT66QzMsGHsmdij2+aje7SKuT4vl40Zj3RPn4tlLBvm+e/riY3x/L/33WVj/xLnY8cwFWPzwWUHzb3v6fOROGINl/xkdch3z/3UGtow/H1vGn4++HZsbkm5KTC2y0kxZbueWWaYs12hf/u1Eq5NgC1np/lXxikfODjnt1HtGaV7uuifOxevXHOf7vPXp8zHngdN157vl40Zj7gOn46XLB/t937Ndtq7lqHnr2ujruy3jz/crvyNZ9ejZWPP4OfjoxuFYGbCPn7poIFY8cjb+eOgMv+Vvf+YCPHXRQABAZpr7OF0w6AjcdmrPkOu5d3QfbHv6fOx8trEOO3tAR8x54HS/6W48ubvf58B6NpR1T5yLdU+ci8UPn4Ut48/HmEGdQk57Ys82OLVPe03LfeGyYzH/X2f4fdeuWSZ2PHMBcieMwepHz8G6J85F7oQxyJ0wxq+O9urfqQXOGXgEMtOcG2Deflpw2yWRTFC0f4jMYtsAs33zTE3TpaemoFlmGrq0aoKz+ndE3yOaIzVFIC01BameMRpDj2rtux+gZZN0NM3UV7kql+V1bNdWYefpHqHiFUKgRZN01d+O7mBuUJKaInwVZSRtsjMghHt/+i0jNfL4l35HtAj6rklGKvp38t8+tYqoS6smSFHs85N7BQeYGRq3Qalts0w0y0zzuz8kVfF322aZyM5MQ0qKQJrKNgbuBzVdWzdFRloKMtJScFTbprrTSMnjqLaxN9DVHOGQAPOkXm2tToIttGma4fdZrezxStdQBgHuToZmmWl+T/NMT01Bj3bZaNdMW/0KAG2zM9C2WSa6t8tG/07+ZXqKxeMgM9JSMPSo1pqnb9U0Ay2y0nFGvw5onZ3hV4c0yUhDm+wMX13fxvN7aorwvXMjw7PvU1NS0KV1k+AVKKSlpvjVM1npqUF11sDOLYLmSdOwT1ME0CwzDUe0zEJGWgr6hOnIPL1vB80dAe2aZ6JNtn9eTE8VvuPcsmm6r+MeUD/+iTAydnT/DlYnwVQdWmg//4miZdsAU0Jqmi5Fw43kAo3vZNK21PiQ0rrUxPwIcROTrjllJqRBWV+Gy1t8fgHZGR+w4SyBxyvc0dNS5ymXqTZ5tEVnSkCLwco6zMuo12F4l+Ldv8pt89YLLs93kdao1n4xcl9pzQOA/oAv1v3Josf++AoZigf7Bpgay2Itp4kQitNJGtPDZkRd4bK+braEUY1frZ0QkSiTo0ybEZ3zSXqIyWJsPjhbuDIyVWP5aVRAo1yKHRumsVQnylm9y/GW+2rbbXSdrXactawicLZI+yCeHQEMMB2Ax4jiwPEBppYhOsoppEFhiRFLMSpAioadKwG13ln1HmFz0xGukad199mgg5+SkJ3Pb4os3OEz4tjqCTiU0yZavlJuT4rviq8nmHQFb7fvCqbF+0HXFUyhr6Mz1m2zYycE+eMRoniwb4CpcTqthWH8h4xp2AILgw+rK8hwtAaTLoOit1AVojG3FzHCpNDM6mRiI8/ZwpXPgc8DCL0MT8Ck8lvUQ2QDFmaH0i2WnK48T8JdwVT7Ti+J4MBe9dhoqNf0DZEVho4Ii7gMFj22x1soKB7sG2BqLBHDNaRCnUMcImutiPevaNwvZu8+PZV4KLyCSZZg+8HRwtVrRpRLekQOiYxcfnyp7Urf/lUkzHs8jB5qGu39sYGBvpk5Qv89nGR3PEYUD/YNMDVOp/cqk50a/FYOkY2VmSnXumzDjmWIPBT+IT8soil2Zl1pjLRUZl97C3d89NZ5qkGMjrJTOW3QspxbhQXxlunect9vhIxviKzfx5A0XzGM8tjoqX/ifq6zcLFcpEPAQ0TxYNsAU2vFpX24UAxpMUmyXsGMRK2X2IqnFRpyr1Psi6AEZtoQ2Qh5N95XwchAFh46M1ZtZaev8jzwPUXW0ypS1s+qQadeFm6nnnIm9nswnc/p9XbEDsaEOEpkd7YNMLUWiFpOExnwd7wfkmDmMqxiZtrVlmzFrjJmiKxzjzE5V6QGBJsX9mZs/K/toWmh+L+uw345J5YSVrk1KQFXMJX7yDudd1cYNYLFsFeshFmMENrvwVSjd1YbZpGkwxFWZAe2DTC10vKkTyml/5NkDWjz22UZZrA8XSrrNzNJoXJQuIvjmp8iqzcxRAbgFUxnCxt4xLnu8XtdhwkP+bH0VhHF9jQ+5Md7tTL4t1hZUbfqSbrqa1N0pjkRShanbwNvkSA7sG2AGcs9DI2/qRWW9mnyh6pYefLbg9bh1+HYKLtREolYhrCMsbVwx8/Sh+LYMOMYVcZ6t8y3700IMM0S6YpVPPMMr55ZL+I9mPFJBiU5+waYGqfT2hMvVHoqYxEpfVoqvWQNPiK+FFrtOxP3VagKMZqKknUr6WFVg53Z1F60vL7CS+99gLE+5MfsQMvKelC5OYFXMJUdwIHtjGh2g1qHcjzqC6Ne56UVyxYH4EGiOLBvgKmxTNT9FFn9SVFlRKHt5If8mFlnqT7kx2aDTbW+AsdeqaZkEfEeTDYwbC1c51a8A7KwQ2Qd3kvqv5+F5zv3p1jqZ2fvldiwbLFe5HvweZDIfLYMMJtnpiEzTVvSmmSkhfytVZN0AO7ex+ZZ7r+7t81GWkrsm50WIbLVUsi2apoe1bKN4N0falo2Cf2bV4/22RGnyc5MDfF96GMGAB1aZAV910olTaH2n16HKmp0zxOqgG4akB8zUlmQ20VWuv2KO7M6Tlo0CX+OBebfDI3lrR0ZMZTdaukB+z/cFmmtH1p4ysw22RlBv3VqGVzGhtK/U3Pf34H5pKNKWR1vsZxDXVo18f2d6SkfvFcr+3Rs3O6sdHdd5m2XpKemoHlW6HNMrQ7NVmmrqLVzendopiXpfpqkq9e1gHt70jXmGbXJOurIK4B6/e00WWH2pxNkRqjr2AlA8WBaq6KnhgDE6+Hz+/n+fvHywZhx32m4aEhn3Du6D9Y9cW7I+c4d2BHXn3hUyN8//esJeOqigWidnYE+HZvjwxuH4emLj8Ftp/X0K0hfunww/nnm0bjw2E545MIBePTCAfjhjpHo0qoJnrl4UNBybx7ZA7ec0hNL/3MW2jXL9H1/Ys82vr+VHbv/Oq8fUlMEvrr1RDTPTMNrVx8HABjevQ3evX4oFj18Jvp3aoH/XjUE7/9lGI5qm42MVPehaeGpxD69ZQRG9W6HL/92ol9arj3hSPxtVA98c/tJOLFnG4wZ1Am/3T0Kg7u1wh1n9MKYYzvho5uG44Fz+uCmkd3xwmXHAgDuO7sPBnRqgatHdMNzlw5C55ZZaNkkHZce3xXv3zAMH900HJ/dcoLfuh770wDceHJ3fHbLCbhmxJG+749q2xQA8PIVg3H7ab3w2S0nYMIlg3BG3w545uJBvgrzrjOPBgCc0KMNnr/0WPz7gn546fLBAIAz+3XwOx5e39x+Esb/+Rhcd+JRePriY/C/q4/DoofPxL/O64d5D5yB5y4d5DsGz14SfKxeuXIwnvrzMWiTnYFXrxzi99uNJ3fH1SO64c/HdQHgnw8D/d/gznjovL6+zy2apOGGk47CL3edgneuH4o/HjoDLZuk49d/jvKb75lLBmF0/w6Bi/N5/tJjQ/4WyYc3DvM1LNo1C25EhvLcpYNww0lH4c9DOvs1sLyuOeFIlbnC6+xphBx/ZKuI0940sjvuPqu3ruVf7clvg7u1wqRbT1SdZsygTr6/n7pooO/vkUe3xeKHz8KUf47CDScdhcFdW2Lk0W2D5u/ZTnuZddnQrkj3dB50axO8D8MZ2LmF3+ebRnYH4G4knjOgIz675QS8fd3xQfOdpThHurVpguOPbIV7Rjfux8FdW/r+Viu3Qjm9b3ss/fdZmqcHgEFdWmLcmP5hpxnRvY3f5/RUgacvPgaAO4+995dhqvOpBURK3nIEAE7t0x6f3jwCPTQeu9H9OwLwb5A//qcBQdOd1qe932dvfvn27ydpWo9XuEDusqFdfX9/c7t7uW9fNxQf3zwCKSnCly8CdWiRhfvO7gMA6NU+G49eOABXj+jm+715ZhpG9W6HJz3nwPDubTC4a0u8e/1Q3zTvXD8U/71qCGbdfxp+/ecoX9l4Vr8OeOrPx+DnO0/BnwZ3xjFdWuCNaxvzYofmWZhwySD0bJ+N0/q0x1vXDcULlx2LXu2z0bV143kw7KjWuGlkd7x0+WA8f1ljGXfewCNw6fFdMfLotvjnmUcjRQBnD+iI5y87Fj/feYpvur+f3sv3922n9sSD5/bFkW2a+u0H5fkOuDscx57fD89cPAhjVcpy5fK9Jt48HM9cPAj/Oq8fTuvtPuapKQJf/PUEfP7Xxvrv7P4d8dB5fbH44bNwyyk98PAF/XDR4C44sWcbTLr1RIwb0x8PntsXn94yAk9ffAxuOKmxXfLJzSPQq302HvnTAHRt3QT/PKs3pvzzFDx4bl+cM+AIvHv9UDz2pwF44xr3fv7q1hPxxd9OwLgx/XH1iG7o3rapb3v+eVZvfHBD8Hlz3YlH4Y4zeuHaE47EO9cPRXqqwMij2yJFuM+1+85prLtevmIwrh5xJB46ry8+uXkEZt53Kj675QTcdmpPnNyrHTJSU3Bqn/a49oQj0TwzDV/+7YSg9Sl5y78FY8/EC5cdiwmKetj7W5+O2oLmthHO/VhlpKZg0q0nYuz5/dC6aTqaZqRiYOcWOKmn+/zu3rYpbj21J47p0tKXB5V1WmedwTbgDtrPHdgRnVpm4YJBR6hOc+nxXVW/V+rUMgtPXTQQQ7q1Ui17j1AE9t/9/eSg3y8f2hUPntsXk28/ya8DK7C8veGko/D2dcejU8ssfHbLCXj0wgF45MLgMlKto8vbFgSAk3q2xWe3nOB3Lgc6tU973/rDtZPUDOzcAn89pQdG9W6HB85xl4dvXzcU7Zpl6qqTR3Rvg2ujaPMA7vQfd2Qr3Du6T9Bv3vPgxpO7+9qo3uM25thOEAK4+6zeuP200PsnVP1xcq+2vjZU7w7NcMWw4PzTumk6Tg2oxwDgquHdcHrf4O8B+LWt/jaqh99vvXTEdF7CjCEuTTv3kZV7txi2vO5jp/j+fuCcPnhx+hb84/ReeOi80AGBnuXmThgT0/Te72fedypGv/w7AGDGvafi7Fd+R6/22Zh1/+kxpTNUOrLSU7DpqfMNXXY06ejZLhs7iiow6/7T0Ku9/t5XAMg7VIlRz89Bl1ZNsGDsmbrmHfX8bOQdqsK8B0/HaS/M9ftt/r/OQNfWTdVn1OC695dg/rYifHLzCNWTVasr3l6EpbmH8NWtJ+LEnm398pIyf3vlThiDIU9OR3FlHVY8cjbu/mol/thaFDSN0qDHpqGsph4540b7CrTAZWvN6wCwOq8YF72xwO+74d1b45vbGyuvkRNmY09xld9+7vfIb6iucwWtN/D8UdvuUEKdc+HWEen8Vts34dJ0/9l9cJdKYFxaXYdjH58efgMUbjutJ96ZtwMAcEyXFvjlrlGq0wWm5b6z++CfEQLzUNv8n+/X4vMlu/HguX3xwrTNaJqRisraBr9plfP+tnYf/v75ipDr8c5z76RV+H7lnpDTaCljA7dz1v2n4ayX5oWc/o+HzsCo5+eoLndnUQXOeHGu6nzv/WUYzh7gDjC3FZRj9Mvz/JaxaX8pznv1j4jpPfPFudhRVIGZ952Goz2dZ2r55pZTeuCRCwfg7JfnYWtBOabdcyr6HtFcVx71KiirxoinZ6Fds0zkjBsd9Pv7f+zA+CkbcfPIHnhUJWCOh6U7D+GKdxZh2FGtMTmggatlOytr6zHg0WkRpwvkPW59OzbHtHtPBQDM2VyAmz5ahsHdWmF1XjGyM1Kx/snz9G5SQtHb3jHCaS/Mwa6DlZjzwOkhz0svb7r+9L/5WLunJOj3cWP6Y/yUjb7PR7Zpit2HKgG4L0ys31uCjxbkIiMtBbX1jfWPWlmnx97iKpw8YTY6tsjEkn+7z71Iddftp/XC2/O2q64zcN5XrhyMo9pm45I3F6ou61/n9VMN0sLVX2p1mTId3nNVWZ9Hmz9C1evK5Xydk4eHJq/BZUO7YvLyfADuTsqf72rs9JFSosfDv4ZMf9vsDBysqPV9PrZrS/yk0mnkdf5//8DGfaVITxWoa2iMc3656xRc+L/5OLJNU/z+0Bm+773l9PR7T/UbvaClvK6oqcfAx6b5PmekpWDLeH1t88DtPatfB3xw43Df93MfOB2ne84hrcdo1sYDuOXjHN/nS47vgpevGAIA+HD+Tjz5ywa/6beMPx99xv3mW4d33eueOBfNMtNUj/Wu5y5cLqVU7S025wpmHC6/8xI/aWGbJ9pFkQzfO9dMXIcZku3+jlSdeSzaV4TEslf1rtLKe8jMuq9P2eGutj+MzreBTyU1Zji0fe/ui7WojXb/N76bUm2ZZCXlq+I0z6PxoCmfg5EiFPnH4FMkmnytZx4r75e38hbqwPLQ6LaaN88FbqP3c+AFWF85HcU+MeMYBS4zmnUEbosyr6ltZqh1RHsXinNvvHEI2wQ4NhfLbgpXQBu19608jEJoK/REwL+mpIVNtiB6A0Yr9qD3uHkrXTsfxUh5PeyrqaKcLxpal2fEOZMM5120x0ctvyT+3nIGI9s/gctSHnchQnfkWJkXtGx+pPrdjPQ37ivniLp8CPrsqQODngwd/PToaBlzzNTTp0e4h5Hq6fSJtlPccQGmwx9aR3Hm5BdkR3slx6hKXXXtIRYdWNknE73bG21hHU/W9myHFy5/a30vstpkZj+p2oh9yvpPHwecaknBiGwbtvNI0fw2+hyJpmGvv7PXmlfJOPkp0FqTHriNkeaL6gqmCd0AhlzBjLDMoHVqTItWjgswvZKhR5diF2s+sUMDRUBoavza5Wq51lTYJLkx030FUzF5vOr34MoqfJqtfC1QpFdARZttlPOpbb/hDVPh/28sy3fSuRLtZkZ/hcI5ZWOyiWava51HWU4or2DG+72f4WjJd5GmMXP4pbW3QsRpPSE+B+5WI8rpwGXFtAwDlhnu/cqqIz9CrCRprmDamY3KtaSkfsLEPx1GUW6OpiGy3gatKanRvuxka8zpvT/Biv1jVu++GWIbIhv6R6OuHDtgF1oi1r0be2dg8PzJVRLZlxmNdv9RM8J3/O1wfuqpiwUiDZE1ZZAsEGG9hrJkBJj/v43fh3+4RTSdq/G5B1P/SoLuwVR2buvYTlsFmGYW6nYoPOzCCY1Fqzm6gRGqq03jbDGvXkMGi+XBGo4+Ngqx3IMZr1gzsPEVabWWDpGNFGCGu+c6zIYpj5PqEFmTt9mIq8KJXOSbcS4k8v5yBN8xNf6+NuX5JBS/26ldpPkeTPOTErROp4u1PA2+Qmjg/cIm3HcfzXBmV5hZ9Ny7nnQP+UmEE4TiIAHyid6H/Jh5XwXPu2Cx3IMZ78aQ1uFjVrbRIg6RjTIPRprP6GHB3gaLL7iPZYisEQmyuWi30U4BBfmL6piGOFEDAwBl4zlFCFudJN7gQEugYcVTZH1tBeMXHX6FClZ16Pk6WYMe8uP5PYHKk+AHXinaHirTh8pr0Qbfjg0w7S6B8qjtRTtkzu78hsja5D4jTftTYzISZSit3u2wYrOD7i9JjF2vi3K/m3GPTKzTJQqrHk6mNney7Xu7Mn+IbOi6ydJ6RusVzDg3GEVQhWAyQ1Zj0C0OIUbIxvQmg6DhrNEvK/Q69C808ApmvJ//4LgAM5F6F8h8hj1F1pjFREXvJhg2RFbPtElwXhqVl6IdbmIErY1/K58uaNbDcJQNULXGqBPysJ2f+hjr+WHGaWHfvZUczA3uAobI2qg3Qe89mFZx8vkR69NgQ+UXGxexuoWrL9QuWhh9vjouwPSyUVmiyu7pSxZOPg7KwkHfEFlz0qO6zlh6/YxLhqNY85AfffdgWsmsp0DGO7D3rs6Yp8ja+YgZw8hNNGJYMhlHz2EIlQ0Cv1denRHCnmOVtL8HM/QeMuPct8NwUAu7MAEEdzKGeo+qFkHLii5hhgv7kB9ewXQWGeJvig/1MeV2OdX1U94roCU/xWNTQ/b6KVPIzB+WWfcQapnXCQ3uSEkM+8TFMDspRRFhxrIv9V5FdHARFFcxD5ENe/WarGBoIBNwgJXnYYqw5/uFNd2DGaF+N2OrYgmmYlpvHNcVast8Q2QDh7XG+8m6cRB8fJXPfzB/Qx0XYFr5frZo2K/ISy6JsP8FoCtoc8o5YsP2QFxY0RDyrtF7dTDiezAtfYps9CsPt1WRrmDyKbLGsGMa7ZimZGBmUac8pu7XlJi3Lr0ay9nI0wpYcA+mRcFULKsz+3YnM0ZQWM3lCv0br2CGY5MDSPbm5GyiLAC0NU593ZKGr9+3hgQshOPNinsw9b5Y28pOCrMaIXHPb777sGJvzDnjTLEmlYl0xSFR6SlPQj7JMnCZfk+Rtdc5EuFVi37cVzDDDZE1Jk1qy3RqR6J7/uiW73Kpd7L6rrZHkxabdmEF3m7i/x5M85kSYLZqmmHGYgEAw7u38fzb2pDlHdOlheZpB3drFfb3Vk3TAQCZaSlo1ywTAHDBoE5Rpy2UDs3dy77w2M6GL1uvvh2b48Jj3dvYxsTjHs4ZfTsAAFpkpQX9lpWeGtOyhx7lzmedWmbFtJzT+7YHAHRp1STot66tg78DgLMHdAQApKem4HTPNgLAOZ7vA40ZdAQAoGlm8H4AgN4dmmlPsCKtZ3jSDgCn9WnvN83/DXbnwVZNGo/9GE9+OKGH+1w9q5877UIATTMaj8eNJ3fXlR416an+lcRJPdv6/h7QSfu5Hej4I1sFfTegc+jlCQFcOayb33eXHN/F7/MYT1kwpFtrnOrZj2cojmugJgF5N9z6vTLS1Iv0k3q598uJnv0zur87DynLtN4dmvnyYve22UHLOKJF8Dlwap92EdOkV+eWwflOqbnKee7VTJH3R/Vu55cHvMsFGstqpXbNtZVf5wx0n2etA8q78485QnX68z3n5RGeMqRNdgZ6tXfv3xGe+iySJp7z5vxj1OuTYZ7ljDLheGjlLSPV8vQFg9T3jZqrR3SLPJFChxbu+vCs/o3lYg9P/vXWTXqXmahG9NCW34zirS9CtQ2854yyTjvlaPU83Kdjc7/PVymOac/2zTDcs21/PaWH33QCwOj+ocvZaASWzYG87QZvWaFmcNeWAIBe7bPRtVXTkNMd27VVxPR4z68e7YLL7W5tgtsXHT1luZ7zMpQTe/rnqW5tmqjWn4B/wD26v3o7ZqCnnvO2mc70tB/+PMTd1vAGSZHSflof//kuH9rVkz73vh4TMP+o3u71tWvmn1fbZDd+bputno9TPYnyttnGRNnu79k+G+097fuRR7f1+y1cvReK95y5esSRABrbZEBjWyCQd38DkeOjI9uEzrcAIMwYhzts2DCZk5Nj2PIqauqRmiLgkhJNM9JQWl2HFlnBDQS9SqrqkJmWojkIqWtwoa7BhaYZ/gf6UEUtSqrq0KNdNg5X1CI1VaBFVjrKquuQnZHmd++PESpq6rGvpApHtc1Geqp1F6ELy2qQnZmKrLRUVNTWo3kMxyT/cCVOeW4OurRqggVjz9Q1b32DCwVlNejcqgnKqutQVduAlBT3dYO2nkA/Wi6XxI6ichzdoXnkicOQUqKovNZXeBRX1kIIgZZN0lFT34AGl0RJVR2apqchM92dJ2vrXThUUYsjWmbB5ZI4UFaNVk0ykJoiUFFTj9YBhV19gwslVXV+21xZWw8pgXqX1JXXvUqr69A8Mw21DS6UVtWjXbMMv54/l0sGHfv6Bhe2FZaje9tslFTVoWWTdGSlp6K6rgFAY9BfW+9CcVUt6hokmqanIjM9BYcr65CdkYqy6npkpadi+NMzAQC5E8b4pav72CkAgI1PnodtBeXo1SEbTTPS/M7R6roG1NS70LKJer6srmtAeU09ho1vXEdlbT1KqurQsXkW9hRXoU12BqrqGlBaVYee7SMH6KXVdaiubUBtgwudWjZBdV0Diqvq0KF5JtJTU3xll8slsSq/GMd1axXyylp1XYNv+sKyGl/FGE5lbT1c0j/QUqatRVY69pVUoW12JoqratE8M90XvJRU1UEI+MrWgrJqFJS6zyspJbIz07BuTwkGd2vlV+6UVtcBAFbtLkbfI5qjSUYqMlLdea2iph4AkB2i08O7nTX1LqSmCKSlCGSlp6K0ug7r9pTgmveW4NiuLbEmvwQAsP6Jc5GdmYbCshq4pPQ1lAK3s7iiDu2bZyI1RaDe5UKDSwaVT8WVtUhLTfHbV+v2lKBD80x0UFmuV4NL4nBlra8TEXCXyZlpKSirrseL0zfj8yW7cftpvTD2/H6QUqKspt63Xw9V1EJKibbNMlFT34DqWhdaqgS8gQ5V1KJFVhrSQpT5NfUNyEyLrUMtVoVlNWibnRFU59U3uFBT7wqbDwB3mZCWInTXmUXlNWjT1H+93rKrrkEiPVUk7YgJr5LKOmRlpMQ1jzS4JPaXVqNLqya+MnvN4+egoUEiMz0FGanucyY7M83XOdbgktheWI4urZqgorYeTdJTsbe4Gn2PaI6y6jqkpaSgSUYqpJSoa5Corm/wnVveMq6kqg6FZTUY/fI8NM9Mw8pHz9aU/9TsL6nGic/OQscWmVjy79EA3OXswfJaZKWnoqa+wZ12CbTOzsDhylp0aJ7lK2cDO/1Kq+uQW1SBQV1a+pULBaXVqKl3oUVWOqrrG3x1T6i2bmVtPVblFaP/ES3QLCsN6akpfnXegdJqpKYINM9Kg5TBne3e88N7Xmgpq9U0uCRcUvrqBG97Xbm+r5fl4aFv1+DyoV3x8AX9UVZdh26tmwad58o2eW29C5W19WiWmYaaeheapKfiYEUtWjRxf1amXU19gwsHympwRIssFFfWomlGGsqq69ChRVbQtnu3Y19JFbq29q9nq2obUO9yoXmWu62mti8Bdz5pnZ2OipqGsOV0KEXlNWiakYoUIbCtoBwDO7eAEAIHy2tQWF6Dfke0wJ7iKjRNTw1q+4VTUFaNDs2zfP8qebfHJaWv3VBb7/K1Lytq6nG4sta3T7znsLc9VlFTj2ZZ6cullMPU1q3/bLNAYIY3IrgEELLhGUp6aopqQNcmO8PXy6E88LEEXOFkZ6bFHPAYwRssAeZtqxZpqSno7Lna1jwr3dC0pKQIQ/a1EMJvfymv8nsr/MCOi4y0FN9Vj5QUgU6KKzAZacEFTFpqSlBAHbhMvbznWmZaKto3Dy5UU1JE0P5OS01BvyPcPV/KgjiwUM5ISwkq8Lzp1ToKoklGKgZ5eoIB/3M0Kz01bECt9nvTjDRfGrwBXXZmml8wEU6LrHS/8ik7M82v/PL+lpIicPyR4UdhKNOnJbj0pj9c2gD48lHgvg8sDzs0zwqaZpjKFTfvck/tE3zFUUtjRe04tMhK9w0tVV4t8C5PeS6ppUd5DDJCDNRRy2PHdGmpMqW/1BQRlB+86WqdnYEuASMShBB+6VH2iGempWpu8LeJ0KiwOrgEQh+XtNQUTQ2uUFfgI1E7P737PCMtuQNLLy2dGEZLTRFBo3YC22+BjeXUFOG78uI9r/oe4Z5HWdcIIZCRJvzyjHfZgWWZ1vynVdOMNDRto162ectMZX2t1CIr3XdVUrkvlJ1aLeH+PtwFhKYZaTi5l//VXmVZqtb5FpgOpWiCb8B9vFIV1yYjLUfZXg6kPG4ZaSm+do732HnLFy1lXVpqii/vedtF3s5UtRgiNUUEBZeN86RGXK+3rRZtOawsw5T1UNtmmb70q42Ai8SbHwPrckA9rcr9Hth+CRTpWDv3HkwiIiKb4T2BRESN7HqPIpmLASYREZHBknxEJhERJTEGmEREREREZDgt7wOlxMMAk4iIiIiIDMchssmJASYREZHB2GdPRETJigEmERHZDnu9iShm7OkhsgQDTCIiIoOY8W5pIiKn44PPkgsDTCIish2nPxiCjSkiokbse0suDDCJiMh2OESWiKLG4oPIUgwwiYiIDMJeeiKiYBzVkVw0BZhCiPOEEJuFENuEEGPNThQREZGTOX2ILxERUbQiBphCiFQAbwA4H8AAAFcLIQaYnTAiIiL2ehNRtFh8EFlDyxXMEQC2SSl3SClrAXwF4CJzk0VEROQ8HCFLRETJLk3DNF0A5Ck+5wM4IXAiIcStAG4FgCOPPNKQxFHy6NSyCc7q1wH/OKOX1UkhGxl7fj80uIKb7E9ffAx2H6o0ZB1vXXs85mwuMGRZZJzjj2yNkUe3xaMXDsTe4ip8v3KP1UnS5JoTjsT8rUX4y8lHWZ0UItt4+7qhmLnxQNzW1zwrDecM6IibT+kR03LaN8/E6P4dcNtpbJtE6/xBnfDtij2468zeVieFYjBuTH+U19Rrnl5EemeXEOIyAOdJKf/q+Xw9gBOklHeGmmfYsGEyJydHcyKIiIiIiIjIGYQQy6WUw9R+0zJEdg+AborPXT3fEREREREREfloCTCXAegthOghhMgAcBWAn8xNFhERERERETlNxHswpZT1Qog7AUwDkArgQynletNTRkRERERERI6i5SE/kFL+CuBXk9NCREREREREDqZliCwRERERERFRRAwwiYiIiIiIyBAMMImIiIiIiMgQDDCJiIiIiIjIEAwwiYiIiIiIyBAMMImIiIiIiMgQDDCJiIiIiIjIEAwwiYiIiIiIyBAMMImIiIiIiMgQQkpp/EKFKAOw2fAFU6JpB6DI6kQQJaGWAEqsTgRREmK9R2QN1nvG6yulbK72Q5pJK9wspRxm0rIpQQghcphPiOJPCPGulPJWq9NBlGxY7xFZg/We8YQQOaF+4xBZIqLk87PVCSAiIooj1ntxxACTiCjJSClZ0RIRUdJgvRdfZgWY75q0XEoszCdERJRMWO8RUaIIWZ6Z8pAfIiIiIiIiSj4cIktE5FBCiG5CiDlCiA1CiPVCiLs937cRQswQQmz1/NtaZd6jhBArhBCrPPPervhtqBBirRBimxDiNSGEiOd2ERERhRKm7rvc89klhFB9mJYQIksIsVQIsdoz7ROK33oIIZZ46r5JQoiMeG1TomGASTGLpZHrme4GzzRbhRA3KL5nI5covHoA90spBwA4EcAdQogBAMYCmCWl7A1gludzoH0ATpJSDgFwAoCxQojOnt/eAvA3AL09/59n6lYQOVAsjVzPdOcJITZ76rixiu/ZyCUKL1Tdtw7AJQB+DzNvDYAzpZSDAQwBcJ4Q4kTPb88BeEVKeTSAwwBuMSn9CY8BJhkh6kauEKINgMfgbuCOAPCYIhBlI5coDCnlPinlCs/fZQA2AugC4CIAH3sm+xjAn1XmrZVS1ng+ZsJTHwghOgFoIaVcLN33UHyiNj8RRd/IFUKkAngDwPkABgC42jMvwEYuUVih6j4p5UYp5eYI80opZbnnY7rnf+m5iHEmgMme31TrTtKGASbFLJZGLoBzAcyQUh6SUh4GMAPu3iQ2col0EEJ0B3AcgCUAOkop93l+2g+go2eaYUKI9xXzdBNCrAGQB+A5KeVeuM/dfMWi8z3fEZFCLI1cuDtUt0kpd0gpawF8BeAiNnKJ9Amo+0JN01kI8avic6oQYhWAArjboEsAtAVQLKWs90zGui8GDDDJUFE0crvA3bj18p7QbOQSaSSEaAbgWwD3SClLlb95Omik5+8cKeVfFb/lSSmPBXA0gBuEEB3jmGyihBFFIzdU3cdGLpFG4eo+JSnlXinlBYrPDZ7bQ7oCGCGEOMb0xCYZBphkmGgbuUQUPSFEOtzn3edSyu88Xx/wjALwDnktCLcMz5XLdQBGAdgDd6Xr1dXzHRGpiLaRS0TRC1H36SKlLAYwB+5bsA4CaCWESPP8zLovBgwwyRAxNHL3AOim+Ow9odnIJYrAM5zuAwAbpZQvK376CYD3gVk3APhRZd6uQogmnr9bAzgFwGbPqINSIcSJnuX/RW1+IoqpkRuq7mMjlyiCMHWflnnbCyFaef5uAuBsAJs8F0LmALjMM6lq3UnaMMCkmMXSyAUwDcA5QojWnkbuOQCmsZFLpMlIANcDOFO4XzeySghxAYAJAM4WQmwFMNrzOXB4en8AS4QQqwHMA/CilHKt57d/AHgfwDYA2wH8FrctInKIWBq5AJYB6O15YmwGgKsA/MRGLpEmqnWfEOJiIUQ+gJMATBFCTAOChqd3AjDH8/yBZXDfg/mL57d/AbhPCLEN7uHqH8RzoxKJcJdlRNETQpwC4A8AawG4PF//G+57Ub4GcCSAXQCukFIe8jy2/XbvMFkhxM2e6QHgaSnlR57vhwGYCKAJ3A3cuyQzLBER2UCYui8TwP8AtAdQDGCVlPJcz2uA3vcOk/V0Br0KIBXAh1LKpz3f94T7oT9tAKwEcJ3iic9ERLbHAJOIiIiIiIgMwSGyREREREREZAgGmERERERERGQIBphERERERERkCAaYREREREREZAgGmERERERERGQIBphERERERERkCAaYRESUVIQQrYQQ//D83VkIMdnEdd0uhPiLyvfdhRDrzFovERGRVfgeTCIiSipCiO4AfpFSHpPMaSAiIjIDr2ASEVGymQCglxBilRDiG++VRCHEjUKIH4QQM4QQuUKIO4UQ9wkhVgohFgsh2nim6yWEmCqEWC6E+EMI0S/UioQQjwshHvD8PVQIsVoIsRrAHYpp7hVCfOj5e5AQYp0QoqmZO4CIiMgsDDCJiCjZjAWwXUo5BMCDAb8dA+ASAMMBPA2gUkp5HIBFALxDXd8FcJeUciiABwC8qXG9H3nmGxzw/X8BHC2EuNgzzW1Sykp9m0RERGQPaVYngIiIyEbmSCnLAJQJIUoA/Oz5fi2AY4UQzQCcDOAbIYR3nsxICxVCtALQSkr5u+erTwGcDwBSSpcQ4kYAawC8I6VcYNC2EBERxR0DTCIiokY1ir9dis8uuOvMFADFnqufRuoNoBxAZ4OXS0REFFccIktERMmmDEDzaGaUUpYC2CmEuBwAhFvgkFe1+YoBFAshTvF8da33NyFESwCvATgVQFshxGXRpI2IiMgOGGASEVFSkVIeBLDA83CfF6JYxLUAbvE8rGc9gIs0zncTgDeEEKsACMX3rwB4Q0q5BcAtACYIITpEkS4iIiLL8TUlREREREREZAhewSQiIiIiIiJD8CE/REREMRJC/AfA5QFffyOlfNqK9BAREVmFQ2SJiIiIiIjIEBwiS0RERERERIZggElERERERESGYIBJREREREREhmCASURERERERIZggElERERERESG+H8YbnsU6K+XPwAAAABJRU5ErkJggg==\n", + "text/plain": [ + "<Figure size 1152x432 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + } + ], + "source": [ + "# get raw data\n", + "df = get_data(hosts=hosts, charts=charts, after=after, before=before)\n", + "\n", + "# filter df for just the dims if set\n", + "if len(dims):\n", + " df = df[[dim for dim in dims]]\n", + "\n", + "# set some variables based on our data\n", + "df_timestamp_min = df.index.min()\n", + "df_timestamp_max = df.index.max()\n", + "\n", + "# print some info\n", + "print(df.shape)\n", + "print(df_timestamp_min, df_timestamp_max)\n", + "display(df.head())\n", + "\n", + "# lets just plot each dimension to have a look at it\n", + "for col in df.columns: \n", + "\n", + " # plot dimension, setting index to datetime so its more readable on the plot\n", + " df[[col]].set_index(pd.to_datetime(df.index, unit='s')).plot(title=f'Raw Data - {col}', figsize=(16,6))" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "### 2. Add some anomalous data<a id=\"add-some-anomalous-data\"></a>" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "Below we will pick the last `n_tail_anomalous` observations and mess them up in some random but noticable way. In this case we randomly shuffle the data and then multiply each observation by some integer randomly chosen from `integers_to_pick_randomly`" + ] + }, + { + "cell_type": "code", + "execution_count": 5, + "metadata": { + "colab": { + "base_uri": "https://localhost:8080/", + "height": 405 + }, + "id": "RDuB5PdjOaAX", + "outputId": "d686cea5-d0a8-4ed4-aa58-64770a063fbb" + }, + "outputs": [], + "source": [ + "# size of anomalous data\n", + "n_tail_anomalous = 500\n", + "integers_to_pick_randomly = [0,1,5,10]\n", + "\n", + "# randomly scramble data and multiply randomly by some numbers to make it anomalous looking\n", + "anomalous_shape = (n_tail_anomalous, len(df.columns))\n", + "randomly_scrambled_data = np.random.choice(df.tail(n_tail_anomalous).values.reshape(-1,), anomalous_shape)\n", + "random_integers = np.random.choice(integers_to_pick_randomly, anomalous_shape)\n", + "data_anomalous = randomly_scrambled_data * random_integers\n", + "\n", + "# create anomalous dataframe\n", + "df_anomalous = pd.DataFrame(data = data_anomalous, columns = df.columns)\n", + "# make sure it has the expected index since we don't want to shuffle that\n", + "df_anomalous.index = df.tail(n_tail_anomalous).index\n", + "\n", + "# overwrite last n_tail observations with anomalous data\n", + "df.update(df_anomalous)" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "In the plot below it should be clear that the light yellow section of the data has been messed with and is now \"anomalous\" or \"strange looking\" in comparison to all the data that comes before it. \n", + "\n", + "Our goal now is to create some sort of [anomaly score](https://github.com/netdata/netdata/blob/master/ml/README.md#anomaly-score) that can easily capture this." + ] + }, + { + "cell_type": "code", + "execution_count": 6, + "metadata": { + "scrolled": true + }, + "outputs": [ + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAA54AAAGECAYAAABeXf8zAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAABzIklEQVR4nO3dd5hU1f3H8c/ZvgtLR6SogCBNBASxK/YCUaNRf/aSxGiiSTQaW6zRiNFEoyYxauwl9gqCIMVCXXrvCyx1advbzJzfH1N2Znba7s7sLMv79Tw87Mxt55a593zvacZaKwAAAAAAEiUl2QkAAAAAALRsBJ4AAAAAgIQi8AQAAAAAJBSBJwAAAAAgoQg8AQAAAAAJReAJAAAAAEgoAk8AaOGMMQ8bY95OdjoQmjHmemPMD029LEIzxowyxkxLdjoAoKUh8ASARjLGTDPG7DXGZCY7Lc2FMcYaY8qMMaXGmN3GmG+NMZfXY/lRxpiCOKSjtScNXzd2XYjOc977JDsdAIDmh8ATABrBGNNT0smSrKQLkpuaZmeItba1pH6SXpf0gjHmoSZOwyWSqiSdZYw5uIm3DcTEGJOW7DQAQKIReAJA41wraZbcgdV1/hOMMa8bY/5pjBlnjCkxxsw2xhzuN/0EY8xcY0yR5/8T/KZNM8Y8ZoyZ4Smx+9IY09EY844xptgzf0+/+f9hjNnsmTbPGHNyuAQbYy4wxiwzxuzzbGeA37SAEivPPjzm+buTMeYrz3J7jDHfG2OiPkestbustW9JukXSvcaYjp713WCMWeE5NuuNMb/yfN9K0teSunn2vdQY080YM9IYM9Oz/W3GmBeMMRlRNn+dpBclLZZ0ddBxyDfG3GuMWe4psX7NGJPlmTbKGFNgjLnPGLPLM+9VfstmGmOeNsZsMsbsMMa8aIzJDlr2D8aYnZ603uC3bEdjzBeeczVH0uFB6epvjJnkOcarjDGXxbpsfRlj7jbGbPGcg1XGmDOMMQcbY8q958kz39HGmEJjTLoxpo8xZrrnut1ljHnfM893ntkXec7Z5Z7vxxhjFnrO2wxjzFFB5+AuY8xi4y4h/68xposx5mtPmiYbY9pHSP8v/a6h5caYo/3WG+7c1qmeHHzdB02bZoz5hd9n3/LG7RnPeS42xiwxxhzpmRbLNXK3MWa7pNdiP2sAsH8i8ASAxrlW0juef+cYY7oETf8/SY9Iai9praTHJckY00HSOEnPSeoo6e+Sxvln9j3LXiOpu9wBxky5M6gdJK2Q5F96OFfSUM+0dyV96M1o+zPGHCHpPUm/l9RZ0nhJX8YQwEnSHyQVeJbrIuk+uUt6Y/W5pDRJIz2fd0oaI6mNpBskPWOMOdpaWybpPElbrbWtPf+2SnJKul1SJ0nHSzpD0q/DbcwYc5ikUao9P9eGmO0qSefIfXyPkPQnv2kHe7bVXe4A9iVjTD/PtLGe+YdK6uOZ58GgZdt6vv+5pH/6BVD/lFQpqaukGz3/vGluJWmS3OfwILmvgX8ZYwZGW7a+PPtyq6RjrLW5nuOQb63dLmmapMv8Zr9G0v+stTWS/izpG7mv6R6Snpcka+0pnnmHeM7Z+8aYYZJelfQrua/z/0j6wgRWS79E0llyH8+fyP3S4T65r7MUSb8Nk/5LJT0s93ltI3eNg91+s0Q6t/FytqRTPOtvK/cx86Yhlmukg6TDJN2UgLQBQLNC4AkADWSMOUnuTOMH1tp5ktZJujJotk+ttXOstQ65g5+hnu9HS1pjrX3LWuuw1r4naaXcGW+v16y166y1RXJnxtdZayd71vWhpGHeGa21b1trd3vW9TdJmXJXcQ12uaRx1tpJniDiaUnZkk4IMW+wGrkDnsOstTXW2u+ttTEHnp7t7ZI7sy1r7TjP/llr7XS5g5mwJbXW2nnW2lmefcyXO4g5NcImr5G02Fq7XNL/JA3yBEL+XrDWbrbW7pH7pcAVQdMfsNZWedI3TtJlxhgjd6Bwu7V2j7W2RNJf5A4SvWokPeo5TuMllUrqZ4xJlTvQetBaW2atXSrpDb/lxsgd/L3m2c8Fkj6WdGkMy9aXU+7rZKAxJt1am2+tXeeZ9oY8JcSe7V4h6S2/fTtMUjdrbaW1NlLnRjdJ+o+1dra11mmtfUPuqs/H+c3zvLV2h7V2i6TvJc221i6w1lZK+lR+13mQX0j6q7V2rucaWmut3eg3Pdq5jYcaSbmS+ksy1toV1tptMV4jLkkPea6vigSkDQCaFQJPAGi46yR9Y63d5fn8roKq20ra7vd3uaTWnr+7SdoYNO9GuUtFvHb4/V0R4rN3XTLG3OmpclhkjNknd+lLpxBpDtiutdYlaXPQdsN5Su5S22+Mu2rsPTEs42OMSZe7FGuP5/N5xphZniql+ySdHybN3uWPMO6qvtuNMcVyZ+TDzq/a0mh5gprpqnt+Nvv9vVHu4+O111P6Gjy9s6QcSfM81Uf3SZrg+d5rt+cFgZf33HeWu9Q3eLteh0k61rtez7qvkrt0LNqyATxVO71Vle8Lnm6tXSt3yffDknYaY/5njPHu/+dyB6S95C6NLLLWzvFM+6MkI2mOcVfZjlTqepikPwTtzyEKPM4xX+dBDpH7ZU84kc5tXFhrp0h6Qe6S6J3GmJeMMW0U2zVS6AmuAeCAQOAJAA3gaat1maRTPYHQdrmrgQ4xxgyJYRVb5c6U+ztU0pYGpOVkuYOByyS1t9a2k1Qkd3AQcbuekplD/LZbLneG2cvXIY+1tsRa+wdrbW+5qzXeYYw5ox5JvVCSQ+6AJVPukrynJXXxpHm8X5pDlaT+W+5S4b7W2jZyV8cMtY8y7vayfeVuU+o9P8dKutIEduRyiN/fh8p9fLzae6q+Bk/fJXdANMha287zr62nI6VoCuU+BsHb9dosabrfett5qq3eEsOyAay1N/tVVf5LmHnetdZ6S+6tpCc931dK+kDuUs9rVFvaKWvtdmvtL6213eSuQvuvcO0jPfvzeND+5HhK+BtrsyK3cQ13bsvkd42b6J1OBcwvv9+EJFlrn7PWDpc0UO6qtXcptmukPtXUAWC/R+AJAA1zkdxVFQfKXX12qKQBclcVDNWWMNh4SUcYY640xqQZd0csAyV91YC05ModkBRKSjPGPCh3m7dQPpA02rg7kUmXu91mlaQZnukL5Q7OUo0x58qvKqtxdxLTxxOsFsm9/65oiTPGdDDujnn+KelJa+1uSRlyV/MslOQwxpwnd3s5rx2SOhpj2gbtZ7GkUmNMf7k7KwrnOrnbSvqfnyPlrlZ8nt98vzHG9PC0ub1f0vtB63nEGJPhCe7HSPrQU0r8stxtUg/y7GN3Y8w50Y6FtdYp6RNJDxtjcjxtN/1LYb+S+7q4xrg78kk3xhxjjBkQw7L1YozpZ4w53fMSoFLuQMn/fL4p6Xq5XzK85bfcpcaYHp6Pe+UOoLzL7ZDU228dL0u62RhzrHFrZYwZbYzJbWi6/bwi6U5jzHDPuvt42vV6hTu3i+Sudj3UuNtBPxxlOwslXew55n3kbrMrSfKcm2M9v6UyuY+jqzHXCAC0VASeANAw18ndBnOTpwRou3V3yvKCpKtMlOERPMHXGLkDv91yl1iO8au2Wx8T5a7Gt1ruKoWVCqxm6L/dVXKXYj0vd6nMTyT9xFpb7Znld57v9sldxfMzv8X7Sposd3vFmZL+Za2dGiFdi4wxpXJXz/2F3O3dHvSko0TuTmM+kDt4uVLSF37pXCl3J0jrPVUVu0m60zNfidyZ+uAgUZLkCSYuk7vt4Ha/fxvkDqD8g7V35W5bul7uapuP+U3b7knbVrmr7N7sSZck3e3Zr1mear+TFbpNbSi3yl19dLvcvSH7ejT1HJez5W4LuNUzz5NyB+kRl22ATLk7wNnlWd9Bku71S8uPcgeU84PaTh4jabbn3H4h6XfW2vWeaQ9LesNzzi6z1uZJ+qXcv4u9ch+z6xuaYE+14ZM96ftQ7rab78p9TXwmT/thj5Dn1lq7WtKjcp+zNZIitVGVpGckVcsdVL8hT/VtjzZyX4t75f7t7Za7SrrUuGsEAFocY2PvFwIAgBbDGJMv6RfW2skhpo2S9La1tkfwtAOJMWaKpHetta8kOy31EencxrDsKEkPW2tHxTdVAHBgY8BiAABQhzHmGElHy902FwCARqGqLQAACGCMeUPuqqG/91T/PZDky12NGQAQR1S1BQAAAAAkFCWeAAAAAICEIvAEAAAAACRUk3Yu1KlTJ9uzZ8+m3CQAAAAANDmXqzzZSUiKBQtW7LLWdg7+vkkDz549eyovL68pNwkAAAAATa6kZF6yk5AUbdqM2Bjqe6raAgAAAAASisATAAAAAJBQBJ4AAAAAgIRq0jaeodTU1KigoECVlZXJTgriKCsrSz169FB6enqykwIAAAAgyZIeeBYUFCg3N1c9e/aUMSbZyUEcWGu1e/duFRQUqFevXslODgAAAIAkS3pV28rKSnXs2JGgswUxxqhjx46UYgMAAACQ1AwCT0kEnS0Q5xQAAACAV7MIPAEAAAAALReBZxy8/vrr2rp1a7KTEdHrr7+uhx9+ONnJAAAAAHAAIvCMg/0h8Ew0h8OR7CQAAAAAaKaS3qutv0e+XKblW4vjus6B3drooZ8MijhPWVmZLrvsMhUUFMjpdOqBBx7Qe++9p88++0ySNGnSJP3rX//SRx99pJ///OfKy8uTMUY33nijDjnkEOXl5emqq65Sdna2Zs6cqeXLl+uOO+5QaWmpOnXqpNdff11du3bVqFGjNGzYMH3//fcqKyvTm2++qSeeeEJLlizR5Zdfrscee6xO2ubOnavf/e53KisrU2Zmpr799lt9/PHH+vTTT1VUVKQtW7bo6quv1kMPPaT8/HyNGTNGS5culSQ9/fTTKi0trVPS+frrrysvL08vvPCCJGnMmDG68847dfLJJ9fZv9tvv13r1q3Tb37zGxUWFionJ0cvv/yy+vfvr+uvv15ZWVlasGCBTjzxRP39739v/AkDAAAA0OI0q8AzWSZMmKBu3bpp3LhxkqSioiI99NBDKiwsVOfOnfXaa6/pxhtv1MKFC7VlyxZfYLdv3z61a9dOL7zwgp5++mmNGDFCNTU1uu222/T555+rc+fOev/993X//ffr1VdflSRlZGQoLy9P//jHP3ThhRdq3rx56tChgw4//HDdfvvt6tixoy9d1dXVuvzyy/X+++/rmGOOUXFxsbKzsyVJc+bM0dKlS5WTk6NjjjlGo0ePVqdOnRp1HELtnyTddNNNevHFF9W3b1/Nnj1bv/71rzVlyhRJ7uFwZsyYodTU1EZtGwAAADjQFFW4lJtllHIAdMzZrALPaCWTiTJ48GD94Q9/0N13360xY8bo5JNP1jXXXKO3335bN9xwg2bOnKk333xTJSUlWr9+vW677TaNHj1aZ599dp11rVq1SkuXLtVZZ50lSXI6neratatv+gUXXODb5qBBg3zTevfurc2bNwcEnqtWrVLXrl11zDHHSJLatGnjm3bWWWf55r344ov1ww8/6KKLLmrUcejdu3ed/SstLdWMGTN06aWX+uarqqry/X3ppZcSdAIAAAD1tLvMqVHPFupXJ7XSrafmJjs5CdesAs9kOeKIIzR//nyNHz9ef/rTn3TGGWfoF7/4hX7yk58oKytLl156qdLS0tS+fXstWrRIEydO1IsvvqgPPvjAV5LpZa3VoEGDNHPmzJDbyszMlCSlpKT4/vZ+rk87yeDhSowxSktLk8vl8n0XbhzNcPOF2r9nn31W7dq108KFC0Ouq1WrVjGnGQAAAIDb7jJ3fvzbVVUHROBJ50KStm7dqpycHF199dW66667NH/+fHXr1k3dunXTY489phtuuEGStGvXLrlcLl1yySV67LHHNH/+fElSbm6uSkpKJEn9+vVTYWGhL/CsqanRsmXLGpSufv36adu2bZo7d64kqaSkxBecTpo0SXv27FFFRYU+++wznXjiierSpYt27typ3bt3q6qqSl999VXI9fbs2VMLFy6Uy+XS5s2bNWfOnLD716ZNG/Xq1UsffvihJHdgvWjRogbtDwAAAIADEyWekpYsWaK77rpLKSkpSk9P17///W9J0lVXXaXCwkINGDBAkrRlyxbdcMMNvtLCJ554QpJ0/fXX6+abb/Z1LvTRRx/pt7/9rYqKiuRwOPT73/9egwbFXo34/PPP1yuvvKJu3brp/fff12233aaKigplZ2dr8uTJkqSRI0fqkksuUUFBga6++mqNGDFCkvTggw9q5MiR6t69u/r37x9y/SeeeKJ69eqlgQMHasCAATr66KMj7t8777yjW265RY899phqamr0f//3fxoyZEi9jjEAAACAA5ex1jbZxkaMGGHz8vICvluxYoUvsGtubr31Vg0bNkw///nPk52UAMG90sa6TH5+fpOO5dmczy0AAACQSCUl8yJOX72zRpe8vFt9Oqfp05sa10loc9KmzYh51toRwd9T4hnG8OHD1apVK/3tb39LdlIAAAAAYL9G4BnGvHmR31Ak0/XXX6/rr7++XssMHTpUPXv2TEh6AAAAACASAs8DxNChQ5OdBAAAAAAHKHq1BQAAAAAkFIEnAAAAACChCDwBAAAAAAnV7Np4FhXNksOxL27rS0trp7Ztj4vb+hJp1KhRevrpp31jcibS9ddfrzFjxuhnP/tZ2Hlef/11nX322erWrVvC0wMAAACg5Wp2gafDsU8ZGZ3jtr7q6sK4retA8/rrr+vII48k8AQAAADQKFS1lXTRRRdp+PDhGjRokF566SXf961bt9b999+vIUOG6LjjjtOOHTskSfn5+Tr99NN11FFH6YwzztCmTZskuUsRb7nlFh133HHq3bu3pk2bphtvvFEDBgwIGP7klltu0YgRIzRo0CA99NBDIdP03nvvafDgwTryyCN19913B6TJ66OPPvKt98MPP9SRRx6pIUOG6JRTTqmzPmutbr31VvXr109nnnmmdu7c6Zv26KOP6phjjtGRRx6pm266SdZaffTRR8rLy9NVV12loUOHqqKiIuR8AAAAABANgaekV199VfPmzVNeXp6ee+457d69W5JUVlam4447TosWLdIpp5yil19+WZJ022236brrrtPixYt11VVX6be//a1vXXv37tXMmTP1zDPP6IILLtDtt9+uZcuWacmSJVq4cKEk6fHHH1deXp4WL16s6dOna/HixQHp2bp1q+6++25NmTJFCxcu1Ny5c/XZZ59F3IdHH31UEydO1KJFi/TFF1/Umf7pp59q1apVWr58ud58803NmDHDN+3WW2/V3LlztXTpUlVUVOirr77Sz372M40YMULvvPOOFi5cqOzs7JDzAQAAAEA0BJ6SnnvuOV+p5ubNm7VmzRpJUkZGhsaMGSNJGj58uPLz8yVJM2fO1JVXXilJuuaaa/TDDz/41vWTn/xExhgNHjxYXbp00eDBg5WSkqJBgwb5lv/ggw909NFHa9iwYVq2bJmWL18ekJ65c+dq1KhR6ty5s9LS0nTVVVfpu+++i7gPJ554oq6//nq9/PLLcjqddaZ/9913uuKKK5Samqpu3brp9NNP902bOnWqjj32WA0ePFhTpkzRsmXLQm4j1vkAAAAAwF+za+PZ1KZNm6bJkydr5syZysnJ0ahRo1RZWSlJSk9PlzFGkpSamiqHwxF1fZmZmZKklJQU39/ezw6HQxs2bNDTTz+tuXPnqn379rr++ut924uFNz2SApZ78cUXNXv2bI0bN07Dhw/XvHnz1LFjx6jrq6ys1K9//Wvl5eXpkEMO0cMPPxwyPbHOBwAAAADBDvgSz6KiIrVv3145OTlauXKlZs2aFXWZE044Qf/73/8kSe+8845OPvnkmLdXXFysVq1aqW3bttqxY4e+/vrrOvOMHDlS06dP165du+R0OvXee+/p1FNPlSR16dJFK1askMvl0qeffupbZt26dTr22GP16KOPqnPnztq8eXPAOk855RS9//77cjqd2rZtm6ZOnSqpNnjt1KmTSktL9dFHH/mWyc3NVUlJSdT5AAAAACCSZlfimZbWLq490aaltYs4/dxzz9WLL76oAQMGqF+/fjruuOhDrzz//PO64YYb9NRTT6lz58567bXXYk7PkCFDNGzYMPXv31+HHHKITjzxxDrzdO3aVWPHjtVpp50ma61Gjx6tCy+8UJI0duxYjRkzRp07d9aIESNUWloqSbrrrru0Zs0aWWt1xhlnaMiQIQHr/OlPf6opU6Zo4MCBOvTQQ3X88cdLktq1a6df/vKXOvLII3XwwQfrmGOO8S1z/fXX6+abb1Z2drZmzpwZdj4AAAAA9WOiz9KimKbsmXTEiBE2Ly8v4LsVK1ZowIABTZYGNB3OLQAAAA5UJSXzIk5fvbNGl7y8W306p+nTmzo1UaoSr02bEfOstSOCvz/gq9oCAAAAABKLwBMAAAAAkFDNIvBsyuq+aBqcUwAAAABeSQ88s7KytHv3bgKVFsRaq927dysrKyvZSQEAAADQDCS9V9sePXqooKBAhYXx68kWyZeVlaUePXokOxkAAAAAmoGkB57p6enq1atXspMBAAAAAEiQpFe1BQAAAAC0bASeAAAAANDETLIT0MQIPAEAAACgiR1oXasSeAIAAAAAEorAEwAAAACQUFEDT2PMIcaYqcaY5caYZcaY33m+72CMmWSMWeP5v33ikwsAAAAA2N/EUuLpkPQHa+1AScdJ+o0xZqCkeyR9a63tK+lbz2cAAAAAQBPbXuyUyzbflqNRA09r7TZr7XzP3yWSVkjqLulCSW94ZntD0kUJSiMAAAAAIIwt+xw66/lC/fu70novW1zp0puzy2QbELRaa/Xu3DLtKXNFnbdebTyNMT0lDZM0W1IXa+02z6TtkrqEWeYmY0yeMSavsLCwPpsDAAAAAESxs8Qd+M3Kr673so9NKNZTk0s0Z2P9l12906EnvinRvV/sizpvzIGnMaa1pI8l/d5aW+w/zbrD45AhsrX2JWvtCGvtiM6dO8e6OQAAAABosZrLOJ7FFe6gtdpR/2VrnO7/iyriVOJpjEmXO+h8x1r7iefrHcaYrp7pXSXtrH9SAQAAAAAtXSy92hpJ/5W0wlr7d79JX0i6zvP3dZI+j3/yAAAAAKDlab7dACVGWgzznCjpGklLjDELPd/dJ2mspA+MMT+XtFHSZQlJIQAAAAAgrHgEsYkOhKMGntbaHxS+CvIZ8U0OAAAAAKAhGtJu1DRRY9N69WoLAAAAAEB9EXgCAAAAQAvQkOqyDRi+s0EIPAEAAABgP9ZchmaJhMATAAAAAPZjjSm0pI0nAAAAALRQiYj3mnPJJ4EnAAAAACChCDwBAAAAoIk1UZ8+sUtwL0MEngAAAABwgDJNVEGXwBMAAAAA9mONKay0TVT2SuAJAAAAAAe6BHdvS+AJAAAAAPuxuMSMjSg2jWVRAk8AAAAAOEDRxhMAAAAAWqjmPOZmfcVS4krgCQAAAABIKAJPAAAAANiPxWMIzkT3bUvgCQAAAAAtQEM6GUpwZ7Y+BJ4AAAAA0MSaZvTM6OJRWhoLAk8AAAAAOMAluuCTwBMAAAAAWoDGlF42puCTcTwBAAAAAGHRxhMAAAAAELOmCiIbsl0CTwAAAABoYkmKEZOGwBMAAAAADnCJ7t2WwBMAAAAAkFAEngAAAACwH4u1sNJaq4krKlXjrLtEfduHbityav7m6pjnJ/AEAAAAgCYWKlgsr3Zp9L8KtWhL7AFdfUxdXaU7P9mnl34obfS6zv1noZ6aXBLz/ASeAAAAANBEvl1VqU8XloectnRrjTbtdeofUxsfGIayr8IlSdpR4mr0ulz1bBOa1ugtAgAAAABi8vuP9kmSPv5lx7its7495IbqSKgxnQvFsiwlngAAAABwAAgVoDbVsC4EngAAAADQxOIZ8MXcuVAct+kvlo6JCDwBAAAAAAlF4AkAAAAAB4CmqlYbCoEnAAAAABxAElXlNhICTwAAAAA4ECSxyJPAEwAAAACaWDJKHZOJwBMAAAAADnCNCYQZxxMAAAAAEFYsQ6HEA4EnAAAAABxAbJwr+jKOJwAAAAA0Q8no5yfUNmOpJhsPBJ4AAAAAsB9rquCxMQg8AQAAAKAFaEh7Tdp4AgAAAADiLwklpASeAAAAANACRKtya5qqeDMEAk8AAAAAaGLxLHSMNZ60ESLTxrQTZRxPAAAAAGjh6FwIAAAAANAkopV8UtUWAAAAAA4gyQsBQ1fzbUxMGsuyBJ4AAAAAcACIFB8murougScAAAAAIKEIPAEAAABgv9b8exci8AQAAACAFiCZ7UajIfAEAAAAgBYg1nLPUO05G1NmyjieAAAAANDixVbWGar32aYaYYXAEwAAAACaWKhCwmS01Ex0b7ZeBJ4AAAAAsF9rfPTYmIJPxvEEAAAAgGYoVKzW2FqvjVk+0QWfUQNPY8yrxpidxpilft89bIzZYoxZ6Pl3fmKTCQAAAACIB/8gszm18Xxd0rkhvn/GWjvU8298fJMFAAAAAAeGm9/bo0krK5t8u795f6+mrq5qkm1FDTyttd9J2tMEaQEAAACAFsdlrRYWVAd8t6+ittzxx/XVuuPjfXGv7lpS6dKanTVhp3+3tjbo3LTHqd1lzjinoFZj2njeaoxZ7KmK2z5uKQIAAACAFuTdueW65o09+mFdbaB349t1y/aqHY3bTnDgesNbe3Txy7tjWvbvU0p09vOFDdtuAsfx/LekwyUNlbRN0t/CzWiMuckYk2eMySssbNiOAAAAAMD+at0ud0S5tSi2EsV4NbtctTN0JBsuUKxOXIFnwwJPa+0Oa63TWuuS9LKkkRHmfclaO8JaO6Jz584NTScAAAAAHBAaWuU2WsDaVB0JhdKgwNMY09Xv408lLQ03LwAAAABAiR+zJNrmk7j9tGgzGGPekzRKUidjTIGkhySNMsYMlfvQ5Uv6VeKSCAAAAAD7ryQWNDaJWEpSowae1torQnz93wakBwAAAACQJPtdVVsAAAAAQPNQ3yq0yahxS+AJAAAAAM1AYwNCE6VIM5lVfgk8AQAAAKA58BRdNjRAtMnsPSgKAk8AAAAAaAKxhoX1DR+T2XZTiq2qL4EnAAAAACRQzIFhsiPIBCLwBAAAAID9WL1r2CahRi6BJwAAAAC0ANE6F0rcdqPPQ+AJAAAAAEnSjPsDiisCTwAAAABoDhIchSazCSmBJwAAAAA0gWhxpXdyS+xiiMATAAAAABIoUiBp/Xr6Mb7vEisZtXsJPAEAAAAADcY4ngAAAACApCPwBAAAAIAkacpebZPZdpTAEwAAAACSxIb5O6HbjPOGGMcTAAAAAPYTDQ0IY12M4VQAAAAAoIWzMYaIDY0Poy3XlNV6gxF4AgAAAEAi1bOoMYnxYcIQeAIAAADAAYCqtgAAAABwILIh/2zsquIyX8zbZRxPAAAAAECyEXgCAAAAQJLEs/QxmeN0RkPgCQAAAABNIFqV1GT2OptoBJ4AAAAAkECRSiJtiDaezbnkMpRYOi0i8AQAAACAJAlVyJnogk+bhKLVtCbfIgAAAAAgbjbsckqSKmpqA8riSldCtlVW5ZKjAasm8AQAAACAJPGvpbp6h6NB63h8YrEkacnWGt93J/5tZ8Rlnp5c3KBtjXp2pyobkEwCTwAAAABoAqVVdau4+n/zr+9L67W+C14sVHZ67C1Cjacx5o/rq1Ve3bDqtqGCzlhq7hJ4AgAAAEATeH56/QLLaDbsdjZouYYGnY1B50IAAAAAkECx9PoaMH9ikpFUBJ4AAAAAkCQteexOfwSeAAAAAJAkyRhOJd4YxxMAAAAAICm5VXgJPAEAAAAgWfa34s0GIvAEAAAAACQUgScAAAAAJFDEKq4toAvbWDpIIvAEAAAAgGQJEbS1gFi0DgJPAAAAADgA1Hc80Xgi8AQAAACAZqQl9jdE4AkAAAAASWJbZJhZF4EnAAAAACRJLB3zNHexVOEl8AQAAACABEpm20p/yUwGgScAAAAAJMm2Yleyk9AkCDwBAAAAoBlpJgWkcUXgCQAAAABosFjaqRJ4AgAAAEAz0gL6G6qDwBMAAAAADgB0LgQAAAAALVRLbLNZXwSeAAAAAIAGYxxPAAAAADjA2Vh6/0kwAk8AAAAAaEZaYtVcAk8AAAAAOBAkMaIl8AQAAACAZiT5FWPrh3E8AQAAAABJR+AJAAAAAInUEhtt1hOBJwAAAAAgoQg8AQAAAKAF8zbBTGbBa9TA0xjzqjFmpzFmqd93HYwxk4wxazz/t09sMgEAAADgwLC/1cw1MSQ4lhLP1yWdG/TdPZK+tdb2lfSt5zMAAAAAIE4cLqsJyytkrVV5tavJtut0WTld8e1bNy3aDNba74wxPYO+vlDSKM/fb0iaJunueCYMAAAAAPZX1Q6rjDR3UeDklZX1WtZlre77Yp9KKq2mranSXZ8WSZIeOLeNLhueU++0OF1ShcOlTxdVRJ23xml10t93qlWG0XmDsjSsR4bO7J/lmxbOrA1V+mJJ+PVHDTzD6GKt3eb5e7ukLg1cDwAAAAC0KN+vKdQ1/92hN6/toCqH1fbi+pVW5m2qkVRT5/uPFpRHDTzXFtaoT+f0gO+OHrsj5m175y2vtnpzdrnenF2uJfcfHHE91kq/fHdvxPU2unMha61VhDFOjTE3GWPyjDF5hYWFjd0cAAAAADRrP6zdJUmav7laRZXxrbIazWMTipt0e7FqaOC5wxjTVZI8/+8MN6O19iVr7Qhr7YjOnTs3cHMAAAAAsH+xktzldE24zabdXMwaGnh+Iek6z9/XSfo8PskBAAAAgP2b8fZL20yDwGSIZTiV9yTNlNTPGFNgjPm5pLGSzjLGrJF0puczAAAAAAB1xNKr7RVhJp0R57QAAAAAAPYz8RrHEwAAAAAQI5PEmrYtrY0nAAAAAKCZaaZxJ4EnAAAAAKDhYillJfAEAAAAgDjyNnlMRrVXqtoCAAAAwAHAv7Od5hoINjUCTwAAAABAQhF4AgAAAEACJKVX2yRsMxYEngAAAAAQR0YxDGzZADEFlc008iTwBAAAAIAEsLbp48BkxJ0mhjibwBMAAAAA9gOJKUdtGgSeAAAAAIAG21XqijoPgScAAAAAxJG36mlSOhdKwkZ3lBB4AgAAAEDSMI6nG4EnAAAAACChCDwBAAAAII58nQAlobTTNtPxVAg8AQAAACCeYhlfJEGaa9VeAk8AAAAASJBmGgc2OQJPAAAAAEiAZFR7ba6BLoEnAAAAAMRR8iraNl8EngAAAADQUjTTIk8CTwAAAABIAGubb2c/TY3AEwAAAADiKImd2jbXAk8CTwAAAABIhGQEgc21hJXAEwAAAADiyNC9UB0EngAAAACAhCLwBAAAAIAEsFZyuJq27uu+CleTbi9WaclOAAAAAAC0JN7Ohaykv31bErf1rtjh0ODHtys30+jlKzuEnGdHiUsllfEPPm0jG49S4gkAAAAACVJUEf8Sz5Iqq/97bXfY6Sf8bWfct9lYBJ4AAAAAgIgaGz4TeAIAAABAHNGnbV0EngAAAACAiBo7PiiBJwAAAAAkQtN2aNusEXgCAAAAQByZFljXljaeAAAAANAMUeBZi8ATAAAAAOLItMAiT9p4AgAAAACaNQJPAAAAAEgAqtrWIvAEAAAAACQUgScAAAAAICLaeAIAAABAM9TYYK0lIfAEAAAAgDjydmrbkuJOxvEEAAAAADRrBJ4AAAAAgLAcLqttRc5GrSMtTmkBAAAAAEgyall1bYc9saPR66DEEwAAAADiyNvGE7UIPAEAAAAACUXgCQAAAAAJYFtKXds4IPAEAAAAgDiipm1dBJ4AAAAAgIQi8AQAAAAAJBSBJwAAAAAkgKWJpw+BJwAAAADEkWlZw3jGBYEnAAAAACChCDwBAAAAAAlF4AkAAAAAcWQ8A6rQxrMWgScAAAAAIKEIPAEAAAAACZXWmIWNMfmSSiQ5JTmstSPikSgAAAAA2F/Rq21djQo8PU6z1u6Kw3oAAAAAAC0QVW0BAAAAII4+mb9FkrSj2JnklDQfjQ08raRvjDHzjDE3hZrBGHOTMSbPGJNXWFjYyM0BAAAAQPO2fFuxJGnSyqokp6T5aGzgeZK19mhJ50n6jTHmlOAZrLUvWWtHWGtHdO7cuZGbAwAAAADsbxoVeFprt3j+3ynpU0kj45EoBPpi0Vat3lGS7GQAAAAAQIM0OPA0xrQyxuR6/5Z0tqSl8UoYav32vQU6+5nvkp0MAAAAAGiQxvRq20XSp8bdV3CapHettRPikioAAAAAQIvR4MDTWrte0pA4pgUAAAAA0AIxnAoAAAAAIKEIPAEAAAAACUXgCQAAAABIKAJPAAAAAEBCEXgCAAAAABKKwBMAAAAAkFAEnmhWXC6rGqcr2ckAAADNTElljXaVViU7GfuF/F1lyU7CfmF7UaUqqp3JTsYBg8ATzcq9nyxR3/u/TnYyAABAMzPqqWka8djkZCej2ft2xQ6Nenqaxi/ZluykNHvHPfGtrnt1TrKTccAg8ESz8n7e5mQnAQAANEO7y6qTnYT9woptxZKkZVuLkpyS/cOc/D3JTsIBg8ATTWLpliJV1lCVAQAOFOXVDi3fWpzsZAAHLGuTnQIgEIEnEm53aZXGPP+D7vpocbKTAgBoIre+u0DnP/c97acAAJIIPNEEyj2Zjvkb98a8jOU1HQDs1+Z6qq9VO+gwDkgGY5KdAiAQgScSriE3PhdxJwDs17y3fitu6EAy8A4fzQ2BZxOauGy77v90SbKT0eSMJ/KsTymmi7tlRMu3FqvnPeO0YFPspcgA0JRSUrz3/iQnBDjAGIo60UwReDahX701T+/M3pTsZCRNffIeBJ6RTV21U5I0cdmOJKcEAEJL8WR+uZ8DACQCTzQBX3WreuQ9yKdE5s3QUYUNQHPlvffTdAIAIBF4ooGstfrP9HUqLKmKOq+3xkd9giQCz8h8x5TjBOz31u4s1abd5clORtw15N4PAGi5CDzRIMu3FeuJr1fqd/9bEHVeo/q386FqVmQpvsCT4wTs7878+3Sd8tTUZCcjAXyRJwAABJ5oGIfTnZMorXJEnbdhvdqSU4nEG8xThQ1Ac5VC3AkA8EPgiQZpSEaiPss0JqMyddVOzVi7qxFraDyH06WlW4oStn6q2gLJs66wVOXV0V+67Y/Kqx0qrqyJy7roXAhIrki/vG1FFdpVGr25FBBPBJ5oEG8Vz1gKMxvUuVAjxhu/4bW5uvKV2Q1fQRz0uf9rjXn+B323ujAh6zd0LgQkhctldcbfputXb81LdlIS4ri/fKujHv4mLuvyviCjZkbjfDyvQCeOnULTCsTV8U9M0YjHJic7GTjApCU7AdjP1asebfSHpjHuALWlvCHfuLtMUue4r7chwTyAxvP+5H5Icq2KRCmujF9Jrq9XWyLPRrnro0VyWXcAn8rwjKgHLhc0N5R4NmPFlTWqcjiTnYxG82Y5rHWXlEZ6a1vb/X7LyKgkai8MnQvFLNo1BzeOU2y8x4hDFZ2vZkacjpXD6VJRRXyqAe9Pap+hzfs3aq3VnrLqZCcDfprv1YIDFYFnM3bUw9/o6iRXGW2IBZv2quc943z/tu6rkCTVOF3qde949bp3fNSHZ0t5QZ6oPIKvxDMxq99vTV25U0f/eZIqqmtf2Jzz7Hca8OCEJKZq//DfHzao173jta+cjGMkLfU3V+1w6di/xLfanfcFmTNON8I7P1ykIY/EpxpwNL95d74mLN0uSVqxrVg97xmnpVuKtHZnqfr96Wtt3hO/4W92llRqwAMTtHRLkWat361rX50jp99D0Hv4Rjw+WSeOnRK37cbb+3M36+g/T9KKbcXJTgqAZorAs5mbm7832UkIKVI24stF2wI+T16xQ1JgFa7dYd6K0nYxNvEuSWgp/jJ+hfaUVWvz3tpM4eodpaqsaUSj4QPE+3M3S5J2xjA274Gspf7m9lVUa0dxfM99vDsX+mzh1risJxbjFm/TzW+72/FOWu5+hk1ctl0f5m1WlcOlrxZvi7R4vXy3epcqapx69ccNuvXd+fpudaF2l9U9F/vKa7S1qDJu242379a4+zRYX1iW5JQAaK4IPNEoodoPBDf7DJXnCJcPSWlhvbUmqlpUiq/TjhZyoOKEo4FEa6kvxTJTU+O+zkQ1CUhmdVPvlhsyTFhs9t8xaFye93spNCxsNsgioLkh8Gwi1706J9lJiKtIN7PgZ06oWcNl3mrHp2yau+XqHSWaumpnTPO+P3eTVm0vqdf6y6qdenbyajmc8S1xM76ShLiuNqIZ63btN52ENEW+p7TKodOfnqYFm5q2VkJxZY0WF+xr0m2iVkNuTZU1Tk1YGr8SslCmrdqphz5f6vv8s3/P0L2fLIm4zI7iSq3dWSopMQF1bZv9+i+7s6RSD3+xTDUh7p31PQdvz9ro289wJi/foQ/yNkddV7Qe3XeXVumhz5eGTLfTZfXIl8u0o7hSe8uq62zP4bS+4S02xbEqb6wqa5x68POlKipvWDta73M7cUE5EmHexuTXrKtxuvTMpNVNPkxVIl5ibdhVppvezFNlzf7fR0siEHg2kekJGlYj2UI9YIK/CxlERvmtN1V8c/Yz3+mG1+bGNO/dHy/ROc9+V6/1PzVxlZ6dvCau1bIk/2PcNAdq8vIduvLl2XptRn6TbG9/sGjzPq3fVaanJq5q0u3+/PW5uuCFH+P+MgOJ8+evluvmt+dr3sY9CdvG9a/N1RszN/o+523cq/fmbIq4zLF/+VZn/n26pMSUjJhGVLV97KsVen1Gvq+aq7/6ru9Pny3V6Oe+jzjPL97M0x8/Whx1Xd5Np4SJrh79arnemLlRE5dtrzNtxrpdeu3HfN398WL99n8L9MePFmvtzlJfEPvFotqqxD97cWbUtMTbx/ML9ObMjXr6m4bd07zPbUPk2WzEciou+feMxCckio/mFegf367RPyavSXZSGu2Bz5bqm+U7NGdD4u73+zMCT8RdLA+dsNmGFtpba7UjziWeato2nluL3B1E5e9q3m13mvK6SdYlOn/TvuRsGJIadt4373X/fuI5VEm8JaKWia9zoQa8SfQuG6pn94aktCpO9+BoVW0dnn0Ntcve4+B0WRV62lLH+9nQGN40N/Ra8N5/wwXlaHr7S1bKWzoYr99prBLzws2z7vivukXYrwPPhvS+WFHt1M7i0I3zN+0u194oXYFv3lOuV75fH/P2tuyr0M6S+HcGUFxZo7z8wLcp24oq6jykV20vUWWNU1v2VejF6evikjH/fk2htns6OHC6rJZuKVJxZY0cTpf2llVr4eZ9gQuEaeP57uxNvnM4Z8Me5e8qCxifssrh1PKttb3jzVi7S3/4YJGKK2u0aPM+WWs1bdXOhAQbM9ftrlevhaVVDq3aXiJrre/YJJJpYW1h4y3WfM/SLUX1Ljn0XXeqrVa2dEtRvXpy3F1apRemrPFdu+sLS2MuDfMN5xFhHpfLNro6bmmVw/fGtqiiJuq9sTlavrU47kNSJbuNp7VWUxNw3wte2xZPb+SxqKxxaofnuVrjdKm0yh1gewOQPWXVnjGNa5VU1kSsfpyR6s6ehArMgnd95fbiJqvW5r/t79cU1qlS6731vDUz32/oHau/jF+h5751l+Y09xLB+l5ZDqdL01cX+gLW1CbIWS4u2Ffvpi/JsHJ7saasrFtqn2iRLrHpqwtD1iSIVcHe8kYd+8oaZ50qtclqxZOIzdZ2/kgGLZS0ZCegofLy9+hnL87Ui1cfrXOP7Brzcpe/NFOLC4qUP3Z0nWmnPDVVuZlpWvLIOWGXv+7VOVq/q0wXDu2uzrmZUbeXqK7Pb3ozT7PW79GKR89VdkaqXC6r45+YonMHHawXrxkuyf1gP+fZ73TuoIM1wVPtJy3F6Bcn927Utq/5b2171cUFRRrz/A+SpEuO7qElW/Zp9Y7AtjSh3p6u3F6s+z5dom+Wb9frN4zUZf9xVyvKSk/xLXP/p0v10bwCzbnvDB3UJktXeoaW+Xh+gSTpuN4dNGv9Hj120ZG6+rjDGrVPwa54eZaMkTY8Ufc6CeW6V+do3sa9uumU3vpswZY60+OdWfV1wsQ7tQZbvaNEY57/Qb86tbfuPW9AzMt9umCL7vhgkc4ffLDvO+9vINR9JZQ/frRY367cqZG9Ompkrw46/W/T67W8FPmlw39/2KDHx6/Qe788Tscf3jHmdfq77d35mrqqUAseOEvD/jyp3ulLtp3FlTr/ue916fAeeurSIXFbb7LzEu/P3ax7Plmipy8dop8N7xG39Qbv14ljp2jpI+eodWb0bMK1r85xvzwcO1o3vj5X36/Zpfyxo31BmPeZ4X/9/PGjxfp66XZNvuNU9TmodZ11pnmilxpn3QPuf98rrqzRuc9+r9GDu+qfVx0dYr/ie8K8z7P5m/bqsXErdPOph+ue8/rXmW9u/l5NW12o0/odpPmb9uql78K/sG4ucWhDk/Gf79YHNDloisD6ghd+lNT870nnPuuu4t2c0tnYPkdOenKqpIbv01nPTNfmPRUBy/vaTjeT30JjMNxdZPttieeSLUWS3CVT9bG4oCji9JKqyFWhvINXJ/vH4d0P70PQ+/83y2vblXjfFM/xKxldnsDxtT6eX1An6HSnre683szEzqDu+2s7F5Lmexq8h6ueNmu9e7/iOZ6av/rkV7yN81/9YUOTDEfhf5zQMN6qbos3R74nBPOOS7tlb+wlQsHKPG97Ha6GVyuK9NJhxXb377w+pVbBvPeKyjiXGDaV4kr3vXp+nDt/SvZPrsBz3W1rxLkNJdT15D8ebiT+bZm+X7PL93ek56S385xYt+HP/95c6Vl+Tn7oGgOJelHgvX8ENz/wD7q8+xZcqcIEzJ+Q5DVKfY9ZQdC9sBnu0gEn2S/IItm8J/y9yzTx1ZPQUslmfA6Sab8KPKscTl/PdN4qPPm7y1UWFCyWVjnqVJ9zuWzMF5jLZbWnrDrkA9HXa5vnc0lljS8Ytda9jaKKGl+mp6FCtYnxr0rknR6pLnmoMdTC9UpaXu3wVaVzuazKqhyqcbrkclmVVjl8x27plvpl0iX5qmD58x4/Z9B5Ceh+P8b7j3cd3n+NUbC33Hc+G8IR5vhGS1ZxZU1MafftY5iqtqVVDt+1Ya1tVODR0qzcHvjSpfatZAPbM/nWE/pCraxxRq3mWVLpqPc16527IZd6jdMVc6+BicgAbCuqUFmVIy7t2qL93mM9PhXVTl91yeB1htpGrOfLu6z/b9t7RKsdrrABV3m1Q5t2lwdsZ9nWotrnTJTrtaE9T4fuA879ZWWNs05V1mjXd0lljUpibNO6ZV9FiOMavgTEf9Zo97j6Ho3g/XSfx7rb846xnRo0doj/J2vd5yN4H4yp3YdIl1N9n2nbiyoD8j7e5V0u63thFklDOq3bUVyptKBjEK2N58rtxSGv0/Lqunm35iLcuaA6ZXx4D2NDX8SUVNY0qDfmaGevzC9PFStqpEW2XwWe93+6VGf+fbr2llX7Tuz01YUa9NBE34XhcLp05EMT1ef+r1XjdKn3veP0xox89b5vvHrdOz6m7fS+b7yO/vMkDXhwglbvKNEfP1qki/7prtbhvYyGPzZZ936yRIMf/kZDHvlGkjTyL9+q173jNeSRb3TUw9+EXf/Rf56kf05dGzENoXrK7P/ABPW8Z5wqa5y+YPLtWRvV855x6nv/12HX5X+DD1FrSbtKqzTwwYka9udJ2rynXL3vG69BD01U3/u/1jOTV+vIhyaq173j1fOecb4qhfURqkfXX7yZ506btbrWr9qH955z+t+mBwxCHRw0+Hvlhw3qde94379Y7QnRZu2kJ6f6zmc4jW0zNmn5DvW8Z5y2eTrs2bynXEc9/I2enLBKPe8Zp573jAu77N8nrVave8fL4fS286s9oVUOp458aKIe/XKZJOnDvAKdOHZKxK7Sf/e/BRr04IQG7ceaHSXqec84rd7RdO1sfv3OPF3z39khp539zHSt810zdZ9e5z77vRb5tz9u4AMuUjUy/3aV/R+YoNOfnh5yPu9D9ldvzavXNRtqHbF45fv1uvw/M3Xly7M08MGJIefxZqinrAwcXijUdhpy3WzdV6Hjn5iiQQ9N1MX//jHsfJf8e4Ze/3FD1PUd8/i3vipfkfifrxtem+NrZ+c14MEJutpTjf+CF35U7/tqz8czk9eo173jdfJfa5tM+B+OnveM07+mhb6X3/ruAvW6d7yOevibgHuZJF387x81IMzxG/jgRJ3y1FR9mFfg+270cz/oypdnubcfJYPmbGBG+N/T1tX5buTj32rR5n3q/8AE9X8gML39H5igEY9NDvjOPxM+7NFJ2hbU3r2wpEo97xmncYu3+fZj+bYinTh2it6atTFgXt9+hviheu97ny/cop/+K3KPnMFNPd6etTHiMDPX/ndOwH48OWGVnpm8WpL0zbIdddrGGeN+edHznnF6a2a+9vr1PbG4YJ963zc+Ys2s85/7Xnd8sCjktL9OXBX1/lBZ4972M5NW67gnvlUfv7xAr3vH6/KXZulf09bqhLFTYu4c7r05m2Pqib+0yqFj//JtnXN37atz1POecbr5rXm+74oqajTisUl6c2a+zn32+5B5oIEPTtSv35kvSbrl7fD3+mAPf7Es4nOzIb5YtFWnPT3Nl3865vHJvvuNw+nSyX+dors+XKRe944PaO84Y+0u9bxnnHaWVEbNS4TzzuyNOvy+8REDnp73jNP9n4a/jpuiJL3nPeNiulfXh3+yL3zhB415PnJv1F7DHp2kIY9+ozHPf68/fRZ5GKlYuVxWgx6aWO/1+Xrzbp7vUJJuvwo8vTfv0ipHnV+V9y2lf4lTSaVDLis99MWyBm/zrxNW6YO8Al+HOf5BXHBX9YUxVrHcU1YddQiGqSvDjy25t7zad0P6y/iVYecLVTLiDPFLWONXPTY4iPDv3j0RnNYGVc0KfbcMFTwFv2murw27Io/rFk55VeMCT+914+04Kd/T6caL0+tm/IK94RnOpNob/PqdW29vcB/Pd7cxneuperYuwvh1ny/cqrIGVHWTal8oxHuomEjGL9kecL3486/mHe6hG+qtfzxfWM9eH1jdLxElzr6Sknq8TX1s3ArN3rDHV0oTSrnnOvgwhrEMG3Ld+Nd8WLol/IukeRv36uEvl0dd367Sqnof36mrCvX3SavrfD/bU1V0yZaigOvhrZn5kgKrhgVfL89/GzrwHLek9ncRnM5I++/l/f16g6BlW2NrJtGQHmSlus8zr5nrwwdNwSWa/psOVftjjef58rZfoJK/213ldlaE7QTznoP5MYw/GHy+/vTZ0ojDzMzJ3xOwzKt+GetVIV6ypRij3WXuZ/+/p63TrtLawHOGJ8/y/ZrAIM4otsDg1R+iZ+r3eUp5/vFt6GEo5mzY47tnBr8ICOYf5E9ZEb3zmfIoTZMm+A0ps3DzPu0qrdaDny/zfQ7lG09g//XS8Pf6YK8nYJivuz5cpA27ylTtKYHdVVrt+x0XVdRo854KfTjP/XJo4eba6/DVH91pWbBpX4NrTz365XI5XTZqzZB3ZkceLqkp/CvEC6uGCPU8W1RQFNO9Uqq93yzdUqy3Z8V+XCI9/70v8fxfAsaCNp6R7VeBp39PnuFiDv+HbkMfwIGCq1nFYZUxiNadebhd8//am2HxX1e0YxI8OdEvzYLTE2p7/tWS/KU28pVeQztASGlAwOuf/HgMsu1NQ6TrhJteZI2tShqpamJToIZXZAk7PDb4Y2K25F1rfR9jDb0uwt2P6rO+qG2WPdvwv295b6fBi0Yq2fVVc49p6K76H5CA+2qUxVNMbdqD01N7rw9RahtDsuJ1ZXm31ch3tXXVY33Bsza0ZL45iJTyeJQ0NrbaacC6EvxMitcwTN77XEPyV4nS2Hsp1bBDa/Jebd+etVGdWmdoYNe2evjLZXrhymH659S16nNQax3cJltXeKoTffuHU3V4Z3dPdzVOl578eqWvAfuDXyzV2QMPDlivlfTXCSt1wuGdfN9Fegje+u58fbV4mz77zYl6f+4mPXrhkSHnm7yituSx35++DnsjiLXdlL/lW4t1/nPf67bT++gPZ/fTM5NWa97GvXrhymFaE6GUakdx+JJVa90X+0fzCnwlaf4ZF//mE38Zv6JOT3t/Cxo42vs2OlEcQXV/w3Xu9KfPltb5rjpKW5BJy3do3OKtmra6UI9ddKTu/HCRKmtcuv6EnlqypUgPjBnomzfUsfCavHxHQLUj783k6Ymr9MLUtTpzQJeI6fD33LdrNG2Ve103vp4X83LBvJfhZwu36rOFW/XN7afo4LZZAfP47nnGXWWlb5dcPe3Xu2dwe91P5hfojg8W6aDcTL187Qhd+M8fde95/fWrUw+Pmpa/jF+h5VuL9cPaXRp6SDuNOaqrr/fkE8dO0RFdWuu1G0aGXP7d2Zt0eOdWOrZ3/XtfLaty6OlvVumP59TtVTKUF6ev06s/btCHN5/g+272hj16f+4mbdpTrjdnbFTPTq300S3HKzMtVdNXF6ptdrp6dWqlIY98o+tP6KkZ69xv4UM90KM9ZzbsKtNpT08LO91bXax3p1Z648aROvmvU/XJr0/Qlr0VKq92KCs91Tfv2K9XqnVWmpwuq8y0FP3h7H511nfnh4v0ZYRaC7/73wKN6NlB1/j1Cr2usEzf+JVU+Lvmv7O1IMQ4opt2l+vGN+bqvV8ep865mXpm0mq9PWuj5j1wlm+evDClrfm7yvTfHzboxD4dI97bvKy1ATVGHE6XrwfUUNbuLNXZz0zXR7fUnvPf/2+Bnv2/YWGXKSypUufczDoBw2s/btDu0sAq+pU1Lr0xI1/XndAzatqfmbRao/od5Pv8n+nrtCfMsGAfzSvQ10u26RG/Z1PPe8bpxhN7SaoNZr5ctFUfzat9Ix+coT/lr1N9Hfn87oy+ap+TrsUFRfr75UN989z7yWJV1oS+nz45obZWTc97xunfVx2tw/16ofUfZifai03f+MN+33nbA05Ytl3l1Q7lZKR55rGe6XXXs7hgn044vFNASZe17nvYhKXb9dK1IyS52877N3s5/W/TfH//9r0Fyt9dpk6tM/Xq9ccErN//2RLtOfPZwq2+kq0t+yoCSre9pdShBpIPVXoaLFyJ15SVO/Srt+apxmn1+zP71pne855xGtKjre+zt+OlVTtKtGDzPl157KG69N8z1TYnXXM27NFvT++j56as1YN+z8Q3Zm7U6h2lKiyt0gtXDtMr32/QQz8ZqOenrFVaitGyrcUxVcftec84fXP7KXXyTtNWFaqi2j3U29uzNgZse/BDoZsDRPPs5NU6sU8ntc5M0+3vL9STlxylf3y7Rv+66mi9NXOjjjg4V6ce0dk3/8NfLFPfLq31+LgV+uBXxyt/d5lufXeBJCk91Z3gy/8zU2/94ljfMr//3wJtCMoXhawOXs+YY9zibSqqqNGVxx7qC+a+W12oswcdrBXbinXeP77X5DtOUc+OrXTyXwObGNz0Zp4O65ij+0cPrLPeV77foIFd22jV9hL98dzYnpPvzN6oY3t1UJ+Dcn3DB14wtJven7O5TinurtJq/fqdebrl1D4a3KOtqh0u/ebd+brjrCM0oGsbfb5wi1ZsKwnZ87PX/E17NfZr930mVBb7jvcX6rJjDtGKbcU6o38XHdoxR5L7fD87eY2+uPXEkOvdW1bt65H9g18dr/5dc/XspDU6tV9n/e2bVfrZ8B51Orj0WlJQpE89IxT4X7tTV+7UN8t36ImLB/u+s9bqb9+s1uXHHKJDOuT49oKwM7QmDzy9AcQ5g7poysqdmr6qUP+c6i6qH9mzg2++Bz9fqnd+cZwkaeKy7XrFr8rJtFWFOndQYODpdFn9a9q6gGL/Gkf40+6tHuhtu3l20PpCiTSw7Svf17+e+18nun9oz09Zqz+c3c9XVSbUQ8rfY19FroY2a/0e3fXRYt/nwBLP2n0IFWit3A/GxYrVL9+sDey8DxOptlqOf4YmUlf3v3gzMED05q1e8LRRmRxDlSTvKQhVza9Bgp7i45ds089P6uXZVt1S5EUFRVpUUBQQeD7x9YqA+bztjHaWVOlCz+/iia9Xhg08/bfif/wWbt6nhZv3+QLP4MxYsPs87VQa0jX7f6av02s/5qtLm6zoM8t9HEK5++PaNhxLthRp4+5yHdEl19ftvDdTFKpKl/+piPageeTL2Kr9r99Vph/WugPc9+ds1vshqr8Gt6sKFXhKipg5/HzhVn2+cGtA4ClJN701T13b1j2m4aq+/feH9Vq7s1RfLd6qG07sFbLa3+PjV4RYUvrd+wu1aPO+OvsTjssGVu+at3Fv1JcWq3eUapZfO7vPFm6NGHg+Pm65nv2/YXUyQY+EqQL80BfLYgo8g6+/J74O31RCksqqnbrzw8D2f3lB473e9t6CgM/Bwd8mv16//c+Lf+D53pzo1au9bnlnvoYe0s73+dnJtfe0cJ2refl+K9b/u9qjvHVfpW9olUhtPK98eXbI+0VwW8kNQW1r/dvaRmpGEvxyIZqpq6IHYP4aO9yI/0vLZyeHrmIb6l7nrebas2OrgMD3uSnuZ1lwR4DeatbeIUF6tM+O+KwM556PF+uOs+ren/ZVVOvnb8zVxt3lut7v9xNtdIFwnp28Rs9OXqPT+x+kldtLfM+xufl7fPcf/+vG/37++oz8gBc43p73FxUU6aXptfv82cLIzY9qz2z9wo7fvOtu23rlsYf6Xh7d9NY85Y8d7btWJy7boStGHlqnyrS3enKowNPpsvrd/xZKkv54bv+YOh+7/9OlykhN0erHz9Nj49zH7bs1u/RdmGfJ+CXbtXxrsabddZpWbCvWpOU7tKO4Ul/cepJv25ECz5v881ghfhqfLNiiTzxB4MvfrdeMe8+QVHvt++fv/PmP4nDZf2bqxhN76dUfN/iqz0ca5eKCf/4Q8uXBDa/PlaSAwHPNzlK9MHWtpq8u1Je3ncQ461EkraptqKoE/iUI/ics1O8kuNe0UD2h1acTmGi9sEUTPIh0LML9/qPdF6K1bazbK1/t36E6FzoQhDpmDT3n8apa0ih1gsvwHXCEy+Q09pr3bTuJNWO8L4MackoipTuWXQq1zWjXRn0OVXPpGS+WrdcOmF3/9afW8/oJDqyilUg1RnMc6iJa0NLQXm3rw78XU//0OKM8YLz3HOt3VYdrMlHfvQjISzSHe3QzFu74RH1x0IjmCaFOs8Npm03mPGLvwvW4GuNZ1Tb0tMYdsFirOAffV6uj5Kd9z4AGpMk/SdGusfq0mw3e1foMDVafw+x97ntjjoa+fDhQNGmJZ7HfBeM9HU9/U/u21L/jixnrdisvf49G9OwQ8jIMvoBCdYBwbT0GyZ1dj44NQnl+St0OJr5eErnTlZ1+bxf9OxOKlnmdHaVE9Fdvzwv47H/T/G51oW57b4EeGD0g4jqaSiydg0xeHr1EMZpQVcCidfAkhS5ddrlsvV803PfpkoBOKhrKuxdPTghMu8taX0+NZdVO/Wf6Ot/M/uNNvvbjBo05qpuMCXyrP2Vl+GO8fGuxvlvtLul6a9ZGbdpTrgd/MtB3Z/4hTCnY375ZpdvPPML3+f25m9QuJ0P9uuTqs4Vb1KtTK6UHVZGct3GP7v90qf5303GasnKnFm3ep3FLtum5K4bpGL8aEa//uEF9DsrVfzxv39+fG9iZwD8mr9G95/fXmzNDl6L9Y/IafbFoS9h9Hv38D3rykto3mk9/U/da8Vaj8+/0pcZhdfUrs3Xt8bUliK//uEHnDe6qD+ZurlfJiLcUKpbqbJJ8vUTefOrhvurc4SzcvC9gOA9vJzr+vPfdxWE6AZHcL/w+XbDFlxl6d84mtctJ903Py9+jicu266ge7eosO2PdLhWV12h+iKq7kvsteHpqijLTUjS8Z3t9vmCr+nZprYuGdQ+Y79P5W5Sbla6M1BQN7NZGkruaarcQJbbB3vAr8fDvrfSzhVv1zOVDAzqKCVf92Gvisu3aUVypovIabd7bsCYKoXqWDebtmfmpiat08dHd60xfuHmfr2OiSG4Jek7Uh387LP9So1Al8/68Y6r6P+v93wk+8uUyFeytUI3TpdaZ7uzJ9DWF+nHdLt0ZVKJ/7yeLAz77d+73yJfLta6w1FcLpL6iPWMbK7jn6Kb2bpjOlaKNiT11VcPSPX/TvpAdBI5bsi2gRD4Ub/Xrgr3lEXto9xcpOHtzZr5e/n69nr/i6MBlIgQJ0d7lVDldenLCShVV1GjiMvd95NsVgcfq84VbtG5nqa47oaemry7U+YO7+ppONGYIt1D7+v7cTSHX+cn8grAdMU1btVN9u+SGvW9mpqWG/N6rpNKhF6ev00ZPE6/lW4s13i8P/Ny3a5SWavTrUX1835VXOzQ3f692+1XX31ZUobdmbdTcML9Bl5UmLN2ukb06hJzuNWPdLt323vyA7+ZF6FxPch+DzrmZWhbUoZGR0ZKCIn2/NvC5ur2oUq/PyNdhnqq/q3eUauPustoXbMSdIZmmfDPYqdcA2/rypyVJZw7oElMVxfyxo/Xloq11qhN1aJURcjiMluD5K4bV2d/GSE0xcepoCZI0694z9M3y7b5qS4kQrtrp4Icnhhwbr2OrjICbtyT9dFh3XxsFf8f17qBZ6xufsfK2C4rkH/831FfVJpr8saN9bRzb5aT7emv0uvnUw2Pq+TeZMtJSQrbLapWR2uDeg+vrb5cO0R+Cqmcmyn3n99dfxq9UTkaqr1fcZMofO1rbitzDtuRmpQX8Vl6+dkRA9fsPbz5el744M+y6Fj14toY82rDhEKKlMV5DPyTrOXj0oe3CvjCorzvPPiLgBXQ4DdnX4GsgnHieEzTM1DtHhWz//tsz+uqOs47QyMcna2eIkQNCnbtR/ToHvHx76+cjdc1/IxdEXDysu686Z7Boz55YrzP/ea89/jBf3yLX/He2rxlD8P7kjx2tJyes1L+nrdNd5/TT5cccEjCM0X+uGa5feYatyR87Wqt3lOjsZ76LKS3B2mana/4DZ+lwz5BS/mk5uW+nmHsZjuTFq4/WzW+7A8Jrjz8s7MvhaIYe0s7XM/KhHXKivsBojIzUlDolwPljR4fNj5135MH6eun2euV/WqKNT46ZZ60dEfx901a1tWE/RBSq6kJpA9sA7A/iXZWzWVQNbUGc1jaLTLa/4KBTCv/Wt7giPr+dWK6qsgYOPRMcdEoNH/6mKYXrDKSpgk73tpru3ui97prT76HK00lOcIYg+DFSUhm5lCFqD63NQLJevsbzPWasvVg2ZF9jDQaQfOHyKd7aRaGCznDineWJVkBTn+vMO+92v3aaayN0JikF3ruCk7KrNPC4RBuCJZKiipqwhRTxOqYb/Tpmasz9K5GBZrBw12a48+6NWch7h9akVW0rHS55+8KL9Xzk5e/Rtn11x55qzI+ruRsfpYpufXHtx9e7szcmPEPzwdzNOn3AQVq5rUTpqUZtc9JV7XDFZbvRHnKxWlcYfT2lVbFXIYoWCDSn4KY5WxinkqhYFIV4QZBM6wpLw3bOtjioF+dov4NEdbTWEmrqhBuDsSHC9XbclGK5lyGxwo3JGu21RKjx04NfGsVSlXV7cfgxThNRY2xtYalmrN2lQd3aBnQWFNyMx+F0+cao3lFcWbfzML9AbvnWYl919ob6fGFtqa9/1ep49TXg33RkXVDnX/XhP5JEooPQUG2f83eFT7u3GYv/+M+o1aRVbTO79rVdr3tWktS9XXZCBlcH4HbBkG4Re24EAKA5+81ph+v43p109X9nJzspTeJnw3sE9K6bm5kW0Mvvaf0617sX5XiIVxMdHDiaR1VbPwSdQGLRrhcAsD9LMcY3dvKBILgTs+ChZZIRdErxrV6PA1vSAk8AiUXgCQDYnxkdWM+yxo7xmjAHzilAgjVpG08ATWdClOEfAABozqL1nN7SNGZolUSaE8MQTUAsKPEEAAAAACQUgScAAAASLtwY1QAODASeAAAAAICEOuACz0Hd2gR8vu74w5KUkvo7uE1WQtc/uHvbes0/sleHBKUkvDvOOkIZaYm7bC85ukfE6VnpKcrJSG30dg7rmNPodQAAEKyp+6fp3bmVOrTK0MCubSLO9/OTekmSRg/u2hTJAtAM7XeBZ32qaeSPHV3n37jfnqwJvz9ZknREl9Z65MIjG7RuScr705nKHztad5/bP+D7RQ+eHXaZOfefEXGdfxo9IGw6bjujT8Rlf3lyr4jTo/n7ZUOiHoNhh7aTJH18y/H64FfHK3/saPXrkuub/uHNx8e0reDg7dNfn1Bn2+N+e1Kd5X57Rl+tfuw8/fnCQZKkq487NKbtRbPskXOUP3a0/nbZEN93o/p19v194dBuyh87Wiv/fJ6WP3puneVvGXW47xoLx/86nHbnqLikG433+g3HJDsJIV0wpFvc1/nni46MPlMz8OQlg5OdhGbhlCM6B3z2ZtxDufLY2O+Fwfeq5Y+673+z7g18Pp09sEtM6wl13xvSo34vMuPpshE96vU8n/j7UwL25fPfnBgwPXgfI+13tO16l/M/l9GWeeXaEXr/puOi7sc5g7oof+xobXgifPpiTWufg1pHnde7jSl/GKX5D5yl8b87OeJ2HxgzUJJ01zn9ou1Ks5Sa0kx7nK2HY3q2Dzvt+z+e1oQpwYFqvws8mxPvLcgG9TOdEuGoGkW+cVU5XGGnpUR5jZkaacMxiOWm6u3V3D8t1c7waQ4neEs1zvr11V3tmT+tkfvslZZad98z/UpWox77er5ibrZdph+AbDPtJj4Rl0hmAmsLxFNzPSdNLSPovhTpHp2R2vBzm5XmfhHocAXey0PdF2O1P42AEfwMb4oAw1WPizwlRXLGMH9GWuNr4/jW1YjrKZqWEMDtryLlMTkvaAr7Ry6kASJVG+3cOlOSdM6ggyVJuVlpDbrJZntK7fyfB/0PzlVmhJt/tMzk0EPaSZLSUow6tsoImBatGku0XYh2T2mbnR55BtW+Ae/kOYaSdNHQ7r6/u7atrQ58tKd0NNhZA7voJ0GlOaGqEXf220Yw77E4NkR136z0+p9L/wC2d6dWkgJLG04NKnnof3BuwGfveZOkLm1q0906kxGLmkr7nOjXbyjNtdrziMPqvpn+6bDuIeaMXX3vc/GoVt4Q/bu2aXTGN/g3uj9qkxV4TR/Xu4OOClOSOPyw9urRPjuGdda9J6V4Hg5tPM8A7z3s7IEHx5zW4G2fMyhyaWksQv0GYjE8zHJXjDwk5Pedgp41B/s9x847svYYhCvF7eB5VrcLugcFX8NHdq99ho84LPDZ1cHveX9av846vndH3+fDOrbSoR2i36dO79856jzh+KdNki4+uvZec/5g9zHo3i769eXl/2zOTk9Vut9LjP01wLl0eA+NOWr/ria8uKAo7LQ2MeQB9wcn9ukY8Llzbvi8JJqesU34ajmza1+7fsVibdtXoWqnS60z05SZlqpqh0vl1Q4d2jFHhSVVykhL0b7yGvU/OFfFFQ4Vllaqz0G5ykhNUXZGqsqqHEpNMer/wATfus8ffLDGL3GPW/jD3aepc25mxABwb1m12manKyXFqMrhdKcvLVV7y6o17M+TJEmz7ztDHVtlaFtRpTLTU9Q2O10V1U6lphjtLavRoZ4M6z+nrtVTE1fp6uMO1Z9GD1RWeqq2FVXo+CemSHI/jPaVu8dmmnPfGRr5l28lSWsfP0/rCst0WMcc7S6rVqoxvgeeN00llQ6lp6bI4XSpY+tMlVY5tHpHiQ7v1FqLt+zTsEPbq7zKobTUFL324wY97xnz6sd7Tld6qlH7nAwVllQpNcWoTVa6yqodstb9hjctJUUZaSmy1qqk0qFunofKnrJq1Thdys5IVVF5jaqdLmWnp6ptdrpyMlJVWFKlg/wCxRqnS7tKq5SZlqoOrTLU855xkqTv7jpNpzw1VZ1zMzXutycpJ8Od4cnylLpsK6qUy1pV1rjUz5NJrKxxyuVJT5c2WapxutT3/q8luaswt/V7sO8sqdRBuVkq9+yTN6g3MjLGvf7Tnp6mg9tkaXtxZcD579kxRx/cfLwyU1NVXFmjQ/we6tUOlzbvLVfvTq1UWFqlqhpXwHRJKqtyaNBDEyVJM+89XV3b1j6Qy6sdqnFYZaanKMUY7S6rUk5GWp3Afm9ZtUqrHDr5r1MlSZNuP0Wjn/tB1U6X3rxxpN6dvanOWJxXjDxUR/Voq3s/WaKcjFS9ePVwXfvqHPd+G/dLkKMPbafXbhipNTtK1CozTRt3l+nmt+crNcVo8h2nandplX724syA9U6+41S1yUpT25x0bdlboc65mVqxrUSdWmdoX0WNiitq1P/gNiqvdqiwpEqXvzRLwab84VSVVDqUmZ6iovIaXf7SLKWmGI377UlyudzHJXi7H918vG58fa6KKx169vKhGtWvs+bm79Uv38yrs/5Q/nvdCHX3ZHgP7ZCjh79Ypg/yCgLmee36Y7R5b7ke/HyZLhjSTQe3zdJL363XFSMP0T3nDVDb7HTfNZ9ijE7+6xRV1tS+FT5zQBfN27hHe8vDj6/21W0nKTsjVa0y0lTjdKmookZZ6ak68+/TY9oPr29uP0VnP/OdJGnDE+drw64ySVJWeqqy0lPVJitNV7w8S3Pz9wYsN/mOU1RZ41JaqlHrzDTlZqarvMahfeU1SksxeuDzpZq1fo+eu2KYhh/WXqt3lKhHu2wZY8Km8fs/uu+jF/3zR63cXqJ7zuuvcwYdrNOenhYw36EdcrRpT7kk6ctbT9KhHXNkrdXQRyeFXO+TlwzWUxNXa1dplW4/8wid2KejBnZro+1FlUpNcae/Y+tMjXx8snaWVPmW+/2ZffXs5DVhj91xvTto1nr3WHPH9uqgf189XE6X9T1T/Pdz9FFdNW7xNt/nGfec7j5WqcZ3/E/vf5BuP/MIVTtduuTfMyS5m0L8dFh3rd1ZKofLqkubTOVkpCkt1ai00qHT/zZd6alG/7pquHIyUnXVK7NDpnXqnaO0cXeZrn9triR3s4Jr/jtHe8qq9c8rj9a8jXv16o8bdM1xh+mmU3orJyNVaSkpapuTriqHU2t2lKqsyqGubbN1ylPu+8f6v5yvGpdLBXsrVFHt1CEdcpRipMEPf+PbZnZ6qlKMfPfvksoalVU5AwKt4soatc5IU3mNU60z07R2Z4ky01LV3hMYuazV3rJqdWqdqVZ+L9aqHE4VVdSovMqpLm2ylJ5qlL+7XG2y0nzPvGl3jlKb7HSlpxqlphi9OXOjxn69Usf37qgnLh6snIxUZaalavPecvU5qLVSjPv57N0Hb1XgXaVV6tg6Q5lpqXK4XNpTVq3WmWmqcrh/wz075sgY43sWLXrobDldVu1z0tXr3vEB52LRQ2eHfOlaXFkj65JyMlOV7gkga5wuOV1WWem1eYvyaodSjFGN06XUFKOcjDQVV9aopNKhDjkZqnG55HBaZaWn+J65Xht3l+mg3CxlZ6Sqotoph8slK3egJrmfRWXVDh2U6z4/pVUOpaUYlVY5VFxRo4PbZmnL3gqlphh1bJUZ8Hz0Kq1yqKLafS73lFfL6bQqq3aoV6dWykpP9R2jxQ+frcoap7LSU1XjcKlDqwyVVTtV43CpdVaa0lNTVFblUHm1U2VVDh3kufbDqXa4NDd/jwb3aOsLwL3HbUdxpY79y7dqlZGqnwzppv/N3Rx2PeN/e7JyMlK1u6za9zuMJCcjVeXVTt/nL289ST954YeQ8z5x8WDd+8kS9Tmotb667SRV1biPd0mlw30tpqdob5n7vt86K00Ht8mSkTRrw251bZvtuxfO+9OZ2lZUqd/9b4HWFZZFTaPkzjeUVjrUJjtdRRU1uuifPwakW5JWPHquBjw4Icwa3M+LsiqHendureKKGrXJSteVr8zSsq3FAdt55IvlmrBsu/54bj/9dcKqgHXce15//Wx4D6WmGLXLqc2/ff/H01Ra5dD1r83RjuIq/eea4Rp+WHtZ6y4Y8dYCK6qoUaXDqWqHS6VVDnVslaEap9ULU9do/JLtGnNUV/3ujL4a8/wPqnK49NbPR+qYnh1UVuXQzpIqnfeP7+vs16e/PkGHH9Ram/eUq1PrTB3rd//4IG+z/jVtnW/e9jnpdZ7Nax4/Txt2lalnx1Zav6tUB+W6z1thqft54r3H+8vNSlNJpUOSO/9cWulQ59xM7Smr0pl/d8//9e9OVsHeCuVmpemRL5drxbZiXXf8YfpuzS5t2FWmX5zUS5cM76E0z7F0WetL+4Fo45Nj5llrRwR/3+TFMd3bZUd8a+afgZekdjkZvgDPq1WIUiT/wKBH++hvBtv7vV30D1D9v+/ieTj7r9s7b25W3Rt82+x0343Vfz9SjVHXtlnaVlQph1/9o7TUFF/AFXxMvNvJbB0YPLfOTNPRh7rf5p7ct7PvOymw5NV/fd38/s4OU4Lhvz/+b16D37hLCgg6JSk9NaXOeZOkTL+SR++D019wMCfVPpi8D7R0vzfGwQ9V7zrDPfz8Sz4752aq0C8Tm5pifMsHrzcjLUWHd24dNt1SbcZAqnvN5mSkSX6F1aGOjeS+1nIya9fTt0uu+nfN1eKCIrXJTleH1hl1ljmudwdf2np2bKXj/N6K9+uSq5XbS9SpdabaZqdrRM8Ovn2V3CW5vTz/gvXsmKM0z7Hu7Vl/uM6jvNMjfV+w1x2IdMnNVP+D3W/Sl22t+6Z1RM8O6tslV/M27lWP9tlql5NRp9QgkuyMVN/6Jal9Tt1j1rtzKxXsq5Dkfrh41982O8OX4fS/5ru1y9Z6v8xD+5x0DT+sgyav2BE2HUcG1bAIXa4SnX8G2BgT8liHuv/1Oahu6V5bpfuuvXbZ7v1LSzFR78Fe3t+n9zd5TM8OIa+d9jnp2uQZW3xwDO36OudmqlenHO0qrdLxh3f0XafB+xr8SjTcdefVOrP22HVpk+U7p6Hedh8etB/d2mUH3Ccl9wvD4P05tEOOOrbOVMcQtTGsdb/cap+TobOitI3s1amVOnp+37mZaRrUra36H5yrGet2q212unp1dqfPZW2d+2RmWmqd601yl1pmpqT67g+hthksNyu9zrPMe8/3PldCXVuhnguZaak6KDdV8ps9uJ1gz6A0HOJ5VrdvlR4wrW1O7f75B2reANk/UJbC36d964tQkhNuWqh9TE9NUXrQI9T3QtVvQpusdN/y2Qr/AvywjrX77H42B86bnpoS8Hv3npOs9FRfKW3fLpFL9ltnpvmW654R/nefm5lWZ59bZ6ZJfpd6q8w0tcpMi6kEKSMtRSf26RRymjdoyUpP1dGHtY8YeA70dAjZJULnit3bZWuL5x4/sGsb5W2sfTEX6Z7kfY4P7t7W93IvXD7D3wmHB+6X955weOfWMQeeXdtmS56kdWmTpdystDqBZ7j8mtcRfufeex0f3CYrIPDs2jbb93sJVRjTLic95P3Me985tEOOdhRXqX1ORp2aAVLd/JNX707u337fg3LVt0uustJTVeVwqc9BrX3H2n+7rTJSVebZ/2GePO6gboHnrmenVr48s9ehHXK0tzwwb5GemuI7NgH5g1YZ2lNWHTK9x/TsoCkrd0oKzD97mxu0zkzTgK5tNMBT265fl9Zasa1YQw5ppx3FVdqwq0zDD2vvm47wWkxV206t4leUflA9i+W9md2OQWnwZvi7t8/2/YgTWcWkPhn2ROrkyVB533IeEkP1r0TwBq3d2mXpsKDMWyzVliLxVk3zr1bbEOmeKr49PS9XvA/X1pmp6tSqbhDVJjvd106vW7tspfldT4d7Mnmdgq5f78M1OLPmL97XpfcB18PvOGcF59g8vNWza0vEG1690+l5seNfrctbUii5MxG1v9e6x1eq++LKGPc11BD1rfYdS/XS+t6fpNrgK5bq9MG9Rnurnofblx71/C3lZtUGxJGq8gb/ZqNVpfav5h/qGPlfE/4vGPseFDpQC5XRbR2imqqX97foHyhG+ll5z3UPvwye5D7+3n0Nd422FN7rMVrgiMTx3hubst+BDL9nWKwiPaP8AwX/31+0ALlNtve5EJ/8Y6RnbDTBLwMbWj20S4g0eO+Nrf1edHubmIQqRAlcNvq9OlI62rdyr3+IpzlSuPMY/FLKn//58d4zvPfLQzuGXy4Ub38cwcc73IuNDL98pL+DPcelVWaa77yHeimMuhpV1dYYc66kf8j9mu4Va+3YSPMPPGqoXb54YYO3F2zj7jJt3lOh7cWVumhoN+Vt3KuDcjOjvhmPZltRhZZvLdYZA2Jro+J0WX0yv0AXH90j4Ee1ZV+Fnp20Wnef118pxmjGul0ac1Q3rdhWrMoap++tTrw4nC49OWGlTut3kE4I86axKWzd5z5+Zw7soglLt2tkrw4BJUr15a360ZCBp8ct3qbjeneQMUbTVu2Uw2WVnZ6qU47oHFMmPJKJy7ZrcPe29Xp4hvLNsu0ackg7dWmTpaLyGk1bvVMXDu2uaodLXy7aqkqHu7pTm+x0/XRYdxlj9PnCLRrV7yC1zU7XhKXbtX5XqX51yuH6bMEWnT+4a503pV8t3qqT+nRSO0/QtbOkUk+MX6nbTu+jdYVlUUtogi3dUiSXtaqodmp7caV6d2pd583yhKXbdGyvjgGZ/Oe/XaPenVurf9dcbdtXqZP6dlJJZY2mrir09eLqclm9M3uj+h3cRusLS5WemqLDD2qtHcWVmr1+j6+qcUWNU+/+4tiAa/3RL5fr1R836I/n9tPanaVql52hB38yUC6X1ScLtujCod2UYow+nlegi4/u7ivl9VdUXqMXpq6R0yW9+uMGXTq8h/580ZF65Mtl+vlJvbRhV7l6dWqlKSt3aHtRla467tCwpUxb91Vo855y5Wala+Ky7RrUrY0652YqLSVFT32zSif16aiT+nTWvvJqdW+frcM6ttLj45brlCM6+2o0BCuvduidWZt0WMcc30Mv3Pa9KqqdGr9kmy4+unudDOaMtbvUrV22qhwu7S2vVvd22Vq7s1Sn9T9IkrSzuFITl+/QVSMPVUqK+3f0wOdLdeaALurXJVeXjjhEN72Zp4Hd2ugPZ9f2Vjl9daG6t8vWv6au1VkDuyglxaii2qmLhnVXaZVDk5fv0EUR2qzuKavWhKXb1SozVU6X1U+HddeyrcVyWasLXvhRkvSz4T300Tx31eqVfz5Xm/aU69UfNujhCwbVedGxcPM+5eXvUb+Dc3XC4Z30yfwCtclO19GHtg/I5K3cXqy3Zm7Ugz8Z6HuBMnv9bn22cKv+8tMjI2bQv16yTcf27ui7323aXa7Ne8vVrV22fli7Sw98tlRS7b1s0vIdGnpIO1+NjK8Wb9W1x/dUipE+nFegi4Z2jzp81OodJdpXXhO2hkJe/h61y8moU/rYlJZuKZLTZX2ZTy9rrT5buEXnHdk17Ispyf2s31ZUGVDDI9bt1jhdAc/aJQVFMsb9QmpfebWvxP1AVbC3XGt3lmpUv4OadLvjl2zTMT07aNqqnbrro8Ua0qOtrjr2MB3Xu6M27y33lWL6l5p+mLdZRRU1Ovqw9qqsdurTBVt06+l9lJuVrpnrdqvG6dLoo7pq0vIdqnG6dGyvjjq4bZZmrtutLm0ytb24UusLy/Qnz+9wwxPn65P5WzRmSNeITbPCCc6bVNY49caMfOVkpqmwpEq7Sqt0cp9Oyt9drsHd26p7+2zVON1Vw4Ov5d2lVXp+ylr938hDtG1fpfp3zVXXttlaXLBPE5dt10+HddfkFTvVr0uuMtJSdEj7nDq1ASX3vf7+z5bo7IFd1CYrXSf06SSH06VP5m/RJcN7aMveCj3x9Qo9+39D9eWibbok6JmwbGuRapzW129FLPfqUJwuq88WbNFFw7orNcWoYG+5ZqzdrcuOCawP5D2GeX86U6//mK8zBhxUJ2+8vahSS7cU6cyBXWSt1cfzt2jMUV01fsk2jT6qqz6aV6D01BQd2a2tqp2ugD43Qhm/ZJtG9uqg2ev36NjeHfTVoq0aM6SbdhRXyuGse5+asHSbjj60fUBtvyqHU18s3KqfDe+hKodL45ds8+XPQu3fgShcVdsGB57GmFRJqyWdJalA0lxJV1hrl4dbZsSIETYvL7a2W4BXYwJPtExXvDRLM9fv1ju/ODYgY/LwF8v0+ox8PThmoG6MMPRELN6fu0l3f7xElw7voacuHRJ9ATQZ7z3hxauH6+a35+nsgV300rV1nm/NDvcyINBH8wp054eLdPHR3fX3y4Y2yTbj9Tvk99x4Lf0YEnjWDTwbU9V2pKS11tr11tpqSf+TdGEj1gcAMQlX6OQdoiCeNYcZ+ab58p7n+gxNAQAAkqMxFZK7S/JvEV4g6djgmYwxN0m6SZIOPTT2Aa4Brz9fOKhOr7Q4sD18wSA98uWyOsMm3DLqcK3aXlLvakGhnDe4qz6Zv0W3nd630etCfN19bn9J0kl9O+nEPh117/kDkpyi2PzipF51OscADmTnDOqij+d11O1nHtFk2xx78WBfj+GN8dhFR2qrp1MjNMxvTjs85HB6LYV/p0mxGNojXVeOyNET3xQrPcVoZ6lLIw/L0NAe6VpQUKMV22tUWlX7orV1pgn4fMHgLFU7pZMOz9SfvnR3unTRUdn6bHHd6/SXJ7RS/h6HJq2sqjPtxf9rr5v/t7fO96Ec1S1di7fW9iycmSZVOcLP35iqtj+TdK619heez9dIOtZae2u4ZahqCwAAAOBAUFIyL9lJSIo2bUbEvartFgWOGtDD8x0AAAAAAD6NCTznSuprjOlljMmQ9H+SvohPsgAAAAAALUWD23haax3GmFslTZR7OJVXrbXL4pYyAAAAAECL0KjRTq214yWNj1NaAAAAAAAtUGOq2gIAAAAAEBWBJwAAAAAgoQg8AQAAAAAJReAJAAAAAEgoAk8AAAAAQEIReAIAAAAAEorAEwAAAACQUASeAAAAAICEIvAEAAAAACSUsdY23caMKZG0qsk2iP1VJ0m7kp0I4ADUVlJRshMBHIB47gHJw7Mv/vpZa3ODv0xr4kSsstaOaOJtYj9jjMnjOgGanjHmJWvtTclOB3Cg4bkHJA/PvvgzxuSF+p6qtgAAry+TnQAAAJoYz74mQuAJAJAkWWt5+AIADig8+5pOUweeLzXx9rB/4joBABxIeO4BaElC3tOatHMhAAAAAMCBh6q2ANACGWMOMcZMNcYsN8YsM8b8zvN9B2PMJGPMGs//7UMse5gxZr4xZqFn2Zv9pg03xiwxxqw1xjxnjDFNuV8AAIQS4bl3qeezyxgTshMvY0yWMWaOMWaRZ95H/Kb1MsbM9jz33jfGZDTVPrU0BJ5IqMZkfj3zXeeZZ40x5jq/78n8ApE5JP3BWjtQ0nGSfmOMGSjpHknfWmv7SvrW8znYNknHW2uHSjpW0j3GmG6eaf+W9EtJfT3/zk3oXgD7mcZkfj3znWuMWeV5vt3j9z2ZXyCycM+9pZIulvRdhGWrJJ1urR0iaaikc40xx3mmPSnpGWttH0l7Jf08Qelv8Qg8kWgNzvwaYzpIekjujO9ISQ/5BahkfoEIrLXbrLXzPX+XSFohqbukCyW94ZntDUkXhVi22lpb5fmYKc+zwhjTVVIba+0s626n8Wao5YEDXIMzv8aYVEn/lHSepIGSrvAsK5H5BSIK99yz1q6w1q6Ksqy11pZ6PqZ7/llPwcbpkj7yTAv53ERsCDyRUI3J/Eo6R9Ika+0ea+1eSZPkfgNF5heoB2NMT0nDJM2W1MVau80zabukLp55RhhjXvFb5hBjzGJJmyU9aa3dKvdvt8Bv1QWe7wB4NCbzK/dL1rXW2vXW2mpJ/5N0IZlfoH6Cnnvh5ulmjBnv9znVGLNQ0k6585+zJXWUtM9a6/DMxnOvEQg80WQakPntLnem18v7YyfzC8TIGNNa0seSfm+tLfaf5nlxYz1/51lrf+E3bbO19ihJfSRdZ4zp0oTJBlqEBmR+wz33yPwCMYr03PNnrd1qrT3f77PT08Skh6SRxpgjE57YAwyBJ5pEQzO/ABrOGJMu9+/uHWvtJ56vd3hqDXirzu6MtA5PSedSSSdL2iL3A9mrh+c7AEEamvkF0HBhnnv1Yq3dJ2mq3M24dktqZ4xJ80zmudcIBJ5IuEZkfrdIOsTvs/fHTuYXiMJTNe+/klZYa//uN+kLSd6Ouq6T9HmIZXsYY7I9f7eXdJKkVZ5aCsXGmOM867821PLAga4Rmd9wzz0yv0AUEZ57sSzb2RjTzvN3tqSzJK30FI5MlfQzz6whn5uIDYEnEqoxmV9JEyWdbYxp78n8ni1pIplfICYnSrpG0unGPSzKQmPM+ZLGSjrLGLNG0pmez8HV3AdImm2MWSRpuqSnrbVLPNN+LekVSWslrZP0dZPtEbAfaEzmV9JcSX09PdhmSPo/SV+Q+QViEvK5Z4z5qTGmQNLxksYZYyZKdaq5d5U01dO3wVy523h+5Zl2t6Q7jDFr5a72/t+m3KmWxLjvZUBiGGNOkvS9pCWSXJ6v75O7vcsHkg6VtFHSZdbaPZ4u5m/2Vrc1xtzomV+SHrfWvub5foSk1yVly53xvc1yMQMAkizCcy9T0vOSOkvaJ2mhtfYcz1BFr3ir23peED0rKVXSq9baxz3f95a7s6EOkhZIutqv92kAaPYIPAEAAAAACUVVWwAAAABAQhF4AgAAAAASisATAAAAAJBQBJ4AAAAAgIQi8AQAAAAAJBSBJwAAAAAgoQg8AQCQZIxpZ4z5tefvbsaYjxK4rZuNMdeG+L6nMWZporYLAECyMI4nAAByB32SvrLWHnkgpwEAgESgxBMAALexkg43xiw0xnzoLXk0xlxvjPnMGDPJGJNvjLnVGHOHMWaBMWaWMaaDZ77DjTETjDHzjDHfG2P6h9uQMeZhY8ydnr+HG2MWGWMWSfqN3zy3G2Ne9fw92Biz1BiTk8gDAABAohB4AgDgdo+kddbaoZLuCpp2pKSLJR0j6XFJ5dbaYZJmSvJWmX1J0m3W2uGS7pT0rxi3+5pnuSFB3/9DUh9jzE898/zKWltev10CAKB5SEt2AgAA2A9MtdaWSCoxxhRJ+tLz/RJJRxljWks6QdKHxhjvMpnRVmqMaSepnbX2O89Xb0k6T5KstS5jzPWSFkv6j7X2xzjtCwAATY7AEwCA6Kr8/nb5fXbJ/SxNkbTPU1oaT30llUrqFuf1AgDQpKhqCwCAW4mk3IYsaK0tlrTBGHOpJBm34KqzoZbbJ2mfMeYkz1dXeacZY9pKek7SKZI6GmN+1pC0AQDQHBB4AgAgyVq7W9KPnk6FnmrAKq6S9HNPJ0HLJF0Y43I3SPqnMWahJOP3/TOS/mmtXS3p55LGGmMOakC6AABIOoZTAQAAAAAkFCWeAAAAAICEonMhAAASxBhzv6RLg77+0Fr7eDLSAwBAslDVFgAAAACQUFS1BQAAAAAkFIEnAAAAACChCDwBAAAAAAlF4AkAAAAASCgCTwAAAABAQv0/4D2e2sbBU3MAAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 1152x432 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + } + ], + "source": [ + "# let's just plot each dimension now that we have added some anomalous data\n", + "for col in df.columns:\n", + " \n", + " ax = df.set_index(pd.to_datetime(df.index, unit='s')).plot(title=f'Anomalous Data Appended - {col}', figsize=(16,6))\n", + " add_shading_to_plot(ax, df_timestamp_max - n_tail_anomalous, df_timestamp_max, 'anomalous data')\n" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "### 3. Lets do some ML!<a id=\"lets-do-some-ml\"></a>" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "\n", + "\n", + "In this notebook we will just use good old [kmeans](https://scikit-learn.org/stable/modules/generated/sklearn.cluster.KMeans.html) from [scikit-learn](https://scikit-learn.org/stable/index.html). \n", + "\n", + "In reality the Netdata Agent uses the awesome [dlib](https://github.com/davisking/dlib) c++ library and the [`find_clusters_using_kmeans`](http://dlib.net/ml.html#find_clusters_using_kmeans) function along with a few others. You can see the Netdata KMeans code [here](https://github.com/netdata/netdata/blob/master/ml/kmeans/KMeans.cc).\n", + "\n", + "The code below:\n", + "\n", + "1. Will initialize some empty objects to use during model training and inference.\n", + "2. Will loop over every observation and run training and inference in a similar way to how the Agent would process each observation.\n", + "\n", + "Of course the Agent implemtation is a lot more efficient and uses more efficient streaming and buffer based approaches as opposed to the fairly naive implementation below. \n", + "\n", + "The idea in this notebook is to make the general approach as readable and understandable as possible." + ] + }, + { + "cell_type": "code", + "execution_count": 7, + "metadata": { + "id": "W6UL8U04ppmM" + }, + "outputs": [], + "source": [ + "# initialize an empty kmeans model for each dimension\n", + "models = {\n", + " dim: {\n", + " 'model' : KMeans(n_clusters=n_clusters_per_dimension, max_iter=max_iterations),\n", + " 'fitted': False\n", + " } for dim in df.columns\n", + "}\n", + "\n", + "# initialize dictionary for storing anomaly scores for each dim\n", + "anomaly_scores = {\n", + " dim: {\n", + " 't' : [],\n", + " 'anomaly_score': []\n", + " } for dim in df.columns\n", + "}\n", + "\n", + "# initialize dictionary for storing anomaly bits for each dim\n", + "anomaly_bits = {\n", + " dim: {\n", + " 't' : [],\n", + " 'anomaly_bit': []\n", + " }\n", + " for dim in df.columns\n", + "}" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "Now we are ready to just loop over each row of data and produce anomaly scores once we have some trained models and train or retrain periodically as defined by `train_every`. \n", + "\n", + "**Note**: The Netdata Agent implementation spreads out the training across each `train_every` window as opposed to trying to train all models in one go like the below implementation. It also avoids some obvious edges cases where there is no need to retrain, for example when the data have not changed at all since last model was trained." + ] + }, + { + "cell_type": "code", + "execution_count": 8, + "metadata": { + "colab": { + "base_uri": "https://localhost:8080/" + }, + "id": "_wxIeEhGiWYv", + "outputId": "8fdfad43-917d-42d1-8997-a49daac25b3d" + }, + "outputs": [ + { + "name": "stdout", + "output_type": "stream", + "text": [ + "train at t=1647981687, (n=3600, train_after=1647981687, train_before=1647978087)\n" + ] + } + ], + "source": [ + "# loop over each row of data in dataframe\n", + "for t, row in df.iterrows():\n", + "\n", + " # get n based on timestamp\n", + " n = t - df_timestamp_min\n", + "\n", + " # for each dimension, if we have a fitted model then make predictions\n", + " for dim in df.columns:\n", + "\n", + " # if we have a fitted model, get anomaly score\n", + " if models[dim]['fitted']:\n", + " \n", + " #################################\n", + " # Inference / Scoring\n", + " #################################\n", + "\n", + " # get a buffer of recent data\n", + " buffer_size = num_samples_to_diff + num_samples_to_smooth + num_samples_to_lag * 2\n", + " df_dim_recent = df[[dim]].loc[(t-buffer_size):t]\n", + "\n", + " # preprocess/featurize recent data\n", + " df_dim_recent_preprocessed = preprocess_df(\n", + " df_dim_recent,\n", + " num_samples_to_lag,\n", + " num_samples_to_diff,\n", + " num_samples_to_smooth\n", + " )\n", + "\n", + " # take most recent feature vector\n", + " X = df_dim_recent_preprocessed.tail(1).values\n", + " \n", + " # get the existing trained cluster centers\n", + " cluster_centers = models[dim]['model'].cluster_centers_\n", + "\n", + " # get anomaly score based on the sum of the euclidian distances between the \n", + " # feature vector and each cluster centroid\n", + " raw_anomaly_score = np.sum(cdist(X, cluster_centers, metric='euclidean'), axis=1)[0]\n", + "\n", + " # normalize anomaly score based on min-max normalization\n", + " # https://en.wikipedia.org/wiki/Feature_scaling#Rescaling_(min-max_normalization)\n", + " # the idea here is to convert the raw_anomaly_score we just computed into a number on a\n", + " # [0, 1] scale such that it behaves more like a percentage. We use the min and max raw scores\n", + " # observed during training to achieve this. This would mean that a normalized score of 1 would\n", + " # correspond to a distance as big as the biggest distance (most anomalous) observed on the \n", + " # training data. So scores that are 99% or higher will tend to be as strange or more strange\n", + " # as the most strange 1% observed during training.\n", + " \n", + " # normalize based on scores observed during training the model\n", + " train_raw_anomaly_score_min = models[dim]['train_raw_anomaly_score_min']\n", + " train_raw_anomaly_score_max = models[dim]['train_raw_anomaly_score_max']\n", + " train_raw_anomaly_score_range = train_raw_anomaly_score_max - train_raw_anomaly_score_min\n", + " \n", + " # normalize\n", + " anomaly_score = (raw_anomaly_score - train_raw_anomaly_score_min) / train_raw_anomaly_score_range\n", + " \n", + " # The Netdata Agent does not actually store the normalized_anomaly_score since doing so would require more storage\n", + " # space for each metric, essentially doubling the amount of metrics that need to be stored. Instead, the Netdata Agent\n", + " # makes use of an existing bit (the anomaly bit) in the internal storage representation used by netdata. So if the \n", + " # normalized_anomaly_score passed the dimension_anomaly_score_threshold netdata will flip the corresponding anomaly_bit\n", + " # from 0 to 1 to signify that the observation the scored feature vector is considered \"anomalous\". \n", + " # All without any extra storage overhead required for the Netdata Agent database! Yes it's almost magic :)\n", + "\n", + " # get anomaly bit\n", + " anomaly_bit = 100 if anomaly_score >= dimension_anomaly_score_threshold else 0\n", + " \n", + " # save anomaly score\n", + " anomaly_scores[dim]['t'].append(t)\n", + " anomaly_scores[dim]['anomaly_score'].append(anomaly_score)\n", + "\n", + " # save anomaly bit\n", + " anomaly_bits[dim]['t'].append(t)\n", + " anomaly_bits[dim]['anomaly_bit'].append(anomaly_bit)\n", + " \n", + " # check if the model needs (re)training\n", + " if (n >= num_samples_to_train) & (n % train_every == 0):\n", + " \n", + " #################################\n", + " # Train / Re-Train\n", + " #################################\n", + "\n", + " train_before = t - num_samples_to_train\n", + " train_after = t\n", + " print(f'train at t={t}, (n={n}, train_after={train_after}, train_before={train_before})')\n", + "\n", + " # loop over each dimension/model\n", + " for dim in df.columns:\n", + " \n", + " # get training data based on most recent num_samples_to_train\n", + " df_dim_train = df[[dim]].loc[(t-num_samples_to_train):t]\n", + " \n", + " # preprocess/featurize training data\n", + " df_dim_train_preprocessed = preprocess_df(\n", + " df_dim_train,\n", + " num_samples_to_lag,\n", + " num_samples_to_diff,\n", + " num_samples_to_smooth\n", + " )\n", + "\n", + " # fit model using the fit method of kmeans\n", + " models[dim]['model'].fit(df_dim_train_preprocessed.values) \n", + " models[dim]['fitted'] = True # mark model as fitted\n", + " \n", + " # get cluster centers of model we just trained\n", + " cluster_centers = models[dim]['model'].cluster_centers_\n", + "\n", + " # get training scores, needed to get min and max scores for normalization at inference time\n", + " train_raw_anomaly_scores = np.sum(cdist(df_dim_train_preprocessed.values, cluster_centers, metric='euclidean'), axis=1)\n", + " # save min and max anomaly score during training, used to normalize all scores to be 0,1 scale\n", + " models[dim]['train_raw_anomaly_score_min'] = min(train_raw_anomaly_scores)\n", + " models[dim]['train_raw_anomaly_score_max'] = max(train_raw_anomaly_scores)\n" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "The hard work is now all done. The above cell has processed all the data, trained or retrained models as defined by the inital config, and saved all anomaly scores and anomaly bits.\n", + "\n", + "The rest of the notebook will try to help make more sense of all this." + ] + }, + { + "cell_type": "code", + "execution_count": 9, + "metadata": { + "id": "0iN0PCPGiWBx" + }, + "outputs": [ + { + "data": { + "text/html": [ + "<div>\n", + "<style scoped>\n", + " .dataframe tbody tr th:only-of-type {\n", + " vertical-align: middle;\n", + " }\n", + "\n", + " .dataframe tbody tr th {\n", + " vertical-align: top;\n", + " }\n", + "\n", + " .dataframe thead th {\n", + " text-align: right;\n", + " }\n", + "</style>\n", + "<table border=\"1\" class=\"dataframe\">\n", + " <thead>\n", + " <tr style=\"text-align: right;\">\n", + " <th></th>\n", + " <th>system.cpu|user</th>\n", + " <th>system.cpu|user__anomaly_score</th>\n", + " <th>system.cpu|user__anomaly_bit</th>\n", + " </tr>\n", + " <tr>\n", + " <th>time_idx</th>\n", + " <th></th>\n", + " <th></th>\n", + " <th></th>\n", + " </tr>\n", + " </thead>\n", + " <tbody>\n", + " <tr>\n", + " <th>1647981888</th>\n", + " <td>0.753769</td>\n", + " <td>0.228337</td>\n", + " <td>0.0</td>\n", + " </tr>\n", + " <tr>\n", + " <th>1647984190</th>\n", + " <td>0.757576</td>\n", + " <td>0.144231</td>\n", + " <td>0.0</td>\n", + " </tr>\n", + " <tr>\n", + " <th>1647983651</th>\n", + " <td>0.753769</td>\n", + " <td>0.198606</td>\n", + " <td>0.0</td>\n", + " </tr>\n", + " <tr>\n", + " <th>1647982084</th>\n", + " <td>0.757576</td>\n", + " <td>0.189867</td>\n", + " <td>0.0</td>\n", + " </tr>\n", + " <tr>\n", + " <th>1647983422</th>\n", + " <td>1.002506</td>\n", + " <td>0.333199</td>\n", + " <td>0.0</td>\n", + " </tr>\n", + " </tbody>\n", + "</table>\n", + "</div>" + ], + "text/plain": [ + " system.cpu|user system.cpu|user__anomaly_score \\\n", + "time_idx \n", + "1647981888 0.753769 0.228337 \n", + "1647984190 0.757576 0.144231 \n", + "1647983651 0.753769 0.198606 \n", + "1647982084 0.757576 0.189867 \n", + "1647983422 1.002506 0.333199 \n", + "\n", + " system.cpu|user__anomaly_bit \n", + "time_idx \n", + "1647981888 0.0 \n", + "1647984190 0.0 \n", + "1647983651 0.0 \n", + "1647982084 0.0 \n", + "1647983422 0.0 " + ] + }, + "metadata": {}, + "output_type": "display_data" + } + ], + "source": [ + "# create dataframe of anomaly scores\n", + "df_anomaly_scores = pd.DataFrame()\n", + "for dim in anomaly_scores:\n", + " df_anomaly_scores_dim = pd.DataFrame(data=zip(anomaly_scores[dim]['t'],anomaly_scores[dim]['anomaly_score']),columns=['time_idx',f'{dim}__anomaly_score']).set_index('time_idx')\n", + " df_anomaly_scores = df_anomaly_scores.join(df_anomaly_scores_dim, how='outer')\n", + "\n", + "# create dataframe of anomaly bits\n", + "df_anomaly_bits = pd.DataFrame()\n", + "for dim in anomaly_bits:\n", + " df_anomaly_bits_dim = pd.DataFrame(data=zip(anomaly_bits[dim]['t'],anomaly_bits[dim]['anomaly_bit']),columns=['time_idx',f'{dim}__anomaly_bit']).set_index('time_idx')\n", + " df_anomaly_bits = df_anomaly_bits.join(df_anomaly_bits_dim, how='outer')\n", + "\n", + "# join anomaly scores to raw df\n", + "df_final = df.join(df_anomaly_scores, how='outer')\n", + "\n", + "# join anomaly bits to raw df\n", + "df_final = df_final.join(df_anomaly_bits, how='outer')\n", + "\n", + "# let's look at a sample of some scored observations\n", + "display(df_final.tail(num_samples_to_train).sample(5))" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "In the dataframe above we see that each observation now also has a column with the `__anomaly_score` and one with the `__anomaly_bit`." + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "### 4. Lets visualize all this!<a id=\"lets-visualize-all-this\"></a>" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "Now that we have our raw data, our anomaly scores, and our anomaly bits - we can plot this all side by side to get a clear picture of how it all works together.\n", + "\n", + "In the plots below we see that during the light yellow \"anomalous\" period the \"[anomaly scores](https://github.com/netdata/netdata/blob/master/ml/README.md#anomaly-score)\" get elevated to such an extend that many \"[anomaly bits](https://github.com/netdata/netdata/blob/master/ml/README.md#anomaly-bit)\" start flipping from 0 to 1 and essentially \"turning on\" to signal potentially anomalous data." + ] + }, + { + "cell_type": "code", + "execution_count": 10, + "metadata": { + "colab": { + "base_uri": "https://localhost:8080/", + "height": 1000 + }, + "id": "zVoR1BJ5nCGv", + "outputId": "ffcc7765-ea39-47c1-da99-ec79647d0871", + "scrolled": true + }, + "outputs": [ + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAABH4AAAEXCAYAAADbdoMsAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAB9c0lEQVR4nO3dd3gUVdsG8PukJ6SShBog9N5DkaIgqFhREUXRV9TXXj4bihULKvb6KqIiFkQUFAuI9F5D7z1AAoT03nb3fH9MyWzNpm7K/bsuLrK7U87Mzs6cec5zzggpJYiIiIiIiIiIqP7x8nQBiIiIiIiIiIioejDwQ0RERERERERUTzHwQ0RERERERERUTzHwQ0RERERERERUTzHwQ0RERERERERUTzHwQ0RERERERERUTzHwQ0REVMsJIe4XQnzk6XKUlxBitRDiv54uR20khHhFCPFjZecVQjQVQhwUQvhXbQlJPX5HeLocRERElcXADxER1QlCiAQhRIEQIlcIcV4IMVsIEVzN65wthCgWQuSo//YJId4SQoSVs9yjK1EGPwAvAnjX5v1gdV/8U9Fl11dCiLZCCIsQ4gtPl6W6SSmTAawCcJ+ny6KpTFCLiIiIqh4DP0REVJdcK6UMBtAHQF8Az9XAOt+RUoYAiAZwF4DBADYIIRrVwLoBYCyAQ1LKJJv3xwEoAnCZEKJZDZWlrvgPgAwAtzSQTJg5AO73dCGocoSCdXMiIqpyvLgQEVGdI6U8D+BfKAEgAIAQYooQ4riamXNACHGD4bNTQoj+6t8ThRBSCNFdfX2PEGKhG+sslFJuA3AdgEgoQSAIIdoLIVYKIdKEEKlCiDlCiHD1sx8AtAbwl5qd84z6/q9q1lKWEGKtVhYnrgSwxsH7dwKYAWAPgNuNH6hZRk8LIfao65gnhAgwfH6vEOKYECJdCPGnEKKF4TMphHhICHFU3Zevq9u4UQiRLYT4Rc1CghAiQgjxtxAiRQiRof4d42gjhBBeQogX1e/ighDiey1zSggxQgiR6GAbRqt/DxRCxKvrTxZCfOBsZwkhBJTAz4sASgBca/O5FEI8JoQ4oX5f72o320KISUKIDUKIz9T9dkgIMcowb5gQ4hshxDkhRJIQYpoQwtsw73ohxHvqvjgphLjSMG9bIcQadZ8uAxBlU67B6j7OFELsFoYuRmXNC2ALgHZCiDbO9osrQogO6vKz1H0yT33/f0KI922m/VMI8YT697PqfsgRQhwWQowSQowB8DyUoFuuEGK3m/tugxDiQ3X7Twghhqjvn1GPlztdlL+VEOI39ThME0J8ZrNcZ9+nVTaecJGpVJljtIzvdrUQ4g0hxAYA+QDaufquiIiIKoKBHyIiqnOEEly4EsAxw9vHAQwHEAbgVQA/CiGaq5+tATBC/fsSACcAXGx47Siw4pCUMgfAMnVdACAAvAWgBYCuAFoBeEWd9g4Ap6FmKkkp31Hn+QdARwBNAOyAkrHhTE8Ah41vqDf4I9T55kAJdNi6GcAYAG0B9AIwSZ33UrW8NwNoDuAUgJ9t5r0CQH8o2U3PAJgJJbjUCkAPALeq03kB+BZAGygBrgIAnznZjknqv5FQbm6DXUxr62MAH0spQwG0B/CLi2mHAYhRt+kXKAEyWzcAiAPQD0pG1d2GzwZBOZaiAEwF8JsQorH62WwAJgAdoGScXQ7gvzbzHlbnfQfAN2ogCgB+ArBd/ex1Y7mEEC0BLAIwDUBjAE8DWCCEiC5rXgCQUpqg/BZ6u9gvrrwOYCmACCj77lP1/e8A3GoIjEUBGA3gJyFEZwCPABigZsRdASBBSrkEwJsA5qnHvFam2Sh73+2BElT9Ccr3N0Cd/nYAnwkHXTvV4NHfUI7jWAAtYX08u/o+q5LDY9SN7xYA7oDSVS9E3Q4iIqIqxcAPERHVJQuFEDkAzgC4AOVGDgAgpfxVSnlWSmmRUs4DcBTAQPXjNVACPIASsHnL8LpcgR/VWSg3cZBSHpNSLpNSFkkpUwB8YFi2Q1LKWVLKHCllEZQgUW/hfNygcAA5Nu/dAWCPlPIAlJvc7kKIvjbTfKLuj3QAf6E0O2oigFlSyh3q+p8DcJEQItYw7ztSymwp5X4A+wAslVKekFJmQQla9VW3I01KuUBKma8GxN5wse0TAXygLidXXe8EIYSPk+mNSgB0EEJESSlzpZSbXUx7J4B/pJQZUAIIY4QQTWymeVtKmS6lPA3gI5QGsgDluPpISlmiHkeHAVwthGgK4CoAj0sp86SUFwB8CGCCYd5TUsqvpJRmKEGT5gCaCiFaQwlivKQeJ2uhfCea2wEsllIuVo/fZQDiAVzlxryaHCjHSkWUQAnetVAz29YDgJRyK4AsAFqWzAQAq9VxhcwA/AF0E0L4SikTpJTHHS3czX13Ukr5rbrv5kEJMr6mbvNSAMVQgkC2BkIJuk5Wl62XX+Xw+yzvDnKDs2PU6XdrmHe2lHK/lNIkpSyphrIREVEDx8APERHVJder2QUjAHSBocuLEOI/QohdaneKTCiZKdrnawAMVzOAvKG0xg9Vgx1hAHaVsxwtAaSr620qhPhZ7b6SDeBH2HfF0QkhvIUQ04XSLS0bQIL6kbN5MqBkAhj9B2qWkDr2zxrYZ7acN/ydDyXDBlBukvWsAjUIk6ZukybZ8HeBg9fB6rYECSG+FEr3rWwAawGEa114bFitV/3bB0BTB9PaugdAJwCHhBDbhBDXOJpICBEIYDxK980mKBlXt9lMesamHC0Mr5OklNLB520A+AI4ZzjGvoSStaXR97mUMl/9M1idP0NKmWezXE0bAOO15arLHgYlcFTWvJoQAJm2bwohWqtdrnKFELkO5gOUrC4BYKsQYr8QwpgB9R1KuxLeDuAHdfuOAXgcSuDygvobMO5HI3f2ne0xpg1cbXzP0WDuraAE3ExO1u3s+6xqzo5RV9+t5gyIiIiqEQM/RERU50gp10DpOvIeoHd9+gpK15NIKWU4lEwVoU5/DErw41EAa6WU2VBu0u8DsF5KaXF33Wp3k9EA1qlvvQlAAuipdvO4XVuvVlybRdwGpXvRaChBp1ht0U5WuQfKDaW2/iFQuok9J5Rxgs5D6c5ym5vZM2eh3Ixqy2sEpXuN7eDR7ngKQGcAg9Rt17rPOdoWq/VC6RpmgnLDnwcgyFAmbyiDaQMApJRHpZS3QgkUvA1gvnA8uPYNAEIBfG7YNy1hHxRrZVOOs4bXLQ3ds4yfn4EymHaUlDJc/RcqpXQ1PpPmHIAImzK3Nvx9BsAPhuWGSykbSSmnuzEv1O+9A4DdtiuWUp5Wu1wFqwOj25FSnpdS3iulbAFlkOjPhRBads2PAMYKIXpD6cq40DDfT1LKYVC+VwnluwHsj/nK7LuynAHQ2sWx7+z7BGyOOwCuBkmv6DHq6rvVZ3e9iURERJXDwA8REdVVH0F5olVvAI2g3DylAIAQ4i4oGT9Ga6AEhrRuXattXrskhPAXygDRC6Fk4XyrfhQCIBdAljqex2SbWZNhPWBrCJSb4DQoN5JvlrHqxbDuPnUnlDGGukHpvtUHyrYGQhn3qCxzAdwlhOgjlCdevQlgi5QywY15bYVAycTIVMdNmepi2rkAnhDKQMXBKB0HxgTgCIAAIcTVQghfKAMz60/jEkLcLoSIVgN0merbjoJ1dwKYBWVcpD7qv6FQutL1NEw3WSgDU7cC8H9QuhZpmgB4TAjhK4QYDyXYsVhKeQ7KODjvCyFChTJYdXshhMtufQAgpTwFpXvPq0IIPyHEMFgPOv0jgGuFEFeoGWEBQhlMOMaNeQGlu1OCOm25CSHGi9JBuTOg/JYsatkTAWyDkumzQEpZoM7TWQhxqXoMFUI5DrTvJBlArFDHBqrMvnPDVijBselCiEbqvhtq+Nzh96l+tgtKd0NfIUQcgJtcrKeix6jT77bSW05EROQmBn6IiKhOksp4Ot8DeFkd6+Z9AJug3HT2BLDBZpY1UAIVa528duYZoYwrlKaubzuAIYauN69CGSQ4C8ogrr/ZzP8WgBfVbh5Pq8s4BSXD5gAAV+PVAMp4Ll2EEC2E8mSumwF8qmZpaP9OQrkxd/rkI42UcjmAlwAsgHLD3B7WY62Ux0dQAk6p6nYscTHtLLWMawGchBIseFQtUxaAhwB8DWW/5AEwPkFpDID9aleljwFM0AIQGjXoNgrKeC7GfbNdLZdx3/wB5XvcBeU7+8bw2RYoGVWpUMYsuklKmaZ+9h8AflC+twwA82HdZceV26BkZqVDCZB9r30gpTwDJQvseSjByzNQAoheZc2rmgjlCW8VNQDAFnX//gng/6SUJwyffwflN/WD4T1/ANOh7KfzUAIsz6mf/ar+nyaE2KH+XZl9Z0UI8bwQ4h8AUMcEuhZKxtNpKMfNLYbJXX2fL0E5/jOg/I5/crbOih6jbny3RERE1U5Yd3smIiKi2kYIcR+AblLKxz1dlrpOCCEBdFS7/9l+NgnAf9XuS3WCUAauXgOgr5SysJrWcTGUzJU2sg5VHCv7fQohVgN4RUq5ugqLRUREVOPcGQuAiIiIPEhKOdPTZaDaSX1CVtfqWr7aren/AHxdl4I+REREVIpppkRERERkRwjRFcp4Nc2hdOtraGaj9Kl7REREdRa7ehERERERERER1VPM+CEiIiIiIiIiqqdqdIyfqKgoGRsbW5OrJCIiIiIiIqI6wmLJ93QR6qSdOw+mSimjHX1Wo4Gf2NhYxMfH1+QqiYiIiIiIiKiOyMnZ7uki1EmhoXGnnH3Grl5ERERERERERPUUAz9ERERERERERPUUAz9ERERERERERPVUjY7x40hJSQkSExNRWFjo6aJQFQoICEBMTAx8fX09XRQiIiIiIiKiBsvjgZ/ExESEhIQgNjYWQghPF4eqgJQSaWlpSExMRNu2bT1dHCIiIiIiIqIGy+NdvQoLCxEZGcmgTz0ihEBkZCSzuIiIiIiIiIg8zOOBHwAM+tRD/E6JiIiIiIiIPK9WBH6IiIiIiIiIiMpr/7kSpOSYPV2MWo2BHyIiIiIiIiKqkybMSsO1M1I9XYxajYGfKjB79mycPXvW08Vwafbs2XjllVc8XQwiIiIiIiKiKpVXLD1dhFqNgZ8qUBcCP9XNZDJ5ughEREREREREZMPjj3M3evWv/ThwNrtKl9mtRSimXtvd5TR5eXm4+eabkZiYCLPZjJdeeglz587FwoULAQDLli3D559/jvnz5+Oee+5BfHw8hBC4++670apVK8THx2PixIkIDAzEpk2bcODAATz55JPIzc1FVFQUZs+ejebNm2PEiBHo27cv1q1bh7y8PHz//fd46623sHfvXtxyyy2YNm2aXdm2bduG//u//0NeXh78/f2xYsUKLFiwAL///juysrKQlJSE22+/HVOnTkVCQgKuueYa7Nu3DwDw3nvvITc31y7TZ/bs2YiPj8dnn30GALjmmmvw9NNPY/jw4Xbb98QTT+D48eN4+OGHkZKSgqCgIHz11Vfo0qULJk2ahICAAOzcuRNDhw7FBx98UPkvjIiIiIiIiIiqTK0K/HjKkiVL0KJFCyxatAgAkJWVhalTpyIlJQXR0dH49ttvcffdd2PXrl1ISkrSAyuZmZkIDw/HZ599hvfeew9xcXEoKSnBo48+ij/++APR0dGYN28eXnjhBcyaNQsA4Ofnh/j4eHz88ccYO3Ystm/fjsaNG6N9+/Z44oknEBkZqZeruLgYt9xyC+bNm4cBAwYgOzsbgYGBAICtW7di3759CAoKwoABA3D11VcjKiqqUvvB0fYBwH333YcZM2agY8eO2LJlCx566CGsXLkSAJCYmIiNGzfC29u7UusmIiIiIiIioqpXqwI/ZWXmVJeePXviqaeewrPPPotrrrkGw4cPxx133IEff/wRd911FzZt2oTvv/8eOTk5OHHiBB599FFcffXVuPzyy+2WdfjwYezbtw+XXXYZAMBsNqN58+b659ddd52+zu7du+uftWvXDmfOnLEK/Bw+fBjNmzfHgAEDAAChoaH6Z5dddpk+7Y033oj169fj+uuvr9R+aNeund325ebmYuPGjRg/frw+XVFRkf73+PHjGfQhIiIiIiIiqqVqVeDHUzp16oQdO3Zg8eLFePHFFzFq1Cj897//xbXXXouAgACMHz8ePj4+iIiIwO7du/Hvv/9ixowZ+OWXX/RMHo2UEt27d8emTZscrsvf3x8A4OXlpf+tvS7PODlCCLvXPj4+sFgs+nuFhYUO53U2naPt++ijjxAeHo5du3Y5XFajRo3cLjMRERERERER1SwO7gzg7NmzCAoKwu23347Jkydjx44daNGiBVq0aIFp06bhrrvuAgCkpqbCYrFg3LhxmDZtGnbs2AEACAkJQU5ODgCgc+fOSElJ0QM/JSUl2L9/f4XK1blzZ5w7dw7btm0DAOTk5OjBoWXLliE9PR0FBQVYuHAhhg4diqZNm+LChQtIS0tDUVER/v77b4fLjY2Nxa5du2CxWHDmzBls3brV6faFhoaibdu2+PXXXwEoga3du3dXaHuIiIiIiIiIqGYx4wfA3r17MXnyZHh5ecHX1xdffPEFAGDixIlISUlB165dAQBJSUm466679GyZt956CwAwadIkPPDAA/rgzvPnz8djjz2GrKwsmEwmPP744+je3f1ubFdddRW+/vprtGjRAvPmzcOjjz6KgoICBAYGYvny5QCAgQMHYty4cUhMTMTtt9+OuLg4AMDLL7+MgQMHomXLlujSpYvD5Q8dOhRt27ZFt27d0LVrV/Tr18/l9s2ZMwcPPvggpk2bhpKSEkyYMAG9e/cu1z4mIiIiIiIioponpKy5593HxcXJ+Ph4q/cOHjyoB1Zqm0ceeQR9+/bFPffc4+miWLF9Kpe78yQkJNg94as61ebvloiIiIiIiGqfnJzt5Zq+5xvnAQB7X2hWHcWpM0JD47ZLKeMcfcaMHyf69++PRo0a4f333/d0UYiIiIiIiIiIKoSBHye2by9flLEmTZo0CZMmTSrXPH369EFsbGy1lIeIiIiIiIiIaicGfhqIPn36eLoIRERERERERFTD+FQvIiIiIiIiIqJ6ioEfIiIiIiIiIqJ6ioEfIiIiIiIiIqJ6qtaN8ZOVtRkmU2aVLc/HJxxhYYPLnG7hwoW44YYbcPDgQXTp0qXK1l9ewcHByM3NrZZlz549G5MnT0ZMTAxyc3PRrl07TJ06FUOGDHE538KFC9GpUyd069atWspFRERERERERNWj1mX8mEyZ8POLrrJ/7gaR5s6di2HDhmHu3LnVu4Eedsstt2Dnzp04evQopkyZghtvvBEHDx50Oc/ChQtx4MCBGiohEREREREREVWVWhf48YTc3FysX78e33zzDX7++Wf9/dWrV2PEiBG46aab0KVLF0ycOBFSSgDAihUr0LdvX/Ts2RN33303ioqKAACxsbF47rnn0KdPH8TFxWHHjh244oor0L59e8yYMUNf36hRo9CvXz/07NkTf/zxh12ZpJSYPHkyevTogZ49e2LevHl6ma655hp9ukceeQSzZ88GAEyZMgXdunVDr1698PTTT5e53SNHjsR9992HmTNnAgC++uorDBgwAL1798a4ceOQn5+PjRs34s8//8TkyZPRp08fHD9+3OF0RERERERERFT7lBn4EUK0EkKsEkIcEELsF0L8n/p+YyHEMiHEUfX/iOovbvX4448/MGbMGHTq1AmRkZHYvn27/tnOnTvx0Ucf4cCBAzhx4gQ2bNiAwsJCTJo0CfPmzcPevXthMpnwxRdf6PO0bt0au3btwvDhwzFp0iTMnz8fmzdvxtSpUwEAAQEB+P3337Fjxw6sWrUKTz31lB5Q0vz222/YtWsXdu/ejeXLl2Py5Mk4d+6c021IS0vD77//jv3792PPnj148cUX3dr2fv364dChQwCAG2+8Edu2bcPu3bvRtWtXfPPNNxgyZAiuu+46vPvuu9i1axfat2/vcDoiIiIiIiIiqn3cyfgxAXhKStkNwGAADwshugGYAmCFlLIjgBXq6zpp7ty5mDBhAgBgwoQJVt29Bg4ciJiYGHh5eaFPnz5ISEjA4cOH0bZtW3Tq1AkAcOedd2Lt2rX6PNdddx0AoGfPnhg0aBBCQkIQHR0Nf39/ZGZmQkqJ559/Hr169cLo0aORlJSE5ORkqzKtX78et956K7y9vdG0aVNccskl2LZtm9NtCAsLQ0BAAO655x789ttvCAoKcmvbjQGnffv2Yfjw4ejZsyfmzJmD/fv3O5zH3emIiIiIiIiIyLPKHNxZSnkOwDn17xwhxEEALQGMBTBCnew7AKsBPFstpaxG6enpWLlyJfbu3QshBMxmM4QQePfddwEA/v7++rTe3t4wmUxlLlObx8vLy2p+Ly8vmEwmzJkzBykpKdi+fTt8fX0RGxuLwsJCt8rr4+MDi8Wiv9bm8/HxwdatW7FixQrMnz8fn332GVauXFnm8nbu3ImuXbsCACZNmoSFCxeid+/emD17NlavXu1wHnenIyIiIiIiIqqrpJRYebgIl3Tyh4+X8HRxKqxcY/wIIWIB9AWwBUBTNSgEAOcBNK3aotWM+fPn44477sCpU6eQkJCAM2fOoG3btli3bp3TeTp37oyEhAQcO3YMAPDDDz/gkksucXudWVlZaNKkCXx9fbFq1SqcOnXKbprhw4dj3rx5MJvNSElJwdq1azFw4EC0adMGBw4cQFFRETIzM7FixQoAyrhBWVlZuOqqq/Dhhx9i9+7dZZZjzZo1mDlzJu69914AQE5ODpo3b46SkhLMmTNHny4kJAQ5OTn6a2fTEREREREREdUXa44W4fEFmZi5vvJP3r77x3T857u0KigV8OSCDFw7I8Xt6d1+nLsQIhjAAgCPSymzhSiNdkkppRBCOpnvPgD3AcrYN2UWyCccxcXub4A7y3Nl7ty5ePZZ60SlcePGYe7cubjlllsczhMQEIBvv/0W48ePh8lkwoABA/DAAw+4XaaJEyfi2muvRc+ePREXF+fw8fE33HADNm3ahN69e0MIgXfeeQfNmjUDANx8883o0aMH2rZti759+wJQgjFjx45FYWEhpJT44IMPHK573rx5WL9+PfLz89G2bVssWLBAz/h5/fXXMWjQIERHR2PQoEF6sGfChAm499578cknn2D+/PlOpyMiIiIiIiKqL9Lzld4257MtZUxZtm2niiu9DM2yQ0Xlml7YDirscCIhfAH8DeBfKeUH6nuHAYyQUp4TQjQHsFpK2dnVcuLi4mR8fLzVewcPHtQDD1S/8LslIiIiIiKi8sjJ2V72RAY93zgPANj7QrMqL8tvu/IxdVE2bugdiNeuCavUsqqynI6WFRoat11KGedoenee6iUAfAPgoBb0Uf0J4E717zsB2D+TnIiIiIiIiIioDnIjT6ZOcKer11AAdwDYK4TYpb73PIDpAH4RQtwD4BSAm6ulhEREREREREREVCHuPNVrPQBnw1ePqopCSClhHDOI6j53uhASERERERERUfUq11O9qkNAQADS0tIYKKhHpJRIS0tDQECAp4tCREREREREVCl1PU3F7ad6VZeYmBgkJiYiJaXqnuRFnhcQEICYmBhPF4OIiIiIiIioQfN44MfX1xdt27b1dDGIiIiIiIiIiHT1pV+Sx7t6ERERERERERFR9WDgh4iIiIiIiIjIRl0f20fDwA8RERERERERkQ129SIiIiIiIiIiqudEHU/9YeCHiIiIiIiIiKieYuCHiIiIiIiIiKieYuCHiIiIiIiIiKieYuCHiIiIiIiIiMiGrCejOzPwQ0RERERERERUTzHwQ0RERERERERko64/zUvDwA8RERERERERkY360tXLx9MFICIiIiIiIiKqDzLzLfDyAkIDqj7PprBEIqvAUu75GPghIiIiIiIionrl09U5yCqw4MUrw2p0vcM/vAAA2PtCsypf9sPzMrD1VHG552NXLyIiIiIiIiKqE06nm9DzjfNYcqDA5XQzN+Rh3g7X09Q1FQn6AAz8EBEREREREVEdcTDZBABYerDQwyWpOxj4ISIiIiIiIiKyUU/Gdmbgh4iIiIiIiIjImbr+WHcGfoiIiIiIiIiInKjrj3Vn4IeIiIiIiIiI6oQ6nnzjEQz8EBERERERERE5wa5eREREREREREQ1qK53v6pJDPwQEREREREREdmqJ8ElBn6IiIiIiIiIiOopBn6IiIiIiIiIqE6o0fF26vjYPhoGfoiIiIiIiIiIbLGrFxERERERERFR/VbXE38Y+CEiIiIiIiKiOqWeJOPUCAZ+iIiIiIiIiIjqKQZ+iIiIiIiIiIjqKQZ+iIiIiIiIiKhOqMnxdupLdzIGfoiIiIiIiIiI6ikGfoiIiIiIiIioTpE1kI5T15/mpSkz8COEmCWEuCCE2Gd47xUhRJIQYpf676rqLSYRERERERERUc1pSF29ZgMY4+D9D6WUfdR/i6u2WERERERERERE7ikxSyzYmQ9LNaQCiUqk/uxJKsa+syVVV5gKKDPwI6VcCyC9BspCRERERERERGQlM9+CRfsKAFh3vzqXZdb//m5zHl5ZnI2+byXXSJksUmL+znyUmF0HmibOTset36bprzeeKMKJVFN1F89KZcb4eUQIsUftChZRZSUiIiIiIiIiIlI9/XsmpvyRhaRM64DJzd+k6n9nFFgAAJYa6p/1995CvLo4G99szCvXfPfPzcDYL1PLnrAKVTTw8wWA9gD6ADgH4H1nEwoh7hNCxAsh4lNSUiq4OiIiIiIiIiJqiJKzlcyeIptEmcwCz43Ck11oUctg8VgZ3FWhwI+UMllKaZZSWgB8BWCgi2lnSinjpJRx0dHRFS0nERERERERETVEDsbYqYmQT008OawmVCjwI4Robnh5A4B9zqYlIiIiIiIiIqpO1RmkqeuPdfcpawIhxFwAIwBECSESAUwFMEII0QdKkC0BwP3VV0QiIiIiIiIiIs+o64k/ZQZ+pJS3Onj7m2ooCxERERERERFRrVeXgkGVeaoXEREREREREVG1cqerVXUGYup6Vy8GfoiIiIiIiIioblCjMJ4eeLkuBYMY+CEiIiIiIiKiWq+mgz3SRR4Ru3oREREREREREVUBUYvTa2px0XQM/BARERERERFRnVDbAi11IfOHgR8iIiIiIiIiqvVcdb2qVrU55cgNDPwQERERERERUa0l3Mnz8VRMyDOrLRcGfoiIiIiIiIiIKoBdvYiIiIiIiIiIyGMY+CEiIiIiIiKiWq+mH+fuDnb1IiIiIiIiIiKqBG1s5ZqO+7gTaKqFsSg7DPwQEREREREREdVTDPwQERERERERUZ2gZ//UQKqNO09xZ1cvIiIiIiIiIqIqUNNj/LCrFxERERERERFRLVAdAZjkHIvD9y1S1mgQymyp3MoY+CEiIiIiIiKiOsGdrlWHk0sqvPzcIgvOZ5uRV2TBrE15AIB52/Otprn4wwt4d3lOmeV569/sCpdDczLNhD5vJePfg4UVXoZPpUtBRERERERERFRNtLF25mzLh59P2aGfm75Oq/C6xn+dhsRMM9pGejudJqug7AycjSeK8FN8fpnTleXgeSWItfwQAz9EREREREREVI/9vrug2teRmGkGAJxMM1dqOQt2VU1ZtTBXZbqWsasXEREREREREdUptX1QZVlFgwC582SxsjDwQ0RERERERES1Vl14ZHp1q0wYiYEfIiIiIiIiIqJarDIZRAz8EBERERERERHVQqIK+nox8ENEREREREREdVoVDalTLzHwQ0RERERERES1lqOcl9oe6Kmq8vGpXkRERERERERE9ZTW04uDOxMRERERERER1RJVlZDEjB8iIiIiIiIiqteqYHzj6uOkbFXd1asyGPghIiIiIiIiIqqIGhpriF29iIiIiIiIiKhecifrpbaN9Vxl5dHG+GFXLyIiIiIiIiKiGlbN3dDY1YuIiIiIiIiIyFNqW6qRAwz8EBEREREREVGdImt5xKXKBndmVy8iIiIiIiIiIg9hVy8iIiIiIiIiokpwI/pRVRk25canehERERERERERVS2PBXrcVNVdvSqjzMCPEGKWEOKCEGKf4b3GQohlQoij6v8RlS8KEREREREREVEdUs1dvTTVPcbPbABjbN6bAmCFlLIjgBXqayIiIiIiIiKiKlVVsZXUXDPyiy1VtDTXqiohSagpP5UZzNqnrAmklGuFELE2b48FMEL9+zsAqwE8W+FSEBEREREREVGDV2KW2H+uBH1i/AAAZzJMOHDeVOHlFZsknlyQifuHNcJts9OtPpv/30h0burr1nLMFglvL8chqH1nS9C6sTe+25zndrky8y1IzjHjpq/T8OglwQgL9EJyjhmPjQjRpzmXZUZSprLtzjJ+lh4sxOdrc12uq8zAjxNNpZTn1L/PA2jqbEIhxH0A7gOA1q1bV3B1RERERERERFTfvbMsBz9vz8fC+6LQPtoHV32eWqnljfsqFQnpZpxKtw8erT9e5HbgZ/LvmfhgnP0oN7mFErd+m4aoRl5IzSvNJiqra9aEWWlIyjIDAL5YlwuTOqsx8HP5Zyllluup3zLLnKbSgztLKSVcZDFJKWdKKeOklHHR0dGVXR0RERERERER1VNHLpQAADIKytcly1lQIiHd7HSe8gycvOxQkcP3i8zKmo1BH3doQR93eeKpXslCiOYAoP5/oRJlICIiIiIiIiKialDRwM+fAO5U/74TwB9VUxwiIiIiIiIiorqtMoMxO1xedT7VSwgxF8AmAJ2FEIlCiHsATAdwmRDiKIDR6msiIiIiIiIiojpB1NSz2KtAZcJI7jzV61YnH42qxHqJiIiIiIiIiOql8mTolGesoYqo9ODORERERERERER1TXUHXKpStXb1IiIiIiIiIiKqTap2BJ2KqwuxIwZ+iIiIiIiIiKhWqUyGi7uqM2hTnuJXd/CIgR8iIiIiIiIiqttqIlJUDlVdHHb1IiIiIiIiIqIGY+OJ4sovpBpTbTaddL98HNyZiIiIiIiIiBqEaguCOFhuVayqpgaIrkwCEQM/RERERERERFTL1K6uW87UVA8zSyVWxMAPERERERERETU4VZGtUxfCUwz8EBERERERERFVRA1Ffji4MxERERERERHVeRVNwvFU5k1VrJePcyciIiIiIiIiqoVq8inyFQ0QMfBDRERERERERA1OVWTaVEnGjxuDDbGrFxERERERERFRDZM1lPIjUfHBqBn4ISIiIiIiIqJapSbiKVXxVK+6gIEfIiIiIiIiIqIKKDHXzHoqEwjzqbpiEBERERERERHVvF92FLj8PCHNPkIzfWkOpi/NAQB8eWsEzme7juKcTjehyGQdgVl9tKicJXUtq8CCsED7HJ3dSSV27+UWWdxaJgM/RERERERERFQruDPQcXW4f25GmdNc/UVqtZfjcHIJBsb6uzXtkgOFbk3Hrl5ERERERERERPUUAz9ERERERERERB5S0SQnd8f9YeCHiIiIiIiIiGqVmnlIesPAwA8RERERERER1QoN5AnrVqp7mxn4ISIiIiIiIiKqpxj4ISIiIiIiIiKqpxj4ISIiIiIiIqJaxd2Bi+sD4+DO1fE0ewZ+iIiIiIiIiIhqgfIEvNydlIEfIiIiIiIiIqpVqiPzpaHy8XQBiIiIiIiIiIiMGlJXL6PCEoknF2SgZbh3mdO6Gxtj4IeIiIiIiIiIaoWGmOlj3OS3luYgMdPs1nzs6kVEREREREREVIdcyHEv6FMeDPwQEREREREREXmKIeWnOnq4MfBDRERERERERLVKAx3ip1rGNmLgh4iIiIiIiIionmLgh4iIiIiIiIjIQ6p7PGsGfoiIiIiIiIiIagELu3oRERERERERUX1XHWPdNFQ+lZlZCJEAIAeAGYBJShlXFYUiIiIiIiIiImpoqiPgVanAj2qklDK1CpZDRERERERERNSgCD7OnYiIiIiIiIjqOykltiQUA1DGuhnzWYqHS1QzsgoqFu55/Z9st6arbOBHAlgqhNguhLjP0QRCiPuEEPFCiPiUlIbxpRERERERERFRxf21twBJWWZPF6NeqGzgZ5iUsh+AKwE8LIS42HYCKeVMKWWclDIuOjq6kqujyioymfH63weQXVji6aIQERERERER6Yzj2+QXc3TnqlKpwI+UMkn9/wKA3wEMrIpCUfWZvz0R36w/iQ+XHfF0UYiIiIiIiIh0DPVUjwoHfoQQjYQQIdrfAC4HsK+qCkbVw2xRfkomM39SREREREREVHtIQ8oPH+dedSrzVK+mAH4XyvDTPgB+klIuqZJSEREREREREVGDwlhP9ahw4EdKeQJA7yosCxERERERERE1UMzyqR58nHsDo/2QlEQtIiIiIiIiotpBMuenWjDwQ0REREREREQex4yf6sHAD5ETM9Ycx87TGZ4uBhERERHVQu8vPYw/diV5uhgNygfLjuD3nYmeLkaDMmXBHmw8nurpYlAlVWZwZ6qDJEOobpv+zyEAQML0qz1cEiIiIiKqbT5deQwAMLZPSw+XpOH4ZMVRAMANfWM8XJKG4+dtZ/DztjM1dk9kvF3lnWvVYcYP1Xv5xSZc8+k67EvK8nRRiIiIGoQnf9mFOVtOeboYRERUxxjH+Fl7rMiDJalfGPhpYEQDHNV51+lM7EvKxhuLDnq6KERERA3CbzuS8MLv+zxdDCIiqgT2Fqk/GPipQ8wWiQXbE2Gx8AdYHlqwy8ITV60mpcT/Vh3D+axCTxeFiIiIiKjB88TtE2/ZqgcDP3XIdxsT8NSvuzF32+kKL0OL2jakvB8tyYknkdrtcHIO3v33MB75aYeni0JERERE1OB54vaJt2zVg4GfOiQ1V+njmJFX7OGSeM6R5Jxyb7+XGvmRPI3UamY1ky23yOThkhARlV9OYQnyeP4iIqJ6xBM9Jti9rHow8FOHaD+BhjhOj+byD9fi6k/WlWseL3V3sYdc7SYaVB4aEdU3PV9Zir6vL/N0MYiIiKqMR7p61fwqGwQGfhqouhw8OlvOMWCEHvjx/GlkX1JWnchoqQtlJCJyV16RqUbGxys2Wap9HURE5B7WZyvPEz0masEtW73EwE8dUpU/goaUQqcFucqzydWxfwpLzLjm0/V48MftVb7sqhQ7ZRF6TP0X87cn1uh6ORYTEVWH3CITuk/9F+8uPezpotQqsVMW4WGOqdbgrDmSgqHTV6KwxOzpohBVq7/3nEWPqf9iX1KWp4tSp3mkXs57gWrBwE8dokVc63Cyjkdou6s8wZzqOMmZ1NbmHacyqn7h1WDVoQs1uj498MOzPRFVoZzCEgDAbztqNphdFyzac87TRaAa9upf+5GUWYDEjHxPF4WoWq05nAIAOHA228Mlqds809WL9wLVgYGfukT9DVRkLJTr/7cBPab+W8UFqn2WHUhG7JRFuP3rLYidsgjfbjhpGNwZ+O932xA7ZRFmrT/pcjm1oVuYp9X0PuAYP9Xr0bk78faSQ3bvd3xhMV75c78HStQw5RebEDtlEeZurfjTGal8tHMLT+uKr9edwKRvt3q6GFUidsoiPPXLbo+W4cNlR/DR8iP665zCEsROWYRlB5IBAFtOpOHid1Yhv7h6u5yYLRKj3l+Nf/Yqwbyft57GlAV77CdUfwcHzuUgdsqiepENMeajtYibxvG1yBpP+VWDXb3qDwZ+6qCKZPzsOpNp1c+1Lo/x48onK44CANYfSwUAvPrXAT3wY5ESyw8qWSyv/X3A5XKq43xT17rXeaq4dWw31Rl/7T6LL1Yft3u/xCwxe2NCzReogUrJUZ7O6Oi7oOpRmk1IADBt0UGsVlvC64MFHs7k+njFUXy0/Kj++kRKHgDg05XKe1P/3I/T6fn6+9Ulr9iE4yl5mDxfCfZM+W0vft52xm467Xew4qASmFq6/3y1lqsmHDqfg9TchvvEWypD/bzlqTEc3Ln+YOCnjrjjmy34Y9fZSi+nLv+Q3AmcOIpn6YM7l2PMzerIdqnouKJSSvxv1TEkZRaUa77Fe8/hr90VP2YsUmLFwWT8Gm9fcawOte3m7PediUjNLfJ0Meqd95cextQ/9nm6GFYOnM3GBjVYXN0Y2Kx5pd19KzZ/scmCz1cfQ5Gp5sdEScstwm1fbcaFnNKHGnyx+jjGfrbe7WXM23YaWQUl1VG8GvP2kkOIT0iv8uVKKfHB0sM4mpzj1vQnUnLx3G97YXZxQbf9JKdQaXQL9vdxuewDZ7Pxyp/7XdZ19iVl4bW/DkBKCSklvlh9HGfS7bts7Txd2qX82AXrbdOW78l74c0n0vABx9yiaqb9lJ6ZvwcZeXUjMPhr/BmsPJTs6WJYqalqS0pOEW6duRlpuUV1rrG8rmDgp45YdzQV57OVil9DDVy7EzhxlclUnlNIdZxvKnoSO52ej3f/PYx7v4sv13wPzdmBR+fuLNc8xjJKAPd8F6+3Hla3iozFVF0uZBfiiXm7cd/35dvnVLZPVx7Dd5tOeboYVq76ZB0mfr3F08Wg6qJfFip2bvl+UwLeWXIY35TRRbg6zN16GhuPp2H2hgT9vbeXHMLuRPe65+xNzMKzC/Y67vJTh3yx+jhumrGpypebU2TCJyuP4ZaZm92a/qE5OzB362kcPu9eoAgAis1Kq1NZR99tX2/G7I0JyMh3HqSbMHMzZm04iZwiE85lFeLtJYdw9+xtdtPd8PlG/e+xn22w+kwrhyczvyfM3IxPVh7z2PqpYTB2UfpsVd043ibP34O7Z9euumdN1ctnbzyJTSfS2BW+GtW7wM+WE2nIq+Sj+9YdTUG6i8jwsQs52Hwize3l/bj5FNYdLX9adbHJgl/iz9g9grYy1+ofNzu/4crKL8GcLafsfuD7krJwPCXXbvqTqXl6K3lCah7unLW1WjIkikxmfLriKAoMT6DYfSYTexIzsfVkut6FbfHeczidZp9KrW2OoxPXnC2nsCcxU3/95+6z2JeU5TDw89fus8jMLz0uElLzcMuXm7Bk3zkUlpjxa/wZSCmx5kiKwz7zFc340VoWnY0P8NuORBxxs7XSVkZeMb5YfRzJalBxw7HS47qm4y+1qfehVlFPzmbGz/6zWdhhaD2uiNwiE37YlGD3G1xzJAUbK5hpk1tkwksL96GguPS8sDcxC3/vqXxmpCtSSvwSf6bC2R/OjvOftpzWzy/HLuTWi3E3XDmanIMt5biOVop62FX0HJxXpHzXxmOtKmUXluDHzfbXXqDyN+faddPVtfnfCnb1Sc8rtqrbnEjJRUKq/TX4THo+1hxxXAf6flMCzpaRzWpbB9IYs6Ac+WNXErILXWc6aV3B3X3ClXY99vV2/r04+8QiJbaeTMfWk44zl7T5pv9z0K4e++Wa43hozna9viNQmpmcrx6XUs1qtj2O8myOW+3j2nTNrQiLReLbDSer7XdZXscu5OCXGsqQril/7Eqq8DXak+ZuPY03Fx+0irZW5nA/cDa7Sh94ci6rAAfP1Z0Bpyt67awMzzcB10+u807rmAs5hbhl5mZc3q0pZv4nrkLLKDKZccc3W9GzZRj+enSYw2lGf7AWAJAw/Wq3lvniwn3lml7z+epj+Gj5Ufh4Vd3V+biLPuZP/boLyw9eQJ9W4ejeIkx//5pPlZRy2/KPfG+1/v6l76+GRQKTvt2Kvx8dXmXlBYBZ6xPw/rIjVu+N/V9pC9bIztGYNWkAHprj+LG0WsTfUfetF363/m4eUzNkDrx2hdV0iRn5eHTuTgzvGIUf7hkEALj3+3gcvZCLLSfTcffQtpi14SSigv1xl9r6Zru/XKWGu1JWxf9JdWDL8h5fAHD/j9ux9WQ63l5yCAnTr8bt35RmPdR05o0eoKvRtVJZrv7E8e+/PF79cz9+3Z6ItlHBVu/fOWtrhZc9Y/Vx/LD5FGIiAnH/Je0BANeq3V+u6dWiwmUty7/7k/HM/D1ISM3DM2O6VMkyD5zNxvO/78WKg8n4ZtIAjP5gDYDK7fPa7rIPy3cdrQyLi+B/eVTXffLzv+3F33vOoUuzEMTFNnY4TXWeF+//YTv+eHgoercKL9d8k77dij2JWTgy7Ur4+Xjh0vcdH7ej3l+DYrPF7v0LOYV4+Y/9mLP5NP594mKn6ylx0k/7kZ+cZ7QePp+D//t5F8Z0b4YZd/R3Op12TJjcvD5r03lXoF5msUjc/KWSteTouNeu9b/EJyKikR+eu7Kr/tlb/9gPzG97OJvdPL71J8Rqg567NVfts+xgMl796wBOpdWOp5ON+WgdTBaJm+NaebooVeb/ft4FoO5di577bS8AICzQV3+vMoHOqz5ZB6Dq9sNFb62s0uVVuxo+SUjJbvHVpc5n/Czee05/VKsW9V99JAW/xJ+xazExWyTmb0/EafUikVdk0jMddp3JRH6xSU/fdTeDYsOxVPyxKwnbEtJhUrMELmQXWg2krNFawhJS87Bk3zk9EJBbZMK2hHScSsvDxmOpej9UbRDQ33YkWS1HQOCkg1Y1Z7RyGZ3LKsCR5BwcPp+DEvXzc1nKvrBYlG3IKSxxOyKt1ZmOXbDPDDJaeSgZ208prV15RSbsP5uF2RtO6q2RR5NzkJRZgPiEdGTmF2PV4Qv6k4gOOCnL+mOp+NAwsKKtpfuVvrJHkq3LlmPTEnjKkC1krAOezypEkUnZR0kZpS2TRw3bulh9ikaO4XvffkrZhoy8Ymw/lV7hwE96nn1LbVZBCeZvT3TrEZWOvn+NcZv3n7XOMHA1zlFBsdkuC0xKibVHUmCxSKTkFGFfUpbTllqj4ym5Sn9efUH202jLM4pPSNd/v2U5kpyDYpP7gzy5yhJLySmyO3Y86WRqnssb2rwik8NWeFu/7Uh0eaxUhpZBWeCkVd12vam59t+33TzqsXUqPR9L9p3Xz2PVTcsgMGZQFJnM+jZuS0h3mXWqfVW289u+52i9pyt5g5OQmof9Z7Ow8ViqW7+H81nu/b40uUWmSj0212KRuODkN73+aKrVcbLjdIbdcXMiJRc7TmfY/T61c1lGfgmy8kscjoliJKVEfEI6Tqfl44SDbFdACVrYnjNtl7Hq8AX8s/ec3e/zr91nrc5daeqgtOU5R1W1jceV7CuzReKPXUkOs3wz84ux60ym/vqQWl8qtvkesgtLsNaQ4WP8vLDErNcTtGtiZkExLBaJJfvs9xUAmMyOz29pTn4vp9Pyseqw0jp/roxrhBZTMl6f84tNTjP6TOoMm5xkq13IKcRew7krMSNfr8t962AQ/cSMfD3Tz3hfWlRiQUZesd34PLblBoCkzAKcyyrQf6/OrgbHLuSq1y/l/FRWIPTw+RyYzBacSc/HH7uSrKYvMVv0cYRcfXdl0eqD5VFYYsYPmxL0+liioV62+0wmTqbmOfyN5xaZkFNYAotFYsH2RKd1sqyCEqss12KTBYkZZZ97bYOH+cUmp+ePqpacXWi1/x3V37PyS1BQbEZydqHDa0mRyayPJWkyW3DofOUzUswW6fZ1KzW3qNzXnLIYxzariq6NWfklbh0L1WH/2axy/8aM5+LTafkVvg9x56leZousUO+WyqyTyq9OZ/wcu5CLh+bs0Ft0tNaLYpMFz8zfgxlrjmPlUyP06T9beQwfqo/cTJh+Na7/3wYcvZCLFU9dguv/t8HRKlwyW6TVuBA39muJD27ug4FvrkDbqEZY9fQIq+lHvLcab4/riWcXKJHoKVd2wQOXtMf9P8RbdbHpHROGPx4Zph/y623SLJcfTMYbiw/ii4n9cGXP5mWW81MH/aj/3Z+Mf9WAyN1D2+Lla7vplSsfb4GBb64oc7mOFJY4r7iuP5qq91tNmH41HvhxO9YdVbbtlb8OIGH61XorsCP/7HOcjl5ilvrTvBxx1q+35ytLrV5f8u5q/W/jyXXwWyvwwlVdraY1dvkCoI+/ZGwEHPeF9XgE913czmkZXbFdDqA8mnutk9R5Wx8sO+I0M8FYX9cyOzSurg8P/7QDKw9dwLE3roSPtxI//nf/eTzw4w68fE03/alpT17WCY+N6uiyfKPeX4MQfx/8+uBFABxXWi/7cA0y80usWkdumrEJYYG+2D31cpfLv5BdiMs/XItbB7bGWzf2dDmtOwa8sRxNQvyx9YXRlV5WZW06noZbv9qMd8b1ws0DHLcy3vXtNmx1Y1DUJ3/ZjeTsIjw4on1VF7PMljbbY/SaT9bjfHahW61hP205jZ+2nMZ/LmpT2WK6Rw8Klr51/w/bsfpwCra/OBrjZ2zC6K5N8fWdrrNO8w3dE9ypkF776XqcSsuvVAvhCDVLEwAmDYnFK9d1dzrtlhNpuGXmZnxya19c19u9DKq7Z2/D1pPpOPnWVRWqZH+++hjeW3oE654ZiVaNg/T3NxxLxe3fbMHjozvi8dGdsC8pCzd+vhEPjWhvddxoGSfdW4Ri0WOlmafGIHbv15Tzvqv9+PO2M3qLMQA8Ptr+HDbq/TXIKTQ5Xc7ivefx8E9KFurnE/vhKvVaXVBsxqNzd6Jjk2Ase/IS6/K5eDiBo/q+lNLt/azN76xb1dtLDuHmuBj8uPm0VT3J6LavtuDAuWy794tNFsC/9PWjP+102rXrqV93Y9Gec9j/amlWrYDAnK2n8dLCfXjnpl52GRPOAj/ObmIufneVw/cd0fa9cVndXv4X7aMbYYWh/qivUy3LC7/vw419YxDo5231+cA3SutOAsCwt0vL8tMW+3Erhr29Sr+epNkMMTDm47VIzi5yeIzZNsxoGQSuaJmEzpZhdDI1D1d8tBb3XdwOM9eeAKAE8O8a2hYA8N6/h/Hl2hNY/NhwbDmZhlf/OoD3x/fGuP4xZZbDaNwXm/DTfwdhSIcot+d5Y9FB/GAYtsA4ML8xG9x2v/V9bSlKzBLTb+yJKb/tRWZBCe4Z1tZu+Xd9uxU7Tmfq9ZvnftuLBTsSsf/VK9CojAG6AeVY8vYSuPd7pW5f3VkdR5JzcPmHazH12m7693PP7HhsTbA+F/d+bSlaNQ7EmXTlHGBbrid/UX6bR6ZdiQ+WHcGMNZV/8uQ7/x7Cl2tOYMOUS9EyPNDltHHTljssV3lVZ7b65R+tcfqbrE5L9p3HAz9ux0e39MH1fVu6Pd9jc3di9eEULHhwCMZ9sRGPjOyAp6/oXO71u7NLZ6w5jnf/PYzv7h6ISzpFl3sdQGkWorLSCi2CyuCRjB9jK51x3JL8YpP+g72QXYgL2YUu++5qn+110jKsPTrTYpGwWCSO2LScaBkbzkZ6zy0yISOvGFJKfRlGtk/JMGbmnEzNc9i3XAt0AKXZI9tOWo+foZXL2clLa4nYp7Y2ZhWUoLDErE8vpcS5rNLK3ZaTrsdR2H4qHVJKFKotXK76rmvcPbFKKXEiJRcFxWZstSmHcV8ArjNTato5m1aHXYZxgAAgwUkLRqaLQRm1DIZ89bsyq8eU9l1l5BUjq6AEJWYLsgpK7LLGzqstOratqbaKTRarluM9hkFAzRaJjLxi/XhJc5BNpHE2plBydiFWqn2dk3OKkJRZgIJiM7afUo7L04aWNmeVf1s5RSb9wmKyWJBbZLJq+Xe2X7XfYEpOkdOn1pxSy6O1LEopkVtkQm6RSf9NX8gptGkZ0v53/Fu4oLbgFhSbUVBshslssfrNGR0tZ7ZReWit8rbHp5E7QR9Nam4RLmQXuvwtasdsXpHJ5bgYeUUm/RjSbqqcnTf22WSJnHfRSl9sUlqgbTPhjONm5BSWIL/YhKz8Er3lPi23CFnqcWQ8nxu31aT+9gDl2HK1H/JLzCg2WVBkMuuPxtYyA43ZShaLtAsUa2wzg2z3TpHJjBKzBWczC5x2Z0hXr1GawhKzW08AtB2cVkoJk9mi/79f/U52nHJvfCeT2aJ/B7YZIGXNp30v2vniWEqu1bGlZcdo+0Ab28X2uNHsN7yfZzi3GBUUm51mJB53krmaaThHGLMmHAUgkjJLv6/T6fl6/UbrtpSUWYCMPCXTRR9s11DpLSwxI7/YZOiOY78Os0Uip7AEydmFsFikfrzmuvhtunqk+NnMQqsx72yzCbWsW+2JUtp222bHuMqY3qRmFhWUmK2+l/Pq+dPR+DfOjqcSJwEhR7Ly7X/PJWaLfn0ArDOIjqfkwWJRtvF8VmHp+cLwXecUuc78zHFzvMkLOaXnJr0secX6GHOOrm2uunXlO6g3OzoHaXUMbQwrQGlQTc4u1LOUNh4vrafFJ2Qgu1A5p65V62/pecV6ndU2Y1E7h+YXm/R96ChbPTGzAPnFJhSbLHq2nnYuMi5HW59tJouzTFKLRVrVY7TjJV3dF9rj7AHr37E2cLpFKlnR/+xTMrqL3LyOa9mnWoOu8bepbQNgXVdzdI+hva/d6xiDtiazBafS8pBryOjdcCxV3wbtum9W94G2Hi3o48jKgxf0eXYbMvvKQ7t+aNYeUY4T20zOU2l5VtvrKHs7K7+kzDFbtfUZz3fOzgvuhMgLS8wus2KM4z4q1xb7LC8j7RruDiml03q39tTBoxdyXF67tHJpy9GyK7XsfuPvWatLOVqWlFI/TvOLTWXGYExmi35tsf0ube9J3MW4T/Wo8Yyff/aew4NzdmD5kxcjq8CEcV9sxLeTBqBzsxAMmb4Sr1zbDbcNamOVcXJ42hj4+5S2qmxLSMd4w9MdkjILMHfraQxz0mLQ5eUlaBURiI5NQtwupwTQY+q/AIDHRnXEL9vOwGSRiH+xtJW/3+vL7OaLnbJI/7vXK0ux8qlLrD433khapERqbpFdpcZXzaBwdl3XTmpKH0iJ3q8qLZhPXdYJj47qiO82JuCVvw7gn/8bjvPZhdh8wvWNnwTw4bIjhhsL56fHEym5uPT9NejbOtzlMjVzt57B87/vtXvf0U3y1D/3u7XMmnC5TebRoj3nrF47yxDTxnNyREullxKYseaE3oUNANY9MxLD31FaBls3DsLp9Hz4+3jh8LQr9WkKSyz4at0JvLnYvq8/oJx4fby90Pe1pVbjDxgDeVP/3IcfNyutjlf3bO4yir8twf6GL7/YhEGG3+bQ6WW3MrpLa308k16g//bcbVUZ8MZyhPj7YO+r1mMzmS1SP1dog3gaj8mW4YF4+opOeGKe9ThJ7jYYdX15id17LcMDsWHKpQCUgNRlH67FLXGt8PZNvZwuJzEjH8PeXmWVGeCO0mwA6wLf+308lh1ILnP/2Q0CWmTCwDdX4PbBrTHteuvsqA7PL8ZF7SNxUftIvLNEeQxv87AAbHpuFADl8bwTZm7GhimXIiTAB73UjLp9r16BVYddBwCdBYS0llOjuGnLkF1oXzkyLsI2my9h+tXob2hNvPLjdTiekouFDw/VxzADlHEBft2eiKNvXInery51+b0t2nPO7rygfR/Gm7KPVxzFxyuOYtsLoxEd4m/Vyt596r/48o7+aBYaYLcNAND5Rfvjy+jYhRyM/mAtpl3fA7cPVjKeHp6zAysOXbDLurENwtq29j8zfw9+3Z6I16/vgZcW7sP9l7Sz2iZX8otN6Pbyv/rr6f8cwtRrnWcTGb30x37M3XoaR6ZdqQc57vp2m9XvSKuX2halrKzH7acyMO6LjXhtrH1Zur68BHcNjXWrnNqu+n7TKbw2tofVZ1+uPYHpZYy/Mv2fQ/o074/vDUC5Oe/7+jLcEtdKr+Ea93XctOXILTLhWS2jycFP5OMVR+0yepc9cTEu+3AtYiODsHrySP39+FMZVvUTR661eUS8No7frw9cZBWYMFskZm9M0G+QbCv1rs6f2nnYePwJURr0mr89EXcMbmM13pDJyRg/xhu0A2ez0a1FKP7abT+4u9ki0fu1pRjfPwbvqvsfAF7764BV5kj/acux2JAp1u75xfrfz4zpjIdGdLAK/Fz+4Vrserk041Qbv0fjKsg2c+1xq2u5lommMW6HVsczskiJedvcH0i4z2v29dXl6o3+rA0nMbxjlD4+IQD8cr+SgbsvqTTIsmjvOSzaa33O2382S89k8vYSiJ2yCLcObIU3b+hpV+4Xr+6KaYsO4m+b8TOfmb8HzxieHrr1+VEY+OYKvH59D9w2sDV6v7oUN8fF4Jf4RLe3Fyj9/va9egWCDZk6qTnKDe3G42k4kpyDTk1D8MCP2/HvfuWaqV2POr34j9Xy3M1htO3yNW3RQczacBLH37wKW06k4bavt2DWpDg8+tNOeHkJ7H3lCtw0YyN2nM60u2a/rWbMvHNTLzwzfw9+uncQooP9rbLjZ6pjWC0/eAHtn19stYz52xMx5Tf7OrgjxuuXr0/F8gK0uu2eVy5HaIAvzOpv94bPN+rlOpmah5Hvrcb/jeqIJy7rhOTsQqt6pab3a0vRuJEfdrx0mcv1bTyeinVHU/XlOw202HyBJrMFHV74B8+O6aJnOnd5aQluiWuF167vjs4vLkGIv4/DAK52L/vGDT0wcZBy7T18PgdXfLQWH0/og7F9lKyczi8uQeemIS7HMNPM2XLa6T2EVqcoKLag68tL8OilHZCRX4w5W07j5Ful3/dfu8/qT/Pd9Nyl+vnWUTDr2QV78PtOJWHh+j4t8NGEvpj49WbEJ2Tg1eu6Y8pve/H5xH54aM4OPHel8/EMtftCfyfHzEVvrUB2YQmOvnGV3WexUxZhbJ8W+HhCX7vPOMZP9ajxjB+tu86+pGzEqxHpTSfS9FaAf/cn27Ue2Wb9LDdE6TVL9593epAUmyw4npLndPC+so6tuVtP43x2YYWeWGXbqmo871gkHI69od2ou0rD1eY3btOsDScBlHYNO5Oej12nM8sso5TAXEMFwtV6lx5Q9v1ON5YLQM8CseXoaUm2FYrqZgxe1fRAxn/ssh63yZjirWXMOGpd0oJHjhSUKJknecVmqxtjP8PJ+HdDVlpF9nd2QeWemOdKZb8CRxdnRxUA4xNskjILsPyA/ZMayvrtuWLMttBaVJ2NB6HRMhQW7kxyOZ0t4aQquuyA/TnSEdvKgFZeR/ObLBLrjqZa3WwbM+N+Uc8hm4+nWWVRGlurne1VZ/vbUdaCo6CPq2U4cjg5ByaLtMsuWLBDubHQWsx/31W+78PYeqtZol7ztOuH7WXI3aw4R7TB+lcbAmsr1Gw82/X8bXNDbLu7ft2ubPtc9SZOy0h1dowZ2WbkfWt49HhZft+prNdksVhdII2/I+271QJZxrK7avnUxiDRWp1t/eLmjbOrI8vZMpwVa6HNMTUv/oxhsN1S+tObXOx+2/H/gNJzibOs1IpYcfACNhhaik3qeIkau8CPiz2mxXHNFuupjNuZYPN0TmddvYz1H+1Jq/EOMhy1OuWv260DB2sdjEdx1MmYOhvV7A1jNoPtce/saV2OvK0GzyvKYoF+01YVtHNfee0xZDcaG1ccHf9afdDR+FFG2rH7x84k/Rpe3qCPUbZNxpRxDDAtq0Eb+qAq2GaWaXXzErNFz9iPT8hAXrFZzxzc4aROrQX3tCdrHTyXo2ckuWOxkyESHNF+gmaLhJ8bmf+O/LxNuX5o45Y5uu/SGn613ggXXDw91dUTlgHl/sy294CzwI/ttUyrY2tDRWjXknnxZ/RhK5xl7Wn1SONxc+Cc8r2stHn612E3x4zVMssc0XajlgE1f3siftx82u46blx3UkaB3nDmqHpknHbhLqV+sOFYGopMFv3cqDVuObrv1mjXHG1/2h45aXnFLrMz/9jl+EmsHOOnetRoxs+Z9PzSlGZRekKYufaE3od404k0u1aCPq8ts3qakpeDmtCqwyl42cGR/T/D+C7GA9fY8mXMHtIYKzJayisAq37/7rC9ef/TUPmeu/U05m617/OdmluMsf/bUGaq5Yw1x9E7Jkx/nZFfgss/XKMPYuzjLdwayMu2q5yzSpaz1kLbirc23bYXRjutTDjKmHHVTao6GINXjjI3HDFZZJmtpu44ZBMQnDDT/hgE7Pf5aheZE3d9uw3xDgJtWgZZdmGJ3WNd3VUV21wWY+aFJqugxOp8oJXjxJulLQcPzdmu//3ITzuwNykLayaPxKz1J5FseNyvlxC46K0Vdt34jBeXi99ZhdFdm+qPBE/KLNDX+emtfXGtYawTV/skdsoizLtvMJqFKZkcp9Pz9enfHtcTi/aex9ojKegdE4bdiVl48WplDCnt1JaWW6RnqBx/8yr0fW0pokP89Rt9rZ+2lrk0d+sZLDuQjBbhgVZP5HNUxtgpi/DP/w3HlR+vs/tMu7FOzi5Cu+cWOay822YQauu4OU4Z2+GpX3dbfW7MCrv/h9LvyjgWg9ki8dxvezF362lMNvQ//zX+DF756wB2v3w5er+2FK0N477YOupiYHnjfvjA8IRAbSwqjba9g9XWx2KTRZ/3wRHt8eyYLnhmwR44o3U5MEuJCTM3ITTAV6/0JWUUONznP205jQnq+EyJGfm46K2yx1eb/s8hbD2ZhgfUp5ktP5iM2CmL8NRlnfRptpxMw21fKWPQOWq1NEuJ1/8+gPVHU60qplp3nr/VCt+sDSf1GxdHZtzeHw/8uN3u/U9XHMWepCyEBfriPTXLIj2vGP1eX4ZvJw3Qp9Mu2xbpuEX98Z936pVSIZTxzYzZEDd8vgF/PDIMH9o8+bHD84v1OoarSusrf+7H7I0JuP/idvhSrYfYcjWGnCOurt+2NylAaXblLTM34+qezXF1r9KsPy1T6Mu1J3BZt6a4ySbb2ZaxelSV520/79IGhAFvLNdvWAHYjc3nqGEHUG74tW6ytmPSGL/7//t5l/40IQCIaxOh/61t05s39LTKBHrt7wN2v2dAGex3syHwrs1/v5Mx9177y34ZQOlTvGzrVB/YHHfuquggq5oHftxeqQYKW3/bZC/e/0O8W/MZsx6N+99RnUpr+C1yMRYkUJo5dSo9H11ecq9u5sql76/G5xP76a+NAcAJMzdbPfkJcB7ovWv2Nix8eCgA5bc3dPpK9HOQ/e6sa2KRyaKf75wFdGOnLEJUsB9Sc4tx++DWen28NOgt7Roq7/vB/vyrcZUVqWUa2xr72Xq7wLFSLn+EBvrgq//EYdT7a7D8yUvQoUnpkzq3n0rXew4YA7x21LdKn+RqPc3X607gv8Ptf5/nsgpw0Vsr8fN9g/X3jEMLGK8Vzjw2dyfMFon/TexnaFBQPjMGqcpqDNbGthRQ9k276EZ6ht+WE+mInbII654pzbjs9OI/KDZZ8NaNPXHrwNb6+99vSsDFHaOtxt/TPDxnh10D7bx4JRBorMfmFpnQ59Wl+PKO/nblts1C3nE6E7d9tdlhI/JyQ4OfFiTT9pGxB8Brfx3ArA0nsfWFUVZjmpWuU+DguWxc+fE6/HDPQKvPpJQY8MZypOYW411DNnXslEXYbcieBOBW4gKVX41m/Jgt1icsZwEGR+cJY2XJWRza0Qnm3X8r16piy1GgxhVnT4Yoi7v9a2fbPCXC+OQqHy8vp49BdaW8ZXaWSVWRpzV4iqtBqY2q+okD5V2/K46CPkBphT3RRd/u2mqPk7FrjMfc4r2lLVp/7zmnVzxe+/sAvlxTeiPn5WU/dhNg3RJyOj0fszac1G9OjLT0WXfN3XraYbbEswv26pUxreVOC6Zo0xszBXMLTcguNOlBH8DxgOWpucXYk5jl1jnqi9VlD9pY3vsSX+/yXU6M5ziLLD23frWu9DvTtlPLADhdxtOY3OHOTbyjMSPc2WdadqrFIrH5RLqeIQm4zrDTvveM/BKHx6itGWuOY8fpTLsxqN433ITONAQxHLVaWqTEN+tPut0a6cyv8Y4zXt5fdgTLDiRbZYZojQzfrC8NJGmHmbMbYWNF3kvAriuP9hv62OZ7dffx3No11FnQpyyObuAqOj4GoBwnC7Y7bjBxJ5OqIo8ZL4sQ1r/vHCdZd2VZ4SQAV1hidpna5Oja9spf+/WBlstivA7o7zn5vm0HWNb4qPvV9rgqb1Cwquw6k1np4JErGZVsiHM1poezMXlspTi4DldEYYkFc7c6z+5zNj6gLeMT7bSxqhxl6ji7tykymfXrqqMGbE2qmi3z4+bTenDTOijhVnHLtMRJNpCzbMHU3CKcSMnDn+o5+U+bc7Gx26lWXGf7wsj2MJ626KDD6bSMujkOBkkHUGbQRwilzNq1WA+qqZ8bA8llXT8CfL30ZQLW3Tq1MQqNmd7a78E2eWDaooNO6wbuZuWfSMmFySLx4fIjdvvSW9ift5z1HLAKnKvb5Si4rDUEuQrMaL+P5TbZ4yVmqR/fn9vUqXacsT7PO3oKIlWeqMkuLv7NO8rmd34EABjeMQp9WoU7fOKUM4+M7ICUnCI94mnronaRZXapqG/6tg53u9tVTWsRFoCz1RQoodqrSYi/XeDktbHd8b9Vx+xagm/qH2N1Y2hreMcohy3kB167wmpMkZoS7O9jN+i2KyufukR/0pC7JgxohdaRQfo4Os5MGhJrF/itDxr5edtlpo3sHF3mOEG1gXbsl/c4KY9p1/fQxwGIaxPhNOBbmwxu17jMseYciYkItHpUszPNwwLcCphVhW/vGoCFO5P09PQOTYL1ATSJqG5zVufQJEy/GmaLRP9py5xmqa9+egRu+2qzw/rvIyM74LNVx9ClWYie+f3opR3KvBfSzoVRwf5lDjux86XL0NfBGKRVLcDXC4UlFnRtHoob+rawGrNq2RMX43hKnlU26OcT+8FLAA/8uEN/766hsbiudwvc8PlGq2W3jWqkDwHy2KiO+GTFUfh6i3IN6G7LmJVTli3Pj3I47lBt9OyYLlZjhjrStXmo3aDolRUR5OswQNwyPBDB/j52jUrDOkQhLMjXbmxEo/bRjawaOaliTr19zXYppcNHy3rsce7rjqaiR8uwsic0cPZYbk1DC/oAZafMehKDPg2To2yZl/9wPHC3q6AP4LhbBOB+a35VK+/NfEVaZH92c9yR+hj0ARw/kaMuBH2A0mO/OlvijYM/1oWgD2DfPdBd7gR9AMeZfNXlrm+3Wb2u6fHhiKj6uAr6aLYlpLscmiAxo8Bp/Xe/+jReY3d/dxrAtXOhO2ONGrNmq5OWqX7wXLZdUKHYbLHrAvzQnB2w9e2GBFzTq4Xd+8anv2lZdZUJ+gCuB1u3VZ3X8KpWVtAHQJUHfQDnWYHOniqqjT/rCoM+1c9jGT9ERBXlKKuIiIiIiDyLmZBEnuMq46fGn+pFRFRZDPoQERER1T4M+hDVTgz8uOn6PvapiHXdwNjGni5CnffgiPYeW/frY7t7bN1ERFT/+ZVz0HYiV6ph7PFyOTxtDBKmX+3ZQhAReQiv6DaGd4xy+P5l3ZrVcEmq3+huTTyyXuPjH8sytEOk1WvjY25rA2fHS01oG+XefowO8a/ydTcLDajyZRIRUe3i4+3hO3WqV+IcNDg2buRXoWVpdZvLujV1ex5fL+W2J65NRIXWSUR1Q5vG3p4uQq3kscGdq8qaySOQlFmA277aAgC4rncLu0cM2urSLARf/Ufp+tYk1B/pecXw9faCxSIRFeyPIpMFyw4m47G5OzGyczQ+va0fAn1LD6CNUy7FuC822g0o+dCI9laPpwv09UZBiRkPXNIeM9Yo729/cTS8vQR8vb3w4Jwd+mOdASD+xdE4n1WIaz5d77TsM+/ojz6twzHwDWW0+T6twvVHTApR+pjHuDYR+PauAcgpNGHI9JUAgFaNA3HG8Ejv0V2bwtfbC6/+dQCubH1+FAZW4ej2Cx4YggA/L8zdchqvlLHu7+8ehPbPLwYAbHthNKKC/fDOuF6wSImeryzVp3t4ZHvERATZPSoRAG7s1xK/7Uiyem/r86Mw9n8b7L7D/a9eAQB44fe9Vo+G3PPK5SgxWdB/2nKr6Ye0j8L2F0cjLNAXuxMzMe6LTQCAD27ujSd/2a1Pd3NcDH6JT8Tjozvio+XWj3/977C2+NrweGPN05d3wntLj1i9d3jaGFzILkJYkC9CA3z19x+4pD32n83SBybc+8rlKCgxIyzQFwICEhKdX1xit44Dr10BLyFQYrYgwNcbHV/4x+pzYz/trc+PQmigL4pMFgT5eSMjr7hKj4uaNOXKLpj+T9kD4pHixau7IiWnqEKPvL6mV3P87eIpDjUh/sXRiLP57QLAN3fG4Z7v4h3OY3zqirtGd22KRv7e+hOfXPnk1r54bO5Oq/fm/HcQJn69pVzrrG7LnrgYJ1LzcP8P28ueuBx6tgzTH+/eUNg+xbCRnzc2PjcKvV9d6nSe6Tf2REQjP4f7f0TnaKx2MPD5oLaNMfM/cRACeOXP/fr1b+dLl8EsJfKLzLjvh3gcOp+DgbGNsTUhHZd1a4plB+wft277ON8VT12C8EBfFJSYUWKW+M+sLVb1CgCYe+9g3PrVZtc7o5w2PXcpLnprpV6vqqitL4yCv7c3vt140u5aDADeXsLpwK7bXhiNgmIzokL8kJFfgiBfbxSazLjorZX6NNtfHA0A8PHywv6zWbjt6y1o3TgI/z5+sX5NPnYhF1d8tNbqCYaHXh+DzPwSDH5LuaY6+273vHI5BAB/H2+YLBb96ZZTruyCWwe0xsj3VyM9rxhX92qORXvOYVy/GFikxO87S+tAh6eNgcks0X2q+0/GPPrGlcjML0F4kC+yC0oQFuiLX7cnOqxzGcW/OBpfrzup14H7tg7XH8tt3K9aPQ8A7hnWFo+M7IAtJ9PtBgje+sIoBPn5wMdLwN/HC9mFJoQG+KDELGGREj5eAn/vOYfH5+0CAIzrF4MFOxL17fZSU47m3jfYrr5TH6146hKMKueTResy7alprrxzUy/0ignDmI/Wlbk8d56iVleM7ByNg+dy9MfNa/x9vFBkqr0PCqqobs18kZ5vQU5h3RmouybU+YyfmIggdIguzXxo4kZ2w+XdmqJV4yC0ahwEfx9vNA8LRFSwP5qEBsDLSyDQzxttGgcBAHrFhCPY3wfe6sWif5sItAgPxIjO0XbLHWDTkqFN07V5iP5eZLA/woP80Mjfxy6FOirYv8zsjJAAXzQJKc22uMaQATOme2lWUv82EQgJ8EWL8ED9vd4x4XbL6t7C8ZPVWhrma1KO7A5/H/tDanRX69aY0EAf+Pt4o7sbT3XT9ntEkC+iQ/whhEAjfx+EBPhiQGxpi02vmHB0bla6n0d3Lc1m6tsq3G65kcH+DluJGvn7oJG/D4Z1tP5+QwN8nbZKRQb7w8fbCzERyjEzrl8MurUItZpmYFslc6lz0xC7+WOjGjlcbssI5TsI8C3dp/4+3mjVOMgq6AMox1gfw3Zqx4m/jzf8fLzg7+PtMNMqyM8HAb7eCAnwha96PPr7eKFHS6X8Fxv2Q5PQAAT4eiMsUJm2PMdFbWM8duq75mFlf0+9HfxGjPq2jkC/CraQhgX6lj1RFWgX7fh3BCjnVkfaOvntAcCoruXPiIwO8cNF7SLLnhBAaIB9u4uzc0FN6do81O69jk1D3LqulkegrzcGtW14XY0H2xwb1/VpUebvIyYiCDERgQ4/c/R9AUBcbATCApXGAePxGNHID1HB/mgdGYSLOynn9it6KPWGEZ2jHZ4XR3a2/h20jw5GZLA/YiKC0DaqkdU1AgBaNw5y+VusCH8fL4So17zKZtk2CQlAWJCvXscx1nU6Nw1x+fuNDlH2XZCfD1qGByKikR+ah1l/NxFBfogM9kdYkC9aRyp1gpGdoxHo543Gjfzg7SX0jNmRXZro56AAX280M5yrr+phnd2s1a1CA3wREuALPx8vBPmVnkM6NQ1GWJCvXvfp11r5Lge3a4yBNr81fx9vNPJ3v913VJcm8PX2QnSIP3y9vfQ6T3/DNcFR3Q9Qzr2D25Wuv1MT+zqQt03/r0FtGyOikR+6OTi+m4QEINhfqbcIIZTGLSHg5+OFAF9v+Hh7WZ3X+7YOt9pujW8D6cLYPtr9DPv6wJ3sr+4tQq3ujVwZ1K56rlMh5fj9VZWWEYEY2UU5X/sZfq+254f6wssLcHJaatBq/Mj77La+CPDxxsbjaYgM9kOL8AAkZRQgLFC5mO1NysIdg9tgxaELKCwxo0V4AOITMnDfxe1wIacIO09nINjfF4PaNYaUEt5eAk1CAzD33sGIiQjENzaZEzNu76+3GHx71wAIAMM72gdtbPVuFY6FDw9FT0NwYsVTl6CpesF+5bru6NYiDC+pj9add99gDGoXibn3DkZYoC/yik2IaxOB+FMZiGsTgaahAXYXGu2Jam/d2FOvEDYNDcDMO/pj/bFUfL/pFAClBUnLNCk2W0dl7xnWFtEh/gj09calXZpg+cEL8BLACENlbfNzo+AlgOAAH1zWrSmGd4zG2cwCRIcogab3xveGn48X+rYKx+yNCRjToxk6RAfjcHKOwy49vz00BAXFZrSJDIKfjxcOnM1GRJAfmoUFwNtLYG9SFjpEByMjvxhmi0SPlmE4cDYbwQE+yCk0QQjlIj8gtjE+ubUvOjcNgY+3gJTA8ZRcpOcVo0OTYDRVA1zLnrjY6iSl+fTWfjifXQiLlHolR/Pe+N7o89oyAMDtg9uga/NQhAX6IjLYH2m5RfD2Enjx6m4Y2bkJIoP9sOpQCq7tXVrRGtevJdpHN0LbqEZ6dFwIgZ/+Owi3qS3ySx4fbrXOpqEB+OPhoejcLAQBvt7465FhaBkRiKyCEsRGKpXkfq3DsXHKpfDxEnq2zG0DW+O1vw7YfbdtIhvpy1u4MwlXdLfvbrjpuUux9WQ6ruvdArlFJnRoEoxODoJLALDgwSF6y3L8i6ORmV9sN83yJy9BWKAvAny9kJJThFaNg9C9RSgu7eL4JnjdMyNxLqsQX607gWUHktGqcSBeu64Hjl3IxRuLDwJQWvOOJufo+83WGzf0wB87z2JrQjpC/H3w8KUdrLJxbujbUm+t3Pr8KOQXm7H8YDJScotwWdemmLn2BJaqLdUfT+gDIQS2nkzDj5tP263r+7sHIjjAB/1aR2DuvYMR6OeNyEZ++HnbafRpFYG8IhPOZxciI78YQ9tHoUmoP1YfTkF2QYlVNp/Gx0vg6zvjcOBcNjo2CUGxyYImof4YP0PJ/Pr2rgHILTTBbJG4pFM0+r6+zG4Zz47pAl9vgWmLlP315R390TQ0AEF+3lh16ALeKmdm0v2XtMPFHaOx/VQG2kcHo1dMGHy8hd4qrbUEa+b8dxDaRAZh2NurENnID7PvGoiHftqOM+kFmHZ9D0QE+ekV/AUPDkGgrzcyC4rRIiwQI95bbbd+26wV20q95pNb+yIrvxhto4KRlleEjk1CcC6rAGczCxAc4AOTWWLy/D0O520f3cjusZ8TBrTCm4uVfbXosWG4+hPrzMm/Hx2G5OxCSAmEBfnC20ugXXSw0xbRK3s0R/voYOQVmRDg6432TYKRmFGAvq3CkZFfjD2JWSgoNqNddCMs3Z+MefFn4OfthVsGtEKJRSIluxD92kTgaHIuMvKL8fnq4+jYJBhH1Qw6H6/Sc9o3d8ahTWQjq5vQ2we3xuB2kSg2WayyBzX3XdwOM9UMrAkDWuH6vi0RogaTbLfd1o/3DMKzC/YgKbMAAb5eeOvGnkjPK8HNcTFYdTgFXkLJ9muk3lg6ai97Z1wvLD1wHssPXnC5rpGdo3Fxp2g9s/TXBy5CaIAvWkYEIjaqEWIiApGZX6K30GseHtke/1tV+pv7fGI/xEQE4tC5HGQWFGNQ20iM/d8GAMAlnaLx3FVd8Nfus/Dx8sLH6uN/+7eJwLTreyC7oARrjqQgv9iMvq3D0b1FGHacysAItRKsZdDOuL0/lh44j9aNg9C3dQTunLXV4TY9NqojOjcNQVZBCZ7/fa++T0+k5uJCdpHe4jz/gYtwJDkXz/++Fy3DAzGuX0sUlJhxba/mSMosQEf1Jnj5kxfjz11nERroiyA/H3RuFqxnjw5pHwkvL4E/HxmKQ+dz0MjPB/3ahONcViEEgC/U89LMO/qjbVQjnMnIx6C2pcGLm/rHQAK4wqa7+uQrOuO63i3Qo2UYBrVtjO4tQjGmezP8s+882kU3Qs+WYTh2IRd9WoVj4/E0nErLx7AO9kGXV67rjuv7tkRekXJt7xMTjrAgX/xwz0CUmC0I9vfFzV9u0r97X28vmC0SsZFByCk0oaDEjCs/Vlre/350GBIzCtAmMghZBSWICvbHqkMXcMvAVgj298Gix4ahXVQwur68RJ++aWgA9iZlIrvAhKhgfzQPD0BogC9OpeXhcHIO4to0xvZTGWgb1QihgaVVXi2TaWiHSEwc1AZBft56Y4ZtBtYXE/s57KKkWfX0CPh6C+QVmfWMEkAJ2i15fLhdgDksyBeLH1PeLzKZrR5WsOixYTiVlo+rejZHh6bBiAkPRH6xGSEBPsgrss90Wv7kxTiVlo9Luyg3vK9f3wMTB7VBr5gw9GkVjn5q4KNb81BEh/hb/Za3vjAKZotETqEJOYUlyCooQfOwQAgBbEvIQMcmwYgI8kNrtSHUVqemIfjzkaEI8FWuoxdyinAkOQedmoZg0/E0jFXHxjTWR2/s1xJt1cBgTEQgcgtNAJT6dbPQABw8l63v69aRQVjw4EVoGhqAlYcu2AUhnendKhwfT+iD/GIzJgxohcu6NbXLXDP64Z6BeOSnncgqcP6IdgB4YnQnmKVyLT+Rkuv0+gTYZ/cB1nUZQPkNtotqhAcdPOZc88fDQ/Xz3Fs39sSork2QXWCCv48XjiTnICmzAO2igtEk1B9JmQVIyS5SG0mhN0DufvlyvLn4IIZ1jMKh89n6eXXt5JHYmpCOAF8vPPLTTqdlMNr6wij9fDn/gYtw9EIurujeDPEJ6bBI5b5G257WjYNwOj0fAPDXI8NQZDLjJrVu5MznE/shMSMfoQG+uKxbUxw6n4OwQF9YpMR1n22wmnbyFZ3RJjIICal5eG/pETQJ8bdqxPp8Yj/9EfJz7x2MdtGNcC6rEN1bhMFkqG/PmhSHrIISxEQE6XU3rW4b1yYCo7o0wcWdopGWWwwfbyXTbMXBC4iJCESRyYLU3CIIIRDi74OcIhNiIgJx17fbACj126YhAcgvMesZvvMfuAjdW4Th0PlseHsJzFhzHIv3ngcAqzoCADx/VRdMGNgaKw4mo0uzUGQXlOCWmUo25fvjeyPA1xuT5+/Wr207T2cCAMb2aeEw83jqtd3Rr3UELu/WDGezCrA3KUsP3m8+odyX703KwjtLDlvN1ysmDHsSs6zK2C6qEaZe1x3JWYUY2aUJ0vOKse5oil6X/ebOOGw6nqZnOjZu5Kd/9sJVXbFgR6KeVf3e+N5Izi5El2YhCAv0RVpeMY6n5NqVozy8BVAbEpluHxiEH7fmO/18ZCd/rDpSc1lllQr8CCHGAPgYgDeAr6WU08ua55peyoVgtJOo7PV9WwJQAhqaG/rGAFBuhG2zajQXtVcqOqE2rWdjepRWdty9aGj62LSCGyPn/j7euGNwGz3wM0gN3Gjl0GjltW3pA4DIYCWDpE3jIKuKweXdmyHDcFMeGeyvX0R8bG6ihBAY26el/tq4vRpjK5I2rTF75ab+MfrfL13TTf/bUZlHdo62C7I06RxgM42yn1sZKgvOMgqu6209aLajrJSOTgIZzcICrLbNKDyodPuEEFaVNm3b/Xy8MFINaPSyyYYSQqCvup3GZQ0xVHy7NLNvjTJuZ8+YMKv1aTfPti0NXl4C1/Rqjt92WndHC/H30bd9wsDWDrezeVig/p2GBPhaHQu2jC3LUcH+DrMgjPtfa2EdZzg+bGmZcysPXcAyJOPpyztjZJcmGNmliR740QKMjjwysgMmDmqD6GB/bE1Ix439WuKBS9ojp7BEr5xMHNRaryxpFfP/Dm+nL6PYZMHSA8kY3z9G3/7rerdAUkYBVtmkymut3ID1b3XyFV2cbqP2PWuBnyu6N8W/+5VAU7OwAIzo3MSqYmvk7JzTKyYM+5KyYJGlA4R/vOIocgpNVgE+7aLYLqoRTqTmOVyWrdAAXwztEIWhDm7SAKUlWQv8xEYGYWiHKCSrwc02kUHoGROGoe2j8HP6GbRuHGS1z/q7kfUztEMU3rihB174XTk3ase/bdepHi1C0c6mNdKYKZdfbMLk+XvQtXkoDp7Ltt6Gns3x6UrrdG5j63f3FmG4pFM01hi60vZoGYYeDrIM20cHo0VYAM6q3T5jI4OQkJaPAF8v3NjP+tjXzn2tGgdZnTNScoowL/4MooKVrMQ7BrfRPxvRuYnehWZohyh0ahqCRXvPoZF/aevzKENWpLb+KVd2RbC/D86kO64wGINEL1zdVf+9lqVJiD+GdYzCrQNb4b2lRzD12u76NRawPycDjlvzr+zZDD7eAssPXsBjl3bAJysdp9cP7RBlda6MaxOhB/9vN+ynVYcv6BXV3q3CcUX3ZlaBn6t6KoF523M1oGS+dmkWqq9HC/yM6tpEz4oZZHM9c3StGdOjmX4NzS9WbkjbRzfCqbR8mAzdfwa1baz/vrTAz7COURjWMQqpuUrgp3uLUMTFNkbryCA8/zsQFWJ9bBivKx2ahODJyzs72n16IKFXTLjVtjcPC9R/F5d1a4rL1fOG7fVSCIGb41rZLdfX20v/PWj/Rwb7W30n2jVQOZ84LB58vb0c1sscNbDZThepXoOahQbgfHYhujUPtfuNGr8n2wxlbVot6GEUHeKvX/eN2cCaQPV8ERlsfbNoUb/nFmEB6NsmAov2nEPz8ECX2diuMgcd1ROA0nNdoJ+31bHQvUWYvp22da1IB8kbHZqEoIMhi8bfx1vfHuP52lEdTMseb+4g+dpZuW0Zj8nIYH/99+YsG00IYbVdWtG1+rVtgK1/G+X1fy6Kdas8GmNdqGkZ2cnDO0bjhr4tMXtjgv6en7eX3hj34Ij2+GL1ccRGBenL7d8mwmXg55kxneElgF/iS4M/4/rFWAV+Hh5p/aMa3jFK766v6d0qHBFBvsjIL8GEAa0ghND3WSubgJyzRr+wIF+8fVMvAECQn3LdGdE5Gq0jg/SsNHcDP8YeB3GxjfXvSzv/7DN0333uyi54cM4OtG6s1CsshnNo56YhOJys1AeM3Te187xmaIfS31276EY4YWjwiY1shKt7NceWE2kAlHOwkfEY1Op72rHgozbEB/l5W50/wgJ9kVVQotdtAej1AGOd+c4hsQ73j62Jg5Tzqda98ca+LfV9pp1fn7miCxbvPY82kUF468aeenDswRHtcd/FSv3QeI3u1jwUB85l49IuTRDRyA9nMvIx/Z9DuKFvSz3wc+vA1vr1dNKQWMzemKA26npjvHo9CAvytdpH2v13dIg/3llyGCM7R+t16PH9Y7AnMQuTr+iM2MhGePinHbisW1NcYqgfRof4I8jPG9MWHcTgdo0xqmtTq7oNAExbdBC+3gL3XtwOYYG+eGbBHjx1WSer+1DNX2UM21IWLyFgrsLAj583UGwGQgMEssvRfaxXC9d1s/DAmk1LqnDgRwjhDeB/AC4DkAhgmxDiTyml00FbYiOrP439oRHtEdnID0PaR+JUmlJh/uf/hlfb45//eHgo8tQKYnm9fG139IoJtwsWAcBN/Vthd2IWhrZXTmSvXNcdPVuGYYg67Zd39Hd6kq8OsybFYe2RVPzfqI41ts6K+P2hIfoFZOkTFyMxw3mU1dP+ffxi/abu1bHd0bdNBBoHKVlwR5NznQa8KuOnewc5TcmujMdHd0SzUH9c26v0pvHHewYh2NCdRctk+XPXWVzUPhLnsgpwywDlAjS6a1O8cm033DJACXA9emlHBPh4I6KRkm2y4MGL4GTYBVzUPhKvX9/D7sl7H9zcB5Pn78aLV3fD4eSccg0q7sjvDw1BscmCLs1CMarLefj7ejkNhMy+a4DDoOTfjw7D1+tO4PmruiKnyIQjhkDIokeHY99Z6zFPLuvaFJOv6IyxfVrgtx1JGNI+Eik5RWgRHoicQhP2nc2ClErL2uJ956wyeZy5skczPD66I5bsO4+f7xsMQKkMvTe+t9499cVruqF7i9Ayu1WseOoS/LTlNMb2aWHVGndLXCscOJuN4R2jMLJLE4QG+OK2Qa3x05bTyCooQWigr13Qx1aQnw8+n9gP/dtEIDm7EKsOpeCi9pHYl5SF2wa1xqVdmuDrdSfRsWkwIhv5YcKAVmgS4o/26vf82W198Z9ZWzHj9v5l7pNfHrgIKw9dQICvN0Z3bYp/95+3upkqy039Y1BQYtYrebZGd22C18d2x7j+MSgxSVzUPhJ9WoXj1wcugm1D9Ge39cPOM5kIVlPBYyIC8dyVXfD9plMY3C4SV3RXuip3aBKMhbuS0KVZqF3Q57eHhsBklvDxFvhm/UncM6wtzmUq2ZFa14d7L26HRv4+GO8isKvp3iIM02/sqd+kZuQV64Hm7IIS3DqotR74eX1sd7z0x34Ayrgjdw6JhY+XwP2XtEPbyEZ60MfWs2O6oEuzUIQG+uDybs0QFeyHt27siW7NQ/XApK0vJvbDphNpdgG6Xx+4CF+uOYH/DmvncD5b/z5+MZIyra8VQX4++PCW3hjSPgr5xWbsOpOBJ+YpmVdehm1Y+dQlVtlnkY388NI13fTsmCYhAXh/fO9yd1H6dtIANA93fcPatXko3hnXy2E2aG3ym3rudGbBQ0Ow41SGVbaMK6ueHoGjyeUbf8vWNT2bIz23yK5RxctL4NNb+6JfmwiEBvhgaPso9I4pu1s6uTb/AefXcE+ZfdcA/WZe+0lPGhKLgW0b6+cdPx8vdG0eiqYh1vUbQLn+/bDpFK7v2xKFJWb4enth0/FU+Hh7oUlIAF6+tjt6xoSjo5o92aNlKKZd3wMxEYFW5+xv7oxD68ZBiAz2x/IDySgoMWPqn/v1z/98ZBj2JGY5PXdWhd8eGoI9ZzIRHuSH0+n5OJmah9sHt8HmE2kIC/RF39bhSMtVGqRnTYpDs1DHXaW6twjF81d1QWGJBWN6NMPHE/roXYm8vAQ+ubUvjl3Ixe2DWmPd0VTkFpkwonM0Dp3PcTgUgtGP9wzCm4sP4q6hsdiXlI0r1SD9wLaNMe36HrhWbbSYNSkOf+0+h7ZRjfDVf+LQ3knX0xm397MLUP796DDsTsx0e7858/3dA62CxX1bh+OZMZ1xQ1/7xlnjz6J/mwi8NrY7svJLcO/Fjq9fs+8egDWHUxChNqrdM6wt/H28cNvA1ujcNAR+Pl7o0yocz13ZBV5C4J5hbdEuupHDBgBHujQLxZs39MRVPZvhfHYhzmUWIi42AlkFJbhtYGuEBfri1eu66/V3o1aNg/DOuF56o7qtGbf30+9dx6n1pgkDHZfLq5LHu7cXnI7XVhnV+DOsEUK6SH90OaMQFwF4RUp5hfr6OQCQUr7lbJ64uDgZH+94IE2iuiJ2yiIA4CNBqVZ5Z8khfL76OJ6+vBMeudQ+QFvdxy1/Fw2b8ftv//ximC0Sh6eNsRpXo64bP2MjtiVk4Jf7L6q34yIQNUSv/rUf325IwItXd7XKKPaU6rqerjyUjLtnx2NE52jMvmtglS6bKuZkah5GvrcabSKDsGbySE8Xp9b4Z+85l90gy3JLv0CsPFKElNyqSfvRMn7CAgWyCkpjJ77egKvnDbxzfRieWej8QRY39A7E77sLnH5eEafevma7lDLO0WeV6erVEsAZw+tEAINsJxJC3AfgPgBo3dpxdxWiuuTpyzs57G5A5En3X9Ie57IKnaYgz7i9P5Iyq/biYvTGDT30LBVqeN4f3xsmi1LB+v2hIfhz11m7BxjUde+N740vVh/Xx00hovrhsUs7Iiu/BLc66VZf02ZNisOR5NyyJyynYR2iMb5/DB6/rFOVL5sqpk3jINwxuA3+c5HjjOGG6lJ1oPpeLXyx56wy/tbHN4Xj/+ZnWk03eXQI3l1emgF6ZbcA/HOgEDf0CcLITgGYt0PJ5g0P9ML5bDPaRflgTLcArD5aBAEgLc+iB15CAgRGdw5AYYnEPwcK0T7KB8dTTegQ7YPpY8Pw264CXN87EL/syMf8nco8X09sjDu/V7ry+XkDTUK8kZhpRpvG3hjQxg+juwSgV4t8fRt8vKzHHnpsRDDMUuLPPepwA429kZBuxoiO/igokTiUXGIVaAKAm/sFIshP4GSqGTsSi/Unlz16STA+XeP6vFGZjJ+bAIyRUv5XfX0HgEFSykeczcOMHyIiIiIiIiJyJidnu6eLUCeFhsY5zfipTHNcEgBjx7wY9T0iIiIiIiIiIqoFKhP42QagoxCirRDCD8AEAH9WTbGIiIiIiIiIiKiyKjwgg5TSJIR4BMC/UB7nPktKub+M2YiIiIiIiIiIqIZUaiROKeViAIurqCxERERERERERFSF6tcjN4iIiIiIiIiISMfADxERERERERFRPcXADxERERERERFRPcXADxERERERERFRPSWklDW3MiFyAByusRUSVU4UgFRPF4KI6qUwAFmeLgQR1TusuxBRdWC9pW7oLKUMcfRBpZ7qVQGHpZRxNbxOogoRQsTzeCWi6iCEmCmlvM/T5SCi+oV1FyKqDqy31A1CiHhnn7GrFxERUc37y9MFICIiInIT6y11HAM/RERENUxKyQoUERER1Qmst9R9NR34mVnD6yOqDB6vREREVJew7kJE1HA5vQbU6ODORERERERERERUc9jVi4iIqIKEEK2EEKuEEAeEEPuFEP+nvt9YCLFMCHFU/T/CwbxthBA7hBC71HkfMHzWXwixVwhxTAjxiRBC1OR2ERERUf3jot4yXn1tEUI4HCBeCBEghNgqhNitTvuq4bO2Qogtar1lnhDCr6a2idzDwA8REVHFmQA8JaXsBmAwgIeFEN0ATAGwQkrZEcAK9bWtcwAuklL2ATAIwBQhRAv1sy8A3Augo/pvTLVuBRERETUEzuot+wDcCGCti3mLAFwqpewNoA+AMUKIwepnbwP4UErZAUAGgHuqqfxUQQz8UINQmVZ5dbo71WmOCiHuNLzPVnmiBkxKeU5KuUP9OwfAQQAtAYwF8J062XcArncwb7GUskh96Q/1miyEaA4gVEq5WSr9sb93ND8R1V+VaZVXpxsjhDis1k+mGN5nqzxRA+as3iKlPCilPFzGvFJKmau+9FX/SfX+51IA89XPHNZ7yLMY+KGGosKt8kKIxgCmQmmRHwhgqiFAxFZ5IgIACCFiAfQFsAVAUynlOfWj8wCaqtPECSG+NszTSgixB8AZAG9LKc9CCRwlGhadqL5HRA1HhVvlhRDeAP4H4EoA3QDcqs4LsFWeiFQ29RZn07QQQiw2vPYWQuwCcAHAMinlFgCRADKllCZ1MtZbaiEGfqhBqEyrPIAroJzY0qWUGQCWQUltZKs8EQEAhBDBABYAeFxKmW38TD0/SPXveCnlfw2fnZFS9gLQAcCdQoimNVhsIqqlKtMqD6WR6piU8oSUshjAzwDGslWeiDSu6i1GUsqzUsqrDK/Nahf1GAADhRA9qr2wVCUY+KEGpwKt8i2htMZrtCg2W+WJCEIIXyiVpzlSyt/Ut5PV4LDWdeuCq2WomT77AAwHkASlQqWJUd8jogaoAq3yzuotbJUnImf1lnKRUmYCWAWlt0MagHAhhI/6MesttRADP9SgVLRVnojIEbUF/RsAB6WUHxg++hOANh7YnQD+cDBvjBAiUP07AsAwAIfVYHS2EGKwuvz/OJqfiOq/irbKExE54qLe4s680UKIcPXvQACXATik3kOtAnCTOqnDeg95FgM/1GBUolU+CUArw2stis1WeSIaCuAOAJeqj2XfJYS4CsB0AJcJIY4CGK2+ts0m7ApgixBiN4A1AN6TUu5VP3sIwNcAjgE4DuCfGtsiIqoVKtEq76zewlZ5InJYbxFC3CCESARwEYBFQoh/AbtswuYAVqljE26DMhTG3+pnzwJ4UghxDEp24Tc1uVFUNqEE6IjqNzW6/R2AdCnl44b33wWQJqWcrj71orGU8hmbeRsD2A6gn/rWDgD9pZTpQoitAB6Dkn69GMCnUsrFICIiIqogZ/UWw+erATwtpYx38JkPgCMARkEJ7GwDcJuUcr8Q4lcAC6SUPwshZgDYI6X8vPq2hIiIagMGfqhBEEIMA7AOwF4AFvXt56EEbH4B0BrAKQA3qwGdOAAPaN29hBB3q9MDwBtSym/V9+MAzAYQCKVF/lHJHxURERFVgot6iz+ATwFEA8gEsEtKeYUQogWAr7XuXmrm4UcAvAHMklK+ob7fDspgz40B7ARwu5SyqIY2i4iIPISBHyIiIiIiIiKieopj/BARERERERER1VMM/BARERERERER1VMM/BARERERERER1VMM/BARERERERER1VMM/BARERERERER1VMM/BARERERERER1VMM/BAREVGdJ4QIF0I8pP7dQggxvxrX9YAQ4j8O3o8VQuyrrvUSERERVYSQUnq6DERERESVIoSIBfC3lLJHQy4DERERkS1m/BAREVF9MB1AeyHELiHEr1rmjRBikhBioRBimRAiQQjxiBDiSSHETiHEZiFEY3W69kKIJUKI7UKIdUKILs5WJIR4RQjxtPp3fyHEbiHEbgAPG6Z5QggxS/27pxBinxAiqDp3ABEREZEjDPwQERFRfTAFwHEpZR8Ak20+6wHgRgADALwBIF9K2RfAJgBal62ZAB6VUvYH8DSAz91c77fqfL1t3v8YQAchxA3qNPdLKfPLt0lERERElefj6QIQERERVbNVUsocADlCiCwAf6nv7wXQSwgRDGAIgF+FENo8/mUtVAgRDiBcSrlWfesHAFcCgJTSIoSYBGAPgC+llBuqaFuIiIiIyoWBHyIiIqrvigx/WwyvLVDqQl4AMtVsoarUEUAugBZVvFwiIiIit7GrFxEREdUHOQBCKjKjlDIbwEkhxHgAEArbrluO5ssEkCmEGKa+NVH7TAgRBuATABcDiBRC3FSRshERERFVFgM/REREVOdJKdMAbFAHdX63AouYCOAedZDm/QDGujnfXQD+J4TYBUAY3v8QwP+klEcA3ANguhCiSQXKRURERFQpfJw7EREREREREVE9xYwfIiIiIiIiIqJ6ioM7ExERETkghHgBwHibt3+VUr7hifIQERERVQS7ehERERERERER1VPs6kVEREREREREVE8x8ENEREREREREVE8x8ENEREREREREVE8x8ENEREREREREVE/9P44ckr5e3L2eAAAAAElFTkSuQmCC\n", + "text/plain": [ + "<Figure size 1440x288 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAABHcAAAEXCAYAAAAnY6jmAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAABi50lEQVR4nO3dd5iU1fnG8ftsp3cQRKWIIoigAipIwF6wd8WCNZpoLNGIJZbEbmLs+tMoWAhiBRVQwUIRUHrvSm/Lwi7by8z5/THvzL5Td7bvwvdzXV7MzNvOzBZ37nnOc4y1VgAAAAAAAKifEmp7AAAAAAAAAKg4wh0AAAAAAIB6jHAHAAAAAACgHiPcAQAAAAAAqMcIdwAAAAAAAOoxwh0AAAAAAIB6jHAHAABEZIx5zBjzYW2PA7XLGGNrewwAACA2wh0AAGqJMeYnY8weY0xqbY+lqhljbjTGrDTGZBtjdhhjJhpjmtT2uGqS8/W9qbbHAQAA9n2EOwAA1AJjTCdJgyRZSefV7miqljFmsKSnJF1prW0i6QhJY6v4GklVeT7UHXxtAQAoP8IdAABqx7WSZksaJek69wZjzChjzGvGmAlO5csvxpiuru0DjDFzjDFZzr8DXNt+MsY8YYyZaYzJMcZ8ZYxpZYwZbYzZ6+zfybX/S8aYTc62ecaYQZEG64zljpDHFhtjLoywez9Js6y1CyTJWrvbWvuetTbbOa6BMebfxpgNznOYYYxp4Gw7zxizzBiT6TyXI1zXW2+Mud8Ys1hSrjEmyRhzvPNcM40xi4wxQ+J58aM8x7ONMcud13yLMeZe5/GlxphzXfslG2N2GWOONsakGWM+NMZkOGOYY4xpZ4x5Ur7w7lXn6/Cqc2x3Y8xkY8xuY8wqY8xlrvOOMsa8boyZ5BzzszHmAGPMi06F10pjzNExxn+i67XYZIwZ7jrvm851s40xU40xhzjbOhljrDtQiVVxFDpVL/R4Y8xwY8xvznV+N8YMc+17gzFmhfNcvvWPwdlmjTF/NsaskbQm3q8ZAADwIdwBAKB2XCtptPPfGcaYdiHbr5D0uKQWktZKelKSjDEtJU2Q9LKkVpJekDTBGNMq5NhrJB0oqaukWZJGSmopaYWkR137zpHUx9n2P0mfGGPSIoz3PUlX++8YY3o7558QYd9fnOf0uDFmoAmfdvYvScdKGuBc92+SvMaYwySNkXSXpDaSJkr6yhiT4jr2SklDJTWX1M65/hPOee6V9Jkxpk2EMcXjHUl/dKqNjpT0g/P4+3I9d0lnS9rmhFfXSWom6SD5vh63Ssq31j4kabqk2621ja21txtjGkmaLN/r3Fa+r9PrxpgernNfJulhSa0lFcr3tZvv3P9Uvq93GCcomSTpFfleuz6SFrp2GSbpn855Fsr3fVelnOf3sqSznNdwgH8MxpjzJT0o6SJnfNPl+1q7XSDpOEk9BAAAyoVwBwCAGmaMOVHSIZI+ttbOk7RO0lUhu31hrf3VWlsi3xvxPs7jQyWtsdZ+YK0tsdaOkbRS0rmuY0daa9dZa7Pke8O/zlo7xTnXJ5IC1R/W2g+ttRnOuf4tKVXS4RGG/aWkw4wx3Zz710gaa60tCt3RWjtdvjfxx8gXvmQYY14wxiQaYxIk3SDpTmvtFmutx1o701pbKOlySROstZOttcXyhUAN5AsJ/F621m6y1ubLF7hMtNZOtNZ6rbWTJc2VL3ypiGJJPYwxTa21e6y1853HP5R0tjGmqeu5f+A6ppWkQ53nMs9auzfK+c+RtN5aO9J5vRdI+kzSpa59vnDOUSDpC0kF1tr3rbUe+aa2RavcuUrSFGvtGGttsfM1XejaPsFaO815nR+SdIIx5qA4X5fy8Eo60hjTwFq7zVq7zHn8VklPW2tXON+HT0nq467ecbbvdr62AACgHAh3AACoeddJ+s5au8u5/z+FTM2StN11O09SY+d2B0kbQvbdIF8Vjd8O1+38CPf955Ix5l5nqkyWMSZTviqU1qEDdsKGsZKudgKaK1UacISx1k6y1p4rX0XN+ZKGS7rJOXeafIFWqKDnZq31StoU8tw2uW4fIulSZxpSpjP+EyW1Dz2xMWaYM9UpxxgzKcqwL5YvGNrgTF06wRnHVkk/S7rYGNNc0lkqrXz5QNK3kj4yxmw1xjxnjEmOcv5DJB0XMt5hkg5w7RP31y7EQYr8mvoFXjdrbY6k3fK93lXGWpsrX0B3q6RtxjeVr7uz+RBJL7me925JRtG/tgAAoBwIdwAAqEHG11vmMkmDjTHbjTHbJd0tqbcz1aksW+V7o+x2sKQtFRjLIPmmRF0mqYW1trmkLPnedEfynnxhxCmS8qy1s8q6hlNR8718U5yOlLRLUoF808VCBT03Y4yRL7RwPzf3stybJH1grW3u+q+RtfaZCOMY7UyPamytPSvKWOdYa8+Xb8rUOEkfhzz3q+Wrspllrd3iHFNsrX3cWttDvgqjc+Sbchc6Vv94p4aMt7G19rZI4ymnTYr8mvoFqnSMMY3lC922Ssp1Hm7o2tcdNoXKjbWvtfZba+1p8gVsKyW97RrfH0OeewNr7Uz34TGuCwAAYiDcAQCgZl0gySNfX5E+zn9HyNeD5NpoB7lMlG961FXG11D4cudcX1dgLE0klUhKl5RkjHlEUtNoOzthjlfSvxWjascYc74x5gpjTAvj01/SYEmznWqcdyW9YIzp4EzVOsHpy/OxpKHGmFOc6pe/ytd3ZmaUS30o6VxjzBnOedKMMUOMMR3L+0IYY1Kc6p5mzpSwvc5z9Rsn3zSzO+XrweM/7iRjTC9jTKJzTLHruB2SurjO8bV8X7trjK8pc7Ixpp9xNY2uhNGSTjXGXOZ8X7QyxvRxbT/b+Boup8jXe2e2M70tXb7w7GrnNbxBsUOihZL+YIw52BjTTNID/g3G10j6fKf3TqGkHJW+Fm9KesAY09PZt5kx5lIBAIAqQbgDAEDNuk6+njgbrbXb/f9JelXSMFPGMtDW2gz5qkP+KilDvsqbc1xTvMrjW0nfSFot33SoApU9NeZ9Sb3kC1ai2SPpZvlWPdrr7Pu8tdY/leleSUvka+a8W9KzkhKstavkq455Rb4Kn3MlnRupr48kWWs3yTfl60H5AqpNku5Txf++uUbSemPMXvmmFgVWenL6wHwmqbOkz13HHCBfo+O98jWrnqrS4OslSZc4q0O97KwWdrp8jZS3yjf17ln5+hyVm/GtqvWgM76N8k0p+6t8r+lCSe5KsP/J10h7t3zNrN0Nom+W73XLkNRT0cM0OX2NxkpaLGmegkPFBEn3OM9tt3yB3m3OcV84z/Uj5/VdKt/0NgAAUAWMtVTAAgCA+BhjrpV0i7X2xNoeS01zKpsOs9ZeXebOdYgxZpSkzdbahyt4vLXWRpuqBwAA6oCYnw4CAAD4GWMaSvqTpNdreyw1zVmC/kb5qnsAAADqFKZlAQCAMhljzpBv6tMO+ab47DeMMTfLN+VrkrV2Wm2PpxY8XtsDAAAAsTEtCwAAAAAAoB6jcgcAAAAAAKAeq5aeO61bt7adOnWqjlMDAAAAAIB6zuvNq+0h1EsLFqzYZa1tE/p4tYQ7nTp10ty5c6vj1AAAAAAAoJ7Lzp5X20Ool5o27bsh0uNMywIAAAAAAKjHCHcAAAAAAADqMcIdAAAAAACAeqxaeu5EUlxcrM2bN6ugoKCmLgnUO2lpaerYsaOSk5NreygAAAAAgHqixsKdzZs3q0mTJurUqZOMMTV1WaDesNYqIyNDmzdvVufOnWt7OAAAAACAeqLGpmUVFBSoVatWBDtAFMYYtWrViuo2AAAAAEC51GjPHYIdIDZ+RgAAAAAA5UVDZQAAAAAAUKet2VmszZkltT2MOqvGeu4AAAAAAABUxEVvZ0iSljx0QC2PpG6icidOo0aN0tatW2t7GDGNGjVKjz32WG0Po05Zv369jjzyyNoeBgAAAAAA1SaucMcYc7cxZpkxZqkxZowxJq26B1bX1Idwp7qVlFACV1G8dgAAAACA6lLmtCxjzIGS/iKph7U23xjzsaQrJI2q6EUf/2qZlm/dW9HDI+rRoakePbdn1O25ubm67LLLtHnzZnk8Hv3973/XmDFjNG7cOEnS5MmT9frrr+vTTz/VjTfeqLlz58oYoxtuuEEHHXSQ5s6dq2HDhqlBgwaaNWuWli9frnvuuUc5OTlq3bq1Ro0apfbt22vIkCE6+uijNX36dOXm5ur999/X008/rSVLlujyyy/XE088ETa2OXPm6M4771Rubq5SU1P1/fff67PPPtMXX3yhrKwsbdmyRVdffbUeffRRrV+/Xuecc46WLl0qSfrXv/6lnJycsIqdUaNGae7cuXr11VclSeecc47uvfdeDRo0KOz53X333Vq3bp3+/Oc/Kz09XQ0bNtTbb7+t7t27a/jw4UpLS9OCBQs0cOBAvfDCC3F9PX799VfdeeedKigoUIMGDTRy5EgdfvjhGjVqlL788kvl5eVp3bp1uvDCC/Xcc89JksaMGaOnnnpK1loNHTpUzz77rCSpcePGuu222zRx4kS1b99eTz31lP72t79p48aNevHFF3Xeeedp/fr1uuaaa5SbmytJevXVVzVgwICgMf3hD3/Qyy+/rD59+kiSTjzxRL322mvq3bt32PinTp2qO++8U5KvyfG0adPUpEkTPfvss/rwww+VkJCgs846S88884wWLlyoW2+9VXl5eerataveffddtWjRQkOGDFGfPn00Y8YMXXnllRoyZEjE7xkAAAAAACoj3p47SZIaGGOKJTWUVO9KWL755ht16NBBEyZMkCRlZWXp0UcfVXp6utq0aaORI0fqhhtu0MKFC7Vly5ZAeJKZmanmzZvr1Vdf1b/+9S/17dtXxcXFuuOOOzR+/Hi1adNGY8eO1UMPPaR3331XkpSSkqK5c+fqpZde0vnnn6958+apZcuW6tq1q+6++261atUqMK6ioiJdfvnlGjt2rPr166e9e/eqQYMGknwBydKlS9WwYUP169dPQ4cOVevWrSv1OkR6fpJ0yy236M0331S3bt30yy+/6E9/+pN++OEHSdLmzZs1c+ZMJSYmxn2d7t27a/r06UpKStKUKVP04IMP6rPPPguMYcGCBUpNTdXhhx+uO+64Q4mJibr//vs1b948tWjRQqeffrrGjRunCy64QLm5uTr55JP1/PPP68ILL9TDDz+syZMna/ny5bruuut03nnnqW3btpo8ebLS0tK0Zs0aXXnllZo7d27QmG688UaNGjVKL774olavXq2CgoKIwY7kC81ee+01DRw4UDk5OUpLS9OkSZM0fvx4/fLLL2rYsKF2794tSbr22mv1yiuvaPDgwXrkkUf0+OOP68UXX5Tk+/rOnTtXxcXFGjx4cNTvGQAAAAAAKqrMcMdau8UY8y9JGyXlS/rOWvtd6H7GmFsk3SJJBx98cMxzxqqwqS69evXSX//6V91///0655xzNGjQIF1zzTX68MMPdf3112vWrFl6//33lZ2drd9++0133HGHhg4dqtNPPz3sXKtWrdLSpUt12mmnSZI8Hk9QBcZ5550XuGbPnj0D27p06aJNmzYFhTurVq1S+/bt1a9fP0lS06ZNA9tOO+20wL4XXXSRZsyYoQsuuKBSr0OXLl3Cnl9OTo5mzpypSy+9NLBfYWFh4Pall15armBH8oVn1113ndasWSNjjIqLiwPbTjnlFDVr1kyS1KNHD23YsEEZGRkaMmSI2rRpI0kaNmyYpk2bpgsuuEApKSk688wzJfle09TUVCUnJ6tXr15av369JKm4uFi33367Fi5cqMTERK1evTpsTJdeeqn++c9/6vnnn9e7776r4cOHRx3/wIEDdc8992jYsGG66KKL1LFjR02ZMkXXX3+9GjZsKElq2bKlsrKylJmZqcGDB0uSrrvuuqDX8fLLL5dU9vcMAAAAAAAVFc+0rBaSzpfUWVKmpE+MMVdbaz9072etfUvSW5LUt29fW/VDrZzDDjtM8+fP18SJE/Xwww/rlFNO0U033aRzzz1XaWlpuvTSS5WUlKQWLVpo0aJF+vbbb/Xmm2/q448/DquusNaqZ8+emjVrVsRrpaamSpISEhICt/33y9N7xRgTdj8pKUlerzfwWEFBQcRjo+0X6fm9+OKLat68uRYuXBjxXI0aNYp7zH5///vfddJJJ+mLL77Q+vXrNWTIkMA292uSmJhY5muSnJwceC3cr6n79fzPf/6jdu3aadGiRfJ6vUpLC28L1bBhQ5122mkaP368Pv74Y82bNy/qNUeMGKGhQ4dq4sSJGjhwoL799tu4n7ub/7Ur63sGAAAAAICKiqeh8qmSfrfWpltriyV9LmlAGcfUOVu3blXDhg119dVX67777tP8+fPVoUMHdejQQU888YSuv/56SdKuXbvk9Xp18cUX64knntD8+fMlSU2aNFF2drYk6fDDD1d6enrgjXpxcbGWLVtWoXEdfvjh2rZtm+bMmSNJys7ODgQWkydP1u7du5Wfn69x48Zp4MCBateunXbu3KmMjAwVFhbq66+/jnjeTp06aeHChfJ6vdq0aZN+/fXXqM+vadOm6ty5sz755BNJviBi0aJFFXo+fllZWTrwwAMl+fr/lKV///6aOnWqdu3aJY/HozFjxgSqYeK9Xvv27ZWQkKAPPvhAHo8n4n433XST/vKXv6hfv35q0aJF1POtW7dOvXr10v33369+/fpp5cqVOu200zRy5Ejl5eVJknbv3q1mzZqpRYsWmj59uiTpgw8+iDjuqvyeAQAAAADALZ6eOxslHW+MaSjftKxTJM2NfUjds2TJEt13331KSEhQcnKy3njjDUm+6T/p6ek64ogjJElbtmzR9ddfH6h6efrppyVJw4cP16233hpoqPzpp5/qL3/5i7KyslRSUqK77rpLPXvGP93s7LPP1n//+1916NBBY8eO1R133KH8/Hw1aNBAU6ZMkeQLPC6++GJt3rxZV199tfr27StJeuSRR9S/f38deOCB6t69e8TzDxw4UJ07d1aPHj10xBFH6Jhjjon5/EaPHq3bbrtNTzzxhIqLi3XFFVdE7UcTj7/97W+67rrr9MQTT2jo0KFl7t++fXs988wzOumkkwINlc8///y4r/enP/1JF198sd5//32deeaZUauNjj32WDVt2jQQ5kXz4osv6scff1RCQoJ69uyps846S6mpqVq4cKH69u2rlJQUnX322Xrqqaf03nvvBRoqd+nSRSNHjgw7X0pKSqW/ZwAAAAAAiMRYW/YMKmPM45Iul1QiaYGkm6y1hdH279u3rw1tZrtixYpAgFKX3H777Tr66KN144031vZQgoSudhXvMevXrw9bOQultm7dqiFDhmjlypVKSIincK3m1dWfFQAAAACoKtnZ0dtkRNLrye2SpCUPHVAdw6k3mjbtO89a2zf08bje3VprH7XWdrfWHmmtvSZWsFOfHHvssVq8eLGuvvrq2h4KasD777+v4447Tk8++WSdDXYAAAAAACiveJdC3yfFaqhb24YPHx5zNadI+vTpo06dOlXLeCRp5MiReumll4IeW7Nmjbp16xb02MCBA/Xaa69V2zgq6tprr9W1114b9Fik51RXxw8AAAAAQCT7dbizr+nTp0+1nv/6668vs1dNfbMvPicAAAAAwP6FuSkAAAAAAAD1GOEOAAAAAACoF+JZFGp/RLgDAAAAAADqBaKdyGqt505W1myVlGRW2fmSkpqrWbPjy9xv3LhxuvDCC7VixQp17969yq5fXo0bN1ZOTk61nHvUqFG677771LFjR+Xk5KhLly569NFHNWDAgJjHjRs3Tocddph69OhRLeMCAAAAAABVr9Yqd0pKMpWS0qbK/os3KBozZoxOPPFEjRkzpnqfYC27/PLLtWDBAq1Zs0YjRozQRRddpBUrVsQ8Zty4cVq+fHkNjRAAAAAAgPJhVlZk+9W0rJycHM2YMUPvvPOOPvroo8DjP/30k4YMGaJLLrlE3bt317BhwwLz+L7//nsdffTR6tWrl2644QYVFhZKkjp16qQHHnhAffr0Ud++fTV//nydccYZ6tq1q958883A9U455RQdc8wx6tWrl8aPHx82Jmut7rvvPh155JHq1auXxo4dGxjTOeecE9jv9ttv16hRoyRJI0aMUI8ePXTUUUfp3nvvLfN5n3TSSbrlllv01ltvSZLefvtt9evXT71799bFF1+svLw8zZw5U19++aXuu+8+9enTR+vWrYu4HwAAAAAAtYVsJ7L9KtwZP368zjzzTB122GFq1aqV5s2bF9i2YMECvfjii1q+fLl+++03/fzzzyooKNDw4cM1duxYLVmyRCUlJXrjjTcCxxx88MFauHChBg0apOHDh+vTTz/V7Nmz9eijj0qS0tLS9MUXX2j+/Pn68ccf9de//jWs+dPnn3+uhQsXatGiRZoyZYruu+8+bdu2LepzyMjI0BdffKFly5Zp8eLFevjhh+N67sccc4xWrlwpSbrooos0Z84cLVq0SEcccYTeeecdDRgwQOedd56ef/55LVy4UF27do24HwAAAAAAtYXKncj2q3BnzJgxuuKKKyRJV1xxRdDUrP79+6tjx45KSEhQnz59tH79eq1atUqdO3fWYYcdJkm67rrrNG3atMAx5513niSpV69eOu6449SkSRO1adNGqampyszMlLVWDz74oI466iideuqp2rJli3bs2BE0phkzZujKK69UYmKi2rVrp8GDB2vOnDlRn0OzZs2UlpamG2+8UZ9//rkaNmwY13N3h0pLly7VoEGD1KtXL40ePVrLli2LeEy8+wEAAAAAgNpTaw2Va9ru3bv1ww8/aMmSJTLGyOPxyBij559/XpKUmpoa2DcxMVElJSVlntN/TEJCQtDxCQkJKikp0ejRo5Wenq558+YpOTlZnTp1UkFBQVzjTUpKktfrDdz3H5eUlKRff/1V33//vT799FO9+uqr+uGHH8o834IFC3TEEUdIkoYPH65x48apd+/eGjVqlH766aeIx8S7HwAAAAAANYHKncj2m8qdTz/9VNdcc402bNig9evXa9OmTercubOmT58e9ZjDDz9c69ev19q1ayVJH3zwgQYPHhz3NbOystS2bVslJyfrxx9/1IYNG8L2GTRokMaOHSuPx6P09HRNmzZN/fv31yGHHKLly5ersLBQmZmZ+v777yX5+vhkZWXp7LPP1n/+8x8tWrSozHFMnTpVb731lm6++WZJUnZ2ttq3b6/i4mKNHj06sF+TJk2UnZ0duB9tPwAAAAAAUHfUWuVOUlJzFRWlV+n5YhkzZozuv//+oMcuvvhijRkzRpdffnnEY9LS0jRy5EhdeumlKikpUb9+/XTrrbfGPaZhw4bp3HPPVa9evdS3b9+IS69feOGFmjVrlnr37i1jjJ577jkdcMABkqTLLrtMRx55pDp37qyjjz5aki9wOf/881VQUCBrrV544YWI1x47dqxmzJihvLw8de7cWZ999lmgcuef//ynjjvuOLVp00bHHXdcINC54oordPPNN+vll1/Wp59+GnU/AAAAAABqA4U7kZnQBr9VoW/fvnbu3LlBj61YsSIQLgCIjp8VAAAAAPu67Ox5Ze/k0uvJ7ZKkOX9rp7RkUx1DqheaNu07z1rbN/Tx/WZaFgAAAAAAqH+2ZJb2xKVyJzLCHQAAAAAAUGdNWVkYuF0ds4/2BTUa7vBFAGLjZwQAAAAAgu3P07DiVWPhTlpamjIyMnjzCkRhrVVGRobS0tJqeygAAAAAUGckMueoTDW2WlbHjh21efNmpadX3QpZwL4mLS1NHTt2rO1hAAAAAECd4Q53qBeJrMbCneTkZHXu3LmmLgcAAAAAAPYBSQml07LIdiKjuAkAAAAAANRZrmyHyp0oCHcAAAAAAECdFTQtq/aGUacR7gAAAAAAgDorMYHVsspCuAMAAAAAAOosd7TDtKzICHcAAAAAAECdRZ5TNsIdAAAAAABQZ7mrdajciYxwBwAAAAAA1Fk2ym2UItwBAAAAAAB1lqVcp0yEOwAAAAAAoF4g54mMcAcAAAAAANRZQT13mJgVEeEOAAAAAACos4J67pDtRES4AwAAAAAA6iwCnbIR7gAAAAAAgHqBoCcywh0AAAAAAFBnkeeUjXAHAAAAAADUWcENlREJ4Q4AAAAAAKgXmJYVGeEOAAAAAACos6jcKRvhDgAAAAAAqLPqU6CzYFOR/jkpS7aGS4wIdwAAAAAAQJ1V00FJZdz7eaY+np+vndneGr1uXOGOMaa5MeZTY8xKY8wKY8wJ1T0wAAAAAAAAd7RT13MeY3z/5hbVzcqdlyR9Y63tLqm3pBXVNyQAAAAAAABHDfTcefTrLL3wfXalz1NcswU7AWWGO8aYZpL+IOkdSbLWFllrM6t5XAAAAAAAACGVO9UT73y+KF8jZ+dW+jzFHt/4arrCKJ7Knc6S0iWNNMYsMMb81xjTqJrHBQAAAAAAUK9Wyyrx+P61NTzSeMKdJEnHSHrDWnu0pFxJI0J3MsbcYoyZa4yZm56eXsXDBAAAAAAA+6P61HOnLlfubJa02Vr7i3P/U/nCniDW2restX2ttX3btGlTlWMEAAAAAAD7qboe6Lh5a2msZYY71trtkjYZYw53HjpF0vJqHRUAAAAAAIDq/lQsN38QVdNjjne1rDskjTbGLJbUR9JT1TYiAAAAAACACL5eWlDbQ4jJH+rUdLVRUjw7WWsXSupbvUMBAAAAAAAI4QpKcgurd63xhZuL1KdjSrVeozrEW7kDAAAAAABQ49xFML2rOXjZlRNfeDR/U5F+WBW9iqhOVu4AAAAAAADUBndQUt0Ni5MT49vv1jF7lF9sNfOvbdUkLbxupq723AEAAAAAAKhx1hWVeKs53UlONHHtl1/sG0duke/fzZklmrgsv0rH8tWSfN0/LjOufancAQAAAAAAdZa7csdTRyp3/DxO2HTde7u10zWlqyqmZT34ZZYk6dkLyt6Xyh0AAAAAAFBnuXMSb/X2U1ZiQnyVO37+QqLdecEDY1oWAAAAAABABN5q7lScmlS+cMc/nAbJIcdV4TCL4yhXItwBAAAAAAB1VnU3VLaVCIz840kJCYWqcpiZeWWXKxHuAAAAAACAOssdlHiqYVpWifuc5Uxl/OFO+ep94tO2sS+y2ZLlKXNfwh0AAAAAAFBnVXflTlFJ6UnLe3r/2EKPq0w1kCRt2lOiJKe5czyBFqtlAQAAAACAOiu4cqfq050iV2FMeUMZfw+gsHCnEuNZm16sC9/KCNyP5zlTuQMAAAAAAOouG/FmlXE3LC7v+aPlLpUZ58bdwdOw4ln+nXAHAAAAAADUWaE9d5ZtK9ZHc/Oq7PzeSoRHgWNDDqzMrKyikDQnnuXfmZYFAAAAAADqrNCeOzeP3q3sQqvzezcIX4K8Cq8Vj+rpARR8n8odAAAAAACwz7BWyi/2pR25hVWzdFZlAprShspVl/IUloRW7tBzBwAAAAAA1GPu4MTKyjjFOl5b+VWppOBzlL9yx0Y8rjLDKgkJc+JZLYtwBwAAAAAA1FnuoMR9u6DY6g//2amnvt1bufNX4tjqaKgcek6mZQEAAAAAgHotNNvwd9nZW2CVmW81ppLNlYPCowoeG7YUehVM9fLzxnEywh0AAAAAAFB3RQlfQqcvVfj0USqD4uGvqgmbllWJ8YRV7jAtCwAAAAAA1Gc25I67505Vn7/8lTtVv1xW6CkJdwAAAAAAQL0WOm3KPy3LUwcqd6L23KnE0MJ77jAtCwAAAAAA1GPRoo14KlrKf/7Se/nFVt8sz495bIknvrOWR2iY443jeSZV+GoAAAAAAADVLLSyxhgjyVZduBOlcueJSVn6ckmBDmqRpJ7tk4OOSU6Uij1SQYmzFHqMc1ZmPBKrZQEAAAAAgHouWk8c97SsyvS+ibZa1rpdJZIkb4S5V2lJvslh+cWRl8uqyobKVO4AAAAAAID6zRV2eG1poOKuaNm216sOzRIreHp3SFT6eF6R705qsgk9RKlJRtmFVgXFlYlxgk1eWaDkBHruAAAAAACAfYw7fCksKb3tnpaVmVfxOVreKJU7/scjZStpycGVO1UxLeuezzJ1xyeZYVVIrJYFAAAAAADqtWg9cTxRQpnKnN/Nv+R6pHDFH+74K3dCz1Gl07LouQMAAAAAAOqzoJ477nAnWslNZa7lOk+sJdeTnDQlP8q0rCpdCj2OdIdwBwAAAAAA1FnuoMRrI0/LqtbKnQjb/cdEm5ZVGVTuAAAAAACAfU6giiZK5U5lVssKKgAKqtwxznXCj/HvVlXLsUcbjySV0HMHAAAAAADUZ1alVTTu8KWkqip3otz2X9MbITjyP+LfFNZzpxIDCg2qIi3FHopwBwAAAAAA1F22tHLHG1S5E7RLpc4fuOmu3HEuujffhgUugVCn7FOWW/hS6GUfQ7gDAAAAAADqLHfljjfqtKzKnT/SbX+gdNdnmRo9Jy/KwdXfUJmeOwAAAAAAoF7zZxtGwVOU4qloiYc3ylrrxrXPhKUFwWMKqdwJq+ypxHhCg6HMvLKb7hDuAAAAAACAOstaX+WOMcFVLF5v8D4VPn+U28aV7oQueW6dPaNNz/q/6TkVHk9opU5GbtnhTlKFrwYAAAAAAFBN/jExS6nJRsmJJlBFE9xQ2TUtqxLXiVK4E1S5k1cUHLCU1XNn8dbiCo8nngbKoajcAQAAAAAAdc4nC/L14a95vobKxhe2BC+FXr3Xd1fuFJRU3bSrslQg26FyBwAAAAAA1B17C7zKLXRX5VgZ+cIWd28bT5SKm/JyhylRp2UVha51HnzdBGNUVZHPJwvyy30M4Q4AAAAAAKgzho3K0PoMT+C+r+eOLzyJulpWJa4XfVpWabpTUBJyTMg5EqtxXlQ8wRXTsgAAAAAAQJ3hDnak4CDFXa1Tkw2Vw44Jq9yp+PV956lc1Q/hDgAAAAAAqLPcq2W5M5DRc/Pce4UdtyvHo4e/ylJ6tidsW+j5I50mVl7jb+bs3z2pkulOrGgnntgn7nDHGJNojFlgjPk63mMAAAAAAAAqw8oXtBgF98fJc/XBiVT48vR32Rq/OF9D39gV+/w2yvSuGHlNUUnwdStbueN+XqkVaKBTnsqdOyWtKP8lAAAAAAAAKsiWTpFyBzEdmiW4dwmzZEuRJCm/OHbtS4l7eleUfUKzm0JP8J4JlZwX5Q6nUhJN1G3RxHV5Y0xHSUMl/bccYwMAAAAAAChTXpFXv6wvjLgtULljgpc/91RRz53te4ObN/sVuwKc0P47xSXB07J2ZlduXfaKLH/uFm+29KKkv0mKOlpjzC3GmLnGmLnp6emVGxUAAAAAANhvPDZhr24avUdbMkui7hM6LctTRsXN4G5pkqSjOiRHPecn8/P06IS9rnOWnqlpWmlk4s52rLUq9E/LqqLlz93XDa00iucaZYY7xphzJO201s6LtZ+19i1rbV9rbd82bdqUeWEAAAAAAABJWrfLl5as2Rke7lh/6Y6CK2vcQU+kyp2GKb6D2jWNHn18uSQ/6L57ilZSlMNKvK4wyUreKGVDZ76WHnVbKPduJRUoAoqncmegpPOMMeslfSTpZGPMh+W/FAAAAAAAQLhEJ52445PMsG2l07KMPK4UpKSMuUz+YCVWWNK8QXAsUuKaiuVuq+O+XVQS3IC5JMpiXFsyPUHVRbHHGn1blfTcsdY+YK3taK3tJOkKST9Ya6+Ob3gAAAAAAACxxVpK3L8Uuv+2X1mVO/5gJVr4IkktG4aEO3H08SksCd4nVsgUby+dmuq5AwAAAAAAUC0SY6QTy7cVB3relKfnjj+ciRW+NA8Ld1yVO1GOKwpZKStWZVBNhTvlWj3dWvuTpJ8qd0kAAAAAAIBS+UXR043FW4uVliQlJJiQcMc1PSpS5Y717xe+rcRrlV9kw1bBcgc10QKXeKdlSZLX62oYFEO8vXmioXIHAAAAAADUKk8Z2UZBSfhqWUWuUCXS4d4YlTuPfp2lAf/eGRbguIOaaHlLccg+VTEtK1a2E88pCHcAAAAAAECt6ndISpn7GBOjwiXk8YJiq7Hz8iRFrqz5ckmBJKmwOHSKVeSGym53fbqn9LKKXBnkR88dAAAAAAAAl6jZTsj91TuLA7cjVdakOU1q8kKmg3miNFTu3CoxcHv97uCSod92hS/f7lcV4U48M7bK1XMHAAAAAACgqpXdlca3T7QqmdAAxH03UsPjtGSjghKr7dnBZT3u49w9fVo3TlQks9cXatLygqhjjtaUOVSNNlQGAAAAAACoaa0aJajIY+Ou3HHvF6lyp1FKgjLzPdq4O7jqxroOdJ/DRrnwnrzYqUw8VTcv/5St8Yvyo5+j7FMwLQsAAAAAANRtp3ZPkxS9wiVWiBKp2qdLa1+tS5Er2wlt2OzuueO/Wd5VrcpqFC1Jb/+cq505MRr3SFqfUaKrRmZE3U64AwAAAAAA6jTj/OeJEq7EylAiNVROcmZZFbqWNfc1bC7dZ/XO0uTHf9lYy55HHFfIwNamF+vbFdGncUU7x1dL8rVka3HUfQh3AAAAAABArTJxNN0xJkaFTox0pzhCuU9you+CBa5wJ8HEPo8UPsUrqYxUJTSMuu+LLN37eab25MWu1AnlrzSKhnAHAAAAAADUqrKyHX/4E3VaVoxjI03LSnEqd4pdlTjGSP5dQ6dfBSp3ypfJhIVRWfm+E2zcE32FrYog3AEAAAAAAHWaf1pWvOFOWQ2VExPC4yT3+UMP8d8t77SsRVuCp1IFQqpyhkRlraZFuAMAAAAAAGpVWeGFMf6eOFF67sQ4PlIgE5rtHHNQctC0rNDwxVpp054Sbc0qX7rzwPgsSdLoObmav6koUKFUnqXPrS171S2WQgcAAAAAALVqdxw9aIxMBadlhW91hzutGyXovWtbqf9zOwLhUegqV1bS2a/vKnOM0TzzXbYkqV0TX41NeVfdKmt/KncAAAAAAECtKqvBsD+LiZZx2NAeOa7bkfrkuBs4+4OeBNdqWd5o87JinCeSoUemRXy8XJU7Krtyh3AHAAAAAADUqN25Xj30ZaZyCn3JS5lhh9N0Z8Pu6NOiCktsIOQJ7rkTIfxx33UCGvdqXJEqdyrikJaRJ0xFavIcCz13AAAAAABAnfLx/Dx9uaRA7/+SKyny1Ck3f0PlaJZuLVbfZ3fo/nG+HjehZwsLa1z3E9zhjvNYpJ47kRSX1YIn5Dh/pU95ZmVZawl3AAAAAABA3dKqkS+O2JkdZ+VOiNCgZ9te33kmLS+QFF6pE9pU2X29Imdb0LSssMqditXuRDsuNGwq8zyEOwAAAAAAoC5p1sAXR/h77ZS1NLgxwYGOu9dN51aJYfuHTnsKXQ7dfW93rm/n4KXQfTdGnN5EJ3ROKVelTdB1Qit3Ao/Hf0IryUNDZQAAAAAAUJf4p0L5mx2XuRS6ggMdd9CTYExYA+SikEqd0LAnUriS4Gq6498/JdEoOdFUuOdONFXdc4el0AEAAAAAQI0KDSvKqkwJXZXKGAXKb4wJXxGroDj4fMXOPCivtRq/KF8FJZGvETotKzHBCZIqWrkT7XGmZQEAAAAAgPrMG5JWeL3SkG6pMY9JdCUY/rBnYJcUJZjwaVf5YeGOr1rnl/VFemTCXn23oiDs/Bm5Xq3b5Ut9/GFTgglutFxe0UKZ8hTuWMtqWQAAAAAAoI7xhx7+ghyPDQ5v/EzgX6O2TRLDHh90aKoSjLRmZ3ApTmjlzug5uTrqqR3asTf28lbzNxVLKu0BlJhggip6yssq8hSwslYHCzsP4Q4AAAAAAKhLQrMNr7WBPjxugcDHSA2SS3cILF8uX2XNjuzgWpjQcOfj+fmSpG1Z4TUzNw1oFHV8/kbOq3dGmMcVj5Cqm4oshe4eTzSEOwAAAAAAoEaFhTteX5VMKH+4Y6Sg8Mc4KUmCMUoMbcgjKS8k3Ckssc5x4WOJ9Fig546JvD1eVpGDmfIuhR46jS0U4Q4AAAAAAKhRoVmFxypK5U7pg9GCGX+fHDd/5c6LlzSXVBqwxFsx4582lZBgVIlsx5mWFen85TiHZVoWAAAAAACoY8IaKkcNd3z/+qdH+QWmZZnw5smSL9xpmmbUomFw7BFpVa5I4U2VVe7Y4Cod/3g27i7fNC+mZQEAAAAAgDrFunraSJLXa5UQIaFIDOmt49eqkW/nSIFQQbFVVoFXaclGqYnBO0SqmIkU3vj3i3T+8hozNzdwO8UZT5GT+GTlRy7hcV/XSsopskpOjLirb/9KjxIAAAAAAKAcQitRPFYRe+f4p2UZ+VbMkqROLRPVNC0h8Hiofs/t0ISlBWqQbJSSFLxt8ZbisP3957j06AZq6YRGgcqdhMi9gOJlJU1bWxi4X+IN/je08bNf6MphO7M9QauFhSLcAQAAAAAANSpSQ+UEI3VsHhxguAtv/NlPy0YJsnJ64sTIXRokG6UmBe/w64aisP38501KNCrxWG3f69HvGSXO+Y16tk+OeP7TuqdGv7jjt/QSNW9QGr2UOBU7/sqgaLOtgip3rG//5BgJTlL0TQAAAAAAAFWvyBPecycxQUoKCTDcS6G7++wExAh30pLjq7jxVwQlJfgqak57JT2wLcFI7ZpETlVO6JyqySsLI27zm7o2eHuxE+r4GzZHa5ScYIzc0Y/XKuK0tcD+MUcBAAAAAABQxZ75LjvovsdaJ9AI5p6W5efeL9IxfmnJRu2bxWhU4xdSueOWkBC9oXJKUvmna21wGimXeHz3oy1xHtpzx+uN/PoE9i/3SAAAAAAAAKpQYLWskPwiaLUsZ5s7+IgVrzRINkpONFErb0LP4a/cCbq+iR4gVaQTT7ET6pQ4oU4807Kk6EvFB/avwFgAAAAAAACqjNcbedqRu7FwaB8aKfYy5f5pWcmJsWMY/zmSE0xYL6CEBFMlK2aFCvTciZLuBD0v69sv1tMg3AEAAAAAALXCH254nfAiNL9wT8valeNLRH5ZX9oUOVa408CZNpVUxsysQOVOhP1KPDbmNSqqrHAnrHLHG/u5Eu4AAAAAAIBaUeL1rx5llRChRMZfrWKMtMi1jLk/E4lVVZOcVL7KnaQIJ0vP8VZT5U5Z07JKL2rl680Ta0l2wh0AAAAAAFCj2jp9cPwZRqByJyS/CKyQFaXDTczgxSmLCV2BK5pIlTv5xTbqdKg2ZfTyiaWkPNOy5Ht9qNwBAAAAAAB1RrsmviRlxjrfFCuPN3JQE61aJbfQBv69uE+DiPv4c5MyK3ecfyOFQKceniYTJVU5sn2yPhzeUmf1TIt5/ohjc01HiyS0v5CXnjsAAAAAAKAucS8Bbq2Vla95cmiFTiDkCAk2/nhiY0lS93bJ6tQqKeI1/Jcos3InxrSsFg2jN1ROTjTqfWBK3JVBkcYWTevGwSf12sgNp/0ivwIAAAAAAADVxB1uRKtekdzTsoKdd1QDnXeUr2JndXqxIvGfN97KncQI4YkxJuJ0qK9ubR1YjasiLXm8gcqdyE/+9CPSdMMJifp8Yb72Fnjl8UavYpKo3AEAAAAAADXMHWn8usE3NevdWbnhPXec1CJWv5nzj4o8LcuvrMoaEyVACowhwoZo1UKS9NIlzTXjnrYxr2mdVyBqzx1JZ/ZoEKgmsjZ2f6Eywx1jzEHGmB+NMcuNMcuMMXeWdQwAAAAAAEBUrlAjv8h3p7AkfLfEONYhTzBGU+9qq/evbRn0eGq8q2U5sU60S5W5WlbI9pQko2YNYsct/lAnWtGSCem546lsuCOpRNJfrbU9JB0v6c/GmB5xHAcAAAAAABDGPRWrZSNfNPHo2U3D9gtU7pRxvpaNEnR4u+BqmjuG+PryJEdYBcstULkTJd2J9nhge8jo4pmm5X/+0St3ggMnb5SG035lhjvW2m3W2vnO7WxJKyQdGMdYAQAAAAAAwrgzDf+y4B2ahacwiYHgpexzNkxJ0OFtfQHPpUc3UONUX+SRFGfPnWjKrNypgGjhTqRrWUkea5UQ40UoV88dY0wnSUdL+iXCtluMMXONMXPT09PLc1oAAAAAALAfcWcaHifpiBRs+HvOxJuv+KuA3DlIckjycW6vND1xbjOd2DVF7pNHC3HKG+7EE0RFWwrdfz+0D1CxR0qJsSRW3OGOMaaxpM8k3WWt3Rs+MPuWtbavtbZvmzZt4j0tAAAAAADYz7grVjxO5U5iQngwkpocnpQ0To2enkSa5RTacyc1yej8oxoEKmH8W/29f0KVFdZUpLDHhvwb85xWKvZYpcSoQIor3DHGJMsX7Iy21n4ezzEAAAAAAACRuMMd/7SsSL1t0pKdG65Nn93cOup5Z//uW3lrwtKCwGOhq2WFLinuv2zXNr7SmNBKnbIqd+Kp1AnlLaujcsi5i0qskitTuWN8r+47klZYa1+Ib5gAAAAAAACRWVeq4Z+WlWjCq2DSksKnZUXqzRMq11WFE9pzJ1oBzLEHp2jGPW11Zd+Gzv1kZ/+qb7rjz3bu/HRP5B1clyz2Stv2epUao3InRu4TMFDSNZKWGGMWOo89aK2dGMexAAAAAAAAQSJNy0qIUH7in4pUmXwldLWsxJDruE/drEGC7j65iU46LFXHdUqVJDVtULmGzJF4rfTa1GztyPZG3O5+fdam+9aIzymMXuZTZrhjrZ2hio0VAAAAAAAgTPBqWf7KndBFxd1LoVc8lkgKmVeVXxwckoT1+UkygWBHkg5qEU9dTPTzReK10pszcqNuL/H4xrh8W3Fc1yzXalkAAAAAAACVFannTsRlwJ39CorLaE4Twn2u0LDl0wX55TpXWSpUVRTl6bRp7Itpip3XZGdOaWVPUozZaIQ7AAAAAACgRsW7WtaEZb7GyG/OyCnX+d3hzryNRTH3reqpSvGcL3QJdL+zeqZJknZme8K2JcRIkQh3AAAAAABAjXJnG/6GypEqd/zTk7xW+tdFzXVxnwZxnd99rgYhy6k/cHqToPvV0C+5TF4bOd2Z5az2NWlZQdi2WKt2Ee4AAAAAAIAa5c42JrqCjND8IsW1QtQZR6TpsaHNYp732uN8K10lu45rkhYcfRzfOTXofjz9fN67tqWevSD2tQPniyMs2pQZXpkjSR2a+uZePTa0adg2wh0AAAAAAFBnuMMdfz+dA5uHN5VJKV8vY919chMlJUh/PaW0Oid0dayw1bLiCGOOOShFx3VKKd9gYsguiFy589CZTXVV34Y6tXta2LakGAkO4Q4AAAAAAKhR1jUxq3OrJDVINmqYkqBzegVPu2rqVN00Solv7lRSgtGCBw7Qpcc0jLpPaAVMvLOyovW8iXdaVzzPoX2zRD1wRtOwFb4kqWFq9AiHcAcAAAAAANQod+VOkccGqlKu6d9Q80e0C2xr0dC34clz45sSFY+w4CTOcCbatKjQh0Pv/294S905pLEObhljuas4HNUhOeq2chY4AQAAAAAAVI57UlJQzx1jlJwYvl/D1Krrelzxyp2KXa/XgSnqdWCKflxTWLETSOrWNiniVC0/KncAAAAAAECNirYUeCh/hU9VLmhV0dWxolbuhIZFzv0r+zbUfaeW9v6J1jPng+talnntz25qFXtsZZ4BAAAAAACgKsUZ7qQl+ZKSxIqWzUQQNo0q3mlZ5RzDg2c01bXHNSo93jn8qfNKp5jde2oT9elYdqNmU8YgCXcAAAAAAECNKivbad/UF1c8NrSpbh7QSMceHL3fTHmFVdrEeVz82U7sHds1SQisDHZ8Fa3ARc8dAAAAAABQo2xIunNR7+BVsib8qY2slVKSjP5yUhNVp7grd+JsqBz9Or493U89dFn2iiLcAQAAAAAANcorKdFIHifpOKRV8EpSyYlV2WUnmP/cDZJ9/5Z44jsuWrhzYPPyRyv+U0VbXr28CHcAAAAAAECNstb6KmaccCdsefJqcP9pTXRIyyQ1a+Arl2nbxPdvfkl8DYCiDfHa4xqqS+tE/WPSXu3M9katBPI/bG1ptVBVVe7QcwcAAAAAANSoYo+UmlSaglRVyBFLswYJGnRoaviGOJs7R2tqnJhgNLhbWpnTs/oe7Ouv07ZJYmDfqoq0qNwBAAAAAAA1qqjEqnFqgnKLrHO/5sfgz2rizHbiP2+Ux/84qJHO6pmmTq1Ko5iqujbhDgAAAAAAqDHWWhV5pBRXIrFuVy2kO1WsrPY5CcYEBTtSeGPpUA+e0US/Z5TdFIhwBwAAAAAA1Jhip4uye1rWiV2rZknw8nD3wKnS88Yx1yreqqEr+zaK65r03AEAAACAKOZt2K3xC7fU9jCAfUqRxyspuM/OmT0aRNm7+rRu7Fuhq3nDqul8U56z9GyfLElqlMJqWQAAAKhFWzPztSevSD07NKvtoQDV5uI3ZkmSzuvdIWozVVStnXsLJCO1bZJW20PZb/zvl43q1KqhBhzaukauV1Dsm2Z0WNtk/bYrznXIq8HV/RuqZcMEndOrar7XyvMr4vGhzTSsX0O1bZJY9s5xoHIHAAAAFTLgmR809OUZtT0MoEbkFdXeG9D9zW2j56v/k9/X9jD2Kw9+sURX/feXGrtedoGvv84fIq1cVYOSEozOO6qBEqo4uI3nbGnJRkcdWHVT0Qh3AAAAUCnFTnk9sC/j+7zmzNuwR5KUT6C2z9qdWyRJapa2b1XDmSpb2Lz8CHcAAABQKUUlvOnFvo/v85pXWEK4s6/6fVeuJOnglvtmp5jamMFJuAMAAIBK4U0v9gdFVO7UOP+KSqg5tqqXjYrC4/X9PKUl10wKsm/VB0VGuAMAAIBK4U0v9geEmDXDHS6UeHnNa1pN/T73Ol/mfS102ZLlqzY7oGnVNEkuD8IdAAAAVEphMW/AsO/LLWSKUE1YtnVv4HYJlTs1wuMtfZ335BbX6DUTjNS9XZK6tt43pmeNOL2JOrVMrJVwZ994BQEAAFCj/MvYSlJ+MW96sW9atT07cPuX3zPUq2OzWhzN/sG9KhlVgTXD3Sx8yZYsHdCs+peg91doGSN9clPNLL9eE4b1a6Rh/RrVyrWp3AEAAEC5LdiYGbi9bGtW7Q0EqEb+FX0kaW9+zVQ07O+87mlZVO7UiG1ZBYHbe1zf89XJXyyUmFA/J2Z1aV3zlTlloXIHAAAgTmt3Ziun0KM+BzWv7aHE5flvV8rjlUac1b3Kz+3+RH3znvwqPz9QF7iDBk8NNZrd33ldU4T2FhCo1YS563cHbtfU97n/Z6umsp2URFNl15t9b1slJda9UIrKHQAAgDhdP2qOLnjt56D+BHXZaz+u05tT11XLuT2uRqf15fUAysv9vc0MoZrh/nUyfXV67Q1kPxJULVVDv8/9P1s1tWT4Pac00fUnNNLpR1R+ylmj1ASlJhHuAAAA1FubdvsqVLZm1q9KlepY2tb9RtdLRUONWbl9b9BUoUistVq0KVMlHq/en7We6odKcFcxePbBlZuWbc3Swk2ZtT2MIO7XvDhK0DBn/W79tGpnTQ1pnxf0+7yGwh3/l7mmKneaNUjQPSc3UXIdrLipKoQ7AAAAkhZvzlRWnD01sgtKqnk0lbMzu0CXvDEzcL+wGpZwdr/RrYpPetel52jNjuywx+8Ys0B//XhRpc9fX2UXFAc1rz7zxek6/T9TYx7z3fIdOv+1n/XUxJV6ZPwy3TN2/339Ksu7j1fuXPeurxqxOgLgigqaChfld8ulb87S8JFzampIVSqnsESZeTXT1yZenlqo3KnpaVn7A8IdAACw38vIKdR5r/6sh8ctjbqP+83PL79nlOv8O/cW6Kb35mrtzvDwojo8980qzd2wJ3C/oBpWs3K/AaiKT3pP+fdUnfafaWGPf7Voqz6bv1kbM/IqfY2KWrgpU98u214r1+712Hf6y5gFQY/tyvG9MUzPLlSnERM0bsGWoO0ZzvZ3f/5dkrR0Cw2vK8odLsxYm67zX/u5zr0xD1VU4g1a5SuWXTmFklRmNVhNcv8+idRQOfT3mbVWH87eEHc4XxMKij3aubcg4ra7Plqgfk9OqeERxeZxJZc1VbnjDVTukO5UFcIdAACw39uZ7XuD89WirVH3+X1XbuD2xt3lCxp+XrdLU1bs0FvTfgvblltYoote/1nzN+6JcGTFHNi8QdB990ooVcX9prcqP+ktiVIe8c2ybWGPfTBrvTZk5EbYu2pd9fZs/fGDeSosiRyS+UOWV75fU6XX9S9P/N3yHUH3/Z6auEKSdNfYhUGPh75XatkopUrHtT9xV5Gs3pGjRZsyNW3NrlocUdn+MmaBznhxmjKc4CaS/CKPRjrhnyTtyatYMGKt1fQ16VF/Nioi+HdL+O+D71eUTsdauiVLv/6+Ww+PW6rb/ze/ysZQWU9NXKH+T32v7AhTIqes2Klij61T0yXdGVp1NlQuKvHq7+OWavnWvVTuVAPCHQAAsN9zT1uKtgxsXlHpm5f8ovK9kVm+da8kacfe0jdb2QXF2p5VoN/SczV/Y2ZQdcaOvQVxV4pYa/Xo+KX60dV/oigkBLjq7dlBn2pbayv9Zsy9Qla8DZXnbdit//2yMeY+O7IjvyENDZBmrNmlv49fpsv+b1aZ192YkRf31+z3Xbm66u3Z2pZV+vz8X/to1RBTVvjCl39PXh3z3Dv2Fuhf367SmF836ue1ZQcEa3fmBG7PXLtLizdnBu5vzcxXUZTpdu43v1LthDsFxR7Nca3AU5cs2ZylF6eslsdrtX5Xbsw32ZGyxiWur0NWBUOR8vpm6TZtKiNUnr9xj3ZmF+gb53fH+pDgs8TjDYShb05dp8e/Wh7YVtGqwh9W7tQ17/yqD2ZtqNDxkbh/1CMFx+7fXS99v0aXvzVbkrR4c92pUJvsBLIrQ35nuF/nzNy6E+4ETz+svnBn9Y5sfTB7gx74YkngmhTuVB3CHQAAsN97ZHzpdKzMKKX97qqJ8vaweXu67xNyf2BQ7PGq12Pf6finvw8EMe6w5I8fzNMfP5gX1zSDN6au03uzNuj20aWfWr/xU/AKWXvyinXze3Ml+YKpzg9M1OEPf1Nm+f1TE1fohKe/D0yDWJeeowUb9+inVTv1/LerAvvF82ZgT26RLn5jlh78YklYsLRi297A7fmu6WTu17y4JPgad431hWHuwCySgmKP/vD8j7rgtZ/LHKMknfPydM1clxGossotLO2vtHTL3rD91+/KVborkFqzI1tTXSv87NhbEJj68vGcTXr1x7V64PMlGvbfX6KOwT8F8IeVpSHNVf/9RVNcoc3cDXvUKDUx4vH+sMkvr6gkcN5dMao5qtJrP67VpW/O0i+/lW8KY7wKij0V7hNz7qsz9OKUNfpx5U4N+ddPGvry9KjTkiJVMczfmClJmv1bhnr/47ugr3exx6tHxy8NCuYqa/OePN364Xxd9d/ZUUPKpVuydNHrM9X/ye8Dj+0N6Q02buFWDX7+J/2wcodeCqkyW1TBYCTDed2emLCiQsdHEtRzx2O1M7sgqHmyO9T0hyiSlJVfrJzC2u+HZq0NVEuGrvaV6QoDd2aXv6Jye1aBjv7Hd3r2m5VRqxz98os8uvKt2ZoZR5BcEke4k1/k0Z9Hz69UA+4lzhTRRZsyAyFeIolEleGlBAAA+z33J77+4GF3bpEmLdkma60+n79ZY37dGLTP0i1ZGr9wS9i5YvEHOO6pRCM+Wxy47Q9R/H88vzSl7Gk+/pW7WpRRnfHr+t0q8XiDppeV9Ub/rWm/aVtWgV50xnHKv6fqwtdnhr1xnbN+twY+80NQSBPKPZXtranB09Pc49jiWonslR/WBm4XeYLf1A4+rK0kqdeBzSRJ4xduidhb5rUffedYFaFZcyS5zptnf7DkHs+yrcHn93ithvzrJ73gqtj56yeLdN27vwaqbI576nud9dJ0WWsDb2z8JizeJo/XBlUJzVy7Sz0f/VaLNmWGVdzMWlcalDw6fqk+nrs5cH/tzhwt3ZIVcQWh7VkFstbq6nd+Ud8npii3sETWWvV7coo6jZhQ6X4r27Ly9eWirUFhyxbne33muoqHO/+ZvFqdRkwI+36buW6Xuv/9m6DXPdSOvQXqNGKC/vZp9GbS/qmQm3bn65h/TtakJeFT/yIFoP7X68EvlkiS3vhpray18nqtft+Vq/dmbdCpL8Ruei35QoB16TlRX/9Xvl+joS9P1w2j5gTGefzTvvAmK79Yd320QOvSfa/NOa/MCDs+dJqpv2F5aPgrSXkVDEUecl4DKfaqfIs3Z+qLBZujbncLXZb77rELNXzknEC1W6xwvazeXM9+s1If/RpePfjVoq267cN5mrlul+4ZuzAo1I3kwS+WqO8TkzV1dXrY72l3lac/CPQrKC4duzsUnLB4m256b66stfrT6HlRp3ge//T32pNXrDd+Wqdnv1npOq8nbGrovA17NOu3DF0VI0jelVOo7n+fpFmuEDbaNNsFm/ZowpJtYUH56z+tVacRE7Q9jum/D3xe+v3in7JG4U7VIdwBAAD7rXdn/K5OIyYEPfb6j+vk8Vo9PXGFbhs9X50fmKh7Pl4U9Ea6qMSrS96cqTs/Whjxk+LlW/cGyu/9U7Ik3x/9z0xaqd2ucvw1rjeuoX8c+6daWWv1wOdLwhrnSlKiU9O+eU++8opKgqZnhTr0oUk6++Xpgfv9n/K9UfR6rc5+abo6jZgQCJvc1TVvTl0XNCUo9FP6lduztSUzX2e95KuAuO+TRYE3nX7uN0vvuHp95BaWaJ3rNdiTW6THvlymc1+Zob2uyqVij9Wm3XnKyCnUi1NWK90JhNbuzNH2rALd+dHCoDe4JR6v1u7Mkfv95pKQ6oQs502SuxKgQ7M0SVKOU/XgrpTYtCdfb0/7Tc9/u1Jer9XmPeFvJP1B4aNfLgt8PdOzC7VmZ07YFI0//2++jntqik54+gdNW52uz+Zt1i0fzFNekUcfzdkU9Cm/pKBPzEN7pCzbmqVzXpmh4SPnqFOrhkHbtmYVaM3OHP281vcG7t/frdYLk1cHKo6O+edk7XA1f12/K1d3j12oTiMm6I8fzNXu3CJ1GjFBF73+c9D3xUe/btSU5Tt08r+m6i9jFuin1enKyivWtNXp+tz5Xp24ZJt25RRqxba9mlvGNK1xC7bo8a+W6f5PF6vTiAmB6hJ/KLB2Z4525RTqoS98lXbu8E/yBXLPfbNSGTmFWuC8qf547uag0MEdpLweEnLc5lS/TV6+Q5/M3SQpchWDP4T9Ld0XlM7+bbc6PzBRw0fNCfo+f/7blfrjB76Kuee+WamjHvs2aCwfzN7gayTuBEHfLN2uR8YvlbVWnUZM0L8nr9ayrXu1ekfpz0dWfrHyizx6acoajVu4Vaf8e6omLA4PpUKfq6RAr6A568P7e+VHaLq+eU9eIDyOptjVrGXZ1r2atyH8a2yt1Xmv/qy7xy7SzLW7gr7XInE3UfZ4vSp0ApHHvlymUT//rj0xGlq7A+bJy3cE/d6SfMHWiM+XBIVA1lrdMWaBJi3drn98tVyfL9iir0LCSr+pq9P17bLt+t8vG7Urp0jXvfur/jNltf7x1XKd9+oMpWcXBq2mmFtUejsjp1BvTi39nvN/fd6Z8bv+/L/5mrJihx4at1QTl2zXvyev1jszfg/rs+XmrwiVFJhi558aWlDs0dXvlIY6D3y+WOe/9rOuent20Dke/HyJCoq9muYKmsYv3BIxFJ22urQCyN1L6LlvfFWcdzu9v5ZuydKFr/8csedTalJp/PDfGb7xG+ZlVRlTHcve9e3b186dO7fKzwsAAFCVQoMdv7TkhKBPWGPpc1BztW2Sqr+f00MPfrFEx3dpFZiy1LpxSmBlI7fjOrfUL79HfqN7ed+DNNZ5Y3l4uyZ69/p+GvjMD4HtX99xonp2aCrJ98bz0IcmBbb97czDA39oV8ZBLRvoqAOba0KESoZQTdKSoi4N/9ltA3TxGzM18NBWSkxI0LTV6UpJTFCRx6u5D58qr7U65V9TlV2FUykm3TlIN4yaE7GJdL9OLdS7Y3P9sGqn3hh2rM54sXR1rkWPnK5duYU65d++N9pdWjfSD/cO0cx1u3TV278oKcGEfaJ9Rs92+nZZ8BSoaB4eekS5p660bpyqrPwiTfjLIJ0eYSUxSfru7j/o9P9MU2pSQsyKhuEDOmnUzPWSpMQEo94dm4VVFUjSN3cN0iVvzAoKLZ+9uJfu/6z0E/dXrzpaQ3u1V+cHJgYde1DLBtq0O3YYMHPEyZqxZpdSkhJ0cKuG6tSqUaBCKdrPoyTddWq3QAWZ25tXH6Mzj2yv71fs0HfLdgR+dtxG33ScurVtrBvemxNxap2b/3vWr0f7ploeoSLts9tO0MVvhPd7urL/wUFVfpJ0WLvGgYDmhct6a+GmTDVrkBwWTvn9/Zwe+ufXyyNuk6Qv/jRAF74+M+r2aJo1SI451dP/s3xE+6ZhVXgDD22l0Tcdr8178vTMpJW6fmAnrdmRo1d+WBtU3SZJcx8+Va0bp+riN2Yqr8ijLq0bhf0uufr4g9WqUap6dmiqWz6Ypz8c1kYvXNZbfZ8IX0XqrCMP0KSlsXuQvXRFH9350cKI23576mwVebz6eO4mPTJ+WeDxh84+Qhcec2DEa/p98acBOvrgFtqWla8Tnv4h6n5+/Tu31KBDWwf137p1cFddcmzHuKq5Ivn96bNljFGJx6s+/5hc5tSzPw7uov8LqY4MNenOQVqzMydsJT631o1T1Ll1I63anq3nLumtWz+cF3aN/p1b6lfX/8seP6+nHv3S9xof0b6pJt05SB/M3qBjDm6uA5qm6dgIr/WShw6IOdb9ySs/ZWt3nlePnt0s5n5Nm/adZ63tG/p4XOGOMeZMSS9JSpT0X2vtM7H2J9wBAAB1XbHHq/5PTin3KjGR3uTHo2ubRlqXHtzg9IQurYLK4avSub076NQj2urJCSt05pEH6P2Qhqe3DekacXpGqJtO7Bz4hNXt5kGddd8Z3XXmS9MCFQzxGH3TcTH7zdQ17ZulaVtWQdSgLla4Fe185/buEHHltGjWPzNUT3y9POzrcF7vDnr5yqNjhiIHNE3T9pBKiRYNk3XOUR30wewNuuTYjvp0XnzTZfwSE0yVN12N9rPQvGFyWAVTqHtOOyzmFK2q1Ltjswr3p4kk3p/Dbm0b64BmaZoeY6WuU49oF+i3dGjbxlXa90cKfuPu1rFFg6CeYTXllSuP1t1jF2rew6epWcNkDXj6e22thpUByyM50QRVM0VTnv+PPHT2EbpuQCe9Pf03Pf/tKj13yVHKLSwJaogdzZ2ndAvrrxSLP3yvCqG/JxokJ0asECPcKb9o4U6Z07KMMYmSXpN0lqQekq40xvSo+iECAADUnMISrw5t2zhw/8RDW+vMnsF/ZPY9pEXYcc9efFS5r/W3Mw/XdQM6SZKapiVJ8r35+vCm4/SXU7rp1sFdyzzHm1cfG3XbD38drC5tGgXuj//zQL10eR+d3+dA/frQqfrH+Ufqq9tPVIrTufIPh7XR/Wd215R7BgedZ9YDJ+uBs7oH7p/Rs50ePqeHbhtSOr5zjmovSbptyKFKSUpQh2aly643cZ5bNI+e20P9OrWMuv2ta45VUsi6uGf3OkBPXHBk0GPn9+kgyVcRccPAzjGvKfleu+TEyKX/I1zP18/9fLdlFeiApmn68d4hapDsa2B8QNO0wPamacka0LWV7jq1W+Cxpy7sFbjdJDX4NXnywiP14NlH6Is/DYi6BLD7a3DtCYdIkh4+p0fY92OzBslhxzYOud6xnYKPeeScHtqTV6wPZvvCvn9d2ltzHjo1bJxX9DtIJ3RpFXF88QY7j5zTQ22bpMa1rz/Y8X+Prn9mqNY/M1Q/339y2PdEKHewc2yEn1m3M3seoAOapmn0TcdJkm75Q5eI+/mn54W6Ocr+rRtXbEWyi44+UFcff3DEx3958JTA92LrxqkadX3/oH0eOvsIzXrg5MD9Wwd30aQ7B6lLm0Z6Y9gxEa83fEAn/eGwNpr+t5N0eo92khS07+DD2gRu33lKt6BjIwU7knTDwM5q1zT213nSnYN03xmHx9wn1OsRnoP/+/uiYw7Uub07aO1TZ6tZQ9/PwU2DfF+b3h1Lqx66uX7H+53Rs51OPLR10GOX9z1Iic732dBe7cv8PpKk3gc1lyR9/qcBgcf8wc6gbq016vp+Ycc8PPQIrfjHmerr/Fx2aJYW9jMb6smJK3TYw5P0/LerlJhgdFnfg3Ry97Zh+3Vp3UjDjiv9Xnr72r7680mHat7Dp+qf5/fUrw+eokNCpmyGmnjnII295fio28/r3SHi4/88v2fYY6G/J/zBznOXlP4/tFOryE3hUTFlVu4YY06Q9Ji19gzn/gOSZK19OtoxVO4AAID6oMTj1X2fLtYXC7ZozZNnKdl5Y/nC5NV6+fs1euGy3lq0KVPvuapeFj16uno//l3QeVo3TtWunMKgCoJFj5yu7MJiPTVxhZ66sJeaNUjW5j35OqhlQ83bsFsHNGugA5v7ghFrrTo/MFEHNm8QmOIw5ubjdaXTH2HZ42eoUWqSPvp1o0Z8vkS3/KGLNmTk6ttlOzTk8DYadX1/fbtsu/74wTwd3LKhpv3tpKjP2eO1MpISnDcyHq/V1NU71a9TSzVJ871J2pKZr2+WbteNJ/qCk53ZBer/5Pc6vUc7vXrVMVqzM1s9O/jeQG3MyNP0tek6v8+BapyapPkb96hr68b68//ma8baXbr2hEO0c2+hTujaKhBwLdi4R09MWKF5zspYix87XbtzitSptS+gmrdht7q1a6I3flqni44+UN3aNdHmPXlKSUxQSlKCUpMS9dTEFbpuwCE6tG0TfbN0uxZtztT8DXsC090OadVQ71zXT41SE9XeCaCy8orVrGGyNu3O03sz12vmugx9fceJmvVbhp6ZtFJFJV69NuxoHdq2ibZnFegvYxbojlMO1bGHtFDDFN8bsMISj1KTEjXq59/12FfL9fEfT1D/zr7A6p0Zv+uF71Zp8j2D1aF5aeh11kvTtWLbXk25Z3BQoPjezPX6adVOPX3RUfpozkb9uCpdH9zYX03TklVQ7FFiglGiMYGvlV9uYYle+n6Nbh7URW2apGprZr4GOFP3LujTQeMWbtVh7Rrr4JaNdNep3TR2ziYVFHt006Au6tqmkc54cZrWpefqzJ4H6M1rSkPDFyav1qQl23RgiwZ6fdgxSkpI0D0fL9TXi7fpo1uO10EtGyrBSCc8/YP6d2qpN64+Rsc+MUUNUxL11R0n6sq3Zuu2IV11eb+DNHNthk7t0U7FHq9uGDVHV/U/WGf1aq8V2/YqJSlBv6XnKq+oJGgqzcEtG+q7u/+gEq8NesObW1iino9+K0n69aFTlJlXrPbN0vTz2ozAVJFHz+2hlo1SdMoR7QLHzv4tQ1e8NVv/d82xOrl7WxlJSRGW5vlm6XYd1bGZfkvP1efzN+vfl/WWMcbX42Xmei165HTlF3t8TWtbN9LizZk671VfU9mxtxyvy9+arZHD++mErq3U/e/fKMGULuf9+rBjlF/k0aBurfXerPV67cd1eumKPsrIKdINJ5YGk/7qq09uPUHLt+7Vxcd2VOPUJBWVePXilNW6tO9B6ty6kZ6etEJb9uTr+oGddfRBzZWQYALfX/P/flpYE+6lW7LUtkmqduUUafLyHbppUGc1cl6fPblF+mD2Bt1+0qFatnWvfs/I1Xm9O6jvE5M1oGvroKqw24Z01eLNmYG+TR2apanYa5WeXaj/3XScBjhhycrte3Xmi76+XgO6tgo01F7/zFAVe7z6ceVOndajnT6cvUEdWzbU9SPnaMo9gwNTlr68faC+WrRVn8/fopkPnKxV27M14rMlev7So7Q9q0CnHNFOv/yWocMPaKLmDYOfq8drNXn5Dp3eo5281ioxwcgYo9s+nKdJS7fr1wdPUfOGKUpx+r7c9N4cTVmxU8v/cYYapiSp7xOTtSunSK8PO0Zn92of+L7r1raxBh/WRmnJifpk3ib93zV91bqx7zyrt+foxG6tZa3V418tD0x9XPvkWYHvtRKPNzB91v//mYJijzZk5OnwA5pIkqatTte/J6/Wok2Z6tG+qcbcfLz2FhRr0HM/Bj3HZy7qpSv6+wKcrLxipSYnKC05UdkFxWqSlixrraat2aUTurQKPE83a62Wbtmrmet2aVdOoU7u3k5tmqQG/V6SfL+z9uYXa0tmvo7v0lKzf/P9Xv3tqbM1bU26Hhm/TJ/dNkD/mbJa//tlo0YO76frncbfD5zVXSlJCXr8q+Xq36ml7jvzcF36pm8K40tX9NG5R3XQW9N/8wVRxYuF8qvwtCxjzCWSzrTW3uTcv0bScdba20P2u0XSLZJ08MEHH7thw4awcwEAANQ1RSVe5RaWBK025fVazVm/W307tZSRVOTxavZvGeraprEOatlQe3KLtD4jV7tzi7Qtq0Dn9+mggmJv4I32uvQcDerWJvpFI1i9I1utG/s+/bbWqlXjVK3anq2ubRpFfEMq+d70JjuBR4nHqzenrtOw4w4pc+Wsipi7frd6dGgaCDnKkltYorkb9kR9kyH5VnPJyCnU6T2rrix/yeYsdWvXWGnJtfOJcEGxJ+zaBcUezVm/u9zfE+WxK6dQO/cW6vADmug/k1fryuMODoSHobxeK2OqppHpr7/vVpc2jQLfu+U1a12G8opKlJFbpHOP6qAGKZG/bl8v3qrUpESd5lSb+GXlFWtrVr66H9Ak4vPxv+mtSkUlXt3+v/nq37lloFrEz98A18gX8Li/971eq8ISb8TnmF/k0U+rduqsXu3LPZ6dewvksTYQYlaldek5yikoCVSpTFm+Q4cf0EQHtWyorPxiLduapeM7twoLIP2KPV7lF3vUtIyvwabdecotKlH3A5pW9VOIqsTjVWZ+ceB798eVOzVj7S6NOKt7IOjPLSxRYoKJ6/fJgo179MLk1brntMN09MHBlT8ZOYXKL/aoY4volTOFJR79uDJdx3dpGQiu0rMLNWrm77ptyKFKinMcVcHrtbJSoJppzY5sNUpNCgqt/fvNWLtLg7q11rasAiUlGLV1KhvX7sxW1zaNZYzRpt15YdWykpSdPU8ov2oPd9yo3AEAAAAAANEQ7lRMhXvuSNoi6SDX/Y7OYwAAAAAAAKhl8YQ7cyR1M8Z0NsakSLpC0pfVOywAAAAAAADEo8xJ09baEmPM7ZK+lW8p9HettZFbpQMAAAAAAKBGxdURz1o7UdLEah4LAAAAAAAAyimeaVkAAAAAAACoowh3AAAAAAAA6jHCHQAAAAAAgHqMcAcAAAAAAKAeM9baqj+pMdmSVlX5iYHq0VrSrtoeBIB9TjNJWbU9CAD7HP5uAVAd+Lul/jjcWtsk9MG4VsuqgFXW2r7VdG6gShlj5vL9CqCqGWPestbeUtvjALBv4e8WANWBv1vqD2PM3EiPMy0LAIDq8VVtDwAAACBO/N1SzxHuAABQDay1/JEEAADqBf5uqf+qK9x5q5rOC1QHvl8BAEB9wd8tALB/i/j/gWppqAwAAAAAAICawbQsAADKYIw5yBjzozFmuTFmmTHmTufxlsaYycaYNc6/LSIce4gxZr4xZqFz7K2ubccaY5YYY9YaY142xpiafF4AAGDfE+Pvlkud+15jTMTG7MaYNGPMr8aYRc6+j7u2dTbG/OL83TLWGJNSU88JZSPcAQCgbCWS/mqt7SHpeEl/Nsb0kDRC0vfW2m6Svnfuh9om6QRrbR9Jx0kaYYzp4Gx7Q9LNkro5/51Zrc8CAADsD6L93bJU0kWSpsU4tlDSydba3pL6SDrTGHO8s+1ZSf+x1h4qaY+kG6tp/KgAwh3sUyrz6bqz33XOPmuMMde5HufTdWA/Zq3dZq2d79zOlrRC0oGSzpf0nrPbe5IuiHBskbW20LmbKuf/vcaY9pKaWmtnW98c6fcjHQ9g31WZT9ed/c40xqxy/j4Z4XqcT9eB/Vi0v1ustSustavKONZaa3Ocu8nOf9Z5/3OypE+dbRH/7kHtIdzBvqbCn64bY1pKelS+T9b7S3rUFQLx6ToASZIxppOkoyX9IqmdtXabs2m7pHbOPn2NMf91HXOQMWaxpE2SnrXWbpUvHNrsOvVm5zEA+48Kf7pujEmU9JqksyT1kHSlc6zEp+sAHCF/t0Tbp4MxZqLrfqIxZqGknZImW2t/kdRKUqa1tsTZjb9b6hjCHexTKvPpuqQz5Pvltdtau0fSZPnKEPl0HYAkyRjTWNJnku6y1u51b3N+P1jn9lxr7U2ubZustUdJOlTSdcaYdjU4bAB1VGU+XZfvg6i11trfrLVFkj6SdD6frgPwi/V3i5u1dqu19mzXfY8znbyjpP7GmCOrfbCoNMId7LMq8On6gfJ9qu7nT6P5dB2AjDHJ8v2BNNpa+7nz8A4nAPZPs9oZ6xxOxc5SSYMkbZHvjya/js5jAPZDFfh0PdrfLXy6DiDa3y3lYq3NlPSjfLMWMiQ1N8YkOZv5u6WOIdzBPqmin64DQCTOJ+HvSFphrX3BtelLSf7+XNdJGh/h2I7GmAbO7RaSTpS0ygmc9xpjjnfOf22k4wHs+yr66ToARBLj75Z4jm1jjGnu3G4g6TRJK533UD9KusTZNeLfPag9hDvY51Ti0/Utkg5y3fen0Xy6DmCgpGsknewsab7QGHO2pGcknWaMWSPpVOd+aFXgEZJ+McYskjRV0r+stUucbX+S9F9JayWtkzSpxp4RgDqhEp+uR/u7hU/XAUT8u8UYc6ExZrOkEyRNMMZ8K4VVBbaX9KPTK3COfG0rvna23S/pHmPMWvmqBN+pySeF2IwvgAP2DU5K/Z6k3dbau1yPPy8pw1r7jLOaREtr7d9Cjm0paZ6kY5yH5ks61lq72xjzq6S/yFcqPVHSK9baiQIAAKigaH+3uLb/JOlea+3cCNuSJK2WdIp84c0cSVdZa5cZYz6R9Jm19iNjzJuSFltrX6++ZwIAqG2EO9inGGNOlDRd0hJJXufhB+ULZT6WdLCkDZIuc0KbvpJu9U/NMsbc4OwvSU9aa0c6j/eVNEpSA/k+Wb/D8sMDAAAqIcbfLamSXpHURlKmpIXW2jOMMR0k/dc/NcupIHxRUqKkd621TzqPd5GvwXJLSQskXW2tLayhpwUAqAWEOwAAAAAAAPUYPXcAAAAAAADqMcIdAAAAAACAeoxwBwAAAAAAoB4j3AEAAAAAAKjHCHcAAAAAAADqMcIdAAAAAACAeoxwBwAA1AvGmObGmD85tzsYYz6txmvdaoy5NsLjnYwxS6vrugAAABVhrLW1PQYAAIAyGWM6SfraWnvk/jwGAACAUFTuAACA+uIZSV2NMQuNMZ/4K2iMMcONMeOMMZONMeuNMbcbY+4xxiwwxsw2xrR09utqjPnGGDPPGDPdGNM92oWMMY8ZY+51bh9rjFlkjFkk6c+ufe42xrzr3O5ljFlqjGlYnS8AAABAJIQ7AACgvhghaZ21to+k+0K2HSnpIkn9JD0pKc9ae7SkWZL806veknSHtfZYSfdKej3O6450jusd8vhLkg41xlzo7PNHa21e+Z4SAABA5SXV9gAAAACqwI/W2mxJ2caYLElfOY8vkXSUMaaxpAGSPjHG+I9JLeukxpjmkppba6c5D30g6SxJstZ6jTHDJS2W9H/W2p+r6LkAAACUC+EOAADYFxS6bntd973y/b2TICnTqfqpSt0k5UjqUMXnBQAAiBvTsgAAQH2RLalJRQ601u6V9Lsx5lJJMj6h06wiHZcpKdMYc6Lz0DD/NmNMM0kvS/qDpFbGmEsqMjYAAIDKItwBAAD1grU2Q9LPTiPl5ytwimGSbnQaIy+TdH6cx10v6TVjzEJJxvX4fyS9Zq1dLelGSc8YY9pWYFwAAACVwlLoAAAAAAAA9RiVOwAAAAAAAPUYDZUBAMB+yxjzkKRLQx7+xFr7ZG2MBwAAoCKYlgUAAAAAAFCPMS0LAAAAAACgHiPcAQAAAAAAqMcIdwAAAAAAAOoxwh0AAAAAAIB67P8BWCNWlbXiM88AAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 1440x288 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAABIQAAAEXCAYAAADcGJ98AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAywElEQVR4nO3debxVZd3//9eHGQREkQhEA80JRUCPaA6JGWZo4hAOOYCS3t45dFeOZdmgTXabemv5tVS0vAnFBO+y+hFqao6MoqChhjGpiIGAogzX74+9OB4O58DhnL3Ze5/9ej4e58Fea13rWtfanGzz3tf1WZFSQpIkSZIkSZWjRbEHIEmSJEmSpK3LQEiSJEmSJKnCGAhJkiRJkiRVGAMhSZIkSZKkCmMgJEmSJEmSVGEMhCRJkiRJkiqMgZAkSdpqIuK7EfHbAvX9YkQMLkTf+khEpGKPQZIkNZ2BkCRJzUhEPBoR/46ItsUeSz5FRO+ISBGxIvt5MyJ+ERGt17dJKe2dUno0a1+w4Kmxsr+bLxd7HJIkSWAgJElSsxERvYHDgAQcV9zRFEyXlFJHoB/wKeCCIo9HBRYRrYo9BkmSmiMDIUmSmo+zgKeB0cCImgciYnRE3BIRf4yI5RHxTETsWuP4wRHxXEQsy/48uMaxRyPimoh4Mpud838R0TUi7omId7P2vWu0vzEi5mXHpkTEYXUNNhvLRbX2PR8RJ2zuRlNKbwETgb41zp0bEZ+NiKOBbwKnZOOdsbn+6hnf0IiYlb1fCyLikmz/CxHxhRrtWkfE2xExMCLaRcRvI2JJRCzN3pvuEXEtubDu5mxMN2fn7hkREyPinYh4OSJOrtHv6GwW1J+yc/4eER+PiBuyWWAvRcTATYz/0OzvbGn29zGyRr+3ZtddHhF/i4hPZMfWz8RqVaOfemc21Z6JVfv8iBgZEa9l1/lnRJxeo+05ETE7u5e/rB9DdixFxAURMQeY09C/M0mS1HAGQpIkNR9nAfdkP5+LiO61jp8KfA/YDngFuBYgIrYH/gjcBHQFrgf+GBFda517JrAjsCvwFHAnsD0wG7i6RtvngAHZsf8F7ouIdnWM9y7gjPUbEdE/6/+Pm7vRiOgJfI5cALaBlNKfgR8CY1NKHVNK/TfXXz1uB/4jpdQJ2Ad4ONt/d81xA0OBRSmlaeSCuG2Bnci9l+cD76eUvgU8DlyYjenCiNiGXKj1v8DHyL3Hv4iIvjX6Phm4CtgB+IDc+z412x5H7u9qI1m48ifgf4Bu5P4+ptdocjrwg6yf6eR+Z/Iqu7+bgM9n7+HB68cQEcPIhXYnZuN7HBhTq4vjgQOpEfpJkqT8MRCSJKkZiIhDgU8A96aUpgCvAl+q1eyBlNKzKaU15AKAAdn+Y4A5KaXfpJTWpJTGAC8BX6hx7p0ppVdTSsvIBQ2vppT+mvV1H1A9UyWl9NuU0pKsr/8G2gJ71DHsB4HdI2K3bPtMciHOh5u41bcjYimwAFhJLhQplNVA34jonFL6d0pparb/t8DQiOicbZ8J/KbGOV2BT6aU1qaUpqSU3q2n/2OBuSmlO7P3ahpwPzC8RpsHsj5WAQ8Aq1JKd6eU1gJjqfG+1/Il4K8ppTEppdXZ38f0Gsf/mFJ6LKX0AfAt4FMRsVMD35ctsQ7YJyLap5QWpZRezPafD/wopTQ7+x36ITCg5iyh7Pg7KaX3CzAuSZIqnoGQJEnNwwjg/0spvZ1t/y+1lo0Bb9R4/R7QMXvdE3i9VtvXyc3WWe/NGq/fr2N7fV9ExCXZUqBlWXizLbmZKBvIQo6xwBkR0QI4jY+ClfrskFLqAnQA/g78ZTPt6xQRp8dHBar/VE+zk8jN/nk9W1b1qWzcC7NrnxQRXYDP89EMm99kY/pdRCyMiJ9GjcLXtXwCODBb0rU0e69OBz5eo02D3/dadiIXCtZn3voXKaUVwDvkfg/yJqW0EjiFXPizKFsiuGd2+BPAjTXu+x0g2PB3bh6SJKlgDIQkSSpzEdGe3NKiwyPijYh4A/ga0D9bhrU5C8n9A72mncnNwtnSsRwGXJaNZ7ssvFlG7h/7dbmLXAhyJPBeSumphlwnmzUyGjgoIjYKm8gV1t7U+fdkS7c6ppQ+X0+b51JKw8gt5xoP3Ftr3GeQm83zVEppQXbO6pTS91JKfcktkTqW3FK+usY0D/hbSqlLjZ+OKaX/3NTYG2geuaV99ameDRQRHckt71tIbtYV5AK39WoGVLWt3FTblNJfUkpDgB7kZp39qsb4/qPWvbdPKT1Z8/RNXFeSJDWRgZAkSeXveGAtuVorA7KfvcjVZTmrvpNqeIjc0q0vRUSriDgl6+sPjRhLJ2ANsBhoFRHfATrX1zgLgNYB/83mZwdVi4i25JZqvQEsqaPJm0DvbObRFouINtksom1TSquBd7Nxrjce2A/4KrmaQuvPOyIi+kVEy+yc1TXOexPYpUYffyD3vp8ZucLUrSPigIjYqzFjruUe4LMRcXL2d9o1IgbUOD40KzrdhlwtoadTSvNSSovJBYFnRETLiDiHTQdL04FPR8TOEbEtcOX6A5Erpj0sqyX0AbCCj96LW4ErI2LvrO22ETEcSZK01RgISZJU/kaQq/Hzr5TSG+t/gJuB02Mzj+1OKS0hN5PlG+TClcuAY2ssP9sSfwH+DPyD3LKzVWx+6c/d5B4j/9vNtANYGhEryIUrnwKOSynVNZPkvuzPJRExtY7jDXEmMDci3iW37Kn6CVnZDKX7gT7A72uc83FydY3eJVds+298FHTdCHwxe6rWTSml5cBR5IpJLyQXbv2EXM2lLRa5p5F9Mxvfv8gtd/sGueVY04Gas8X+l1wh8HeA/dmwSPa5wKXkfhf2BmrO2tlASmkiuWV/zwNT2DBEbAF8Pbu3d4DDgf/Mznsgu9ffZe/vC+SW3kmSpK0k6v4MJUmStHVExFnAeSmlQ4s9li2RzX7aPaV0xmYbl5CIGA3MTyld1cjzU0qpviWAkiSpTGzyG0NJkqRCiogOwFeAXxR7LFsiIrYHRpGbRSRJklR2XDImSZKKIiI+R67W0JvkljCVhYg4l9wyuD+llB4r9niK4HvFHoAkSWo6l4xJkiRJkiRVGGcISZIkSZIkVZiSqCG0ww47pN69exd7GJIkSZIkqUStW/desYdQdqZNm/12SqlbXcdKIhDq3bs3kydPLvYwJEmSJElSiVq+fEqxh1B2Oneuer2+Yy4ZkyRJkiRJqjAGQpIkSZIkSRXGQEiSJEmSJKnClEQNobqsXr2a+fPns2rVqmIPRdoq2rVrR69evWjdunWxhyJJkiRJauZKNhCaP38+nTp1onfv3kREsYcjFVRKiSVLljB//nz69OlT7OFIkiRJkpq5zS4Zi4g7IuKtiHihxr7tI2JiRMzJ/twu2x8RcVNEvBIRz0fEfo0d2KpVq+jatathkCpCRNC1a1dnxEmSJEmStoqG1BAaDRxda98VwKSU0m7ApGwb4PPAbtnPecAvmzI4wyBVEn/fJUmSJElby2aXjKWUHouI3rV2DwMGZ6/vAh4FLs/2351SSsDTEdElInqklBblbcSSJEmSJKmiLF+1mvunvcd7qxMvLlrNgB3bFPR6C5etpV1r2L5Dyw32v7F8LS0CPtaxZT1nbuz1f6/hE9vVHb8sW7WOjm2Dlg2YIPDPJWvo1rEFHdvm5vbMXPQh+/RoTdC4yQWNrSHUvUbI8wbQPXu9IzCvRrv52b6NAqGIOI/cLCJ23nnnRg5DkiRJkiQ1d398fhHffejdj7ZfsNwGwIPPN/59aHJR6ZRSiojUiPNuA24DqKqq2uLzy8Ho0aM56qij6NmzZ7GHUq/Ro0czd+5cvvvd7xZ7KCVj7ty5HHvssbzwwgubb1zDd7/7XTp27Mgll1yywf6FCxdy8cUXM27cOKZPn87ChQsZOnRoPocsSZIkSc3a6rXrNtgesmdbvnV054Jdb/ANiwF49L+6NWh/fa6ftJwHZ67igk93ZPh+7Tc49vyC1Vx839IG9bfs/cSw//d2ddvxM97nhkdWMHTvdlw2pFO95/X5Sf19NjYQenP9UrCI6AG8le1fAOxUo12vbF9FGj16NPvss09JB0KFtmbNGlq1KtmH2W0VPXv2ZNy4cQBMnz6dyZMnGwhJkiRJUhNs06YFXbdp+LKtxqrvGg29dvvWueVc27SNjc7p3G5tg/trGR8FYl23aUmnbNnYNm027rehGvsv9QeBEcCPsz8n1Nh/YUT8DjgQWJaP+kHf+78XmbXw3c033AJ9e3bm6i/svck2K1eu5OSTT2b+/PmsXbuWb3/724wZM4bx48cDMHHiRH7xi18wbtw4Ro0axeTJk4kIzjnnHHbaaScmT57M6aefTvv27XnqqaeYNWsWX//611mxYgU77LADo0ePpkePHgwePJiBAwfy+OOPs3LlSu6++25+9KMfMXPmTE455RSuueaajcb23HPP8dWvfpWVK1fStm1bJk2axP33388DDzzAsmXLWLBgAWeccQZXX331RjNefvazn7FixYqNZgWNHj2ayZMnc/PNNwNw7LHHcskll3DYYYdtdH9f+9rXePXVV7ngggtYvHgxHTp04Fe/+hV77rknI0eOpF27dkybNo1DDjmE66+/vkF/J88++yxf/epXWbVqFe3bt+fOO+9kjz32YPTo0Tz44IO89957vPrqq5xwwgn89Kc/BWDMmDH88Ic/JKXEMcccw09+kos/O3bsyH/+53/y0EMP0aNHD374wx9y2WWX8a9//YsbbriB4447jrlz53LmmWeycuVKAG6++WYOPvjgDcb06U9/mptuuokBAwYAcOihh3LLLbfQv3//Ou9hxowZfOpTn+Ltt9/msssu49xzz61+/6dOncp3vvMd3n//fZ544gmuvPJKTjnllAa9N5IkSZIk5dNmA6GIGEOugPQOETEfuJpcEHRvRIwCXgdOzpo/BAwFXgHeA84uwJi3mj//+c/07NmTP/7xjwAsW7aMq6++msWLF9OtWzfuvPNOzjnnHKZPn86CBQuqA5elS5fSpUsXbr75Zn72s59RVVXF6tWrueiii5gwYQLdunVj7NixfOtb3+KOO+4AoE2bNkyePJkbb7yRYcOGMWXKFLbffnt23XVXvva1r9G1a9fqcX344YeccsopjB07lgMOOIB3332X9u1zU8+effZZXnjhBTp06MABBxzAMcccww477NCk96Gu+wM477zzuPXWW9ltt9145pln+MpXvsLDDz8MwPz583nyySdp2bLhSeWee+7J448/TqtWrfjrX//KN7/5Te6///7qMUybNo22bduyxx57cNFFF9GyZUsuv/xypkyZwnbbbcdRRx3F+PHjOf7441m5ciWf+cxnuO666zjhhBO46qqrmDhxIrNmzWLEiBEcd9xxfOxjH2PixIm0a9eOOXPmcNpppzF58uQNxjRq1ChGjx7NDTfcwD/+8Q9WrVpVbxgE8Pzzz/P000+zcuVKBg4cyDHHHFN9rE2bNnz/+9/fIHSTJEmSJKkYGvKUsdPqOXRkHW0TcEFTB1Xb5mbyFEq/fv34xje+weWXX86xxx7LYYcdxplnnslvf/tbzj77bJ566inuvvtuli9fzmuvvcZFF13EMcccw1FHHbVRXy+//DIvvPACQ4YMAWDt2rX06NGj+vhxxx1Xfc299967+tguu+zCvHnzNgiEXn75ZXr06MEBBxwAQOfOH62bHDJkSHXbE088kSeeeILjjz++Se/DLrvsstH9rVixgieffJLhw4dXt/vggw+qXw8fPnyLwiDIBW4jRoxgzpw5RASrV6+uPnbkkUey7bbbAtC3b19ef/11lixZwuDBg+nWLbfW8vTTT+exxx7j+OOPp02bNhx99NFA7j1t27YtrVu3pl+/fsydOxeA1atXc+GFFzJ9+nRatmzJP/7xj43GNHz4cH7wgx9w3XXXcccddzBy5MhN3sOwYcNo37497du354gjjuDZZ5+tnl0kSZIkSWqcci08XKhxp1p/NkZlF3fZjN13352pU6fy0EMPcdVVV3HkkUfy5S9/mS984Qu0a9eO4cOH06pVK7bbbjtmzJjBX/7yF2699Vbuvffe6pk/66WU2HvvvXnqqafqvFbbtm0BaNGiRfXr9dtr1qxp8Jij1qPqIoJWrVqxbt1H6w1Xraq7Cnl97eq6vxtuuIEuXbowffr0OvvaZpttGjzm9b797W9zxBFH8MADDzB37lwGDx5cfazme9KyZcvNvietW7eufi9qvqc138+f//zndO/enRkzZrBu3TratWu3UT8dOnRgyJAhTJgwgXvvvZcpU6Zs8rp1vf+SJEmSJJWaFsUeQClbuHAhHTp04IwzzuDSSy9l6tSp9OzZk549e3LNNddw9tm5FXFvv/0269at46STTuKaa65h6tSpAHTq1Inly5cDsMcee7B48eLqQGj16tW8+OKLjRrXHnvswaJFi3juuecAWL58eXXIMXHiRN555x3ef/99xo8fzyGHHEL37t156623WLJkCR988AF/+MMf6uy3d+/eTJ8+nXXr1jFv3jyeffbZeu+vc+fO9OnTh/vuuw/IBV4zZsxo1P2st2zZMnbccUcgV89ocwYNGsTf/vY33n77bdauXcuYMWM4/PDDt+h6PXr0oEWLFvzmN79h7dq1dbb78pe/zMUXX8wBBxzAdtttt8k+J0yYwKpVq1iyZAmPPvpo9Syu9Wr+TkiSJEmSGqdcvnuPWn9ucGwL7qF2203121AGQpswc+ZMBg0axIABA/je977HVVddBeSWJu20007stddeACxYsIDBgwczYMAAzjjjDH70ox8BMHLkSM4//3wGDBjA2rVrGTduHJdffjn9+/dnwIABPPnkk1s0nqFDh7Jw4ULatGnD2LFjueiii+jfvz9Dhgypns0zaNAgTjrpJPbdd19OOukkqqqqaN26Nd/5zncYNGgQQ4YMYc8996yz/0MOOYQ+ffrQt29fLr74Yvbbb79N3t8999zD7bffTv/+/dl7772ZMGFCnf021GWXXcaVV17JwIEDGzQrqkePHvz4xz/miCOOoH///uy///4MGzaswdf7yle+wl133UX//v156aWX6p3VtP/++9O5c+fqAHBT9t13X4444ggOOuggvv3tb2/0hLkjjjiCWbNmMWDAAMaOHdvgsUqSJEmSlE+RK/tTXFVVVal2Md/Zs2dXBy6l5sILL2TgwIGMGjWq2EPZQO2nhDX0nLlz5270xDF9ZOHChQwePJiXXnqJFi0Km6GW8u+9JEmSJBXL3U/N5TsTPlplc0L/9nz/2G0Ldr1+174BwMxvfbxB++tzzZ+WMXbq+1w+pBNnDNpwEsLUeR8y4u53GtTfsvfXcej1b1W3vXfKe/zgz+8yfGB7vjO0/vehc+eqKSmlqrqOOUNoC+2///48//zznHHGGcUeiraCu+++mwMPPJBrr7224GGQJEmSJKluJTCXpVEKXVS6KSwqvYU2V1S4mEaOHLnZp2DVNmDAAHr37l2Q8QDceeed3HjjjRvsmzNnDrvtttsG+w455BBuueWWgo2jsc466yzOOuusDfbVdU+lOn5JkiRJao7KpIRQtbrqBRX7HgyEKlyhH4l+9tlnN6j2TjlpjvckSZIkScq/QoU++ejXNTCSJEmSJEkVxkBIkiRJkiSpwhgISZIkSZKkklYKT0hvDItK58GyZU+zZs3SvPXXqlUXtt32oM22Gz9+PCeccAKzZ89mzz33zNv1t1THjh1ZsWJFQfoePXo0l156Kb169WLFihXssssuXH311Rx88MGbPG/8+PHsvvvu9O3btyDjkiRJkiSpLnUVaS43xb6HspkhtGbNUtq06Za3n4aGS2PGjOHQQw9lzJgxhb3BIjvllFOYNm0ac+bM4YorruDEE09k9uzZmzxn/PjxzJo1ayuNUJIkSZKk8pKvzKd2eGRR6QJbsWIFTzzxBLfffju/+93vqvc/+uijDB48mC9+8YvsueeenH766dXT1yZNmsTAgQPp168f55xzDh988AEAvXv35sorr2TAgAFUVVUxdepUPve5z7Hrrrty6623Vl/vyCOPZL/99qNfv35MmDBhozGllLj00kvZZ5996NevH2PHjq0e07HHHlvd7sILL2T06NEAXHHFFfTt25d9992XSy65ZLP3fcQRR3Deeedx2223AfCrX/2KAw44gP79+3PSSSfx3nvv8eSTT/Lggw9y6aWXMmDAAF599dU620mSJEmSpNJjILQJEyZM4Oijj2b33Xena9euTJkypfrYtGnTuOGGG5g1axavvfYaf//731m1ahUjR45k7NixzJw5kzVr1vDLX/6y+pydd96Z6dOnc9hhhzFy5EjGjRvH008/zdVXXw1Au3bteOCBB5g6dSqPPPII3/jGNzZaJ/n73/+e6dOnM2PGDP76179y6aWXsmjRonrvYcmSJTzwwAO8+OKLPP/881x11VUNuvf99tuPl156CYATTzyR5557jhkzZrDXXntx++23c/DBB3Pcccdx3XXXMX36dHbdddc620mSJEmSpNJjILQJY8aM4dRTTwXg1FNP3WDZ2KBBg+jVqxctWrRgwIABzJ07l5dffpk+ffqw++67AzBixAgee+yx6nOOO+44APr168eBBx5Ip06d6NatG23btmXp0qWklPjmN7/Jvvvuy2c/+1kWLFjAm2++ucGYnnjiCU477TRatmxJ9+7dOfzww3nuuefqvYdtt92Wdu3aMWrUKH7/+9/ToUOHBt17zSDqhRde4LDDDqNfv37cc889vPjii3We09B2kiRJkiRtifIsKW1R6bL0zjvv8PDDDzNz5kwigrVr1xIRXHfddQC0bdu2um3Lli1Zs2bNZvtcf06LFi02OL9FixasWbOGe+65h8WLFzNlyhRat25N7969WbVqVYPG26pVK9atW1e9vf68Vq1a8eyzzzJp0iTGjRvHzTffzMMPP7zZ/qZNm8Zee+0FwMiRIxk/fjz9+/dn9OjRPProo3We09B2kiRJkiRVklKsge0MoXqMGzeOM888k9dff525c+cyb948+vTpw+OPP17vOXvssQdz587llVdeAeA3v/kNhx9+eIOvuWzZMj72sY/RunVrHnnkEV5//fWN2hx22GGMHTuWtWvXsnjxYh577DEGDRrEJz7xCWbNmsUHH3zA0qVLmTRpEpCrS7Rs2TKGDh3Kz3/+c2bMmLHZcfztb3/jtttu49xzzwVg+fLl9OjRg9WrV3PPPfdUt+vUqRPLly+v3q6vnSRJkiRJlShvRaUL0G/ZzBBq1aoLH364OK/9bcqYMWO4/PLLN9h30kknMWbMGE455ZQ6z2nXrh133nknw4cPZ82aNRxwwAGcf/75DR7T6aefzhe+8AX69etHVVVVnY+5P+GEE3jqqafo378/EcFPf/pTPv7xjwNw8skns88++9CnTx8GDhwI5EKaYcOGsWrVKlJKXH/99XVee+zYsTzxxBO899579OnTh/vvv796htAPfvADDjzwQLp168aBBx5YHQKdeuqpnHvuudx0002MGzeu3naSJEmSJKm0RO2ixcVQVVWVJk+evMG+2bNnVwcSUqXw916SJEmSNnbHE//k+3+YVb190oD2fPeYbQt2vX7XvgHAzG99vEH763PNn5Yxdur7XHlUJ750wDYbHJs+/0POvOudBvW3fNU6Dv7vt6rb3jvlPX7w53cZPrA93xla//vQuXPVlJRSVV3HXDImSZIkSZJUAKVcVNpASJIkSZIklZUoxSrNm1DXeIt9DyUdCJXCcjZpa/H3XZIkSZKal7wVla7VUT76LdlAqF27dixZssR/JKsipJRYsmQJ7dq1K/ZQJEmSJEkVoGSfMtarVy/mz5/P4sX5e7KYVMratWtHr169ij0MSZIkSSo55TpVpJRrCJVsINS6dWv69OlT7GFIkiRJkqQSU2YlhEpSyS4ZkyRJkiRJag6ijgir2KGWgZAkSZIkSVIB5K2odAH6NRCSJEmSJEmqMAZCkiRJkiSppJXrE8hLuai0gZAkSZIkSSorUewCPM2AgZAkSZIkSdJWVuxMq0mBUER8LSJejIgXImJMRLSLiD4R8UxEvBIRYyOiTb4GK0mSJEmSVC7yVlS6VkdFLSodETsCFwNVKaV9gJbAqcBPgJ+nlD4J/BsYlYdxSpIkSZIkKU+aumSsFdA+IloBHYBFwGeAcdnxu4Djm3gNSZIkSZKkstMsi0qnlBYAPwP+RS4IWgZMAZamlNZkzeYDO9Z1fkScFxGTI2Ly4sWLGzsMSZIkSZJUYYpdf6c5aMqSse2AYUAfoCewDXB0Q89PKd2WUqpKKVV169atscOQJEmSJEkqO1HkR6U1ZcnYZ4F/ppQWp5RWA78HDgG6ZEvIAHoBC5o4RkmSJEmSpLJTqMinqEWlyS0VOygiOkQu1joSmAU8AnwxazMCmNC0IUqSJEmSJCmfmlJD6BlyxaOnAjOzvm4DLge+HhGvAF2B2/MwTkmSJEmSVKFSoaozF1gpF5VutfkmmxhASlcDV9fa/RowqCn9SpIkSZIk1avI9Xeag6Y+dl6SJEmSJElbqNiRloGQJEmSJElSAeQr9Kn9RLJiF5WWJEmSJElSGTIQkiRJkiRJJS0VrDxzYZVyUWkDIUmSJEmSVFaKXX+nOTAQkiRJkiRJ2tqKnGoZCEmSJEmSJBVA3opKF6BfAyFJkiRJkqQKYyAkSZIkSZJKWirPmtIWlZYkSZIkScqXsKp0kxkISZIkSZIkbWXFzrQMhCRJkiRJkgogb0Wla3VkUWlJkiRJkiRtMQMhSZIkSZJU0sq0prRFpSVJkiRJkvKl2PV3mgMDIUmSJEmSpK2s2E9KMxCSJEmSJEkqgLwVlS5AvwZCkiRJkiRJFcZASJIkSZIklbRUplWlLSotSZIkSZKUJ8Wuv9McGAhJkiRJkiRtZcXOtAyEJEmSJEmSCiBvRaVrdWRRaUmSJEmSJG0xAyFJkiRJklTSUsHKMxeWRaUlSZIkSZLypNj1d5oDAyFJkiRJkqStrNhPSjMQkiRJkiRJKoBCZT4WlZYkSZIkSdIWMxCSJEmSJEklLdWuolwmRYQsKi1JkiRJkpQnZZIHVStUvaCm9NukQCgiukTEuIh4KSJmR8SnImL7iJgYEXOyP7dryjUkSZIkSZJqKreH0G80w6kE+m3qDKEbgT+nlPYE+gOzgSuASSml3YBJ2bYkSZIkSVJFydfEoNozgYpaVDoitgU+DdwOkFL6MKW0FBgG3JU1uws4vmlDlCRJkiRJUj41ZYZQH2AxcGdETIuIX0fENkD3lNKirM0bQPe6To6I8yJickRMXrx4cROGIUmSJEmSKkm51BBqrkWlWwH7Ab9MKQ0EVlJreVhKKVHPOFNKt6WUqlJKVd26dWvCMCRJkiRJUiUpVJHmQqlrvPm4h2IVlZ4PzE8pPZNtjyMXEL0ZET1yA4sewFtNuIYkSZIkSdIGClWkuVCaVVHplNIbwLyI2CPbdSQwC3gQGJHtGwFMaPzwJEmSJEmSylPeikoXoN9WTTz/IuCeiGgDvAacTS5kujciRgGvAyc38RqSJEmSJEnKoyYFQiml6UBVHYeObEq/kiRJkiRJ66Vaa6PKpYZQcy0qLUmSJEmStNWVSR5Urc6i0gXqt6EMhCRJkiRJUlkps5rSzauotCRJkiRJkuqXt6LStTrKR78GQpIkSZIkqaSV22Pmy4GBkCRJkiRJKivlUkPIotKSJEmSJEl5Ui5PGVuvzqLSebgHi0pLkiRJkqSKUW5LyCwqLUmSJEmSVCHyVlS6AP0aCEmSJEmSpJJWZhOCyoKBkCRJkiRJKivlUkPIotKSJEmSJEl5EmXznLGcOotK5+EeLCotSZIkSZIqRiqzRWQWlZYkSZIkSVLRGQhJkiRJkqSSVm6PmV8vb08Zq7U2zKeMSZIkSZKkilMuNYQsKi1JkiRJkpQv5ZEHVauzqHQe7sGi0pIkSZIkqXKU2RIyi0pLkiRJkiSp6AyEJEmSJElSSSu3x8yvV6iVbRaVliRJkiRJladMaghZVFqSJEmSJClPyiQPqpaPAtL57tdASJIkSZIklZVyW0BmUWlJkiRJkiQVnYGQJEmSJEkqaYWaYVNoFpWWJEmSJEnKk3KpIWRRaUmSJEmSpDwpVJHmQqlrvPm4B4tKS5IkSZKkilFuS8gsKi1JkiRJkqSiMxCSJEmSJEklrcwmBJUFAyFJkiRJklRWyq2GUCkyEJIkSZIkSWWl3PKgOotKF6jfhmpyIBQRLSNiWkT8IdvuExHPRMQrETE2Ito09RqSJEmSJEnrldsSsuZaVPqrwOwa2z8Bfp5S+iTwb2BUHq4hSZIkSZKkPGlSIBQRvYBjgF9n2wF8BhiXNbkLOL4p15AkSZIkSRWu3J4zXwaaOkPoBuAyYF223RVYmlJak23PB3as68SIOC8iJkfE5MWLFzdxGJIkSZIkqVKUWw2hUtToQCgijgXeSilNacz5KaXbUkpVKaWqbt26NXYYkiRJkiSpAkQ9r8tBnUWl83ATTemjVROuewhwXEQMBdoBnYEbgS4R0SqbJdQLWNCEa0iSJEmSJG2g3BaQNaui0imlK1NKvVJKvYFTgYdTSqcDjwBfzJqNACY0fniSJEmSJEnKt3w8Zay2y4GvR8Qr5GoK3V6Aa0iSJEmSpApRbjOCykFTloxVSyk9CjyavX4NGJSPfiVJkiRJkmortxpCpagQM4QkSZIkSZLyKsq4qnSdRaUL1G9DGQhJkiRJkiRVGAMhSZIkSZJUXsqsqFCzesqYJEmSJEnS1lCoQKWSGQhJkiRJkqTyUmY1hEqRgZAkSZIkSSp5ZVxTuu6i0nm4CYtKS5IkSZIkqcEMhCRJkiRJUlkpt5JCFpWWJEmSJEnaQqnsIqDSZyAkSZIkSZJUYQyEJEmSJElSyatZQLk5FJUudr8GQpIkSZIkSRXGQEiSJEmSJJWVcqsoZFFpSZIkSZKkLVSoQKWSGQhJkiRJkqSy0hxqCOWjrpA1hCRJkiRJktRgBkKSJEmSJEkVxkBIkiRJkiSVlXIrKWRRaUmSJEmSpC1UbgFQOTAQkiRJkiRJJa9mAeVmUVS6QP02lIGQJEmSJElShTEQkiRJkiRJqjAGQpIkSZIkqayUW00hi0pLkiRJkiRtoUIFKpXMQEiSJEmSJJW8qOd1OaizqHRTKkJvot+GMhCSJEmSJEmqMAZCkiRJkiRJFcZASJIkSZIklbRUq4x0uZUUsqi0JEmSJEmSis5ASJIkSZIklbyaBZSbRVHpAvXbUI0OhCJip4h4JCJmRcSLEfHVbP/2ETExIuZkf27X+OFJkiRJkiQp35oyQ2gN8I2UUl/gIOCCiOgLXAFMSintBkzKtiVJkiRJklQiGh0IpZQWpZSmZq+XA7OBHYFhwF1Zs7uA45s4RkmSJEmSVMnSJjdLXrMtKh0RvYGBwDNA95TSouzQG0D3es45LyImR8TkxYsX52MYkiRJkiRJaoAmB0IR0RG4H/ivlNK7NY+llBL1BHcppdtSSlUppapu3bo1dRiSJEmSJKkZi3pel4M6i0rn4SaKUlQ6d+FoTS4Muiel9Pts95sR0SM73gN4qynXkCRJkiRJUn415SljAdwOzE4pXV/j0IPAiOz1CGBC44cnSZIkSZKkfGvVhHMPAc4EZkbE9GzfN4EfA/dGxCjgdeDkJo1QkiRJkiRVtNq1aCwq3fR+Gx0IpZSeoP5le0c2tl9JkiRJkiQVVl6eMiZJkiRJklRIUaOCcnMoKl3sfg2EJEmSJEmSKoyBkCRJkiRJUoUxEJIkSZIkSSUt1aqebFHppvdrICRJkiRJklRhDIQkSZIkSVJZaQ5FpfNxDxaVliRJkiRJUoMZCEmSJEmSJFUYAyFJkiRJklTSahdPtqh00/s1EJIkSZIkSaowBkKSJEmSJKnk1Syg3CyKSufhJiwqLUmSJEmSpAYzEJIkSZIkSaowBkKSJEmSJKmk1a6dbFHppvdrICRJkiRJklRhDIQkSZIkSVLJi3pel4M6i0oXqN+GMhCSJEmSJEmqMAZCkiRJkiRJFcZASJIkSZIklbTaxZMtKt30fg2EJEmSJEmSKoyBkCRJkiRJKnk1Cyg3i6LSebgJi0pLkiRJkiSpwQyEJEmSJEmSKoyBkCRJkiRJKmmpVhlpi0o3vV8DIUmSJEmSpApjICRJkiRJkkpe1PO6HOSjgHS++zUQkiRJkiRJqjAGQpIkSZIkSRXGQEiSJEmSJJW02sWTLSrd9H4NhCRJkiRJkiqMgZAkSZIkSSp9UefLslBX8ed8FJouuaLSEXF0RLwcEa9ExBWFuIYkSZIkSZIaJ++BUES0BG4BPg/0BU6LiL75vo4kSZIkSZIap1UB+hwEvJJSeg0gIn4HDANmFeBakiRJW81DMxfx26dfL/YwJEmqOP98e2Wxh9AorVrk1nSV4hK3QgRCOwLzamzPBw6s3SgizgPOA9h5550LMAxJkqT8WrsusXrtumIPQ5KkitNru/b07Z5b5HTXM+8x4qBtCnq9K47qRNdtNl5UdfXQzrRp2fB457SqDix6dy1H7N52o2Nd2rfg833bcWDvNg3q6yuHdWTATq0BOG7f9kyf/yEXfLpTg8dSW6Q8P/ssIr4IHJ1S+nK2fSZwYErpwvrOqaqqSpMnT87rOCRJkiRJUvOxfPmUYg+h7HTuXDUlpVRV17FCFJVeAOxUY7tXtk+SJEmSJEkloBCB0HPAbhHRJyLaAKcCDxbgOpIkSZIkSWqEvNcQSimtiYgLgb8ALYE7Ukov5vs6kiRJkiRJapxCFJUmpfQQ8FAh+pYkSZIkSVLTFGLJmCRJkiRJkkqYgZAkSZIkSVKFMRCSJEmSJEmqMAZCkiRJkiRJFSZSSsUeAxGxHHi52OOQtsAOwNvFHoSkZmdbYFmxByGp2fFzi6RC8HNLedgjpdSprgMFecpYI7ycUqoq9iCkhoqIyf7OSsq3iLgtpXRescchqXnxc4ukQvBzS3mIiMn1HXPJmCRJpeP/ij0ASZKkBvJzS5kzEJIkqUSklPxgJUmSyoKfW8pfqQRCtxV7ANIW8ndWkiSVCz+3SFLlqvf/A0qiqLQkSZIkSZK2nlKZISRJUrMRETtFxCMRMSsiXoyIr2b7t4+IiRExJ/tzuzrO/URETI2I6dm559c4tn9EzIyIVyLipoiIrXlfkiSp+dnE55bh2fa6iKizMH1EtIuIZyNiRtb2ezWO9YmIZ7LPLWMjos3Wuic1jIGQJEn5twb4RkqpL3AQcEFE9AWuACallHYDJmXbtS0CPpVSGgAcCFwRET2zY78EzgV2y36OLuhdSJKkSlDf55YXgBOBxzZx7gfAZ1JK/YEBwNERcVB27CfAz1NKnwT+DYwq0PjVSAZCqmhN+RY/azciazMnIkbU2O+3+FIFSyktSilNzV4vB2YDOwLDgLuyZncBx9dx7ocppQ+yzbZk/18dET2Azimlp1NuvffddZ0vqflqyrf4WbujI+Ll7PPJFTX2+y2+VMHq+9ySUpqdUnp5M+emlNKKbLN19pOyf/98BhiXHavzc4+Ky0BIla7R3+JHxPbA1eS+wR8EXF0jOPJbfEkARERvYCDwDNA9pbQoO/QG0D1rUxURv65xzk4R8TwwD/hJSmkhuUBpfo2u52f7JFWORn+LHxEtgVuAzwN9gdOyc8Fv8SVlan1uqa9Nz4h4qMZ2y4iYDrwFTEwpPQN0BZamlNZkzfzcUoIMhFTRmvItPvA5cv/Beyel9G9gIrkpkn6LLwmAiOgI3A/8V0rp3ZrHsv8+pOz15JTSl2scm5dS2hf4JDAiIrpvxWFLKlFN+Raf3JdXr6SUXkspfQj8Dhjmt/iS1tvU55aaUkoLU0pDa2yvzZa69wIGRcQ+BR+s8sJASMo04lv8Hcl9e7/e+tTbb/ElERGtyX2ouiel9Pts95tZaLx+Cdhbm+ojmxn0AnAYsIDcB631emX7JFWgRnyLX9/nFr/Fl1Tf55YtklJaCjxCbnXEEqBLRLTKDvu5pQQZCEk0/lt8SapL9o377cDslNL1NQ49CKyvNzYCmFDHub0ion32ejvgUODlLKR+NyIOyvo/q67zJTV/jf0WX5LqsonPLQ05t1tEdMletweGAC9l/4Z6BPhi1rTOzz0qLgMhVbwmfIu/ANipxvb61Ntv8SUdApwJfCZ7fPz0iBgK/BgYEhFzgM9m27VnH+4FPBMRM4C/AT9LKc3Mjn0F+DXwCvAq8KetdkeSSkITvsWv73OL3+JLqvNzS0ScEBHzgU8Bf4yIv8BGsw97AI9ktQ+fI1dS4w/ZscuBr0fEK+RmI96+NW9Kmxe54E6qTFkafhfwTkrpv2rsvw5YklL6cfYUju1TSpfVOnd7YAqwX7ZrKrB/SumdiHgWuJjcNO6HgP9JKT2EJElSI9X3uaXG8UeBS1JKk+s41gr4B3AkucDnOeBLKaUXI+I+4P6U0u8i4lbg+ZTSLwp3J5KkUmAgpIoWEYcCjwMzgXXZ7m+SC3LuBXYGXgdOzoKeKuD89cvGIuKcrD3AtSmlO7P9VcBooD25b/AvSv6PTZIkNcEmPre0Bf4H6AYsBaanlD4XET2BX69fNpbNVLwBaAnckVK6Ntu/C7ki09sD04AzUkofbKXbkiQViYGQJEmSJElShbGGkCRJkiRJUoUxEJIkSZIkSaowBkKSJEmSJEkVxkBIkiRJkiSpwhgISZIkSZIkVRgDIUmSJEmSpApjICRJkpqtiOgSEV/JXveMiHEFvNb5EXFWHft7R8QLhbquJElSY0RKqdhjkCRJKoiI6A38IaW0TyWPQZIkqTZnCEmSpObsx8CuETE9Iu5bP1MnIkZGxPiImBgRcyPiwoj4ekRMi4inI2L7rN2uEfHniJgSEY9HxJ71XSgivhsRl2Sv94+IGRExA7igRpuvRcQd2et+EfFCRHQo5BsgSZJUFwMhSZLUnF0BvJpSGgBcWuvYPsCJwAHAtcB7KaWBwFPA+qVftwEXpZT2By4BftHA696Znde/1v4bgU9GxAlZm/9IKb23ZbckSZLUdK2KPQBJkqQieSSltBxYHhHLgP/L9s8E9o2IjsDBwH0Rsf6ctpvrNCK6AF1SSo9lu34DfB4gpbQuIkYCzwP/L6X09zzdiyRJ0hYxEJIkSZXqgxqv19XYXkfuM1ILYGk2uyifdgNWAD3z3K8kSVKDuWRMkiQ1Z8uBTo05MaX0LvDPiBgOEDm1l4DVdd5SYGlEHJrtOn39sYjYFrgJ+DTQNSK+2JixSZIkNZWBkCRJarZSSkuAv2fFpK9rRBenA6Oy4tAvAsMaeN7ZwC0RMR2IGvt/DtySUvoHMAr4cUR8rBHjkiRJahIfOy9JkiRJklRhnCEkSZIkSZJUYSwqLUmStAUi4lvA8Fq770spXVuM8UiSJDWGS8YkSZIkSZIqjEvGJEmSJEmSKoyBkCRJkiRJUoUxEJIkSZIkSaowBkKSJEmSJEkV5v8H1TEd+Tl4kpoAAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 1440x288 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAABIEAAAEXCAYAAAA6MVQ4AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAC4FUlEQVR4nOzdd3gUVdsG8Pvsbhq9BaSoFOktQMCCCEgRRUVBbKCC7bXBa6OoKBawYUFfLJ+NiCKCqKCCIL1ITYDQOwFCDQnpbcv5/pid2dnd2ZZCErh/16Xs7szOnJ3Mzs4885znCCkliIiIiIiIiIjo4mYq6wYQEREREREREVHpYxCIiIiIiIiIiOgSwCAQEREREREREdElgEEgIiIiIiIiIqJLAINARERERERERESXAAaBiIiIiIiIiIguAQwCERERXUBCiNeFED/6mb5LCNGrFNbbSwiRHGCeWUKIO0p63ZcyIcQVQohsIYTZx/QIIcReIUT0hW7bxU4IESeEGFHW7SAiIipPGAQiIiICIIS4XwgR77xgPyWE+FsIcf2FboeUsq2UcuWFXq8QogOAjgDmO5+PEELYndsjUwiRKIS49QK3KVwI8aEQItnZjiQhxNQL2YZAPLZTthDisBDiSXW6lPKYlLKKlNLunH+lEOJR3fQCAN8BGH/hW2/M+ZnWlnU7iIiIqOQxCERERJc8IcTzAKYCeBtAPQBXAPgcwKAybNaF9h8AM6WUUvfaeillFQA1oGyPn4UQNS5gm14CEAugG4CqAHoB2FKSKxBCWEpgMeudgZ4qAIYAeF8I0SmE9/8E4CEhREQJtIXKkK+MLyIiovKCQSAiIrqkCSGqA3gTwNNSyt+klDlSSquU8k8p5RjnPBFCiKlCiJPO/6aqF+xqNyshxFghxFlnFtEdQohbhBD7hRBpQoiXPVYbKYSYLYTIEkJsEUJ01LUnSQjR1/n4dSHEHCHEDOe8u4QQsbp5GwghfhVCpAghjgghRuumRTm7w5wXQuwG0DXAprgZwCqjCVJKB4AfAFQG0Ny5/GZCiOVCiFQhxDkhxEw1QCSEGCmE+FPXlgNCiF90z48LIWICtAfONv8upTwpFUlSyhm65VwuhPjN+flThRDTnK+bhBAThBBHnX+TGc6/M4QQjYUQUgjxiBDiGIDlztcfFkLscW6vxUKIK4Non9G22gpgD4DWHuuzCCEmA+gBYJoza2ia8z3JAM4DuKYo6xRC1BFC/CWESHfub2uc22CMEOJXj3k/FUJ84nw8wpm5lOXcf4YJIVoD+BLAtc42pjvnjRBCfCCEOCaEOCOE+FIIEeWcVpTvgL5NtYQQ053frfNCiHkey33ZuY8lCSGG6d7nllUl/GQw6f8ORu8XQlwlhFglhMhwrmu2br5WQoglzs+xTwhxt25anBDiCyHEQiFEDoDeQfzJiIiIygyDQEREdKm7FkAkgN/9zPMKlAv0GChdproBmKCbfplzGQ0BvAbgawDDAXSBctH/qhCiiW7+QQB+AVALShbIPCFEmI913w7gZyjZOH8A0AIdAP4EkOhcbx8AzwohbnK+byKAZs7/bgLwkK8PJ4SoDKAJgH0+ppsBjARgBXBUfRnAOwAaQAl4XA7gdee0VQB6OAMRDQCEQ9nOEEI0BVAFwHZf7dHZAOB5IcRTQoj2Qgjh0aa/nO1p7NwGPzsnj3D+1xuAur5pHsvu6Wz3TUKIQQBeBjAYQDSANQBmBdE+L0KIrgBaAIj3nCalfMW57GecmUPP6CbvgbJvFcULAJKhtL0elM8iAfwIYIAuOGcBcC+AGc6/+acAbpZSVgVwHYBtUso9AJ6AK7uphnMd7zo/VwyAq+Da11Whfgf0fgBQCUBbAHUBfOyx3DrO5T4E4CshRMuQtk5w3gLwD4CaABoB+B+gfTeWQPme1oWy/T4XQrTRvfd+AJOhZKuxGx0REZVrDAIREdGlrjaAc1JKm595hgF4U0p5VkqZAuANAA/oplsBTJZSWqEEIuoA+ERKmSWl3AVgN9wv8BOklHOd838E5eLZVxbIWinlQmdNmR90y+kKIFpK+aaUslBKeRjKhfe9zul3O9uUJqU8DuWC35cazn+zPF6/xpkJkg/gAwDDpZRnAUBKeVBKuURKWeDcJh9BCazA2ZYsKAGDGwAsBnBSCNHKOc8aZ3ZRIO8AeA/K9o8HcEIIoQazukEJQI1xZm/lSynVC/BhAD6SUh6WUmZD6VZ2r3Dv+vW68315UIIe70gp9zj3g7cBxISQDXSNMwsnC8AmKH+nA0G+V5UF198hVFYA9QFc6cxiW+PMnDoFYDWAoc75BkDZ1xOczx0A2gkhoqSUp5z7qhdn8O1xAM8596csKNvoXt1soX4H1GXXh5KF9oSU8ryz/Z4Zaa8697NVABZA2bdLmhXAlQAaeOxLtwJIklJOl1LanJlev8K1TQFgvpTyXymlQ0qZXwptIyIiKjEMAhER0aUuFUAd4b82TAO4MmDgfNxAvwy18C+APOe/Z3TT86Bko6iOqw+cwZBkj+XpndY9zoXSlcwC5wWrM/iQ7gzWvAwlE0Rt83Hde/Xt95Tu/Leqx+sbnJkgNaFkIfVQJwgh6gkhfhZCnBBCZELJOqmje+8qKDV8bnA+XgklANQTPrqdeZJS2qWUn0kpu0MJkEwG8J2zy9LlAI76CN4Z/b0scG0bwH3bXAngE912TIOS6dQwmHbCuZ2cGTWXQcloeTvI96qqwvV3cCNcRaezhRBXGMwyBcBBAP84u3fpi0x/DyUjB85/fwAAKWUOgHugBMBOCSEWOIN0RqKhZOok6LbRIufrqlC/A6rLAaRJKc/7WPd5Z1tVnt+9kjIWyt98k1C6XT7sfP1KAFd7fM+GQfk7q46DiIiogmAQiIiILnXrARQAuMPPPCehXAyqrnC+VlSXqw+c3boaFWF5xwEccQYf1P+qSilvcU4/pV+Ps82GnBfZh6B09zGang3gSQAPCFfB47ehdDlqL6WsBiXAIHRvU4NAPZyPVyHEIJBHG/KklJ9BqZ3TBsrnv8JH8M7o72WDe1BCXwD7OID/eGzLKCnluiK08wyUTJHbfM3i4/XWULr2GS2ziu6/YwbTs6SUL0gpm0LpPvi8EKKPc/I8AB2EEO2gZLXM1L1vsZSyH5Qsor1QMsmM2ngOShCnrW77VJdKIeziOg6glvBdcLyms0uWSv/dy4ESnFLpAzOe1ECS4fxSytNSyseklA2gFEn/XAhxlbN9qzz2jSpSyid1y/H1NyUiIip3GAQiIqJLmpQyA0oNk8+cxWwrCSHChBA3CyHed842C8AEIUS0EKKOc/4fi7HaLkKIwc4AxrNQglAbQlzGJgBZQohxQikCbRZCtHPWpAGAOQBeEkLUFEI0AjAqwPIWwtmdy4iUMg3AN3DVgakKIBtAhhCiIYAxHm9ZBaUmT5Sz8PEaKN2RagPYqs7kLM77utE6hRDPOosDRwmlsPJDzvVudX7+UwDeFUJUFkJECiG6O986C8BzQogmQogqUAJWs/10+fsSyrZq61xvdSGE1t3HXxsN2lwbwJ0ADLtWQQlENfV4T0Mo9aFC3QfU99/qLGwsAGQAsEPp6gVn96S5UGrabFKDSM5MrkHOAEsBlL+l2kXvDIBGQohw5zIcUAJEHwsh6qpt1tWfKjJnl7W/oQRdajq/ezd4zPaGECJcCNEDSiBLLTK+DcBg53f2KgCP+FlPCoATAIY7vysPQ6mXBefnGer8ngBKoFFC2R5/AWghhHjA2bYwIURXZzYaERFRhcMgEBERXfKklB8CeB5KsecUKHf/n4GSRQEAk6DUpNkOYAeUYconFWOV86F0xTkPpbbQYGctlVDabIdyQRwD4AiUbI1vAFR3zvIGlK4zR6AUvP0hwCK/AjDMGUjwZSqAW4QQHZzL7wwl6LAAwG8e7dsPJbCwxvk8E8BhAP/qug0BSrbSvz7WlwvgQyhd4s4BeBrAEGetHzuUbJurAByD0qXuHuf7vnN+3tVQPn8+/ATBpJS/Q6k99LOza9tOKHVqgmkj4BpJKxtKgecUP+v7BMBdQhkFS63TdD+A76WUBX7W4U9zAEuhbO/1AD6XUq7QTf8eQHu47wMmKPv8SSjd33pCyfYClBHTdgE4LYQ453xtHJQuZxuc22gpgCIVaBbKKGT6INkDUGry7AVwFkpgVHUayvfkJJQspieklHud0z4GUAglaPU9dFlOPjwGJViZCqXLnj7TqyuAjc6/4R8A/uvcz7IA9IdS/+iksz3vAYgI4SMTERGVG0JKZrASERERIIT4CcAcKeW8C7S+Rs71XXch1lcUpd1GIUQElG5gN6hFt0thHVdACbBc5gzGVQhCiF4AfpRSNgowq6/3xwFYKaWMK7lWERERVWz+imASERHRJURKef8FXl8ylKHJy63SbqMz+8dXQeZic9aceh7AzxUpAERERESlg0EgIiIioouQs97PGSjdAgeUcXPKwjwASWXcBiIionKF3cGIiIiIiIiIiC4BLAxNRERERERERHQJKLPuYHXq1JGNGzcuq9UTERERERERUTnncOSWdRMqnK1b95yTUkYbTSuzIFDjxo0RHx9fVqsnIiIiIiIionIuKyuhrJtQ4VSrFnvU1zR2ByMiIiIiIiIiugQwCEREREREREREdAlgEIiIiIiIiIiI6BJQZjWBjFitViQnJyM/P7+sm0JUbkVGRqJRo0YICwsr66YQERERERFRBVKugkDJycmoWrUqGjduDCFEWTeHqNyRUiI1NRXJyclo0qRJWTeHiIiIiIiIKpCA3cGEEN8JIc4KIXb6mC6EEJ8KIQ4KIbYLIToXtTH5+fmoXbs2A0BEPgghULt2bWbLERERERERUciCqQkUB2CAn+k3A2ju/O9xAF8Up0EMABH5x+8IERERERERFUXA7mBSytVCiMZ+ZhkEYIaUUgLYIISoIYSoL6U8VVKNJCIiIiIiIqJLS3ZhNv44sgp59nzsOZ+E9rWu8jv/uWwrKmUmo1KDopXOOJ17DhHmcNSMqOb2+tm8NJiECXUiawS9rOScM2hUuZ7htExrDipbomAWgfNyjmafQp3IGqhsiQIA7Dl/GK1rNgFQtOSAkqgJ1BDAcd3zZOdrXkEgIcTjULKFcMUVV5TAqomIiIiIiIjoYrQ4aTHe3Tpde/7P8fXBvTFlbSm1qHxYeOzfIr/3ghaGllJ+BeArAIiNjZUXct0XSlxcHPr3748GDRqUdVN8iouLQ1JSEl5//fWybgoRERERERGRIavD6va8V4NYvBjzoM/5Z037Fo+ZF6AwdigKu94X8vpuXTgaAPDXLZ8G9bovn+2cjb+P/YvHWt+JQU16u03blXYI4zZ8EtTyMq3ZuH/Jy9q8C46uwRe7fkH/y6/B6Pb3+3xfY9zoc1pJBIFOALhc97yR87VLUlxcHNq1a1eug0ClzWazwWIpVwPPERERERERUQVXOSwKtSKr+ZxutkWhtnCgAGYU+pkvEF/r8LduvUhzBACgUlik13uqhlcKenn67mK1IquhSpjSJaySxXu5wSqJK/U/ADwjhPgZwNUAMkqiHtAbf+7C7pOZxW6cXpsG1TDxtrZ+58nJycHdd9+N5ORk2O12vPrqq5g1axbmzZsHAFiyZAk+//xzzJ07F4888gji4+MhhMDDDz+Myy+/HPHx8Rg2bBiioqKwfv167N69G88//zyys7NRp04dxMXFoX79+ujVqxc6deqENWvWICcnBzNmzMA777yDHTt24J577sGkSZO82rZ582b897//RU5ODiIiIrBs2TL8+uuv+P3335GRkYETJ05g+PDhmDhxIpKSknDrrbdi505lULcPPvgA2dnZXtk/cXFxiI+Px7Rp0wAAt956K1588UX06NHD6/M999xzOHToEJ5++mmkpKSgUqVK+Prrr9GqVSuMGDECkZGR2Lp1K7p3746PPvqo+H8wIiIiIiIioiA51LGvpKNsG1KOBQwCCSFmAegFoI4QIhnARABhACCl/BLAQgC3ADgIIBfAyNJq7IWwaNEiNGjQAAsWLAAAZGRkYOLEiUhJSUF0dDSmT5+Ohx9+GNu2bcOJEye0IEt6ejpq1KiBadOm4YMPPkBsbCysVitGjRqF+fPnIzo6GrNnz8Yrr7yC7777DgAQHh6O+Ph4fPLJJxg0aBASEhJQq1YtNGvWDM899xxq166ttauwsBD33HMPZs+eja5duyIzMxNRUUoUcNOmTdi5cycqVaqErl27YuDAgahTp06xtoPR5wOAxx9/HF9++SWaN2+OjRs34qmnnsLy5csBAMnJyVi3bh3MZnOx1k1EREREREQUKruzWLJw2Mu4JeVXMKOD+e1I5xwV7OkSa5FToIyd0tK+fXu88MILGDduHG699Vb06NEDDzzwAH788UeMHDkS69evx4wZM5CVlYXDhw9j1KhRGDhwIPr37++1rH379mHnzp3o168fAMBut6N+/fra9Ntvv11bZ9u2bbVpTZs2xfHjx92CQPv27UP9+vXRtWtXAEC1aq7Ur379+mnzDh48GGvXrsUdd9xRrO3QtGlTr8+XnZ2NdevWYejQodp8BQUF2uOhQ4cyAEREREREREQlQiK0UsL2cpMJVDolkNWlymIsnoVbPLRo0QJbtmzBwoULMWHCBPTp0wePPvoobrvtNkRGRmLo0KGwWCyoWbMmEhMTsXjxYnz55ZeYM2eOluGjklKibdu2WL/euIJ5RITST9BkMmmP1ec2my3oNgshvJ5bLBY4HK4dPz8/3/C9vuYz+nxTp05FjRo1sG3bNsNlVa5cOeg2ExEREREREZUkdgcLLPCg9JeYkydPolKlShg+fDjGjBmDLVu2oEGDBmjQoAEmTZqEkSOV3m7nzp2Dw+HAkCFDMGnSJGzZsgUAULVqVWRlZQEAWrZsiZSUFC0IZLVasWvXriK1q2XLljh16hQ2b94MAMjKytICRUuWLEFaWhry8vIwb948dO/eHfXq1cPZs2eRmpqKgoIC/PXXX4bLbdy4MbZt2waHw4Hjx49j06ZNPj9ftWrV0KRJE/zyyy8AlCBXYmJikT4PERERERERUShEgOlaJpCjrINAwuNf/ZRAn0I3r8eswsfroWAmkIcdO3ZgzJgxMJlMCAsLwxdffAEAGDZsGFJSUtC6dWsAwIkTJzBy5Egti+add94BAIwYMQJPPPGEVhh67ty5GD16NDIyMmCz2fDss8+ibdvgu7rdcsst+Oabb9CgQQPMnj0bo0aNQl5eHqKiorB06VIAQLdu3TBkyBAkJydj+PDhiI2NBQC89tpr6NatGxo2bIhWrVoZLr979+5o0qQJ2rRpg9atW6Nz585+P9/MmTPx5JNPYtKkSbBarbj33nvRsWPHkLYxERERERERUUljJlBgDAJ5uOmmm3DTTTd5vb527Vo89thj2vOOHTtq2T96Q4YMwZAhQ7TnMTExWL16tdd8K1eu1B736tULvXr1Mpy2cOFC7XHXrl2xYcMGr2U1atRIG71Mb/To0Rg9erTX63pCCMycOdNwmtHna9KkCRYtWuT1elxcnN/1EBEREREREZUmV00gFob2hUGgIHTp0gWVK1fGhx9+WNZNISIiIiIiIrokyBArINugDFRU9qODlW5h6OJgECgICQkJZd0En0aMGIERI0aE9J6YmBg0bty4VNpDREREREREVBpCqadTHhi113NgpwuNQaBLUExMTFk3gYiIiIiIiOgiVVKBHuHnWdFwdDAiIiIiIiIiuohUrIyhC4lBICIiIiIiIiKq8EQp1eK5mDAIRERERERERETljgwxqFN+8n/Kb2FoBoGIiIiIiIiIqPwLEOUpb5lARjWgyzpQxSBQCYuLi8PJkyfLuhl+xcXF4fXXXy/rZpQrSUlJaNeuXVk3g4iIiIiIiIpIDQLJMh6Bq6RCPZ5LKYmllt/Rwf4eD5zeUbLLvKw9cPO7JbtMD3FxcWjXrh0aNGhQquspz2w2GyyW8rtrlWfcdkREREREREVT1qGfioCZQB5ycnIwcOBAdOzYEe3atcPs2bNxxx13aNOXLFmCO++8E3a7HSNGjEC7du3Qvn17fPzxx5g7dy7i4+MxbNgwxMTEIC8vDwkJCejZsye6dOmCm266CadOnQIA9OrVC8899xxiY2PRunVrbN68GYMHD0bz5s0xYcIEw7Zt3rwZ1113HTp27Ihu3bohKysLcXFxGDRoEHr16oXmzZvjjTfeAOCd2fLBBx8YZv/ExcXhmWee0Z7feuutWLlypeHnA4BDhw5hwIAB6NKlC3r06IG9e/cCAEaMGIEnnngCV199NcaOHRv09t60aROuvfZadOrUCddddx327duntWvw4MEYMGAAmjdv7rbMWbNmoX379mjXrh3GjRunvV6lShWMGTMGbdu2Rd++fbFp0yb06tULTZs2xR9//KFtlx49eqBz587o3Lkz1q1b59WmG264Adu2bdOeX3/99UhMTDRs/6pVqxATE4OYmBh06tQJWVlZAID33nsP7du3R8eOHTF+/HgAwLZt23DNNdegQ4cOuPPOO3H+/HkAyr7w7LPPIjY2Fp988onPfYaIiIiIiIh8K2/dwcqj8ptyUMoZO74sWrQIDRo0wIIFCwAAGRkZmDhxIlJSUhAdHY3p06fj4YcfxrZt23DixAns3LkTAJCeno4aNWpg2rRp+OCDDxAbGwur1YpRo0Zh/vz5iI6OxuzZs/HKK6/gu+++AwCEh4cjPj4en3zyCQYNGoSEhATUqlULzZo1w3PPPYfatWtr7SosLMQ999yD2bNno2vXrsjMzERUVBQAJZCyc+dOVKpUCV27dsXAgQNRp06dYm0Ho88HAI8//ji+/PJLNG/eHBs3bsRTTz2F5cuXAwCSk5Oxbt06mM3moNfTqlUrrFmzBhaLBUuXLsXLL7+MX3/9VWvD1q1bERERgZYtW2LUqFEwm80YN24cEhISULNmTfTv3x/z5s3DHXfcgZycHNx4442YMmUK7rzzTkyYMAFLlizB7t278dBDD+H2229H3bp1sWTJEkRGRuLAgQO47777EB8f79amRx55BHFxcZg6dSr279+P/Px8dOzY0bD9H3zwAT777DN0794d2dnZiIyMxN9//4358+dj48aNqFSpEtLS0gAADz74IP73v/+hZ8+eeO211/DGG29g6tSpAJS/b3x8PKxWK3r27OlznyEiIiIiIiJj5ScIVH4LQ5ffIFAZad++PV544QWMGzcOt956K3r06IEHHngAP/74I0aOHIn169djxowZyMrKwuHDhzFq1CgMHDgQ/fv391rWvn37sHPnTvTr1w8AYLfbUb9+fW367bffrq2zbdu22rSmTZvi+PHjbkGgffv2oX79+ujatSsAoFq1atq0fv36afMOHjwYa9eudcteKoqmTZt6fb7s7GysW7cOQ4cO1eYrKCjQHg8dOjSkABCgBNkeeughHDhwAEIIWK1WbVqfPn1QvXp1AECbNm1w9OhRpKamolevXoiOjgYADBs2DKtXr8Ydd9yB8PBwDBgwAICyTSMiIhAWFob27dsjKSkJAGC1WvHMM89g27ZtMJvN2L9/v1ebhg4dirfeegtTpkzBd999hxEjRvhsf/fu3fH8889j2LBhGDx4MBo1aoSlS5di5MiRqFSpEgCgVq1ayMjIQHp6Onr27AkAeOihh9y24z333AMg8D5DRERERER0qRIBOny5gkCl0zHs30MF6NAwDFUjg+tUZdzesu20xiCQhxYtWmDLli1YuHAhJkyYgD59+uDRRx/FbbfdhsjISAwdOhQWiwU1a9ZEYmIiFi9ejC+//BJz5szxytaQUqJt27ZYv3694boiIiIAACaTSXusPrfZbEG3WXgUvRJCwGKxwOFwaK/l5+cbvtfXfEafb+rUqahRo4ZbVym9ypUrB91m1auvvorevXvj999/R1JSEnr16qVN028Ts9kccJuEhYVp20K/TfXb8+OPP0a9evWQmJgIh8OByMhIr+VUqlQJ/fr1w/z58zFnzhwkJCT4XOf48eMxcOBALFy4EN27d8fixYuD/ux66rYLtM8QERERERGRsdLOBHri5/O4vlk4vri3VsCWlASva32DeT5ZkYXv1ucg8eXLglomawJ5OHnyJCpVqoThw4djzJgx2LJlCxo0aIAGDRpg0qRJGDlyJADg3LlzcDgcGDJkCCZNmoQtW7YAAKpWrarVhWnZsiVSUlK0C3qr1Ypdu3YVqV0tW7bEqVOnsHnzZgBAVlaWFthYsmQJ0tLSkJeXh3nz5qF79+6oV68ezp49i9TUVBQUFOCvv/4yXG7jxo2xbds2OBwOHD9+HJs2bfL5+apVq4YmTZrgl19+AaAELHzVyglWRkYGGjZsCECpAxRIt27dsGrVKpw7dw52ux2zZs3SsmuCXV/9+vVhMpnwww8/wG63G8736KOPYvTo0ejatStq1qzpc3mHDh1C+/btMW7cOHTt2hV79+5Fv379MH36dOTm5gIA0tLSUL16ddSsWRNr1qwBAPzwww+G7S7JfYaIiIiIiOhSIrwelLykVONryLLyzbocOEKIfTETyMOOHTswZswYmEwmhIWF4YsvvgCgdDtKSUlB69atAQAnTpzAyJEjtSyad955B4CrQHJUVBTWr1+PuXPnYvTo0cjIyIDNZsOzzz6Ltm3bBt2eW265Bd988w0aNGiA2bNnY9SoUcjLy0NUVBSWLl0KQAmMDBkyBMnJyRg+fDhiY2MBAK+99hq6deuGhg0bolWrVobL7969O5o0aYI2bdqgdevW6Ny5s9/PN3PmTDz55JOYNGkSrFYr7r33Xp/1coIxduxYPPTQQ5g0aRIGDhwYcP769evj3XffRe/evSGlxMCBAzFo0KCg1/fUU09hyJAhmDFjBgYMGOAze6lLly6oVq2aFvTzZerUqVixYgVMJhPatm2Lm2++GREREdi2bRtiY2MRHh6OW265BW+//Ta+//57PPHEE8jNzUXTpk0xffp0r+WFh4cXe58hIiIiIiK6GEgZWmZP+akJVH6JUDdqSYmNjZWeBXn37NmjBVnKm2eeeQadOnXCI488UtZNcRMXF4f4+HhMmzYtpPckJSUZjhZGipMnT6JXr17Yu3cvTKbylzBXnr8rREREREREJeHH3T/ivc3vac9vb9wT4zv7vlEf/kF/RAgbCtvfgoL+L4a8vut+GwEAWDc4zvD1rD3volENM/5+OtrvcqZs/R6/H1mB5zsOx13N+rpN25F6EP9ZNclwPZ6yrbno/+dT2ry/HV6OD7bNwB1NemFsJ6VN7SefVpb7iqs7WLVqsQlSylijZZa/q9tyqEuXLti+fTuGDx9e1k2hC2DGjBm4+uqrMXny5HIZACIiIiIiIroUBSoMHSGCr617IRiWhS7butDsDhYMf4WBy9qIESP8jl5lJCYmBo0bNy6V9gDA9OnT8cknn7i9duDAATRv3tztte7du+Ozzz4rtXYU1YMPPogHH3zQ7TWjz1Re209ERERERERlqYQKQyNwYehQMQh0CYqJiSnV5Y8cOTJgLZ2K5mL8TERERERERBen0ku3KetMnuJiXxciIiIiIiIiKndkhS30XDrtLomlMghEREREREREROVe0Fk4FT1dpxQxCEREREREREREVOK8g1GBiluXNgaBiIiIiIiIiIhKTOkEekpiqQwClbC4uDicPHmyrJvhV1xcHF5//fWybka5kpSUhHbt2oX8vtdffx0ffPCB1+snT57EXXfdBQDYtm0bFi5cWOw2EhERERERERVHuR0d7L1N72Fv2t4SXWarWq0wrtu4El2mp7i4OLRr1w4NGjQo1fWUZzabDRZLud21LogGDRpg7ty5AJQgUHx8PG655ZYybhUREREREVHFIWURSyFLR8k2RCe4bBwWhq4wcnJyMHDgQHTs2BHt2rXD7Nmzcccdd2jTlyxZgjvvvBN2ux0jRoxAu3bt0L59e3z88ceYO3cu4uPjMWzYMMTExCAvLw8JCQno2bMnunTpgptuugmnTp0CAPTq1QvPPfccYmNj0bp1a2zevBmDBw9G8+bNMWHCBMO2bd68Gddddx06duyIbt26ISsrC3FxcRg0aBB69eqF5s2b44033gDgndnywQcfGGb/xMXF4ZlnntGe33rrrVi5cqXh5wOAQ4cOYcCAAejSpQt69OiBvXuVQN2IESPwxBNP4Oqrr8bYsWOD3t6bNm3Ctddei06dOuG6667Dvn37tHYNHjwYAwYMQPPmzd2WOWvWLLRv3x7t2rXDuHGuoF6VKlUwZswYtG3bFn379sWmTZvQq1cvNG3aFH/88Ye2XXr06IHOnTujc+fOWLdunVebbrjhBmzbtk17fv311yMxMdHnZ0hMTMS1116L5s2b4+uvv9bW065dOxQWFuK1117D7NmzERMTg9mzZwe9bYiIiIiIiMgl6Ho6JnPpNqQCK7fpGqWdsePLokWL0KBBAyxYsAAAkJGRgYkTJyIlJQXR0dGYPn06Hn74YWzbtg0nTpzAzp07AQDp6emoUaMGpk2bhg8++ACxsbGwWq0YNWoU5s+fj+joaMyePRuvvPIKvvvuOwBAeHg44uPj8cknn2DQoEFISEhArVq10KxZMzz33HOoXbu21q7CwkLcc889mD17Nrp27YrMzExERUUBUAIpO3fuRKVKldC1a1cMHDgQderUKdZ2MPp8APD444/jyy+/RPPmzbFx40Y89dRTWL58OQAgOTkZ69atg9kc/BeuVatWWLNmDSwWC5YuXYqXX34Zv/76q9aGrVu3IiIiAi1btsSoUaNgNpsxbtw4JCQkoGbNmujfvz/mzZuHO+64Azk5ObjxxhsxZcoU3HnnnZgwYQKWLFmC3bt346GHHsLtt9+OunXrYsmSJYiMjMSBAwdw3333IT4+3q1NjzzyCOLi4jB16lTs378f+fn56Nixo8/PsH37dmzYsAE5OTno1KkTBg4cqE0LDw/Hm2++ifj4eEybNi3o7UJERERERESh2edohJamZECU3yBQhSgMLYQYIITYJ4Q4KIQYbzD9CiHECiHEViHEdiFEhe330r59eyxZsgTjxo3DmjVrUL16dTzwwAP48ccfkZ6ejvXr1+Pmm29G06ZNcfjwYYwaNQqLFi1CtWrVvJa1b98+7Ny5E/369UNMTAwmTZqE5ORkbfrtt9+urbNt27aoX78+IiIi0LRpUxw/ftxrWfXr10fXrl0BANWqVdO6XPXr1w+1a9dGVFQUBg8ejLVr1xZ7Oxh9vuzsbKxbtw5Dhw5FTEwM/vOf/2iZTQAwdOjQkAJAgBJkGzp0KNq1a4fnnnsOu3bt0qb16dMH1atXR2RkJNq0aYOjR49i8+bN6NWrF6Kjo2GxWDBs2DCsXr0agBJwGTBgAABlm/bs2RNhYWFo3749kpKSAABWqxWPPfYY2rdvj6FDh2L37t1ebRo6dCj++usvWK1WfPfddxgxYoTfzzBo0CBERUWhTp066N27NzZt2hTSNiAiIiIiIqLiE1qHqdLpjhW8kgn0CI+h7ktiqQEzgYQQZgCfAegHIBnAZiHEH1JK/dXzBABzpJRfCCHaAFgIoHEJtO+Ca9GiBbZs2YKFCxdiwoQJ6NOnDx599FHcdtttiIyMxNChQ2GxWFCzZk0kJiZi8eLF+PLLLzFnzhwtw0clpUTbtm2xfv16w3VFREQAAEwmk/ZYfW6z2YJus9eOIQQsFgscDlc/yPz8fMP3+prP6PNNnToVNWrUcOsqpVe5cuWg26x69dVX0bt3b/z+++9ISkpCr169tGn6bWI2mwNuk7CwMG1b6Lepfnt+/PHHqFevHhITE+FwOBAZGem1nEqVKqFfv36YP38+5syZg4SEBL/rNdr+REREREREdGHxSiywYDKBugE4KKU8LKUsBPAzgEEe80gAaipMdQDle3gsP06ePIlKlSph+PDhGDNmDLZs2YIGDRqgQYMGmDRpEkaOHAkAOHfuHBwOB4YMGYJJkyZhy5YtAICqVasiKysLANCyZUukpKRoQSCr1eqW6RKKli1b4tSpU9i8eTMAICsrSwtsLFmyBGlpacjLy8O8efPQvXt31KtXD2fPnkVqaioKCgrw119/GS63cePG2LZtGxwOB44fP65lsRh9vmrVqqFJkyb45ZdfAChBLn+1coKRkZGBhg0bAlDqAAXSrVs3rFq1CufOnYPdbsesWbPQs2fPkNZXv359mEwm/PDDD7Db7YbzPfrooxg9ejS6du2KmjVr+l3m/PnzkZ+fj9TUVKxcuVLL1lLp9wkiIiIiIiIKjgwxo0fLBCrrRKAKXhi6IQB936Rk52t6rwMYLoRIhpIFNMpoQUKIx4UQ8UKI+JSUlCI0t/Tt2LED3bp1Q0xMDN544w2tSPOwYcNw+eWXo3Xr1gCAEydOoFevXoiJicHw4cPxzjvvAHAVSI6JiYHdbsfcuXMxbtw4dOzYETExMYaFiP255ZZbcPLkSYSHh2P27NkYNWoUOnbsiH79+mlZO926dcOQIUPQoUMHDBkyBLGxsQgLC8Nrr72Gbt26oV+/fmjVqpXh8rt3744mTZqgTZs2GD16NDp37uz3882cORPffvstOnbsiLZt22L+/Pmhb2SdsWPH4qWXXkKnTp2Cyn6qX78+3n33XfTu3RsdO3ZEly5dMGiQZ0zSt6eeegrff/89OnbsiL179/rMXurSpQuqVaumBf386dChA3r37o1rrrkGr776qtfIcL1798bu3btZGJqIiIiIiKhY/Of6lJ/uYOWXCDTkmhDiLgADpJSPOp8/AOBqKeUzunmedy7rQyHEtQC+BdBOSt/jssXGxkrPgrx79uzRgizlzTPPPINOnTrhkUceKeumuImLiwu56HBcXBySkpIMRwsjxcmTJ9GrVy/s3bsXJlP5G0SvPH9XiIiIiIiISsL3u77HB/EfaM/vbHIjxnR60Of8Z6cMQzPTKRR2vA0FfZ8LeX3X/TYCALBucJzh61l73sUVNc1Y8FS03+VM2fo9fj+yAi90fABDmvVxm7Y77TAeXfmm4Xo85dry0fePJ7R5fzu8HB9sm4E7mvTC2E5Km9pPPg0A2PHKZdr7qlWLTZBSxhotM5ir2xMALtc9b+R8Te8RAHMAQEq5HkAkgOINT1WOdOnSBdu3b8fw4cPLuil0AcyYMQNXX301Jk+eXC4DQEREREREROTtQnQHC64ErDJTgU0iLcdnbkwQS/FdGNrmkDiRHnwtYVUwQ8RvBtBcCNEESvDnXgD3e8xzDEAfAHFCiNZQgkDls79XEQQqDFyWRowYEXD0Kk8xMTFo3LhxqbQHAKZPn45PPvnE7bUDBw6gefPmbq91794dn332Wam1o6gefPBBPPige3TZ6DOV1/YTERERERFd2tyjQL9sycWqAwWYdo//eq8lbdqqbLyTctYtS6ekfLw8CzM25ob8voBBICmlTQjxDIDFAMwAvpNS7hJCvAkgXkr5B4AXAHwthHgOytYeIQP1M6MyExMTU6rLHzlyZFC1dCqSi/EzERERERERVWQFNonY987giesr4+meVXU1gdy9+XfmBW6Z0o58W8mGRfRLW3e4sEjLCCYTCFLKhVAKPutfe033eDeA7kVqARERERERERFRAJ5dsXIKlLDI7C25ziCQE3NSfGLBEyIiIiIiIiKqsNSYT0UYHUwEV1QoiOUU7X0MAhERERERERFRhXdBCkOX4FyhLqUklhpUd7CykpGxATZbeoktz2KpgerVrwk437x583DnnXdiz549aNWqVYmtP1RVqlRBdnZ2qSw7Li4OY8aMQaNGjZCdnY2mTZti4sSJuO666/y+b968eWjRogXatGlTKu0iIiIiIiIiKgpXkKT0okAluWRz8nbYG3UowSUGVq4zgWy2dISHR5fYf8EGlGbNmoXrr78es2bNKt0PWMbuuecebN26FQcOHMD48eMxePBg7Nmzx+975s2bh927d1+gFhIREREREdGlKtB4U55dooQoL93AgmtHpdnPlsJS/SvXQaCykJ2djbVr1+Lbb7/Fzz//rL2+cuVK9OrVC3fddRdatWqFYcOGaTvksmXL0KlTJ7Rv3x4PP/wwCgoKAACNGzfGSy+9hJiYGMTGxmLLli246aab0KxZM3z55Zfa+vr06YPOnTujffv2mD9/vlebpJQYM2YM2rVrh/bt22P27Nlam2699VZtvmeeeQZxcXEAgPHjx6NNmzbo0KEDXnzxxYCfu3fv3nj88cfx1VdfAQC+/vprdO3aFR07dsSQIUOQm5uLdevW4Y8//sCYMWMQExODQ4cOGc5HREREREREVNJEsJ2xSrEwdMl09Co7DAJ5mD9/PgYMGIAWLVqgdu3aSEhI0KZt3boVU6dOxe7du3H48GH8+++/yM/Px4gRIzB79mzs2LEDNpsNX3zxhfaeK664Atu2bUOPHj0wYsQIzJ07Fxs2bMDEiRMBAJGRkfj999+xZcsWrFixAi+88IJXtPO3337Dtm3bkJiYiKVLl2LMmDE4deqUz8+QmpqK33//Hbt27cL27dsxYcKEoD57586dsXfvXgDA4MGDsXnzZiQmJqJ169b49ttvcd111+H222/HlClTsG3bNjRr1sxwPiIiIiIiIqILRb2CLu3C0M3ECczNewIi+1yRlxFsIKu0MAjkYdasWbj33nsBAPfee69bl7Bu3bqhUaNGMJlMiImJQVJSEvbt24cmTZqgRYsWAICHHnoIq1ev1t5z++23AwDat2+Pq6++GlWrVkV0dDQiIiKQnp4OKSVefvlldOjQAX379sWJEydw5swZtzatXbsW9913H8xmM+rVq4eePXti8+bNPj9D9erVERkZiUceeQS//fYbKlWqFNRn1wefdu7ciR49eqB9+/aYOXMmdu3aZfieYOcjIiIiIiIiKk2ilEcFe8C8BHXkeVj2rw4wZ0mNAOa+HOHjcSjKdWHoCy0tLQ3Lly/Hjh07IISA3W6HEAJTpkwBAERERGjzms1m2Gy2gMtU32MymdzebzKZYLPZMHPmTKSkpCAhIQFhYWFo3Lgx8vPzg2qvxWKBw+HQnqvvs1gs2LRpE5YtW4a5c+di2rRpWL58ecDlbd26Fa1btwYAjBgxAvPmzUPHjh0RFxeHlStXGr4n2PmIiIiIiIiISpMWGCml7mAONY9G2ktl+aEoahCImUA6c+fOxQMPPICjR48iKSkJx48fR5MmTbBmzRqf72nZsiWSkpJw8OBBAMAPP/yAnj17Br3OjIwM1K1bF2FhYVixYgWOHj3qNU+PHj0we/Zs2O12pKSkYPXq1ejWrRuuvPJK7N69GwUFBUhPT8eyZcsAKHWGMjIycMstt+Djjz9GYmJiwHasWrUKX331FR577DEAQFZWFurXrw+r1YqZM2dq81WtWhVZWVnac1/zERERERERERWHDJDZ4z2Eeul2B7OrIRRdMoax0ll/SSy1XGcCWSw1UFiYUqLL82fWrFkYN26c22tDhgzBrFmzcM899xi+JzIyEtOnT8fQoUNhs9nQtWtXPPHEE0G3adiwYbjtttvQvn17xMbGGg5Jf+edd2L9+vXo2LEjhBB4//33cdlllwEA7r77brRr1w5NmjRBp06dACiBmUGDBiE/Px9SSnz00UeG6549ezbWrl2L3NxcNGnSBL/++quWCfTWW2/h6quvRnR0NK6++mot8HPvvffisccew6effoq5c+f6nI+IiIiIiIioJAXKfint7mBqEEjIQEGg8qtcB4GqV7/mgq5vxYoVXq+NHj1ae9yrVy/t8bRp07THffr0wdatW73em5SUpD0eMWIERowYYTht/fr1hu3Jzs4GAK1LmtotTe/999/H+++/7/X6pk2bDJfpqz2ennzySTz55JNer3fv3t1tiHhf8xERERERERFdSGqQSOSml8ryXd3Bih4EKuvRxdgdjIiIiIiIiIgqLM8SQJYk3wMpFYeWCZSdGmDO0gn1uBWGLuIqGAQiIiIiIiIiogrvQnUHC982r1TXU5rKXRBIllIVb6KLBb8jRERERER0KQhUGNroHQDgiKpR4m0BALsMNoSitMMEB/5j/hPIyyyR9ZfElWC5CgJFRkYiNTWVF7lEPkgpkZqaisjIyLJuChERERER0YXl0QfKs0uU+lRWql4qq7eHGEK5DGl4KWwWouZNKJX2FEW5KgzdqFEjJCcnIyWl5EYEI7rYREZGolGjRmXdDCIiIiIionJF6w4WcAj3orHDHNL8alDKlH5Ce81yZEMJtggIgw0/hr8N84mnYG/YLuD85SoIFBYWhiZNmpR1M4iIiIiIiIioglD7EqlBoNIawj34TCAtJ8n5jxqcsiPi3+lAw/rOqf6rOwuP6UZzXyHO4GrTXjgWv4+ch2cEbFm56g5GRERERERERFQUWpCklIJAoRaucQVt1GBQybVLXXaejFAeWAuCeh+DQERERERERERU7oRaL1jogi3zEnORW1iywaBw2JXFR1YLMKf0aI/y75FzVvfZQhzn3WhrWJ1d1ISNQSAiIiIiIiIiukgICBTaJOZuzYXDI0CUkefQgi6FVjte/SsTV085W6LrD4cSxLHXb+017a+decjIMw46qaGeu7/xrn+886TV67VQqMsW+cGNQMYgEBERERERERFVCF+uzcYbCzOxeHc+9HGgV/7IcHW/KqXC0OHCGbDxyOBJSrXhpfkZGD8/3e11LRNIGzLevQqQ3QHcNz21WG0SIXZSYxCIiIiIiIiIiCqE87lKgCcr3z34cSbLDpRyYehw2JQHHllIBTbl+dksdb0e3bykGgRyb1fAwtDCT2FoAVRBLqJFeqBmuylXo4MREREREREREfliGDaR7tNKLwikdt0KLvvGszC0yeN9oRaa9rQi4gVEi4yQ3sNMICIiIiIiIiIqd2SAMInnVFfXqNIJAoVpmUCB5nTvBuYKUhUv7OP57lADQACDQERERERERERUAQQaS0u4dQeTeNo8DyLjVImt3+QZ3AnYHnV2h/P9oXUHKw0MAhERERERERFRhSLhVZrHrTtYdeRgTNgcVPrpmRJbpyuo49Gty0dMSAj/haEDh7WCaEuIGAQiIiIiIiIiogpBBBX9kFpWkCn3fImt25XJEygTyLMwtPr+0GoCeX5U/fPgtoM3BoGIiIiIiIiIqMJSgylCV4PHu/5Occsw6wIvnhlIAQMyzm5qJdCG4mIQiIiIiIiIiIjKPf2Q6VJ6F44WumCLPuvmEfNCJEUOg8hJK976fQRxvLuDeQZ9ijZEvPFSi4dBICIiIiIiIiKqAITfsInw8fgZyzwAgOn88WKu339haJ/dt6RuiPgSiOT43wr+BRUEEkIMEELsE0IcFEKM9zHP3UKI3UKIXUKIn4rcIiIiIiIiIiIiL4EiKK4gjdBl3aTI6soDu61Yaw80Olig1pmEZ02gogVzPDOgQmEJNIMQwgzgMwD9ACQD2CyE+ENKuVs3T3MALwHoLqU8L4SoW+QWERERERERERH5ISENRgfTB4FcbGrow24t1jpdNYeCK+nsmt/hfO7ZHSzwGn0/K5pgMoG6ATgopTwspSwE8DOAQR7zPAbgMynleQCQUp4tgbYREREREREREbn4qcLsGiLevX6PzRn6EMXMBAoUhPE5Xd8dTP9ysYaIL9p7gwkCNQSg7ziX7HxNrwWAFkKIf4UQG4QQAwwbKcTjQoh4IUR8SkpKkRpMRERERERERBc/6ZVxYxz4UGfTB35MbkEgs/LAUdwgkHEmUJWzO9FYnNKtUS0M7XyflglUvIJA5akwtAVAcwC9ANwH4GshRA3PmaSUX0kpY6WUsdHR0SW0aiIiIiIiIiK62AXOxNF3BzMIAhWzO5ivmkCtl7yAlREv+GmP6/3C43lRlHZh6BMALtc9b+R8TS8ZwB9SSquU8giA/VCCQkRERERERERExaYPmRiV5dENIO9WhDlXRirT8zNLpgU+agJ5h2aMh7BXnZS1i9iKoucEBRME2gyguRCiiRAiHMC9AP7wmGcelCwgCCHqQOkedrjIrSIiIiIiIiIi8qAGWiTcYzFSuo++daNpi/Y4DVUBAOazB4u5boPgi8PuaoNHKz2DQp6ZP2q7fK5PGBeGNp/cjXAU+m+sDwGDQFJKG4BnACwGsAfAHCnlLiHEm0KI252zLQaQKoTYDWAFgDFSytQitYiIiIiIiIiIqIiEBN4M+971XK3Rk1e8TCCTUSaQLgjkzbM7mMPHfCG2I+UQBhQsLdJ7Aw4RDwBSyoUAFnq89prusQTwvPM/IiIiIiIiIqJi8ez25KsSjoRnlo6vbljFK61suH7pMJguPZ4rPDOBQi0U7Tm2WFGUVGFoIiIiIiIiIqJSI4RwGyHeLQzio04PUPQCzF7r14I7Hv3QjNrjyW7zKgxd1PLOAoBdLXYdIgaBiIiIiIiIiKjc8x4y3sU9uOI9KpdzAcVav9EQ8dLPsPNu7bDlQ3h0ByvqkPESgINBICIiIiIiIiK6FKkZQg5plF9TtO5gBTaJ5HRXkMcoaPPM7DTddO9Hqh83ZIackeS5FJuu/JBNBFXdx0vR3kVEREREREREVIqMMn/UwMiCnfnIt3rXAXJAeAVbXJlAoa3/pfnpWLK3AFVbq+v2DibtSC4AIn0twTXfV2uzcaVwb0ComUD6z2s3yumREhD+O5kxCERERERERERE5Z5+yPQdJ63YcdLqmuYMqEiDLBxTETOB1h5yH4ZdW7IuOKUPOIVLdX7vwtAC3qODhVwTSBdEchgGgRyA8N9NjN3BiIiIiIiIiKjc8zk6mHRNcxjMZVTLJxiemUhGmUD6wM6fWcM95nd/r/AqDF20mkACMM748TtcvYJBICIiIiIiIiIq9yR893YqjUwgn8uRBq8Zck0ThvMWvTC0Z1YRAIj8zIDvZRCIiIiIiIiIiCo0NWvHKAiEItYE8mScCWS0UKH7v+u9nvPGmA6jCnL9rM/9s5h0ETCTNAgC5Zz3uSxXe4mIiIiIiIiIyhkZRNTmSnEaq01Poq7jHADj7mAllQlk1K3MLDyCMTb3OkIuEibPeQG0EseK1JZQRxpzvY+IiIiIiIiIqJwzyvEZbl6KaJGOXrZ1AIwLJht1nSq5NnkUey7Mg6swdODRwIwzl3xw64Zm9JkCB4YYBCIiIiIiIiKick94dJBqLpIRDmWEMBuUUbF8d87yNTV4rsCLLhPIMxhjdXXv8h4dTHoFgkIKAgnXP52s24J/nw6HiCciIiIiIiKick/fPayRSMGSiLHac7sWBDLqDuYM1IQ4Opgn1xDx+mV7ZPsU5vl4ryx2RpK6fgmge+GGIi2DmUBEREREREREVKGEweb23CGU8IZRdzALAg+dHoxAQ8Qrk/TP9aODeReGVuYIIROoBDATiIiIiIiIiIjKHcPC0D5iJjZneMOoMPR15t3OBRpnAoUl/gmjrmKerxh1K/MK7EipzanvKiYQek0gIYTHc9fj06a6uMxx1mDd/jETiIiIiIiIiIjKPX1FIM8MHFeOjjLPAns3AECyrGMwl7vIpR8jcunUgOvXRvfSLcarJhCkNoPFLQhk3B3MKGjliz7Gk2aqFfT79BgEIiIiIiIiIqLyT7jCQJ4ZOGrwR/3XMLRilCkTQp0gs0FhaH9DtXt2QzMZ5P0UpTuYUmS6aKODsTsYEREREREREZV/UqJB7kFEI8ogA8c9CKROD1iMWfqe7hkfika61wTPIeL108y6IJCARAuR7L0O/60zbheMu5YFg5lARERERERERFQhPHnwRSyPeNEruOPQgkAKk0GXLONMoOBH7LrS5KzB43AFd4y7g8G5bl0QSABjwuZ4r76IhaFb2g54v8iaQERERERERERUIfmIaVQVeQY1gZRgijo6mDDIBDLMninCsPHC4RqZzF9haIvQdweT+MnW22tZCyJegWXn38GttwQGEmMQiIiIiIiIiIjKP10UpJ85wW2SGoxxeHQHc6vLY5gJVITh43WZQP5q81g8uoOlo6rh4iL/+TCo1RYhXuWFQSAiIiIiIiIiKvf0iTD/tfzuNi1cFgBwZQSpQaGANYEcwXcHc71HHwQyygRSuAeB3GsE6YkQuqSpyyoqBoGIiIiIiIiIqNzzlwjzRMEMZR6pjg5mUBOohLqDQdcdzCx81wTyDPqE+QgCOSrXDmq10uNf7xlYE4iIiIiIiIiILhGe3cHMAQtD++8OVhW5Xq/pawJ51RnSrSPMozuY55DxWptrXe63DSWJQSAiIiIiIiIiKndkEYZBv0ycB+DqphUhrG5LVKXnOpCR54Dwkz1jggM7Ih/1nmD3XRNI6ApDexaltsAGQ0F2BwvcDSzw9rIEtSYiIiIiIiIiogtIegRoCq2Bgxxq0Mfk1U1LSdJ59c8M9G4Rgf/OTQcAjDb/hufDjJclfNUT0ncH85jn+HkrCmzKa+1NSbpleXZN0y3OIbHjRCEe/jEN/VpHok+LSKw6WIA3b62uzZOaY8fZbP9ZS0fO2fDgnLN+52EQiIiIiIiIiIjKnd2nMt2eL91XgNeCfK/RcPAHz1ox72ge5m3P0157Pmyuz2V4FX12cvgpDP3qnxnYeVkezDXcM3dqIBvRIt0wm+fQ2ULcH5cGAPhzRz7+3JEPAG5BoNu+PIf8yFxE1vedEfTaXxlIk/V8fh6AQSAiIiIiIiIiKocy8qwez4MfRcszQwcArPZQR+EyDgIJ3cte3cEA2CVghnvnrN8jJgIAjhiEYXILA2c4ZeVLhEUqj4szUjxrAhERERERERFRuecrKKM33XYTAOMsnlCHVvc1vLxJSK0AtOd6hAg9RBNwGHsA1ZCD1yzf+50nmO3DIBARERERERERlXvBBDmyEOWc1zuwEsz73ef3R1mWZ8ZRqOsIvB5FK3EM4cJ/TSAAGG/5ye90BoGIiIiIiIiIqNzxDI4Ek2QjPYaI97e8QPxm6Dgzga437Qhxqd6MAlbDzUsgctK053mICGI5Ek9Y/vI7D2sCEREREREREVEFEEyWjTo8u1F3sFAzgfzM7wwCqUPSG73HKOhkFMjynK8OMjApbDocsxYBtZShy/IR7ne5wQoqE0gIMUAIsU8IcVAIMd7PfEOEEFIIEVuMNhERERERERERuQkmiOOQvoNAoZZU9h8EUrJ3dssrfL4n2LV5ZhxZoAxBb8o4ZbgsX8sVAA47LguwrgCEEGYAnwG4GUAbAPcJIdoYzFcVwH8BbAy0TCIiIiIiIiKiUAQVBHLmyRjNG2oGjZCBM4G8CkOHuA4AaGdKcntuFMDyNVx9qPMFkwnUDcBBKeVhKWUhgJ8BDDKY7y0A7wHID6plREREREREREQ+SK+ARuBAiP+aQKFlAhkFVDY4Wru1xXM9ZjgQjfSQ1qO6XJzBWMvPMBsUgA4mCCQgA440FkwQqCGA47rnyc7XXCsSojOAy6WUC/w2SIjHhRDxQoj4lJSUIFZNRERERERERAREoTDgPFKrCeTQuoapilsT6GXrI1hm7+RckZoJ5B50eci8GDeZ40Naj+qDsP/DU5Y/0E4keU0LZhh5wDl8vb/pRWmYnhDCBOAjAC8EmldK+ZWUMlZKGRsdHV3cVRMRERERERHRRUzqAjmRIQSBBCTsHiGPkLuDeQSBHBBadzO1JpBnJtCV4ozf9flrQ4FUikBHi3S/bfG1DGHQZk/BBIFOALhc97yR8zVVVQDtAKwUQiQBuAbAHywOTURERERERETF4R78CL4mUFPTaYR5dKtS3i8REUQwCfDugiWdYRbliXF3sALdKF6h5R0BqagGAIgWGX7b4m+5JVETaDOA5kKIJkKIcAD3AvhDW7mUGVLKOlLKxlLKxgA2ALhdSlm0/CciIiIiIiIiIoQeBJJ+cm2uMp3ESPMi7IscgerIDrgszy5YbplAMO4OZitGh6t0WQUAUAtZAdtiRIgSqAkkpbQBeAbAYgB7AMyRUu4SQrwphLg9YCuIiIiIiIiIiIopuCCQf49blFLGLURyyOuTEHCoYRRndzDPzBtLkLV7jKjd18woWmHoYOYLKkQlpVwopWwhpWwmpZzsfO01KeUfBvP2YhYQEREREREREZUkX0Egm3SFNhw+whxnZA0AQK6MAADUEpkhr68S8rVXhK47WIqshnsKXnU+9w7gBMeVw2QUyAkmAFZSo4MREREREREREV1wwsdjPTvM2mNfoRL1vWqQKBy2gOv2DMZEiwxdkMnVHcwBE3KhBJcsuiBQqIWhVWbhHcjRB3f8LaNEMoGIiIiIiIiIiMqSmn3jyaoLAvkKkeQ4M4BUATNmzhxArGmf22s1keXK19FlAtl1oRfPQtHBClT7KPjuYMwEIiIiIiIiIqIKTg2OzLT1cXtdPxS8e0DIZaptiNsy/NbukRKVf/wPPrB84fZyDZHjCgI5lIwfs1AygaSzDRbdiGShjA6mD10ZBZJMIrjRwUpiiHgiIiIiIiIiogvMPaChBjg8Az023fPTspbhknIRCUAZIQwAzMJ37Z6oea8Yvr7M3gl9TQkAgPCEuQCUzBu7LNlMIKNlBFMTSGkPg0BEREREREREVMGpgRC7nyBQjjPY48nh0U3MXyaQ5fAGw9f/dFyL+iJVaUuGEkwyQcIBoWUI1Rdp/j6CT+5BIKPRwYIYIh6SQSAiIiIiIiIiqpjcCkM74xs2j1CGFRbtsa/RwewerytBlVA6bCnjd7naozwyQ+0O5l2LKJTC0PrXjQJUJreaQb4FChZZ/E4lIiIiIiIiIioHHA7jTCC7NGmREaNgjPK6exDIAjsiYAUAzLD1Q2vTUQD5AdugBllScyWyM+1Kd7Cgyzb7ps8EshiMXBbMGpR8JGYCEREREREREVFF4xHPEc6h0z0zgfRdvRzSOAgUiUK352bYtdcOy/ookGEBmyMhtGBMwnErRv6YphsdzHu9oRWGlohwtseoJlA9XTczf8tldzAiIiIiIiIiqnikcWFom3Tv1KTvPuVZ+0e3MK/31BPnAQB5iEABwgM3B8DnttsBADsdTXE2S8kE8tUdLFTDLcsAABHC6jXt/bCvA76/EgoQ5qfgNcAgEBERERERERFVAGqY5Ryqu72uH+lLXxPobet92mPPDJkHLEvwT8Q4AECeDEcBgssEWuPoAADIQhQEoGUC+RqavijCDbqDLbfHeL3mmfWkBrX8YRCIiIiIiIiIiMolfZhDDeRscLR2m0efCaTPyNEXjPasldNInNMe5yECLcXxoFqjBnsssKMr9sACOxwwIUlehmwZ6TG3EePuWnWQoT0OMwgCpcgaAZYb3PD0DAIRERERERERUTkkPJ4pARTPrBt9IWW3+kC6kIe/Wjl5iEAz06mgWqQOR3+jaSt+sLyFG8w7nOsUOCNrBrUMI/9G/ld7bBQEMir47PkKg0BEREREREREVCFVsqa5PVcDIXbpMTqYLrTh67HfIJAMx2p7+6DapGYXNRIpXuvxHJ6+qCOGtTQle71mEq6lqYEuzzpEgYaHV+YhIiIiIiIiIipnIq3uNW60wtAemUD64d/1gRG7W8jDfybQX45rgmqTuu4rxFntNYcWBCp+cWhf9JlAvj6JBf6LQgMMAhERERERERFROeQQ7qOAaZlAHqEMexBBoEDdwaweI475oi7TIlxZN3ZpHAQyCgkVPUykbz8zgYiIiIiIiIjoIuIQ7hk/Jh81gXx1AdMHSYxq6qjyZLhXdpFv3mGc68y7nesrvRCLURCLNYGIiIiIiIiI6KKkhl/snkEg6Qpt6Ovy6F/3lwmUiwgUIrhMIH8uVHcwX5/FLBgEIiIiIiIiIqIKyDOk4qsmkHv2j4t+vvOo4nM9+YgIIRPIN88gkNoWmyx+6MVoyewORkREREREREQXCfeMF19BIIfPmkCu+ZY7OvlcSyEs2qhfxeEZlFFdU/AZehZ8VKxlBxPgCaY7WPE/JRERERERERFRiXMPq5hCLAx9XEYDAJbYO8N/SWZRrCDQX/ZrnOv2XCqwydES51Ad52R17bWiEIaP3ZdmDmJQegaBiIiIiIiIiKjcq4pc5yP34Ie/TKDG+T8FtWyrLHp3MM9C1aotjqvwRuFov++1SZPbSGO+CB9ZPn0KpuBq0168HfYtu4MRERERERERUcXkOaJXa9Mxw/l81QQq8Mh7edpPQMZWjBwZmxZAcg9OpcpqyEWkz/d1yf8Ck23DglqH8XDzDhySDbHT0RgAu4MRERERERER0UVC+uhLZYPx6GCeXbwWOK7ByYLaGGpehfsty92mFac7mK9aQIE6Z6WiulfXNl/0ATH1kWfQh5lARERERERERFQxSfcwSqasbDibw9foYAZdvLbK5shClPZ8ovUhACjWEPGeGUv6KYH4CiB5MhoW3izcRwmzwB7EcoiIiIiIiIiIyh0JoYt9ZMpKSHA095rLV00gX8O+JzhaaI8X2q/2O28oPAM6RgGeoheGlrrHxtgdjIiIiIiIiIgqJM9gh4B0G/ZdZZXGoQ2Hj7wXdaQuwBWoMSru/EThs84uVvP8t7OokR0Enwnk3h3MM9ikCBe2gMthEIiIiIiIiIiIyj0TpGFgJx9h2mN9sMRXFy+7Ww0hZxDIIJCU4GiOyiI/6PZ5dtgKPGC7v65kvufz9Z5wWAMuh93BiIiIiIiIiKgccg92SAE4DKpD5yFCe6yfmoEqhkvVd/2SBq+p7DAbZuqkyqqwSV0XNB9xHEcQWT7BdOEC3D+Xd7BJmRrBIBARERERERERVUSHU7LdnpsgDUfTykO49ljNkjnqqOtzufouZWpmkVF3MF8jd11X8D+0K/hWe/6d/WYAwXft0jMHUcwZAPqYtwacp6k4FXAedgcjIiIiIiIionJHSukM6ijBFZM07g5WKL27g/nLwrEZjCZmhcUrQGKHyTCwU+AMOt1c8A7SZFWcQS0AQJas5DGnd1uFRxpPsJlAbsvw8Upz04mA7w0qE0gIMUAIsU8IcVAIMd5g+vNCiN1CiO1CiGVCiCuDWS6VLSklPvxnH46n5ZZ1U4iIiIiIiIj8Ej4ygfSBITVA4i8rx+7WHUx5r80gR8ZuODC7yx55pRYAAoCdsrHb9GCq/ViKEAQqjoBBICGEGcBnAG4G0AbAfUKINh6zbQUQK6XsAGAugPdLuqFU8g6lZON/yw/iiR8TyropRERERERERG48CyD7DgIJt3kA/0Eg40yg4GsC+ZIvw92eBxMECrY7mF6SvCzk9aiCyQTqBuCglPKwlLIQwM8ABrmtUMoVUko1nWQDgEYhtIHKiMO5pxTaLmzkkYiIiIiIiCggj75TQhh3B3ObJ4iQiF161wQy6mSlBJyCDwJ5D90eRGFooVyPJ8s6Qa9HXwMpVMEEgRoCOK57nux8zZdHAPxtNEEI8bgQIl4IEZ+SkhJ8K4mIiIiIiIjokiZgXKxZH/g5KuthuT0Gz1uf9Lkcm1thaH/dxkw+R/4ykoHKbs+DywRSgkDr7G2DXo9noCuUbKUSLQwthBgOIBZAT6PpUsqvAHwFALGxsaFkLBERERERERHRJUTAPQ+nNjJxi/k4PEdC189jgwUPW8f6Xa4+WOM/gCJCCrD8bO+NCFhxQm4AUAjfJZxd1CBQYSjhmWJEU4LJBDoB4HLd80bO19wIIfoCeAXA7VLKgqI3iS4UNaIpQh/FjoiIiIiIiKhUGV2q+hv6PVgFCMdk6/1Il5VhDRB8CSUIZIMF39pvgcOZaRRUdzBnTaBChAWY093r1gfxQOH4kNsYTKhpM4DmQogmUII/9wK4Xz+DEKITgP8DMEBKeTbotRMRERERERERGfJOeZlp7+P1WjB1gDx9bb8VX9tvLUILAgvlPa5MoNCCQHH2ASHNrwqYCSSltAF4BsBiAHsAzJFS7hJCvCmEuN052xQAVQD8IoTYJoT4o0itISqn5mw+jhV7Gd8kIiIiIm8z1ifhmzWHy7oZl5QfNhzF16u5zS+kDxbvw/xtXp2CSplH7RvhGsr9qvwZmGAdeQFaUPSuM8EMwaQGgc7KGphmG4RhhS8FfpNHk8whDDMfVKczKeVCAAs9XntN97hv0GukckMWpyPhJWbsr9sBAEnvDizjlhARERFRefPa/F0AgEd7NC3jllw6Xp23EwDw2A3c5hfKtBUHAQCDYvyNE1X61KHcbbAEHCmsJBQnCBTMyGK1RBYAIBOV8J3tZlRHdshr0Q8zf1fBawBe9Dlv6W8xonJESolh32zA0t1nyropREREl4T3F+3FR//sK+tmEBFRBeRZGFpIoIk4rT2XBo9KWnG6gwUTQJpmuwPbHM3wjz0WgO8C0RsdrbDE3tmwUWom0B7H5YiXrfyuj0GgS5goVkSzYnJI4N+DqXjsh/iybgoREdEl4fOVh/Dp8oNl3QwiIqqAjGr9VBeuTBk1yFL+rmyDb9EB2Qh3FL6FTOeIZfraQN/ZXHV/Hi4cgwIfdYNMziBQLiIDro9BoArsj8STyC20lXUzKhTpHBJNsidcuffDhqPYdzqrrJtBRERERETlyCFHA+3xDkcTAMBqRweMsT6OuwteLYU1Fj3EVJTLTruzuxsAfGC7W3ucgyifLVIzgWy69/oSwkD0VJ5sPXYeo2dtxdAujTBlaMciLUOtCXQpZQQx9lNxqP28WYeJiIiIiIgApTD0l/bbtee7ZBO0yf8uqAyYIq+zCNfLoXQH88cOk2FYR3oWhhZKEMghA+f5MBOogsrKVzKATmXkl3FLys7R1BycysgL6T0OpgAREVEpyyu0IyPPWtbNICIiqvA8u4PZpNmrGHRpBYBSZHUAQB7Ci/BuJUpT3KvPYDJ7AH0mUOAQDzOBKih1ZxKXThKPl55TVgIILVOEMSAiIiptvT9YidOZ+cxkJCIiKibPIJDjAvViua/wFa3bWQ6iULXIS3Jvb9+C91E7LBnAvKDebfcR1BEe17UW5+hgwYyWxkwguqQDSWXp4NkspGYXlHUzAsopsMHhYPSMiC4OeYV22OyOUl3H6cxLN0uXiKg8yi5gHdWKyuQRBIrAhflbrne0xVnULPL7fV09HZSNcFxGB7WMU7IWvKv/GF+8q4WhfQWN3OelCkmWYErLpZQdU566g/X9aDX6fLSqrJvhV9fJS9F24mK88/eesm4KEVGJaP3aIjz+Q0JZN6Ncaf/6YvT/uHz/HlHJO3AmC53fWoIzDFrSRW7PqUy0m7gY87edKOumUBGo3ZwqKuOQTeAsjK75n6F/wftBr8esBYECdx9jEKiCcnUHYxpPKMpRDAgAkJ5bvmtGpGQpmUq/bbmwP5olGeQkIvK0fO/Zsm5CuZKVb8P+M9mBZ6SLyvR1SUjLKcQ/u8+UdVOIStXuk5kAgFX7Usq4JVQUJmc3J5VnQeTyylUQ2vu6JphLnRTURBYq+V6+x3ZY52iLrY6r8J7tnoDLZhCoonLuOEX5Doz5JRGNxy8o0eaUR3tOZaLx+AV4OG4zGo9fgMkLdrtlAn2x8hAaj1+A52ZvK7tGVhAXOoOKMaDS9c7fe/Dfn7d6vd7/41V46LtNZdCiS1fj8Qvw9kJm2lHZWLD9FAZMXV3WzSgR7V9fjEGf/VumbZi16Rhe+m2H22ud31qCb9ceAQAkncvB1W8vxcn00Aa1KIrh32zEN2sOAwBW7DuLkdM3ed1gUZ+m5xSi8fgFWLjjVKm3q7SNmrX1kjjHpdDwtLJiU0e9upgUd8QwIzmIwp2Fb+KgbBRwXgaBKriiJAL9kpBc7GVUBL9tUT6nesf36zVH3H4E3lu0FwDw+1amhgZyoX88y1O3vYvR/606jPnbTnq9vv9MNlbt512yC+2r1YfLugl0iXrxl0TsPZ1V1s0oEVn5NiQeTy/TNrz02w7M2nTM7bW0nEK89dduAEDcuiScySy4IMGWtQfPYdICJcD8cNxmrNiXArtXfT/l+cEUJQss7t+kUm9Xafsz0fu37UIJgw3/Mf8JZDGzqty6SK95LnZmj1LQW+zNy6wtReFZ2BoAZAmEYUQxrpcYBKqAxs5NxJerDhV7ORf7dbZRV7mL4TP/uOEodp3MCOk96w6dw4z1SUVep8MhkXD0PL6+QBer5e3PtGT3GSSdyynrZlx0Zm48isdnxJd1M9wcT8vFop2ny7oZVE5JKfHNmsNIyym84OsusNkxcvom7D2dqb32Z+JJdJu8NOhC1wu2n8IJXRZK9aiwEm+nLz1M2wFb8QdD+GbN4VL7jk7/9wg2Hk4Nat7zOYV4fvY25IRQbDYzX+kCXi3Adj+dkY8Xf0lEgc3uc55TGXlu8/y08Rh2nvA+NziamqOd+2xOOu82TRYjq7ykHDiThQnzdlwUA1D0MG3HS2GzgPXTyroplxCJ1uJowBN8NQvuty0ncDilYnR9XbbnDOZ63LgvDxrgHJ63zAGspVdLLN9qx4PfbcKBM8pNCjMcbpkzhbhwv13FobbZ6BhbnCNeSRwtGQSqgObEJ2PjkTQAxfvhvtizLYwynC6GWjMT5u3EwE/XhvSe+7/eiNfm7yryOiWAIV+sw+QL1G2lvO2bj82IR68PVpZ1My46r/y+s9zVohgwdTWe+JFFg8lYYnIGJi3Yg7FzEy/4unckZ2DFvhS8rOtu9Or8nTibVYDM/OACEU//tAWDP3d1mYoIuzCngdeaduGH8HeBtR8Xe1mTFuwpte/oG3/uxj1fbQhq3k+WHcBvW09gTvxxn/N4nnNY7crzCIv/7f76H7swNyEZy/b4rl316rydmJuQrNU4efn3Hbj1f97nBv/RFUG/72v3z6YFgcowJfyxGfH4ccMxJKVeRDdaTmwp6xZcMrqI/fg74iVg3f/8zqf/Jo6a5d0dvjx65Pt4vPjLhf+tCeQ283qMtswDtv5QauvYnJSG1ftT8MafShZlONxrqBpl1pRLfppZ1p/gog4CbU9Ox7liDsGdcPQ8jqfl+px+KiMPy/YEfxGzYPupIlWml1JibkIy8q3ud4WK88Nt1B1EVWhz4Lu1R7zuLh5OycaOZO87TWez8rF4l3JnLi2nEA98uxFHS+EHXUqJ/1t1yO0u7MGz2Vh36Bx2JGdohYzXHEjBrhOZBu/3vewF209hta4rzMp9Z7Hu4DnDeVfsPYvk8679Ij23EMO/2YgfNhyFlBJz4o+j0OZAwtHzWH8ouLuKJWHp7jPYnJRWpPcW2Oz4bMVB7e/mlm10gY9U5SwGRE5HU3Ow5kDxuovZHRLT/z3idYd72/F0LNpZtC4SNrsDb/y5y22Em6OpOZi58WjIy8op9H3n3ciC7adwvoSzQv5MPKn97pzKyMOmI0X7TlcUof6OlqUC529wRl7pFPW32h2Y/u8RWA0ye4x+7rWSk0EcNNVMizOZvs+LFmw/VaSMjHyrXTsHAJS/6Z5Trt/g6lB+VwqPxfvsCjVv6wm3LKdQ1+/Psj1ncCqjZOvwqF2rLCbf52H+NuWeU5lYvtd4v1f/1p8sPeDV7jmbj+OJHxKQcPS8c17/54FG+5JKOn/cL4ayAHM2H9fOActKmLN4baHNjm/WHL4objyqVu1PKZc1o6oL57XG/kWG05fsPoNxc7ej0Ob6HhRnfz+elluiI4yl5xZiy7HzgWcsR6KE83uWc+HKB0SKwlKpoXPhGB0LSuDzFGMRluKvvfy6fdq/uKxaJDa83KfIyxjyxToAQNK7Aw2n3/nZOpzOzPc53dPTPyl3BwbFNAypHasPnMOLvyQapvoWlb86FF+vOYwpi/chzGLCA9dcqb1+44fKELKen/eBbzZh35ks7H1rAMb8kog1B86h55SVQW+XYMUfPY93/t7rdsDsqxtmvXblcCS82g8PfGtc3Nbfz7H6t1HbPGL6ZrfneiPjNqNKhAU737gJADBl8T6sPXgOaw+eQ42oMIydux3Jabn4dPlBn8soDY86u9YUZX0fLdmP/1ul/N2T3h3olm3EwtAEAD2nrARQvP15TvxxvPHnbmR5ZC7c4SzoWpRlrz+ciun/JuFYai6+HdEVAHDvVxtwKiMfQzo3QmRY4KEyi+JMZj6e/mkLrm1aG7Mev6bEljtq1lbUqBSGba/1R98PVyGn0H7BjiFl4bb//Ytz2QUV6jOKUjoZ/XHDUbzx525Y7Q48fkMzw3n0h0c1ABDMIdPoOG7yuBp6+qcteOP2tnjousZBtlgxecEe/LDhKH576jp0vqImrn1nOQDX91kdtnbniXQ8tXsLNr3cB3WrRbot41nnIA1F2Q8CdZF/5Pt41KsWgY0v9w152b7YHMpnMpt830/199t58ydrABh/XvXPsu9MFp75aSt+ffI6bdrYX7e7zxugnf6CRGrzTNp+dOF/fEsiC+lsVj7G/rodHRpVL4EWFV0YlN+1QylZmHRoD3q2iEbzelXLtE0lRR00orwdp9Vt7stjzvPiFftcWXXFOX7f8dm/SM0pDPk6zpd7v9qAvaezyt129cchncc8R2g3zYpCPSZVQy4cCIP6a1dRMoG00bz9TCsrF1Um0Mp9Z3E6w71/4unMfPy44SjSc73v1P6ZeFK761Rgs2uZHXtOZSIz3xpU3ZXTzjvPUkrsPJGBOfHH8e/Bc1rE+XxOoeG6k87lQEqJE+l5+GfXaa1PudXuwKYjaThwJgtbj53X2pTpvOvoWXBQQLnj7V3sz5jRXYn0XCsSj6fjyLkcrR1qpk1+oR1pOYXIyPW/PY6mKZF4h5RB3yGNT0rDCmfRZpvdgS3HzuPXhGQccdZeOZ6Wi0Mp2Ug4eh6Z+Vb8e/Ac3nSmBR5KMc4ySs0pxBcrfZ8MLvVxt/lspsd+k2Hcz/VsZr52lzRbVwdAf8dz3SEle+icLjtA/Qxns/KxIzkj4F1LX7Lyvbdtoc2BOfHHg7qTkFvo+8dS/5n1nwfwfzfT7pBe8wPAxsOpyCu0IyPPiu3J6W53YXxJPp+LE+l5fk9Es/KtSDjqnhmx62SGtt8EknQux+1vVxzpuYUlngVSHMfTcv3WBrHaHdh/JnAR2IU7Tmm1K0patjP44+s44VlfI7vAFjC7TT3+ncrIx8Idp5BTYNOOmYVB1kopCnWf1tdYsTskzmYp36UdyRkhZ6Oqx+j0XKX9RplJ+VY7Dp4tXjHfs5n5iE9Kw5Zj54M6Zp/Nyg/6dwZQ9rVtQRbp9bWNfB2H45PS3L7Du05meO03J9LzkHD0vN/aPZn5Vhw8G7g2xJZj53EqI8/nb6DRMcnTxsOp+CPxpNdxcMW+s25tyMxTPke2Yfcu79NI9ZVg/jZGsxgdN/X1dhbtPG148ynfanfLcj2a5n6uorLaHVi087R2oVZgdf5rc8Dh47cDUDJ3QvmdzPORwZeSVaBl+PrLgPIl32r32Q6bs2vXyn3GXbYy861uharTcgqxwVlvaOaGY17zn83K185F9BepOQU25BbafN4E9IyhHEvNdfvuGF18JJ/Pxcn0PKQ7/16BLomPnMtBbqENqdkFmJuQ7LYfSykRn5SmHbuW7g7tb6eKP3o+5Cw0KSVmbjyKI85zwiO6c8OdJzJwNDUHhwzqv+Rb7dq5+V/bT/o8Jyi0OdwywqWUfusDWpyZQA7n7476+2OzO7DvAhVgP5dd4Jb9ZXQszi6wISvfioxcq+E5gcMhtaxwKWXIdSh9CfY8LTPfimOpvnth6EWoQSDh/5L2rC5LrDhxx1Tnb0pOga1EaguphflDyRrbdzrLb4afEavdgcW7TkNKiZPpeUW+DgEAuxo+kL6XseaAUSH6ojPB4RY1qcg5QS4lEIYpxia+qDKBRkzfbHinZ8K8nZgwb6dblHXF3rNan9Ckdwdi7NztmL/tJPa+NUC7OxMKm0O69cVudVlVLHr2BnR6a4m2Dr1eH6zEG7e3xcQ/lDotN7e7DF8M74IPFu/D/3lk6CS9O1D7Gxd4nEAeS8tFzykrMerGq/BC/5YB27lyn3fq3unMfG1Y1W5NamHOf67VLiQtZoHOzs/gj3rCYnMEdx/pbGY+7vpyPQAgcWJ/fLnqkFvwJundgejx/gqf7/d34q6O+mVk7Nzthq93e3uZ2/Nr3lnmc74xN3lv5y3H0rXHszYp9QH0GeJqRpnqzk5Fu4Nw1xfrvV77bMVBfLLsQFDvf/LHLfj+4W6G0/QHa8/vgL+7mVOX7sf/lh/EP8/dgBbOO17H03Jxz1cbcEdMA6w/nIozmQXaPu7P9e8pf3M1w8rI0z9txer9Kdj+en9Ui1QKw6lZS8HcSen1wUp0bFQd85+5PuC8gcS8afz9LgspWQXo8f4KjLiuMV6/va3hPG8v3IPpQYz+8tTMLejfph6+ejC2hFsZ+OTriR8T8MMjV2vPn5+9Df/sPoP4CX1Rp0qE3/fuPpWJp2ZuQecraiDcYkJOoXIBp+4nJU39WuiPelMW78OXqw5h8yt9cdu0tahbNQKbXjHOPjA66QvmnOn5OduwcMdp7H7zJlQKL9rP+IBP1mgBkk5X1MDvT3X3Oe/ZrHx0m7wMT/ZqhnEDWgW1/Hf/3otv1x5xOy4EIqXUsgKW7TmDR76Px/SRXdG7ZV1tnvM5hbjry/Xo06ouvh3RFQU2OwZ+uhY9mtdx22+6v7tce+zr+9nh9X8AKL9Bvgokb09Ox+DPXcfvnw0yvp74MQH/HkzFrjduQuUI77/H0dQcrc7Mf25oipduaa1NG+mRcepwFWnxWo76kn63UV8L5oIg2IzO9YdTse7gOeTb7FrtHc9t+Pofu/Dz5uNY+vwNuKqu77/v/5YfxKfLDmCoWblQ03+qL1cfwvuL9mHe090Rc3kN7fXtyel45Pt4DLv6Cky+s31QbfZl8Bf/4nha0buBXf32MmTkWQ33IfU385/dZxCflIbYxrXcpt/31QbsOukKct3/9Qatu9Img8B2t8nKeUfSuwO9LtBGz9qKpXvOYpfBb6NnNtcNU1b4nQ64fmtV/o7LUkr0/mAlul9VG4fO5uB0Zj42Hk7FlKEdAQB/bT+FUbO2YspdHdCsbhU8OiMeD117Jd4Y1M73QvXrdv47du52nM8pxH96GmfAGZmbkIxXft+pPc/SBXP05+QHJt+MMLPrguvu/1uP7ckZ+Pu/PfDMT1txW8cG+N99nbyW//bCPYhbl4S/Rl2Pdg2r47t/k/DWX7vx5zPXo71B1lGYcO7nQtk31K/cFOe5/fIXeqJpdJWgP1+o8q12xE5airtjG+H9u5S/zzsL9+K7f49gyXM3aFlJHV5fDIcEmtapjMPncrz27y9WHcKUxfvwz3M3YL8zG6245m87gf/+vA1xI7uil+6YbmTw5+tw8Gx2UOdWTYSzi1qAIFBJe+LHBKw5cA4HJ98Mi7n467Y7JCzmwKGNpHM5uGnqajzWowleGdgm6OVPW65cK3w3IhYPx8XjxlZ18Z0zczpUamanr0yg1ftT8OB3m/BCvxYY1adoo3h5Zmt5bpmKkwnkuzB0WecClXkmkP6udW6hTTspziu0a3cEzucU4mR6nt8RGNT3ncks8Bt5dDgkHA6J5HT3k4KlzuKkviKjec6MGJtduXvluY7zHtk+nkOuGt1p1d/dVoMau33cFfMVIVbvcKxz3pHLLrC5bTsAbv3JtxvU89FTa0/kW5W/S1gQBzYppXZyqd4Z8+XIuRzkW+04oAviWO0OLSNIv8zywrM//iqPQJpRdg4AnM/1fXdd7csPKAd+db886dwvM/OtSM8tRIHNjpwCm3bHap/ujo3V7kBOgQ1rfdQtApTvl36f/tfjjlZaTqGWHeQvY8Ez+KhKyynUhmM9dDYbx9NykVto0wo87j2dpd19/TuE0Vz0f/98q92t/pJ6N9Tqo00ZuVak+vgs6t2+RN33IKfAhuwCm/adScspLNLIPwU2O7ILbLA7JE5l5Bnuw0dTSy4LyZN6jFntp2ZPvMfIMP6cSM9DWk5hwLtF6h0lf1lm+Va79j1RjxW+vuIbPerf7HFmaxod/212B05l5HlljGw5lq4duzJyrcjKt2rHRkDZVur+LqXreK7/PXI4pJbllV1g8ztKT16hXfuuLdmt7Ofqb8JZjxoV+n1L/zOSlW91a4snq92BQpvyeRfvUn6vPOfNyLW6vWbX3c31pG+H511iKaW2LWx2B85lKfN6Hqd9sTuk9j0NpUaHQ0Lb5mqbNh9Jc9u38pz7o/pbqf7meO43RvTnGHoZuVafGXRnfWSPnMtxvb79uPJZbQ5puBz97//uU5nIt9q9Mh7OO88vjFLHC20Ot98Zoz3E7pDIKbDhdEY+bHaH1g79d9MzCOQvi3H7iQwcOOP6nT54Nttt39rqvPGR4cxcsjuMt59a20qtlWKCaz51H9Ef35VlKp915b6U4M8FfFw7GQWAsvKtXt9nKaXbXX31N0Rti3rel5JVoGXB2HTb4/h576wFfQAI8D4v9CUr34pcXWZTWk4hljoLRJ/JNMiOC3Dd6BngMfp9U9eXU+Ba7/G0XBxLzdWOU/8eTNWy35fuOYPMfCvyrXYt2+loai6Szyvb+5hHLU31GGq1O7R9wiiLYu/pLOQVKvNlOM+hbHaHth/oj8UZeVafWeGe1O+HSj0XVo8nC3ec0vZv/XH4gDPjMj3XihPpeVrWl9HfGwAaQDkXb2xLAuD6zqnn++p1hOp8TqF2vFV/a/39DqjfZf05ht0hcTwtFxm5Vi3zaOGO09oy1O+Zer5ntTu0v+lhH5k58c72njifh0Nni17fU/9Z1WO653XOCY+slHPZBV43erMLbNr+4Om5sF8BKDdjHA7pMytQL5gsknyr3W9m9ZoDyvl0gc3hdd0FwOs19TfcF7vHsc7XOVWK89i05Vg68q12v9e8uYU2bTlqxrL6m7Zc93uuHv98LUs9ZqifyeIMdiI/3ftzOKR2nDjicf7heU0SCs+gT5K8rEjLKStGQatMVC6DlriUaSbQnlOZuPmTNfjmwVh0vLwGuk5eipduboXHb2iK1q8twn3drsA7g9tr2TQAvKLopzLytL7nqjf/3OXzDsSgz/7FjhMZeP029+iput+rwQ9P17yj3A0a0PYy5BTasObAObcItXoHR6/x+AXa445v/IPvRrjfVdd/2dQfCvWg4snXeZC6CPXHoN3ExQCg3dVYfygV9329AZ/e1wmdLq+Bj5fuN16Qzh+JJzHbOdpFmJ+odGa+FR1e/wfXX1VHCxLYHA6fJ21bj53HnZ+v83pdSu+To5kbvVOly4rn/uV5B6+9826ypwXbfRfQ058gvTBnG/7eeVrbhtNHdtXuDgNA3aoROJvlXS9j7Nzt+H2rcXG642m5uLxWJQz9v/XayTrgHtSbufEYJsxT7qDd0CIaGw4HV3xWf7denyX25MySGw1D/zvU6lWl2J/n3RZfP3sd31T+HkZ3kNTvh2pzUhqGfunKrvrjme64fZp7bZpgL0IGTfvX8CRf346eU1aiXcNq+GtUD5/LsdodaP7K33i+XwuMDuEOilGWAKBkxn2x8hCOvHNLyCnQnd9agi5X1nSrRwEoI2hl5lkx+c72GBnn2lfVz3osNRc3TFmBuU9ci9jGtbS/4aJne+Dthb4z9ZT2u38Ai7PehtUgwHzf1xu8hjxWqft6v49Xu72e9O5AdH93ObILbEh6dyBG/7wNfyaexNZX+7n91nyz9jDeXrgXq8f0xg1TVvjNHjuXXYirXvkbANA0WvlRN6oVu2jnKTzx4xb88sS16Nq4lttvQPvX/8GL/Vvg0R5NDdfR470V2omVSn/dnW+1o+Ob/+CBa67EW3cov3+fLN2PT5cfxMoXe6FxHdfJhufFl+c+8/Ua5bP/3wNd8J8fErTlBVu7o9nLC7XHj8+Ix643BwT1vrh1yl32ZS/01E7SP195CJ+vPOSVKaN1g3I+L7Q5kJpdgNo+ssVSsgrQdfJSjL/ZO5Pphikr0P2q2pj5aOC6Tuq2OpySA4dDwmRyndot33sGz832HslFv33XHDinfR8mDHRlBHV6awmiq0bgvq6XK59Pt6nv/3oD4o+ex9wnrvVeoHNLLNxx2isL9usHY/HiL4laJov+uKo/PzHy7t/uy1Jr770/pAO6NK7pdkNi5b6z+Peg8QAI6vf5drPy22+G6wJAzVDxvO5Q7wCfSM/DL/HJuNu5TYK1cMcp3NK+vs/uN+1f/wftG1bHn6Nc3+efNx/HS7pR17pMWopPdZkhTXX7tHp+ZdN9AZ+bnYg7OzVyvT+IDGrVN2sOY9IC18ibnucU+kCyWpdRT8B10W7E83trlN39l/N8ZfepTPyReBKjdaMnGWXmns+1apl0qsx8q/Y+s0kg5s1/cFV0Fcx98jqv397P7u+Mp3/agg+HdnS7Iv996wm385q9bw1Aq1cX4cFrr8Sbg9qh3cTF6NioutuNnGDof4NaXVZNe13tnmd3SCzZfQYD2l2Gj5Yo2c173xqgfdWGf7vRbXm+joRqQKISlAtudd9W//11ywnc9eV6/Dv+RpiEcn45dkBLLNl9BluPpSPp3YF46bcd+Hnzca9zmN+2JOP5OYnatpt4WxvcHXs52uq2beLE/gCUoEmzlxfiwOSbtUzVHScygh75TmjfTYkwS9E63izdfQaPzojH3//tgdb1q2m/d+8v2oenel2lLN8h0f3d5ejXph6+dmYex05a6rWsa95epv1me8qREagsCpB4TuCvhXvwzdoj2DdpACIsfmoBGvyWtXjlb9zRqYGWQdXq1UXoeHkNzH+6O1q88jciw0yGozDO2nQMkxbs0fZRQLlp1XbiYjzVqxnGOrNn1d9wX9lN+t/zjYdTff6t1O1oFgKtXl2E/m3q4ZqmtfHmX7vdPvfuk5m45VMlq//nx6/RzkmMush/u/aIdgxSz1Ff/2MX4tYl4dcnr8OQL9bho7s74vk5iXisRxPUVo/jJ7e5LSffakerVxehYY0ow7Y/+N0mrDuUargNrn57KepUicCC0T7Oj4WE8s1TPv9p1DSer5zxl7FkhQX+89uDWkGRlWkmkHpxunTPGS0DYsGOU9oO+vNm70DA/jPuJ69GF11z4pN99iveccJ1x05PPUj6iryqd4MW7TrtM1ATiOf79BcAUvrv0x8ojdvzrWp2htqPd9uxdO0OTSBLdEM2+yt4eNh5B0afieIvE8hXFy6jNPa1RdzGJeFCZyHN23bSLdPG88TVM5NA9befkZSSUpULFH0ACADCdcPS6u/q60dFC6QEu/j6ZrAO9TvrGg2n+KvxzIxJNKhhEuznDfYu706DUev01Duy36zxXbjdiK/fAbWbpd0hQ9pm6jmSPmtNtfd0Fk5m5CMxOd3wveqJ9ezN7kMn60fs89Vx1HN7qyPv2AwyDXwFgAD/QzDrs7HUY+Upj2yipbuV74casDW66DA8Lmsvef9F1Boq6p1Zz/f/tvWEz98BzwAQ4H7nUD2GzNNdQKmBXc/sAc/jgqfftijL+HGDMrraRuffsyjnGqGMtqZm5B5NzfHZP8VzSGv9b86JdN+/ceo2mOcjcO4riOG1ft1+q56rqL8Zi3ca15zz9fv9/fokt+cpWQW6TCDX5493fgeNAqHqZlphUJdm2Z4zbllIJVHg/6dNx7x+y/XdzD3XoT67xqRcYFzpULa/lLogkMc+r//TbzXIUgtE/Rv7q9exw6O+zjaD74SvkT3/do6Q5O98JzWEbNJ3/vYfGA9ECOH3vDTU7+0/u9yzdguCvHOv/8wmIZCea9X2XU/bjiuv+5quUrM6Zqx3jfQYagBIb7dHdpa+hpBan+oH53Ev18+xy1c8/IDD1dVfwOHKLnK+9td25ffm4NlsnHCeky91BoBUP3v8bqr+cWaAqrUt1x1K9eqF4JlpUmhzaMfMQMd9Pf15VngRuzqp1xJqBpDndRfgOobqrzuM+Mug3u5Qug+eTM/Ttp2vG/oqoz9fod2BOfHJbq+p54SFdodhAAiANiqi/u+m1lT8dYtreUa/4Xr633N/I4Kqx1j18uyf3Wfw+UplEBr98X7HiXTtcXxSGszOcymjbCR9zxT1HDVuXRIA13XkMmc24i8JyWggnMebXPd2qgN+qL/Fnl261vkZLflMZoFX9qReRa0BlIIaAICj0n8XyLJQZplAh1Ny3IamVE/wtydnoOUEJWIvpffdqid+TEC42YT9k28GYNzXOc9q9xp5BgDGznXdodPfddGvw+guiy8PeNwZCMTz3OUf3UHv8Lkct7unevd/vcHvFwdQDrLfO7+wqru+WKf9wFrMIugCXepFEeA7E8jXXUS7R00gdb6lz9+AMT7q8Vz37nKv1xbtCr7rUEnzvGPlT6C7qUXheQfW17r8/ch9+M9+PHDce4Q0fSbQsiC7dnjytZ+WJDWbR6/A5tDu5gFA18nK3SL9HYV3Frq+1x/+sw//W34QSe8OxF/bT2qBCdU9/7feqwuJft/tOWUFBrav73ZXUv0bjB3QUruTpX/dSOPxC/D+XR1wd6zrbnaLCX+j0ObA6BuvQmpOIWZuPIb2Datjx4kMfPWAUjdJG/VHSjR5Sdnm8RP6Yvg3ynFHDTqpd6XVkXWOnMtBt8lLkWe149m+LbR1qpkqnm1bOLqHdrfIF7W9nqYuda9FpW6Hj+5W7qT9kpCMXxJcJ0Ev/OI6ButrE72oe93ukPh27RG89ddu3BHTQDtx2XwkDQOmrsE/z92AR7+P93uCDvhOc9f/rV6Y41qv5zZQM/70d4DV9w5sXx+fDeuMR77fDF/0QasX5iTifG6hln6dW2g33GcOp+S4pUr3/mClz+UDyrb6ccNRfLLsABY/ewMApSZG4/ELMFhXd+xEep62vpb1qrplcaji/j2CL1YdQkaeVTu2qBeW+iwBf/v6mJtauqWYq178JRFVIy3YfTITs/+jZLNIKdH05YWYeKsrK9euZfkYj92ifqcB5bzhg8X7MG3FQW367dP+xaG3b8ECj2GMG49fgOiqyv02f8Fa9U77iOsaayfAnu7/2rU/5FvtiAwza8cN/Um8gAM3mzZhzE+18ct2499vo65K6uf7eOl+/LTpqFvNhvu+Vu4MJyZneN0pNrpo0GeABPqtaixO4b2wr/GS9VEclg38zqu/KLzvqw1ud5Yfjot3m3f+NuV8Yq/jcrQyHUdNmQ5AuUj6w3mu8ezsbdrxC3A/2Z+16ZjbgBgddbWDuk5eipSsAvynZ1PYdQGZf3af8fl5/9Cd36jzdL+qNhrVqOQ1r+dAHCr1mOR5TvXsz1uNZg+ouMVTH/puE0bdeJXP6b7KDPjyl0cWc3+PbEpf9NnP+vNbo7/F12uOAFACTIf9dOnSZ2eWxPnW83MS0USXFan/ffpk2QH8tjVZK8ovpe8bJ0/8uEU791CzHzpdUQMvwdVTwQxXZrz6r3pt4tCdK/vKsFSPWylZBeh4eQ1EVwkH4LoxIqX3dYV6XqRySNd6PI+LenmFdrR+zXuI9ad/2uK1fzZ9aQEur1UJR1NzkTixP2InLcG3D3XFDS2itXmOp+VqPQrUDBS7QdDUMyvFMyD8+h+7DGscFtjsaDlhEd4f0gFXCmUZMaaDWrDovUV78VOAHgVTFu/FmgPn8Ecx60Oq2coCwPXvLYfZJHDUWdT6TGYBGo9fgFmPubJM209cjKwCG0b3aY7n+7nO0d74Yxdeu60NOr25xCtg9s7CPV71YvXZ++eylWCglEC3yUvxZK9miPIYFVXdz/Q3nft/vAqnMvK9rpn1wVJ171SDT+m5VnSOUM79MvPy0WH8Avz9X+U80nN/FELpbt3xzX/whsHf8b6vNmD94VQ81ctVB6zx+AVY9kJPt/mUshye+0/FCAsdkg0QjuM4K2t5T5Ql8BmK8fNRZplASrch9ZkIWEtGT3/Q8LX5jPrrekZ4i6uoGUGhChQAUnl29dLfYbGYBKw++uz7E0xNID2r3WH4o7l6f9ll9oQqlDvX5ZWvUXnCgyg6V14F089b/yOpXkwBwDM/bcWPHqOxGNUQ0e+7R1Nz8fnKQ14ZIoCSzhyKj/7Z73ZyowZUPl1+UOv6qN6ZVu8mqeeF+pOBpHM52Hs6y+1CVg3a6ut9nc0qQFa+Tcvk8MfX0Mr6y/BgRnbTC/W4MTfB/dj81l/KKIDztp3UljXXmZ2yYu9ZHEvLDXnULSP6u3ShUE+mjepRqH8t/f7665Zkt+CIv8L26bo7eYFGUnFIiQnzdiIlq8CrZtJvW09oP5DqHTwAhgEgAHj9z904k1kQ8A6qP1OX7jfMHJubkIzp/ya5fecKnHeo9TdktIsNH4cp/XfaJIRbAEiVZ7Xjp43e+30wtYmedwYFfQWAPKkn01qBcN0BpI04hs/DP8U1e94KallGzmQWYJ2PDCXPLCIjoXwN+5i24GrTXtxn9r4poyeE+/c72NH3CqAU3jYLCUB61YxxX4nvSfpsTfVv+n+rDhtmGRh5W7e/qYLNAlO5shPd1zlv20mj2S+IkhyFx1MoWU2hyivGCEVF9e3aIz6n6QOzwW5T9bdo67F0V8FcKEEgdRmeGXJqLUjAuOuwSt3HE4+na/tbmJblGji712aXQWXP+fpNKrA5vPZzh4QW5Nh9MhNWu/Q6FusDTuq5hNE1SIHH743nunwdi9X6QFP+2afVGWsg0iCcjwMFgIQAPltxKGCd1GB0ubKmtszk83nattH7JcGVJaQWL//UY0CXXxKSsf9MluGxzDMA5IvV7sDZrAK88edur6xqs/DOBNp/JtswaSJunes7oi5G3y51mxcUKscGZdQx4zapWUFGf5P1zpuzn3uM6jwn3j0bbtW+lApTCPpCK85VnSirArwR9ZvLmFFfaEVjZz56NYZ9E3xmzVt3tMOGw6nYeDhVi4Dq9W1dz+dw4BerGpXCtDsYROXV6Buvwu5TWV7fzx7N6/gNrN7c7jLD4tJJ7w70e4fQbAo+Cy4U6h26YKm1DUIxtEsj3NiqbsB6S31b19UKh5YHTepUDnoo2EBiLq8R9FDj5YmvjJuS9Oj1TfCN84Kma+OafrvHlRcDO9T3Wy/Nly5X1jQMMJWlz4d1xt87T2uB2Btb1dWCfV3FXvwS8SZOyVq4tmBakdcRbjGFHIQtiofMi/FG2PeYZeuNl2yPlfjy/wp/Ge1MSQCApvk/wlH245K4qVMl3PBc0h91ZKXyKhIFaCWOY5v0nSUEAHWQgSiRj2rIQ7Q4j5UO71GyLkWBzknUTKCxcxO1m8zzwl9FjEm5oG2T/x2+ebQnvl5zGCsMRuZVa66ZhKsb9LN9m3tl2Hq6snYlw0CDkXXjbzTMtvfU6YoaAbuLmWHHQNNGLHbEogBKVlLr+tW0bnQAUKdKBEb3uQqvzd+lvfb+XR3QtE5lbURgAHj9tjZoXb8ahn2zUQsu9GwRjc+HdXarcQRAy5IGlPPHT5cfRGSYSbth8Vv4a+hsUoJQLfK/RyHcR3oMgw0PmRfjJ3sf5CIy4LbwFOgcsySFm01BB9aNPN+vBT5a4r/2q8Ukgg6a+7Ix4inUE+lIk1XQueArv/MObF/fKwutZ4tomE3CMHNYpf89bVgjCjdXegy/V6mCQrMzAHXuRhSm9C/W5/CnauvxAICsPe8G9bovEZf9jvCaG5F/6g5Y093rDgpzFqq0mBz08vTr7l5rOrbX24eY9OpYc+oln+85+t6tCVJKw6F+y7Qw9BndqBuh7pCvztvpd/qlFgACSvdOEFFJ+XS59917IHBmXSiji+mV1vcilABQUeYHvLtT+VKeAkBA4AyWUPgrTl+elXYACIAWAAL810cqT4oSAAKMa1OVlSrIRTNxEk/NdH9df6yJFEpAIQzFGw3wQgSAhphW442w7wG4hrMtafqC0BbYUVisIJBEX9MWLHd0cgsmtROH8X34e7i78DUckg39vN9bqAEgwHeX07JUGxlIRXUAwP3m5Xgt7AfcUfCm30BQfOSTAIACaUGEsKFZ/g+ww09R3UtEMNn+Vo86MiaPTCCrQxoGgADgZ2d3Q/0pSqAAEICgA0AAsMbPaKF6wdQLihX78Wn4NEy33YQ3bA8BgFsACFCyovQBIEDJVNAHgAAl89TTqv0php9NX79LPX/UZ6yadBkiynHGPQh0j3kFJoTNhAkOfGW/zc8nLHtGAaAGOIeTqI1gcj4CBYCA0K+3jaj7uQWBf5+MuiGuCqIOqT5AdCI9D6jk2e4Kds0rSqe9xelRVm5uxTz0nXf9EgqNUUof0cWu30fB1/EqSz3eX1HWTaiQjOqmEJWln8InY37EawiHe+at/sS2hVAuDOuI0OqxAMBI89943jKneI0MwYfhX2qPHaUUBNJfLJiCuHDwp49pC74J/xBPmP/weH0raossLIsYU6zlF4eAA4+aF6A6fHf5LC0jzIuQEPkkmgjloqutM/OqlUkJNoyzzMLaiNGoBOMCtRHOYZ8biorTfb8sNR6/AM09au3pu4N9Hf4hVnz/ps/3+woOlaRxv+4IOM+V4jSqIHBgKUooN7K6mAIHGvR81QM1Eqg+oRH98cQoKNHNpNTZrCfSAQAtxTH0NgVfvyuUOqFF1QDnDI+LLcUxrIscjRHm0m9DKNTtXNxjeSgq5u3A8q3cBIGIiIrigJ/6KlTxBRpRg+hC62BSMrBihHFWIwC8Gvaj9rgaQssYmRj2A0Zb5sHoTuf95mX4MOzzkJYXisHmtaWyXM9MoOKo4hx+W+1epsqCd3FnVTNxAvcGqHdUElqLY5gQNhPTwj71Oc8rlh+RFHk/aiH0AKE/PU1KTauWQqmnkSOVri+VndvrScufaCTOoYfJf2CgKhh4Lyr9RfE1pj14PWxGGbYmsAgUYlXE85gW9j+/811r2oXuJqUHRhSKXiOqAc6hlfBfrydUZrcgkPfN8NvNShbSIxYlYLc4Yjymh08xnNeIv5HJSkIECrEucrThMaOrSak/ebt5Xam2IVTqNjeXchCol2kbnrPMBWA01HoFCwuVRBFoA8VJMGIQqAjev6tDWTehxF3dxKBqOYWkf5t6ZbbuSXe0K7N1ExFdiuZE+C76vMdxhfY4CsF3BdVfmOiDR03FSQg48HbYtxhiXut2576/aTPqIrjucleLPXjb8rW2ngiPC7pKogB9TQlur6kZT1UjilZBoBLyUVuXERXM3WMBB0aZf0Mj4d3V9TKhfNZIj7b7OxdeFjEG74Z9g6oBMh7CYdUyaa5tWjtgO8dYfnbLSFLbdLXJuwC16jGLMtrjLWb/dTCHmlfiFtMGjLPM8so6M9LbrASBvgyfCgB40KKMrKUELfUj17kee/79lc9Q/KL7oWomTuAyhFagu7hmPXaN2+iiRsyw47/mX9FOHEY4rGghjIdvd83vvW+r3+MIFBpu75LWAOdws8n/vlUVuegs9mNy2HcAgF7mRK95LkMqopAPQGJW+GRtv73c4DsZrHWRo7EoYnyR329E3x0sUPck/XFSPY6UtWrOY9ItZu8eMZPCpgMI7TfkQjBpQaDSLew+Newz/NfyG6oi13ncqmCBn3KOQSA/+rSqa/h6J90QpReLdg2rl3UTAvI8AR0U438Y2wttaOzl8DHSZ6lr26BaUPPFOkcxKEnhFh5GqOKoGlmmpfCogtMHZtbb2/ic74x0HWsjRPADNuiDB1cJpeD0CPMiLI94EWMts7VpHZ3FZy2w4avwj/F7xGtBLF1idsRbuN+yAk3Eaec6TnjN9U34h1rQ4QXLHOyPfAgjzIu8RjjSq4c0JEXej1tNau0PiYGmDYhAIXZHPozqwhV8CaaOxN/hL+GFsLn4Kuxjr2kvhc0CADQW7nXi3DODPOuEKAJ1dZps+RYrIl5AM3EClQMEvRqJFDxt+QPjw37W1vcfy18AgHDhfXEUgUK0FUlurw0xrdZ1HZNoLVwj200J+wqfh3+KJy1/4gHzPz5aIWEU/tJ3d2knjqCyrgtYdZGjm2+b13srObv9VEd2sWta+dNFdz6yLGIMZoa/XeRl1akSAUApQutJwGEYRLuitpI5dv/VV3hNUw03L8VzYb/ir4gJ+K/lV/wTMQ6txVFncMSbURCog0kZ2emf8LFYG/Fft2k3mBLxpEe3xuL6O2I8vgj/BO2F7xGldkQ+it8iXsdd5tU+51kZ8TziI55EP4+gcKSwFjuY1UEYj0paFO51mOzoZdqK2nDVETqlG5p7U+TT2uPxllkl1obi6Gt2bV/P/apQKrW51ELcoXrJMhMrwp8LGLwEgMGm1fgsbGpQy1WzOf1lAt1i2oC3LN8FtTxjEjWcx6pB5n+LFf7hZYqxi2qzfHJvDNaO6609HzugZVDvWzO2N1aP6Y29bw3Appf7IH5CX6wbfyO+eSgWu964CZtf6QsAqBJhQeLE/mher6r23n/H34g7DIIRnpk1agCjQyNXsGXN2N7Y/np/JE7sj/E3t3KbP35CX+ybNMBvux+/oanWNsA9KBLuMTbs9tf7Y/1LN2rPh3Ru5Da9WXQV/P3fHobrMevGr9QvoyTMe7o7Dk6+GQtGXx9w3oRX+2mPN73SB5/c2wm737wJiRP7o351V8X/2CtrYtkLPd3eq36GCQNbey3382GdcVtH77/hzjduwp43B+C9Ie3dXl8w+nps1bVF1a9NPWx9tR8OTL4Zm17po72+Zmxvt/lG3XiV1k5PHw7t6PUaYHySsvetAVg3/kYkTOiLTle4ltXlypp4oV8L7fncJ67Fplf6YO9bA/Dz49dg71sDEBnm/dVfM1b5Dux84ya3fe/yWlEAgO5Xue6KbnqlD3a/eRO2v94fO1+/CfET+notr6J4rm+LwDOR5sZWdfHdCMOBBgLyPM6VhbVjjY9hI7s39vmedg2DC7LqVYu04J3B7QPPCGCYwff71yevDXmdpW3p8z19/k4UxyPXNynxZZaWOsJ1cZGOytrj7qYduEKcQS1k4i3Ld6inu8scASseMS9AtO4u9Ed3ex/rEyf2d+tq0cakBATULiV3RbkuFrqblOKrNaEUIG8oUg0v2E1C+S1LmNAXn9zl+v2b+8BViJ/QF782nmf4OcdGKRemoyzK9Bcsv8DuEQRa8WIv7Xzp7xuSAADTwv8HExwYYNqMz8I/xdbO3iMifhI2DR+GfeE3I6iV6bjbNjBSX6S5FY4fYnbVE9F3Oaus695UW2SgLs5jpPlvzH60K7a82g8/PnK1Nn2oRbkobiZO+r2pEz+hL34f5Drv2DzmWmx6uQ9uMsdrr/14bxMkTOiLxIn9se21fhhjmY0FES9r09/skosPw79EYuTjAICnopbi74iXsG5QDjY/4/679LhlAaoiF9FI1wIaiRP742Crr3C440/Y+9YApEvX/vhNvd+0x3XDcrEr8hHt+QDTJgg48ID5H/zvzqZen+0ykYYayEJi5OOYYPkBgNLVLCnyfjxlnoeDk29GgvMcNX5CXxx6+xavcy4jG17qg+8f7oabTJtxhTiD4dcoxz318zQznUL8ePdzwTb1qyFxYn+v8yhA+RskTuyPvW8NwMax3ZEUeT8+S38S+yfdjL1vDcCByTdjw/gbcSRyOPZHPoTLq7kKBu99awAa1lDObSYNaoe3Ld8gKfJ+t++oui1UT1uU78TfES9hT+TDhp/RaJ+uhUxE4zyuNJ1FtMhwDmOufJdmhL+HcWE/43ZT4O4+ShDReHj7asjBvxGjMNi0Wgu4/hkxAS2dXa9uNa3Hlus3wQSHz26I+rYLOBAprKgsCvCAeYnXvEXJTLlCuAbsGWX53ed8YbB5HS/90WcCRYpCxIVPQULkk+jauCaqR4X5DFg1EOdwR0wDbHvN+3weAJqLZHwV9qEW+K9ZKUxr34ywd3C9aQfesXyNASb/NW1rIhNJkffjdtO/eNvyDZp5BN6fs/yqPW4j3I93ibIZACWQq36OMNjwXdj76G3aim5iDxaFj3MLeqkuF2fwH8sCNDGdwT8R49ymjTb/hoNRD7kdGz8K/xIDzZtwl9l3nc1XLD9iRtg7CHf+1piFcRAaAD4P/xQPWJaio67bdDXk4EDEA/jSILjv6QpdxllHw6Bh8P2gakSZcGOLiKDnLxWlVBi6OMu9qIJAretXQ6Oarj7hTetUCfieG1vVxeW1KuGK2pUQGWZG3WqRqFMlAg1qREEIgcoRFlRxBnCublIL1aNcPyIRFhMa1ohCV4OuVN2vqmP4XB8calAjCtUiw1A9KgwWk/vZRp0qEYiweI/OoL94jwozI7qqa6fu3dKVudSntetx96tqo1pkGOpXj9Lugjev575trqhVCQ2qR3mtDwB6tYjWHtf3MQ+gbH+9LgZBDs8uUw1qRMJiNrn93XwJd25vAKhbVTn5qhRuQfWoMLe07eua1UZd3XZpFl0ZZufZXKvLvC/mmkVXQQ+PvxegBP2iws1o37CG2+vRVSNQs7JxVL5GpXCEmU1a+1rWq+oWoAKAHs2V7dmtSS3t76mebF5W3Xj4ymjnXS591k1kmBkNakShdhX3A1vnK2rgqrquv+9l1SNRt2okIsPMsJhNiAwzY0Dby7zXUTUCkWFmVImwuO171zVVts0NzV37Qd2qkagUbkG1yDCEW0yoUyWizLKgiqtrk5LPjirPavvYd1U3tfXfrbF3q7poXreq33l8UU+iSludKr4/Y3UfbYi90neX2E6Xh76P1K4SEXSGXtVI7zY1CeL3qzR1bOSdHXpV3Sq4snbgY3Wo2tQPPchWGvx9tnBYsStiJF51XhQDwM3mzWgmTsAMO2aGv4PVEc9hS+QTeMCyFK1NrroXLUQyXg2bie/Cp2ivqb+XZtgxwLQJHRpURfWoMHwY5irS/KzlV3QW+7HT0RgAEG09qU2rL5SuM0N1J+yxzvoR3cQefB42FVHIR/82l6FKhAW1q0SgRU3Xcb36tq9RJ8qMyFObDT/vo/JXbI54UnteVeRhWGMlY6WDOISkyPvRZFoD1LGdQYMaUaiV5upOcr95mdYlqdLun72W3cO8E0PMa3C9aQcGmjbgOcsvAKTb9zbR4QpOdNfVsLlCnAHqKDf4okQh2oSfRVLk/ehncgVfAKAGclAX53GzaSOG6rIdYsQhPGOZh4lhP6B5zmbUqhyOK2pVQkOkoE6462Lxq/CPvfbLAaZN6CyUorh1qkQgurIrUyga6ahbLRIr7K7gXrPcRNRe8Ciqp+9G9agwPGpxLyJsOu+64IutlY/rqykXybWP/IHoVPfsi3oiHTsiH8XmyKfwffWv0EIcR/Vl42BJWgXTvgWItOcgEoXIdtYBMp93XTRVtbtfIF4pzuB60068FRaHsAWj4amb2IspYcqwzw9ZliAChfg+/D0AwNiwObCs/RC1neeodapEwLzp/9Dss4ZIirwf9ZCGly0zkRR5P64SyVpgoT5Scdmmd9Ahdz3+L/xj/BD2Dq6sVQldxV4876z5AQA1981GGGwYaNqAKshF3zb1UD0qDJfXcv9uVkEu6swfjurHVyByci2Y33ae06TsRbiwIxJWhJ3aihphrgyg+y5P1c7HIsPMwOGVQOLPMJkE7rco9aLULk+A8p33HG5cr5U4hqrIxUuWmajpDKwYZUZEikI8qlvuvoiHkBQ5DG10WWEjLIuwNmI0OokDqIw8JEXej6Hmldr0CBRiX+QILIh4BdeZdiIMNnwWNhUdxCH0Nm3F9sjH0FCk4iNdkXfAFWyZFv4/1IqfisORw9HeZBxI0mfW6bN/bjB715Dyrgsknd8N3xekaoFmADgkG+B207+GAZpnLXPxathMbI58GpWRh6rIRVSY8Wh1Ag634FV1Xabm6Mt2oW3BVkT66ErZ2XQQ3a+qgxqVwlEN2Rhp/tttWfebl6G/OQHLI14AAHRtrJwj9DQl4gbzDswIexf3WVbgy/CphsG/CBTiKfN8vBf2NQDg0/DPcL9lOZZFjMFky7d42jwPALAVroBvZeHKBLrFtAFdnUW4LcKBqshDdWTjQOSDuNG8DdPDp+A5y69oZTqOL8M/Rhexz239TT0yJdVjl4ADz4fNhUVaMdy8FADQR/f3/iDs/3CraT2SIu93y9iywIbHLAtxg3kHTLrAw4ywd7Vlq/TbQ/8bdblIQZiwY4B5M2o4b2C8YZmOp8zzvbafeoMDcAXni8pkAswXVcSjZAjpJ723NEXUby6/n78MDWtGYfX+FFSLVA7yR87loE6VcFSvFI74pDQ81qMpFu86DYeUiK4agYSj53F37OUQENh+Ih3Z+Tb0bVMP+VY72jZQTlp3nsiASQgcS8vFEz+6duxP7o3Bf3/eBgD4cnhnRIaZcXWT2ogKDzwU5p5TmbiydiVUCld+9JPP56JSuAW1KodDSok58ce1Kvxz/nMtulxZE3tPZyIr34YwswkdG1XH9hMZaN+wOg6cycaZrHy3oM3Xqw9j8sI9uDu2ER6+vokWrNhwOBVJ53Iw/jdl2Zte6YM7pv2Lkxn5eLJXM4wb0AqNxy8AACS9OxDL955BRp4Vd8Q0xPK9Z2F3SFx3VR0tkJWWU4icAhsa1IjCX9tP4obm0TiSmoPOzkySf3adRnquFdddVRtzE5LRsl5V9GwZjR3JGahRKRwtL6uqrQ9Q+lRLKXFZ9UjUrhKBrcfOo2alcNSoFIZalcMRf/Q8mtWpgtScAtgcErFX1sTW4+moXz0SSedycW0zV/Bmxb6ziHYGE6pHhWHniUzkFtpQr1ok6laNQPN6VZF8PhdZ+TavgFN6biH2ns5CZJgZ7RtWh9kktHauf+lG9Hx/JQrtDux9awB2ncxEzUphqFEpHCfT89CuYXVIKbFqfwpqV47AukPn0K1JLbfsmh3JGWgSXRkHz2YjxtkdcOeJDNz6v7XadtB/FgDYdzoLl1WPRPWoMOw/k4XalcNxLrsQLS+rim3H09GuQTWk51mRV2hHzykr4JDK3an//JDgNXzi2AEt0adVPVxWPRJrDqSgQ8MaWiqzKi2nECv3ncVtHRtASmDZnjOoUzVC++HSy7fa0epV5Q7tjtf742hqrleXwOTzyt2k6KoROHIuBy3rVcUfiSfRrUktw2Dg2ax8HEnJwZZj6XhvkfJj//3D3bDvdCbeXqg83/RKH+w7nYUHvjW+c/LWoLY4nZmPz1YoPzwTBrbGrE3HcChF+WGvVy0CZzKVO1BrxvZGhMWEPxJPIjWnED1bRGPniQxMWqB0p3j/rg6oFhmGtQdT8OMG70KEsx67BjaHAz2aR2P3yUycyy5Aq8uq4tctJ1CvWgTMJoHsAhv2nc7Cdc1qo+Vl1bD24DkcS83B12uUk6halcORluM6ifn58Wuw9Vg6rqpbBXaHA+EWEx6OUy5Opo/oiqwCG/IKbRjYoYHhiBP3xF6Oq+pWweSFymd45PomGNy5ISIsJpxM///27ju8rep84Pj3lWxZ8rYcj9hx4iTO3tiZhBVWwgoEQgqUQhnpANpCKT9oaSltKaGUUmYpm1J2KTuM0AbKCiRAQoCQRWKyh0e8p87vj3NlyZbkmGzw+3mePJHu0t2+5z3vObeB733NtygOzk3hjzNGsODLMvLTfQzpmUpmkofiP9g//FdMHcSfXgk9OPz97GKOGZpD36vsA+uzFx3M0x+u5+EFpcws7sWEfpnMOCgfEWHp+h144lyU1TaSl+bj8D+/EfH7z150MHNeXsaCL21t6l9OH8VlT0b2PfCDw/qRneJlZK80VmypZmK/TFZuraGspglPnIuCDB+z7l7Q5e0+ZmgOr31uC1QvXDyZ619exrurbaF57ZzjWbW1ho2V9dQ0tuBP8uB2CSV9MthQWc8593/Qdr4FXX38EAozkygtryMzyUPPNC9bqhsZU5BOhXPvqahtok9mIpV1zVz576UMyknh1UsP5fklG/liUxXFfTJYva2GwbmpbccxM8lDWW0TFx9RxO3zbW3Z3WcXk5/hY1heGkW/nEtLwDCxXybnTe6LN94V9dr521kH8aNHPgJs4Pmq4waTneLFYDj+1s47+v3n+eN5YclGnlhkMy/+dNpIdtQ1c8pB+SzdsIPKuiYG56YS7xaKslNobg1EvBFnxph8RhWkc83zn0X7iTZpvnie+MEEpv7VZmzMmTGCgbkpDMtL5YUlm8hIjKeirpmb562wr4R13HrGGH7yWKh5y1XTBnNQnww2VtazvqKeSf0zOeXOUE36O1dO4ZEFpbhE2vYrwDM/noTP4+a5xRupaWhhfD8/eek+tlY1UJSdTFaKl1HX2mY3D5w7lhc/2USvDB9jeqfzxwf/HVGbGrRkyM8ZteymiOEBceMyrcxrLeZoJ+V/UWAgt7dM58FZA6iedz3S9xCSlzqdx2YNhm1fRCxnRSCfga7IZlu1ifm4U7LxbrH75odNP+NI10dtD8yNibnUXrQUf2K8rWl4/Cz44sXQAsZ8Fz7+Z8Ryv7ZZj8ATZ+3WImr6HI0kJJG04llmNv6GpxJ+R1NCBp7GCjYPOIPaw6/l86UfceKC73S6nKaETDyNXexbZuLF4PbQtOwVPGWRr6xu/eF7tPztEG5pOZWtcT35s/wVgLLj7iFz8GR48AQodwpJp94HI06j8Z5jiStbgbuhvP3ChpwIy17o2nr5+0FGX1j9n65ND+DvD+WrWT78MgZ9+peok5jMgcjQE+GtmzDuBKQ1ejZHdc5YUraEgoOvjb2XYxZeEDnh0JNhzNnwyKltg+ryJpG4MXQtNqQP4OkJT3HipttIXXJf+/U57s/I3MtjblJVz0kknX437o8ehOEzWL1hM57Ciby3uozDN9xF9uLbo884+TJ4O/o+qLh8KzXb11PQtAoePT1ifG1OCVeaS1i3rpRnd9LEclXWURRte73te/h1Hm61q5B3vYdxdt1D7YZvMJnkS+fn6p0tJ7HDJHG6+w36uyJftR1ISMPVGJkFElSZOYZPD7mTyc9GZpa2xiXiboneR1ase040T7ce0paF1+rrgbt+O68f9TJDho/hgRt/TgAXZSaFQa71/DiufdO3TcbPxMbbOUhW8O+E33JJ08Xc5ok8rmXH3kFtfQO5H1yPp2E7BzfeynTX21wR3/4tilt6H0/OVy9FzL8yqZgBtfbYNHszkXgvcdWR2/fpsF+wZfiFZJctxPvaFQwI2wcNP/mc9f+9h6JPo2exlGVN4L/j7qGivpkj1t3BgJX3RZ0u3KLTF1Ly5Nh2w37RPJv1JovHPNftdP6Ors3+Kw98ZcuWZ7lf57r4+6nz5ZJYvznmPM05o4jfEvlcFnR3y/Hc1XIit8ffyiR36D5ZYZLJkPYvZlnVeyZ9d7zP2sk30v+lWQC81lrM0e6PEAwNrkS8AXvO/ad1DKUmh/PibFlkcMMD5EkZfxq1hSX5ZzLzg5mkVof+fs/xZ/Cv5DQa3TbA1Lh9Ck3bjunSfumZ6mJIbjz/XdH1DLaUIbbvquplc7o0PJaE3GfwZLxPw6aTOTr/cOZ+Fgr0ibuG5IF/aFueP8lFeW3sDNnw385In09Lz1fxVoxg2+bYf39LbzjhQ2NM1PT9LnWOICJTgVsAN3CvMWZOh/EJwD+AYqAMmGWMWbuz5c4aW4CItGVGdHSS00TngkNCNUKnjAk1YxoRpaYSQv3bbKlu37by8EHZ9EhOYHtNI1OHR7Yb7kzHoEN45oqIMGts77Yg0Dgn2ycYlAoKBlqG5qUylPbLS3YydHr7E9tlq0zol9mudiw5IY6Lpwzgl88sJTFKZHzK4FAt/pFDImv0/Uke/E4mwPTR+QDtslqOCcsQ+VlYM5nxUTpITPXGRQQ+Dg8LbEEoOyk8YBHcDx0DCUd0mDdadlCsjKH0RA8TYnTi2DPNR890L6VldYi0z1AK7gsRaVv3aOdVcNjosP6gwoMmHfcDwKDcULbEQKcJYTBrJ7icYDv2vHQf6yvqcbuEo4bmRASBMpM8bcs7YWT0vpD8SR5mhDXzmxalbXyQN+zcSfHGR+0TKnxfB8/J4DkTTXaKzTjaUW9rXc6dVMhhA7M4bGBWWxAoOE00k/pncvbEQrbXNHLH/NWMyE/jgkP60bdHEuc/ZAMp50/u27asYM1g+P1hVK90/vDSMvpnJXF6SQEAU4fnkpPi5aZ57Wsqwo/Z0LCMjR8d3j/mNvbtYdPtg0Gg2Yf2Y87LoULbhH6ZMc/DIzr0MZbocVPXZJssFPfJ4MPSCi49eiC5aV7eXrWdN1ds44xxvduyutwuV9s6rNnetbcNZaUkcFDvjLZrrqMTRuS1CwId2yFDbHRBOis2O81NMnycWhzt/mvPyxH5aSzdsCNi/mtOHMa0W+wDYjCTcnBuCl9sDtXyDMxOaVt2MGjZL6trmTAHF2Xyzqr2D9LhmTUjeqUxbUTPtiAQ2IyW8Gy5oF4ZiQzumdoWBAru6xRvHEfF6Pi9wJ/IyF7pbd+XO9uVl27P85NG5bX9LTtySA7ba+xDyKiCdE4alcfvX/yc9LDspPB78BGDs5n3+RauOWkog3NTaQ1Er7QJv1avPmFIzL+p0Uwe0AOXwBOL1jGzuFfbdQOR92QgImsV4OQx+W3X4+SiHry9Knq/K5OLelCYGWqyMqogve1v62lh51Z5bWPbdQ5w4sie7YJAJ43Oi5mVesa43uSn+7hiqm16GAwCHTUkpy2wP3hq7Myj3v5Eviqv4+CiHu2u2Wc7pOmHixYAAnDlDodNS9oVDEtcK3jQcyM841w5S8Nq5YMBoOyhsDX0sD3QtYHnWicxvcMbYpLqNkBdqJASzL4JSqjbTMKNnZwL4QGg4/4MgRZ45Uo49np49arQuGP+AK9dHXs54QGgjEKoWGs/ixuM0yzrlxth+cvw9Pkd5wYguTTU5OSpBPtabc/4C2DZi+SufAxWPkbsO3OIp89YWBHZBC2q92xhMyJv0OeH+nLcd03ELXBF/BPtRmfOvRDmdpjn6fPh6fNJABg4NXIduhoAAij/0v4DOORyWPkabN7Ja7adYNSg/kUwcT7cE9l8Sn78Hiy2xzxWAAhPcrsAEMAxiStDXw76HnzkBC0/f9b+CxMeAALwVq7krFdGR/2pzgJAAKmb3oVbnJdevPXntuNfAJBWEGMuYgaAADI2vknGozNjjk/asojbOAe60HIkPAAERASA1gZyKHRtoX9gLf3r1kbMv7MAEBARNOkoZgCo+Pvw4QOkl30cNQAE0DD9XpKePjPquI4BoG0mlaywzt3DhTfDdNfbe/9RK6/DVA3j6vhHOl3/nmL7EguKFgACyHz1IsKfrN5JaJ/BFsCFi0DUABBAxeDvsHLhZuYHRjP7ykdh6zK4c0LEdMM/u5HhnzkZmx0yR7y3DqWok23J3LaAmS91rQl4UFsAKGc4bLFvXwtm4QXd1zKt7c1mO3PN1p/xOPdz/Mh8rlz+GJtNBuk/+RhuiFIeEBeYQPsA0I/eg7+1P19mx73E7LjI/ep1B+iYAFX01VMAbQEggGPCrotgAAjgSHfobzrAXfF/tR2UfwElLIOwAFDQrr6NzOUSWmPMmu4TKuv3TULMyPz4dkGgjhLjhfKYY9urwYcXqOrkrZg7s9MgkIi4gTuAo4H1wEIRed4YE15tcj5QYYwpEpHvADcAsyKXFtLbn4js5fYjhw/M4vcnD+eQoh58vK6CNF88z140iSXrYkfNd8d/fn4Yq3bxddWnlxTQ1BLgjHGRfUMUZafw0yMHkOqLJ9ETx6yxBTQ0t3KW05760QvHt2X67AtP/mAic5duOuD7cXj9skPbCnOPz57AB2vKozaxOxA8+YOJvL+mjHi3izPGFtDSGqC3P5H0RA9L11dyWnEnDzy76MVLJrOtZs+/ceCoITlce9IwZpaECnXPXXQwVQ2hlNxHLxxPQpybeZ9voSg7mYAxHOUELXskJ3DjaSM5bJAtvBwxKJtfnzCU5tYA3z+4L4cPym7LUurI53Hz11mj2wKxQbMP68dnG6v40eH9qW1qIcmze9fL65cdytrtdRw2KIskj5vcNB+9MqIXSp/+0USiJVy+/NNDuHneCi6eMoBUXxxvfLGtrTngzbNG87qzb4IKMxO5atpgjhmWy6ufbaakTwZfbq+lpE8GyzdXU9/cyvLN1Yzv5+eLzdXtgjuxFPh9XHfKcO59aw0PnBuqjfr72cUMcgKXpxb3oq6phTM66TwT4L5zSvj7/77kyMHZnHlv6M0kQ3qm8rOjBpDui2fK4GyuPWkYpxb34pmPN9DY3Ep5bRMnj4kdXAx66Lxx5Kf7cLuE5xdvZGRBGlt2NHD00Bwq6pq4843VZDpNO6aPyee04l4kOlmeZ4wtYO4nm7jmpNgd+Qb98eQRjCv0Y4zhO+N68+j7X32t629QbgrXzxjBtOGRTS7Bnt9/OX0Uk4t6kJHkQYCzJ/Zh8oAebKho/2rmXx8/lOI+GQx0mt+5XcL1M0bwj/dKyU5J4NxJhSQlxDE8P5UZY/JZX1nP5A5NW+ddeijrKuro7U/k5tdXct7BfVm1tZrsVG9b04iJ/TP5/fRhnNKhr7hoRITbzxxDa8CQ5otnfUU9hwzogYhww6kjOHZYLqN/Zwv0N80cxZ1vrGL1tlpOHp3HtdOH4413c+1JwyirbYqoXAmaVdKb5lbbPGhsoR8R4bYzxlDgT+TLbTVRA0CPz57Avz5cH9Hv2+uXHcq1L3wes7+1aMtZuLY8osP78w4bCO+Fvl/K5dxkbmqXFl958sOkP3t2aKL8EtgUu4Y1ph+9C9emtxs05NjZMPAv8NZNsPSp9tP3OwK+nB/6XnwurF/UVqhop+domH473OX0vTL4BJh6PaQ71/cEpwnYhkXwqdNXxbBTbNbMG3PgTacO8LQHoOhImBN2X/jJYkjpCdc5AdOjfwev/QryxoAnCTLDwjg9BsF25x419kJYeE/kuh78U0jKgpeviBw3+ARIzoZFHToenXZD+wBMci7UOLXgXc1YmnE3PHJaxOBWlwd3oEPzlcJDYO1b7YeNOgOGzYBnZkP2MNgaliE380GYewUccRW8eKkdNuh4WO4UskbOgk+coFN6b5hyNUy+FN69Fd68IXJdp90IL/8i9L3voZBeAL9YDTf2h1FnwpJH7Th3nM0y6kxT2DNsznCorwz97gk3Q8l5kNoL3ujQifOEi2DBHZ0v21GfPQbf1o8jR0z7U/RjHc2OdRCfBM21cMrdMMopcnz0D3j+ksjpM/pCxRroGAAa/d22wFg02wqORVJ6gjueHkvvwSRmInVltIw8k7hPnP06cBqsCBXSd/Q9jrQ1c6ka/j22rX6SrMYoAeQTb4UXIpviBZmUnkh1+8yfllFnUXvwVaTdGeVtsJcts4X6m5y+UKf8GhL99n4R9H+l8P5d8Mb1kN4HM+AYnmudxBIZxG9KAvDRQxGLfbffT9lRVUXa1KvJ+qe9fmsGTCd5ZWTzHVzxEHCe80rfRkpjZKF24Tpcen4pI+7r0+k07X56J8GB4ikz+WDoqUxIcMoA2WF/J5KyoXYrdVmjSdy2uN18DR4/3qJDI4Kd7a6rsRfapoVlK4mlvOAY/Otes9meCamwvkNG74X/hQePh/XtA7Dzjn4VqWiARc755U2D5gaIFcQF21/VCkBg48TfketLpCEhE2/HDMkL/wt3H24/H/tH+3ckZyic5TTPTMkN/Z0IY5JzkZrNVE9/EJ9UseLjNxm45uGI6QDqEvNIrNsYOaLoKFjVPoja7g11wYzVI38D//ld22DbPLPrL1oIcgu0xKhEc7mEr9O/0LfJTpuDichE4LfGmGOd71cBGGOuD5vmVWea90QkDtgMZJlOFl5SUmIWLVoUa7RS3wjhTfGUOlD8b8U2vnf/B0wu6sE/LxgfMX5vn7d6XXRv4cf/rHsX8M6qMh4+f9zXylA60Ly29jWeXPYIlL4LqfmUSk/WV9TT259IQeVCcHugYHz7gEDeGKjdbgusQeHZMcHaX3e8nbdqI7jibCCltTnUWVxjFfgyaHs97rZlULMVUvPsPFmDYJsTUPH3s1kSgWbYuBham+x0lU6T2ILxEOeFNU4/DX0m2cJbTAHaVYm31ENLky2MBFVvtN/jnSyvde9DSwP0PQya6+z2ueIBA7XbwJ1gpw802/GelNB+yxkOVRtsYcntsfOUrbbDABJ7gL8vxCXYfdna5PxrtgGMtAK7fwOtNrMp3gf1FdBQBRl97PDy1bYgtt3JDo3z2sBJfCJ4052NMnZalxvqyu08GYU2KLXlM7t9Pr8TVDGwY73dloxCu33BZQSXU/ou+NIh1wlGmlZY9wEkZ4E/LL+gtQm+es+eB30ODjsMLbB5CaQXOvt8M3hTnYwYQ1tNg0Tp+KJuu50/2QlMV22AslX2GDQ4laL+fva3k7Nh+ypbAEzJtedvMCutV0noGLc2wuZP7XZkFNqCdGMVbPzY7qMeA+3xrd0G5Wvscd2xzv5en0k2W6yhCnKH20JtXII9DvXl9lzNHWHP/7oKSEixx7BjU8leY+1+cnfI5dqwCJpqIa2XXbfmehuEXBPsV0QgbzSYQNjxxp63ppVy/2i+2FJLRlICQzr2I9naaNc7qYddn+Rce22aVlj7tg02pRfY7fSm2d8KXg9g52ussddhxRq7rb50G2zL6Bu6XuMS7PISUtnYEMdGk8lB/XviQuw+2rzUHuuc4fb4+5yKr/oKex6m5ttrddMnkFlktz/Oa8dv/gQS/bRmD2fBl2W4RGy/moFmeyw8ifYcSUhrf53XbnWu3VR7vifnQGO1vYcVjIOmOvvZmwae5NA168sIrVtcAhQEM3CM3Y56pwPo9D5QWWr/zyi017O47HSNNVCzxX73ptpzCuy5VPquvV8kZ9tjEp9o1yHOa6dvqbfb0lFTjT3H4pPsbyB22nUf2HMnvY89v8Dum9J37fHLHgZN1bDBNsGmr9Mp+tbP7PWSNRgaKu3+8KVDYmboHE5ICQXLSp2subT8sHuA4YvVXzLY5ezfLOdlGs21dt+74uy5VrHWHgOA3JF2ueVfQofAIYWT7X0SY++Rbo8978HZNw323uCJkXnd2ggtjfYenDXQHofkbNq9qr1hB2xabJcRHkT297Pn4dbP7THJKAzd5zOL7D0ovbcdV77arl/2ELsN9ZXOvj0UmmpoaaxnYWU54mpE3PZa+jrNwQZlx9Ezzc0bKyODZ9nJLrbWRAYRd6U5WLRwUkLO83j879Kw6WR+Pu5o5rwWyoLv2BysV7qb9ZWRb5aM9tvx6Qvw9nyWporxNG4+JeY8nTUH60oQ6DRgqjHmAuf72cB4Y8zFYdN86kyz3vm+2plme4dlzQZmA/Tu3bu4tDR2erVS3wSPffAVvnh3lzIZlNpXmlsD/OqZpVwyZUBEh5oAC9eW88byrfzi2L3ztq5XPt3ExsoGzjvAswXV3jF/+VaWbarix4cXsb6ijlteX8kfZ4wg/hvcM+Mra17hsS8es4U0dzwtAcNXZXX0zkwkLpgdEud1AhABWyBOdBowNFZBnM8WgtN62WnivBAs0AULBl1lAraQm5BiC7jx3lDQIy56c9tQUCMutE6tTTaosqe1NtvCQ6yCRTRNNTbgEhfr5RPGBrySc0LbsLsCLXYfxO/5zs67xAScQF+HrPimGhs4awsm7QWNVaFCW1OdDfjEXtHIddwVgRZ73nqjFMi7wrRCXZldl3hf7PMr0GILyOkFTgG4bQH2enHF2/0bsXxbEAwgrC2rpVeGD497D2SP15fb9ckeGnnumtZQYFjcUca5qGlspaK2iV5+HxI8Do3VNrMr5vUSi7HHwJOEAdaV15OZ5CFpj7QmMPb4+Pw2wNDa5NwHnXtMYw3E7eS8DjQ7+6iT8y14/4v37bl7QVe0Ntt7lNOMioo1kJhlg1JBgeau38uDgSx/IeHbu6GijvS4ZpJSUul0PzTXQWtL+9+v3W7XMSFl3+4bEwgFoE3Anp/eKOvf4mQ7x3md89C5hgMtdr5gkKqpxo5zlmkwLP6qkkTTm4q6AJ7Mt/hp35v4w9z2WUFXT03lD6+Emi2eNNLL85808LfvZOBPdHHX2zUIkOZzsbW6lVSfix9OTuYf79dSmBnHV+UtPPWxXcf4jHcYX5BJJmN47pN6MhKFijpDdt4iTh6RTHx9CSPz41m9vYU/zbOBnUfO9XPBIxXUNxvcAv2y4lhVuYmk3JeZkDKL644r4LpXq3j+ExvISvEamv2P01rXn+bKcfz7wkzeXNXILfNtMK3Q72ZteSsT+3qIdwtLal+iZkcfWusGgDTh7fkMI72nMLGPn8XrmimtaGFtmQ0iXXlMCnNeqz5wgkDhNBNIKaWUUkoppZRSnamujux4XXUuNbUkZhCoK9VyG3D6YXP0coZFncZpDpaG7SBaKaWUUkoppZRSSh0AuhIEWggMEJG+IuIBvgN07K7+eeAc5/NpwH876w9IKaWUUkoppZRSSu1bO20waIxpEZGLgVexr4i/3xjzmYj8DlhkjHkeuA94WERWAeXYQJFSSimllFJKKaWUOkB0qdcoY8xcYG6HYb8J+9wAzOw4n1JKKaWUUkoppZQ6MHxzX9WhlFJKKaWUUkoppbpMg0BKKaWUUkoppZRS3YAGgZRSSimllFJKKaW6AQ0CKaWUUkoppZRSSnUDsr/e5C4i1cDy/fLjSu2aHsD2/b0SSqlvnTRgx/5eCaXUt44+tyil9gZ9bvlmGGSMSYk2oktvB9tLlhtjSvbj7yv1tYjIIj1nlVJ7mojcbYyZvb/XQyn17aLPLUqpvUGfW74ZRGRRrHHaHEwppZTav17Y3yuglFJKKdVF+tzyDadBIKWUUmo/Msbow5RSSimlvhH0ueWbb38Gge7ej7+t1K7Qc1YppZRS3xT63KKUUt1XzL8B+61jaKWUUkoppZRSSim172hzMKWUUmoPEJECEZkvIp+LyGci8lNnuF9E5onISuf/jCjz9hGRj0RksTPvD8PGFYvIUhFZJSK3iojsy+1SSiml1LdPJ88tM53vARGJ2rm8iHhF5AMRWeJMe23YuL4i8r7z3PKEiHj21TaprtEgkFJKKbVntAA/N8YMBSYAF4nIUOBK4D/GmAHAf5zvHW0CJhpjRgPjgStFJM8Z9zfgQmCA82/qXt0KpZRSSnUHsZ5bPgVmAP/rZN5GYIoxZhQwGpgqIhOccTcANxtjioAK4Py9tP5qF2kQSHU7u1Nb70x3jjPNShE5J2y41tYr1Y0ZYzYZYz5yPlcDy4B8YDrwkDPZQ8DJUeZtMsY0Ol8TcP4+i0hPINUYs8DY9tv/iDa/Uurba3dq653pporIcuf55Mqw4Vpbr1Q3Fuu5xRizzBizfCfzGmNMjfM13vlnnPLPFOBfzriozz1q/9IgkOqOdrm2XkT8wDXYmvpxwDVhwSKtrVdKASAihcAY4H0gxxizyRm1GchxpikRkXvD5ikQkU+AdcANxpiN2CDS+rBFr3eGKaW6j12urRcRN3AHMA0YCpzhzAtaW6+UcnR4bok1TZ6IzA377haRxcBWYJ4x5n0gE6g0xrQ4k+lzywFIg0Cq29md2nrgWOxNrtwYUwHMw6Y/am29UgoAEUkGngZ+ZoypCh/n3B+M83mRMeaCsHHrjDEjgSLgHBHJ2YerrZQ6QO1ObT22wmqVMeZLY0wT8DgwXWvrlVJBnT23hDPGbDTGHBf2vdVpxt4LGCciw/f6yqo9QoNAqlvbhdr6fGwtfVAwuq219UopRCQe+yD1iDHm387gLU6gONi8a2tny3AygD4FDgE2YB+ugno5w5RS3dAu1NbHem7R2nqlVKznlq/FGFMJzMe2gigD0kUkzhmtzy0HIA0CqW5rV2vrlVIqGqdm/T5gmTHmL2GjngeC/YedAzwXZd5eIuJzPmcAk4HlTmC6SkQmOMv/XrT5lVLffrtaW6+UUtF08tzSlXmzRCTd+ewDjga+cMpQ84HTnEmjPveo/UuDQKpb2o3a+g1AQdj3YHRba+uVUgcDZwNTnFe9LxaR44A5wNEishI4yvneMctwCPC+iCwB3gT+bIxZ6oz7MXAvsApYDby8z7ZIKXVA2I3a+ljPLVpbr5SK+twiIqeIyHpgIvCSiLwKEVmGPYH5Tl+GC7HdZbzojPs/4DIRWYXNOrxvX26U2jmxwTqlug8n6v0QUG6M+VnY8BuBMmPMHOftGX5jzBUd5vUDHwIHOYM+AoqNMeUi8gHwE2yK9lzgNmPMXJRSSimldlGs55aw8W8AlxtjFkUZFwesAI7EBnkWAmcaYz4TkaeAp40xj4vIXcAnxpg7996WKKWUOhBoEEh1OyIyGXgLWAoEnMG/xAZvngR6A6XA6U5wpwT4YbBJmIic50wPcJ0x5gFneAnwIODD1tRfYvQCU0oppdRu6OS5JQG4DcgCKoHFxphjRSQPuDfYJMzJSPwr4AbuN8Zc5wzvh+0o2g98DHzXGNO4jzZLKaXUfqJBIKWUUkoppZRSSqluQPsEUkoppZRSSimllOoGNAiklFJKKaWUUkop1Q1oEEgppZRSSimllFKqG9AgkFJKKaWUUkoppVQ3oEEgpZRSSimllFJKqW5Ag0BKKaWUUkoppZRS3YAGgZRSSin1rSIi6SLyY+dznoj8ay/+1g9F5HtRhheKyKd763eVUkoppXaFGGP29zoopZRSSu0xIlIIvGiMGd6d10EppZRSqiPNBFJKKaXUt80coL+ILBaRp4IZOSJyrog8KyLzRGStiFwsIpeJyMciskBE/M50/UXkFRH5UETeEpHBsX5IRH4rIpc7n4tFZImILAEuCpvmUhG53/k8QkQ+FZHEvbkDlFJKKaWi0SCQUkoppb5trgRWG2NGA7/oMG44MAMYC1wH1BljxgDvAcFmXXcDlxhjioHLgTu7+LsPOPON6jD8FqBIRE5xpvmBMabu622SUkoppdTui9vfK6CUUkoptQ/NN8ZUA9UisgN4wRm+FBgpIsnAJOApEQnOk7CzhYpIOpBujPmfM+hhYBqAMSYgIucCnwB/N8a8s4e2RSmllFLqa9EgkFJKKaW6k8awz4Gw7wHsc5ELqHSyiPakAUANkLeHl6uUUkop1WXaHEwppZRS3zbVQMquzGiMqQLWiMhMALE6Nu+KNl8lUCkik51BZwXHiUgacCtwKJApIqftyroppZRSSu0uDQIppZRS6lvFGFMGvON0CH3jLiziLOB8p4Pnz4DpXZzv+8AdIrIYkLDhNwN3GGNWAOcDc0QkexfWSymllFJqt+gr4pVSSimllFJKKaW6Ac0EUkoppZRSSimllOoGtGNopZRSSqmdEJFfATM7DH7KGHPd/lgfpZRSSqldoc3BlFJKKaWUUkoppboBbQ6mlFJKKaWUUkop1Q1oEEgppZRSSimllFKqG9AgkFJKKaWUUkoppVQ3oEEgpZRSSimllFJKqW7g/wEz1g2rt6JVHgAAAABJRU5ErkJggg==\n", + "text/plain": [ + "<Figure size 1440x288 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + } + ], + "source": [ + "figsize = (20,4)\n", + "\n", + "for dim in models:\n", + "\n", + " # create a dim with the raw data, anomaly score and anomaly bit for the dim\n", + " df_final_dim = df_final[[dim,f'{dim}__anomaly_score',f'{dim}__anomaly_bit']]\n", + " \n", + " # plot raw data, including the anomalous data\n", + " ax = df_final_dim[[dim]].set_index(pd.to_datetime(df_final_dim.index, unit='s')).plot(\n", + " title=f'Raw Data (Anomalous Appended) - {dim}', figsize=figsize\n", + " )\n", + " add_shading_to_plot(ax, df_timestamp_max - n_tail_anomalous, df_timestamp_max, 'Anomalous Data')\n", + " \n", + " # plat the corresponding anomaly scores\n", + " ax = df_final_dim[[f'{dim}__anomaly_score']].set_index(pd.to_datetime(df_final_dim.index, unit='s')).plot(\n", + " title=f'Anomaly Score - {dim}', figsize=figsize\n", + " )\n", + " add_shading_to_plot(ax, df_timestamp_max - n_tail_anomalous, df_timestamp_max, 'Anomalous Data')\n", + " \n", + " # plot the corresponding anomaly bits\n", + " ax = df_final_dim[[f'{dim}__anomaly_bit']].set_index(pd.to_datetime(df_final_dim.index, unit='s')).plot(\n", + " title=f'Anomaly Bit - {dim}', figsize=figsize\n", + " )\n", + " add_shading_to_plot(ax, df_timestamp_max - n_tail_anomalous, df_timestamp_max, 'Anomalous Data')\n", + "\n", + " # finally, plot it all on the same plot (which might not be so easy or clear to read)\n", + " df_final_dim_normalized = (df_final_dim-df_final_dim.min())/(df_final_dim.max()-df_final_dim.min())\n", + " ax = df_final_dim_normalized.set_index(pd.to_datetime(df_final_dim_normalized.index, unit='s')).plot(\n", + " title=f'Combined (Raw, Score, Bit) - {dim}', figsize=figsize\n", + " )\n", + " add_shading_to_plot(ax, df_timestamp_max - n_tail_anomalous, df_timestamp_max, 'Anomalous Data')" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "The last concept to introduce now is the \"[anomaly rate](https://github.com/netdata/netdata/blob/master/ml/README.md#anomaly-rate)\" which is really just an average over \"anomaly bits\".\n", + "\n", + "For example, in the next cell we will just average all the anomaly bits across the light yellow window of time to find the anomaly rate for the metric within this window. " + ] + }, + { + "cell_type": "code", + "execution_count": 11, + "metadata": {}, + "outputs": [ + { + "name": "stdout", + "output_type": "stream", + "text": [ + "n_tail_anomalous_anomaly_rate = 96.6%\n", + "\n", + "This means the \"anomaly rate\" within the yellow period of anomalous data was 96.6%\n", + "\n", + "Another way to think of this is that 96.6% of the observations during the yellow \n", + "window were considered anomalous based on the latest trained model.\n" + ] + } + ], + "source": [ + "# average the anomaly bits within the n_tail_anomalous period of the data\n", + "n_tail_anomalous_anomaly_rate = df_final_dim[[f'{dim}__anomaly_bit']].tail(n_tail_anomalous).mean()[0]\n", + "\n", + "print(f'n_tail_anomalous_anomaly_rate = {n_tail_anomalous_anomaly_rate}%')\n", + "print(f'\\nThis means the \"anomaly rate\" within the yellow period of anomalous data was {n_tail_anomalous_anomaly_rate}%')\n", + "print(f'\\nAnother way to think of this is that {n_tail_anomalous_anomaly_rate}% of the observations during the yellow \\nwindow were considered anomalous based on the latest trained model.')" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "### 5. So, how does it _actually_ work?<a id=\"so-how-does-it-actually-work\"></a>" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "In this final section of the notebook below we will dig in to try understand this a bit more intuitivley.\n", + "\n", + "First we will \"[featureize](https://brilliant.org/wiki/feature-vector/)\" or \"preprocess\" all the data. Then we will explore what these feature vectors actually are, how they look, and how we derive anomaly scores based on thier distance to the models cluster centroids." + ] + }, + { + "cell_type": "code", + "execution_count": 12, + "metadata": {}, + "outputs": [], + "source": [ + "# preprocess/featurize all data\n", + "df_preprocessed = preprocess_df(\n", + " df,\n", + " num_samples_to_lag,\n", + " num_samples_to_diff,\n", + " num_samples_to_smooth\n", + ")" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "Now that we have preprocessed all of our data, lets just take a look at it.\n", + "\n", + "You will see that we have essentially just added `num_samples_to_lag` additional columns to the dataframe, one for each lag. The numbers themselve also are now longer the original raw metric values, instead they have first been differenced (just take difference of latest value with pervious value so that we are working with delta's as opposed to original raw metric) and also smoothed (in this case by just averaging the previous `num_samples_to_smooth` previous differenced values).\n", + "\n", + "The idea here is to define the representation that the model will work in. In this case the model will decide if a recent observation is anomalous based on it's corresponding feature vector which is a differenced, smoothed, and lagged array or list of recent values." + ] + }, + { + "cell_type": "code", + "execution_count": 13, + "metadata": {}, + "outputs": [ + { + "name": "stdout", + "output_type": "stream", + "text": [ + "(7192, 6)\n" + ] + }, + { + "data": { + "text/html": [ + "<div>\n", + "<style scoped>\n", + " .dataframe tbody tr th:only-of-type {\n", + " vertical-align: middle;\n", + " }\n", + "\n", + " .dataframe tbody tr th {\n", + " vertical-align: top;\n", + " }\n", + "\n", + " .dataframe thead th {\n", + " text-align: right;\n", + " }\n", + "</style>\n", + "<table border=\"1\" class=\"dataframe\">\n", + " <thead>\n", + " <tr style=\"text-align: right;\">\n", + " <th></th>\n", + " <th>system.cpu|user_lag0</th>\n", + " <th>system.cpu|user_lag1</th>\n", + " <th>system.cpu|user_lag2</th>\n", + " <th>system.cpu|user_lag3</th>\n", + " <th>system.cpu|user_lag4</th>\n", + " <th>system.cpu|user_lag5</th>\n", + " </tr>\n", + " <tr>\n", + " <th>time_idx</th>\n", + " <th></th>\n", + " <th></th>\n", + " <th></th>\n", + " <th></th>\n", + " <th></th>\n", + " <th></th>\n", + " </tr>\n", + " </thead>\n", + " <tbody>\n", + " <tr>\n", + " <th>1647983445</th>\n", + " <td>3.330669e-16</td>\n", + " <td>0.167293</td>\n", + " <td>0.499561</td>\n", + " <td>0.167504</td>\n", + " <td>0.000633</td>\n", + " <td>0.253165</td>\n", + " </tr>\n", + " <tr>\n", + " <th>1647980613</th>\n", + " <td>5.967300e-03</td>\n", + " <td>0.000422</td>\n", + " <td>0.166665</td>\n", + " <td>0.335848</td>\n", + " <td>0.083963</td>\n", + " <td>0.083542</td>\n", + " </tr>\n", + " <tr>\n", + " <th>1647984383</th>\n", + " <td>2.531518e-01</td>\n", + " <td>0.083327</td>\n", + " <td>0.001899</td>\n", + " <td>0.251886</td>\n", + " <td>0.083963</td>\n", + " <td>0.082700</td>\n", + " </tr>\n", + " <tr>\n", + " <th>1647984447</th>\n", + " <td>1.696266e-01</td>\n", + " <td>0.083542</td>\n", + " <td>0.081459</td>\n", + " <td>0.082074</td>\n", + " <td>0.082280</td>\n", + " <td>0.168344</td>\n", + " </tr>\n", + " <tr>\n", + " <th>1647983270</th>\n", + " <td>5.101800e-03</td>\n", + " <td>0.082498</td>\n", + " <td>0.082703</td>\n", + " <td>0.004262</td>\n", + " <td>0.174051</td>\n", + " <td>0.001050</td>\n", + " </tr>\n", + " </tbody>\n", + "</table>\n", + "</div>" + ], + "text/plain": [ + " system.cpu|user_lag0 system.cpu|user_lag1 system.cpu|user_lag2 \\\n", + "time_idx \n", + "1647983445 3.330669e-16 0.167293 0.499561 \n", + "1647980613 5.967300e-03 0.000422 0.166665 \n", + "1647984383 2.531518e-01 0.083327 0.001899 \n", + "1647984447 1.696266e-01 0.083542 0.081459 \n", + "1647983270 5.101800e-03 0.082498 0.082703 \n", + "\n", + " system.cpu|user_lag3 system.cpu|user_lag4 system.cpu|user_lag5 \n", + "time_idx \n", + "1647983445 0.167504 0.000633 0.253165 \n", + "1647980613 0.335848 0.083963 0.083542 \n", + "1647984383 0.251886 0.083963 0.082700 \n", + "1647984447 0.082074 0.082280 0.168344 \n", + "1647983270 0.004262 0.174051 0.001050 " + ] + }, + "execution_count": 13, + "metadata": {}, + "output_type": "execute_result" + } + ], + "source": [ + "print(df_preprocessed.shape)\n", + "df_preprocessed.sample(5)" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "The model works based on these feature vectors. A lot of ML is about training a model to define some [\"compressed representation\"](https://en.wikipedia.org/wiki/Data_compression#Machine_learning) of the training data that can then be useful for new data in some way.\n", + "\n", + "This is exactly what our cluster models are trying to do. They process a big bag of preprocessed feature vectors, covering `num_samples_to_train` raw observations, during training to come up with the best, synthetic, `n_clusters_per_dimension` feature vectors as a useful compressed representation of the training data.\n", + "\n", + "The cell below will just show you what those `n_clusters_per_dimension` (in this case 2) synthetic (made up by the kemans algo) feature vectors are." + ] + }, + { + "cell_type": "code", + "execution_count": 14, + "metadata": {}, + "outputs": [ + { + "data": { + "text/html": [ + "<div>\n", + "<style scoped>\n", + " .dataframe tbody tr th:only-of-type {\n", + " vertical-align: middle;\n", + " }\n", + "\n", + " .dataframe tbody tr th {\n", + " vertical-align: top;\n", + " }\n", + "\n", + " .dataframe thead th {\n", + " text-align: right;\n", + " }\n", + "</style>\n", + "<table border=\"1\" class=\"dataframe\">\n", + " <thead>\n", + " <tr style=\"text-align: right;\">\n", + " <th></th>\n", + " <th>system.cpu|user_lag0</th>\n", + " <th>system.cpu|user_lag1</th>\n", + " <th>system.cpu|user_lag2</th>\n", + " <th>system.cpu|user_lag3</th>\n", + " <th>system.cpu|user_lag4</th>\n", + " <th>system.cpu|user_lag5</th>\n", + " </tr>\n", + " </thead>\n", + " <tbody>\n", + " <tr>\n", + " <th>centroid 0</th>\n", + " <td>0.182626</td>\n", + " <td>0.169506</td>\n", + " <td>0.100484</td>\n", + " <td>0.178778</td>\n", + " <td>0.177843</td>\n", + " <td>0.100711</td>\n", + " </tr>\n", + " <tr>\n", + " <th>centroid 1</th>\n", + " <td>0.115532</td>\n", + " <td>0.141029</td>\n", + " <td>0.276627</td>\n", + " <td>0.122611</td>\n", + " <td>0.124448</td>\n", + " <td>0.276112</td>\n", + " </tr>\n", + " </tbody>\n", + "</table>\n", + "</div>" + ], + "text/plain": [ + " system.cpu|user_lag0 system.cpu|user_lag1 system.cpu|user_lag2 \\\n", + "centroid 0 0.182626 0.169506 0.100484 \n", + "centroid 1 0.115532 0.141029 0.276627 \n", + "\n", + " system.cpu|user_lag3 system.cpu|user_lag4 system.cpu|user_lag5 \n", + "centroid 0 0.178778 0.177843 0.100711 \n", + "centroid 1 0.122611 0.124448 0.276112 " + ] + }, + "metadata": {}, + "output_type": "display_data" + } + ], + "source": [ + "# lets pick the first model to look at\n", + "model = list(models.keys())[0]\n", + "\n", + "# get the cluster centroids and put them in a dataframe similar to above\n", + "df_cluster_centers = pd.DataFrame(models[model]['model'].cluster_centers_, columns=df_preprocessed.columns)\n", + "df_cluster_centers.index = [f'centroid {i}' for i in df_cluster_centers.index.values]\n", + "display(df_cluster_centers)" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "At inference time we can now use our `n_clusters_per_dimension` cluster centers as a sort of set of \"reference\" feature vectors we can compare against. \n", + "\n", + "When we see a new feature vector that is very far away from these \"reference\" feature vectors, we can take that as a signal that the recent data the feature vecotr was derived from may look significantly different than most of the data the clusters where initially train on. And as such it may be \"anomalous\" or \"strange\" in some way that might be meaningful to you are a user trying to monitor and troubleshoot systems based on these metrics.\n", + "\n", + "To try make this visually clearer we will take 10 random feature vectors from the first half of our data where things were generally normal and we will also take 10 random feature vectors from the yellow anomalous period of time. Lastly we will also include the cluster centroids themselves to see how they compare to both sets of 10 feature vectors. \n", + "\n", + "Basically this is represented in the heatmap below where each row is a processed feature vectors corresponding to some timestamp `t`." + ] + }, + { + "cell_type": "code", + "execution_count": 15, + "metadata": { + "pycharm": { + "name": "#%%\n" + } + }, + "outputs": [ + { + "data": { + "text/plain": [ + "<AxesSubplot:>" + ] + }, + "execution_count": 15, + "metadata": {}, + "output_type": "execute_result" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAt0AAAKiCAYAAAAKQ2DmAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAEAAElEQVR4nOydd3hVVfaw35UQSAJEekgBoiAoSg/FglKkmYioIGLXsYwz9jLqqOjgz7GPo+PM+Cn2sdNEQIoCCiIoIL1JCySE0HuAkKzvj7MTbm7ajZKbwnqf5zy5Z9e119nnZu1119lHVBXDMAzDMAzDMMqOkPIWwDAMwzAMwzCqOmZ0G4ZhGIZhGEYZY0a3YRiGYRiGYZQxZnQbhmEYhmEYRhljRrdhGIZhGIZhlDFmdBuGYRiGYRhGGVOtvAUwjKrC1AatbP/NADh8uLwlMKoaBw6WtwSVh1o1y1sCoyox8MBqCWZ/Hbv+J2j/ZxfO+9MJH5t5ug3DMAzDMAyjjDFPt2EYhmEYhlHhkZCgOtZPOObpNgzDMAzDMIwyxjzdhmEYhmEYRoVHQs3TbRiGYRiGYRhGMZin2zAMwzAMw6j4hFRuX3Hllt4wDMMwDMMwKgFBN7pF5B0R2SYiywIs315ELj5RfYjIXSKySkSWi8gLfnlNReSAiDzozluJyCKfY5+I3Ovy2onIjyKyVES+EpEolx4mIu+79JUi8qhP+/1FZLWIrBWRR3zSP3Lpy5zsYT55PVzfy0XkO5cWLiI/ichil/63YnTxTxG5wOe8gYhkicgf/crd7GRe4uS4NGCFF6I7l1ZHREY5fa8UkXNc+vOunw98yl6bq9sA+xskIioiZ/ikJYhIptPXYhGZIyKtStFmJ6eDtSLymoiIS39JRHoF2k6wqN+rO+fNncz5P00l4e5bC+Q3u+NGzv1hIud8N55OY94jPD42L69Pxgq6zRhHtxnjaP+//wZT7KDT8KLu9Fo4md6Lp9Li/oJ6qndeIhfMHkPynuXEDOqXl17/gq5cOGdc3pG0YwmNk3sHU/SgYno6ccT0607yqslc8utUWj9cUJcnCzanAsd0FRgSKkE7ykR+1eC+z8MZgAeAD1T17ADK3wgkquqdv7cPEekJPAYkqeoREWmkqtt88kcBCsxT1Zf82gwF0oCuqpoiIj8DD6rqdyJyM3Cqqj4hIlcDA1X1KhGJBFYAPYDNwBqgD5AK/AwMU9UVblHxtevqY+B7Vf2viNQB5gD9VXVTrrzOGKypqgecgT4buEdV5/rJXB+YqKrdfNLuAK4GclT1QpcWD3wHdFTVvSJSC2ioqhtKofMCuhOR94FZqjpSRKoDka7MKFXtIyIjgVeBtcAEN86sAPv7DIgFpqvqky4tAZiQe81F5HbgXFW9IcA2fwLuBuYBk4DXVPVrEWkGvKWqfYurH9SX44SEcP68KSwYfBOHt2TQbdooltx2PwfXrMsrUvf8ruxdsJiczMPE3zSMeud1Yckt9wHQa+NCpid0DJq4vgT15TghIfReNIUfB95EZloGF3w/igU33c+BVcf1FNE0jrDatWh+z81snTSd9HFTCjQTVvcUei+eyrRWF5KdWQXf7lPJ9VSRXo4jISEkr5nC9D43kZmaQb+fR/HDsPvZt3JdyZWDQNBejlPJ51RQqcS6CvbLcTr3fCto/2d/nnFr5X85jqp+D+wKpKwz1EYAQ533cujv7OMO4DlVPeLK+Rrcg4ANwPIimu0NrFPVFHfeEvjefZ4GXJHbPVBTRKoBEcBRYB/QBVirqutV9SjwKXCpk2OSOoCfgHjX1tXAGFXd5CuvK3rAlQlzR2ET8Qpgsl/aMOABIM4Z2wCNgP14CxVU9UApDe5B+OlORE4BLgDedm0eVdU9QA4Q5hYOkUAW8CDwr1IY3LWA84E/AFcVUzQK2B1gmzFAlKrOddfhA2CQkz0FqC8ijQNpKxic0rEthzakkJmSimZlsXXsRBoNyO/d2D17Hjnui3fv/EXUiKkw4geNuoltObg+hUMbPT2ljZpI46T8esrclMa+5avRnJwi24kd1I9t02ZV2X/6pqcTR/0ubTmwNoWDG1LJycoi5dOJxF9adT2PRWFzKnBMV4EjIRK0oyyo0DHdzjgdDnymqu1V9TMR6ekX8pF7zAmgyZZAdxGZJyLfiUhnyDPiHgaKDNPAM+4+8TlfjjOagSFAE/d5FHAQSAc2AS+p6i4gDs/bnUuqS8vDea2v47ih3BKoKyIzRWSBiFzvUzZURBYB24BpqjqvEJnPAxb41GkCxKjqT8DnQO4iZjGQAWwQkXdF5BKfOg8Voe/XXH5RujsV2A68KyK/iMhIEampqvvxvMi/OB3txfv1YFwh8hfFpcBkVV0D7BSRTj55zZ1864D7gX84Of1DhXyPOnjXItWnHf/rs9Dps0IQHhPN4S1b884Pb8mgRkx0keXjrhnMjm+/zzsPCa9B129G02XyZzQcUHUNgvDYaDJTffSUlkFEbNF6KorYwUmkfTHhRIpWoTA9nTgi4qI5uPm4Lg+lZhAZV3pdVnZsTgWO6erkodLtXqKqM4D2v7F6NaAe0A3oDHwuIqcBTwGvuHCNApWcx30g8KhP8s3AayLyBDAez6MNnkc7Gy/0oS4wS0S+CVC+/+CFlszykbcTnpc9AvhRROaq6hpVzQbaO4NxrIicrar+MewxeIZvLkPxjG3wPO3vAC+raraI9Hc66Q28IiKdVPUpVX0ReLEYmZ+icN1VAzoCd6nqPBF5FXgEeEJVXwBeAHAhJsNF5BagL7BEVf+vBD0NwwtLyR3HMI4vLtapanvX9lDgTbywldUUM28Ku+5+bMO7pv71bgNuA7inZiMuDq9TUjtBJ2bIQKLan83PA6/NS5vVvidHtm4jolk8iWPf58DKNWRu3FxMKycvNaIbEnVWS7Z9M7u8RanQmJ6ME43NqcAxXVUOKp3R7eKyXykk65CqnltC9VS8cA0FfhKRHKAB0BUYLN6DlXWAHBE5rKqvu3oDgIWqmpHbkKquwjMSEZGWQJLLuhrPC5sFbBORH4BEPC93rjccvBCSNJ9xPQk0BG73k3enqh4EDorI90A7vNjwXDn2iMgMoD/gb3RnAuE+58OAxiJyjTuPFZHTVfVXn9CWn0RkGvAu8JSIPARcQ0G+V9W7i9Idnsc/1ccDPwrP6M5DRDoAAqwGnlXVfs7Tfrqq/lpIn4hIPaAX0EZEFAgF1Mnpz3g3DsR7oPKzwtrEi7lP43hYD/hdHzw9ZvpXVNU38Qz7oMZ0H07PIDz2eLhIeGw0R9IzCpSrd8E5nHrfH5k/8Fr06PHonSNbvciqzJRUdv3wE1FtWldJo/vwlgwi4n30FBdN5paCeiqO2CsGkP7VNPTYsRMtXoXB9HTiyEzLoGaT47qMjI/mUFrpdFkVsDkVOKarwLGX45Q9+4HauSeqOsOFmvgfJRncAOOAnpBnKFcHdqhqd1VNUNUE4J/A330MbvCMVd/QEkSkkfsbAjwOvOGyNuEZhYhITTyv+iq8BydPF5FTnef8KjyjEOfl7Yf3YKVvwNaXwPkiUs09lNkVWCkiDZ2HGxGJwHs4c1Uh410JtPAZby1VjfMZ67PAMBGJFRHfp+raAykAqvpiEfq+2+UXqjtV3QpsluO7h/TGe6jUl6eBJ/Bi0kNdWg4QKSJxIvJtIWMaDHyoqs1cv03w4sm7F1L2fGCdk3N1EeNor6p7VDUd2Cci3Vy8+fVO/7m0pOCiptzY98tSIk9LIKJpPBIWRuPLktg2eXq+MrXbnEnrl0ew6No7OLrj+CMO1U6JQqp7G+SE1atLna4dObB6bVDlDxZ7FiylZvMEIpt5eoobnETGpOklV/QhbnASaV9MLCMJKwampxPHzp+XUvv0BGomxBMSFkazq5JIG186XVYFbE4Fjunq5CHonm4R+QTPs9hARFKBJ1X1bXFb2KnqG35VZgCPuPjlZ1W1KG9liX3ghVO8I95WgkeBG5yHt7i2auIZtbf7ZQ0TkT+7z2NwHlXg33hxzMvxvLjvquoS19adwBQ8A/MdVc198PANPCP3RxfmMEZVR6jqShGZDCzBM0ZHquoyEWkLvC/ejiohwOeqWlgg10Qn90i8hcNYv/zReN7f94GXRCQWOIwXkvJHfj93AR+5RcZ64KbcDPEevpyvqlvc+SIRWYoXXrJYRBKBwpbsw4DnCxlHbnpzN1cE7xrfUgp5/wS8hxfK87U7cmPtWwDzS9FWmaLZ2ax6ZAQdvxiJhISS9vFoDq5eS/NH7mbfomVsnzydlk/9hdCakbR924vEOZyWzqJr76Bmy+a0fvlvkKMQImx89a18u55UJTQ7m6UPjKDbuJFIaCibPhzN/pVrafX43exZuIyMSdOp07ENnT95nbA6UTQe0JNWj93FzM7JgLdjQER8DDtn/VTOIylbTE8nDs3OZv6dI+g5xdPl+ndGs3dF1VzUFofNqcAxXZWCSv5ynKBvGWgEFxGZDSS7nUMqDW6BsklVx1cAWS7D207xieLKBXXLwEpMULcMNE4KKtKWgRWdoG0ZaJwUBHvLwK793w3a/9l5k2864WOrdDHdRql5AGgK7ClnOUqFX3hPeVMNeLm8hTAMwzCMkxmL6TYqNKo6Lze8xfhtqOoXle2XAsMwDMMwyhYp4s3bRWGebsMwDMMwDKPCU1YvrfkdvIq3Y91gOf7m7SIxo9swDMMwDMMwSoEcf/P2jZD3QsejxdUxo9swDMMwDMOo8FSwmG7fN2+3w3tJ3z3u3SqFYjHdhmEYhmEYhuGDiNwmIvN9jtv8iuS+efu/qtoBOIjfSwD9MU+3YRiGYRiGUeEJZky37xuniyCVEt687Y95ug3DMAzDMAyjFAT45u18mKfbME4Q9tKXwLAXmQSOvcgkMExPgXM0q7wlqBzUr1ehYoeNXEIrnK+4yDdvF4YZ3YZhGIZhGIZRSlR1EZAYaHkzug3DMAzDMIwKTwXcp7tUVDg/vWEYhmEYhmFUNczoNgzDMAzDMIwyxsJLDMMwDMMwjApPBXs5TqkxT7dhGIZhGIZhlDFmdBtGJaXhRd3ptXAyvRdPpcX9txbIr3deIhfMHkPynuXEDOqXl17/gq5cOGdc3pG0YwmNk3sHU/QKRUy/7iSvmswlv06l9cMF9XiyYPMpcExXgRHdtzv9lk6m/4qptHqwoJ5CqofR9X+v0H/FVHrN+pzIZnEASFgYiW/+nT4LxnPRz1/S8IIuwRY96NTreT5dZ31N1zlTaHpnQV3FXj+UztPHkzhtLB2+/IjIls0BqN2+DYnTxpI4bSydvxlHgwEXBVv0oCIhErSjLAiq0S0iTURkhoisEJHlInJPAHXai8jFpeznHRHZJiLLCsm7S0RWuf5f8MtrKiIHRORBd95KRBb5HPtE5F6X105EfhSRpSLylYhEufQwEXnfpa8UkUd92u8vIqtFZK2IFHhrkYi8JiIHfM5vFJHtPv3f4lc+SkRSReT1YnQxSkRO8zlvLyIqIv39yj3mdLLE9dW1SAXnr9dDRPb6yDjcJ6/Q6yAiz7t+PvBJuzZXtwH2O8iN4wyftAQRyXRyLBaROT6b1gfSZid33da6ayEu/SUR6RVoO0EhJIS2/xjO3MtvYXpiEnFDkql1RvN8RTI3p7Po9kdJ+3xCvvSd38/ju3MH8d25g5iTdAPZhzLZ/u0PwZS+wiAhIST+ezgzBtzCxNZJNBuWTNSZzUuuWNWw+RQ4pqvACAmhw6vDmT3wFqa0S6LJ0GRq++kp4aYhHN2zj8mt+7Lmtfdo88yDAJz2hyEATOs0kFkX30Tb5x8GqdxhBcUSEkLLvw9n8TW38tOFyUQPSsozqnPJGDOBn3sNZH6fy9j075G0eMozIQ6u/pUF/Qczv89lLL76Vlq98DckNLQ8RmEEQLA93ceAB1S1NdAN+LOItC6hTnugVEY38B7Q3z9RRHoClwLtVPUs4CW/Iv8Avs49UdXVqtpeVdsDnYBDwFiXPRJ4RFXbuLSHXPoQoIZL7wTc7ozBUODfwACgNTDMd+wikgjULWQsn+XKoKoj/fKeBr4vSgkichYQqqrrfZKHAbPd39xy5wDJQEdVbQtcBGwuqt1CmOUj4wif9Pfwuw4icopPP0dFpI2IROBtKP/vUvRZYByOdU6OdsD7wF9L0eZ/gVuB092RK/u/KOHVrsGmbmJbDq5P4dDGVDQri7RRE2mclN9jlrkpjX3LV6M5OUW2EzuoH9umzSI78+R8s0/9Lm05sDaFgxtSycnKIuXTicRfWnU9j0Vh8ylwTFeBUa9zWw6s8+4tzcpi8+cTib0kv55iL+lFyofev9S0MVNo1PMcAGqf2YJtM703ax/Zvousvfup2+ns4A4giER1aEvmxk0c3uTpKuPLSTTol19X2T5vFQuNjARVAHIyD6PZ2QCE1Kiel15VkVAJ2lEWBNXoVtV0VV3oPu8HVgJxRZV3b/gZAQx13suhAfbzPbCrkKw7gOdU9Ygrt82nr0HABmB5Ec32xjPoUtx5S44bvNOAK3K7B2qKSDUgAjgK7AO6AGtVdb2qHgU+xVsA4AzyF4G/BDI+V6cTEA1MLabYNcCXPnUEb1FwI9BHRMJdVgyww0cvO1R1S6CyFEUR1yEHCHOyRAJZwIPAv1Q1oHeliUgt4HzgD8BVxRSNAnYH2GYMEKWqc1VVgQ+AQW4cKUB9EWkcSFvBIDw2mszUrXnnh9MyiIiNLnU7sYOTSPtiQskFqygRcdEc3Hxcj4dSM4iMK70eKzs2nwLHdBUYEbHRZPrcW5lpGUT43VsRsdFkpqYDoNnZZO3bT/X6ddm7ZBWxyb2Q0FAiE+Kp0+EsIuNjgip/MKnROJrDael550fSt1KjccE5FXfj1XT7cSrNH3+QXx9/Ji89qkNbusz8is4zxrP64afyjHCj4lFuMd0ikgB0AOYVVcYZp8M57u39TER6+oV85B5zAui2JdBdROaJyHci0tnJUgt4GPhbMXWvAj7xOV+OM5rxDNkm7vMo4CCQDmwCXlLVXXiLC1/vcSrHFxx3AuNVNZ2CXOFCMUaJSBMnbwjwMp6xWhznAQt8zs8FNqjqOmAmkOTSpwJNRGSNiPxHRC7MrSAirxShb1/P7zkunONr510vErfYmgT8gqejvUBXVR1Xwlh8uRSYrKprgJ1uAZJLcyffOuB+vF8vCgsV8j3q4F2LVJ92fK8PwEI8fVYZakQ3JOqslmz7ZnZ5i2JUAWw+BY7pqng2vjeazLSt9P5xNO1f+is75/6C5pghmfbex8w9py/rnnmZZvfekZe+75cl/NTjEhYMGEKzu27zPN5VlZCQ4B1lQLlsGeiM3NHAvaq6rzR1VXUGXsjJb6EaUA8vtKUz8LmLd34KeEVVD0ghcWPO4z4QeNQn+WbgNRF5AhiP59EGz6OdDcTihYvMEpFvihJIRGLxjPYehWR/BXyiqkdE5Ha8cIlewJ+ASaqaWpi8PsQA233Oh+F52HF/rwdGu3F3AroDPYHPROQRVX1PVe8rrgM8Y7SZa+NiYBxeaEaRqOoLwAsAIjISGO7i1fsCS1T1/0rocxjwqs84hnF8cbHOhQPhfhl5E+ivqqspZt6UoEeAbXjX1L/ebcBtAH+q3oh+YXVKaueEcHhLBhHxxx3v4XHRZG7JKFUbsVcMIP2raeixYydavEpDZloGNZsc12NkfDSH0kqnx6qAzafAMV0FRuaWDCJ87q2IuGgy/e6tzC0ZRMTHkJmWgYSGEhZVm6M7vR8nFz/0bF65njM/Yf+ajUGRuzw4sjWD8LjjnvwaMY05srXoObVt3ERaPfckq/zSD/26nuyDh6h5Rkv2Ly7wSJtRAQi6p1tEwvAM7o9UdcxvqP97PN2pwBj1+Akv1KEB0BV4QUQ2AvcCfxWRO33qDQAWqmreXaCqq1S1r6p2wvOAr3NZV+N5YbNc+MoPQCKQxnFvOEC8S+sAtADWuv4jRWSt62NnbsgHXgx5rkf3HOBOV/4l4HoRea6Q8WYC4U5voXghMMNdvX8B/UWktusrW1VnquqTeJ73K1y9Yj3dqrpPVQ+4z5PwQkcaFHkFfBCRDoAAq4Ehqnolnqe6SKNdROrhLTxGunE8BFyZ+9CjH+OBC1y9kjzdaXjXJJfc65NLuNNnPlT1TVVNVNXEYBncAHsWLKVm8wQim8UjYWHEDU4iY9L0UrURNziJtC8mlpGElYOdPy+l9ukJ1EyIJyQsjGZXJZE2vnR6rArYfAoc01Vg7J6/lFotEohM8PTU5Mok0ifk11P6hOk0u+4yAOIu78e2mXMBCI0IJzQyAoBGvc8l51g2+1eto6qyf9FSIk5tRniTOCQsjOhLL2bHlPy6iji1Wd7n+hf14NAGL9I1vElc3oOTNeJjiWxxGoc3p1JVqey7lwTV0+0Mo7eBlar6jwCr7Qdq5578Tk/3ODxP7gwRaQlUx4tl7u4j41PAAVX13RFkGPlDSxCRRqq6zYV6PA684bI24RmFH4pITTyv+j+BFcDpInIqnjF3FXC1qi4HGvu0e0BVW7jPMT4hJwPxYuBR1Wt8yt8IJKpqYQ/6rcQz6DfixaQvUdV+PnXfBy4TkXlAjqr+6rLaAymur2I93S7OOUNVVUS64C3kdhZXx4en8bzEYUDu49Y5eAuPOOADVfV/qm0w8KGq3u4jw3d4XvpNfmXPxy2GSvJ0A3vE252mG17I0/V4C5NcWgJfBDiuMkezs1n6wAi6jRuJhIay6cPR7F+5llaP382ehcvImDSdOh3b0PmT1wmrE0XjAT1p9dhdzOycDEBE0zgi4mPYOeunch5J+aLZ2cy/cwQ9p3h6XP/OaPauWFveYgUdm0+BY7oKDM3OZtG9I+g+wdPTxvdGs2/lWloPv5vdC5eRPmE6G94dRZd3X6T/iqkc3bWXedd5/25qNKpP9wlvozk5ZG7J4OebA37cqVKi2dms+evTtPvkbSQ0hPRPR3NozVpOfegu9i1exs6pM4i7+RrqdT+HnKxjHNu7j5V3e//yT+naiWZ33kpO1jHQHNY8+jeydu0p3wEZRSIaxCddReR8YBawFM+4Avirqk4SkT8CqOobfnXqAVPwDLNnVfWzAPr5BC9cowGQATypqm+7MJF38Iyvo8CDqjrdr+5TeEb3S+68Jp4xd5qq7vUpdw/wZ3c6BnjUGZ61gHfxdigR4F1VfdHVuRjPAA8F3lHV409CHG/3gKrWcp+fxTO2j+E9kHiHqq7yK38jntF9ZyFtXQe0UtXHReRdYJ6vfkVkIN7DpY/jGZh1XF9rgdtUdUch6vXv407XxjE8T/D9qjrH5RV6HVzeIKC9qj7lzl8C+uEtDK4RbzeXZ3wXCa7cDOB5VZ3sk3Y3cCbwPN5CYzWe7o8Cd6pqkc8N+LWdiLfjSgTeLjZ3uWsaBiwB2qhqkb8Hj6/Vqmo/Nn6C8HkI3yiBWjXLWwKjqnE0oMfVjfr1qvAWhSeQnumrgqqonreNDtr/2RlvXnHCxxZUo9sILuJtxTcDOE9VK9VTKM6Y36Sq4yuALJfhbXP4RHHlzOgODDO6A8eMbuNEY0Z3YJjRHRhmdJeOcnmQ0ggOqpopIk/i7cLhH3pRofEL7ylvquHtFmMYhmEYRjlRVrHWwcKM7iqOqk4pbxkqO6paYWK5DcMwDMOonJjRbRiGYRiGYVR8Qsvt9TInhMotvWEYhmEYhmFUAszoNgzDMAzDMIwyxsJLDMMwDMMwjApPZX+Q0jzdhmEYhmEYhlHGmKfbME4Qtv90YNje04FjeyoHRlTtkssYHjanAiN9q712oSIioebpNgzDMAzDMAyjGMzTbRiGYRiGYVR4LKbbMAzDMAzDMIxiMU+3YRiGYRiGUeGxmG7DMAzDMAzDMIrFPN2GYRiGYRhGhUdCKrevuHJLbxiGYRiGYRiVgKAa3SISLiI/ichiEVkuIn8LoE4PETm3lP1MFpE9IjLBL11E5BkRWSMiK0Xkbr/8ziJyTEQGu/OeIrLI5zgsIoNcXi8RWSgiy0TkfRGp5tJPEZGvfMZ4k18fUSKSKiKv+6TNFJHVPv00cunNRORbEVniysT71HnBtb9SRF4TkUIDnURklIic5nPeXkRURPr7lXvMtbfEydC1FPru4eosF5HvXFoTEZkhIitc+j0+5Z93/Xzgk3atiNxbij4HuXGc4ZOWICKZTpbFIjJHRFqVos1OIrJURNb66lREXhKRXoG2U1GI6ded5FWTueTXqbR++NbyFqfcaHhRd3otnEzvxVNpcX9BPdQ7L5ELZo8hec9yYgb1y0uvf0FXLpwzLu9I2rGExsm9gyl60Inu251+SyfTf8VUWj1YUFch1cPo+r9X6L9iKr1mfU5kszgAJCyMxDf/Tp8F47no5y9peEGXYIseVOr36s55cydz/k9TSbi7oJ6a3XEj5/4wkXO+G0+nMe8RHh+bl9cnYwXdZoyj24xxtP/ff4MpdtD5zfOpWjUSRz5HnwXj6bt4Eq0eui3Yolc47PvcIyREgnaUifxl0mrRHAF6qWo7oD3QX0S6lVCnB1Aqoxt4EbiukPQbgSbAGap6JvBpboaIhALPA1Nz01R1hqq2V9X2QC/gEDBVREKA94GrVPVsIAW4wVX7M7DCjbEH8LKIVPeR4Wng+0Jkuya3L1Xd5tJeAj5Q1bbACOBZJ+u5wHlAW+BsoDNwoX+DInIWEKqq632ShwGz3d/ccucAyUBH19dFwOZCZCyAiNQB/gMMVNWzgCEu6xjwgKq2BroBfxaR1iJyik8/R0WkjYhEADcB/w6kz6LG4VjndNgO7xr9tRRt/he4FTjdHbkLk38Bj5SinXJHQkJI/PdwZgy4hYmtk2g2LJmoM5uXt1jBJySEtv8YztzLb2F6YhJxQ5KpdUZ+PWRuTmfR7Y+S9nm+NTo7v5/Hd+cO4rtzBzEn6QayD2Wy/dsfgil9cAkJocOrw5k98BamtEuiydBkavvpKuGmIRzds4/Jrfuy5rX3aPPMgwCc9gfvtp/WaSCzLr6Jts8/DIX7ASo/ISGc+fxwFg69hR/OSyLm8mRqtsyvp31LVzL3oiv48cKBZHw1hZZPPZSXl515mLk9BzG35yAWXXtHsKUPHr9jPsVf0Z/QGtWZ1mkg33a7nNNuGZpnkJ+M2Pd51SGoRrd6HHCnYe4o8rVPIpIA/BG4z3kvuwfYz7fA/kKy7gBGqGqOK7fNJ+8uYDSwrZB6AIOBr1X1EFAfOKqqa1zeNOCK3O6B2s5LWgvYhWeAIiKdgGh8DPsSaA1Md59nAJf69BEOVAdq4Okxo5D61wBf5p44mYbgLT76iEi4y4oBdqjqEQBV3aGqWwKU8WpgjKpucnW3ub/pqrrQfd4PrATigBwgzMkSCWQBDwL/UtWA3pUmIrWA84E/AFcVUzQK2B1gmzFAlKrOVVUFPgAGOflTgPoi0jiQtioC9bu05cDaFA5uSCUnK4uUTycSf2nV9tIWRt3Ethxcn8KhjaloVhZpoybSOCm/HjI3pbFv+Wo0J6fIdmIH9WPbtFlkZx4ua5HLjXqd23JgnTdnNCuLzZ9PJPaS/LqKvaQXKR+OBSBtzBQa9TwHgNpntmDbzHkAHNm+i6y9+6nb6ezgDiBInNKxLYc2pJCZ4ulp69iJNBqQX0+7Z88jx82VvfMXUSOm0nx1nDB+z3xCldCaEUhoKKER4eRkZZG174B/FycN9n1+HPN0lxIRCRWRRXjG7TRVnVdUWVXdCLwBvOK8l7NE5Bq/kI/cY1QA3TcHhorIfBH5WkROdzLFAZfheTqL4irgE/d5B1BNRBLd+WA8DzrA68CZwBZgKXCPquY47/jLeAZmYbzrxvGET6jIYuBy9/kyPGO+vqr+iGeEp7tjiqquLKTN84AFPufnAhtUdR0wE0hy6VOBJuKF3fxHRPK85iLyShH6zvX8tgTquvCXBSJyvb8QbvHUAZjnDPBJwC9O9r1AV1UdV4ReCuNSYLJb9Ox0i5lcmjv51gH3A/9wMrQqYhyLnLc+Dkj1aSfVpeWyEE+flYKIuGgObt6ad34oNYPIuOhylKh8CI+NJjP1uB4Op2UQEVt6PcQOTiLtiwklF6zERMRGk+kzZzLTMojwmzMRsdFkpqYDoNnZZO3bT/X6ddm7ZBWxyb2Q0FAiE+Kp0+EsIuNjgip/sAiPiebwFp85tSWDGjFFz6m4awaz49vjP26GhNeg6zej6TL5MxoOqLqG0++ZT6ljppB9MJPklNlcvHYGa155h6zde4Mqf0XCvs+rDkHfvURVs4H2ztAZKyJnq+qyUtT/CPjoN3ZfAzisqokicjnwDtAd+CfwsDOOC1RyXtA2wBQng4rIVcArIlIDz2jNdsX7AYvwwlGaA9NEZBZwPTBJVVML6eMaVU0Tkdp43vbr8DytDwKvi8iNeCEpaUC2iLTAM+xzY7yniUh3VZ3l124MsN3nfBjHQ2o+dTKNVtUDznDtDvQEPhORR1T1PVW9r2h1At4c6gT0BiKAH0Vkbu6vAM4rPRq4V1X3Of29ALzg8kcCw0XkFqAvsERV/6+EPocBr/qMYxjHFxfrXDgQIjIUeBPor6qr8UKaCqWw6+7HNiC2pEJG1aNGdEOizmrJtm9ml7coFZaN740m6ozm9P5xNIc2bWHn3F/QnOySK1ZxYoYMJKr92fw88Nq8tFnte3Jk6zYimsWTOPZ9DqxcQ+bGgKL5ThrqdW6LZucwIaE71etG0WP6x2ybPoeDG1JLrmxUaSr7Pt3ltmWgqu4RkRl4cbMBG90icg3wUCFZa1V1cAnVU4Ex7vNY4F33ORH41BleDYCLReSYj/f1SmCsb/iD8zZ3dzL1xfP4gheb/JwLUVgrIhuAM4BzgO4i8ie8sJPqInJAVR9R1TTX5n4R+RjoghfLvQXn6XbG6xVOb7cCc3NDdUTka9e+v9GdiReGkhuzfgVwqYg8BgheyERtVd3vFkMzgZkishQvRv09EXkFzxD351NVfc7pdKeqHgQOisj3QDtgjYiE4RncH6nqGP8GRKSDk2M18Kyq9hORd0XkdFX9tZA+EZF6eAuaNiKiQCigIlLYnBiPu8bugcrPCmsTL/Y+jeOLGNznNJ/zcDx9+stzG3AbwB9oRC/qFNFFcMlMy6Bmk+M/aUfGR3MorbAIpKrN4S0ZRMQf10N4XDSZW0qnh9grBpD+1TT02LETLV6FInNLBhE+cyYiLppMvzmTuSWDiPgYMtMykNBQwqJqc3SnF8G1+KFn88r1nPkJ+9dsDIrcweZwegbhsT5zKjaaI+kF51S9C87h1Pv+yPyB16JHj0fOHdnqRTBmpqSy64efiGrTukoa3b9nPjW56i62Tp2FHjvGke272DFnIXU7tjlpjW77Pq86BHv3kobOw417eK4PsKqEavuB2rknqvqRzwOHvkdJBjfAOI4bkBcCa1ybp6pqgqomAKOAP/mFOwzjeGhJ7lhydxipATyMFwYDsAnP64uIRAOtgPWqeo2qNnV9PIhnVD8iItVEpIErH4b3QOMyd97AhaUAPIrnmc/t40JXN8yNpbDwkpVAC/e5N54XuYkbazM8g/gyF3pxuk+99ngPh6Kq9xWh7+dc2S+B850skUBXYKULkXkbWKmq/yhENvAeKn0CLyY91KXlAJEiEici3xZSZzDwoao2c+NoAmzALYD8OB9Y58axuohxtFfVPaqaDuwTkW5O9uvxiYfHW1QVWByq6puqmqiqiRXF4AbY+fNSap+eQM2EeELCwmh2VRJp46eXXLGKsWfBUmo2TyCyWTwSFkbc4CQyJpVOD3GDk0j7YmIZSVhx2D1/KbVaJBCZ4OmqyZVJpE/Ir6v0CdNpdt1lAMRd3o9tM+cCEBoRTmhkBACNep9LzrFs9q9aF9wBBIl9vywl8rQEIpp6emp8WRLbJufXU+02Z9L65REsuvYOju7YlZde7ZQopHoYAGH16lKna0cOrF4bVPmDxe+ZT5mb0mnUw9tAKzQygvpd27F/9XpOVuz7vOoQbE93DPC+87qGAJ+r6gQAERkBzFfV8X51vgJGicilwF2FhFAUwIVznAHUEpFU4A+qOgV4DvhIRO4DDgC3BNBWAl689nd+WQ+JSLIbx39VNfcOeBrPQ7wUz4v7sKruKKaLGsAUZzyHAt8Ab7m8HsCzzqP7Pd7OKOAtDHrhxYwrXnzzV4W0PdG18Q3ewmGsX/5ovIdLlwP/cguiY8BanPe2JFR1pYhMBpbgGcwjVXWZiJyPFyazVLwYfoC/quok8Lb8w7veW9z5IqezJaq62MXLF+ZaHIa3y4z/OHLTm7v+BDhKANfYhz8B7+GFyXztjtzFUAtgfinaKlc0O5v5d46g55SRSGgo698Zzd4VVfOfe3FodjZLHxhBt3GeHjZ9OJr9K9fS6vG72bNwGRmTplOnYxs6f/I6YXWiaDygJ60eu4uZnZMBiGgaR0R8DDtn/VTOIyl7NDubRfeOoPsET1cb3xvNvpVraT38bnYvXEb6hOlseHcUXd59kf4rpnJ0117mXedFn9VoVJ/uE95Gc3LI3JLBzzf/pZxHU3ZodjarHhlBxy9GIiGhpH08moOr19L8kbvZt2gZ2ydPp+VTfyG0ZiRt3/ai4A6npbPo2juo2bI5rV/+G+QohAgbX32Lg2uq5uLk98yntW98ROe3nqXPLxMQETZ+MIa9y1aX84jKD/s+P05ZPeAYLMSLgjCqIu7XhBnAeS58pNIgIncCmwpZhJWHLJfhbXP4RHHlPpZWdjMFQK2a5S1B5eFoQPv5GFG1Sy5jeOwrbF8vowBHj5a3BJWDq3V1UK3ggU9NDdr/2fFP9T3hY7PXwFdhVDVTRJ7E24VjU3nLUxpU9fWSSwWNang7zxiGYRiGUU5Udk+3Gd1VHBdWY/wOVPWL8pbBMAzDMIzKjRndhmEYhmEYRoWnsnu6g/5yHMMwDMMwDMM42TBPt2EYhmEYhlHhCQmp3L7iyi29YRiGYRiGYVQCzNNtGIZhGIZhVHhCKvlr4M3TbRiGYRiGYRhljHm6DeMEYS99CQx74Uvg2EtfAsNe+BI49tKXwKhevbwlMArDdi8xDMMwDMMwDKNYzNNtGIZhGIZhVHjEPN2GYRiGYRiGYRSHeboNwzAMwzCMCo/FdBuGYRiGYRiGUSxmdBuGYRiGYRhGGWPhJYZhGIZhGEaFx8JLfgMiEioiv4jIhADK9hCRc0vZ/mQR2ePfvng8IyJrRGSliNztl99ZRI6JyGB33lNEFvkch0VkkMvrJSILRWSZiLwvItVc+iki8pWILBaR5SJyk0/7N4jIr+64wSe9uoi86eRaJSJX+ORdKSIrXFsf+6S/4NJWishrIlLoTBSRUSJyms95exFREenvV+4x194SN9auAeq6h4js9dHRcJ+8d0Rkm4gs86vzvOvnA5+0a0Xk3kD6dOUHuXGc4ZOWICKZTo7FIjJHRFqVos1OIrJURNb66lREXhKRXoG2EywaXtSdXgsn03vxVFrcf2uB/HrnJXLB7DEk71lOzKB+een1L+jKhXPG5R1JO5bQOLl3MEUPKtF9u9Nv6WT6r5hKqwcL6imkehhd//cK/VdMpdesz4lsFgeAhIWR+Obf6bNgPBf9/CUNL+gSbNGDSv1e3Tlv7mTO/2kqCXcX1FOzO27k3B8mcs534+k05j3C42Pz8vpkrKDbjHF0mzGO9v/7bzDFLhd+85yqVo3Ekc/RZ8F4+i6eRKuHbgu26BWKmH7dSV41mUt+nUrrhwvq8WTC5tTJQXmFl9wDrAywbA+gVEY38CJwXSHpNwJNgDNU9Uzg09wMEQkFngem5qap6gxVba+q7YFewCFgqoiEAO8DV6nq2UAKkGtE/xlYoartnOwvO6O6HvAk0BXoAjwpInVdnceAbaraEmgNfOdkOh14FDhPVc8C7nXp5wLnAW2Bs4HOwIX+gxWRs4BQVV3vkzwMmO3+5pY7B0gGOqpqW+AiYHMh+iuKWbl6UtURPunvAf7G/Sk+/RwVkTYiEgHcBPy7FH0WGIdjnZOjHd41+msp2vwvcCtwujtyZf8X8Egp2il7QkJo+4/hzL38FqYnJhE3JJlaZzTPVyRzczqLbn+UtM/zr213fj+P784dxHfnDmJO0g1kH8pk+7c/BFP64BESQodXhzN74C1MaZdEk6HJ1PbTU8JNQzi6Zx+TW/dlzWvv0eaZBwE47Q9DAJjWaSCzLr6Jts8/DIWvbSs/ISGc+fxwFg69hR/OSyLm8mRqtsyvp31LVzL3oiv48cKBZHw1hZZPPZSXl515mLk9BzG35yAWXXtHsKUPLr9jTsVf0Z/QGtWZ1mkg33a7nNNuGZpnPJ1sSEgIif8ezowBtzCxdRLNhiUTdWbzkitWRWxOBUxIqATtKBP5y6TVYhCReCAJGBlA2QTgj8B9znvZPZA+VPVboLB3lN0BjFDVHFdum0/eXcBoYFsh9QAGA1+r6iGgPnBUVde4vGlArndagdrOS1oL2AUcA/oB01R1l6rudnVyjbqbgWedTDmqusOl3wr825X3lVeBcKA6UAMIAzIKkfka4MvcEyfTELzFRx8RCXdZMcAOVT3i+tmhqluK0EPAqOr3eOP3JQcIc7JEAlnAg8C/VDWgdxWKSC3gfOAPwFXFFI0CdgfYZgwQpapzVVWBD4BBbhwpQH0RaRxIW8GgbmJbDq5P4dDGVDQri7RRE2mclN9bnbkpjX3LV6M5OUW2EzuoH9umzSI783BZi1wu1OvclgPrUji4wdPT5s8nEntJfj3FXtKLlA/HApA2ZgqNep4DQO0zW7Bt5jwAjmzfRdbe/dTtdHZwBxAkTunYlkMbUshM8fS0dexEGg3Ir6fds+eR4+bJ3vmLqBFTYW6HoPJ75hSqhNaMQEJDCY0IJycri6x9B4I9hApB/S5tObDW02NOVhYpn04k/tKq+4tbcdicOnkoD0/3P4G/4BlfxaKqG4E3gFec93KWiFzjF/KRe4wKoO/mwFARmS8iXztPMiISB1yG5+ksiquAT9znHUA1EUl054PxPOgArwNnAluApcA9zsiPI7/3OBWIE5E67vxpF67yhYhEu7SWQEsR+UFE5uaGhKjqj8AMIN0dU1S1sF8OzgMW+JyfC2xQ1XXATLzFD3je/SYuvOU/IpLnNReRV4rQt6/n9xwXzvG1864XiaruByYBvzjZ9wJdVXVccfX8uBSY7BY9O0Wkk09ecyffOuB+4B9uHK2KGMcidw3i8K5JLqkuLZeFePqsEITHRpOZujXv/HBaBhGx0cXUKJzYwUmkfVFilFelJSI2mszNx/WUmZZBRFx0wTKp6QBodjZZ+/ZTvX5d9i5ZRWxyLyQ0lMiEeOp0OIvI+Jigyh8swmOiObzFZz5tyaBGTNHzKe6awez49vu885DwGnT9ZjRdJn9GwwFV23D6PXMqdcwUsg9mkpwym4vXzmDNK++QtXtvUOWvKETERXPQR4+HUjOIjCv9d1hVwOZU4ISESNCOsiCoD1KKSDJeGMUCEenxW9pQ1Y+Aj36jCDWAw6qaKCKXA+8A3fEWAg+rak5hodHOC9oGmOJkUBG5CnhFRGrgGa3Zrng/YBFeOEpzYJqIzCpGpmpAPDBHVe8XkfuBl/DCY6rhhTn0cGW+F5E2QAM8wz7etTFNRLqrqn8/McB2n/NhHA+p+RS4Hhitqgec4dod6Al8JiKPqOp7qnpfMbKDZ4w2c21cDIxzMheJqr4AvAAgIiOB4SJyC9AXWKKq/1dCn8OAV33GMYzji4t1LhwIERkKvAn0V9XVQPuiGizsuvuxDYj1TxSR24DbAP5UvRH9wuqU1E6FoUZ0Q6LOasm2b2aXtygVko3vjSbqjOb0/nE0hzZtYefcX9Cc7JIrVnFihgwkqv3Z/Dzw2ry0We17cmTrNiKaxZM49n0OrFxD5sbSRKidHNTr3BbNzmFCQneq142ix/SP2TZ9Dgc3pJZc2TAKweZU5SLYu5ecBwx0xlk4ECUi/1PVa0uol4eIXAM8VEjWWlUdXEL1VGCM+zwWeNd9TgQ+dYZXA+BiETnm4329EhjrG/7gvM3dnUx98bzS4MUmP+dCFNaKyAbgDCANz3jOJR7P27wTL1Y8V64v8MImcuWd5/rdICJrOG6Ez1XVA67/r4FzAH+jOxNPz7kx61cAl4rIY4DghUzUVtX9qprt5JkpIkvxYtTfE5FX8Axxfz5V1edUdZ+PTiY5T3kDnxCZIhGRDk6O1cCzqtpPRN4VkdNV9dci6tTDW9C0EREFQgEVkcLmxHjcNXYPVH5WhCg98K5PvE9avEvLJRxPn/lQ1TfxDHvG12qlRbR/wjm8JYOI+OM/74fHRZO5pbAIo6KJvWIA6V9NQ48dO9HiVRgyt2QQ0eS4niLioslMyyhYJj6GzLQMJDSUsKjaHN3pRSUtfujZvHI9Z37C/jUbgyJ3sDmcnkF4rM98io3mSHrB+VTvgnM49b4/Mn/gtejR49FgR7Z6kW+ZKans+uEnotq0rrJG9++ZU02uuoutU2ehx45xZPsudsxZSN2ObU5KAykzLYOaPnqMjI/mUFrpvsOqCjanAickpHLvdB1U6VX1UVWNV9UEvHCN6QEY3PuB2j5tfOTz0J7vUZLBDZ4XNteAvBBY49o8VVUTnFyjgD/5hTsM43hoCQAi0sj9rQE8jBcGA7AJ6O3yooFWwHo8L3lfEanrHqDsixcWosBXHDfIewMrfOTt4dpqgGfYr3d9XCgi1UQkzI2lsPCSlUALn3aXqGoTN9ZmeDHsl7nQC1/vdHu8h0NR1fuK0PdzTq7GLj4bEemCN6d2FiJLYTwNPIEXkx7q0nKASBGJE5FvC6kzGPhQVZu5cTQBNuAWQH6cD6xz41hdxDjaq+oeVU0H9olINzee6/GJh8fT/bKCXZQPexYspWbzBCKbxSNhYcQNTiJj0vRStRE3OIm0LyaWkYQVg93zl1KrRQKRCZ6emlyZRPqE/HpKnzCdZtddBkDc5f3YNnMuAKER4YRGRgDQqPe55BzLZv+qdcEdQJDY98tSIk9LIKKpp6fGlyWxbXJ+PdVucyatXx7Bomvv4OiO449qVDslCqkeBkBYvbrU6dqRA6vXBlX+YPJ75lTmpnQa9fA2hgqNjKB+13bsX72ek5GdPy+l9ukJ1EyIJyQsjGZXJZE2vnTfYVUFm1MnDxVmn24RGQHMV9XxfllfAaNE5FLgrkJCKApraxaed7mWiKQCf1DVKcBzwEcich9wALglgLYS8OK1v/PLesiFy4QA/1XV3DvkaTwP8VI8L+7DuV5fEXka+NmVG6Gquf+5HgY+FJF/4oWD5G4zmGuor8ALX3lIVXe6+PVeeDHjihff/FUh4k/EM9q/wVs4jPXLH433cOly4F8utvkYsBYXMhEAg4E7ROQYnif4KreQQEQ+cf03cNfhSVV92+UNwrveW9z5IqezJaq62MXLF+aCHYa3y4z/OHLTm4vIIjzdHyWAa+zDn/B2XIkAvnYHbmHTAphfirbKFM3OZukDI+g2biQSGsqmD0ezf+VaWj1+N3sWLiNj0nTqdGxD509eJ6xOFI0H9KTVY3cxs3MyABFN44iIj2HnrJ/KeSRli2Zns+jeEXSf4Olp43uj2bdyLa2H383uhctInzCdDe+Oosu7L9J/xVSO7trLvOu8iKoajerTfcLbaE4OmVsy+Pnmv5TzaMoOzc5m1SMj6PjFSCQklLSPR3Nw9VqaP3I3+xYtY/vk6bR86i+E1oyk7dteZNfhtHQWXXsHNVs2p/XLf4MchRBh46tvcXBN1VycwO+bU2vf+IjObz1Ln18mICJs/GAMe5etLucRlQ+anc38O0fQc4qnx/XvjGbviqq7WCsOm1OBI5V8n25x9pFRBRFvK74ZeFsOVqpgVBG5E9hUyCKsPGS5DG+bwyeKKxfM8JLKzNGA9qgxAKJql1zGgH2F7VVlFMrRo+UtQeWgevXylqByMPjI6qBawbe8OTdo/2dH3tbthI+twni6jROPqmaKyJN4u3BsKm95SoOqvl7eMvhQDXi5vIUwDMMwjJOZyv5GSjO6qzgurMb4HajqF+Utg2EYhmEYlRszug3DMAzDMIwKT1m9KTJYVO69VwzDMAzDMAyjEmCebsMwDMMwDKPCU9ljus3TbRiGYRiGYRhljBndhmEYhmEYhlHGWHiJYRiGYRiGUeGp7OElZnQbhmFUUMLCKvc/mGBx9Ki9lypQatUsbwkqBwcOlrcERlXEjG7DMAzDMAyjwlPZPd0W020YhmEYhmEYZYx5ug3DMAzDMIwKj4RUbl9x5ZbeMAzDMAzDMCoB5uk2DMMwDMMwKjyV/TXwZnQbhmEYhmEYRikRkY3AfiAbOKaqicWVt/ASw6ikNLyoO70WTqb34qm0uP/WAvn1zkvkgtljSN6znJhB/fLlRcTH0O3Lt+m5YBI9508komlcsMQOOtF9u9Nv6WT6r5hKqwcL6imkehhd//cK/VdMpdesz4ls5ulCqlUjceRz9Fkwnr6LJ9HqoduCLXrQqdfzfLrO+pquc6bQ9M6Cuoq9fiidp48ncdpYOnz5EZEtm+fLrxEXQ/e1C2jyx5uDJXK5ENOvO8mrJnPJr1Np/XDhc+q8T1/hkl+n0nfu59R0c6p6vTr0nv4BQ/YvJPFfTwRb7KBj31EnjpLm3MlCSIgE7SgFPVW1fUkGNwTZ6BaRjSKyVEQWicj8AMq3F5GLS9nHOyKyTUSWFZJ3l4isEpHlIvKCX15TETkgIg+681ZOztxjn4jc6/LaiciPbixfiUiUS7/Gr06OiLR3eUNFZInr+/lCZLtCRFREEt15gohk+rT1hk/ZYtvyKTdIRIb7pS0SkU/90rqJyDyXt1JEnipBzb5164jIKKfXlSJyjl/+A25cDXzGuVxEZolIfZfWXEQ+K0WfDUQkS0T+6JfuO7+WisilpWiznohME5Ff3d+6Lj1ZREYE2k7QCAmh7T+GM/fyW5iemETckGRqnZHfAMrcnM6i2x8l7fMJBap3eOt51v3zbWZ0upjvLxzC0e07gyV5cAkJocOrw5k98BamtEuiydBkavvpKeGmIRzds4/Jrfuy5rX3aPPMgwDEX9Gf0BrVmdZpIN92u5zTbhmaZ5BXSUJCaPn34Sy+5lZ+ujCZ6EFJBYzqjDET+LnXQOb3uYxN/x5Ji6ceyZff4qlH2DV9VjClDjoSEkLiv4czY8AtTGydRLNhyUSdmV9Pzf8whKO79/HV6X1Z/cp7tH/em1PZh4+w5IlX+eXBFwprumph31EnjEDmnFE5KA9Pd8ArAqA9UCqjG3gP6O+fKCI9gUuBdqp6FvCSX5F/AF/nnqjqaidne6ATcAgY67JHAo+oahuX9pCr85FPneuADaq6yBmXLwK9Xd+NRaS3j2y1gXuAeX4yrcttT1X/6MoW25YffwH+49PPmUAo0F1EfF+R8D5wm5P7bODzItorjFeByap6BtAOWOnTXxOgL7DJp/xdQGfg/wFXu7T/Ax4vRZ9DgLnAsELyerpxDAZeK0WbjwDfqurpwLfuHGAicImIRJairTKnbmJbDq5P4dDGVDQri7RRE2mclH8aZG5KY9/y1WhOTr70Wmc0R0KrsX3GHACyDx4iO/Nw0GQPJvU6t+XAuhQObvD0tPnzicRekl9PsZf0IuVD79ZOGzOFRj3dulGV0JoRSGgooRHh5GRlkbXvQLCHEDSiOrQlc+MmDm/ydJXx5SQa9Muvq2yfN4aERkaCHn8pTYP+vTm8KZWDq9cGTebyoH6XthxY682pnKwsUj6dSPyl+fUUf2kvNrzvzalNo6YQ3dubU9mHMtn+wwKyDx8JutzBxr6jThyBzLmThQro6VZgqogsEJESfw6tsOElIlIdGAEMdZ7LoYHUU9XvgV2FZN0BPKeqR1y5bT59DQI2AMuLaLY3ngGc4s5bAt+7z9OAKwqpMwzI9SifBvyqqtvd+Td+dZ4GngcC+VYpqS0ARKQlcERVd/jJ9CEwFW8BkksjIB1AVbNVdUUAciAipwAXAG+7ukdVdY9PkVfwDH/f18XlADWASCBLRLoDW1X110D69BnHA0CciMQXUSYK2F2KNi/FW3zg/g4CUFUFZgLJpWirzAmPjSYzdWve+eG0DCJiowOqW6tFAll799H5439x4Q9jaf1/f4FKvg1TUUTERpO5+bieMtMyiIiLLlgmNR0Azc4ma99+qtevS+qYKWQfzCQ5ZTYXr53BmlfeIWv33qDKH0xqNI7mcFp63vmR9K3UaFxwTsXdeDXdfpxK88cf5NfHnwE8A7zpn29l48v/Dpq85UVEXDQHfebUodQMIv3nVFw0Bzf7zKm9+6lRv25Q5Sxv7DvqxBHInDNOPCJym4jM9zkKM6rPV9WOwADgzyJyQXFtBnsWB7wiUNWjwHDgM+fp/UxEevqFb+QecwLouyWeh3eeiHwnIp0BRKQW8DDwt2LqXgV84nO+nONG6xCgSSF1hvrUWQu0ciEj1fAMuiau/45AE1WdWEgbp4rIL07e7iW15cd5wMJCZPrUyeXrJX4FWC0iY0XkdhEJd7KVpO9Tge3Au07OkbkedBfakaaqi/1keBZvoXCJk+MJvEVHQDjveYyq/oTnkfdfjM0QL7ToO3y85y6cpbCxXOSKRKtqrsWxFfD9RpsPdKeKINWqUf/cRJb/9Xm+v2AwkafG0/Tay8tbrApHvc5t0ewcJiR05+tWvWl5783UPLWoNd7JQ9p7HzP3nL6se+Zlmt17BwAJD97J5jffI/vQoXKWzqgK2HeUURTB9HSr6puqmuhzvOkvj6qmub/b8CIfuhQnf7B3LzlfVdNEpBEwTURWOc90QKjqDLyQk99CNaAe0A0vvOFzETkNeAp4RVUPiBT8OcF53AcCj/ok3wy8JiJPAOOBo351ugKHVHWZk3u3iNwBfIbn6Z0DNBeRELywlhsLkTcdaKqqO0WkEzBORM4qqq1C6sfgGcS5MiUCO1R1k4ikAe+ISD1V3aWqI0TkI7xQkKvxDPIeAei7GtARuEtV54nIq8AjIvIs8FfXXj5UdRrerwOIyPXAJKCleLH0u4F7VLW4/9xDOR7+8inwDvCyT35PVd0hIs2Bb0VkpqoeUNWAjWZVVRHx9c5vA2ILK+sWj7cB/Kl6I/qF1Qm0m9/F4S0ZRMQ3zjsPj4smc0tGYHXTtrJ36UoObUwFYOtX31K3Szv4oExELVcyt2QQ0eS4niLioslMyyhYJj6GzLQMJDSUsKjaHN25myZX3cXWqbPQY8c4sn0XO+YspG7HNhzckBrsYQSFI1szCI+LyTuvEdOYI1uLnlPbxk2k1XNPsgqI6tiWhsn9aP7EQ1SLqg05OeQcOULaux8FQfLgkpmWQU2fORUZH80h/zmVlkHNJj5z6pTaHNlZmh/eKj/2HXXiCGTOGcHHORlDVHW/+9wXL0KjSILq6S7tisCf3+npTgXGqMdPeAZrA6Ar8IJ4277cC/xVRO70qTcAWKiqeTNcVVepal9V7YTnrV3n15e/ZxxV/UpVu6rqOcBqYA1QGy+GeqbrvxswXkQSVfWIqu50dRe4PloW05Y/mUC4z/kw4AzXzzq88Iu8sBRVXaeq/8ULpWknIvUD0HcqkKqqubHoo/CM8OZ4XvDFrr94YKGI5H1ruBjpG4F/4/3KcAMwG7imkLH4Mgy40bU7HmgrIqf7F1LVdUAG0Nr1V5KnO0NEYlzZGDxDO5dwp88C+K6Eg2VwA+xZsJSazROIbBaPhIURNziJjEnTA6q7e8FSwk6JonoD7+fuBhd2Zf+qqhmHu3v+Umq1SCAywdNTkyuTSJ+QX0/pE6bT7LrLAIi7vB/bZs4FIHNTOo16dAUgNDKC+l3bsX/1+uAOIIjsX7SUiFObEd4kDgkLI/rSi9kxJb+uIk5tlve5/kU9OLTBi7j7ZdC1zO3Sm7ldepP61gekvPZmlTS4AXb+vJTapydQMyGekLAwml2VRNr4/HpKHT+dU2/w5lTTwf3ImD63PEQtV+w76sQRyJw7WQgRCdoRANHAbBFZDPwETFTVycVVCJqn+7esCPD2Pqyde/I7Pd3jgJ544Qctgep4nt88D6h4u3YcUNXXfeoNw8+AFpFGqrrNeaofB3x3FgkBrsQvHMGnTl3gT8CVqroXz/DPLTMTeFBV54tIQ2CXqmY7j/zpwPqi2ipkvCuBa/1kaqOqW1xaT7zQjrdEJAmY5OKXT8fbb3JPSfpW1a0isllEWqnqajyDfYWqLsWLE88d10Yg0S++/CHgNVXNEpEIvNCjHLxYb0TkW+D63IWaS2sJ1FLVOJ+0v+Fdo3xzyf2aciqQ4mQtydM9Hs/wf879/dInryVQYDec8kSzs1n6wAi6jRuJhIay6cPR7F+5llaP382ehcvImDSdOh3b0PmT1wmrE0XjAT1p9dhdzOycDDk5rPjr85w74X0Q2PPLclLe/aK8h1QmaHY2i+4dQfcJnp42vjeafSvX0nr43exeuIz0CdPZ8O4ourz7Iv1XTOXorr3Mu+4+ANa+8RGd33qWPr9MQETY+MEY9i5bXc4jKjs0O5s1f32adp+8jYSGkP7paA6tWcupD93FvsXL2Dl1BnE3X0O97ueQk3WMY3v3sfLuR0puuIqh2dnMv3MEPad4c2r9O6PZu2Itbf52N7vmLyPtq+mse3sU5374Ipf86s2p2Vfdl1d/4IZvCYuqRUj1MOIHXcT0vjezb6W/36byY99RJ46i5pxRvqjqerwNJAJGVLXkUicAZzjm7v5RDfhYVZ9xeX8EUNU3/OrUA6YAYcCzqlritnIi8gnQA8+YzQCeVNW3XZjIO3hG5FE843a6X92n8Izul9x5TbydN05zBnJuuXuAP7vTMcCjzmBFRHrgPbDZrRC5ci/OCFXNt22fKzOT40b3FXiGZBaeMfqkqn5VirYigZ/xPOkXAM/7yiQioUAa0AEvprsj3g4tx4DHVHWKf5uFId6WiCPxFjHrgZtUdbdfmY34GN0iEgu8papJ7nwIXpjPHrwY9Z14D7aeoaqZPu08CUSo6iM+aW3x4v7PlPyb1IcBL6vqOwGOoz5e2EpTPEP9SlXd5fIm4F3jpcW1Mb5Wq+DcTJWco1nlLUHloX69yv32tWCRvtVuvUCpVbPkMgb4bNRjFMPVujqoX1KPfbU8aDf7M5ecdcLHFjSj2wg+Lsb6K1X9prxlKQ0icjZws6reXwFkicZbIJa4P5MZ3YFhRnfgmNEdGGZ0B44Z3YFhRndgmNFdOk7ePXhODv6OC9eoTKjqsopgcDua4m1PaBiGYRiG8ZsJ9u4lRhBxD3+OL285KjOq+nN5y2AYhmEYBoSW7vXsFQ7zdBuGYRiGYRhGGWOebsMwDMMwDKPCU4rXs1dIzNNtGIZhGIZhGGWMeboNwzAMwzCMCk+AL62psJin2zAMwzAMwzDKGPN0G8YJon79yr0CDxY7d9qeyoESHl7eElQObO9p40TToH55S2AUhsV0G4ZhGIZhGIZRLObpNgzDMAzDMCo85uk2DMMwDMMwDKNYzNNtGIZhGIZhVHhCKrmruJKLbxiGYRiGYRgVH/N0G4ZhGIZhGBWeUNun2zAMwzAMwzCM4jCj2zAqKXUuPJ+O07+m43dTiLvj1iLL1R/Ql/NSVlGrzdkAVKtTh7M/fZ9uKxZw2ogngiVuudHwou70WjiZ3oun0uL+gnqqd14iF8weQ/Ke5cQM6peXXv+Crlw4Z1zekbRjCY2TewdT9KBT54Lzaf/t13SYMYXYPxY9p+r178s5G1ZR082pU84/lzbjR9Pu6/G0GT+aqHO6BkvkcsHmVGCYngKnfq/unDd3Muf/NJWEuwvqqtkdN3LuDxM557vxdBrzHuHxsXl5fTJW0G3GOLrNGEf7//03mGIHnZAQCdpRJvKXSavFICJ1RGSUiKwSkZUick4J5duLyMWl7OMdEdkmIssKybvL9b1cRF7wy2sqIgdE5EF33kpEFvkc+0TkXpfXTkR+FJGlIvKViES59DARed+lrxSRR/36CBWRX0Rkgk/aqSIyT0TWishnIlLdpd8oItt9+r/FRyc/ujEsEZGhxejinyJygc95AxHJEpE/+pW72cm8RESWicilAer6Gj8d5YhIe5dXXUTeFJE1TudX+FyDZSIyyWes54vIK4H06aMDFZH+funZTo7FIrJQRM4tRZtFXYc7ReTmQNsJCiEhnPb0cJbfcCu/XJRMw4FJRJzevECx0Jo1ibnpOvYvXJSXlnPkCCkvvcrGZ14oUL7KERJC238MZ+7ltzA9MYm4IcnUOiO/njI3p7Po9kdJ+3xCvvSd38/ju3MH8d25g5iTdAPZhzLZ/u0PwZQ+uISEcOqI4ay88VYW9U2mwcAkIloUnFMhuXPql0V5aVm7drPqljtYPGAgax98hNP/UYXnls2pwDA9BU5ICGc+P5yFQ2/hh/OSiLk8mZot8+tq39KVzL3oCn68cCAZX02h5VMP5eVlZx5mbs9BzO05iEXX3hFs6Y1SUB6e7leByap6BtAOWFlC+fZAqYxu4D2gv3+iiPQELgXaqepZwEt+Rf4BfJ17oqqrVbW9qrYHOgGHgLEueyTwiKq2cWm5d8AQoIZL7wTcLiIJPn3cQ8ExPw+8oqotgN3AH3zyPsuVQVVHurRDwPVuDP2Bf4pInULGWx/opqrf+yQPAeYCw3zKxQOPAeeralugG7DEv73CUNWPfHR0HbBBVRe57MeAbaraEmgNfOfSrwHaAnOAfiIiwBPA04H06RgGzPYdhyPTydMOeBR4thRtFnUd3gHuKkU7ZU7t9m05vHETRzanollZbP9qEvX6FPQENX3gbtLeGEnOkaN5aTmZmeyfvzBfWlWlbmJbDq5P4dBGT09poybSOCm/njI3pbFv+Wo0J6fIdmIH9WPbtFlkZx4ua5HLjVrt2nI45fic2vHVJOoWNqfuLzinDq1YSda2bQBkrvmVkPAaSPWwoMkeTGxOBYbpKXBO6diWQxtSyEzxdLV17EQaDcivq92z55HjdLB3/iJqxDQuD1GN30lQjW4ROQW4AHgbQFWPquqeYspXB0YAQ533skiPri/OyNxVSNYdwHOqesSV2+bT1yBgA7C8iGZ7A+tUNcWdtwRyjdlpwBW53QM1RaQaEAEcBfa5PuKBJDyDPbdfAXoBo1zS+8CgEsa3RlV/dZ+3ANuAhoUUvQKY7Jc2DHgAiHPyADQC9gMHXJsHVHVDcTIUwTDgU5/zm3FGr6rmqOoOly5AGBAJZAHXAl+ramHXrABOZ0OAG4E+IlLUy7Kj8IznQNss9Dqo6iFgo4h0CaStYFC9cTRH09Pzzo+mb6VG4+h8ZWqe3ZrqsTHsnv6df/WThvDYaDJTt+adH07LICI2upgahRM7OIm0LyaUXLASU71xNEd859TWQubUWa2pHhPDnhlFz6l6A/pxYNkK9GhWmclanticCgzTU+CEx0RzeIuPrrZkUCOmaF3FXTOYHd8e96WFhNeg6zej6TL5MxoOqNphOJU9vCTYu5ecCmwH3hWRdsAC4B5VPVhYYVU9KiLDgURVvRPyvNWFhSEcUtWSQglaAt1F5BngMPCgqv4sIrWAh4E+wINF1L0K+MTnfDme13wcngHYxKWPcunpeEblfT7G5D+BvwC1fdqpD+xR1WPuPBWI88m/woWHrHFtbfYVyhmC1YF1hch8HseNSESkCRCjqj+JyOfAUOBlYDGQAWwQkW+BMar6lavzEJ5n2p/vVfVuv7Shbuz4eN6fFpEeTr47VTUDeB3P274c+AH4EuhH4JyL51FfJyIz8RYyo11ehIgsAsKBGDxDGhGpDcwqor2r8RYuxV2H+UB34KdSyFl+iHDq44/w64OPllzWKJYa0Q2JOqsl276ZXd6ilC8iNHv8EdYVM6ciTm9Bs4cfYMX1fyiyjGFzKlBMTwWJGTKQqPZn8/PAa/PSZrXvyZGt24hoFk/i2Pc5sHINmRs3F9OKUV4EO7ykGtAR+K+qdgAOAo+UpgFVneETbuF7BBK7Ww2ohxc+8RDwufNwPoUXVnCgsErO4z4Q+MIn+WbgTyKyAM+Izv2ttQuQDcTiLTIeEJHTRCQZL9RiQSmG+xWQ4EI+puF5X33ligE+BG5S1cJ+n4vBW+TkMhT43H3+FBeaoarZeGEqg/GM+1dE5CmX92IR+s5ncItIV7yFT24cfTUgHpijqh2BH3HhPKr6oap2UNVrgfuA14AB4sX6vyIiJc1LX4963jgcueElZ7gxfSAioqr7ixhHe1VdUUJ/4Bnlsf6JInKbiMwXkflfHtgTQDMnhqNbM6geE5N3Xj2mMUe2ZuSdh9aqSWSr0zn70w/oNPtbandox5lv/yfvYcqThcNbMoiIP/4zbHhcNJlbMoqpUZDYKwaQ/tU09NixkgtXYo5uzaCG75xqXMicank6rT/9gA6zvDl1xlv/yXuYsnrjaFr9v9dZ+8DDHNlUdf/h25wKDNNT4BxOzyA81kdXsdEcSS+oq3oXnMOp9/2RRdfeke+XpCNbXWhXSiq7fviJqDaty17ociJEJGhHmchfJq0WTSqQqqrz3PkoPCM8YESkp9+De7nHnAD7H6MePwE5QAOgK/CCiGwE7gX+KiJ3+tQbACx0XloAVHWVqvZV1U54HvBcT/PVeDHrWS585QcgEc/rPND18SnQS0T+B+wE6rhwFPAM1TTXx87cUBi8kJROPnqIAiYCj6nq3CLGm4nn8c1lGHCjk2E80FZETnd9qar+pKrP4nn1cx96fKgIfb/m15f/LwE78WLPx7jzL/C71iISC3RR1XF4IS9DgT14oTyFIiKhTrbhbhz/Avo7T3Y+VPVHvOvbUERqFzGORSLSmmKugyMcT5/+fbypqomqmnhprTpFiX3C2b94KRGnNqNGkzgkLIyGl1zMrmnT8/Kz9x/gpw7nsOD83iw4vzf7f1nMyj/8iQNLCzxbXKXZs2ApNZsnENksHgkLI25wEhmTppdc0Ye4wUmkfTGxjCSsOBxYspTwhGbUiPfmVINLLmb3N/nn1PxO5/BL99780t2bU6tu/RMHly4jtHZtznjn/7Hp+ZfZv+CXchxF2WNzKjBMT4Gz75elRJ6WQERTT1eNL0ti2+T8uqrd5kxavzyCRdfewdEdxyMxq50Slff8RFi9utTp2pEDq9cGVX4jcIIaXqKqW0Vks4i0UtXVeMZVSV7G/fiEY6jqDLyHK38L44CewAwRaYkXlrFDVbvnFnAe3gOq+rpPvWHkNygRkUaqus15ZR8H3nBZm/BCGj4UkZp4XvV/qurneA/24cItHnSeXkRkBp6X+VPgBrxwC0QkRlVzgywH4h7AdJ73scAHqpoXPlIIK4EWwEw33lqqmhcyISJ/A4aJyEigsaoudFntgRTwPN3Ai8X0gdPBlXjhF7h6KiJfAT2A6RR+rZ8GhrvPEXjx8Dl4YTmIyCrnsfalN7BEVfPCUUTkfeAy4AM/uc4AQoGdzpvfvoRxFHodHC3xFlAVg+xs1g9/mrM+eBtCQ9j2+Wgyf11L0/vv4sCSZez6Zkax1TvN/pbQ2jUJCQujXt/eLL/uD2T+WliEUuVGs7NZ+sAIuo0biYSGsunD0exfuZZWj9/NnoXLyJg0nTod29D5k9cJqxNF4wE9afXYXczsnAxARNM4IuJj2DmrckQV/S6ys9nw5NOc+cHbSEgI277w5lST++7iwNJl7C5mTjW+4RrCmzUl/u4/EX/3nwBYcf0fOLYzoMc0KhU2pwLD9BQ4mp3NqkdG0PGLkUhIKGkfj+bg6rU0f+Ru9i1axvbJ02n51F8IrRlJ27dfBeBwWjqLrr2Dmi2b0/rlv0GOQoiw8dW3OLim6n2X51JWsdbBQlQ1uB1628mNxDN41+OFRuwWt4Wdqr7hV74eMAXvwbtnVfWzAPr4BM/Ya4AXq/ykqr7tjNV38Iyvo3iG73S/uk/hGd0vufOaeIb0aaq616fcPcCf3ekY4FFnaNYC3sXbrUOAd53h6ttHD9d3sjs/Dc/Qqwf8AlyrqkdE5Fk8Y/sY3oOhd6jqKhG51vXh+9DnjXp815DcfroDt6vqtSLyJBChqo/45LcFPsMLw3gXL3ziMF5Iyh9VNaA7143nOVXt5pfeDC/8pY5r8yZV3eTyOuDFeP/Bnd8L3ApsxosLrw38oKqt/Np8F5jnO09EZKDTzQARyQaW5mYBf1XVgFwlRV0Hl7cQ6KOqO4uq/0OzM4J7M1VSdu40NQVKw4aV+x9MsNi+3eaUcWIJL+rxfCMffXesDuqX1L/mbAjazX7Xuaee8LEF3eg2gouIzAaStZhdYioiLgb+NFX1D2MpD1k6APer6nXFlTOjOzDM6A4cM7oDw4xu40RjRndgBNvo/vfcjUG72f/cLeGEjy3Yu5cYwecBoClerHSlQVUr0h5RDfD2ETcMwzAMw/hNmNFdxfF5aNX4jajqtPKWwTAMwzBOdkIreUx3ebyR0jAMwzAMwzBOKszTbRiGYRiGYVR4ymr/7GBhnm7DMAzDMAzDKGPM020YhmEYhmFUeCr7Pt3m6TYMwzAMwzCMMsY83YZxgjh40PYKDgTb/zZwDh8ubwmMqkbt2pXbUxgsdu6y7/OKiHm6DcMwDMMwDMMoFjO6DcMwDMMwDKOMsfASwzAMwzAMo8Jj4SWGYRiGYRiGYRSLeboNwzAMwzCMCo+9HMcwDMMwDMMwjGIxT7dhGIZhGIZR4bGY7lIgIq1EZJHPsU9E7i2hTnsRubiU/bwjIttEZFkheXeJyCoRWS4iL/jlNRWRAyLyYEnyikg7EflRRJaKyFciEuXSw0TkfZe+UkQedenhIvKTiCx2ff/Np9+PRGS1iCxzsoe59DNcH0dyZfKpc48rv7w4HYrIvSJyvc95NRHZLiLP+ZVLFpFfnHwrROT2Uui7qYhMdeNdISIJfvmvicgBn/O7nOyTRKS6SztfRF4pRZ/tRURFpL9fera7VotFZKGInFuKNk8VkXkislZEPvOR7U4RuTnQdoJF/V7dOW/uZM7/aSoJd99aIL/ZHTdy7g8TOee78XQa8x7h8bF5eX0yVtBtxji6zRhH+//9N5hiBx3TU+DU63k+XWd9Tdc5U2h6Z0FdxV4/lM7Tx5M4bSwdvvyIyJbNAajdvg2J08aSOG0snb8ZR4MBFwVb9KDS8KLu9Fo4md6Lp9Li/oJ6qndeIhfMHkPynuXEDOqXl17/gq5cOGdc3pG0YwmNk3sHU/SgYvMpcKL7dqff0sn0XzGVVg8W1FVI9TC6/u8V+q+YSq9ZnxPZLA4AqVaNxJHP0WfBePounkSrh24LtuhGKRDV8tkAXkRCgTSgq6qmFFPuRiBRVe8sRdsXAAeAD1T1bJ/0nsBjQJKqHhGRRqq6zSd/FKDAPFV9qTh5ReRn4EFV/c4ZZKeq6hMicjUwUFWvEpFIYAXQA0gBaqrqAWdUzwbuUdW5blHxtevqY+B7Vf2viDQCmgGDgN25MonI2cCnQBfgKDAZ+KOqrvWTuRqwEOioqsdc2gDgcaAx0EJV1cmTAnRR1VQRqQEkqOrqAPU9E3hGVaeJSC0gR1UPubxE4B7gMlWt5dLmAucCfwUWAxPcGIap6q4A+3zetbFeVW/wST/g008/4K+qemGAbX4OjFHVT0XkDWCxuw6RwA+q2qG4+lMbtArezRQSwvnzprBg8E0c3pJBt2mjWHLb/Rxcsy6vSN3zu7J3wWJyMg8Tf9Mw6p3XhSW33AdAr40LmZ7QMWjilhuVXE9hYUH06oSE0O2HySwaejNH0jNI/PoLlv/pAQ756Cq0Vk2yDxwEoH7fnsTdeDVLrr6VkIhw9GgWmp1N9UYN6fztOOa0vwDNzg6K6Pv3B/H/WEgIvRdN4ceBN5GZlsEF349iwU33c2DVcT1FNI0jrHYtmt9zM1snTSd93JQCzYTVPYXei6cyrdWFZGcG7y1IQXs5TiWeTxDkl+OEhNB/+RRmXXwTh1Iz6D1nFPOuu5/9PnPqtNuv5pQ2rfjlzieJH3IxcZf2Yd6199FkaDKxyb2Yd939hEaE03fRRL7rez2HUtKCIvrgI6uD6nr+ZMXWoF2YYa0bn/CxlWdMd29gXQkGd3VgBDDUeS+HBtKwqn4PFGa83QE8p6pHXDlfg3sQsAFYHqC8LYHv3edpwBW53QM1ncEbgWcU71OPXG9vmDvUyTHJ5SvwExCfK5+q/gxk+clyJt7C4JAzpr8DLi9E5l7AwlyD2zEMeBXYBJzj0mrjhRrtdP0eKYXB3RqopqrTXN0DPgZ3KPAi8Bf/am78kW5s1wJfl8LgFmAIcCPQR0SKesdhFLC7FG32Aka5pPfxFju48WwUkS6BtBUMTunYlkMbUshMSUWzstg6diKNBuT3mO2ePY8c98987/xF1IhpXB6iliump8CJ6tCWzI2bOLzJ01XGl5No0C+/rnINJIDQyEhwTpuczMN5BlFIjep56VWRuoltObg+hUMbPT2ljZpI46T8esrclMa+5avRnJwi24kd1I9t02YF1eAOJjafAqde57YcWJfCwQ2erjZ/PpHYS/LrKvaSXqR8OBaAtDFTaNTT/ftWJbRmBBIaSmhEODlZWWTtO+DfhVFBKM+Y7quAT4oroKpHRWQ4Pp5u560uLAzhkKqWFErQEuguIs8Ah/E81T877+zDQB/gwSLq+su7HLgUGIdnADZx6aNcejqeUXlfrjHpjNAFQAvg36o6z7cD53G+Ds8zXBzLgGdEpD6QCVwMzC+k3Hmuv9z2w4GLgNuBOngG+BxV3SUi44EUEfkWz/P8iarmiMg1wEOFtL1WVQfj6XSPiIwBTgW+AR5R1WzgTmC8qqZL/ieOXwfm4unwB+BLoB+Bcy6wQVXXOS97EjDa5UWIyCIgHIjBM6QRkdrArCLauxrYBuzxWaCkAnE+ZeYD3fEWReVOeEw0h7dszTs/vCWDUzq1LbJ83DWD2fHt93nnIeE16PrNaPTYMTa8+ibbv/62TOUtL0xPgVOjcTSH09Lzzo+kbyWqQ7sC5eJuvJomt9+IhIWxaMiNeelRHdpyxivPUCM+lpV3PRxUr2QwCY+NJjPVZ06lZVC3c9FzqihiByex/l/vnkjRKhQ2nwInIjaazM3H51RmWgb1urQtWCbV06dmZ5O1bz/V69cldcwUYi/pTXLKbEIjw1n80LNk7d4bVPmDSWXfvaRcjG7nwR4IPFrauqo6A2j/G7uuBtQDugGdgc9F5DTgKeAVF/oRqLw3A6+JyBPAeDyPNnghH9lALFAXmCUi36jqemeItheROsBYETlbVX3jzv+DF1pSlHEIgKqudOEVU4GDwCLXpz8xwEqf82Rghqpmisho4AkRuVdVs1X1FhFpg2eUP4i3ALlRVT8CPipGnGp4xmgHPO/5Z8CNIvI13mKkRyHyfwh8COAWVa8BA1zs+WbgAVUt2kXkLRY+dZ8/Ba7nuNGdqartXdvnAB84Pe+nmHkjIg2K6Q88o/yMQurdBtwGcE/NRlwcXqeEZoJPzJCBRLU/m58HXpuXNqt9T45s3UZEs3gSx77PgZVryNy4uRylLH9MT4GR9t7HpL33MY0uS6bZvXew6p5HANj3yxJ+6nEJkaefxpmvPseu6d+Tc+RoCa2dnNSIbkjUWS3Z9s3s8hal3LH59Puo17ktmp3DhITuVK8bRY/pH7Nt+hwObkgtb9GMQiiv8JIBeGEPGaWtKCI9Jf/DjbnHnACqp+LF7Kqq/gTkAA2ArsALIrIRuBf4q4j4xpAXkFdVV6lqX1XthOcBzw2+uhqYrKpZLnzlByDRVwhV3QPMAPIeAhSRJ4GGwP2B6EFV31bVTqp6AV4IxZpCimXieXxzGQZc5Ma5AKiP8wS7Npeq6it4BvcVTq5ritB3bhhGKrDILSqO4Xn+O+IZ4S2Ata6/SBHxjzmPxYsjHwc8AAwF9uCF8hSK+7XgCmC4a/dfQH/nyfbX0Y9417ehiNQuYhyLXIjMTqCOCwsCL8THNygu3OnTv483VTVRVRODaXAfTs8gPPZ4GER4bDRH0gveTvUuOIdT7/sji669Az16PErpyFYvsiozJZVdP/xEVJvWZS90OWB6CpwjWzMIj4vJO68R05gjW4v+it42biIN+xe8VQ/9up7sg4eoeUbLMpGzvDm8JYOIeJ85FRdN5pbS/SuLvWIA6V9NQ48dK7lwJcXmU+BkbskgosnxORURF01mWkbBMvGePiU0lLCo2hzduZsmVyWzdeos9NgxjmzfxY45C6nbsU1Q5Q8mISEStKNM5C+TVktmGCWElviwHy/mGPA83aravpAjkF0qxgE9AUSkJVAd2KGq3VU1QVUTgH8Cf1fV14uT1z3kiIiE4D2Y+IbL2sTxkIaaeF71VSLS0Hm4EZEIPMN2lTu/BS+8YlgJHt7C+m+KF8/9cSHFVuIZvoi3u0p3oKnPWP8MDBORWiLSw6dee7wHK1HVj4rQ92BX9mc8Y7WhO+8FrFDViara2KevQ6rawk++p4Hh7nMEXox7Dl5YDiKyqpAx9QaWqGoT13YzPC/3ZYXo6AwgFNipqvuLGEd7VV3h4ulnALnjugEv7CWXlnhhPRWCfb8sJfK0BCKaxiNhYTS+LIltk6fnK1O7zZm0fnkEi669g6M7jofLVzslCqkeBkBYvbrU6dqRA6vzrYeqDKanwNm/aCkRpzYjvEkcEhZG9KUXs2NKfl1FnNos73P9i3pwaIP3iEt4kzgkNBSAGvGxRLY4jcObq6anbc+CpdRsnkBkM29OxQ1OImPS9JIr+hA3OIm0LyaWkYQVA5tPgbN7/lJqtUggMsGbU02uTCJ9Qn5dpU+YTrPrvH9zcZf3Y9vMuQBkbkqnUY+uAIRGRlC/azv2r14f3AEYARP08BJniPbBiyv2Tf8jgKq+4VdlBvCIi9N9VlU/C6CPT/DCGhqISCrwpKq+DbwDvCPeVoJHgRucsVVqefGM1T+7z2OA3OC8fwPvishyvAcG31XVJSLSFnjfeWpDgM9VdYKr8waekfujC28Zo6ojRKQxXixxFJAj3taArVV1HzDaxXRnAX923nN/vsaFceAZpdPVPUTq+BJ4AbgP+IuI/D88b+5BvIcUS0RVs8XbzvBb9zDiAuCtkuqJSAdXf6FL+hhYihde8oIL9yhsqTkMGOuXNhrvIdkPOB7Tjat/gwvrCYSHgU9F5P+AX4C3ffLOwwtDqhBodjarHhlBxy9GIiGhpH08moOr19L8kbvZt2gZ2ydPp+VTfyG0ZiRt334VgMNp6Sy69g5qtmxO65f/BjkKIcLGV9/Kt5tHVcL0FDianc2avz5Nu0/eRkJDSP90NIfWrOXUh+5i3+Jl7Jw6g7ibr6Fe93PIyTrGsb37WHm3FwpwStdONLvzVnKyjoHmsObRv5G1a0/5DqiM0Oxslj4wgm7jRiKhoWz6cDT7V66l1eN3s2fhMjImTadOxzZ0/uR1wupE0XhAT1o9dhczOycD3s4mEfEx7JxVIR4PKTNsPgWOZmez6N4RdJ/gzamN741m38q1tB5+N7sXLiN9wnQ2vDuKLu++SP8VUzm6ay/zrvN2WFr7xkd0futZ+vwyARFh4wdj2LssoH0QKiUhlfyVjuW2ZaARHERkLPAXVf21vGUpDSKSDJymqq9VAFk6APer6nXFlQvqloHGSUFQtwysxAR1y8BKTtC2DKzkBHXLwEpMsLcMHP3rtqBdmCtOb3TCx2ZvpKz6PIL3QGWlMrp9fgWoCDQAnihvIQzDMAzjZMZ2LzEqNG6/7ar7W1MQyN2D3DAMwzAM47dSyaNjDMMwDMMwDKPiY55uwzAMwzAMo8JTRjv5BQ3zdBuGYRiGYRhGGWOebsMwDMMwDKPCU9kfpDRPt2EYhmEYhmGUMebpNgzDMAzDMCo8ld3TbUa3YZwg9u0vbwkqB0ePlrcElYd2bcpbgsrBzl3lLUHlIX2rvfQlEBITQ8tbBKMKYka3YRiGYRiGUeGx3UsMwzAMwzAMwygW83QbhmEYhmEYFZ7QSh7TbZ5uwzAMwzAMwyhjzNNtGIZhGIZhVHgsptswDMMwDMMwjGIxT7dhGIZhGIZR4ans+3SXiadbRO4TkeUiskxEPhGR8BLK9xCRc0vZx2QR2SMiE/zSRUSeEZE1IrJSRO72y+8sIsdEZLA77ykii3yOwyIyyOX1EpGFbhzvi0g1l/6QT/llIpItIvVc3j0ubbmI3OvT79MissTVmSoisSXI1V5EfnTtLBGRocXo4p8icoHPeQMRyRKRP/qVu1lElrr2lonIpQHqur6IzBCRAyLyul/eZBFZ7OR8Q0RCffLuEpFVLu8Fl3ae63++iJzu0uo4nQQ0H0WkmohsF5Hn/NJnishqp+OVInJbIO25uhe4a513DVx6QxGZHGg7wSS6b3f6LZ1M/xVTafXgrQXyQ6qH0fV/r9B/xVR6zfqcyGZxAEi1aiSOfI4+C8bTd/EkWj0UsJqqJDH9upO8ajKX/DqV1g8X1OPJQq3zzqfF+K9pMWEKDW4uqIc6Ay+j1cw5nPb5WE77fCx1Ls+7TYi+9wGajxlP8zHjieo3IJhilwt2750Y7N47TuQ555MwaiIJYyZT94ZbCi1T66L+NPvsK5p9Np7GT7+Ql97grgdo9tl4mn3+FQ0f+GuwRDZ+Ayfc6BaROOBuIFFVzwZCgatKqNYDKJXRDbwIXFdI+o1AE+AMVT0T+NRHtlDgeWBqbpqqzlDV9qraHugFHAJyDcD3gavcOFKAG1ydF33qPAp8p6q7RORs4FagC9AOSBaRFrnyqmpbV2cCMLw4uZwc16vqWUB/4J8iUsd/sCJSH+imqt/7JA8B5gLDfMrFA48B56tqW6AbsKQQ/RXGYeAJ4MFC8q5U1XbA2UBD1zci0hO4FGjnxvCSK/8AcDFwL5C7KHgc+Luq5gQoTx9gDTBEpMCy9xqn4/OA50WkeoBtbsKbOx/7JqrqdiBdRM4LsJ3gEBJCh1eHM3vgLUxpl0STocnUPqN5viIJNw3h6J59TG7dlzWvvUebZ7zLF39Ff0JrVGdap4F82+1yTrtlaJ5RcLIhISEk/ns4MwbcwsTWSTQblkzUmc1LrljVCAkh5q/DSbnjVtYNSuaUAUnUOK2gHvZO+Zr1V17G+isvY8+YUQDU6n4h4We2Zt2Qy1h/zVAa3HAzITVrBnsEwcPuvROC3Xs+hITQ6C+Pk3bP7Wy88hKi+l5M9VPz6yKsSTPq3Xgrm2+5hpShA9n+D8/nFN62PRHtOpAybBApV11KeOuziejYuTxGERRCRIJ2lIn8ZdKqF7YS4TzDkcCWogqKSAKe8XWf81B2D6QDVf0WKOwdgHcAI3INOFXd5pN3FzAa2FZIPYDBwNeqegioDxxV1TUubxpwRSF1hgGfuM9nAvNU9ZCqHgO+Ay53cuzzqVMT8H0tWAG5VHWNqv7qPm9xeQ0L6f8KwN8TOwzPuI1zxjZAIzx9HXBtHlDVDYUpwR9VPaiqs/GMb/+83HFVA6r7jOsO4DlVPeLK5Y4tC29ORAJZItIcaKKqMwORxWd8r+IZyucUUaYWcBDIDqRBVd2oqkuAwgz/ccA1pZCvzKnXuS0H1qVwcEMqmpXF5s8nEntJ73xlYi/pRcqHYwFIGzOFRj2dqlQJrRmBhIYSGhFOTlYWWfsOBHsIFYL6XdpyYK2nx5ysLFI+nUj8pb1LrljFiDi7LUc3bSIrLRU9lsXeyZOo3TMwPdRo3pxDC+ZDdjaamcnhNaupdV5AX+OVErv3Tgx27x0n/Kw2ZG327j+OZbFv2tfUvLBXvjKnDBrMni8+Jme/9y83e7d7DasqUr0GEhaGhFVHqlUje9fOYA/BCJATbnSrahqeV3MTkA7sVdWpxZTfCLwBvOK8x7NE5Bq/kI/cY1QAIjQHhrrwha99QhjigMuA/xZT9yqOG9A7gGoikujOB+N50PMQkUg8L/Rol7QM6O7CMSLxPLpNfMo/IyKb8Qy44YHKJSJd8AzadYVknwcs8CnbBIhR1Z+Az4HcsJTFQAawQUTeFZFLfOo8VIS+XytKJj/5puAtCvYDudeopdPFPBH5TkRyl97PAh/g/ULwOvAMnqc7IMQLVboI+ArvWg3zK/KRiCwBVgNPq2q2q/dZEWO8PoBu5wMVyoqIiI0mc/PWvPPMtAwi4qILlklNB0Czs8nat5/q9euSOmYK2QczSU6ZzcVrZ7DmlXfI2r03qPJXFCLiojnoo8dDqRlE+unxZCAsOpqsjPS886yMrVRrVFAPURf1ofmoL4l/+VWqRTcG4PBqz8iW8HBC69ShZpeuhDWOCZrswcbuvROD3XvHqdYwmmMZx3VxLGMrYQ0b5StTvWkC1Zsm0GTk/2jyzidEnnM+AIeXLubQgp847evvOG3ydxyc+wNHN64PqvxG4JzwBylFpC5eWMGpwB7gCxG5VlX/F2gbqvoR8NFvFKEGcFhVE0XkcuAdPIPpn8DDqppTMCIBRCQGaANMcTKoiFwFvCIiNfBCP/y9ppcAP6jqLldnpYjkhokcBBb51lHVx4DHRORR4E7gyQDl+hC4oYjwixhgu8/5UDxjG7zQmneAl1U1W0T6A52B3m5cnVT1KVV9ES9c5zehqv2cMfwRXojONLy5VQ8vjKUz8LmInKaqi1waLg493fson+F5wR9Q1YxiuksGZqhqpoiMBp4QkXtzjWu88JL5ItIQmCMik1U1RVWLjIkPgG1AbGEZLm78NoDbQhvRJ7TO7+gmONTr3BbNzmFCQneq142ix/SP2TZ9Dgc3pJa3aEYFZv93M9j79QQ0K4u6g4cS98xzpNxyIwd//IH9Z5/NqR98QvbuXRxavAjNCegHppMOu/eM30xoKNWbNGPz7TdSLTqaJm9+QMpVgwitU5fqCaexPsnzjMe/PpJD7TuRuWhBCQ1WTmzLwIJcBGxQ1e2qmgWMoZTx2r/T053q+gQYC7R1nxOBT0VkI57X+j/iHph0XAmMdTIDoKo/qmp3Ve0CfI8XR+yLr2c8t87bqtpJVS8AdhdSBzzjNDdUpUi5RCQKmAg8pqpzixhvJuD7oOow4EbX3nigba63Xz1+UtVnnexXuH5+l6fbtX0Y+BJvwQXuOuT2iRe20SC3vIvFfhx4Gm/x8RfgLbznAYpjGHCRG98CvDCgXv6FXCz2QqCr6+/3eLrD8fRc2LjfVNVEVU0MpsGduSWDiCaN884j4qLJTMsoWCbe8zhKaChhUbU5unM3Ta5KZuvUWeixYxzZvosdcxZSt2OboMlekchMy6Cmjx4j46M5lFbcmq9qkpWRQVj0ce90WHRjjm3Lr4fsvXvQLO/rcfeYL4g486y8vB1v/T/WX3kZKbf/AUQ4unFjUOQuD+zeOzHYvXecY9sz8n45AqgW3Zis7fmjYI9ty+DArBmQfYxjW9LI2pRCWNNm1OpxEYeXLUYzD6GZhzj44yzC27QL9hCMACkLo3sT0E1EIp1h1RtYWUKd/UDt3BNV/Sj3QUW/Y3AxbeQyDujpPl+IM3pV9VRVTVDVBLwQiD+p6jifer6x2QCISCP3twbwMF4YTG7eKa79L4uo0xQvnvtjd366T7FLgVXFyeUeABwLfKCqxS02VgItXB8tgVqqGufT5rPAMBGJFZGOPvXa4z0cmu/BUL+jWANYRGo5Tzwufj8pd1z4XAcnV3W8kJ1crgcmuV8JIvGM8hz3GRH5wIXV+PYXhferRVOf8f2ZgiEmuaE/HXAhOao6tIgxflDcGB0t8UKHKgy75y+lVosEIhPikbAwmlyZRPqE6fnKpE+YTrPrLgMg7vJ+bJvprdsyN6XTqEdXAEIjI6jftR37V5+cP0fu/HkptU9PoGZCPCFhYTS7Kom08dNLrljFyFy+lOrNmhEWF4dUC+OU/hezf2Z+PVRrcPyRkto9enFkg4t2Cwkh9JQ6ANQ4vSXhLVty4McfgiV60LF778Rg995xDq9YRljTZlSLjYNqYUT1GcDB72fkK3Pgu2/zHpAMOaUOYU2bkZW2mayMLV56aCiEViOyY+cqHV5S2R+kPOHhJao6z3mkFwLHgF+ANwFEZAQwX1XH+1X7Chgl3hZ2d6nqrJL6EZFZwBlALRFJBf6gqlOA5/Dieu/De2iw8L138reVgBd7/Z1f1kMikoy3OPmvqvp+I1wGTFXVg351Rou3o0gW8GdV3ePSnxORVniGZQrHd+4oiiuBC4D6InKjS7vRhWf4MhG4HRiJZ3yO9ZcH+AxvJ5aXxNuq8DBeSEpJMuThPMtRQHXnie8L7ATGu0VJCDCD4wuTd4B3RGQZcBQvPEZdW5F4O4X0dWX/AUxy5a52aW0p+ADuZcD03IczHV8CLzgZwLv2mXhhRu+pakC/sbmY87FAXeASEfmberuugLd4mBhIO8FCs7NZdO8Iuk8YiYSGsvG90exbuZbWw+9m98JlpE+YzoZ3R9Hl3Rfpv2IqR3ftZd519wGw9o2P6PzWs/T5ZQIiwsYPxrB32epyHlH5oNnZzL9zBD2neHpc/85o9q5YW95iBZ/sbNL//jTN/vs2EhrC7nGjObJuLQ3/dBeHVyxj/8wZ1Lv6Omr36AnZ2WTv3Uva448C3jZ4Ce950YM5Bw+Q9uhfILvqhpfYvXdisHvPh+xstr/wDPGvvQWhIewbP5aj69dS//Y7ObxyOQe/n8GhH2dTs+u5NPvsK8jJZserL5Gzdy8Hvp1KZGI3mn0yDhQO/TiLg7NmlvOAjKIQZwcZlRgRmQ0k+xj4lRrn0X5bVYeUtywAIvI9cKmq7i6u3KgarexmCoCjR8tbgspDuzaVPIAxSKxcbbdeoNj9FxiJiaElFzJo+fOKoH5JzUnfG7Sb/dyYU0742Ow18FWDB4Cm5S3EiUJV91Ugg7sh8I+SDG7DMAzDMIzisNfAVwFUdV55y1BVcQ9kjitvOQzDMAzjZMdeA28YhmEYhmEYJyEiEioiv4jIhJLKmqfbMAzDMAzDqPBUUE/3PXg7yUWVVNA83YZhGIZhGIZRSkQkHm+75JGBlDdPt2EYhmEYhlHhqYBvpPwn3sv9apdQDjBPt2EYhmEYhmHkQ0RuE5H5PsdtfvnJwLZA3wcC5uk2DCPI1KpZ3hJUHtatt/2nDaM82Lih6r7g6UTSMsj9BTOmW1XfxL3csQjOAwaKyMVAOBAlIv9T1WuLqmCebsMwDMMwDMMoBar6qKrGq2oCcBXeG7OLNLjBPN2GYRiGYRhGJaACxnSXCjO6DcMwDMMwDOM3oqozgZkllbPwEsMwDMMwDMMoY8zTbRiGYRiGYVR4KujLcQLGPN2GYRiGYRiGUcaYp9swDMMwDMOo8IRWbke3eboNo7IS3bc7/ZZOpv+KqbR68NYC+SHVw+j6v1fov2IqvWZ9TmSzOAAkLIzEN/9OnwXjuejnL2l4QZdgix5UGl7UnV4LJ9N78VRa3F9QT/XOS+SC2WNI3rOcmEH98tLrX9CVC+eMyzuSdiyhcXLvYIoeVExPgWP33okhpl93kldN5pJfp9L64YJ6PJmo36s7582dzPk/TSXh7oK6aHbHjZz7w0TO+W48nca8R3h8bF5en4wVdJsxjm4zxtH+f/8NpthGKQm60S0i94jIMhFZLiL3BlC+vdt4vDR9vCMi20RkWSF5d4nIKtf/C355TUXkgIg86M5bicgin2Nfrswi0k5EfhSRpSLylYhEufRr/OrkiEh7lzfMlV8iIpNFpIFLf0pE0nzqXOzSw0TkfVdnpYg86tKbiMgMEVnhxnFPMbq4V0Su9zmvJiLbReQ5v3LJIvKLiCx27d5eSp1HiUiqiLzukzZTRFb7jKuRzzVYJiKTRKS6SztfRF4pRX/tRURFpL9ferbra7GILBSRc0vR5qkiMk9E1orIZz6y3SkiNwfaTlAICaHDq8OZPfAWprRLosnQZGqf0TxfkYSbhnB0zz4mt+7Lmtfeo80zDwJw2h+GADCt00BmXXwTbZ9/GCp5nFyRhITQ9h/DmXv5LUxPTCJuSDK1/PSUuTmdRbc/StrnE/Kl7/x+Ht+dO4jvzh3EnKQbyD6UyfZvfwim9MHD9BQ4du+dECQkhMR/D2fGgFuY2DqJZsOSiTqzeckVqyIhIZz5/HAWDr2FH85LIubyZGq2zK+LfUtXMveiK/jxwoFkfDWFlk89lJeXnXmYuT0HMbfnIBZde0ewpQ8qISJBO8pE/jJptQhE5GzgVqAL0A5IFpEWJVRrD5TK6AbeA/r7J4pIT+BSoJ2qngW85FfkH8DXuSequlpV26tqe6ATcAgY67JHAo+oahuX9pCr85FPneuADaq6SESqAa8CPVW1LbAEuNOn71dy66nqJJc2BKjh+ugE3C4iCcAx4AFVbQ10A/4sIq0LGW814GbgY5/kPsAaYIiIN6tEJAzvrUuXqGo7oAMBbH3jx9PA94WkX+Mzrm25aUBbYA7Qz8nxhGsjUIYBs91fXzJdX+2AR4FnS9Hm83jXoQWwG/iDS38HuKsU7ZQ59Tq35cC6FA5uSEWzstj8+URiL8nvXYy9pBcpH3rTNW3MFBr1PAeA2me2YNvMeQAc2b6LrL37qdvp7OAOIEjUTWzLwfUpHNro6Slt1EQaJ+XXU+amNPYtX43m5BTZTuygfmybNovszMNlLXK5YHoKHLv3Tgz1u7TlwFpPjzlZWaR8OpH4S6v2LyRFcUrHthzakEJmijento6dSKMB+XWxe/Y8ctx9tXf+ImrENC4PUY3fSbA93WcC81T1kKoeA74DLi+qsPM0jgCGOu/l0EA6UdXvgV2FZN0BPKeqR1y5XCMQERkEbACWF9Fsb2Cdqqa485YcNzKnAVcUUmcY8GluF+6o6YzMKGBLSUNx5asBEcBRYJ+qpqvqQjeG/cBKIK6Q+r2AhU7XvjK9CmwCznFptfHi+3e6No+o6uoSZMtDRDoB0cDUQKsAYUAkkAVcC3ytqoVds8L6E7wFyY1AHxEJL6JoFJ7xHGibvYBRLul9YBCAqh4CNopIhfktOCI2mszNW/POM9MyiIiLLlgmNR0Azc4ma99+qtevy94lq4hN7oWEhhKZEE+dDmcRGR8TVPmDRXhsNJmpx/V0OC2DiNjoYmoUTuzgJNK+mFBywUqK6Slw7N47MUTERXPQR4+HUjOIjCv9nKsKhMdEc3iLz/23JYMaMUXrIu6awez49riPKyS8Bl2/GU2XyZ/RcEDVXrhUdk93sB+kXAY8IyL1gUw8D/b/Z+88w6Oqtgb8roSEFHoLCQGiSBGlGuwoRZogYkUUOxb8ELtiuejFa72Wa7t6FbCLiCAiIKAUBQWVEghdkBogodcQksn6fuydMBlSJkJmkrDf5zlP5uy69jrnTNZeZ+098wsqrKpHRGQokKiqgyDXW51fGMIhVS0qlKAJ0F5EngMOAw+r6h8iUgl4DOMFfriAutcBo7zOl2G85uMxBmD9fOr0tWVQ1UwRGQgkAweBP4H/8yo7yIaBzMd4sXdjDMDLga0YA/UBX8PUer7bAL/l0/8FwAKvshHAJcBdQDWMAf6rqu4SkQnABhGZDkwERqlqtojcgPXi+7BGVa8WkRDgVYzhfEk+5T4UEQ8wFviXqirwNjAPo8NfgG+BbvnULYjzMW8Q1orILKCnbR8gUkSSgAggFmNIIyKVgdkFtHc9kAbs8ZqgbCbvRGY+0B74vRhylkrWfzSWKs0a0XnuWA5t3MLOeYvQbE+wxSq1VIypTZUzmpD245xgi1KqcXoqGvfsOY6X2Gt6U6X1mfzR++ivjc9u3ZGMbWlENown8ZuPObBiNenrNwVRSkdBBNToVtUVIvISxiN6EEgCivWNo6ozMSEnf4cKQA1MSEY74CsRORV4BhNWcEDymd1Yj3tvTLhCDrcBb4rIP4AJGC+0d51zMBOBpfY8DONpbwP8Bbxl2/sX8C4mtELt31dt+2dj9BMHVAdmi8iPqvqXbbMSxti8X1X35TPeWIwXPIdewExVTReRscA/ROR+VfWo6gARaYExnB/GTEBuUdXPgc8LVin3AJNVdXM+urtBVVOswTsWE27ziap+CnxqxzAUeBPoYScdmzCTjoLfYed9g/AlcBNHje50G9qDiJwHfCIiZ9o3Aq0LajAnvr4Q0oBm+dS7E7gT4M7QOnQJrVZEMyeG9C2pRNY/+noxsl4M6Smpx5aJjyU9JRUJDSWsSmWO7DSO/8WPHI266ThrFPtXrw+I3IHm8JZUIuOP6imiXgzpW1ILqXEscVf1YOt3P6BZWUUXLqM4PfmPe/ZODOkpqUR76TEqPoZDKcW758oLh7emEhHn9fzFxZCx9Vhd1LjoPE554G7m9+6PHsnMTc/YZl7ap2/YzK5ffqdKi+bl1ugu6z8DH/CFlKo6QlXPUtWLMK/+Vxenvoh0lLwLFXOOX/2ovhkYp4bfgWygFnAO8LKIrAfuB54QEe946x6YMI3cp0BVV6pqV1U9C+MBX+vTl69nvLWtt9Z6e7/CeGxR1VRr+GYDH2CMbTAe2CmqmmlDYX4BEq0ewjCG5ueqOq6A8aZjPL459AMuseNcANTEeoKtHMmq+jrG4L7K9uO7MDTnyAnDOA/jpV+PiZG/KWeRpqqm2L/7MXHlecIzRCQOOFtVxwMPYd4M7MGE8uSLiIRa2YbaPt8CulvDPg+qOhdzfWuLSOUCxpFk4+F3AtVsKA9APJDi1VyE1advH++raqKqJgbK4AbYPT+ZSqclEJUQj4SFUf/anmydOCNPma0TZ9DwxisAqHdlN9JmzQMgNDKC0KhIAOp0Pp/sLA/7V/revuWDPQuSiW6UQFRDo6d6V/ckdfKMoit6Ue/qnqSMmVRCEpYOnJ78xz17J4adfyRTuXEC0QnxhISF0fC6nqRMKN49V17YtyiZqFMTiGxg7qm6V/QkbUpeXVRucTrNXx1GUv+BHNlx9IV3hapVkPAwAMJqVKfaOW05sGpNQOV3+E/A9+kWkTqqmiYiDTDx3OcWUWU/JuYYOG5P93igIzBTRJoA4cAOVW3vJd8zwAFVfdurXj/yGtDe4wgBngLe88oLAa7FhCPkkAI0F5HaqrodY9iusOVjVXWrLXcFJgwHTNx1J+BTEYnG6Oo/Nv54BLBCVV8rZLwrgNNsH1WsPPVzYtpF5Fagn4jMxYTwzLL1WgMbwCwMpRBPt6re4DXuW2w7Q6zxWk1Vd9gJQi/gR5/qzwJD7edIjKc/GxNKg4isVFVf73JnYImq5oajiMjHGL194l1QRJoBocBOVfVQxH0jIjOBqzHe85sxYS85NMFMekoF6vGQdP8w2k8cjoSGsv6jsexbsYbmQweze+FStk6cwboPv+bsD/9N9+XTOLJrL7/d+AAAFevUpP3EEWh2NulbUvnjtkeDPJqSQz0ekh8axrnjjZ42fjqW/SvW0PSpwexZuJTUyTOo1rYF7Ua9TVi1KtTt0ZGmT97LrHa9AIhsUI/I+Fh2zi7zUUWF4vTkP+7ZOzGox8P8QcPoONXo8a+RY9m7/OQ0FtXjYeWQYbQdMxwJCSXli7EcXLWGRkMGsy9pKdunzKDJM48SGh1FyxFvAHA4ZStJ/QcS3aQRzV/9J2QrhAjr3/iAg6vL70SurP8ipRinawA7FJmN8bBmAg+q6nSbfjeAqr7nU74GMBWz8O4FVR3tRx+jgA4YL2cq8LSqjrBhIiMxxtcRTEz3DJ+6z2CM7lfseTTG+D1VVfd6lbuPozHZ44DHrQcbEemAWbCZZ0Jhx3ifHfsGTPjGThH51MqkwHrgLlXdasNHPgSaYxYffqiq/xaRCzHxyckYIxXgCa9dT3L6awh8qqoXicjNQA9Vvc5Ht6swhvkooBHGm3sQuE9VC4y3zw8vo3uQ1dvPmOsWijG4H7TGLyLSBhikqrfb8/sxO9tswsSxVwZ+UdWmPn18iFmM6z3J6Q0MVNUeNn48OSfL6sUv95sNNfoSE4K0COjvNUFZCHRR1Z0F1f+6YtPAPkxlFOuUcThOGF5v2h1FcORI0WUcUKtmsCUoG3TdsSqgVvDafYcD9n+2UZWIEz62gBvdjsAiIt8Aj6rqn8GWpTiISC/MROfNUiBLG8yE4cbCyjmj2z+c0e040Tij23+c0e0fzuj2j0Ab3ev2B87oPqXyiTe63c/Al3+GYBZUlimjW1VL075jtTD7iDscDofD4XD8LZzRXc6x+237vee241hU9Ydgy+BwOBwOx8lOWY/pDvjuJQ6Hw+FwOBwOx8mGM7odDofD4XA4HI4SxoWXOBwOh8PhcDhKPUJhv5tX+nGebofD4XA4HA6Ho4Rxnm6Hw+FwOBwOR6lHpGx7up3R7XCcINz+t/7h9un2n9q1y/ZK/UCRssVtke8vbv9phyN4OKPb4XA4HA6Hw1HqCcETbBGOCxfT7XA4HA6Hw+FwlDDO0+1wOBwOh8PhKPWU9Zhu5+l2OBwOh8PhcDhKGOfpdjgcDofD4XCUetw+3Q6Hw+FwOBwOh6NQnKfb4XA4HA6Hw1HqcTHd+SAiI0UkTUSW+qTXEJEfRORP+7d6Ee1UE5F7itn3IBFZIyIqIrV88jqISJKILBORn3zyQkVkkYhM9EqbbcsnicgWERlv06uLyDciskREfheRM73qPGDbXyoio0QkwqaPEJHFts7XIlLJq861IrLc1vvCK72BiEwTkRU2P8GmdxKRhbaPj0Uk38mTiLQRkRE+aeNFZJ5PWlMRmWXHuUJE3i+GvsNF5H0RWS0iK0XkKp/8q+y1SLTnF1gdzBeRxjatmh2nX/ejiFQQke0i8qJP+iwRWeU1jjuLMY6KIjLa3ju/eem6hYh85G87pYnYbu3ptXIKl/05jeaP3RFscYJG7Uva02nhFDovnsZpDx6rhxoXJHLRnHH02rOM2D7dctNrXnQOF/86PvfouWMJdXt1DqToAafaRRfSevr3tJk5lbi7C75nanTvynnrVhLdwnz1Vb3wfFpMGEur7yfQYsJYqpx3TqBEDgoxXdvTLXkK3ZdPo+nDx+opJDyMcz57ne7Lp9Fp9ldENawHgISFkfj+83RZMIFL/viW2hedHWjRA0rNTu25YN4ULvx9GgmDj9VTw4G3cP4vkzjvpwmcNe4jIuLjcvO6pC7n3JnjOXfmeFp/9m4gxQ4KTlcnByUVXvIR0D2f9CHAdFVtDEy354VRDSiW0Q38AlwCbPBOFJFqwH+B3qp6BnCNT737gBXeCaraXlVbq2prYC4wzmY9ASSpakvgJuAN20c9YDCQqKpnAqHAdbbOA6raytbZCAyydRoDjwMXWLnu9xLhE+Dfqno6cDaQZg3Tj4HrbB8bgJsL0MUTwJs+OjgLqCoip3qVexN43Y71dOCtAtrLjyeBNFVtAjQHciczIlIZo9ffvMo/BFxqx3m3TXsKeF5V/Z3CdgFWA9eIiO+vh9xgr9cFwEsiEu5nm7cDu1X1NOB14CUAVU0G4kWkgZ/tlAokJITEd4Yys8cAJjXvScN+vahyeqNgixV4QkJo+dpQ5l05gBmJPal3TS8qNcurh/RNW0m663FSvpqYJ33nz7/x0/l9+On8Pvza82Y8h9LZPv2XQEofWEJCOGXYUFbccgdJXXtRq3dPIk879p4JiY4m9tYb2b8oKTctc9duVg4YyOIevVnz8BAav/ZyAAUPMCEhtHljKHN6D2Bqq57U79uLyj73VMKt13Bkzz6mNO/K6jc/osVzDwNw6u3m384PZ/Vm9qW30vKlx+CYr7ByQkgIp780lIV9B/DLBT2JvbIX0U3y6mlf8grmXXIVcy/uTep3U2nyzCO5eZ70w8zr2Id5HfuQ1H9goKUPLE5XfhOCJ2BHychfAqjqz8CufLIuxxiM2L99imjqRaCR9Vz+28++F6nq+nyyrgfGqepGWy4tJ0NE4oGewPD82hSRKkAnYLxNag7MsO2sBBJEJMbmVQAirfc5Cthiy+2zbQkQCeT8hNodwDuquttbLhFpDlRQ1R9s+gFVPQTUBI6o6mpb/wcgj3fZ1q8MtFTVxV7JVwLfAV9ydDIAEAtszjmxhqa/3Aa8YOtlq+oOr7xnMcbrYa+0TIxeooBMEWkE1FfVWcXosx9morMROK+AMpWAg+D3k+N9b34NdPYy6L8jr75KPTXPbsmBNRs4uG4z2ZmZbPhyEvGXl28vbX5UT2zJwb82cGj9ZjQzk5SvJ1G3Z149pG9MYd+yVWh2wXO+uD7dSPthNp70wwWWKetUatWSwxs2krHJ6GrHd5Op3uXYe6bBg4NJeW842RlHf4L10PIVZKaZr9T01X8SElERKac/PVqjXUsOrDXPlmZmsumrScRdlldPcZd1YsOn3wCQMm4qdTqar6nKp59G2izjg8jYvovMvfupftaZlEeqtm3JoXUbSN9g9LTtm0nU6ZFXT7vn/Ea2fab2zk+iYmzdYIgadJyuTh4CvZAyRlW32s/bgJjCCmM84WutB/YREansFe7hezQvoq0mQHUbgrBARG7yyvsP8CgUuCy2D8ZDv8+eL8YYsIjI2UBDIF5VU4BXMMbgVmCvqk7LaUREPrTjbsZRb3IToImI/CIi80Sku1f6HhEZZ8Ne/i0iocAOoEJOuAZwNVA/H5kTgaU+af2AUfbo55X+OjBDRL634THVrLxNC9F3tZxywLM23GVMzuRDRNpijOlJPjK8gPHgPw68DTyH8XT7hQ3XuQRjCPuOA+BzEVkCrAKeVVWPrTe6gHHk3Af1gE0AqpoF7MVMcADmA+39lbE0EFkvhoObtuWeH9qcSlS9oh638kdEXAzpm4/q4XBKKpFxxddD3NU9SRkzseiCZZjwujFkbN2ae35k2zYq1s2rq+gzmhMeG8uemT/5Vs+lRo9uHFi6HD2SWWKyBpPIuBjSvZ6t9JRUIn2erci4GNI3G12qx0Pmvv2E16zO3iUrievVCQkNJSohnmptziAqPjag8geKiNgYDm/xeva2pFIxtuBnr94NV7Nj+s+55yERFTnnx7GcPWU0tXuUb4eB05X/iGQH7CgJgraQUlVVRLToknnq7Ada/80uK2BCKzpjPM1zbWxzE0x4xAIR6VBA3X7k9YK/CLwhIklAMrAI8IiJUb8cOAXYA4wRkf6q+pmV/1ZrOL8F9AU+tHI1BjoA8cDPItLCprcH2mCM+NHALao6QkSuA14XkYrANPL35sYC23NOrDHcGJhjdZ8pImeq6lJV/VBEpmJCgi4H7hKRVqq6ikL0LSZmPh74VVUfFJEHgVdE5GbgNeAW3zqqmgSca+tfhJmciIiMxnjBH1LV1IL6BHoBM1U1XUTGAv8QkftzjGtMeMl8EakN/CoiU1R1g6r2LaTNokgD4oos5SiXVIypTZUzmpD245xgixJcRGj41BDWPvx4gUUiG59Gw8ceYvlNtwdQsLLD+o/GUqVZIzrPHcuhjVvYOW8Rml22f9b6RBB7TW+qtD6TP3r3z02b3bojGdvSiGwYT+I3H3NgxWrS128KopSlA6ersk2gje5UEYlV1a0iEosxZvzGhkzMLiD7elVdXkj1zcBOVT0IHBSRn4FWQFugt4hcCkQAVUTkM1Xtb/ushYmnviKnIevxvtXmC7AO+AvoBqxT1e02bxxwPvCZV12PiHyJ8ax/aOX6TVUzgXUishpjHG/GxI3/ZdsajzFWR6jqXKznVUS6YiYOvqTb8eRwLVDd9gFQBTOZeNLKtQUYCYwUswD2TBE5gDH286MDsBM4xNFY9zGY2OjKwJnALNtXXWCCiPRW1fleensKE7bxltVHAiYm/skC+sTKfKGIrLfnNTGhPz94F1LV7SKyEDgH2GCN+qb5tPeaqn4CpGDeGGy2oUFV7fjA6DE9P2HELNa8E+B26tCJaoWIHjjSU1KJrn/09WNUfAyHUgqby5RPDm9JJTL+qB4i6sWQvqV4eoi7qgdbv/sBzco60eKVKo5sS6Vi7FGva3jdumRsO6qr0ErRRDVpTPMvPzH5tWvR7IP/svKOeziYvJTwujE0/d/brHnoMTI2lt9/+OlbUon0erYi68WQ7vNspW9JJTI+lvSUVCQ0lLAqlTmyczcAix95Ibdcx1mj2L96fUDkDjSHt6YSEef17MXFkLH12GevxkXnccoDdzO/d/88b0cyttlwpQ2b2fXL71Rp0bzcGpJOVycPgQ4vmcDRRX83A98WUX4/xoADjKc7Z2FjPkdhBje2rwvF7HwRhTHGVqjq46oar6oJGANwRo7BbbkamKiqucGcNrQiZ4HeAOBna4hvBM4VkShrVHYGVojhNFtXgN7ASlt/PMaAzTHwm2AM+D+AatZjC8awXG7L1bF/KwKPAe/lM94VwGle5/2A7qqaYMd6lh0vItJdRMLs57oYQzZFVVcVou89qqqYMI8Oto/OwHJV3auqtbz6modZwDrfS56bgMmqugsT351tjygrxyc2dCcXMbH17YEGXm3/H8eGmGCvcRtgLYCq9i1gHJ/YKt735tWY+yDnTUwTjg3Vwbb7vqomqmpiaTG4AXb+kUzlxglEJ8QTEhZGw+t6kjJhRrDFCjh7FiQT3SiBqIbxSFgY9a7uSerk4umh3tU9SRnjGyVV/jiwJJmIhIZUjK+HhIVR67JL2f3jUV159h9g/lnnsah9Zxa178z+RYtzDe7QypVpNvJ/bHzpVfYvWBTEUZQ8u+cnU+m0BKISzD1V/9qebJ2Y957aOnEGDW80fpp6V3YjbZbZMCo0MoLQqEgA6nQ+n+wsD/tXrg3sAALEvkXJRJ2aQGQDo6e6V/QkbUpePVVucTrNXx1GUv+BHNlxdBlYhapVctcEhNWoTrVz2nJg1ZqAyh9InK78R8gO2FESlIinW0RGYQyxWiKyGXhaVUdgwjK+EpHbMbtuXGvLJwJ3q+oA73ZUdaeNdV4KfK+qj1AEIjIY4zWtCywRkcmqOkBVV4jIFGAJxrgbrqr5GlI+XGfl9uZ04GMbHrMM491FVX8Tka+BhUAWJuzkfUBs+Sr282IgZ4nxVKCriCzHhIk8oqo77VgeBqZbQ30B8IGt84iI9MJMmt5V1WOsCFVdKSJV7duBmpi483le+etEZK+InAN0xYTL5EwsHlHVbb5tFsBjwKci8h9MOMutRVWwBvEttl8woSiTgSOYBa8ALbGLUL24AmMMZ3ilfQu8bCcgYGK604GKwEequsDPcYyw41iDWQTsvXCyI1CmrC71eJg/aBgdpw5HQkP5a+RY9i4vv1/EBaEeD8kPDePc8UYPGz8dy/4Va2j61GD2LFxK6uQZVGvbgnaj3iasWhXq9uhI0yfvZVa7XgBENqhHZHwsO2f/HuSRBACPh3VPP8vpn4xAQkJIGzOW9D/XUP+BezmQvJTdP84ssGrdm28gomED4gffQ/xgs+HU8ptuJ2tnfuvpyzbq8ZB0/zDaTzT31PqPxrJvxRqaDx3M7oVL2TpxBus+/JqzP/w33ZdP48iuvfx24wMAVKxTk/YTR6DZ2aRvSeWP2x4N8mhKDvV4WDlkGG3HDEdCQkn5YiwHV62h0ZDB7EtayvYpM2jyzKOERkfRcsQbABxO2UpS/4FEN2lE81f/CdkKIcL6Nz7g4OryOTkBp6uTCTnqzHOUN0TkAWC/qua7K0tpxU5ORqiq77aOwZClImYbxAvtAssC+UKauofJDypFB1uCskPt2uV0O7kTTMoW9+j5S5XKRZdxOPyl645VAf2S2pmxKWAPe82K9U/42NzPwJdv3gUyiixVylDVfaXB4LY0AIYUZXA7HA6Hw+FwFIb7GfhyjI1D/zTYcpRlVPVP4M9gy+FwOBwOx8mOlNCP1gQK5+l2OBwOh8PhcDhKGOfpdjgcDofD4XCUekJK6EdrAoXzdDscDofD4XA4HCWM83Q7HA6Hw+FwOEo9JbV/dqBwnm6Hw+FwOBwOh6OEcZ5uh8PhcDgcDkepR8p4TLczuh2OE0TvzHHBFqFMIA/eF2wRygzy2uvBFqFMkDjiuWCLUGY4smxHsEUoE+xwenKUAM7odjgcDofD4XCUetw+3Q6Hw+FwOBwOh6NQnKfb4XA4HA6Hw1HqKesx3c7T7XA4HA6Hw+FwlDDO6HY4HA6Hw+FwOEoYF17icDgcDofD4Sj1hLgfx3E4HA6Hw+FwOByFUaTRLSIjRSRNRJb6pF8jIstEJFtEEv3pTESeKI5whfUhIi1FZK7NTxaRCJ/8Cd4yi8hoEUmyx3oRSbLp4SLyoW1jsYh08KrTz6YvEZEpIlLLpj8jIile7V1q07uIyAJbZ4GIdPq7beWji1gRmeiT9h9bN8QrLUZEJtqxLBeRycXQ9yARWSMimiOfTRcRedPmLRGRtl55N4vIn/a42Ss9XETeF5HVIrJSRK6y6feKyFIRmSwi4TbtQhHxe0NiEWltZezuk+6xOlwsIgtF5PwTMPZeIjLM33aCQUbGEW7q+yjXXfEA1/S+j/fe/rLAstOnzeWsM65k+dI1AZSw9BB+/cNEPTeGyCEf5Jsf2uJ8Ih97n4hH3yPi4XcIOfXMAEtYOsjIOEL/vkO49oqHuKr3/bz79uhjyowZPZVr+jxI3ysf5tb+T7F2zaYgSBpcnpq6gYveTabPxyvyzR/5RypXfbqSqz5dSZ+PV9Dy9UXsTc8KsJSlA/fsFU5Eu/OJ+2g8cZ9MoMp1tx6TH1qnLjGvfkDse18S+8FXRJx9oal31rnUffcLYj8YQ913vyCidbtAix5QhOyAHSWBP+ElHwFvA5/4pC8FrgT+V4z+ngCeL0b5fPsQkQrAZ8CNqrpYRGoCmV75VwIHvOuoal+v/FeBvfb0DpvfQkTqAN+LSDvMhOQNoLmq7hCRl4FBwDO23uuq+oqPvDuAy1R1i4icCUwF6ll5i9uWLw8Cud9W1tC+AtgEXAzMtFnDgB9U9Q1brmUR7XrzCzARmOWT3gNobI9zgHeBc0SkBvA0kAgosEBEJqjqbuBJIE1Vm1hZa9i2bgBaYu6FbnYi8Q+gXzHk7AfMsX+neKWnq2prABHpBryA0Y0/FDT2ScCzIvKiqh4qhowBIzw8jPdG/pOo6EgyM7O4/cYnuaB9G1q0apqn3MGD6Yz6bBJntmwcJEmDT9ZvU8n6eTwV+z+Wb75n1ULSk38FQOJOIeLWf5D+3G2BFLFUEB4exvsjn869p2678SkuaN+Glq2a5Jbp0bM91/TtBsCsGX/w2ssf8877TwVL5KDQ54yaXN+6Nk9M2ZBv/m3tYritXQwAs9bu5ZOFaVSNPDmjOt2zVwghIdQY/Dhpj95N1vZUYv/7OelzfyJzw1+5RarecAcHZ03jwHdjCGt4KnWef5uUGy7Fs3c325+6D8/O7YQlNKLOS++S0rdrEAfjKIwiPd2q+jOwK5/0Faq6yt+ORORFINJ6Ij/3p04hfXQFlqjqYltup6p6bD+VMAbqvwqQQ4BrgVE2qTkww7aTBuzBGJFij2hbpwqwpQh5F6lqTplldrwV/05b+XAVeQ3MDraPd8lrsMYCm71kWuJvB1b+9flkXQ58ooZ5QDURiQW6YQz8XdbQ/gHI8T7fhjF6UdVsVc35eS8BwoAozESpP/C9qh5zj+WH1d81wC1AF983HF5UAXb706aVMd+xq6piDPFe/rYVaESEqOhIALKyPGRlZYHIMeXeffMLbr69DxUrhgdaxFJD9tpk9ND+ggscOZz7UcIjQDUAUpU+jr2nPMfcUpUqReV+Tk/PME/2SUZifCWqRoT6VXbyyt1c2rR6CUtUenHPXsGENzuTrJRNZG1NgawsDs6cSuT5HXxKKSHR0QBIdCWydm4HIHPNKjw5n9evRcIrQlhYAKUPLCLZATtKgoBNuVV1iIgMyvFEAojIbKByPsUfVtUfC2muCaAiMhWoDXypqi/bvGeBV4GCvJLtgVRV/dOeLwZ6i8gooD5wFlBfVX8XkYFAMnAQ+BP4P692BonITcB84CFrdHpzFbBQVTPsWP92WyJyCrA7py1LP8zE4VvgeREJU9VM4B1gtIgMAn4EPrSe98rA7AJ0cr2qLi8gD6AexqOew2ablm+6iFSz58/acJ21wCBVTcW8NZmHmTD8YuXvVkjfvpwPrFPVtSIyC+gJjLV5kWLChiIwk49OAMc5djDXpT3wVTHkDCgej4f+1zzCpo3buLZfd1q0bJInf8XytaRu20n7ixP59MNvgyRl2SC05QWEX3Y7Uqkah//3ZLDFCRoej4frr3mMTRu30bdft2PuKYDRX3zPZ59MJDMzi/+NfCbwQpYR0jOzmbN+H092ig+2KKWak/XZq1CrDlnbt+Wee7anEn56izxl9n78HnVeepfKffohEZGkPXLXMe1EXXQJR/5cAZmZx+Q5SgdBXUipqu1VtXU+R2EGN5jJwoWYUIULgStEpLOItAYaqeo3hdTNMVZzGIkxFucD/wF+BTwiEgYMBNoAccAS4HFb512gEdAa2Iox8nMRkTOAl4C77PnfbssSC2z3aj8cuBQYr6r7gN+whquqTgVOxYSiNAMWiUhtVd1fgK5b+2F0FpcKQDzwq6q2BeYCr1j5PlXVNqraH3gAeBPoISJfi8jr3vHpBdAPyAla/pK8Xv50O55mGI/7JyIiJ2DsaZjrdgwicqeIzBeR+SM/GONHUyVDaGgoo8a9xvczPmBp8hrW/Hn0dXd2djavv/wRDzx6S9DkK0t4lvxC+nO3cXj404T3PDa28mQhNDSU0eNeYeqM/9l7auMxZfpe34PvprzDfQ/0Z/h7XwdByrLBrL/20qZe9EkbWuIv7tkrmKhO3TkwbQIp13Uj7YlB1Hz8X3neaIY1bES1O+5j1+v5vuQvNwiegB0lQVCNbhGZ7bWA0Pu4pIiqm4GfVXWHjbOdDLQFzgMSRWQ9Jua3ifWG5vRXARMjnrsqSFWzVPUBa4BdDlQDVmOMYFR1rQ0x+ArjZUVVU1XVo6rZGOP2bK8+4oFvgJtUda1N/ltteZGO8d7m0M3KmWzHeiFexqcN9/hCVW8E/gAuEpHKBeg6SUSaF6HvFMxbgBzibVpB6TsxbxrG2fQxmOuTi4jEAWer6njgIaAvJrSnc0FCiEgo5g3CUDvut4Du1pOdB1WdC9QCah/n2MHoPj2/DFV9X1UTVTXxtjuu8aOpkqVylWgSzz6TX+csyk07eDCdNX9u5M5b/kGvLneRvHg1Dwx64aRdTOkv2WuTkZqxEF0l2KIElfzuKV+6XXoBs2b8EUCpyhbfn+ShJcXlZHv2snakUaF23dzz0NoxeHak5SlTqccVHJo1DYAjy5cgYRUJqVrNlK9Vh9rDXmPni/8ga+tmHKWXQBvdmdbrCxyXp3sq0EJEoqwhfTGwXFXfVdU4VU3AGKKrVbWDV71LgJWqmntX2jai7ecuQJb1fqYAzUWkti3aBVhhy8V6tXkFZsEnNqxiEjBEVX/xKlPstnxYDSR4nfcDBqhqgh3rKZj45igR6SQiUbbtyhgv+sbj9PZOAG4Sw7nAXlXdirkOXUWkuohUx8TaT7UTi+8wcedgDGnfPp4FhtrPkZiFmNmYWG9EZGU+cnTGxPLXt2NviAktucK3oIg0A0KBnSfA092E/K9LqWD3rr3s33cQgMOHM/ht7mISTjn6Grty5Whm/PIxE3/4HxN/+B8tWjXh9bcfp/mZpwVL5FKL1Dr6QiMk/jSoEAYH9wVRouCwK997ql6eMhs2bM39PPunhdRvWBfHsezP8DB/8wE6nlY12KKUak7mZ+/IymVUqNeACnXjoEIFojt2I/3Xn/KU8aRtJaLtOQBUaHAKEh5O9p7dSHRl6jz/Frs/eIOMZUlBkD6whEh2wI6SoMh3XTbWuQNQS0Q2A0+r6ggRuQLjaawNTBKRJFXtZj2Yw1U1v63v3geWiMhCVb3Bj77z7UNVd4vIaxgvrgKTVXWSH+O9jryhJQB1gKliouZTgBsBbBz0P4GfRSQT2IBZvAfwsg1lUWA9NowEsyPJaRhPbI5B2fVvtpWLqh4UkbUichpmAWZ34G6f/DnAZUAD4G0RycJMqoarql8uKBEZDDwK1MVcp8mqOgDzJuFSYA3Gg32r7XeXiDyLuQ4Aw/TogsjHgE9F5D+Y0JhbvfppY+svtElfYOLdN1l91CL/ZVn9MG8RvBmLCd35hKMx3dj6N6tdYHscYwfoyNFwoFLHju27efqJt/BkZ6PZ2VzS7QIu6pDIu2+NovkZjbi4U34vT05OKt78BCGntUIqVSVy2CgyJ38MoeZrMOuXiVRo3Z4K7bqgnizIPELGR+X7VW1B7Ni+m6FPvE12djbZ2UqXbudzUYdE/vvWlzQ/oxEdOrVj9Bff89vcJVSoUIEqVaJ59vl7gy12wHlk0jr+2HyAPelZdH5/KfecF0tWtlkA2LeV2Xl0+po9nJ9Qmagw/xZcllfcs1cI2R52vfUidV56F0JCOPD9t2RuWEvVWwZyZNVy0uf+xO73XqPGg0OpctUNoLDz5acBqNKnLxXiGlDtxruodqMxH1Ifu5vsPX7vI+AIIKIn0QrhsoydgJylquV+Ty4R6QWcqqpvlgJZYoAvVLXAsJccDmQtcw+TH8iD9wVbhDKDvOb39vUnNWEjngu2CGWGI8t2FF3IwQ6nJ79oOD0poPsWZWXPC9j/2Qoh557wsblVHWUEVf1GzH7k5R5VnVh0qYDRABNz7nA4HA6Hw/G3cUZ3GUJVhwdbhpMNf0NzHA6Hw+FwlCwltX92oAjq7iUOh8PhcDgcDsfJgPN0OxwOh8PhcDhKPSW1f3agcJ5uh8PhcDgcDoejhHFGt8PhcDgcDofDUcK48BKHw+FwOBwOR6nHLaR0OBwOh8PhcDgcheI83Q7HCaLiiGeDLUKZYP53m4MtQpkhJqnIH+51APNmZwRbhDLDK2e7H6fyh/FVPgi2CI58EA2gp7sEfvbHebodDofD4XA4HI4Sxnm6HQ6Hw+FwOBylH+fpdjgcDofD4XA4HIXhPN0Oh8PhcDgcjtJPID3dJYDzdDscDofD4XA4HCWM83Q7HA6Hw+FwOEo/qsGW4LhwRrfDUcZ5auoGfv5rHzWiKjD+5tOPyR/5RyqTVu4GwJOt/LXrMLPvbkHVyJPj8a920YUkPP0kEhJC6uiv2fJe/luB1ejelabvvsmS3ldzMHkpVS88nwaPPkRIWBjZmZlseOFl9s39LcDSB47Isy+g5uDHkJAQ9k0ax97PR+bJrznoESLatANAIiIIrVaDDT0vBCC0Tl1qP/YMFerUBVW2Pfp/ZG3bEvAxlBZiu7XnrDeeREJDWDt8DMtfctvPVaoUztAnO9Lo1Bqg8M9/zWDJ0tTc/B7dGnPLjW1B4NChTJ5/+Sf+/HNnECUOLBGJ51P9nkcgJISD349n3+gP8+SH1q5LzUeHEVKpMoSEsGfEWxz+fU6e/NgRY9n7yXvs//rTQIt/UiIiEcDPQEWMPf21qj5dWJ0iw0tEZKSIpInIUp/0f4vIShFZIiLfiEg1P9p6oqgyPuWvEZFlIpItIok+eS1FZK7NT7aD986f4C2ziIwWkSR7rBeRJJseLiIf2jYWi0gHrzr9bPoSEZkiIrVs+jMikuLV3qU2vYuILLB1FohIJ6+2wkXkfRFZbfV2lU1vICIzRWSR7efSAnQRKyITfdL+Y+UI8UqLEZGJdizLRWRyMfQ9SETWiIjmjNWm32BlSxaRX0WklU1v6qWDJBHZJyL327x8r52IXGDbmi8ijW1aNRGZ5j2OIuSsICLbReRFn/RZIrLKyrJCRO4sxtgvEpGFIpIlIld7pdcWkSn+thMM+pxRk/eubFRg/m3tYhh7YzPG3tiM+y+MIzG+0kljcBMSwinDhrLiljtI6tqLWr17EnnasboKiY4m9tYb2b8oKTctc9duVg4YyOIevVnz8BAav/ZyAAUPMCEh1HrgCbY9MpBNN/WhUucehDU8NU+RnW//m5TbryXl9mvZN3YUh36enptX58nn2DvqIzbf2IeUu67Hs3tXoEdQapCQEBLfGcrMHgOY1LwnDfv1osrpBT+fJwuPPHghv87dyFV9R9G3/2j+Wr87T37Klv0MGDievjeM5oOR83lqSIfgCBoMQkKofu8Q0p4YxNYBVxHVsTsVGuR9/qreMIBDP/3AtoH92PHc49S49/E8+dXvfojDf/wSSKmDg2YH7iiaDKCTqrYCWgPdReTcwir4Y+R8BHTPJ/0H4ExVbQmsBh7Pp4wvxTK6gaXAlZiZRC4iUgH4DLhbVc8AOgCZXvlXAge866hqX1VtraqtgbHAOJt1h81vAXQBXhWRENvHG0BHO8YlwCCvJl/PaU9VcwzbHcBltq2bAe/p5pNAmqo2AZoDP9n0p4CvVLUNcB3w3wJ08SCQ6y6xBuoVwCbgYq9yw4AfVLWVqjYHhhTQXn78AlwCbPBJXwdcbMf1LPA+gKqu8tLpWcAh4BtbJ99rBzwEXArcD9xt054Cnlf1e4VEF8w9d42I+G7qc4OV5wLgJREJ97PNjcAtwBfeiaq6HdgqIhf42U7ASYyvRNWIUL/KTl65m0ubVi9hiUoPlVq15PCGjWRs2oxmZrLju8lU79L5mHINHhxMynvDyc44kpt2aPkKMtPSAEhf/SchERWR8LCAyR5IKp5+JpkpG8namgJZWRycPoXoCzsWWL7SJT04MP17AMIanoqEhpI+fx4Amp6OZhwOiNylkZpnt+TAmg0cXLfZvCH5chLxlx97z51MVIoOp22bOMZPWAFAVlY2Bw4cyVNmSfI29u83P3KUvDSVmDrRAZczWIQ3PZOsLZvwbDPP36FZU4k6v0OeMqqKRBudhERXwrNze25e5PkdyNqWQub6tYEU+6RHDTm2Zpg9Co1/KdLoVtWfgWPcFqo6TVWz7Ok8IL6wdqxXMtJ6IT8vql/bxwpVXZVPVldgiaoutuV2qqrH9lMJY6D+qwA5BLgWGGWTmgMzbDtpwB4gEbNDowDRtk4VoND3paq6SFVzyiyz461oz28DXrDlslV1R0412zZA1UL6uArw9rh2sH28C/TzSo8Fcn/yT1WXFCZzPvKvzyf9V1XNcUsUdK07A2tVdYOtU9C1ywSi7JEpIo2A+qo6y185MeN9A2Mon1dAmUrAQcDjT4Oqut7qKj/DfzxQ5n8aMD0zmznr99GlcbVgixIwwuvGkLF1a+75kW3bqFg3Jk+Z6DOaEx4by56ZP/lWz6VGj24cWLocPZJZYJmyTIVaMWSlHX3Vn7U9ldDadfIvGxNLhdh6pC/8HYCw+g3xHNhPzL9eo97w0dQY+CCEnLxr9CPrxXBw07bc80ObU4mqF1NIjfJPXFxldu9O55l/dOKLT67hH090ICKi4LdtfXqfzi9zNwZQwuASWqsOnu1ez9+OVEJr1c5TZu+n/yO686XEfTGFOs+9xa53XgJAIiKp0vdW9n76v4DKHDSyswN2iMid9q18znHM23MRCbWRE2kYh2ehMYgn6pvxNuD7wgqo6hAg3XpGb7DCzvYJT8g5LimivyaAishUGxLwqFfes8CrGK9rfrQHUlX1T3u+GOhtQxZOwXhs66tqJjAQSMYYws2BEV7tDLJhEiNFJD/X4VXAQlXNkKOhN89aeceISM638DNAfxHZDEwG7vVtyMq1W1W9f+u4H2bi8A3QU0RyXHDvACNsyMqTIhJn26hcgK6TRKR5AbrKj9vJ/1pfx9GJTGG8AHyCeTPyNvAcxtPtF2LCiC4BvrP99fMp8rmILAFWAc96TcZGFzD2m/zodj7mvinTzPprL23qRZ88oSX+IELDp4aw4bmXCiwS2fg0Gj72EH89WWio3klDdOfuHJz1g/nHBEhoBSJbtmXnO6+Sctf1hMXFU7nH5UGW0lGaCA0NoVnT2nw9binX3zSG9MNZ3Hpz23zLJp4VR5/LTufNt+cGWMrSTXTH7hyc9h1bru9O2pP3Uuuxf4EIVW+6m/1jP0MPpwdbxHKHqr6vqolex/v5lPHYt+vxwNkicmZhbR630S0iTwJZgF/ea29Utb1XiIb38WMRVSsAF2K8jxcCV4hIZxFpDTRS1W8KqZtjrOYwEuMZng/8B/gV8FgjdiDQBojDhJfkhNC8CzTCxPBsxRj5uYjIGcBLwF1e8sYDv6pqW2Au8IqXPB+pajwm7OLTfGKbY4Hcd0k2ZOJSYLyq7gN+A7oBqOpU4FRMKEozYJGI1FbV/QXourWqLi9EX97j6ogxuh/zSQ8HegNjimpDVZNU9VxV7Wjl3GqakNEi8pnXZKQgegEzVTUdEybUR0S8YytusOFADYCHRaSh7bdvAWP/xI+hp2HugWPwngkPn126X+19f5KFlgAc2ZZKxdjY3PPwunXJ2HbUoxRaKZqoJo1p/uUntJk9ncptWtHsg/8S3eJMWz6Gpv97mzUPPUbGxk0Blz9QZO1IpUKdo49ehdoxeLan5Vu2UqfuuaElYLziGWtWmdAUj4eDs2cQ3uTYBb0nC+kpqUTXr5t7HhUfw6GU1EJqlH/S0g6QlnaApcvMPTV9xlqaNa19TLnGp9XkH0905IFHJrN3X8Yx+eUVz440Qmt7PX+1YvDs2J6nTHT3Phz6aRoAR1YsQcLDCalajfBmZ1LtjvuJ+3QSla+8gSr9bqfS5X0DKn9AKV0x3UfFUt0DzCT/cOxcjsvlJSK3YIygzqrF38dFRGYDlfPJergIw3sz8HNOiIaYxYJtMXHciSKyHjO2OiIyS1U72HIVMHHGZ+U0ZENkHvCS6VdMvHBrm7/Wpn+FjY9W1VSv8h8AE73O4zHe55ty6gI7MZ73nDjyMRjjFfu3u213rvXk1sIYejmkA94LRbsB1YBkG9IcZctMtO3swsQmfyFm8eVFIjINmF2APq8vyvAWkZbAcKCHqvouKe+B8er7/Z/Fhuw8hfGQvwU8CiQAgzHx7wXRD7jQXmOAmkAnzBqDXFR1u4gsBM4BNojIaKBpPu295ofhHYHR7zHYme/7AJn/u67U7mW0P8PD/M0HePHShsEWJaAcWJJMREJDKsbX40hqGrUuu5Q/73s4N9+z/wDzzzoaodR81CdseP5lDiYvJbRyZZqN/B8bX3qV/QsWBUP8gJGxchlh8Q2pEFuPrO2pRHfuTtqwY5eDhDVIIKRyFTKWLvaqu5SQSpUJqVqd7L27iWx7NhmrlgVS/FLFzj+Sqdw4geiEeNJTUml4XU9+vf6hYIsVVHbuSic17QANG1Rjw8Y9nJ0Yz7p1eaNW68ZU4pUXu/OPZ6azcdPeIEkaHI6sWkZYvQaE1o3DsyONqA7d2PlC3mVynrRtRLQ5m4PTvqNCg1MgvCLZe3aT9uDtuWWq3ngX2emHOPDt6EAP4aRERGoDmaq6R0QiMevNCn5tynEY3SLSHWMoXayqBYVy+JIpImE2dANV/buv7KcCj4pIFHAEs5DwdVWdhPFCIyIJwMQcg9tyCbBSVXNjnm0boqoHRaQLkKWqy21YRnPrJd6OUeYKWydWVXMCRa/ALBrEhpFMAoaoau4yYlVVEfkOE4c9AxP/nGPkbrTnH4nI6RgDL+8U10wCErzO+wEDVHWU7TcaWGfHci4wT1UPiUhljEd+o6rux04kiouINMBMGG5U1dX5FPF9e+APNwGTVXWXlTvbHlG2z0+At1X1dy85qmDCPOrnhNqIyK22/zxGt22zDfAyGE93MeXzpgn2GpdGHpm0jj82H2BPehad31/KPefFkpVt7P++rcwmNNPX7OH8hMpEhfm34LLc4PGw7ulnOf2TEUhICGljxpL+5xrqP3AvB5KXsvvHmQVWrXvzDUQ0bED84HuIH3wPAMtvup2sneVwZw6Phx3/eZ66r7yLhISyf/J4Mtevpfpt95CxajmHfpkFQKXOPTg4w2czn+xsdv33VWL/8wEiQsaq5ez7bmzgx1BKUI+H+YOG0XHqcCQ0lL9GjmXv8jXBFivovPTKbJ4bdglhFULZvGUvzzw7k6uuOAOAsd8s447bE6latSKPP3oRAB5PNv1v+TqYIgeObA+73n6JOi/812wZOPVbMjf8RdWbB3Jk9XLS5/7E7v+9Rs0H/0HlK/sDyq5/Dw221MGhdP0iZSzwsX3bHoLZFGNiYRWkKAe1iIzCGIu1gFTgaVUdISJrMHsT5ng956nq3dZYHa6qx2x9JyIvYcIQFubEdRfR9xUYL2htzALHJFXtZvP6Y8I9FGO8PepTNwFjdJ/plfaRlfM9n3JTMQZfCnB7zmJAEbkbuA+z+G8DcIuq7hSRTzEGrALrgbtUdauIPGVlyokXB+iqqmk2zOFTjId6O3Crqm608dQfYBb+KfCoqk7LRxfTMeEqWzCe/gQbWpKTPw4YjQmruBUT8hMCfKiqr/q2lx8iMhgzkaqL8bRPVtUBIjIcE6Oes6tJlqom2jrRmInDqaq616utwq5dFGZy0lVVM0WkPWbXliMYr/sqMQsTevlMkG7GeNqv80qrgYnfjsdcx1iMV7oi8KmqPu/n2Nth3lBUBw4D29TsjIOIPAxkqOpbhbVRmj3dpYn5LyYFW4QyQ0x9fzffObmZN/vkCUU4Xl45+75gi1AmGF/F7a3uDw1+WOS7g1jJkj4hcP9nI3uf8LEVaXQ7SgfWiD1LVf1edFhWsR7tEap6TbBlARCRn4HL9egOLvnijG7/cEa3/zij2z+c0e0/zuj2D2d0+4czuouH28agjKCq34hIzWDLEQisB7+0GNy1MXHfhRrcDofD4XA4SpjSFV5SbJzRXYZQ1eHBluFkw8bzjw+2HA6Hw+FwOMo2zuh2OBwOh8PhcJR+ssu2p/vk/dkwh8PhcDgcDocjQDhPt8PhcDgcDoej9FPGN/9wnm6Hw+FwOBwOh6OEcZ5uh8PhcDgcDkfpx+1e4nA4AMbcXb5/KvxEcUpCYLd1Lcss/M3tP+0Pl99bP9gilBkqjXwj2CKUCVZGBFuCskGDYAtQxnBGt8PhcDgcDoej9FPGPd0uptvhcDgcDofD4ShhnKfb4XA4HA6Hw1Hq0QB6uksiENJ5uh0Oh8PhcDgcjhLGebodDofD4XA4HKUf94uUDofD4XA4HA6HozCcp9vhcDgcDofDUfpxu5c4HI7SSGy39vRaOYXL/pxG88fuCLY4QaPaRRfSevr3tJk5lbi7C9ZDje5dOW/dSqJbnAlA1QvPp8WEsbT6fgItJoylynnnBErkoBHTtT3dkqfQffk0mj58rK5CwsM457PX6b58Gp1mf0VUw3oASIUKJA5/kS4LJtB18WSaPnJnoEUPCuHXP0zUc2OIHPJBvvmhiZ2IfOx9Iod8QMQDbxASd2qAJQwutS9pT6eFU+i8eBqnPXjs/VTjgkQumjOOXnuWEdunW256zYvO4eJfx+cePXcsoW6vzoEUPeDU7NSeC+ZN4cLfp5Ew+FhdNRx4C+f/MonzfprAWeM+IiI+LjevS+pyzp05nnNnjqf1Z+8GUmxHMTkuo1tERopImogs9Ul/VkSWiEiSiEwTkbiC2rDlq4nIPcXse5CIrBERFZFaPnkdbN/LROQnn7xQEVkkIhO90mbb8kkiskVExtv06iLyjR3L7yJypledB2z7S0VklIhE2PSPRGSdV3utbXozEZkrIhki8rBXOxG27cW2vX965YmIPCciq0VkhYgMLkAXbURkhE/aeBGZ55PWVERmWblWiMj7fuo6SkQmichKK+OLXnl3i0iybXOOiDS36TVFZKaIHBCRt73KVxSRKVZv93ilvy8ibf2Rx5b/j4ikiEiIV9otIrLd69p/LSJRxWhziojs8b43bPqXItLY33ZKAxISQuI7Q5nZYwCTmvekYb9eVDm9UbDFCjwhIZwybCgrbrmDpK69qNW7J5GnHauHkOhoYm+9kf2LknLTMnftZuWAgSzu0Zs1Dw+h8WsvB1DwIBASQps3hjKn9wCmtupJ/b69qNwsr64Sbr2GI3v2MaV5V1a/+REtnjNfZfFXdSe0Yjg/nNWb6edeyakD+uYa5OWZrN+mcvjdxwvM153bSH/zQdJfvIPMKZ8Rft0DAZQuyISE0PK1ocy7cgAzEntS75peVPK5n9I3bSXprsdJ+SrPVy47f/6Nn87vw0/n9+HXnjfjOZTO9um/BFL6wBISwukvDWVh3wH8ckFPYq/sRXSTvLral7yCeZdcxdyLe5P63VSaPPNIbp4n/TDzOvZhXsc+JPUfGGjpHcXgeD3dHwHd80n/t6q2VNXWwERgaBHtVAOKZXQDvwCXABu8E0WkGvBfoLeqngFc41PvPmCFd4KqtlfV1lbeucA4m/UEkKSqLYGbgDdsH/WAwUCiqp4JhALXeTX5SE57qppk03bZOq/4yJMBdFLVVkBroLuInGvzbgHqA81U9XTgywJ08QTwpo8OzgKqioi3a+VN4HUr1+nAWwW0lx+vqGozoA1wgYj0sOlfqGoLq7uXgdds+mHgH8DDPu10A+YALYEbrbytgFBVXeiPINbQvgLYBFzskz3aju8M4AjQ1/8h8u8cmXx4F3i0GO0EnZpnt+TAmg0cXLeZ7MxMNnw5ifjLy7enKD8qtWrJ4Q0bydi0Gc3MZMd3k6ne5Vg9NHhwMCnvDSc740hu2qHlK8hMSwMgffWfhERURMLDAiZ7oKnRriUH1pp7RjMz2fTVJOIuy6uruMs6seHTbwBIGTeVOh3PMxmqhEZHIqGhhEZGkJ2ZSea+A4EeQsDJXpuMHtpfcP665ZBu9OBZvwKpVjtQogWd6oktOfjXBg6tN/dTyteTqNsz7/2UvjGFfctWoYUsjovr0420H2bjST9c0iIHjaptW3Jo3QbSNxhdbftmEnV65NXV7jm/kW11sHd+EhVj6wZD1OCjGrijBDguo1tVf8YYk77p+7xOo4GipH8RaGQ9lP/2s+9Fqro+n6zrgXGqutGWS8vJEJF4oCcwPL82RaQK0AkYb5OaAzNsOyuBBBGJsXkVgEgRqQBEAVuKkDdNVf8AMn3SVVVz/juF2SNHXwOBYWo3pvQei5fMlYGWqrrYK/lK4DuMke49GYgFNnv1nVyYzF7lDqnqTPv5CLAQiLfn+V5rVT2oqnMwxrc3mRh9hXF0G8xnMQa6v3QAlmGM4X75FbDXJRrY7W+jqjodyO8/6GzgEttmmSCyXgwHN23LPT+0OZWoejGF1CifhNeNIWPr1tzzI9u2UbFuXj1En9Gc8NhY9sz8ybd6LjV6dOPA0uXokcwCy5R1IuNiSPe6Z9JTUon0uWci42JI32z0qR4Pmfv2E16zOpvHTcVzMJ1eG+Zw6ZqZrH59JJm79wZU/tJOhfN64Fnxe7DFCBgRcTGkbz56Px1OSSUyrvjfQXFX9yRlzMSiC5ZhImJjOLzFS1dbUqkYW7Cu6t1wNTum/5x7HhJRkXN+HMvZU0ZTu8fJ51wpS5SYESEiz2G8w3uBjkUUHwKcab2lOYbk7ALKXq+qywtpqwkQJiKzgMrAG6r6ic37D8ZjWbmAun2A6V6G5GKMATtbRM4GGgLxqrpARF4BNgLpwDRVnebVznMiMhSYDgxR1YxC5EVEQoEFwGnAO6r6m81qBPQVkSuA7cBgVf3Tp3oisNQnrR8wDEgFxgLP2/TXgRki8iswDfhQVfeISFNgdAHidVDVPV6yVgMuw3r9bdr/AQ8C4ZhJS2H8gPEmzwP+LSK9gYWqWuikJZ/xjQK+BZ4XkTBVzbGG+orIhZgJxmrM5AMRuQF4JJ+21qjq1YV1pqrZIrIGaIW5To7ygggNnxrC2ocLDhGIbHwaDR97iOU33R5AwcoWNdq1RD3ZTExoT3j1KnSY8QVpM37l4LrNRVc+CQhp3Iqwc7uT/p+TKLzkBFAxpjZVzmhC2o9zgi1KqSH2mt5UaX0mf/Tun5s2u3VHMralEdkwnsRvPubAitWkr98URClLELeQMn9U9UlVrQ98DgwqZt39XuEZvkdhBjeYicRZGI92N+AfItJERHoBaapamNGUY8zl8CJQTUSSgHuBRYBHRKoDlwOnAHFAtIjkPAGPA82AdkAN4DE/xuuxE4544Gyv2PGKwGFVTQQ+AEbmUz0WY5ADYD3xjYE5qroayMxpT1U/BE4HxmC8xfNEpKKqripE33u82q5g9fOmqv7lJf87qtrIjvWpIsaaparXq2obK8f9wKsi8pqNwe5dWH0RCQcuBcbbydFvmOucw2iry7pAMtbQVtXPCxhfoQa3F2mYa+0rz50iMl9E5s9gj59NlTzpKalE1z/6+jEqPoZDKalBlCg4HNmWSsXY2Nzz8Lp1ydh2VA+hlaKJatKY5l9+QpvZ06ncphXNPvhv7mLK8LoxNP3f26x56DEyNpbTf2KW9C2pRHrdM5H1Ykj3uWfSt6QSGW/0KaGhhFWpzJGdu6l/XS+2TZuNZmWRsX0XO35dSPW2LQIqf2lF4k6hYr+HOPzBUDi0r+gK5YTDW1KJjD96P0XUiyF9S/G+g+Ku6sHW735As7JOtHilisNbU4mI89JVXAwZW4/VVY2LzuOUB+4mqf/APG/dMrbZMLgNm9n1y+9UadG85IV2/C0CsXvJ58BVxakgIpW9FiL6HkXdTZuBqTa8YQfwM8ZDeQHQW0TWY8IuOonIZ1591gLOBiblpKnqPlW91RpxNwG1gb8wseTrVHW79bCOA863dbbakJEM4EPbpl9YA3cmR+PkN3M0vvwbTBy0L+lAhNf5tUB1YJ0dawJeIRiqukVVR6rq5UAWcKZdYFmQvqt5tf0+8Keq/qeAIXyJeVvgL/cAnwDnYt6I9AUeKqJON8wagGQ7vgvJJ8REVRXj5b4IjKe7gPF97aesERhd+/bzvqomqmpiJ6r52VTJs/OPZCo3TiA6IZ6QsDAaXteTlAkzgi1WwDmwJJmIhIZUjK+HhIVR67JL2f3jUT149h9g/lnnsah9Zxa178z+RYtZecc9HExeSmjlyjQb+T82vvQq+xcsCuIoAsPu+clUOi2BqIR4JCyM+tf2ZOvEvPfM1okzaHjjFQDUu7IbabPMWu30jVup08Hs7hIaFUnNc1qxf9VfnOxI9TpE3P4MGZ++iG5PCbY4AWXPgmSiGyUQ1dDcT/Wu7knq5OJ9B9W7uicpYyYVXbCMs29RMlGnJhDZwOiq7hU9SZuSV1eVW5xO81eHkdR/IEd2HI3qrVC1Su5ak7Aa1al2TlsOrFoTUPkDimYH7igBSiS8REQae4VBXA6sLKLKfrxCPlR1P2ZR4d/hW+Bt65UNB87BLB4cg/FCIyIdgIdVtb9XvauBiaqaG4NsDc5DNo55APCzqu4TkY3AuXZnjHSgMzDf1olV1a0iIhgD1Df0Iw8iUhvItGEekUAX4CWbPR4TmrMOs2BwdT5NrCCvodoP6K6qc237pwA/Ak+KSHdM+EymiNQFagIpqrqNIvQtIv8Cqlo9eKd7X+uegG/4S0HtVQd6YYzoy4BsTDx4pM2/AjhbVX3f+/cDBqjqKFsuGjPByG+XkguBtWA83ZgJ4N+lCUVcy9KEejzMHzSMjlOHI6Gh/DVyLHuXl+Mv4oLweFj39LOc/skIJCSEtDFjSf9zDfUfuJcDyUvZ/ePMAqvWvfkGIho2IH7wPcQPNuu8l990O1k7j1nGUi5Qj4ek+4fRfqK5Z9Z/NJZ9K9bQfOhgdi9cytaJM1j34dec/eG/6b58Gkd27eW3G024xJr3PqfdBy/QZdFERIT1n4xj79JVQR5RyVPx5icIOa0VUqkqkcNGkTn5Ywg1/1azfplIWPf+SHQVwq+xG09lezj8yv8FUeLAoR4PyQ8N49zx5n7a+OlY9q9YQ9OnBrNn4VJSJ8+gWtsWtBv1NmHVqlC3R0eaPnkvs9r1AiCyQT0i42PZObv8x8Grx8PKIcNoO2Y4EhJKyhdjObhqDY2GDGZf0lK2T5lBk2ceJTQ6ipYjTGTn4ZStJPUfSHSTRjR/9Z+QrRAirH/jAw6uXhvkETkKQvQ4VmiKyChMmEItTPzw06o6QkTGAk0xhtQG4G5VTRGRRPt5QD5tfYHx5H6vqvnF3vqWH4yJz66LefU/OaddEXkEuNX2P9zXM+tldPfySpsFvKiqU7zSzgM+xhiDy4DbVXW3zfsnxjObhQk7GaCqGSIyA+MRFyDJjveANXLnA1WsXAcwCzUTbB+hmDcPX6nqMNtHNYyh2MCWv9tnwWSOnMkYT3tNzK4u8ep1YUVkIWZRZl+MYZwzsfi3qn5GEdgFqJswk6ec+PS3VXW4iLyB8fxnYhYtDlLVZbbeejvecGAP0DUnPEhEXge+VdVZYrZbnADUA95T1bfEbKsYpqoveMkRhfH+J3gv4BSRcZiY9EjMDiQpVpebgVs0nwWoBYxzNiY0qBKwE3O9p9qQne9UtdC3Fl9I05JZ7lzOOCVBii7kACBli7ul/KHHXfWDLUKZYfrI8h0mdaKIiCi6jAO67lgV0C903TY8YF+KUnfACR/bcRndjtKBiDwA7FfVfHdlKYvY0J8HVHV7kYVLXpYHgH2qOqKwcs7o9g9ndPuPM7r9wxnd/uOMbv9wRrd/OKO7eJSZLdAchfIux+5HXqbxCf0JNnuAT4MthMPhcDgcJzVlfPcSZ3SXA2wcujMKSwi764vD4XA4HA7H38YZ3Q6Hw+FwOByO0k8Z93QHYstAh8PhcDgcDofjpMZ5uh0Oh8PhcDgcpZ8yvvmH83Q7HA6Hw+FwOBwljPN0OxwOh8PhcDhKP9llO6bbGd0OxwmiaRO3/7Q/7NtXdBmHod3OJcEWoUyQ0rFNsEVwlDOmvvdVsEUoE3QNtgBlDBde4nA4HA6Hw+FwlDDO0+1wOBwOh8PhKP24LQMdDofD4XA4HA5HYThPt8PhcDgcDoej9OM83Q6Hw+FwOBwOh6MwnKfb4XA4HA6Hw1H6KeNbBjpPt8PhcDgcDofDUcIUaXSLyEgRSRORpQXkPyQiKiK1iminmojcUxzhRGSQiKzJr30R6SAiSSKyTER+8skLFZFFIjLRK222LZ8kIltEZLxNry4i34jIEhH5XUTO9KrzgG1/qYiMEpEIm/6RiKzzaq+1TRcRedPKvERE2nq11UBEponIChFZLiIJNr2TiCy0fXwsIvm+fRCRNiIywidtvIjM80lrKiKzrFwrROT9Yuj7ORHZJCIHfNIftDIvEZHpItLQK+9mEfnTHjd7pYeLyPsislpEVorIVTb9XjvWySISbtMuFJHXiyFna3tPdPdJ99hxL7Y6Pb8YbeZ7r4lILxEZ5m87waJK+ws5Y8r3nDFtKjF33HFMfs0rrqDl3F85ffw3nD7+G2pefXUQpAwONTpeyDmzv+ecX6fSYNCxuom7qS/tZkwg8YdvaPPt50Q1aQRA5dYtSPzhGxJ/+IZ2P46nVo9LAi160DiSkcG9N13P3dddzR3XXMEn771zTJm0rVt55M7bGXj9tdzV9yp+nzM7CJIGh6jzLiTh60kkjJtC9ZsH5Fum0iXdaTj6OxqOnkDdZ18GIPKss2nw+bjc47Q5i4i+uHMgRQ8otS9pT6eFU+i8eBqnPXjss1fjgkQumjOOXnuWEdunW256zYvO4eJfx+cePXcsoW6v8qsnf3iyx+k83KUJD17ShPs7NQ62OMEjOztwRwngT3jJR8DbwCe+GSJSH7M3+kY/2qkG3AP813/x+AWYCMzy6beabae7qm4UkTo+9e4DVgBVchJUtb1X/bHAt/b0CSBJVa8QkWbAO0BnEakHDAaaq2q6iHwFXIfRB8Ajqvq1T789gMb2OAd41/4Fo7/nVPUHEakEZItICPAx0FlVV1vj7mZgBMfyBPAvHx2cBRwQkVNV9S+b9Sbwuqp+a8u1yKetgvgOc63/9ElfBCSq6iERGQi8DPQVkRrA00AioMACEZmgqruBJ4E0VW1ix1nDtnUD0NKOp5udGP0D6FcMOfsBc+zfKV7p6araGkBEugEvABf72Wa+9xowCXhWRF5U1UPFkDFwhITQYOhQVt96G5mpqTT7egx7Z8zg8Nq1eYrtnvw9m559NkhCBomQEJo8P5SkvreRsTWVxO/HsGPaDA6tPqqb1HET2fLJaABqdu3Iac8MYcn1d3Bw1Z8s6H416vEQXqc27aaPZ+e0majHE6zRBIyw8HBefm84kVFRZGVm8sDtN9Puggs5vUWr3DKfj3ifi7p05bJr+rLhr7U8Nfj/+HTilEJaLSeEhFDn0adIGTSAzNRUGn48moM/z+TIuqP3VFj9htS45Q42DbiB7P37CK1uvv7SF/zOxhuuNM1Uqcop46ZwaN4vQRlGiRMSQsvXhjK3962kp6Ry0c9fs23yDA6sPKqn9E1bSbrrcRrdd1ueqjt//o2fzu8DQFj1qnRePI3t08upnorBuz+t5eCR8v/9U54p0tOtqj8DuwrIfh14FGNwFcWLQCPrify3P8Kp6iJVXZ9P1vXAOFXdaMul5WSISDzQExieX5siUgXoBIy3Sc2BGbadlUCCiMTYvApApPU+RwFbihD5cuATNcwDqolIrIg0Byqo6g+2nwPWgKsJHFHV1bb+D8BV+chcGWipqou9kq/EGMlfYiYDOcQCm3NOVDW5CJlzUdV5qro1n/SZXgbnPCDefu4G/KCqu6yh/QOQ432+DWP0oqrZqrojZzhAGEafmUB/4HtVLegey4OICHANcAvQJeftQz5UAXb706aVMd97TVUVY4j38retQBPdsiWHN2zkyObNaGYmuydNplrnk9srlEOVNi1JX7+RwxuNblK/nUytbnl14zlwMPdzaFQUqPk6y04/nGtgh1QMz00/GRARIqOiAMjKysKTlYV5dPOWOXTQ6O7ggQPUrF070GIGhYgzWpC5aSOZKZshK5N9P3xP9MWd8pSp2udq9oz5guz95udXPbuP/Xqr3LkrB+fORjMOB0TuQFM9sSUH/9rAofXm2Uv5ehJ1e+Z99tI3prBv2Sq0EK9iXJ9upP0wG096+dSTo5icBJ7ufBGRy4EUVV1s7KAiGQKc6eWJrAwU9D7yelVdXkhbTYAwEZkFVAbeUNUcT/x/MBOBygXU7QNMV9WcH6NejDFgZ4vI2UBDIF5VF4jIKxgvfjowTVWnebXznIgMBaYDQ1Q1A6gHbPIqs9mmxQN7RGQccArwo9XHDqCCiCSq6nzgaqB+PjInAr7hPf2AYUAqMBZ43qa/DswQkV+BacCHqrpHRJoCowvQSQdV3VNAni+3A9/bz/mO13rhwXiIOwBrgUGqmorxpM8DlmG8y99ijHd/OR9Yp6pr7fXviRk/mAlSEhCBmXx0guO+1wDmA+2BUvm7wGExMWRuOzpXOpK6jeiWrY4pV71rFyq1SyRj3Xo2vfACmdu2BVLMoFCxbgyHU47qJmPrNqq0OVY39W65nvp33YKEhZF0zS256VXatKTZ689RMT6OFfc+dlJ4uXPweDz8X//r2LJpI72vvY7TW7TMk3/jnQN5/P/u4tvRX3A4PZ0X3/0gSJIGlgq1Y8hKPfrsZKVuI/LMvLoJb5AAQP3hn0FIKDs/eIdDc+fkKVO5Sw92f/FxicsbLCLiYkjffFRPh1NSqd6uZSE18ifu6p789daHJ1K0Momi3Nn+VBSY99dO5q3zy0/lKGX8rYWUIhKFCQ8Y+nc7VtX9qtq6gKMoI6gCJrSiJ8Zg+4eINBGRXpiQhgWF1O0HjPI6fxHjkU4C7sWEUnhEpDrGc30KEAdEi0h/W+dxoBnQDhM28Zgf8rYHHrZ1TgVusV7U64DXReR3YD+Q33/1WGB7zon1xDcG5lgveabYWHRV/RA4HRgDdADmiUhFVV1ViL73FCF/Tr/9MROAot5UVMBMNH5V1bbAXOAVK9+nqtpGVfsDD2DCYXqIyNci8roNRSmMfhjvPvavd1hKuh1PM4zH/RMRkeO81wDSMPfAMYjInSIyX0Tmj9uzx4+mgsOemTNJ7tSZFb0vZ9+vv5Lw0ovBFqlUkfLRF8w7rytrn3uVhvcPzE3ft2gJv3e4jAU9rqHhvXcaj/dJQmhoKO+NGsMX3//AqqVLWbcmb9TZzKnf0/Wyy/ni+x/515v/5eV/PEF2Gd9Z4IQRGkp4/YZsuusWtj71MDFP/pOQSkf9QKE1axF+WhMOznUhE4VRMaY2Vc5oQtqPc4ouXM55e+YaXp/+J8PnrOOCRrU4tVZ0sEUKDtkauKME+Lu7lzTCGKOLRWQ9xsBaKCJ1/W1ARCrL0YWIvkfzIqpvBqaq6kEbtvAz0Aq4AOhtZfoS6CQin3n1WQs4GxOnC4Cq7lPVW60H/iagNvAXcAnGo7pdVTOBcRgvK6q61YaQZAAf2jYBUsjrqY63aZsxceN/qWoWJrSlrW1rrqq2V9Wz7ThWcyzpGO9tDtcC1YF1dqwJeBmfqrpFVUeq6uVAFnCmmAWWBem7WqHaNrq7BBOn3duOu7Dx7gQOWZ2BmQC09SqHiMQBZ6vqeOAhoC+wBygwLkJEQjHhN0PtuN8CultPdh5UdS5QC6h9nPcaGN2n55ehqu+raqKqJl5ZrZofTZ14MlNTCasbm3seHlOXzNTUPGU8e/agmZkA7BgzhugzzgiojMEiY1sqEfWO6qZibF0ytqUWWD5t/CRqdz/2Fjz05194Dh4iulmTEpGzNFOpchVaJbZj/q95DcSp337DRV3MS6rmLVtx5EgGe/f4HdFVZsnankqFmKP/6irE1CVze1reMmmpHJg9EzxZZG1JIXPjBsIa5K4/p3KX7hyY9SN4sgImd6A5vCWVyPijeoqoF0P6loKfvfyIu6oHW7/7Ac0qv3ryl32HjQ4OZGSRvGUvDWpEBVkix9/hbxndqpqsqnVUNUFVEzBGZVtVLex99X68Qj6O0/v4LXChiFSwXvdzgBWq+riqxluZrgNmWI9qDlcDE1U1NzhMzK4qOe6rAcDPNvRkI3CuiETZOOLOmMWZiEis/SuYcJWc0I8JwE1iOBfYa2Ok/8B403OCHjsBy20bdezfihiP+Xv5jHcFcJrXeT/MItIc/Z9lx4uIdBeRMPu5LiZuPOV4PN0i0gb4H8bg9v7vMhXoKmYHmOqYRbVTrQf/O4ynHas732v6LEfflERi1gVkY2K9EZGV+YjSGViiqvXt2BtiQkuuyEfmZkAosPMEeLqbcGx4T6nhYHIyEQkNCY+vh4SFUb3npeyZMSNPmQpe8bbVOnUi3WeRZXllf1Iykac0JKK+0U3M5ZeyY2pe3USectQYqnlJBw6t2wBg6oSGAlAxPo6o007l8KbNnAzs2b2LAzYeOePwYRb+Npf6CafkKVO7bl2Sfv8NgI3r/uJIxhGqVa9xTFvljcPLlxLWoCEV4upBhTCqdOnBwZ9n5ilz4KfpRLZtB0BI1WqENWhIZsrRSLzKXXuyf+rkgModaPYsSCa6UQJRDeORsDDqXd2T1Mkziq7oRb2re5IyZlLRBcs54aEhVKwQkvu5aUxltu49SWPcy3tMt4iMwhhPtURkM/C0qua3u0ZO+UTgblXNs4+Squ4UkV/EbD34vao+4kffgzHx2XWBJSIyWVUHqOoKEZkCLMEYasNV1R+j6DpMOIk3pwMfi4hi4oxvt/L+JiJfAwsx3uJFQM72e59bA1qAJOBumz4ZuBRYg/H03mrb8ojIw8B0a6gvAHICIB+xYTEhwLuqesy3kqquFJGq1qNbExN3Ps8rf52I7BWRczCG7xsikvNEPlLEZCgXEXkZs0g1yl7r4ar6DCacpBIwxsbvb1TV3qq6S0SexUwqAIbp0QWRjwGfish/MKExt3r108bKvdAmfQEkY+LDX7ZvJPJbKNAP+MYnbSwwELM7TE5MN7b+zarqVxBuQfeaze6ICSkqnXg8bBz2LI2Hj0BCQ9gxdiyH16whdvC9HFq6lL0zZlLnxhup1qkj6vHg2buX9Y+X3uGcSNTjYfUTz9JqlNHN1i/Hcmj1Gk555F72LV7KzmkzqXfbDdRofx7ZmVlk7d3HisFDAKh6zlk0HHQH2ZlZoNmsfvyfZO7aE9wBBYhdO3bw76efItvjIVuzufiSbpx70cV8/O47NGnenPMu7shdDzzM6//6J+O++BREePiZZxH/1veUbTwetr/8HPFvfgChIeyb8A1H/lpDzbsGcXjFMg7+PJNDc+cQfc75NBz9HWR72PHGK2Tv3QtAhdg4wmLqkr7wjyI6Ktuox0PyQ8M4d/xwJDSUjZ+OZf+KNTR9ajB7Fi4ldfIMqrVtQbtRbxNWrQp1e3Sk6ZP3MqudWbMe2aAekfGx7Jz9e5BHEnwqRVTg1vMSAAgRYeGm3axK3R9coRx/C9GTaEV+WUZEHgD2q2q+u7KUJ+wk5FRVfbMUyBIDfKGqRW4HsqBpM/cw+cG+fUWXcRhO/XNx0YUcZHRsE2wRygwrV5w8i4GPh58+KpXr5ksdr17dKqAzbV32fMD+z8oZT5zwsbmfgS87vIvZKq/co6oTiy4VMBpgYs4dDofD4XA4/jbO6C4j2Dj0T4Mtx8mGqpbvd8AOh8PhcDgCgjO6HQ6Hw+FwOBylnzK+Lenf3TLQ4XA4HA6Hw+Fw+InzdDscDofD4XA4Sj/O0+1wOBwOh8PhcDgKw3m6HQ6Hw+FwOBylH+fpdjgcDofD4XA4HIXhPN0OxwkiJcX9No4/dL6tfrBFKDN8X7NlsEUoE1w55qJgi1Bm2Hnf7GCLUCbodve1wRahbHD1qsD2l122/886T7fD4XA4HA6Hw1HCOE+3w+FwOBwOh6P042K6HQ6Hw+FwOBwOR2E4T7fD4XA4HA6Ho/TjPN0Oh8PhcDgcDoejMJyn2+FwOBwOh8NR6lENnKdbSqBN5+l2OMootS9pT6eFU+i8eBqnPXjHMfk1Lkjkojnj6LVnGbF9uuXJi4yP5dxvR9BxwWQ6zp9EZIN6gRI7qIRf/zBRz40hcsgH+eaHtjifyMfeJ+LR94h4+B1CTj0zwBIGl5iu7emWPIXuy6fR9OFj76mQ8DDO+ex1ui+fRqfZXxHV0Nw3UqECicNfpMuCCXRdPJmmj9wZaNGDwpNfreKCZ+Zy2Svz883feyiTQR8t4/JXF3Dtm4tYve1ggCUMLtUuupDW07+nzcypxN197P2UQ43uXTlv3UqiW5jnreqF59NiwlhafT+BFhPGUuW8cwIlctCo2ak9F8ybwoW/TyNh8LG6ajjwFs7/ZRLn/TSBs8Z9RER8XG5el9TlnDtzPOfOHE/rz94NpNiOYnJcRreIjBSRNBFZ6pP+jIikiEiSPS71o60nitn3NSKyTESyRSTRJ6+liMy1+ckiEuGTP8FbZhEZ7SXrehFJsunhIvKhbWOxiHTwqtPPpi8RkSkiUquwsYtIFxFZYOssEJFOXm09JyKbROSAj5wXichCEckSkasL0UWkiPwkIqFeafeLyGERqeqVFiUin1sZlorIHBGp5KfKc9p4SETUa7w3WB0ki8ivItLKptcXkZkistxeh/u82njJ1vnEK62/iNxfDDn6WDmaeaUliEi61ftiK0/TYrRZ0HUYJCK3+dtOQAgJoeVrQ5l35QBmJPak3jW9qNSsUZ4i6Zu2knTX46R8NfGY6m0+eIm1/xnBzLMu5eeLr+HI9p2BkjyoZP02lcPvPl5gvmfVQtJfupPDL99NxhevULHfgwGULsiEhNDmjaHM6T2Aqa16Ur9vLyr73FMJt17DkT37mNK8K6vf/IgWzz0MQPxV3QmtGM4PZ/Vm+rlXcuqAvrkGeXmmT2IM7w8oeGL2/oxNnB5XiW8fOosXr2vKC9+uDaB0QSYkhFOGDWXFLXeQ1LUXtXr3JPK0RscWi44m9tYb2b8oKTctc9duVg4YyOIevVnz8BAav/ZyAAUPAiEhnP7SUBb2HcAvF/Qk9speRDfJq6t9ySuYd8lVzL24N6nfTaXJM4/k5nnSDzOvYx/mdexDUv+BgZY+sGRnB+4oAY7X0/0R0L2AvNdVtbU9JvvRVrGMbmApcCXws3eiiFQAPgPuVtUzgA5Aplf+lUAeo0pV++bICowFxtmsO2x+C6AL8KqIhNg+3gA6qmpLYAkwyKvJ/Ma+A7jMtnUz8KlX+e+As/MZ40bgFuCLInRxGzBOVT1eaf2APzA6yuE+IFVVW6jqmcDteOmmKESkPtDVypXDOuBiO65ngfdtehbwkKo2B84F/k9EmttJQFurtyMi0kJEIoFbgXf8lcWOb479681aq/dWwMcU774q6DqMBO4tRjslTvXElhz8awOH1m9GMzNJ+XoSdXt2zlMmfWMK+5atQn2+PCo1a4SEVmD7zF8B8Bw8hCf9cMBkDybZa5PRQ/sLLnDkqB4kPAK0bP8QQ3Go0a4lB9Zu4OA6c09t+moScZflvafiLuvEhk+/ASBl3FTqdDzPZKgSGh2JhIYSGhlBdmYmmfsO+HZR7mh3ajWqRYUVmL8m9RDnnFYNgFPrRJGy6zA79h8JkHTBpVKrlhzesJGMTeZ+2vHdZKp36XxMuQYPDiblveFkZxzVy6HlK8hMSwMgffWfhERURMIL1nNZp2rblhxat4H0DUZX276ZRJ0eeXW1e85vZNvv6b3zk6gYWzcYojqOk+MyulX1Z2DX8QohIi8CkdZD+bmffa9Q1fx+CqkrsERVF9tyO3OMUevVfRD4VwFyCHAtMMomNQdm2HbSgD1AIibUR4BoW6cKsKUIeRepak6ZZXa8FW3ePFXdmk+d9aq6BChqynUD8K3XOBoBlYCnyGuUxgIpXu2vUtWMItr25nXgUSDXElHVX1V1tz2dB8Tb9K2qutB+3g+sAOrZsYRZvUVhjP6HgbdU1a8JgL2OF2ImDdcVUrQKsLuQ/DwUch0OAetFJD+DPChExMWQvnlb7vnhlFQi42L8qlvptAQy9+6j3RdvcfEv39D8X49CiIs0yyG05QVEPjmSiLueI+OLV4ItTsCIjIshfdPReyo9JZXIejHHltlsHhH1eMjct5/wmtXZPG4qnoPp9Nowh0vXzGT16yPJ3L03oPKXRprFRfPD0h0ALNm4jy17DpO6tzhfuWWX8LoxZGw9+nV6ZNs2KtbNez9Fn9Gc8NhY9sz8qcB2avToxoGly9EjfvuHyhwRsTEc3uL1fb4llYqxBX+f17vhanZMP+pvDImoyDk/juXsKaOp3ePYiY2j9FCSCykHichNwHyMx7NA40dVh4jIIOtpBkBEZgOV8yn+sKr+WEi/TQAVkalAbeBLVc15N/Us8CpwqIC67TGe4D/t+WKgt4iMAuoDZwH1VfV3ERkIJAMHgT+B/yvG2K8CFhbT4M0XEQkHTlXV9V7J1wFfArOBpiISo6qpGI/tNBuqMh34OGesRelbRC4HUlR1sbGX8+V24Pt8ZEwA2gC/qep+EZkMLLIy7AXOUdVnizHsy4EpqrpaRHaKyFmqusDmNbLhQZUxRv05VoamwOgC2uugqnuK6HM+5v74vRhylkqkQgVqnp/ITxf0IX3TVs765HUa9L+SjZ98HWzRSgWeJb+QvuQXQhq1ILznrRx+59Fgi1TqqdGuJerJZmJCe8KrV6HDjC9Im/ErB9dtDrZoQeWOjvV5/tu1XPHaAhrHRnN6XCVCCv7+PLkQoeFTQ1j7cMHhXpGNT6PhYw+x/KbbAyhY6Sb2mt5UaX0mf/Tun5s2u3VHMralEdkwnsRvPubAitWkr98URClLkDK+ZWBJGd3vYgxc5aihW6yYWFVt/zf7roDxgrbDGNfTRWQBsBNopKoPWCMwP/px1MsNxkg9HWNwbQB+BTwiEgYMxBiSfwFvAY9jPOiFjl1EzgBewnjkTwS1MB5433FcoarZIjIWuAZ4W1WTRORU2/clwB8icp59a1CgvkUkChOmUaDMItIRY3Rf6JNeCROyc7+q7gOwk6CXbf5wYKiIDODoW4p830T4jO8N+/lLe55jdK/NmbyJSF9MuEt3+1akdRHtFkYa0Mw3UUTuBO4EuCe8Dt3Cqh1HF/5zeEsqkfFHXy9G1IshfUuqf3VTtrE3eQWH1huDaNt306l+div4pIiKJxnZa5ORmrEQXQUO7gu2OCVO+pZUIusfvaci68WQnpJ6bJn4WNJTUpHQUMKqVObIzt3Uv+5etk2bjWZlkbF9Fzt+XUj1ti1OeqO7UkQFnu9rlpWoKpe88Dv1a0YUUat8cGRbKhVjY3PPw+vWJWPb0fsptFI0UU0a0/xL88UTXrsWzT74LyvvuIeDyUsJrxtD0/+9zZqHHiNjYzk1IC2Ht6YSEef1fR4XQ8bWY7/Pa1x0Hqc8cDfze/fP4/nP2GZDcTZsZtcvv1OlRfPya3SXcUrknbKqpqqqR83eLh+Qf5xsoYjIbK/FiN7HJUVU3Qz8rKo7bFjAZKAtcB6QKCLrMbHATURklld/FTDxz7neUFXNUtUHbIzw5UA1YDXWeFPVtaqqwFfA+UWNXUTigW+Am1T1RK2oSQdyv8VFpAXQGPjBjvU6vEJMVPWAqo5T1Xswse85Cz0L03cj4BRgsW0zHlgoInVt3ZbAcOByVd3pJUsYxuD+XFVz4uTxym+DCdNZBVyjqtdiPNWNCxqsiNQAOgHDrSyPANdK/u73CcBFtl7TAsaXJCLVCurPiwiMrvOgqu+raqKqJgbK4AbYsyCZ6EYJRDWMR8LCqHd1T1Inz/Cr7u4FyYRVrUJ4reoA1Lr4HPavXFOS4pYZpNbRHQFC4k+DCmEnhcENsHt+MpVOSyAqwdxT9a/tydaJee+prRNn0PDGKwCod2U30mbNAyB941bqdDA7TIRGRVLznFbsX/VXYAdQCtmXnsWRLOOZG/P7NhJPqUqliJNjp94DS5KJSGhIxfh6SFgYtS67lN0/Hr2fPPsPMP+s81jUvjOL2ndm/6LFuQZ3aOXKNBv5Pza+9Cr7FywK4igCw75FyUSdmkBkA/Ps1b2iJ2lT8j57lVucTvNXh5HUfyBHdhyN6q1QtUpuvHtYjepUO6ctB1aV4+/zbA3cUQKUyNMvIrFesbFXYBY9FkWmiITlxPUeh6d7KvCo9c4eAS7GLGychPFC54Q7TFTVDl71LgFWqmqua8a2Iap6UES6AFmqulxE4oDmIlJbVbdjFlmuKGzs1rCbBAxR1V/+5tiOQVV3i0ioiESo6mGMgf2Mqr7gNY51ItIQYywvt3XCMTHrs2w7Rem7jld764FEVd0hIg0wC09vVNXVXmUEGAGsUNXXCmjzWYyXOAzI2XklG4gSkXrAJ6rqG6B2NfCpqt7l1ddPmNCPjT5lLwTW2vEdr6e7CXDCrtvxoh4PyQ8N49zxw5HQUDZ+Opb9K9bQ9KnB7Fm4lNTJM6jWtgXtRr1NWLUq1O3RkaZP3susdr0gO5vlT7zE+RM/BoE9i5ax4cMxwR5SQKh48xOEnNYKqVSVyGGjyJz8MYSar8GsXyZSoXV7KrTrgnqyIPMIGR8V9dKl/KAeD0n3D6P9RHNPrf9oLPtWrKH50MHsXriUrRNnsO7Drzn7w3/Tffk0juzay283PgDAmvc+p90HL9Bl0UREhPWfjGPv0vyW3JQvHvp8Bb+v3cueg5l0+Nc8BnVtSJbH/LO+7rw41qYe4vHRqxCB02Ki+Nc1TYIscQDxeFj39LOc/skIJCSEtDFjSf9zDfUfuJcDyUvZ/ePMAqvWvfkGIho2IH7wPcQPvgeA5TfdTtbO415CVipRj4eVQ4bRdsxwJCSUlC/GcnDVGhoNGcy+pKVsnzKDJs88Smh0FC1HmJe8h1O2ktR/INFNGtH81X8aIzFEWP/GBxxcfRLtklPGED2O1fk21rkDJsQhFXhaVUeIyKcYA0eB9cBdqrrVGqvDVfWYLQRF5CWgNybW+QY/+r4CE9ZRGxNekaSq3Wxef0y4hwKTVfVRn7oJGKP7TK+0j4B5qvqeT7mpGEMwBbhdVTfYvLsxu4FkYkJPblHVnYWM/SkrU068OEBXVU0TkZeB64E4zILM4ar6jIi0w3jGqwOHgW1qdmTx1cUIYJSNvf4LuFRVV3rlv4a5PlsxixYF85ZjEvCYFvMm8DG6h2Ni1DfY7CxVTRSRCzEx5ckcXQj6hNrdXESkD9BaVZ+x568A3TDhJTeI2QbyuZxr6tX3TOAlVZ3ilTYYEwb0Embys8qO8QgwSFV/83Nc+V4Hm7cQ6OLtyfdlQqWmJ89WF8dB59vqB1uEMsP3/3OviP3hyjEXBVuEMsNv980Otghlgv373de5P3TdsSqgixSyZz0YsAsT0uG1Ez624zK6HaUDEWkLPKCqNwZblhOFiAwCNqrqhFIgSxvgwaL064xu/3BGt/84o9s/nNHtP87o9g9ndPuHM7qLx8kRXFbOUdWFYn6IJlTz7tVdZlHVt4Mtgxe1gH8EWwiHw+FwOE5q3O4ljtKAqo4MtgzlFVX9IdgyOBwOh8PhKNs4o9vhcDgcDofDUfop455u9zN0DofD4XA4HA5HMRCR+ja0d7mILBOR+4qq4zzdDofD4XA4HI7ST+nydGdhfnV8oYhUBhaIyA+qurygCs7T7XA4HA6Hw+FwFANV3aqqC+3n/Zgti+sVVsd5uh0Oh8PhcDgcpZ8AerpF5E7MD/jl8L6qvl9A2QSgDVDo74I4o9vhOEH0eLVNsEUoE3w7uPz/rPOJ4vI33T3lD19e/nOwRSgz1KoZbAnKBh2fc8/eyY41sPM1sr0RkUrAWOB+Vd1XWFlndDscDofD4XA4Sj+lK6YbEQnDGNyfq+q4osq7mG6Hw+FwOBwOh6MYiIgAI4AVqvqaP3Wc0e1wOBwOh8PhcBSPC4AbgU4ikmSPSwur4MJLHA6Hw+FwOByln2wNtgS5qOocQIpTx3m6HQ6Hw+FwOByOEsZ5uh0Oh8PhcDgcpZ9StpCyuDhPt8PhcDgcDofDUcI4T7fDUcZ5auoGfv5rHzWiKjD+5tOPyR/5RyqTVu4GwJOt/LXrMLPvbkHVyJPj8Y/p2p7Wrz6JhIawbuQYVr3yQZ78kPAw2o18meptz+DIzj3M6/8AhzakIBUqcNZ7/6J6m+ZIhQps+Gw8q/5d5Jat5QJ3Tx0fsd3ac9Yb5p5bO3wMy1/6oOhK5ZCandrT7PknkZAQNn82hvVv5tVDw4G3UK//NWiWhyM7d7Fs8BMc3rwFgC6py9m/fDUAh1O2ktR/YMDlDwbu2SuCk9nTLSIjRSRNRJbmk3eviKwUkWUi8rIfbT1RzL6vsW1ni0iiT15LEZlr85NFJMInf4K3zCIy2mvl6XoRSbLp4SLyoW1jsYh08KrTz6YvEZEpIlLLpj8jIim+K1lFpIuILLB1FohIJ5te2atskojsEJH/2Ly7bfkkEZkjIs0L0EWsiEz0SfuPlSPEKy1GRCbasSwXkcnF0PdHIrLOS87WNv0Gq4NkEflVRFrZ9AgR+d32tUxE/unV1ue2zvNeaU+JSJ9iyHO/iBwWkapeaR1EZK+Vb4mI/CgidYrRZr73s4i8knO9SiN9zqjJe1c2KjD/tnYxjL2xGWNvbMb9F8aRGF/p5PmCDgmhzRtDmdN7AFNb9aR+315UbpZXVwm3XsORPfuY0rwrq9/8iBbPPQxA/FXdCa0Yzg9n9Wb6uVdy6oC+RDUs9Bd+yw3unvr7SEgIie8MZWaPAUxq3pOG/XpR5fSCdVluCQnh9JeGsrDvAH65oCexV/YiuklePexLXsG8S65i7sW9Sf1uKk2eeSQ3z5N+mHkd+zCvY5+TxuAG9+yVd443vOQjoLtvooh0BC4HWqnqGcArfrRVLKMbWApcCeT5KTIRqQB8Btxt++4AZHrlXwkc8K6jqn1VtbWqtsZscp6zwfkdNr8F0AV4VURCbB9vAB1VtSWwBBjk1eTrOe2pao5huwO4zLZ1M/CpbXu/V9nWwAav/r9Q1RY2/WWgoH0gHwRyXQjW0L4C2ARc7FVuGPCDqrZS1ebAkALaK4hHvGRNsmnrgIvtuJ7l6K83ZQCdVLUV0BroLiLnikhLIN3qrZ2IVBWRWOAcVR1fDFn6AX9g7gFvZlv5Wtr8/ytGmx+Rz/0MvEXxdRUwEuMrUTUi1K+yk1fu5tKm1UtYotJDjXYtObB2AwfXbUYzM9n01STiLuucp0zcZZ3Y8Ok3AKSMm0qdjueZDFVCoyOR0FBCIyPIzswkc98B3y7KJe6e+vvUPLslB9aYey47M5MNX04i/vLORVcsZ1Rt25JD6zaQvsE8e9u+mUSdHnn1sHvOb2SnHwZg7/wkKsbWDYaopQr37BVBdnbgjhLguIxuVf0Z2JVP1kDgRVXNsOXSCmtHRF4EIq2H8nM/+16hqqvyyeoKLFHVxbbcTlX12H4qYQzUfxUghwDXAqNsUnNghtcY9gCJmC1iBIi2daoAW4qQd5Gq5pRZZsdb0af/JkAdYLat4/1zotFAQXvlXAVM8TrvYPt4F2Oc5hALbPaSaUlhMvuDqv6qqrvt6Twg3qarquZYKGH2UMwEKNJODMIAD2Yy8LS/fYpII6AS8BR5x+ddRoDKwO788gsYS773s6puAGqKSJn+j5Cemc2c9fvo0rhasEUJGJFxMaRv2pZ7np6SSmS9mGPLbN4KgHo8ZO7bT3jN6mweNxXPwXR6bZjDpWtmsvr1kWTu3htQ+Us7J+M9VRSR9WI46HXPHdqcSpTPPXcyEBEbw+EtR/VweEsqFWML1kO9G65mx/SjPrSQiIqc8+NYzp4ymto9Tr5JS1G4Z69sUlLvJJoA7UXkOeAw8LCq/lFQYVUdIiKDrEcXABGZjTGafHlYVX8som8VkalAbeBLVc0Jb3kWeBU4VEDd9kCqqv5pzxcDvUVkFFAfOAuor6q/i8hAIBk4CPxJXo/qIBG5CZgPPORllOZwFbAwZ1LixXXAaFXNNa5F5P8wE4Vw4JgQBxE5Bdjt01Y/zMThW+B5EQlT1UzgHWC0iAwCfgQ+VNUtIlIZa+jnw/Wqutx+fk5EhgLTgSH5yH878L2XbKHAAuA04B1V/c2mbwcWYrz9pwEhqrqwgP7z4zrgSytzUxGJUdVUm9fehgfVxFybJ2yfHYHX82nrkKqe70efCzEb4Y8thpylill/7aVNvWj3KtJParRriXqymZjQnvDqVegw4wvSZvzKwXWbi658kuDuKceJIPaa3lRpfSZ/9O6fmza7dUcytqUR2TCexG8+5sCK1aSv3xREKUsXJ+uzp57Ss0/336Gkdi+pANQAzgUeAb6ynke/UdX23mEXXkdhBndO3xcCN9i/V4hIZxuD3EhVvymkbo6xmsNIjGd4PvAf4FfAIyJhGG9+GyAOE17yuK3zLtAIE1KxFWPk5yIiZwAvAXfl0/91Pv2jqu+oaiPgMYxn15dYYLtX++HApcB46yn/Dehm25oKnIoJRWkGLBKR2r4hLj5HjsH9uK3TDnNtH/MZV0eM0Z2brqoeO5GKB84WkTNt+v227VcxE6F/iMiTIvKViNyRzxh96YeZTGVjjOBrvPJywkvqAx9iwnJQ1ZkFjM8fgxsgDXOt8yAid4rIfBGZP3z2Wj+bCg7fn4SvItO3pBJZ/+gLish6MaSnpB5bJj4WAAkNJaxKZY7s3E3963qxbdpsNCuLjO272PHrQqq3bRFQ+Us7J+M9VRTpKalEe91zUfExHPK5504GDm9NJSLuqB4i4mLI2HqsHmpcdB6nPHA3Sf0HokdyI0HJ2GZekKdv2MyuX36nSot8lzSdtLhnr2xSUkb3ZmCcDTH4HcgGahWnARGZ7bPAMOe4xI++f1bVHap6CJgMtAXOAxJFZD0wB2giIrO8+quAiQ8enZOmqlmq+oA1zi4HqgGrMQY1qrrWeqW/As63aanW2MzGGLdne/URD3wD3KSqeSw0uwCxgqouKGBcXwJ98klPB7wXinazcibbsV6IVwiGqu5S1S9U9UZMzPNFcuxiTu+jua231V7PDIwx6z2ulsBw4HJV3ekroKruAWbiEy8tIpdjPOGVMBOia4GrRSSqAB0gIi2AxsAPdnzXUUCICTABuMjW61jA+H4tqC8fIjC69h3b+6qaqKqJA9qX3sVS+zM8zN98gI6nVS26cDli9/xkKp2WQFRCPBIWRv1re7J14ow8ZbZOnEHDG68AoN6V3UibNQ+A9I1bqdPhHABCoyKpeU4r9q/6K7ADKMWcrPdUUez8I5nKjROITognJCyMhtf1JGXCjKIrljP2LUom6tQEIhuYZ6/uFT1Jm5JXD5VbnE7zV4eR1H8gR3YcjeyrULUKEh4GQFiN6lQ7py0HVq0JqPylmZP62cvWwB0lQEm9lxgPdARm2jjlcMxCwsLI9AqDQFXb/82+pwKPWsPtCGYh4euqOgnjhUZEEoCJqtrBq94lwEpVzX13bNsQVT0oIl2ALFVdLiJxQHPrJd6OWWS5wtaJVdWttokrMAs+EZFqwCRMWMYv+cjt62VHRBp7hbr0xISx+LIaSPBpZ4CqjrJtRAPr7FjOBeap6iEbUtII2Kiq+7ETiYLIGZd9Y9HHa1wNMAs/b1TV1V7lawOZqrpHRCKtjl7yyg8D7rfjaszRePVQINx6xQep6k356OkZVX3Bq611ItIwH7EvBNaC8XQXNcYiaAKMOY76JcYjk9bxx+YD7EnPovP7S7nnvFiy7BdG31Zmrjt9zR7OT6hMVJh/C3TKC+rxkHT/MNpPHI6EhrL+o7HsW7GG5kMHs3vhUrZOnMG6D7/m7A//Tffl0ziyay+/3fgAAGve+5x2H7xAl0UTERHWfzKOvUvzW0ZS/nD31N9HPR7mDxpGx6nmnvtr5Fj2Lj/5DEb1eFg5ZBhtxwxHQkJJ+WIsB1etodGQwexLWsr2KTNo8syjhEZH0XLEG8DRrQGjmzSi+av/NIZPiLD+jQ84uLp0v0k8Ubhnr3wjXuHDxa9sYp07YLzYqcDTqjrChjiMxBg5RzBx2DOssTpcVS/Np62XgN6YWOcb/Oj7CsyuErUxCxyTVLWbzeuPCYdQYLKqPupTNwFjdJ/plfYRxiB9z6fcVIynPgW43S6qQ0TuBu7DLAzcANyiqjtF5FM7bgXWA3dZY/UpK5O34dxV7SJTEfkLuFRVV3r1/wZmMpCJWRA4SFWX5aOL6ZhwlS0YT3+Cei3CFJFxGA9+A+BWIAvzluNDG+JRJCIyA6NrAZIwu8McEJHhmBj1DbZolqomWu/3xxgjOgT4SlWHebV3P7BHVT+yhvwXwJmY6/WYiFwNdFHVPGE4BejpNcz99xsmjn2dlXMvZgKyGj8o5H4Ow4QQtVDVrILqZ/7vurIdbBYgvh28KNgilBkuf7NNsEUoE4y5291T/lKrZrAlKBt0fM49e/4QdteXxQodPl48X9wUsP+zodd/csLHdlxGt6N0YCcgZ6lqfjHfZRIR+TfwqZ6AHVZOgCxXAG1V9R+FlXNGt384o9t/nNHtH87o9h9ndPuHM7r9wxndxePkWvZaTlHVb0SkXH2VquojRZcKGBXwWRDrcDgcDocjsGgJxVoHCmd0lxNUdXiwZSivqGqpjOV2OBwOh8NRdiip3UscDofD4XA4HA6HxXm6HQ6Hw+FwOBylH/fjOA6Hw+FwOBwOh6MwnKfb4XA4HA6Hw1H68WQHW4Ljwnm6HQ6Hw+FwOByOEsZ5uh2OE8SRZUX96KoDoOfjjYMtQpnB7T/tH5ffWz/YIpQZQmpEBFuEMsHu6RuKLuSgzl1FlzmRlPUtA52n2+FwOBwOh8PhKGGcp9vhcDgcDofDUfpxu5c4HA6Hw+FwOByOwnCebofD4XA4HA5H6cfFdDscDofD4XA4HI7CcJ5uh8PhcDgcDkepR11Mt8PhcDgcDofD4SiM4zK6RWSkiKSJyFKf9NEikmSP9SKS5EdbTxSz72tEZJmIZItIok9eSxGZa/OTRSTCJ3+Ct8wFySsi4SLyoW1jsYh08KrTz6YvEZEpIlLLpj8jIile7V1q02uKyEwROSAib/vIU6y28tFFrIhM9En7j60b4pUWIyIT7ViWi8jkYuj7IxFZ5yVLa5suIvKmiKyx8rf1qvOyvQYrbBkRkYp2jEtF5B6vsu971/VDnvzGd4uIbLfyLRORr0UkqhhtThGRPfno8ksRKbWbS4df/zBRz40hcsgH+eaHtjifyMfeJ+LR94h4+B1CTj0zwBKWHsIuv4+IRz6j4j3vFFpO4hoTMfRbQppfECDJSgex3drTa+UULvtzGs0fu+OY/JDwMC748nUu+3MaXed9RXTDegDUveR8us8fy6VLJtB9/lhiOp4baNGDhnv+/MM9e3+fygOfpNYHk6jxymfBFiX4ZGcH7igBjtfT/RHQ3TdRVfuqamtVbQ2MBcb50VaxjG5gKXAl8LN3oohUAD4D7lbVM4AOQKZX/pXAAT/lvcPmtwC6AK+KSIjt4w2go6q2BJYAg7yafD2nPVXNMWwPA/8AHs5H3uK25cuDQO43vjVErwA2ARd7lRsG/KCqrVS1OTCkgPYK4hEvWZJsWg+gsT3uBN61MpwPXAC0BM4E2llZugFzbPqNtmwrIFRVF/ojRCHjAxht5TsDOAL0Lcb4/p0jkw/vAo8Wo52AkvXbVA6/+3iB+Z5VC0l/6U4Ov3w3GV+8QsV+DwZQutKFJ+lHMj57uvBCEkJYl1vIXnty/TCNhISQ+M5QZvYYwKTmPWnYrxdVTm+Up0yj26/hyO59fNe4K6te/4jWL5mvs4wdu/npsoFMbtmbuTcP4bxPXw7GEIKCe/78wz17f5/Dsyax5/kHgi2G4wRwXEa3qv4M7CooX0QEuBYYVVg7IvIiEGk9lJ/72fcKVV2VT1ZXYImqLrbldqqqx/ZTCWOg/stPeZsDM2w7acAeIBEQe0TbOlWALUXIe1BV52CM7zzdFretfLgKmOJ13gFYhjEW+3mlxwKbvWRaUsx+8uNy4BM1zAP+v737DpOqPN84/r23AEtHUKoUQVQURAU7drBAFFsUNbHEEhN77C3G/IwlltiisZdgiYgVFbtgVxCpFkQ6LL3vwpbn98d5F2aXLWeV3Zkdns917QVz6nPu2Zl9zzvvOdNcUlvAgAZAPaA+kA3kEp0ANQyPFbbxd6ITkrgOoPzjWy+czDQClsbdqJm9B6wsZ9Zo4JCwzZRT/NMEbE15ZQfrNvzKqV4DsLo9Ju7XKJ4xCfIqyQrI3GMQRZM/xVYvq52iUkTL3XuxauoMVv88m+KCAmY8N4IORx1capkORx3Ez0++BMDMYSNpffBeACwdN4W8eQsAWD7pRzJz6pNRL7t2DyBJ/PUXj7/2frmCKeMoXrUi2WWkhiKrvZ8aUNNjuvsBuWb2Y2ULmdmVQF7ooTwZQNLohKEMiT+HVLHP7oBJGilprKTEHsq/A3cAa2LW+y1wpKQsSV2A3YCtzawAOBeYQNRA7gE8mrCd88JQi8cktaji2H/VtkJdS81sbcLkIUQnDi8BAyWV/PW7H3g0DHO5RlK7sI0mFWQ9TlKPhO3eFGq5S1L9MK09UY9zidlAezP7DPgAmBd+RprZFOAdoDPwOXCPpCOBsWZWnRONio4P4ARFw4PmAFsAr4VjPLmC4xtW1c7MrBiYCuxcjRpTSmavfci55jEanHMTa5+5PdnlpK4mLcncfi+Kvo498ipt5LRvzepZ89c/XjM7l4btW5ezzDwArKiIguUrqd+y9NvS1sceytKxkyleV4CL+Osvhs34tec2HzXd6C5pHFWbmfVLGMqQ+PNuFatmAfsCJ4d/j5Z0cBiD3NXMXqpGvY8RNSK/Bv4FfAoUhUbeucAuQDuiISElny8+AHQFehM1Nu+orNhNsK22wMKE7dUDjgBeNrMVwBdEQzows5HANkRDUbYHvpG0pZmtrCDr3mY2OWz6qrBOX6LG7BVVHFc3YAegA1HD/CBJ/cys0MxOMrNdgBeAi4iG7dwZxmAfWcV2Kzy+4PkwTKgN0YnMZeHYh1ZwfMdVtr8EC4ienzqpaPwn5N10BvmP/JV6A09Pdjkpq95hZ1Hw7hObbW/kr9WsRzd633opX55zfbJLSSn++quav/bc5qDGPi4PH8UfQ9Q7/EvWHw00KWfWpVU0vGcDo8xsUdjOG8CuROO4+0iaTnTcW0n61wVfmQAAX/JJREFU0MwOqKheMysE1g+kkvQp8ANRIxgz+ylM/x9hfLSZ5SYs/zBQ6qK8cvzabeURDeMocSjQHJgQjVahYVjm9bDNJcAzwDPhgsH9JL1NNISiPCeZ2WQzmxcer5X0OBvGps8Btk5YvkOYdgrwuZmtCvW/CexVZj9/Ap4C9gSWE42/fh94tYJaqjy+EmZmkl4DzgdukXQyoQFextSYDe8GYT+lSDqbaCw79xy4PWfs1D7GppKn+KcJqGVbaNQUVvvHlWWpXTfqHRd9OKaGTcnctg/rioso/u7zJFdW8/Lm5NJo6zbrHzfs0Jo1c3LLWaYteXNyUWYm2c2asHZxNIIrp31r+r10H5/9/gpWTZuF25i//iq2Ob/2XHxWx78cpybHqB4CfGdms6tcMlIgKTsMt8DM+v3C/Y4ELg93rVhHdKHdXWY2gg0X+XUGXi9pcFdUb9iGzGy1pP5AoZlNDsMyeoRe4oVEF1lOCeu0TWigHk10wWdl5vzKbf1ANFyjxBDgTDN7NmyjEfBzOJY9iRrCayQ1IepFn2lmKwmN/4qU1BLGnQ9OqOVVoiEwzwF7AMvDcjOBsyTdTDR2e3+iTwtKttcCGETUiP4NUEw0DjwnzD8a2N3Myl6hVNnxlbUv8BNEPd1ArOsFKtCdcvI3s4eAhwBWX3BISr4bqFU7bFE0eiejQzfIyvY/+BVYe/eZ6/+fPfgiin74arP5o7/4qwk02bYzjTp3IG9OLp1OHMinJ/2l1DKzX32fLqcezaLPx9HxuEPJfT/KJrtZEw4Y8RDjrryDRZ/Guh56s+Gvv3g259ee23z8qka3pGeJLmprJWk28FczKxmPfCJlhpaExuojZlbere8eAsZLGlsyrruKfR8N3AtsCYyQNM7MDjWzpZLuBL4iasS9ERrcVdmoXmArYKSkYqLG8e8AzGyupL8BoyQVADOA08I6t4WhLAZMB85JqHk60YWS9SQNBgaERny1t1UinBD8FIZzzCW6m8wfy8z/mKhh2xG4T1Ih0dCiR8zsqxjZAAyVtCVRA3pcwj7eIBruMZVorHzJZ6fDgIOIhngY8JaZvZawveuBm8ysWNJI4M9h2QfD/K5Aqb9MoWFd2fFBNKZ733B8s9mQZZXCpyvbA43D7/MfzGykpNZE1xzMr3wLyVH/1KvJ6LYzatyMnBufpeCNJyEzemkXfvI6Wb37kdW3P1ZUCAXrWPtEudcRbxayj72MzM49oWFTGlzyBAUfDF2fVdHXbya5uuSyoiK+Pu9GDhz5CMrMZNpjL7J88lR6/u0Clnw9kTmvvc9Pjw5j76f/yW9+fJt1S5bz8YnRB4HdzzuFJt060vP6P9Pz+j8D8P6AM1i7sMLr7NOGv/7i8dfeL9f0wr+R3WNXMpo0p+UDr7D6f4+Q/8FrVa+Yjur4l+PIfPxUnRdOQHYzs2uTXcumIum/wMWh9z/ZtVwMrEg4oSxXqvZ0p5qMLRpUvZAD4KW/VXoNuguOOn/rqhdygL/+4lo5eXGyS6gTtvrfZ6p6qU1n7W1H19rf2fqXv7TJjy0lb4HmqsfMXpLUMtl1bEpmdkqya0iwDHg62UU455xzm7U63tPtje40YWaPJLuGdGVmjye7Buecc87Vbd7ods4555xzKa+u372kpu/T7Zxzzjnn3GbPe7qdc84551zqKypOdgW/ivd0O+ecc845V8O8p9s555xzzqU8H9PtnHPOOeecq5T3dDu3iayevzrZJdQJLft1SHYJdcaQ8Xsmu4Q6Yc3DHya7hDpjwejZyS6hTli7Yl2yS6gTtqrtHdbx+3R7T7dzzjnnnHM1zHu6nXPOOedc6vMx3c4555xzzrnKeKPbOeecc865GubDS5xzzjnnXMozv5DSOeecc845Vxnv6XbOOeecc6lvc76QUtJjkhZImlhmem9Jn0saJ+lrSbtXsZ3mkv5UzX2fJ2mqJJPUqsy8A8K+J0n6qMy8TEnfSHo9YdrosPw4SXMlvRymt5D0kqTxkr6UtFPCOheH7U+U9KykBmX2c4+kVQmPO0l6L2zrQ0kdEua9JWlZYk1h+sGSxoa6PpbUrYIsBku6vsy0cZKeKzNtT0lfhHlTJN1QUb7l7KO5pGGSvgvr7hWm/z0c0zhJb0tql7DORs+DpC3DsUyUNDhh2VcS141Rz8uSPi8z7QZJc8I+v5P0gKRYv+OSWkr6QNIqSfeVmfeupBZxa0sFTc69hlYPj2CL2/+b7FJSyjXDp7LvzV9x5D3jyp2/PK+Q84d+x+B7v+WEB8bzY+6a2i0wRcxbtJrf//VtBl70KoMuepWnRkzZaJn3vpzFkZe8xuBLX+fYy0cwZsqCJFSafPVOupSGN71AzpUPlzs/s+fe5FzxEA0uf5AGl95PxjY7lbtcOmrQd2/aPfEy7Z56laYnnr7R/Myt2tD6jodp++BztH34fzTYfV8AMpo2o/UdD7P165/S4vwra7vspGi41750HjaCzsPfosWpZ5a7TONDDqPT86/R6flXafP32wDI2W13Og4dvv6n28ff0Gj/g2uzdFcNv7an+wngPuCpMtNvA/5mZm9KOiI8PqCS7TQH/gT8uxr7/gR4HfgwcaKk5mE7h5nZTEll791+ITAFaFoywcz6Jaz/IvBKeHg1MM7Mjpa0PXA/cLCk9sAFQA8zy5P0P+BEojyQ1Aco20i7HXjKzJ6UdBBwM/C7MO+fQEPgnDLrPAAcZWZTwknJtcBp5WRxOXBkwjHsAGQC/SQ1MrOSb215EvitmX0rKRPYrpxtVeRu4C0zO05SvVAvwD/N7Lqw3wuA64E/VvI8DAEeBIYDbwAvS/oN8I2ZzY1TSNj2bsAqSduY2bSE2XeZ2e2hsT0K2B/4IMZm84HrgJ3CT6KniX4/b4pTXyrI/3AEeW+9QNM/X1/1wpuRo3fZipP3bMOVw6aWO/+hj2azfdtG3Hvy9kxbmMffX5vG42fsWMtVJl9mprji1N3YcZuWrMor4NjLR7B3r7Z027r5+mX27NmGg/oOQhLfT1/KRXeO4s17jkpe0UlS+MVICke9TP1Trih3ftH3Y8mb8CkAateFBqdfR95NZ9RmicmRkcEWF1zFgsv/SOHCXNr+eyh5n31EwYwNb9fNTj6L1R++zarXXiC70zZs9Y/7mHPyEdi6tSx7/H6yO3cju0u5fU3pJSODrS6/ljnnnUlBbi6dnnye1aM+YN3PP61fJHvrTmxx2lnMOvNkileuILPFFgDkjfmSmScfE22maTO6DH+LNZ9/kpTDqBVFxcmu4Ff5VT3dZjYKWFLeLDY0apsBVTWmbgG6hh7Kf8bc9zdmNr2cWScBw81sZlhuffdL6F0eCDxS3jYlNQUOAl4Ok3oA74ftfAd0ltQ6zMsCciRlETVA54ZtZBI1oi8vs/n12yJqBK7/62Rm7wEryztMqshRUndgrZktSpg8hKih+Hbifoi+PGpe2GeRmU0uZ58bkdQM2A94NKy7zsyWhf+vSFi0UagZKn4eCojyqg8UhfwuIjoxi+sY4DXgOaKTnfLUAxoAS+Ns0MxWm9nHRI3vsl4lyrTOKJgyjuJVK6pecDPTp0tTmuVU3Nfw04I89timGQDbbJnD3KVrWbRq8/tmuq1aNGTHbVoC0Dgnm67tm5G7pHSvf6OcbCQBsGZtIeG/m53inyZga8p7+w7WbXhLUb0GYHX74/G46m2/E4VzZlE4bw4UFrL6g5Hk7H1AmaWMjEaNAFCjxhQuXhhNzc9n7cRxWMHm8dprsGNPCmbNpGDObCgsYMU7b9Jo/4NKLdNs8HEse+EZildG7+tFSzduejU5eACrPxuNrS3vz5hLBTU1pvsiYKSk24ka9ntXsfyVwE5m1htAUhNgdAXLnlRFY7E7kC3pQ6AJcLeZlfTE/4uoMdykgnUHA+8lNCS/JWrgjVY0RKYT0MHMxoRjmwnkAW+b2dthnfOAV81snkr/FSrZ1t3A0UATSS3NbHElx3Im8IakPGAFUN53Qu8DjC0z7QSgP7A9cD7wTJh+F/B9yOYt4Ekzy5d0YJhX1hoz2xvoAiwEHpe0MzAGuLCkB13STcDvgeXAgWHdip6HZ8LP2cAVRD3IT5tZdT7HHwLcCOQCLwL/SJh3saRTiJ6rN81sXKjxMuDkcrY1yswuqGxnZrZUUv0Yz5er47Zr04h3Jy+hT+emjJ+9krnL15K7fB2tGtdLdmlJM3vBKqZMX8LO27baaN47X8zkzqHfsGRFPg9edVA5azuAzF77UO83f0CNm5P/n2uSXU6tyGq1FYUL569/XLQwl3o79Cy1zPInH2SrWx+gyeAhqEEOCy4r+2Hv5iFry9YU5m7IqjB3Pjk79Sq1TL2OnQHY+pH/QkYmix++nzWffVxqmSb9D2fpM0/WeL3JZJvzmO5KnAtcbGZbAxcTekjjMrOVZta7gp+qemeziIYeDAQOBa6T1F3SIGCBmY2pZN0hwLMJj28BmksaR9R4/Yaod7YFUQ9yF6Ad0EjSKWFM8vHAveVs+1Jgf0nfEA15mAMUVXEsFwNHmFkH4HHgznKWaUvUIAbWD21ZFHqY3wN2kbQFgJndCPQh6gE/iajhjZl9UEHWJSdLWcCuwANmtguwmuhEibD+NeG5Hkp00lGyzkbPg5ktN7OBZtaH6GThN8AwSQ+HMeN7VRZI+KRhW+BjM/sBKFDCWHui4SW9iXr1G0k6MdT4zwqOsdIGd4IFRM912XrOVnTdwtdPTcuNuSmXqs7arx0r8go5+r5vGfrZfHZo24iMjM20CxdYnVfABbd/xFWn9aVxw41PPPrv0ZE37zmK+y4/gHueG1f7BdYRReM/Ie+mM8h/5K/UG7jx2ObNVcODDmPV268y58RDWXD1ebS86v/YbD8yqUpmJvW27sSsc05j3rWX0vqav5HReEP/YWbLVtTr1p3Vn6Xx0JI0UFM93acSjZ0GeIEKhnNU5Ff2dM8GFode2NWSRgE7EzUajwxjzBsATSX918xOCftsBexO1AsNrB86cXqYL+BnYBpRI/JnM1sY5g0n6s1fCnQDpoZe7oaSpppZtzBe+ZiwfGPg2JIhGhVksCWws5l9ESY9T2gkl5FHNPSkxBBge0nTw+OmwLHAw+GYfgIekPQwsFBSS6AXlfd0zwZmJ9QyjIRGd4KhROO0/0rFz8MPCctfRzROegjwcdjucKJ8K/JbovHyP4eMm4b1S3UfmVmBpLeIhsU892t6uoMGRFmXYmYPAQ8BLPjtXnX7FNzRuEEW/zg2GkNqZvS/4xu2blE/yVUlR0FhMRfc/hG/6deFAXt2rHTZvj1aMyt3FUtX5NOiaYNKl92cFf80AbVsC42awur0Hv5VuGgBWVu2Wf84c8vWFC0qfbFt48OPZsGV0T0U1k0ej7Lrk9GsOcXLYo0KTBuFC3PJar0hq6zWbShYWDqrwgW55E8aD0WFFM6dQ8HMGWR37MTaydF9LJr0P4xVH74LRYW1Wnut8/t0l2suUW8uRGOkf6xi+ZUkDPn4lT3drwD7SsqS1BDYA5hiZleZWQcz60w0Dvj9kgZ3cBzwupmtHwyl6I4dJd07ZxI10FYQDSvZU1LD0Bg/OOxjhJm1MbPOYT9rzKxb2FarhDtpXAU8VsVxLAWahTHbEA0X2fgWAtG0kn1kEDVKeybUcBRhPLKkgdow5mVbop72ZVX1dJvZfGCWpJILLw8GJodtbptQy1HAd+H/5T4PCdluSzRU50OiMd7FROPBc8L88ySdx8aGEF2cWXJ8u1HOuO5wnPsAP4Vj+MU93WFbbYDpVS3r6rYVeYWsK4wu1Bn29QL6dG5C4wab351VzYxr//0ZXTs04/Tf9Ch3mRnzVmBhfPKkaYtZV1hE8yab5wlKZdRqwwdkGR26QVZ22je4AdZ9N4ms9h3JatMOsrJodOCh5H1a6mZiFC2YR4Nd9wAgq2MXVK/eZtfgBsifPJHsjp3IatcesrJp2v9wVo8qff3/qo/eI2fXvgBkNGtOdsdOFMyZtX5+kwEDWTnyjVqt21Xfr/prIulZoruStJI0G/irmT0KnAXcHS6Syycav1sy9OGPZlbqfjhmtljSJ4puPfimmV0WY98XEI3PbgOMl/SGmZ1p0Z0+3gLGEzXkHjGziZVtKziRaDhJoh2AJyUZMAn4Q6j3C0nDiIZHFBINO3moiu0fANwctjUK+HPCsYwmGn/dOOT4BzMbKeks4EVJxUSN8PIueR8F3BEahv2AOVb6LiCjgB6S2hLdLeUuSWtC3SebWVVDXEqcDwwNJyHTCJ8AALeExngxMAP4I0CM5+EmNvROP0t08eqVRHc/IeRR6nMySZ2Jxmqvv1Wgmf0sabmkPcKkkjHd2WHfse+IEz4daArUU3Q7wwHhJG834HMzqzNdCE0v/BvZPXYlo0lzWj7wCqv/9wj5H7yW7LKS7tLnf+DLn1ewbE0hB942hvMO6kBBGCN44u5tmLYwj6tenIoE3bZqyN+P7prkipNj7HcLeWXUNLp3bM7gS6M7mV580i7MWxjdCOnEQ7vz9uczeeWjaWRlZVC/XiZ3Xbzf+gsrNyf1T72ajG47o8bNyLnxWQreeBIyoz+thZ+8TlbvfmT17Y8VFULBOtY+8X9JrriWFBex5N5b2OrWByAjg1VvvkLBjJ9odtq5rPt+MnmffcTSB+9ki0uup+mxJ4PB4tv+un719kPfQA0boexsGu5zIAuuOLfUnU/SSlERC2+7iQ73PAyZGax49SXWTZtKy3POI3/KJFaP+oA1n31Moz32ptPzr0FxEYvuvp3i5csByGrbjuzWbcgb+1WSD6Tm1fUx3bLN5ErqdCbpbuA1M3s32bVsKoruWX6MmSX98vWQ76sW3WWmQj68JJ6Wx1fnTpWbt4ztN4PbpW0Cax7+MNkl1BmLJi2qeiHH2hVJ/9NTJ3T/anKtnmmvOu/gWvs72/i+9zb5sW1+n5ump38QDd9IG2Y2KNk1JJhYVYPbOeecczXL6viYbm90pwEzyyW6l7SrAWZW/lfNOeecc87F5I1u55xzzjmX8ur6mO6aunuJc84555xzLvCebuecc845l/KK6/iYbu/pds4555xzroZ5o9s555xzzrka5sNLnHPOOedcyqvrF1J6o9u5TSSzfmayS6gTipfkJ7uEOkOLlyS7hDrhk2dmVb2QA6BzF3+fiqPLmb2SXYJLQ97ods4555xzKc+Ki5Ndwq/iY7qdc84555yrYd7T7ZxzzjnnUl5d/xp47+l2zjnnnHOuhnlPt3POOeecS3l1/e4l3tPtnHPOOedcDfOebufquEZnXkW9XfameMVSll/1+43mZ7TtSOOzriarc3fWDHuY/DeeTUKVqeHakTMYNW0FWzTM4uVTd9ho/mNf5TLiu6UAFBUb05bkM/qPPWmWs3m9Vc5bkseVj49j8cp1APy2X0d+f3CXUstMm7+Kq5/4lsmzVnDRUd05Y0DXZJSaFC0P6sf2/7gGZWQw+78vMP2eh0vN73TuabQ/5XissIh1i5cw6YKryZ89F4D+uZNZOfkHAPLnzGPcKefWev21peFe+7LVX66CjEyWvzKMpU8+stEyjQ85jJZn/Rkw1v7wHfOvu5yc3XZny0uuXL9MvU5dmHfNpaz+6L1arD45/D2qcpv1mG5Jj0laIGlimek7S/pM0gRJr0lqGmNbV1dz38dLmiSpWFKfMvN6hf1PCjU0KDP/1cSaJT0vaVz4mS5pXJheT9LjYRvfSjogYZ0hYfp4SW9JalVmH3+RZCXTJbWQ9FJY/ktJOyUse6GkiaHei8ps53xJ34V5t1WQRVtJr5eZ9i9JcyRlJExrLen1cCyTJb1RecqltidJN0n6QdIUSRckTL9H0tRwbLsmrHNrOK6Jkk5ImD40LPuPhGnXShpcjXoukpQvqVnCtAMkLQ/P43hJ70raqhrbrOj3+XZJB8XdTm1bO/oNVtz2lwrn2+oVrH76X+S98VwtVpWaBu/YkgePqbhxeEbf1rz4u+158Xfbc9G+7ejTofFm88csUWamuPz4Hrx+w/48f+U+PPPhDKbOXVlqmWYNs7nmxB05o3+XCraSpjIy2OHW6xl7wpl8ss9A2h4ziEbdS/9OrZgwhc8POZbP9j+S3NdG0v2Gy9bPK8rL5/MDB/P5gYPTusFNRgZbXX4tcy48h+m//Q1NBxxBvS6lc8reuhNbnHYWs848mRknHMnCO28BIG/Ml8w8+RhmnnwMs889HcvPZ83nnyTjKGqdv0fVLRW1Gyrya4eXPAEcVs70R4Arzawn8BJwWTnLlFWtRjcwETgGGJU4UVIW8F/gj2a2I3AAUJAw/xhgVeI6ZnaCmfU2s97Ai8DwMOusML8n0B+4Q1JG2MfdwIFm1gsYD5yXsI+tgQHAzDLHNy4s//uwPqHxfRawO7AzMEhStzDvQOAoYOdwLLdXkMUlwPqultDQPhqYBeyfsNyNwDtmtrOZ9QCuJL7TgK2B7c1sB6CkBXc4sG34ORt4INQwENgV6A3sAVwqqamkXkBeyKGvpGaS2gJ7mNnL1ahnCPAV0e9AotHhuewV5v+5Gtt8gvJ/n++lelnVqsLvv8VWr6hwvq1YRtHP30FRYS1WlZr6dGhMswbxvhzkje+WcsR2LWq4otS0VbMG7NgxOp9t1CCLrm0bk7us9JcatWxan56dm5OVuXmNUmy2ay/W/DyDvBmzsYIC5r80gq0OP7jUMks//oLivCiv5V+Po37bNskoNaka7NiTglkzKZgzGwoLWPHOmzTav3TfRbPBx7HshWcoXhm9fxUt3fjLoJocPIDVn43G1m4eX6rl71GVs2KrtZ+YnqD8dkO5ftW7pZmNAsr7yrTubGgMvwMcW9l2JN0C5IQeyqEx9z3FzL4vZ9YAYLyZfRuWW2xmRWE/jYkaqP9XQR0CfguUfP7eA3g/bGcBsAzoAyj8NArrNAXmJmzqLuByIPFZS9zWd0BnSa2BHYAvzGyNmRUCH7GhIXkucIuZrU2ooTzHAm8lPD4AmETUAB6SML0tMLvkgZmNr2B75TkXuNHMisvUchTwlEU+B5qHRnQPYJSZFZrZaqITk8OIToBywolBNlBEdDLw17iFSOoKNAauLXN8icsIaAIsjbvdin6fzWwG0FLS5veXczOVV1DMx9NX0H/b5skuJenmLFrDlJnL2blL82SXkhIatG1N/tz56x/nz82lftvWFS7f/uTjWPTehr6hjAb12ePdF9n9refZskxjPZ1kbdmawtwNORXmzid7y9IfPNbr2Jl6HTuz9SP/ZevHnqXhXvtutJ0m/Q9n5cgRNV5vXePvUamhknZwuWqqi2ISUWMM4HiiHtIKmdmVRL2fvc3sZABJoxOGfCT+HFLFvrsDJmmkpLGSLk+Y93fgDmBNBev2A3LN7Mfw+FvgSElZkroAuwFbm1kBUSN0AlFjuwfwaKj7KGBOSaM/wbeExrSk3YFOQAeiHvt+klpKaggcwYa8uod5X0j6SFLfsgWHupaWNMyDIUQnDi8BAyVlh+n3A49K+kDSNZLahW00qSDrcZJ6hHW7AidI+lrSm5K2DdPbE/Wol5gdpn0LHCapoaIhNgeG7KYAC4GxwGtANyDDzMaW83xU5ESinvbRwHbh5KVEP0XDg2YChwCPhWM8sILj+zTmPscC+1SjRleHfThtObu0b7TZf2y7Or+QC/4zhit/24PGOdlVr+BKaXv8kTTtvRPT79swlnl07wP54pBjmXDOX9j+pqvJ6Vzpn8f0lplJva07Meuc05h37aW0vuZvZDRusmF2y1bU69ad1Z9tHkNLqmNzfY8qLrZa+5F0dmjzlPyc/Wvrr6ln6wzgHknXAa8C66q7ATPr9wv3nQXsC/Qlaly/J2kMsBjoamYXS+pcwboljdUSjxH1RH8NzAA+BYpCI/ZcYBdgGtHwg6sk3Uk0jGRAOdu+Bbg7NAgnAN8ARWY2RdKtwNvAamAcUe9vybFsAewZjud/krYxs8Qe9LZEjVggGodO1HC/xMxWSvoCOBR43cxGStqGqMf5cOAbSTuZ2UKiYSCVqQ/km1mfMETnMaKTlHKZ2dvhJOHTUN9nJcdlZhcl1PsacI6ka4iG17xjZg9vvMVShgBHm1mxpBeJTuzuC/NGm9mgsO0rgNuIhhp9EOMYK7MAaFd2YngRng1wxx5dOXVb7wxPB29uhh/bllVQVMyF/xnDb3Zvz4Bd2ya7nJSRPy+XBu02vM4btGvN2nm5Gy23xX570eXiP/L1kadg69aPcGTt/OhDwrwZs1nyyZc07dmDvOmzNlq/ritcmEtW6w05ZbVuQ8HC0h/WFi7IJX/SeCgqpHDuHApmziC7YyfWTo6GxzbpfxirPnzXh8aVw9+jap6ZPQQ8tCm3WSM93Wb2nZkNMLPdiBqxP1V3G7+ip3s20bCGRWa2BniDaGzxXkAfSdOBj4Hukj5M2F8WUU/08wnHUWhmF4ce+KOA5sAPhMabmf0UGsD/A/Ym6g3uAnwb9tMBGCupjZmtMLPTw7jx3wNbEjXYMbNHzWw3M9uPaDjEDwnHMjwM3fgSKAZKXbAJ5AGJF4oeGuqcEGrYl4QhGGa2xMyeMbPfEY153i9mT/dsNox1fwnoFf4/h9KfZHQI0zCzm0J2/YmG4/yQsFzJpwJjiIaKdDWz3wLHhR7/cknqSTR+/J1wfCdSwRATohO+/cJ6v7anuwFR1qWY2UNm1sfM+niDOz2sXFvE17NXcWC3ZlUvnKbMjGufGs82bRpzWv9tkl1OSlnxzQQabtOZnI4dUHY2bY4eyIK33i+1TJOeO9DjjhsZd8q5rFu04ZPnrGZNUb3oE4PsLVrQfI9dWfX91Fqtv7bkT55IdsdOZLVrD1nZNO1/OKtHfVBqmVUfvUfOrtEHuBnNmpPdsRMFczacgDQZMJCVI2Nf77/Z2Jzfo6zIau2nJtRIT7ekrcxsQRi3ey3wYIzVCiRlh6Ebv6aneyRweWi4rSO6kPAuMxvBhov8OhP1/B6QsN4hwHdmtn7Mc9iGzGy1pP5AoZlNDsMyekjaMvQS9wemmNkEYKuE9acDfcxskaTmwBozWwecSXRisCIsV5JXR6KG/55hEy8TDcv4QFJ3oB6wqMzx/gB0Tng8BDjTzJ4N224E/ByOZU/gczNbI6kJ0UnCTDNbSdW9wCW1/BwyLWlAvwqcJ+k5ogsml5vZPEmZQHMzW6zo4sleRL35JdlkAxcBA4ka0SW/4ZlAPUUXmJ5nZmXvgTcEuMHMbk7Y1s+SOpVT876EE75N0NPdHXjhV6xfYxr/6Qayd+iNGjen+d3DyRv+KGRGL+2177+Cmm1BsxsfQTmNoLiYBocez/IrTsHyKxpllb4uG/EzX81exbK8Qg5+aCJ/2qstheGCmRN2js5n35u6jL07N6FhdryLmdLR2J+W8urnc+jevglH/300ABcN3o55S6LzzhP378TC5fkc/49PWJVfSIbgqfem8/oN+6X9MBQrKuK7K29k1xceQRmZzHnmRVZ/P5WuV17AinETWfjW+3S/4XIyGzWk16N3AxtuDdioe1d63PE3KDbIENPvfpjVP1S7T6puKCpi4W030eGehyEzgxWvvsS6aVNpec555E+ZxOpRH7Dms49ptMfedHr+NSguYtHdt1O8fDkAWW3bkd26DXljv0rygdQuf49Kbyo9UqGaK0vPEl201wrIBf5qZo9KupANd40YDlxlZhYaq4+Y2RHlbOtW4EhgbMm47ir2fTTRsI4tiS5wHGdmh4Z5pwBXETXk3jCzy8us25mo0Z14274niBqkD5ZZbiRRD/Mc4A/hojok/RG4kOjCwBnAaWa2uMx+prOh0b0X8GSoaVLY1tKw3GigZdjWJWb2Xphej2gYR2+iE4hLzax0l0q03HvAOUTjy2cDnUsa9GH+cKIe/I7A6UAh0accj5vZHRWGXHofzYGhYRuriIZsfCtJREM7DiMaznO6mX2t6DaNJeO0V4TlxyVs7yJgmZk9EbbxDLAT0fN1haTjgP5mdk6ZOqYBR4SLUUum3Un0+/cF8ArRiYGA5UQnIKV62Cs5xop+n7OJLgTtadHFruVa/Lt96/YNRGtJ0307JLuEOiNzu41GNLlyvHucX2gXV+cu3lCLo8uZvapeyJF9znOqzf3NO3qPWvs72/alL6o8toraDRUu/2sa3S41hBOQ3czs2mTXsqlI+ifwtFXvDis1VcvRwK5mdl1ly3mjOx5vdMfnje54vNEdnze64/FGdzy13eiee9TutfZ3tt0rX27yY9u8LntNU2b2kqSWya5jUzKzOPd2ry1ZRHe9cc4555z7RbzRnSbMbOPv13WbhJml5Fhu55xzbnNSjS+tSUmb11eJOeecc845lwTe0+2cc84551JeTd3Kr7Z4T7dzzjnnnHM1zHu6nXPOOedcyrPi4mSX8Kt4T7dzzjnnnHM1zO/T7dwmYhP+z19MMcy65MVkl1BnrMzNS3YJdUK3Idsnu4Q6Y+xD31W9kCM/P9kV1A0HzvuuVu/TPbP/LrX2d7bjO99s8mPznm7nnHPOOedqmI/pds4555xzKc/v0+2cc84555yrlPd0O+ecc865lFfsPd3OOeecc865ynhPt3POOeecS3n+jZTOOeecc865SnlPt3N13LxFq7ni3k9YvDwfAb/tvy2/H7hDqWXe+3IWdz83jowMkZkhrj69L7vtsFVyCq5lDfrsTYs/XQYZGax+82VWPP94qfmZW7ah5eU3ktG4CWRksOzRe8n/8uNS89s++iLLn3qQlcOeru3ya03jffalzRXXRBkMH8aixx4uNb/5kUfT+pLLKFiQC8CS54aybPgwAFpf9Bca77c/AAv/8wArRr5Zu8UnSdYR55HRrQ+2ZjkFj1y40Xx13InsY6/Cli8AoPj7zyj65H+1XWbSNN9vXzr/9RqUkUHu88OY++DD5S63xWED2O6Bexh/5HGsnjCRZvvuTcfL/0JGdjbFBQXMuPk2Vnz2RS1XX7u2OHBftr3xGsjMYN4zw5h5X+ms2v3+BNqfdjJWVETRmjV8f9n1rPnhp/Xz67dvy+4fvc702+9n1oOP1Xb5LqZf3NMtaWtJH0iaLGmSpAsT5m0h6R1JP4Z/W1SxreaS/lTN/Z8naaokk9SqzLwDJI0LdX1UZl6mpG8kvZ4wbXRYfpykuZJeDtNbSHpJ0nhJX0raKWGdi8P2J0p6VlKDMP0JST8nbK93mL69pM8krZV0aTnHP0zSd5KmSNorTD8+7KNYUp9KsmibeDxh2r8kzZGUkTCttaTXJX0bnrc3qpF3uceVML+vpEJJx4XHnSSNTXge/him15f0VsjtTwnrPyRp12rUU97xnSZpYcI+h0lqWI1tviVpWTlZPidp27jbqW2ZmeKKU3djxL+O5LmbD2foW98zddayUsvs2bMNr9wxiJdvH8Q//rQ31z7wWXKKrW0ZGbQ4/0oWXH0e8848loYHHkZWx21KLdLs5DNZ89E7zD93CItuuootzr+q1PwWf/wL+V99UptV176MDNpefT0zzj2LnwYPotnhA6m/TdeNFls+8k2m/fZopv326PUN7sb99qfBDj346fijmXbyCbQ69QwyGjWq7SNIiqIJ71Pw/I2VLlM8ezIFj11MwWMXb1YNbjIy6HLj9Uw57SzGDRhEqyMHktNt49+pjEaNaHv671j5zbj10wqWLOW7M8/l28OPZOqlV7LtnbfVYuFJkJFB939cz7cnn8WX+w+i9eCBNOxeOqvc4a/z1UFH8nX/o5l5/yN0u+HKUvO73XAlS94fXZtVJ4UVW6391IRfM7ykEPiLmfUA9gT+LKlHmHcl8J6ZbQu8Fx5XpjlQrUY38AlwCDAjcaKk5sC/gSPNbEfg+DLrXQhMSZxgZv3MrLeZ9QY+A4aHWVcD48ysF/B74O6wj/bABUAfM9sJyAROTNjkZSXbM7NxYdqSsM7t5RzL3cBbZrY9sHNCfROBY4BRlSYBlwDrT4tDQ/RoYBawf8JyNwLvmNnO4Xmr6nkpq7zjQlImcCvwdsKy84C9QqZ7AFdKagccCnwM9AJ+F9bfGcg0s7Fxiqjk+ACeD/XtCKwDTqjG8f2zpKYyHgAur8Z2atVWLRqy4zYtAWick03X9s3IXbKm1DKNcrKRoi/XWrO2ENXqd4glT73tdqJw7iyK5s+BwkLWfDiShnsfUGoZM0OhkZjRqDFFixeun5ez9wEUzp9DwfSfSGc5O/Vi3cyZFMyZjRUWsPytN2hy4MGx1q3ftStrxnwNRUVYXh75P3xP43361XDFqcFmTcbyVyW7jJTUeOde5M+YydpZs7GCAha99gYt+m/8O9XxkguY8+AjFK9dt37amslTKFgQfTqQ98OPZDSoj+pl11rtta3pLr3Imz6T/JlRVrmvvEGrQ0tnVbRq9fr/ZzZsCAnfJt7qsIPJnzmb1d9PrbWa3S/zixvdZjavpJFkZiuJGortw+yjgCfD/58EBlexuVuArqGH8p8x9/+NmU0vZ9ZJwHAzmxmWW1AyQ1IHYCDwSHnblNQUOAh4OUzqAbwftvMd0FlS6zAvC8iRlAU0BOZWUe8CM/sKKCizz2bAfsCjYbl1ZrYs/H+KmX1f2XaDY4G3Eh4fAEwiaiwOSZjeFpidUNP4GNuO43zgRWB91uE41oaH9dnwu1ZAlFc2UNL0+ztwXTX2dwDlH9964XlpBCyNu1Ezew9YWc6s0cAhYZspbfaCVUyZvoSdt2210bx3vpjJ4Re8wh9vfp+b/rR3EqqrfZmttqJoYe76x4WLcslstWWpZZY//R8aHXwE7Z55i61uupcl998KgBrk0PSE01n+9H9qteZkyG7dmoLceesfF+TOJ2ur1hst1/SQ/nQd9god7ribrNZtAMj/Pmpkq0EDMps3p9Hue5Ddpm2t1Z7qMtpvR/YZd5H92+tQq62TXU6tqdemNWvnbfidWjd/PvXblP6darRjD+q1bcuyDz4qu/p6Wxx+KKsmTsbWFVS4TF1Xv01r8udsyGrtvI2zAmh/2kns+dnbdL32Un689iYgaoB3/PNZTL/j/lqrN5msyGrtpyZskgspJXUGdgFKBl21NrOS36D5wMa/PaVdCfwUeigvk9QkYRhD2Z8eVWyrO9BC0oeSxkj6fcK8fxH1WBZXsO5goh76FeHxt0Q9zUjaHegEdDCzOUQ91jOJenSXm1liL+9NYUjKXZLqV1FvF2Ah8HgY9vKIpNifzUrqAixNaOBC1BB9FngJGCippIvgfuBRRcOCrgk9z1Qj742OK/T6H03UAC5b29aSxhP1SN9qZnOBd4DOwOfAPZKOBMaGeXFVdHwAJ0gaB8wBtgBeC7WcXMHxDatqZ2ZWDEwl+hQiZa3OK+CC2z/iqtP60rhhvY3m99+jI2/ecxT3XX4A9zw3rvYLTFGNDjyM1W+/xtyTDmPBNefT6or/A4lmv/8jK1/8L5afl+wSU8LKjz7gx8MO5qfjjmL1Z5/S/qZbAFj92Ses/Pgjujz1LB1uvYM1347DiouSXG1qsPk/se7+s6OhJWPeIOvYq6peaXMh0enaK5lx060VLpKzbTc6XfEXpl3z11osLHXNeeIZPt9rAD/ddAedLjoXgM6Xnsesh56gaM2aKtZ2qeBXN7olNSbq5bwoobG6npkZUK1TBjNbmTCMoezP5CpWzwJ2I+rRPhS4TlJ3SYOABWY2ppJ1SxpzJW4BmodG3PnAN0CRojHqRxE1mNsBjSSdEta5Ctge6EvU6LsiRr27Ag+Y2S7Aaqo37KMtUaMdAEn1gCOAl8Pz8QVRDpjZSGAboqEo2wPfSNoyZt4VHde/gCtCw7QUM5sVhuZ0A06V1NrMCs3spHCsLwAXAXdIujOMwT6ysoOt7PiC58OQljbABOCyUMvQCo7vuKoCDhYQPddl6zlb0teSvn5o2FcxN7XpFRQWc8HtH/Gbfl0YsGfHSpft26M1s3JXsXRFfi1VlzxFixaQueWGc/6sVq0pWrSw1DKNDhvMmo+ic+Z1U8ajevXIaNacetvvRPOzLqLd0yNocszJNB3yBxofVZ3RSnVHQW4u2a039E5nt25D4YLcUssULV+GFUS9jUuHv0DODjuun7fo4f8w7bdHM+OcP4DEuunTa6XulLcuDwqi11nxT2NQRhbkNElyUbVj3fxc6rfd8DtVr00b1s7f8DuV2bgRDbtvS4/nnmKX0e/RZJed2f7hf9Oo505h+dZs95/7mPqXK1g7c1at11+b1s7PpUH7DVnVb1s6q7IWvDyCLQ+Lhp803bUXXa+7jD2/fI8OZ/2eThecTfvTT67xmpOlro/p/lUfl4cexheBoWY2PGFWrqS2ZjZPUlsShh3E3G4Too/0y3NSFQ3v2cBiM1sNrJY0iqiHclfgSElHAA2AppL+a2anhH22AnYn6rUFIDTqTg/zBfwMTCNq5P1sZgvDvOHA3sB/E3r410p6HCh10WQF9c42s5JPCYZRvUZ3XjieEocSjZGfEMbwNgzLvB6OaQnwDPBMuGBwP0lvU0XelRxXH+C5sK9WwBGSCs3s5ZINmNlcSROBfuH4SvwJeIromoDlROOv3wdereR4Kz2+hH2apNeITpZukXQyoQFextSYDe8GYT+lmNlDwEMANuH/knIDUTPj2n9/RtcOzTj9N+V/EDRj3go6tmmCJCZNW8y6wiKaN6nqQ5i6b933k8hu35HMNu0oWrSAhgccyuKbS/c2Fi2YT4Nddmf126+R1bEL1KtP8bKlLLjkD+uXafa7cyjOW8OqV56v7UOoFXmTJlCvUyey27enMHcBzQ47gtlXln7rymq1JYXhhKXJAQex9ucwzj0jg8wmTSlavoz623anQffuzPkszS88jatRc1i9DAC13RYkyCtvBFv6WTV+Ag06d6J+h/asy11Aq98cwY8XbvidKlq5iq9322v94x7PPsWMf9zG6gkTyWzShO0f+w8zb72DlWO+SUb5tWrluAnkdOlEg63bs3b+AlofdQST/lT69ZfTpRN5P0eXsLU85ADWhP9/M/iU9ct0/st5FK1ew5zHh9Ze8a5afnGjOzRCHwWmmNmdZWa/CpxK1FN8KvBKFZtbCaw//Q9jxHv/wtJeAe4L42/rEV3Ed5eZvUDUW4ukA4BLSxrcwXHA62a2vvsvXJS5xszWAWcCo8xshaSZwJ7hzhh5wMHA12GdkpMNEQ1XmVhZsWY2X9IsSduF8dsHA1X15if6gWi4RokhwJlm9myopxHwc6h1T+BzM1sTTmy6AjPj5F3RcZlZl4RlniDK8OUwfn6xmeWFTwb2Be5KWLYFMIioEf0boiE/BuSE+UcDu5tZ2c9jKzu+svYFfgp1DgV+zTtRd6p4LpNl7HcLeWXUNLp3bM7gS6Nzj4tP2oV5C6MLb048tDtvfz6TVz6aRlZWBvXrZXLXxfutv7AyrRUXseS+W9nq5n9Htwwc+QoFM6bR7NRzWffDZPI++4il/7mTlpdcR5NjTgGMJf+8PtlV176iIub94+90euBRlJnB0pdfZO1PU9nyT+eTP3kiKz/8gC1O+h1NDjgQioooWr6cOddGL01lZdH5if8CULx6FXOuuhyKNo/hJVlHXUJGx50gpyn1/vwIhaOfg8xMAIq/GUnG9nuTucthUFwEhesoeKW86+jTVFERP//17+zw1KMoI4MFL7xI3o9T2fri81k1YSJL3/2gwlXbnHoyDTp1pMMFf6LDBdE9Fib//g8ULl5SW9XXKisq4oer/87Oz0avv3nPvciaH6bS5bLzWfHtRBa//QHtzziZLfrtRXFBIYXLVzDlgureByE91FQPdG2R2S87AEn7EvWOTmDDGOmrzewNSS2B/wEdie4u8lszW6Lotnd/NLMzy9neM0R3tHjTzMrrkSy7/AVE47PbEPWkv1GyXUmXEfVQFwOPmNm/yqx7AFGje1DCtA+BW8zsrYRpexFdCGpEF+79wcyWhnl/I+qZLSQadnKmma2V9D6wJdFFguPC8a6S1IaoYd401LUK6BEa8b2JLu6sR9STfrqZLQ0Nz3vD9pYR3UklcShFSZ3vAecQXcw5G+icONQn9MQ/T/R8nB5qzgAeN7M7qso6bKPc4yqzzBNEje5hkvoDd4TsBNwXeoVLlr0LeMXMPlR0u8VXiS7EfdDM7lV0W8VsM7s5YZ2GVRxfDtEdSOaE45sNnJZ4MW0VxziaaAhNY2Ax0fM9UtHFs6+Z2e6VrZ+snu66ZtYlLya7hDpjZa6PJ4+j25Dtk11CnTH2oe+SXUKdkJ/+o+82iQPnfVervTc/9O1Ra39nu381eZMf2y9udLvUERrnu5nZtcmuZVOR9F/g4pIhPEmu5WJghZk9Wtly3uiOxxvd8XmjOx5vdMfnje54vNEdT203ur/fdYda+zu73dgpm/zYUv4WaK5qZvZS+HQhbZQZ+pNsy4D0/SpC55xzztU4b3SnCTMr997j7tczs8erXso555xzNam4jo/p3iT36XbOOeecc85VzHu6nXPOOedcyiuu6KsN6wjv6XbOOeecc66GeU+3c84555xLed7T7ZxzzjnnnKuU93Q7t4mM2MfvKhhHXe+pqE2Fm8cXO/5qP988JdkluDSzriDZFbh05I1u55xzzjmX8up6p40PL3HOOeecc66GeU+3c84555xLeXX8u3G8p9s555xzzrma5j3dzjnnnHMu5fmYbuecc84551ylvKfbOeecc86lPO/p3gQkbS3pA0mTJU2SdGHCvOPDtGJJfWJu7+qaq7bS/Z4mqd0vWO8NSc3LmX6DpEvLmV5f0vOSpkr6QlLnCrbbVtLrZab9S9IcSRkJ01pLel3St+E5eKMatQ+V9L2kiZIek5QdpjeT9FrY5iRJp4fp20kaI2m8pL3CtCxJ70pqWI39jpP0XJlpT0j6Ocz7TtJfq7E9SbonZDpe0q5h+paS3oq7ndq05SH9OGDMWxw47m26XnzWRvO32LsP/UYN54glk2h71KGl5u1w42Xs/8Xr7P/VG+x42zW1VXJSbHlIPw4a+xYHf/s23S4pJ6d9+rDfx8MZtGwSbQdvyKnlfnuw/6cvr/8ZuGg8bQYdXJulJ1Xr/v3o/+1bDJj4Nt0v3Ti3lvv04aBPhzN45STaHX1oOVtIX/7ai8dz+mX8tZe+UqLRDRQCfzGzHsCewJ8l9QjzJgLHAKOqsb2kNLqB04ByG92SMitaycyOMLNl1djPH4ClZtYNuAu4tYLlLgEeTqghAzgamAXsn7DcjcA7ZrZzeA6urEYtQ4HtgZ5ADnBmmP5nYLKZ7QwcANwhqR5wDnAhcARQckJxLvBfM1sTZ4eSdgAygX6SGpWZfZmZ9QZ6A6dK6hLzOA4Htg0/ZwMPAJjZQmCepH1ibqd2ZGSw0x3X8+WxZ/Jh34G0P24QjbfrWmqRvNnzGHfuVcx9odR5Fy1234UWe+7KR3sdyUd7DKL5rj1pue/utVl97cnIoNed1/P5MWfyfp+BtD9+EI23L5PTrHmMO+cq5vyvdE6LR33BR3sP5qO9B/PpwFMpWpPHwvc+qc3qkycjg53/dT2fHHUm7+wykA7HD6JJObl9ffZVzHr+9Qo2kqb8tReP5/TL+GuvUsXFtfdTE1Ki0W1m88xsbPj/SmAK0D48nmJm38fdlqRbgJzQ2zk05jrdQk/rt5LGSuoapl8m6avQ8/m3MK2zpCmSHg49uG9LypF0HNAHGBr2nSNpuqRbJY0Fjpc0RNKE0Ct8a8L+p0tqFf5/jaQfJH0MbFdByUcBT4b/DwMOlqRyljsWSOylPQCYRNSgHJIwvS0wu+SBmY2Pk1tY9g0LgC+BDiWzgCahrsbAEqKTqwKgYfgpCD38vwGeirvPUPvTwNtEWZSnQfh3dcxtHgU8FQ7lc6C5pLZh3svAydWor8Y179OL1dNmsGb6bKyggDkvjqD1wNK9sHkz57By0vdYmXcPw8ioX4+Metlk1K+HsrJZu2BRbZZfa1qUzWnYCNqUk9OKcnJK1G7woSx4ZzRFefk1XXJK2KJvL1b/tCG32S+MoG2ZXv41M+ewYuL3df/z3mry1148ntMv46+99JYSje5EYajELsAXv2R9M7sSyDOz3mZ2ctjm6NAQLvtzSFhtKHB/6JXdm6hncwBRr+fuRL2mu0naLyy/bVh+R2AZcKyZDQO+Bk4O+84Lyy42s12JeupvBQ4K2+sraXCZY98NODHMPwLoW8FhtifqrcbMCoHlQMsy2+pC1Bu+NmHyEOBZ4CVgYMlQEOB+4NEwxOeakiEykppUkNu4hE8iSvaXDfyODY38+4AdgLnABOBCMysO+7qa6KThH8B1wD/CvLhOAJ4LxzKkzLx/ShpHdBLxnJktCPXdVcFxlPTqr880mB2mQfS89qtGfTUup21r8mfPX/84f24uOe1ax1p32ZfjWDz6C/r/8DH9f/iYhe+NZtUP02qq1KRq0K41eYk5zYmfU6J2xw1kzgubT69S2dzy5uSS0776uaUjf+3F4zn9Mv7aq1xd7+lOqQspJTUGXgQuMrMVm2q7ZlZhg0lSE6C9mb0Uls0P0wcAA4BvwqKNiRrbM4GfzWxcmD4G6FzJ7p8P//YFPgzDFQi98PsR9aKW6Ae8VDLMQtKrsQ6wfG2BhSUPwtCOI4BLzGylpC+AQ4HXzWykpG2Aw4iGWXwjaadQa++Y+/s3MMrMRofHhwLjiE4yugLvSBptZjOJetyR1I2oZ3yKpKeBesB1ZvZDRTtRNK5/kZnNlDQHeEzSFma2JCxymZkNC79L70na28w+NbOLYx5HeRZQ8bChs4mGo/Dn+ltxWL3mv2I3taPhNh1pvF1X3t0hGmG05yuPsfDd3Vjy2ZgkV5aa6rfekqY7dmfBux8nuxRXx/lrLx7PyaWrlGl0h57SF4GhZjZ8E297NNCknFmXUnGPuoCbzew/ZbbVGUjsPS4iGstckbjDG6pjDrA1MFtSFtAMWFxmmTw2DLGAqBHcHJgQRqI0DMu8DhAarc8Azyi6+HI/SW8DoynfSWY2GSBcsLgl0XjtEqcDt4RhJ1Ml/Uw09vvLhGVuAq4FLgAeAaYT9X5XNpRjCLC9pOnhcVOiYTQPJy5kZqskfQjsC3wq6S7gwHK295yZ3cKGTEt0CNMgyjGv7IphPw8BDwG83nS7WvuurLx5uTTo0Gb94wbtWpM3NzfWum0G9WfZV99StDoaQr/gndG02H2XtPyDlj83l5zEnNrHz6lEu2MPZ95r72CFhZu6vJRVNrec9q3Jm1O93NKVv/bi8Zx+GX/tVa6uj6hJieElYdzvo8AUM7tzE2yyIGHoBGbWLwz5KPvzbhhDPrtkqIeiO4M0BEYCZ4QeUyS1l7RVFftdSfmNe4gam/tLahUuqhwCfFRmmVHA4DAevAnRWOfyvAqcGv5/HPB+aNwm+oHSPfBDgDPNrLOZdQa6AP0lNZR0UDjmkp7/rsBMM1tZQW69ExrcZxI16IeUGSIyEzg4LNOaaHz6+s8HJe0PzDWzH4lOAIrDT0kdN0s6OvGAFF0I+lugZ8JxHMXGQ0wIJyN7AD8BmNnFFRzHLQmZ/l6RPYHlZjYvzOtOdEFvylg+ZgKNtulMTqcOKDub9scOJPeN92Otmzd7Llvs0xdlZqKsLFru05eV3/9UwxUnx7IxE2jUtTMNS3I6Ln5OJdofN5A5L4yooQpT09KvJ9C424bcOhw/kHkjqpdbuvLXXjye0y/jr730po3bakkoQtqXqEd1AlHDC+BqM3sjNLzuJepJXQaMM7NDw7jjR8zsiHK2dytwJDC2ZFx3FfvfFvgP0IroQr/jzWyaolsXltyNYxVwClHP9utmtlNY91KgsZndIOlYop7aPGAvogtC+5jZorDsEKLxzAJGmNkVYfr0kuUkXUPUoF5A1HAda2a3l6m3AdGFhLsQXaB4opltNOBN0ntEvc9zicYod04ctiNpONHwl45EPdOFRCdij5vZHVXlFrZRCMwgOuEAGG5mN4bn5wmiYS4i6vX+b1hHRBdBnmBmSxTdjWQo0Scv55rZJ6G3/SYz+yxhX/sDt5rZngnTMol6pHcBbia6K8tyoqEq7wEXlHNCUt5xiGgc+mHAGuB0M/s6zLsUWGtm91a2jdrs6QbYasB+9LjlapSZyaynX2Tq7Q/S/ZoLWD52Irlvvk+zXXvSZ+h9ZDdvSvHatazNXcRHewyCjAx63vlXttinL5ix8N3RTL76lqp3uInUdk/FVgP2Y6dbo5xmPv0iP/7zQba79gKWjZ1I7hvv03zXnvR9NuSUv5b8BYv4sO8gAHI6tmffd5/lne32hyS8VxYW1fou12t96H70+meU24wnX+T72x5kh+ui3OaNeJ8Wu/Vkz+ej3Iryo9+vd3cblJRa62VXvcymVFdfe7WtLue0rqBWd1dKXXrtHZP3fXk3cagxo7fevtbeiPvN+m6TH1tKNLpdzQgnLLuZ2bXJrqW6JI00s5S4AamkUcBRZra0suVqu9FdV9X1jwdrUzIb3XVJbTe6XfpLZqO7LvFGd/WkzJhut+mZ2UuSWla9ZOpJoQb3lsCdVTW4nXPOOecq443uNGdmjyS7hros3MHl5WTX4Zxzzm3u6vonpSlxIaVzzjnnnHPpzHu6nXPOOedcyvOebuecc84551ylvKfbOeecc86lvLp+xz3v6XbOOeecc66GeU+3c84555xLeXV9TLc3up3bRPzLFOLJqNWvUqjbmjZJdgV1w4qVVS/jXHX4a8/VBG90O+ecc865lFfXe7p9TLdzzjnnnHM1zHu6nXPOOedcyvOebuecc84551ylvKfbOeecc86lPO/pds4555xzzlXKG93O1VGt+/ej/7dvMWDi23S/9KyN5rfcpw8HfTqcwSsn0e7oQ9dPb9Zre/b/8DkOGfM6B3/5Ku2PO7w2y651W/Xvx8Hj3uKQCW+z7V/Kz+mAT4dz5IpJtBt86Ebzs5o04tAfP6LXndfVRrlJ1fLAfuz16Vvs/cXbdDp/46w6/vE09hw9gj0+fJVdhz1Bgw7t1s/rdv1l7Dnqdfb6+A2633RNbZZd6/y1F4/nFJ+/9uIpLq69n5qQEo1uSVtL+kDSZEmTJF2YMO+fkr6TNF7SS5Kax9je1TVacMX7PU1Su6qX3Gi9N8o7Lkk3SLq0nOn7SRorqVDScZVsN0fSR5IyE6ZdJClfUrOEaQ0lDZU0QdJESR9Lahyz9nKfH0nZkp4M25wi6aowfcuw/YmSBids55XqZCfpZUmfl5l2g6Q5ksaFmh6QFPt3XNJVkqZK+l7SoWFaPUmjJKXWUKyMDHb+1/V8ctSZvLPLQDocP4gm23cttUjerHl8ffZVzHr+9VLTi9bk8/UfruDd3QbxyVFnsvNtV5PdLE1vSpuRwc53Xc9ng8/kvV0rzmns2Vcxu0xOJXa4/iIWffxVbVSbXBkZbHfr9Ywbciaf7TuQNscMolH30lmtnDCFLwccyxcHHEnu6yPpdv1lADTruwvNd9+Vzw84ks/2G0TTXXrSYu/dk3EUNc9fe/F4TvH5a2+zkRKNbqAQ+IuZ9QD2BP4sqUeY9w6wk5n1An4AroqxvaQ0uoHTgHIbjokN37LM7AgzW1aN/cwM+3qmiuXOAIabWVHCtCHAV8AxCdMuBHLNrKeZ7QT8AYj7VS8VPT/HA/XNrCewG3COpM5h/w8CuwMXAUj6DfCNmc2Ns8PQsN8NaCZpmzKz7zKz3kAPoCewf8xt9gBOBHYEDgP+LSnTzNYB7wEnxNlObdmiby9W/zSDNdNnYwUFzH5hBG0HHVxqmTUz57Bi4vcbnbKvmjqd1T/NACB/3gLyFy6hXqstaq322tSiTy9WJeY0bARtYuYE0GyXHam/VUsWvvdJbZWcNM127UXezzPImxFllfvSCLY8rHRWSz/5guK8fABWfD2OBu3aRDPMyKhfj4x62dG/WdmsXbiotg+hVvhrLx7PKT5/7W0+UqLRbWbzzGxs+P9KYArQPjx+28wKw6KfAx0q25akW4Cc0Ns5NM7+JXWT9K6kb0MPctcw/TJJX4Ve3L+FaZ1Dz+3DoVf+7dCjfBzQBxga9p0jabqkWyWNBY6XNCShN/nWhP1Pl9Qq/P8aST9I+hjYroK8ppvZeKCqD0BOBl5J2E9XoDFwLVHjt0RbYE7C9r83s7Vxsqvk+TGgUeghzgHWASuIGvMNgfpAUZh/EXBbnP0FxwCvAc8RNZTLUw9oACyNuc2jgOfMbK2Z/QxMJToxAHiZKMuU0aBda/Jmz1//OG9OLjntW1d7Oy369CSjXjarp83clOWljJx2rcmbsyGn/Dm55LSLmZNEz5uvYOLVt1a9bBqo36Y1+YlZzculftuKs2p38nEsfm8UAMu/HsfST76g34SP2W/Cxyz+YDRrfpxW4zUng7/24vGc4vPXXnw+vGQTC72huwBflDP7DODNytY3syuBPDPrbWYnh22ODg3hsj+HhNWGAveb2c7A3sA8SQOAbYkaXr2B3STtF5bfNiy/I7AMONbMhgFfAyeHfeeFZReb2a7AKOBW4KCwvb6JwytCnbsRNSJ7A0cAfSsNqxKS6gHbmNn0hMknEjVURwPbSSp5VT8GXCHpM0n/J2nbhO1UlV2ixOdnGLAamEfUM3+7mS0h6p0/iqiH/B/An4CnzWxNNQ5vCPBs+BlSZt7FksaF/f5gZuPCcVxWwXHcE9ZrD8xK2M7sMA1gIr/iuUhVDdpsSZ9H/8mYc64Cs2SXk3K6nHMS80eOIn9ObrJLSTltjjuSpjvvxPT7HwEgp0tHGm3blY9778/onfejRb89ab7HbkmuMnX5ay8ez2lj/tqr21JqnGoYR/wicJGZrSgz7xqiYSixeq8TmVm/SvbZBGhvZi+FZfPD9AHAAOCbsGhjosb2TODnksYcMAboXMnunw//9gU+NLOFYftDgf2IelFL9ANeKmmASno11gGWrxXRCUGiIcDRZlYs6UWiISD3mdm4MExjAHAI8JWkvcxsSmXZJSrn+dkdKCIabtMCGC3pXTObBgwM67QArgSOlvRwWO4OM/uskv20JnoePjYzk1QgaSczmxgWucvMbpeUDQyTdKKZPWdm/wT+GedYyjKzIknrJDUJn8Qk1nM2cDbAOVlbMSCr+S/ZRbXlz80lp0Ob9Y9z2rcmrxqNw6wmjdh7+H+YdMNdLP3y25ooMSXkzc0lp/2GnBq0b03e3Hg5bbH7LrTcZze2OXsImY0akVEvm8JVa5h8/R01VW5SrZ2fS4PErNq2Zu28jbPaYr+96HLRH/l68CnYumgU2lZH9Gf5mG8pWh2dOy9+bzTN+u7Csi/G1E7xtchfe/F4TvH5ay8+v2XgJhIaSS8CQ81seJl5pwGDiHqRq326W83e2vWrATeHXuveZtbNzB4N8xKHXhRR+cnL6urWu4nkEQ2vAEBST6LG6juSphP1eq/vJTazVWY23Mz+BPyXqKc9VnYVPD8nAW+ZWYGZLQA+IRp+k+g64KZQx8fAqcANVRzXb4ka5z+H4+jMxr3dmFkB8BbRiU2cnu45wNYJm+hAwpAbouEw+eXs5yEz62NmfWqrwQ2w9OsJNO7WmYadOqDsbDocP5B5I96Pta6ys9nz+fuZ8cwrzH1pZA1XmlzLxpTJ6biBzI+Z05gzLuXt7Q7k7R0OZtLVtzLrmZfTtsENsOKbCeRs05kGHaOsWh89kIUjS2fVZKcd2P72Gxn3u3MpWLRk/fT82XNpvndflJmJsrJosVdfVv/wU20fQq3w1148nlN8/trbfKRET7ckAY8CU8zszjLzDgMuB/avxhCEAknZoeFVaU932MdsSYPN7GVJ9YFMYCTwd0lDzWyVpPZUfXHhSqCiS6y/BO4JY7eXEjUU7y2zzCjgCUk3Ez03vwH+U8U+y2VmSyVlSmoQeu+HADeY2c0ly0j6WVInogbm5LBOPaKLED8M26kqu4qen5lEQ2meltSI6ALZfyWsty3Qwcw+lLQzUYPWiMZ/I+m8sP/7yuxyCHBYSW+4pC7Au0Cp+ySF36l9CJ9UxOjpfhV4RtKdRL3z2xI9Z0hqCSwq+X1KBVZUxLiLb2Sf1x5BmZnMePJFVk6Zyg7XXcCysROZN+J9WuzWkz2fv4/s5k1pc8SB9Lj2fN7dbRAdjj2cVvv2od4Wzel0ytEAjDn7SpaP/y7JR7XpWVER4y+5kb1fDTk9FeW0fchp/oj3ab5bT/Z4bkNO2197Pu/3GZTs0mudFRXx/ZU3ssvzUVZzn3mR1d9PZZsrLmDFuIksGvk+3W64nMxGDen16N0A5M+ex7e/P5fc10bSot+e7PnRa5gZiz8YzaK3P0jyEdUMf+3F4znF56+9+Irr+Cgj/YKO401fhLQv0TjjCWy4OPBqM3tD0lSiXsbFYfrnZvZHRbeXe8TMjihne7cCRwJjS8Z1V7H/bYkat62IGtbHm9k0RbcuPDMstgo4hahn+/Vwlw8U3dKvsZndIOlYonHKecBeRBeE9jGzRWHZIUR3VhEwwsyuCNOnlywXhmmcCiwgariONbPby9TbF3iJqMc3H5gfxpeXPa5HgWfN7F1J04AjzOy7hPl3ArlE458vDXVlACOAK+J8qlDJ89MYeJyoAS/g8dDwLVnvf8A1ZvajpK2Ihtk0A643sxcl3Qd8YmbPJqzTmajHvENibYouVD0XOBw4C1gIZAPjgTMSxtdXdSzXEI1LLyQa4vRmmH4csJeZ/aWy9YfnbJf8F1MdkKFkV1B3NI514063YmXVyzhXHU3T+A6Fm9IhC76v1Xf02vw7e0zepj+2lGh0u5ohaVfgYjP7XbJrqS5JrwPHhFv2JbuW4cCVZvZDZct5ozseb3TH543ueLzR7TY1b3THU9uN7mH1a+/v7HFrN/2xpcyYbrfphdswfqBK7hGeqsxsUIo0uOsBL1fV4HbOOeecq0xKjOl2NcfMHkt2DXVZaPg/lew6nHPOuc2d373EOeecc845Vynv6XbOOeeccynPe7qdc84555zbzEg6TNL3kqZKurKq5b2n2znnnHPOpbxU6ukON6m4H+gPzCb6Nu9XzWxyRet4T7dzzjnnnHPVszsw1cymhZsuPAccVdkK3tPt3CZSEzfS/7UknW1mDyW7jrrAs4rHc4rHc4rPs4rHc4KTrPb+zko6Gzg7YdJDZfJvD8xKeDwb2KOybXpPt3Pp7eyqF3GBZxWP5xSP5xSfZxWP51SLzOwhM+uT8POrT3i80e2cc84551z1zAG2TnjcIUyrkDe6nXPOOeecq56vgG0ldQnfXn0i8GplK/iYbufS22Y9/q+aPKt4PKd4PKf4PKt4PKcUYmaFks4DRgKZwGNmNqmydWRmtVKcc84555xzmysfXuKcc84551wN80a3c84555xzNcwb3c4555xzztUwb3Q755xzzjlXw7zR7VwakbS9pCsk3RN+rpC0Q7LrqksknZ7sGlJJ+J06WFLjMtMPS1ZNqUjS7pL6hv/3kHSJpCOSXVddIOmpZNeQ6iTtG36nBiS7FvfL+d1LnEsTkq4AhgDPEX0dLUQ36z8ReM7MbklWbXWJpJlm1jHZdaQCSRcAfwamAL2BC83slTBvrJntmsTyUoakvwKHE92G9x2ir4L+AOgPjDSzm5JYXkqRVPY+xgIOBN4HMLMja72oFCTpSzPbPfz/LKLX4UvAAOA1fz+vm7zR7VyakPQDsKOZFZSZXg+YZGbbJqey1CNpfEWzgO5mVr8260lVkiYAe5nZKkmdgWHA02Z2t6RvzGyX5FaYGkJOvYH6wHygg5mtkJQDfGFmvZJZXyqRNBaYDDwCGNFr7lmizgHM7KPkVZc6El9fkr4CjjCzhZIaAZ+bWc/kVuh+Cf9yHOfSRzHQDphRZnrbMM9t0Bo4FFhaZrqAT2u/nJSVYWarAMxsuqQDgGGSOhFl5SKFZlYErJH0k5mtADCzPEn+2iutD3AhcA1wmZmNk5Tnje2NZEhqQTQMWGa2EMDMVksqTG5p7pfyRrdz6eMi4D1JPwKzwrSOQDfgvGQVlaJeBxqb2biyMyR9WOvVpK5cSb1Lcgo93oOAxwDvadtgnaSGZrYG2K1koqRm+AlvKWZWDNwl6YXwby7eFilPM2AM0cmtSWprZvPCtRV+wltH+fAS59KIpAxgd6B9mDQH+Cr0wjlXLZI6EPXizi9n3j5m9kkSyko5kuqb2dpyprcC2prZhCSUVSdIGgjsY2ZXJ7uWukBSQ6C1mf2c7Fpc9Xmj27k0I2mLciavLDvW23lWcXlO8XhO8XlW8XhO6cUb3c6lGUnTga2JxisLaE50cVcucJaZjUlacSnGs4rHc4rHc4rPs4rHc0ovfp9u59LPO0RXurcys5ZEtzJ7HfgT8O+kVpZ6PKt4ystpBJ5TWf77FJ9nFY/nlEa8p9u5NCNpQtnbSUkab2a9JI0zs95JKi3leFbxeE7xeE7xeVbxeE7pxa8Ydi79zAtflPNceHwC0V0oMvE7KZTlWcXjOcXjOcXnWcXjOaUR7+l2Ls2EOyb8Fdg3TPoE+BuwHOhoZlOTVVuq8azi8Zzi8Zzi86zi8ZzSize6nXPOOeecq2E+vMS5NCNpS+ByYEegQcl0MzsoaUWlKM8qHs8pHs8pPs8qHs8pvfjdS5xLP0OB74AuRB9DTge+SmZBKcyzisdzisdzis+zisdzSiM+vMS5NCNpjJntVnKFe5j2lZn1TXZtqcazisdzisdzis+zisdzSi8+vMS59FPyTWXzwlcszwXK+1Yz51nF5TnF4znF51nF4zmlEW90O5d+/k9SM+AvwL1AU+Di5JaUsjyreDyneDyn+DyreDynNOLDS5xzzjnnnKth3tPtXJqQdC9Q4Vm0mV1Qi+WkNM8qHs8pHs8pPs8qHs8pPXmj27n08XWyC6hDPKt4PKd4PKf4PKt4PKc05MNLnNvMSLrXzM5Pdh11gWcVj+cUj+cUn2cVj+dUt/h9up3b/OyT7ALqEM8qHs8pHs8pPs8qHs+pDvFGt3POOeecczXMG93OOeecc87VMG90O7f5UbILqEM8q3g8p3g8p/g8q3g8pzrEG93OpRFJmZJur2Kxu2ulmBTnWcXjOcXjOcXnWcXjOaUfv3uJc2lG0udmtmey66gLPKt4PKd4PKf4PKt4PKf04vfpdi79fCPpVeAFYHXJRDMbnrySUpZnFY/nFI/nFJ9nFY/nlEa80e1c+mkALAYOSphmgL9Jb8yzisdzisdzis+zisdzSiM+vMQ555xzzrka5hdSOpdmJHWX9J6kieFxL0nXJruuVORZxeM5xeM5xedZxeM5pRdvdDuXfh4GrgIKAMxsPHBiUitKXZ5VPJ5TPJ5TfJ5VPJ5TGvFGt3Ppp6GZfVlmWmFSKkl9nlU8nlM8nlN8nlU8nlMa8Ua3c+lnkaSuRBfbIOk4YF5yS0pZnlU8nlM8nlN8nlU8nlMa8QspnUszkrYBHgL2BpYCPwOnmNn0ZNaVijyreDyneDyn+DyreDyn9OKNbufSlKRGQIaZrUx2LanOs4rHc4rHc4rPs4rHc0oPPrzEuTQj6UJJTYE1wF2SxkoakOy6UpFnFY/nFI/nFJ9nFY/nlF680e1c+jnDzFYAA4CWwO+AW5JbUsryrOLxnOLxnOLzrOLxnNKIN7qdSz8K/x4BPGVmkxKmudI8q3g8p3g8p/g8q3g8pzTijW7n0s8YSW8TvUmPlNQEKE5yTanKs4rHc4rHc4rPs4rHc0ojfiGlc2lGUgbQG5hmZssktQTahy9VcAk8q3g8p3g8p/g8q3g8p/SSlewCnHOb3L7h316SfwpZBc8qHs8pHs8pPs8qHs8pjXhPt3NpRtJrCQ8bALsDY8zsoCSVlLI8q3g8p3g8p/g8q3g8p/TiPd3OpRkz+03iY0lbA/9KTjWpzbOKx3OKx3OKz7OKx3NKL34hpXPpbzawQ7KLqCM8q3g8p3g8p/g8q3g8pzrMe7qdSzOS7gVKxo2VXIQzNmkFpTDPKh7PKR7PKT7PKh7PKb34mG7n0oykUxMeFgLTzeyTZNWTyjyreDyneDyn+DyreDyn9OKNbuecc84552qYDy9xLk1I+isbPoaszIdmNqqm60llnlU8nlM8nlN8nlU8nlN68ka3c+ljeszlltVgDXXF9JjLLavBGuqC6TGXW1aDNdQF02Mut6wGa6grpsdcblkN1lAXTI+53LIarMFtYj68xDnnnHPOuRrmPd3OpRlJ15c33cxurO1aUp1nFY/nFI/nFJ9nFY/nlF680e1c+lmd8P8GwCBgSpJqSXWeVTyeUzyeU3yeVTyeUxrx4SXOpTlJ9YGRZnZAsmtJdZ5VPJ5TPJ5TfJ5VPJ5T3ebfSOlc+msIdEh2EXWEZxWP5xSP5xSfZxWP51SH+fAS59KMpAlsuNVUJrAl4OP/yuFZxeM5xeM5xedZxeM5pRcfXuJcmpHUKeFhIZBrZoXJqieVeVbxeE7xeE7xeVbxeE7pxRvdzqUhSbsC+xL1kHxsZt8kuaSU5VnF4znF4znF51nF4zmlDx/T7VyaCbeYehJoCbQCnpB0bXKrSk2eVTyeUzyeU3yeVTyeU3rxnm7n0oyk74GdzSw/PM4BxpnZdsmtLPV4VvF4TvF4TvF5VvF4TunFe7qdSz9zie7nWqI+MCdJtaQ6zyoezykezyk+zyoezymNeE+3c2lG0stAX+AdojGA/YEvgdkAZnZB0opLMZ5VPJ5TPJ5TfJ5VPJ5TevFGt3NpRtKplc03sydrq5ZU51nF4znF4znF51nF4zmlF290O5dmJDUC8s2sKDzOBOqb2ZrkVpZ6PKt4PKd4PKf4PKt4PKf04mO6nUs/7wE5CY9zgHeTVEuq86zi8Zzi8Zzi86zi8ZzSiDe6nUs/DcxsVcmD8P+GSawnlXlW8XhO8XhO8XlW8XhOacQb3c6ln9XhyxQAkLQbkJfEelKZZxWP5xSP5xSfZxWP55RGfEy3c2lGUl/gOaJbTQloA5xgZmOSWlgK8qzi8Zzi8Zzi86zi8ZzSize6nUtDkrKBki9P+N7MCpJZTyrzrOLxnOLxnOLzrOLxnNKHN7qd2wxIamNm85NdR13gWcXjOcXjOcXnWcXjOdVdPqbbuc3Do8kuoA7xrOLxnOLxnOLzrOLxnOoo7+l2zjnnnHOuhmUluwDn3KYnqQWwNQmvcTMbm7yKUpdnFY/nFI/nFJ9nFY/nlD680e1cmpH0d+A04Ceg5KMsAw5KVk2pyrOKx3OKx3OKz7OKx3NKLz68xLk0I+l7oKeZrUt2LanOs4rHc4rHc4rPs4rHc0ovfiGlc+lnItA82UXUEZ5VPJ5TPJ5TfJ5VPJ5TGvGebufSjKQ+wCtEb9ZrS6ab2ZFJKypFeVbxeE7xeE7xeVbxeE7pxcd0O5d+ngRuBSYAxUmuJdV5VvF4TvF4TvF5VvF4TmnEe7qdSzOSvjKzvsmuoy7wrOLxnOLxnOLzrOLxnNKLN7qdSzOS7iT6GPJVSn8c6beYKsOzisdzisdzis+zisdzSi/e6HYuzUj6oJzJZmZ+i6kyPKt4PKd4PKf4PKt4PKf04o1u55xzzjnnapjfMtC5NCOptaRHJb0ZHveQ9Idk15WKPKt4PKd4PKf4PKt4PKf04o1u59LPE8BIoF14/ANwUbKKSXFP4FnF8QSeUxxP4DnF9QSeVRxP4DmlDW90O5d+WpnZ/wi3lzKzQqAouSWlLM8qHs8pHs8pPs8qHs8pjXij27n0s1pSS8AAJO0JLE9uSSnLs4rHc4rHc4rPs4rHc0oj/uU4zqWfS4huL9VV0ifAlsDxyS0pZXlW8XhO8XhO8XlW8XhOacTvXuJcmpFUn+jjx+0AAd8DGWa2ttIVN0OeVTyeUzyeU3yeVTyeU3rxRrdzaUbSWDPbtappzrOKy3OKx3OKz7OKx3NKLz68xLk0IakN0B7IkbQLUa8IQFOgYdIKS0GeVTyeUzyeU3yeVTyeU3ryRrdz6eNQ4DSgA3AHG96kVwJXJ6mmVOVZxeM5xeM5xedZxeM5pSEfXuJcmpF0rJm9mOw66gLPKh7PKR7PKT7PKh7PKb34LQOdSz8dJDVV5BFJYyUNSHZRKcqzisdzisdzis+zisdzSiPe6HYu/ZxhZiuAAUBL4HfALcktKWV5VvF4TvF4TvF5VvF4TmnEG93OpZ+SsX9HAE+Z2aSEaa40zyoezykezyk+zyoezymNeKPbufQzRtLbRG/SIyU1IXyFsNuIZxWP5xSP5xSfZxWP55RG/EJK59KMpAygNzDNzJaFrxBub2bjk1tZ6vGs4vGc4vGc4vOs4vGc0ov3dDuXfl4A2gIrAMxssb9BV8izisdzisdzis+zisdzSiPe6HYu/TwAnAT8KOkWSdslu6AU5lnF4znF4znF51nF4zmlER9e4lyaktQMGAJcA8wCHgb+a2YFSS0sBXlW8XhO8XhO8XlW8XhO6cEb3c6loTDu7xSi20vNBYYC+wI9zeyAJJaWcjyreDyneDyn+DyreDyn9OGNbufSjKSXgO2Ap4EnzGxewryvzaxP0opLMZ5VPJ5TPJ5TfJ5VPJ5TevFGt3NpRtJvgbfMbIWka4Fdgf8zs7FJLi3leFbxeE7xeE7xeVbxeE7pxS+kdC79XBveoPcFDgEeJboYx23Ms4rHc4rHc4rPs4rHc0oj3uh2Lv0UhX8HAg+Z2QigXhLrSWWeVTyeUzyeU3yeVTyeUxrxRrdz6WeOpP8AJwBvSKqPv9Yr4lnF4znF4znF51nF4zmlER/T7VyakdQQOAyYYGY/SmpLdJX720kuLeV4VvF4TvF4TvF5VvF4TunFG93OOeecc87VMP+IwjnnnHPOuRrmjW7nnHPOOedqmDe6nXPOOeecq2He6HbOOeecc66GeaPbOeecc865Gvb/CMMMiMlPVecAAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 720x720 with 2 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + } + ], + "source": [ + "# prepare heatmap\n", + "df_heatmap = pd.concat([df_preprocessed.sample(10),df_preprocessed.tail(n_tail_anomalous).sample(10), df_cluster_centers])\n", + "df_heatmap = df_heatmap.round(2)\n", + "\n", + "# get scores\n", + "heatmap_scores = np.sum(cdist(df_heatmap, models[dim]['model'].cluster_centers_, metric='euclidean'), axis=1)\n", + "heatmap_bits = [1 if score >= dimension_anomaly_score_threshold else 0 for score in heatmap_scores]\n", + "\n", + "# add anomaly score to index\n", + "heatmap_index_inputs = list(zip(range(1, len(df_heatmap)+1), df_heatmap.index, heatmap_scores, heatmap_bits))\n", + "df_heatmap.index = [f'{x[0]}. t={x[1]} (AS={round(x[2]*100)}%, AB={x[3]})' for x in heatmap_index_inputs]\n", + "\n", + "fig, ax = plt.subplots(figsize=(10,10))\n", + "sns.heatmap(df_heatmap, annot=True, ax=ax, cmap='RdYlBu')" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "You should see from the above heatmap that the top 10 rows all tend to have lower anomaly scores (AS) and anomaly bits (AB) that are 0. While its the opposite for rows 11-20.\n", + "\n", + "The final two rows are the cluster centroids themselve which should look more similar to the first 10 rows, fairly different to rows 11-20. And of course, you would expect that each cluster centroid itself has a low anomaly score and non-anomalous anomaly bit." + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "Another way to present this visually is via line or bar plots. Below we just plot each of the rows above as a line. First all at the same time on one plot and then each one individually as a bar plot." + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "In the plot below the dotted lines correspond to the feature vectors sampled from the yellow anomalous period and as such we expect them to look very different to the solid lines (sampled from the normal period) and the solid circled lines which correspond to the two centroids. (Admittedly its not the clearest of plots to read since the normal lines all bunch together)." + ] + }, + { + "cell_type": "code", + "execution_count": 16, + "metadata": {}, + "outputs": [ + { + "data": { + "text/plain": [ + "<AxesSubplot:>" + ] + }, + "execution_count": 16, + "metadata": {}, + "output_type": "execute_result" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAnYAAAFMCAYAAABGXfGvAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAD6HklEQVR4nOzdd3zT1frA8c83SZPuvRctlFX23qCAIAgq7oUD3Bv1XvXqHfpz3Ot14eKiKIJbQRRxAbKHUsqmFChddO82adLM8/sjUEVGS9s0Hef9evVVbb75fp+UNHlyznmeowghkCRJkiRJkto/lbsDkCRJkiRJklqGTOwkSZIkSZI6CJnYSZIkSZIkdRAysZMkSZIkSeogZGInSZIkSZLUQcjETpIkSZIkqYPQuDuAPwsNDRUJCQnuDkOSJEmSJKlBqampZUKIMHfHcVKbS+wSEhLYuXOnu8OQJEmSJElqkKIoOe6O4Y/kVKwkSZIkSVIHIRM7SZIkSZKkDkImdpIkSZIkSR2ETOwkSZIkSZI6CJnYSZIkSZIkdRAysZMkSZIkSeogZGInSZIkSZLUQcjETpIkSZIkqYOQiZ0kSZIkSVIHIRM7SZIkSZKkDkImdpIkSZLUHJU5sPJBMFa4OxJJkomdJEmSJDWLxQC7lsCO99wdiSTJxE6SJEmSmuzYerBboMc0+G0BmA3ujkjq5GRiJ0mSJElNIQT88Bfn17hHwFTpHLmTJDeSiZ0kSZIkNUXWJig/CkPnQtxwSBgH294Em9ndkUmdmEzsJEmSJKkpdr4PXkHQZ5bz/8c/Br1mgNXk3rikTk3j6gsoihIILAL6AgKYI4TY7urrSpIkSZLL1BTCoVUw8h7w8HT+rOsFzi9JciOXJ3bAfOAnIcRViqJoAe9WuKYkSZIkuU7xQdD6wtA5p/5cCMjZBghIGOuW0KTOzaWJnaIoAcB44FYAIYQFsLjympIkSZLkct0nw1+OgkZ36s+FgO8eAo0n3L0ZFMU98UmdlqvX2CUCpcBiRVF2K4qySFEUHxdfU5IkSZJcx1TpTOD+nNQBqFQwdh4U74eMta0fm9TpuTqx0wCDgQVCiEFALfDEnw9SFOVORVF2Koqys7S01MUhSZIkSVIzLJsDH19x9tv7XQ3+sbD5ldaLSZJOcHVilwfkCSF+O/H/y3AmeqcQQrwrhBgqhBgaFhbm4pAkSZIkqYnKj8GxdRA38uzHaLQw+gHI3X5ivZ0ktR6XJnZCiCLguKIoPU/8aBKQ5sprSpIkSZLLpC4GRQ2Dbz73cYNvhrBeoC9qnbgk6YTWqIp9APjkREVsJnBbK1xTkiRJklqW1QS7P4Zel4B/1LmP1XrDvb/K4gmp1bk8sRNC7AGGuvo6kiRJkuRSh75zFk4Mm9u44xUFHHbIS4H4c0zdSlILkjtPSJIkSVJjJF8G134CiRMaf5+tr8Piac61eZLUCmRiJ0mSJEmNodFB7xnnN7068CZQeTgTPElqBTKxkyRJkqSGbPg3bH/7/O/nFwGDZ8Oez6A6v+XjkqQ/kYmdJEmSJJ1LXQ1sfQOKm9jUYfSDIBxNSwwl6TzJxE6SJEmSzmXfF2CthWFzGj72TIK6OJsW52wBh6NlY5OkP2mNdieSJEmS1D4JASnvQ9RAiBnS9PNMfwm0vs4txyTJheQzTJIkSZLOJmcblB5qfIuTs/EMAJUazAawGFsmNkk6A5nYSZIkSdLZeHg525z0vbL55zKUwOv9YOf7zT+XJJ2FTOwkSZIk6WxiBsM1S0Hr0/xz+YZDZF/Y9hbYzM0/nySdgUzsJEmSJOlMsrdAZU7LnnPco2Aogj2ftux5JekEmdhJkiRJ0p857LDiHlh5f8ueN3ECRA92Niy221r23JKETOwkSZIk6XQZa6E6F4Y2scXJ2SiKc9SuMhsyN7TsuSUJ2e5EkiRJkk6X8j74RkCvGS1/7p7T4fZfIHZoy59b6vTkiJ0kSZIk/VFlDhxdDYNvBrVHy59fpfo9qZMNi6UWJhM7SZIkSfqjvBTQ6GDIra69zsaXYOmlzibIktRCZGInSZIkSX/U7yp47AgExLr2Ol5BkL3ZWX0rSS1EJnaSJEmSdJLV5PzuGeD6aw26CXzCYcurrr+W1GnIxE6SJEmSTvr4Smebk9bg4QWj7oVj66Bgd+tcU+rwZGInSZIkSQDFaZCzFcJ7td41h84FXQBslqN2UsuQ7U4kSZIkCWDnB6DWwcCbWu+anv5w+TsQ3rv1ril1aDKxkyRJkiSzAfZ+Dn0uB5+Q1r12bxf0ypM6LTkVK0mSJEn7vwKL3jk16g7lx+CLm6DquHuuL3UYcsROkiRJkvpc7uxdFzfcPddXa+Hwj+AfA9P+454YpA5BjthJkiRJklcQDLzBuZerOwTGQf9rIXUJ1Ja5JwapQ5CJnSRJktS5bfov7PvK3VHAmIfBVge/LnB3JFI7JhM7SZIkqfMyVsDG/0LudndHAmE9oPdM2PEe1NW4OxqpnZJr7CRJkqTOa/fHYDfDMDcVTfzZuEchrBX76EkdjkzsJEmSpM7J4XD2rosbCRF93B2NU/RA55ckNZGcipUkSZI6p8z1UJnVdkbrThICDq2CQ9+5OxKpHZIjdpIkSVLnpFJDt4mQfJm7Iznd1vlgKIIeF4Paw93RSO2IHLGTJEmSOqeuF8DsFc7+dW2JosC4R6AqFw4sd3c0Ujvj8sROUZRsRVH2K4qyR1GUna6+niRJkiQ16HgKmCrdHcXZdZ8K4cmw5TXnWkBJaqTWGrG7UAgxUAgxtJWuJ0mSJElnZrc6t+/65j53R3J2KhWMfQRK0+HwD+6ORmpH5FSsJEmS1Lkc/sG5fm3wbHdHcm59ZkHiBEC4OxKpHWmNxE4AqxVFSVUU5c5WuJ4kSZIknV3K+xAQB92nuDuSc1Nr4JaVzqbF0nmpS0uj+KX/Ytfr3R1Kq2uNxG6sEGIwMA24T1GU8X8+QFGUOxVF2akoys7S0tJWCEmSJEnqlMqOQtZGGHKLsyq2PbDWOdufSI1WtuB/VC/vnIUnLk/shBD5J76XACuA4Wc45l0hxFAhxNCwsDBXhyRJkiR1VsfWg8oDBt3s7kgaL3UxfHEj5KW6O5J2I/LZZ4h54w3Ufn7uDqXVuTSxUxTFR1EUv5P/DUwBDrjympIkSZJ0ViPuhHkHwC/C3ZE03qCbwDMAtrzq7kjaPCEEQgg0QUH4jDhtHKlTcPWIXQSwRVGUvcAO4HshxE8uvqYkSZIknc5hd373i3RvHOdL5wfD74L0VVCS7u5o2jTDunVkX30N1qIid4fiNi5N7IQQmUKIASe++gghnnfl9SRJkiTprBZPhzX/dHcUTTPibvDwhq2vuzuSNkvY7ZS89hoOgwFNaKi7w3Eb2e5EkiRJ6vgKdsPxX8E/2t2RNI1PCAy5FSoywW5zdzRtUvV332HJOEbYww+haDrvjqmd95FLkiRJnUfK+84RrwHXuTuSppv8L1BrnVuOSadwWCyUvfEmnn364DeljbexcTE5YidJkiR1bKYq2L8M+l3tLEJorzQ6Z1JXWw7GCndH06ZUr/gGa0EBYfPmoag6d2ojR+wkSZKkjm3v52AzwbC57o6k+UxVMH+A87Fc9Iy7o2kzAmZdjtrfD58xo90ditvJxE6SJEnq2Hpd4mxGHDXA3ZE0n1cgdL/IObU8dp7z/zs5IQQqrRb/adPcHUqb0LnHKyVJkqSOLzAOht/h7ihazth5YNFDynvujsTtbJWVZF16KbXbtrk7lDZDJnaSJElSx7XldTi2zt1RtKyo/s59bn9dABaju6Nxq/J338N8LBNNeLi7Q2kzZGInSZIkdUz6Ilj3f5Dxi7sjaXljHwFjOWRucHckbmMtLKTyk08IuOwydElJ7g6nzZBr7CRJkqSOaddH4LDB0DnujqTldRkFD+6G4K7ujsRtSt9+G4Qg7P773B1KmyJH7CRJkqSOx2GH1A+h6wUQ0s3d0bjGyaTOWufeONzAcvw41V+vIPD66/CIiXF3OG2KTOwkSZKkjufIz1CTB8Nud3ckrrXuOXh3wu/74HYSHrGxxL75BqF33eXuUNocmdhJkiRJHY/dAnEjoUcHb4ERngyl6ZC+yt2RtBohBIqi4DdpEpqQEHeH0+bIxE6SJEnqePpcDnN/BnUHX0qefBkEd4PNr4AQ7o6mVeQ/+CDlHyx2dxhtlkzsJEmSpI6laD/YzO6OonWo1DDmISjc2/HaupxB7fbt6NesRVHL9OVs5G9GkiRJ6jisdbD0MvjuYXdH0noGXAd+0bDtTXdH4lJCCEpefQ1NVBSB113n7nDarA4+Ri1JkiR1KmnfOvu79b/G3ZG0Ho0Ornq/w7c+0a9ZQ93+/UQ9/zwqnc7d4bRZMrGTJEmSOo6d7zvXnCVOcHckravLaHdH4FJCCErfeANtt24EXHapu8Np02RiJ0mSJHUMRQfg+G8w5XlQdcKVRmUZ8N2DMP2/ENHH3dG0KEVRiHnpJRwmE4pGpi7n0gmf+ZIkSVKHdGglaDxh4A3ujsQ9vIOdRRRbXnN3JC7hmZyM95Ah7g6jzZOJnSRJktQxXPAk3L3VmeB0Rt7BMPQ2OLAcKrLcHU2LqVi6lILHH8dhsbg7lHZBJnaSJElS+ycEKAqEdvLN4EfeByoNbJ3v7khahN1goOydBdhKS1Fpte4Op12QiZ0kSZLUvgkBi6fBtrfcHYn7+UfBwBthzyegL3J3NM1WsfhD7FVVhM2b5+5Q2g25AlGSJElq347/BrnbYcD17o6kbRjzEIT2AJ2fuyNpFlt5ORWLF+M3dSpe/fq5O5x2QyZ2kiRJUvuWsgh0AdDvKndH0jYEJ8Koe90dRbOVv/seDrOZsIcecnco7YpM7CRJkqT2q7bM2ZR4yG2g9XF3NG3L7k/AbnEWVLRDwXPm4NknGV3XRHeH0q7INXaSJElS+7X7oxPJyxx3R9L2HFoJvzwLllp3R9IkHhHhBFwqmxGfL5nYSZIkSe1X0kUw+RkI7+XuSNqesY+AqQJSl7g7kvNiPnqUnFtuxZKT4+5Q2iWZ2EmSJEntV2RfGPuwu6Nom+JHQJexsO1NsJndHU2jlcyfT93Bg6j8/d0dSrskEztJkiSpffp1ARTsdncUbdu4eaAvgH1fuDuSRjHt3Yth7S8Ez7kNTVCQu8Npl2RiJ0mSJLU/Vcfh57/Boe/cHUnb1m0S9L8O/KLcHUmDhBCUvPIq6uBgQm65xd3htFuyKlaSJElqf1I/dH4fcqs7o2j7FAWuWOjuKBqldts2jDt2EPHUU6h8ZIVzU7XKiJ2iKGpFUXYrirKqNa4nSZIkdWA2C+xaAt2nQmC8u6NpH0xVkPK+c5eONsp70CAi/vYkgdde4+5Q2rXWmop9CDjUSteSJEmSOrL076C2FIbNdXck7cfhH+D7R+DoGndHclYqb2+Cb75Z7gnbTC5P7BRFiQUuARa5+lqSJElSJ2CqgqiBzvVjUuP0vQr8Y2HLq+6O5DTCZiP3rrswbNrk7lA6hNYYsXsd+CvgONsBiqLcqSjKTkVRdpaWlrZCSJIkSVK7NWwu3LkBVLL+r9E0WhjzoHNP3Zxt7o7mFFUrVlC7cRPCZnN3KB2CS/8qFEWZAZQIIVLPdZwQ4l0hxFAhxNCwsDBXhiRJkiS1Z+XHnOvEFMXdkbQ/g2aDdyhsbjujdo66OsreehuvgQPxvfBCd4fTIbj6484Y4FJFUbKBz4GJiqJ87OJrSpIkSR2RpRbevQB+fsrdkbRPWm8YeQ8g2kzD4spPPsVWXEzYI/NQZLLeIlza7kQI8STwJICiKBcAjwkhbnLlNSVJkqQOav8yMNdA75nujqT9GvdomxnttOv1lL/7Lj7jxuEzfLi7w+kwZB87SZIkqe0TAna+D+HJED/S3dG0XyeTuqpcUNQQEOO2UFQ+PkT8/e/ouie5LYaOqNVWngohNgghZrTW9SRJkqQOJH8XFO51Fk60kRGndstsgHdGwcZ/uzUMRaUiYMYlePbs6dY4OhpZUiRJkiS1ffs+B60v9L/W3ZG0fzpfGHAd7PkMqvPdEkLJ669T/sFit1y7o5OJnSRJktT2TX0Bbv0edH7ujqRjGP0gCAdsf7vVL205fpzy9z/AkpPT6tfuDGRiJ0mSJLV9ag+IHujuKDqOoC7Q72pIXQy15a166dI330RRqQi9995WvW5nIRM7SZLOyF5TQ+2vv7o7DKmzczhgyUzntKHUssbOA4cNcluvYXHd4SPUfLeK4Jtn4xER3mrX7UxkYidJ0hmZ9u0n99bbqFq2zN2hSJ1Z1kbI2gSKfLtqceG94NHDrdo+pvT111H5+hJy++2tds3ORrY7kSTpjHxGjsB75EgKn3kWj/h42WdKco+d74NXMCRf5u5IOibvYOd3Y8Xv/+1CIXfcgf8ll6AOCHD5tTor+RFIkqRTGDZvpmzhu6BSEfvGfLSxseQ/+BCW48fdHZrU2dQUQPoPMOgm8PB0dzQd19pnnO1PWmE3Cu/BgwiYcYnLr9OZycROkqR61qIiCv76ODWrViEsFtT+/sQteAchBMfvuQdhsbg7RKkz2bUUhB2G3ubuSDq2rhPAUAR7PnXZJQybN1P4r39h1+tddg3JSSZ2kiQBIGw28h99DIfZTMz811F5OkdItAkJxM6fT+hdd6FotW6OUupUuoyBC56E4K7ujqRjS5wA0YNh6+tgt7X46YXDQckrr1K7dRsqna7Fzy+dSiZ2kiQBUPrGm5hSU4l65l/oup76RuozcgQBM50LrK357mloKnVCiePggifcHUXHpyjOPWQrsyHtmxY/fc0PP2JOTyfswQflh8NWIBM7SZKw5udTvngxgVdfVZ/AnYlp716OXTxNVspKrrdzMVRkuTuKzqPndAjrBSmLWvS0wmKhdP58dD174n/J9BY9t3RmsipWkiQ8YmJI+PgjdA3s2ejZpw/ew4dT+MyzaLt0wXvYsFaKUOpUyo/Bqofhwqdhwl/cHU3noFLBVR9AQGyLnrZq+XKsx48T+78FKCo5ltQa5G9ZkjoxYbNh3LkTAK8BA+rX1Z2NotEQ89qraGNjyXvgQVkpK7nGzg9ApYHBN7s7ks4log94BoAQzq8W4DNuHGEPPYjvhAktcj6pYTKxk6ROrPSNN8m5aTZ1hw41+j5/rpS1G2pdGKHU6VhNsPtj6DUD/CLcHU3nU5YBC8ZAztYWOZ02NpbQe+5BUZQWOZ/UMJnYSVInZdi8mfJ33yXw6qvx7N37vO57slLWb+IkVN5eLopQ6pQOroC6Khg2192RdE4BMVBbAptfbdZp7NXV5D30MObMzBYKTGosmdhJUid0sl+drkcPIp76W5PO4TNyBOGPzENRqWRvKqnlVOdBZD9IGOfuSDonDy8YeS8c+wUKdjf5NOWLFqFfvRphtbZgcFJjyMROkjqZk/3qhNlMzOuvN7iuriGW3FyOTZ8uK2WlljHhr3DHBmcLDsk9hs0FXQBsea1Jd7cWl1Dx0cf4z5iBZwMFWVLLk4mdJHU2ajUBM2cQ+X/Pouua2OzTeURH49mzF4XPPIsxJaUFApQ6LX2x87taNmxwK88AGH47pK2EsqPnffeyBe8gbDbCHnzABcFJDZGJnSR1IsJqRVEUgq67joBLWma/RkWjIebVV2SlrNQ8ddXwxiDY/Iq7I5EARtwDl78DQQnndTdLTg5Vy5YTdM01aOPiXBObdE6dMrE7XmFEXyfn/aXOxVpUxLGLp6HfsKHFz316payhxa8hdXB7vwBrLXSb6O5IJADfMBh4A6g9zutu6pAQQu+8k9B77nZRYFJDOl1iZ3cIbl+yk1nvbCOrTLZpkDoHYbOR/8ij2Cor0cZ3Ob/7NrKflbNS9nW0XRKaEKHUqQnh3PEgejBED3J3NNIf/bYQNr7U6MPVvr6EPfgAmrAwFwYlnUunS+zUKoV/XdqHcoOZy97awqYjpe4OSZJcrnT+G5h27TqxD+y519VZ7Q6eW5XGocIahBDc8/EuXv75MHVWe4PX8Rk5kri330Lt6yur4aTGy9kKZYdli5O2qHCvs/VJbVmDhxa98AKGzZtbISjpXDpdYgcwqlsIK+8fS3SgF7cu3sGizZmNHpWQpPbGsHkz5e+9R+DVV59zH1iAcoOZmxb9xqItWWw8UorF7sBbp+at9RlMf2MzO7IqGnVNW2Ul2dddLytlpcbZtdS5YL/PFe6ORPqzMQ+DrQ5+XXDOw4wpKVQu/QjzkSOtE5d0Vp0ysQOIC/Zm+T2jmZIcyXf7CrHaZWIndUzGHSnoevZssF/dgfxqLn1rK3uOV/HatQO4e0I3dBo1r14zkKVzhmOxObhm4Xae/mZ/g2tU1X5+qAMDZaWs1DjTX4brvwCtt7sjkf4srAf0ngk73oO6mjMeIoSg5NXX0ISHE3Tjja0coPRnSlsbqRo6dKjYeWLvytbgcAj0ZhsBXh5Um6yYLHYiA5rX10uS2hpHbS0qH5+z3r47t5Lr3v2VEB8tC2cPpV9swGnHGC02Xll9hO/2FrB63ngCvbXnvKa9pobsa6/DXllJwldfygo5SWqvCnbDuxfA5H/B2Hmn3axfv568e+4l8plnCLr2mlYPz90URUkVQgx1dxwnddoRu5NUKoUAL2fVz5Nf7+PSt7awK7fSzVFJUvNVLFlCXVoawDmTOoA+0QHMHtmFlQ+MPWNSB+Ct1fD3Gcmse+wCAr212OwO/vNTOqV68xmPl5WyUoMcdvjkGjjys7sjkc4lepAzoYsddtpNwm6n9NXX0HbpQuAVs9wQnPRnnT6x+6OHJvXA00PNdQt/5audsheX1H4ZNm2i+MV/n3ONW5XRwl+X7aWi1oJWo+LpGcmE+uoaPLevztk8dm9eNe9vzmLyqxtZlpp3xnWqJytlFbUGR3V10x+Q1DEdXQNHf3au4ZLatsn/goSxZ7wp+JabCX/icRSP82uNIrlGp5+K/bPKWgv3f7aLrRnl3DYmgaem90ajlvmv1H5Yi4rIunwWmogIEr74/Ixbhh0u0nPnRzspqDKxcPYQJvaKaNK1Mkr0PLF8PztzKhnXPZQXZvUjLvj0dVLCbkdRqxFCoMitoqSTPrkaCvfBvAPn3S9NcgN9EaR+COMelf9efyCnYtu4IB8tS24bzm1jEvhhfyGVRtmyQWo/TvarExYLMa+9dsak7qcDhcx6ZytGi53P7xzV5KQOICncjy/vGsX/XdaHXTmV3P/prjOO3ClqNQ6zmYK//FVWykpOldnOEbsht8gkob0o2A0bXoQDywGoWvENFUs/Qjgcbg5M+iO5Id8ZaNQq/jmzDw9M7E6wjxa7Q5BXaaRLyLnXKUmSu1V++SWmXbuIfvnlM/arW5aax2Nf7WVgXCALZw8hwr/5hUIqlcLsUQlM6h1BTZ1zyzKD2cbxCiO9o/zrj1PUauyVlRQ+8yzaLl3wHnb6eh2pE9m5GBQVDL7F3ZFIjdV9KoT3gS2v4eh6CSWvvIKua1eCZt/k7sikP3DpiJ2iKJ6KouxQFGWvoigHFUV5xpXXa2nBPs6qv7fWZTB9/mZWHyxyc0SSdG5BV19NzBvzCZhx5n1gL+wZxl0TuvL5nSNbJKn7o+hAL3pFOhO5N9cdZeabW05pbKxoNMS89qrcU1ZyihkMYx+GgBh3RyI1lkrlLKIoTafitX9gLysj/JF5cnlFG+PqqVgzMFEIMQAYCFysKMpIF1+zxV07LI6kcF/u/CiVN345isPRttYlSpK1uARbRQWKhwf+U6acctuxUgOPL9uH1e4gxFfHk9N64+mhdmk8d4/vxqUDo+sbG6dkOxsby0pZqV7yZTDpH+6OQjpffWZh8+pC+bKf8Z00Ca+BA90dkfQnLk3shNPJV26PE1/tLiuKDPDki7tGccWgGF5dc4T7Pt1Frdnm7rAkCTixrm7ePHJumo2wnfq8XJdezOVvbWXNoWJyyo2tFlOQj5ZXrxnIkjnDMVsdXP2/7Xy0PRv4vVLWXlGJJSu71WKS2pB9X4KxcbuYSG2MWkN5ySAcVkH4fXe6OxrpDFxePKEoilpRlD1ACbBGCPGbq6/pCp4eal65ZgBPX9KbDYdLySqrdXdIkgRA6fz5mHbtIvTee1E0zmWzQgjeXp/B3CU7iQ/x5rsHxpIU7tvqsU3oEcbqeeO5Y1wi43s4NwU32+z4jBxJ0to1ePXr2+oxSW5WfBC+vgN2f+zuSKQm8r36HsIeehhdcn93hyKdQau1O1EUJRBYATwghDjwp9vuBO4EiI+PH5KTk9MqMTVVmcFc3+8rt9xIfIjcBkdyD8PGjRy/624Cr72WqGf+Vf/zZ79L44OtWVw2MJp/X9EfL61rp14bSwjB7Ut24qVV88+ZfQj11VL+3iI0IcEEXnmlu8OTWsP3j8Kuj+DRdPAOdnc0UnMUHwSVh3PbsU6s07Y7EUJUAeuBi89w27tCiKFCiKFhYWGtFVKTnUzqftxfyMRXNrB0e/YZWzxIkitZCwspePwJdL16EfHkE6fcdvXQWJ6+pDevXzuwzSR1AA4BA+ICWX2wmMmvbmT5zlyMv/1G4b+ekXvKdgZmPez9AvpeIZO6dsicmUXxi//GXl0N1jr48BL4pV3VRHYKrq6KDTsxUoeiKF7ARUC6K6/ZmsZ2D2VCjzD+8e1B/rZiPxab7OUjtR7F0xPvESOIee1VVJ6ebDlaxr9/dP559Y7y5/ZxXdtctZpapfDgpO788NBYuof78tjyAzw7+AZU0THkPfgQlrw8d4coudK+L8Gih6Fz3R2J1ASlb7xB5VdfOdfyenjCsDsgfRWUdJi39Q7B1SN2UcB6RVH2ASk419itcvE1W42fpwfv3jyU+y7sxmc7jnPDe7+edd9MSWpJQgg0QUHEzn8dbUICizZncvMHv7EuvRh9Xdtvqv3HxsbHTCpC5r+BcDjIk5WyHVtpOkT2h9g2M2slNZLpwEH0P/1EyK23oAkJcf5wxN3g4Q1bXnNvcNIpXF0Vu08IMUgI0V8I0VcI8awrr+cOapXCX6b24s3rB3GwoIbfssrdHZLUwRk2biTnptnYysups9p55Mu9PPf9IaYkR/L1vWPw82wfXfxPNjZeM288ob26E/Xqq9Rm5XDk543uDk1ylen/hbmroY2NJEsNK33tNdSBgQTfdtvvP/QJgSG3wv6voLJtr43vTOSWYi1k5oBoNv7lAmb0jwYgr7L1WktIncfJdXWO2loUHx9uXbyDFbvzefSiHrxz42B8de1vM5mTezEXJ/Xj4Zn/YGaqwiurf29sLHUQdTXO7x5e7o1DOm+1v/5G7dathNx1F2o/v1NvHHU/6PygcK97gpNO02pVsY01dOhQsXPnTneH0SyHCmu47O2tzB2byGNTeqJWyU+nUvMJq5Wcm2/BfPgwiV8vR5uQwM8Hi1ArCpOTm77fa1tSUWvhue/TyPthDd10dq548k6GJchF9u1ebTm83g8ufsE5wiO1K5bsbMrf/4CIp59CpdOdfoC1zrnmrpPqtFWxnUm3MF+uGhLLgg3HuH1JCjXtYM2T1PaVzp+PafduMm5+kGXFzj/dqX0iO0xSB85t/F65egB/sxzkhs0f88HbX8udXjqCPR+DtRbiRrg7EqkJtAkJRP3fs2dO6sCZ1AkBFVmtG5h0RjKxcwGtRsULs/rx3OV92Xy0jMvf3kpmqVwQLjWdw2ikZs1aDg+/iPuKQll/uKTDtthRFIV+C+bjGR/Hg5sWYcvPQ19nZX16ibtDk5rC4YCdiyF+NIT3dnc00nkQdjtFL7yAObMRCdsvz8DC8WCqcnlc0rnJxM6FbhrZhU9uH0GV0cqK3fnuDkdqx8psKv4x7S/8JWIi913Yjf/dNKTNtTJpSeqAALr8bwEq4Pg99/DR2jRu+zCF+z/dRZlBVp63K5nroDILhskWJ+1N9bcrqVz6EeajRxs+uM8sMNdAyiLXByadk1xj1wqKa+oI9dWhVikUVdcR4a/r0G/KUssRViuF7y/mutI4Si0KL189gEv6R7k7rFZT++uv5M69ndAnnuCz6BG8tS4Db52apy9J5srBMfLvqD34/EY4/hvMOwias0zlSW2Ow2Lh2MUXowkOIeGrLxv3t/bxVVCwGx7eD9rOsyOTXGPXCUX4e6JWKVTUWrj0rS3M+2KPrPiTGqX0jTeofv01Hg2p5ut7R3eqpA7AZ+RIEr9eTuhNN9Y3Nk4K8+Wxr/byyuoj7g5PaoxpL8EV78mkrp2p+vxzbAWFhD8yr/EfoMY9AsYy2P2Ra4OTzkkmdq0oyNuDW0Yn8O3eAq5ZuJ3CapO7Q5LaKKvdwbsvfUT5e4sIvO5aLrv3OnpH+bs7LLfw7NkTRVEwZ2QQnrqFL+8axbOX9eGaoXEAVJus2GWBRdsVEAPdLnR3FNJ5sBtqKVvwP7xHjcRn9OjG37HLaIgf5dxhRHIbmdi1IkVRuO/CJN6bPZTM0lpmvrmV1JwKd4cltTHlBjP3vf4jAz56nZqYRCKefNLdIbUJpW+8Sf5fH6cudSc3j0ogPsQbIQSPfLGHKxZsI72oxt0hSn9kt8JXt0Lub+6ORDpfwkHAZZcRPm/e+d/3ivfg1u9bPiap0WRi5waTkyNYce9ofHRqFm7MdHc4UhtysKCaS9/ayoSV7+GjFgx6/52ztxjoZKL+71m0MafvKXvZoBjyKozMeGMLr6w+jNkmlzm0Cemr4OAKqKtydyTSeVL7+RHxxON49e9//ncOjHO2P7FbnRXRUquTxRNuVGW0oCgKAV4eVNZa8PXU4KGWuXZndbhIz2VvbyHIW8vCC8Poaq7Ed8IEd4fVpliys8m69jo8wsPo8tlnqH19AaistfB/36fx9a58uoX58L+bhtA9wq+Bs0ku9eEM5zZTD+0Bldrd0UiNVPHJJ+gSE89vCva0k2TCkstg6nOQfFnLBddGyeIJqV6gt5YALw9sdge3fpjCze/voLLW4u6wJDfpHu7Lw/38+Pa+MfQf2V8mdWegTUggdv7rmDOzKH/3vfqfB/loefWagSyZMxx/Lw/C/TpvF/w2ofQIZG+GobfKpK4dsRYUUPKfl6j+vplTqYFdQO0Bm191Ni6WWpVM7NoAjVrF7JFdSM2t5NK3t8i1Qp1ItdHKg5/t5niFEXtxERNfeQwWL3R3WG2az8iRxL+/iND77zvttgk9wvj6ntEEeDs/MN2+ZCe/HCp2Q5Sd3M4PQOUBg252dyTSeSh9+20Awu47/W/rvKjUMOYhKNwDx9Y1PzDpvMjEro24akgsX9w5ErPVwRXvbOOnA0XuDklysSPFei59ews/HijkYG45+fMeQdhsBF7W8acumstn5EhUWi32qioMGzeectvJ1gwlejPHK4zMXbKTBz7bLRsbt6bQJBh5D/iGuTsSqZHMx45RveIbgm64AY/o6OafcMB14BcFW15r/rmk8yITuzZkUHwQ3z0wlh4Rfry8+jBWu1x42lH9fLCIWW9vxWix8/mdoxi05nNMe/Y4CwQSEtwdXrtR8sqrHL//AYxnWJcbHejFdw+M5ZGLevDzgSImv7qR5al5HXYrtjZl2O0w5f/cHYV0Hkpfn4/Ky4uQu+5smRNqdDD6AeeUfP6uljmn1CiyeKINqrPaqai1EB3oRZ3Vjs0h8NVp3B2W1EJ+2F/IvZ/sYkBcIAtvGoLPru3k3XMvgddfR9Q//+nu8NoVe3U12ddeh726moSvvkQbG3vG444W63ni6/3o66ysemAcWo38TOsy6T9At4nOykipXRBCUPnxJyAEwTfPbrkTmw3OxK77VFB13L+5tlY8IRO7Nu6xr/ayP6+a924eSnxI59mipSMzWmws3JjJPRd0w9NDjWHzFioWf0DsggWytUkTnK1S9s8cDkGZwUy4vyf6Oivf7M7nhhFdUKvktmQtJj8V3psIl7ziHLWTpE6grSV2HTeF7iAuGxhNUU0dl769hW0ZZe4OR2qizFID936SSq3ZhrdWw7yLeuDp4awW9B03lrj335dJXRP9sVK25D//OetxKpVCuL9zFGnF7nz+/u1B2di4paV8AB4+0O8ad0ciNZIxJYWqZcsQNpvrLrL5Ffj+UdedXzqFTOzauHHdw/j2vjGE+eqY/cEOPtyaJdcItTPr00u47K2t/JpZQU65sf7nJa+9TtnCdxFCyM3sm8ln5EhiXnuVsAcfbNTxs0d2Yf51Azl+orHxq7KxcfOZKuHAcuh/NXh2zu3v2hshBMX//g9l7yxAuLKZsKnSWSldkeW6a0j1ZGLXDiSE+rDivjFM7BXOq2uOUCqr+9oFIQRvr89gzpIU4oK9WXn/GJKjnW94+g0bKF+4EGtRoUzqWoj/lClowsIQNhvG3bvPeayiKFw2MIa1j0zg0gHRvLEug3+tTGulSDuoPZ+BzQRD57o7EqmR9D+vpu7gQUIfeACVVuu6C428D1Qa2DrfddeQ6nXKNXa7amoJ0Kjp5t2+Fvc6HIKs8lq6hfkihKDaZCXQ24V/jFKzvPzzYd5an8HMAdG8dGV/vLTOqVdrQQFZs65AEx1NwueftckpWCEElZWVWCwWIiIi2lXyWTJ/PuWL3qfL4g/wHtq4ZS8bj5SSGOJDfIg3pXoznh4q/Dw9XBxpB/PFbNAXwu1r3R2J1AjCZiNz5qWgVtH1229R1C5uJP3dw7DnE3h4P/hFuvZaraytrbHrdImdEIJpqUc5aDBxZ1wY87pE4Ktpf53RF23OZNHmLBbOHsKAuEB3hyOdQV6lkZ8PFjNnTEJ9YiSsVnJm34z56FESly9rE61NbDYbJpMJPz8/HA4HS5YsoaioCLPZOTIcHh7OpEmT6Nmzp5sjbZzGVsqeze1LUjhYUMPzs/oysVeEi6LsgIRwTrl5B7s7EqkRqpYto/DpvxP71pv4TZ7s+gtWZMKbQ2DUfTDlOddfrxW1tcSu003FKorC0n6JXBkRxNu5JYz+7RBfFlXgaGMJbkNGdQtBrVK4euF2VuzOa/gOUqvYmlHG48v24XAIYoO8mTs28ZTRLmPqLkz797u1X11OTg7btm3j66+/5p133uGFF15g5cqVAKhUKnx9fenfvz8zZ85kxowZqFQqrFarM36jkdLSUrfE3VjqgABiF7yDsNvJu+ce7AbDed3/3guT8PPUMOdD2di40WxmUBSZ1LUjmqgoAi6/HN9Jk1rngsFdYeoL0OeK1rleJ9bpRuz+aFdNLU8fzWdXjZH3+iQwMzywVa7bUsoNZu79ZBe/ZVVw5/iuPH5xL9m6wU2EEHywNZsXfjhEtzAfPr9zFME+Z54mt+Tmoo2Pd2k8DoeDyspKiouL60ffpk2bBsDixYvJycnBz8+PyMhIIiMjiYuLo0ePHmc8lxACIQQqlYpNmzaxbt06EhMTGTZsGD179kTt6imcJqrdto3cO+7E76KLiH39/LrfW2wO/rfxGG+ty8Bbp2bRzUMZmiCTljPSF8HbI+DSNzrFhu+S9GdtbcSuU3e9Hezvw6rB3fmxrJqLQwMA2FKpp6ePJ2Hatr++JsRXx8e3j+D/VqWxaHMm0/tFMVBOy7a6Oqudv329n6935zO1TwSvXDPwtIbS1oICzEeP4jthQosndVarldLSUqJPbAO0fv16tm/fjsViAZyj1JGRkTgcDlQqFTNnzsTLywsfH59GnV9RlPpRx8GDB6MoCjt37uTLL7/E39+foUOHMm7cuDa3Ds9n9Giinn8OXffu531frUbFg5O6M61vJC+vPkz3cD8AWcF8JruWQl0VRPR1dyRSI9j1eiqWLiX45ptR+/m1fgCV2bDtTbjoWdA27jVIOj+desTuzywOB0O3p2GyO3gsMZI5MWF4tJMRsMNFenpGOv9Ia+qs+MuF363mtsU7WH+4lEcu6sH9Fyah+tNzRlit5Nw0G3NmJklr16AOCGjW9UpLSzly5AhFRUUUFRVRVlaGEIJHH30UPz8/9u3bR15eXv1oXFhYGB4eLft8cDgcHDlyhJSUFNRqNTfccAMAJSUlhIWFtcnkx5Kd3azpb6vdwfXv/sq0flHcOjpBjo4D2G0wvz+E9YTZK9wdjdQIpW+8Qdk7C0hYtgyvvn1aP4DjO+D9i2DqizDq3ta/vgvIEbs2TKtSsWJQEn8/ms8/Mwr4uKCcZ5NiuDCk7fdkOpnUbThcwoOf7eb16wbKhd+t5O4J3bhhRBcuSj7z77vktdcx7d1LzGuvNjqpczgcVFRUUFRUVD+dOnnyZCIiIsjPz2fNmjX4+/sTGRlJ7969iYyMRHeiurZ///7079+/xR7fmahUKnr16kWvXr2w25393yorK3nnnXeIiIhg2LBh9OvXrz4md6v88kuK/u+586qU/bNasw0/Tw3/tyqNlXsL+M+V/egV2fZfG1zqyE9Qkw/TXnJ3JFIj2MrKKP9wCX7TLnZPUgcQNxy6jHWO2g2b69xTVmpRcsTuLNaUVfOPjHyyTBZWD+1Bf7/2sZ1XfpWJO5fuJK2whr9M7ck9E7q1ydGT9u6T33KoMFh4YNK5p/n069aTd++9BN1wPZH/+McZj7FYLJSUlODr60tgYCB5eXksWbKkvmBBURTCwsKYPn06CQkJmM1m7HY73t5t6zlpsVjYv38/O3bsoLi4GJ1Ox8CBAxk7dix+7pjy+YPmVsqeJIRg5d4CnvkujRqTlXsv6MZ9E5PQtcPK+hbx0SwoPQwP7QO1HCdo64qee57Kzz6j66rv0CUmui+QjLXw8ZVw6Zsw+Gb3xdFC2tqInUzszsHscLCmrIYZJ4oq1pXXMCLAB582/iJustj56/J9fLe3gEsHRPOfP/RQk5rHYnPwz5UH+WxHLhf2DGPRLcPOOiVnKy/n2PRL8IiJJuGz3/vVWSwWduzYUT+VWl5ejhCCiRMnMn78eIxGIxs3biQiIsJlU6muJITg+PHjpKSkcPjwYR588EF8fX2pqanBx8fHbcUW5qwssq+9Do+I8HPuKdsYFbUW/m9VGmkFNXz3wFi0mk7XYMCp6ADUFECPKe6ORGqAJS+PY9OmE3j55UT937PuDUYIeHcCmA1wfwqo2vf7k0zsGtCWErs/KrVYGbItjWAPDf9IimZWeGCbHgkTQrBg4zH++/NhXr5qAFcOadoIhfS7En0d93y8i9ScSu69oBuPTul51qTO4XBQXl5O5opvqAoJptRkIjo6mokTJ2K323nxxRfx8fGpXwcXGRlJTEwM/v4da2rPbDbXT8d+8MEHVFVVMWTIEIYMGYJvMxKrpjpZKes7bhyxC95p9t+wwWzDV6ehps7Kgg3HuPeCbrKxsdQmWXJyKH7pv0T+/Wk8IttAg+D07+HYOpj8L9C5d0S/uWRi14C2mtgB7Kyu5W9H89inNzE8wIfnu8fQr41P0R7Ir6ZPtD+KotS/CUnnr85q56LXNlKmt/Dfq/szo390/W0Wi4Xi4mLMZjNJSUkAvDl/PuWVlYBzPVpYWBh9+vRh/PjxwKkJT1tWVZ1KgP/gZidAQgjS09NJSUkhMzMTlUpFcnIyo0aNIiYmpoWibZzKL75E7eeL//TpLXbOH/YXct+nu4j09+wcjY2tdfDjX2HkPRDe293RSJJbdarETlGUOGApEAEI4F0hxDk3i2vLiR2AQwg+L6rg+WOF6G12Ukcnt4vWKMdKDVz9v+38ZWpPrh/u2h5qHdU3u/PpEeFHcrQ/e/fura9MLS8vByAoKIiHHnoI/br1bHrzTcLm3Eb8sGGEhoai0bTNhNpozEJvOISx9hi1xkyMxmOo1b4MGfwpQgh2pl6NThtKr14voNW2TB+3srIyUlJS2LNnDxMnTmTEiBFYrVaEEGhduV/lGdgqK9EEBbXIuXblVvLE8n0cKTYwc0A0/5yZTKhv20/em2Tv57DiLrj5W+h6gbujkRpQsWQJvpMmNXltqUvlbAO1DmKHuDuSJmtriZ2r321swKNCiF2KovgBqYqirBFCtNvdtlWKwg1RIVwSGsD2qtr6pG51WTUXBvu32fYoob46+sUE8OTX+0krqOEfM5PxUHfSdUGN4HA4KC4pZeHPu4jyqMPbbqC8vJxLH3wQgNzcXPLz84mMjKRfv37106nWggIKnnyS3jHRJEyZ4vZ9YIUQWK3l1NY6k7ZaYyYWcwl9+zo/Xx079golpT8CCp6eMfh4d8XP72S1nCAyYgZHM/7NbzsuoU/yywQHj2l2TKGhoUybNo1Jf+h4v2/fPlavXs3AgQMZdiIZdjXD5s3kP/Qwce8ubHKl7B8Njg9i1QPjWLDhGG+tP4pDCN6+YXALRNoGpbwPId0hcYK7I5EaYNy1m+IX/43DZCL07rvdHc6p7FZYfgcExsOcH90dTYfRqlOxiqJ8C7wlhFhztmPa+ojdmezVG5m68wg9fTx5LimGccFtc72A3SF46ad0Fm7KZERiMO/cOJiQjjqicB7MZnN9S5H+/fvj6enJj2t+4betm50HKCoiI8KJjIzk4osvxtPTs77Z7x/V96vLyCDx6+Vou3RptcfgcFipq8ujtvYYRuMx4uJuRaXSkZHxH3Jy360/TqXyxNu7K0OHLEOt1mEwHEYIB97eCajVXmc8t16fxoGDD2M0HiM+bi7duj2GStWyI2sFBQVs27aNtLQ0HA4HXbt2ZdiwYfTq1ctla1lbqlL2TI4W6/HSqokN8qaw2oTNLogLbtvLNhqtcB8sHNeh+pB1VEIIcmffjDk7m6Sff0LVyKbkrerX/8FPj8NtP0GXUe6Opkk624hdPUVREoBBwG+tdc3W0t/Xiw/7JvLPjHyu3nuMS8IC+Ge3aOK92lbSpFYpPDm9N72i/Hh8+X7e3ZTJk9M7z/qYP26NVVhYyObNmykqKqKioqL+mPDwcGq1QbyeYgR7V2ZPHMB14/qcNpX656QOTu1X56qkzmqtwWg8ho9PEhqNH6Wla8g49l9MplyEsNYfFxo6CR+fJEJCJ6LVhePj3Q1v7254ekahKL/H7uvbs8Fr+vklM3zYtxzNeJEa/X4UpeUr2KKjo7nqqqswGAykpqaSmprKli1b6N3b+fy0WCwtPk17ck/Z7GuvI++ee5pdKftH3SN+/3D3f6vSWJ9eymNTe3aMxsY73weNFwy83t2RSA2o3bIF486dRPz96baZ1IGz3cmml2DLq9DlK3dH0yG0yoidoii+wEbgeSHE12e4/U7gToD4+PghOTk5Lo/JFersDhYeL+X1nGL8NSpSRiWjPUMC0BakFdTQNcwHTw81Jou9w7VDcTgclJWV1bcUOfk1bdo0+vXrR35+PsuWLTulKjUyMpJqm4Ypr28iyFvLwtlD6B8b2KjrCSEoevZZ5/ZdZ+lX11hCOBDChkqlxWjMIjf3/fr1bxZLGQADBywmJGQ8lZU7OJ63GG/vbvh4d8Xbx/ldo3HNqLHDYUal0mG2lFFW9gvRUde4ZETNbrdjMBgICAjAaDQyf/58evTowbBhw4iLi2vRa9ZXyo4dS+w7b6O0cDuW/CoTT6/Yz/rDpQyIC2z/jY3XvwgWA0x93t2RSOcgHA6yrrwKh15Ptx++R2nl9avnZdN/Yd1zcNdmiHJtc3VXaGsjdi5P7BRF8QBWAT8LIV5t6Pj2OBX7ZwV1Fo4Y67gg2B+HEPxSXsPkEP822R6l2mRl1ttbmdE/iocn9zhtO6z2oK6urn4qNSQkhKSkJKqrq3ntNefG72q1mvBw51TqoEGDiG9gr9YPtmQxc0A0YX7nP+IqHA6U80jm7XYjpWW/YKzNpNZ4DKMxE6Mxi549/kl09DXo9YfYtfvGU5I2b+9uBAYOwcOjZRb9N0Vm5nyyst8gNHQyvXu9gFYb4rJrGQwGNm/ezJ49ezCbzURGRtbvbNFSo3iVn32GtbiYsAcfPK9/v8b6c2PjBTcNOetOJQ1xOES7/DuVWpfDaKT4pZfwHjqMgBmXuDucczNVwbsXwJTnoPcMd0dz3jpVYqc4M5klQIUQ4uHG3KcjJHZ/tLKkijsPZjMywIfne8TSx/fM65jcxWyz8/SKA3yVmsfk3hG8du2ANtuHSwiBxWJBp9MhhGDZsmUUFBRQeaKtCDg3qb/00ksRQnDgwAHCw8MJDQ09Z1PcaqOVx5fv44FJSfSJPr99XIXFQsHfniJkzm14JiefJeZSZ9L2h+QtNORC4uJuwWqtZNPmoYAKL6/Y+pG38PBpBAQM4uTfZ1v7UCCEg+N5S8jIeAkPjwCSe/+XkJBxLr2mxWJh3759pKSkUFxczH333UdYWBh2u71Fmx47LBZULhrdqKi1MH/tER6Z0pMALw/MNvt57VpxNKWYjZ8dZsINPek+tJVbqggB2VugyxhoozMRUjvmcLTb51VnS+zGApuB/YDjxI//JoT44Wz36WiJnV0IPi0s58XMQqqsdmZHh/B41yiCPdpO+wshBB9uy+a57w/RNdSHRbcMpUuI+9djlJaWUlBQcMpUamRkJLfccgsAn376KRqN5pSpVD8/v/NKgo4U67lz6U7yq0y8fPUALht4fj3Viv/zEhWLFxP1+n/RjOuJ8UT1qVYbRnT01QjhYMPGfjgcdQCo1d54e3clKupK4mKdW+kYDEfw8uqCWt221mQ2hl5/iINp86itPUpy7/8SFXWFy68phKC4uJjIE01Wv/zyS+rq6hg+fDjdu3dvVpJXd+gQx++5l5iX/9silbLnYrU7uPztrQzpEsRfL+51zh6Tljobmz8/QvqvRfiHeXH9P4aj8VBTnF1DYLgXOu9W+DCWsw0WT4Mr3oP+17j+elKT6devRx0QiPfgQe4O5fw47FC4B2LaV+uTTpXYNUVHS+xOqrLaeDm7iMX5ZQzw8+aHIT3cHdJptmaUcd+nuxgUF8ji24a32nUdDgcFBQXk5+djMBjq22AsXbqUzMxMNBpN/VRqfHw8AwcObJHr/nywiEe+2IOXVsP/bhrM0ISG+7RZrZXUGjOx22rR7rWRd+99VD8fijG4GCHs9ceFhV5E//7/A6CoaCVabQje3l3R6SLb3Ohbc9ntdWRlv0WX+Ll4eAQhhGjVx7h582Z27NiBXq8nICCAIUOGMHjw4CbtbOHKStk/q7Pa+feP6SzZnn3OxsbFWTWs/uAg+jITQ6YnMGx6Aiq1CrvdwcdPb8duczDysm70Gh3l2inaZXPh6Bp49BBo3f/BTzozh8nEsSlT8YiLo8snH7ev15t1z8OW1+DhfeAf3fDxbYRM7BrQURO7kw4ZTBjsDoYF+FBrt7NPb2JUYOtvrXQ2ueVGPD1UhPt7Ume1o9OoXPbCUFRUxO7du0lLS0Ov1wPg6+vLvHnzUKvVFBYWolarCQkJafH9RdcfLuG2xSkMiA1g4eyhRAZ41t8mhB2zuRhPT+cLS07uIkpL12A0ZmK1OitodR6RhD1mRxsTA/+9EIdiOVF52hVv70Q0mrbzb9qaHA4ru/fcQkT4dGJibmy1NxW73c7hw4dJSUkhKyuL8ePHM3HixCZNZf++p2wEXT77tMUqZc/mj42NLx0QzXOz+uL/h+UQu1fnsm/DcS66rQ/R3QNPuW9prp7NXx6hMKOasHg/xl3bg6hu57ecoFEMpfBqbxg2F6b9p+XPL7WY8kWLKHn5Fbp8/JHLR51bXGUOvDHIuaNJOyrOkYldAzp6YvdHb+YU83xmITPDAvlnUjSxnm2naslmd3DbhymE+zlHEjw9mp9Y2e12cnJyiIyMxNvbm5SUFH766SeSkpJITk4mMTHxvKdSm8pqd/D+lixuHZ1AXe1uyss3YjRmUWs8hsmUjRBw4QUHUBQ1Gcf+S3VVKt4+XeuTN+MHP2D6coOzX10DxRididVaw8G0hykv30ho6CR693rRpYUVZ1JaWoqXlxe+vr6kp6ezYcOG8y62cHWl7J9ZbA7e2ZDBL4dKWH7PaCx6C9WlJmJ6BCEcAovZjs7rzFO1QgiO7ixm2/Jj1FaZueqJoUQktHDV7eZX4Zdn4L4UCGt7sw2Sk72mhoyLpuA1cADxCxe6O5ym+fouOPQdzDsA3i2z242rycSuAZ0psTPZHbyTW8JbucUA3B8fwb3x4Xi1gR0hHA7B/F+OMv+XowyMC2Th7CFE+Hs2fMc/sdvtZGVlkZaWRnp6OkajkZkzZzJkyBDMZjOAy/dMtVqr0OsPkltyiK3pqQyNrcFqzmbY0G/Q6cLIyn6brKz5eHrG4ePjTNx8vLsRGXkpKtWZYxNWK+Zjx/Ds1culsbdHQgjy8paQcew/aDT+JworxrslliNHjrB27VpKSkrw9PSs39kiJKThZLPi00+p3bKVmFdeRuXVOkVPNruDnL1lrPs4nVq7g1lPD6VLWONGDK1mO0dTiuk9JgpFUSjMqCK8iz9qjxZ4PfngYlBp4NZVzT+X5DIlr71O+cKFJH6zov2+NpUcgndGwoQn4MIn3R1No8jErgGdKbE7Ka/OwrPHClhZUsUVEUG8k9x6OxY05Mf9hTz61V58dRoWzh7CoPjGt9gwmUzMnz+furo6tFotPXr0IDk5maSkpBZvNmu3mzGZsk9Unzq3zkrocg++vj0oLPyatEN/ccZk88TPN4mwwB507ToPT89obLZaVCrNWZO4PzLu2oU2IQFNcPv4JOlOBsNhDhx8GCEcjBj+PSqVewqGhBDk5uayY8cODh06REBAAA8++GCjRoZPtq9pjXWDVrOdzV8e4dDWQrwjvXjPUk2VBh6b0pNbzrOxsUlvYenftuEdqGPs1d1J6BfSvPjtNjCWgV9k088huVzF0qVYsrOb3UvT7T67AWpLYO4aaAdrBGVi14DOmNidtK3SQIhWQ08fT4rMViqtNnq3gfYohwpruGPpTtQqhbWPTDjjHrNWq5WMjAzS0tJQqVTMmjULgHXr1hEdHU23bt3w8Ghe5Z5z39MKZ7Pe2mMEBAzC17cnVVU7Sd11HfD7c9nTM4bevV4kKGg0725IYUXKNnx8uvHadROJb2LFrzU/n8wrrsR70CDi/regWY+ls7Db67BYSvHyisNuN2Kqy8fXp7vb4tHr9VRWVhIfH4/VamXx4sX07t2bwYMH43OWzvzW4hLyHnyAiL/+Fe8hrqnWq6u1svylVKpKjAye0oXhMxMpMph5asV+NhwuZWBcIP+5sj89IxvfePp4WgWbvzxCZZGR+D7BjL26O0GRTXjut+M2FFI7ZawAzwBQtY/G+TKxa0BnTuz+6NH0XD4vquDW6FD+khhJoJvbo1TUWijVm+kZ6YfN7uxco1GrOHbsGLt27eLIkSNYrVa8vLzo27cvl1zS9IaYDoeNurrjKIoGL684LJYy9u2/h9raTGy2qvrjunX7Kwld7sJiKScv7+M/rIFLQK127sv5zoYMXvrpMDP6R/HSVf3x1jbt9ygsFrJnz8ZyLFOuq2uio0dfIC//I5KSniQ2Zrbbq/Wqqqr49ttvycrKQq1W06dPH4YNG0ZsbOwpsbVGpawQgq3LMkjoH0psz6BTfn6ysfHAuEA+uHXYeZ3XbndwYEM+O77LxG4TzH5+FD4B57H0oTLH2eLk8gXQdcJ5XVtqPZbjxzHt3Yf/9GkuabDtNpZa5xIATdtuBSUTuwa0RmJXsXcdnsEReMf1cel1mqPCauOlrCKW5pcR6KHmicQobowOQe3mN8O6ujpe+mIDGVZ/3rxhGLt+20JKSgq9e/cmOTmZhISE865gFcJOZtYb1NYeobY2E5MpByGsxMbMpmfPf+FwWNmz9za8vRPr17+dad/TM6motbBqXwGzR3ZpViJR/O//UPHhh8S8/hr+F1/c5PO0J0XHjpJ7YC8Dp16C1rP5I8dmSxmHDj1OefkGQkIuoHfv/6DThrZApM1TWlpKSkoKe/bswWKxcMcddxATc2o/w1MrZT9D7dv8dh+1VWY2fHqYUbO6ERx17vNV1Fqw2BxEBniSV2nk+32F9IjwIyncl5hArwbbnBhrLBxPK6fnyCgACo5WEdUtAKWh6d21z8DW1+Hh/RDgutYvUvPk/+Wv6NesIWnNajRhYe4Op2VUHYeF42HS32HonPO+u9lYi4enByqV64sSZWLXAFcndkIIPr1zBlW1NiYMjaTPLf9ACenmsus110GDiaeP5rG9qpZHEiL4a2JUq8dgMpk4fPgwaWlpHDt2DLvdznpbD5SAKBZcP4Ce0YGoGvEpUQhBXd1xqqpSqa5ORa3xpXvSEwBs2z4RRdGcsnWWn3//Jk3bbcso48Nt2bx1w2C0muZ/etVv2EDe3fcQdMMNRP7j780+X3uRe2AvX/3fU/iHRTDlzgfo0n9gs88phCAv/yMyMl5ErfajX7+3CQo8v1EoVzGbzRw+fJh+/fqhKApr167FZrPVF1vUV8qOG0fs2281q1I2c08p6z9Kx2axM3lOMt0GhTf6vk+t2M8nv+XW/7+Xh5qkcF8+vWMEfp4eZJfVIoD4YO8zrssryzPwxXM7CE/wZ9y13YlMPEt7FJsFXkuG2GFw/Wfn+xClVlKXnk7WrCsIueMOwh+Z5+5wWo4QsGgSGMvh/lRQN262xWqu49fV/6TK+AOR8aMYNupdFwcqE7sGtcaIXVnab6xZ8DIFJSZivauZfEEPQi55EkKTXHrdphJCsLK0ilEBvoTrPMgw1uGtUhHtwvYoJxeLl5aWsmDBAhwOB/7+/iQnJ5OcnEyJw4e7P95NndXO69cOZPIZ9r0Uwo6iON/8MjJeorDoayyWUgDUal/Cwi6iT/LLgHP6tbmL64UQLN6azfM/HCIx1IeP5444pT9dU9kqKyn/30LCHpmHysUVvO4khODwtk1UlxQzYpZzZ4HcA3tZu+gdKgvz6XvhFCbMnoOnT/P7uhkMh0k//Hf6JL+Ml1fbnNZeuXIle/bsweFw0K1bN4YPH05oairVn31G/IcfomlEZe2fWS12ti7L4OCmfELjfJkyt0+T1r1VGS1klBg4WmLgaLGB45VG3p09BEVReOSLPXy9Ox+tRkXXUB+6R/iRHOXPPRc4P8A67A6OphSzbcUxjNUWeo2MZOSsbqdP0e5fBsvnwo3Lofvk845Rah3H77ob4549JK1Zjdq/hdvcuNuhVfDFjXDFIuh/9VkPE0Jg0B8id3chW774iJCBe/GPUZGQOJceyfe6PEyZ2DWgtdbYCYeD/T8uY9Pnn2C1Wrn66nHEXtk+Squv3pPBzmojD3UJ5+64cDxbqD2KwWAgPT2dtLQ0QkNDmT59OkIINm7cSFJSEtHR0aeMzBVUmbjro1QySgxsfvxCAnQmqqt3UVW9i+rqVGprMxg7ZhsqlQdZ2W9jrM0kIHAIgQFD8PFJqk/6WkKd1c5TKw6wfFceFyVH8Oo1zd/zVlitACjNLPpoD6qKi/jl/XfI3ruLqKSeXPvMf1BrnIm21WJm+1efsvO7FfSfPJXJt9/XItc8+eFBCEFGxotERV2Jr2/PFjl3S9Hr9aSmppKamoper2f06NFMnjChyQn+zh+z+e3bTAZeFM/IS7u2TCuSP0kvqmFfXjXHTiZ+JXp8tBp+etjZcubmD3ZQWGWiR7APPSocaDJq0flouO2FMafGs3g61OTDA7tl8UQbZdy5k5ybZhP26COE3nGHu8NpeQ4HLBgFigru3nra89BiKaeo6BsKCr6k1pjBoS+6Ehjcl/E33kBcn6Gtto5XJnYNaO3iidqqSlK/+Ywx196M2ssX05b38CrYAuP/ApF9Wy2O85FrMvPMsQK+L60m3lPLM0nRXBwa0OQn8d69e9m9ezc5OTkIIQgODmbIkCGMGTPmrPcRQjgb+arCSSsyE6n+jiNHnwVAUTT4+fUhIGAwXRMfQqNpfCVfU93/6S5W7Svk4cndeXBi9xbZWqn43//BtG8f8Ys/6LAjdXablZ3freDX5Z+j0qgZc+3NDJw6HdUZqtGKMo7gFxqGT2AQ1SXFeHh64u3f/F0O6uoKSNk5C5uthqRujxMbe4vbCyv+7OTOFmFhYYSFhZF77BibFi9m5AUX0G3SpHPGKxyC2moLvkE6bFY7Jdk1RHdvfNuglmCzO9Cc+AD4v43HSM2pJKPEQE55Lf42hQkRgcx/bDRCCJ5dvBvPaG9GK/uJ84XwYbOaXHQkuVbttm2UvvMO8e+912q9Flvd3s9hxV1w6/eQMBZwvmYczXiR0pLVCGz4+w9E6Pvhox5B8tiprV5AIhO7BrizKtZsrOXD+28mTlvIBaFH8O471ZngRQ90SzwN2VKp56mj+RyureON3vFcE9m43mrV1dUcPXqUIUOcUzcrV64kNze3fpo1IiLitDcqh8NCjX4/1VWpVFWnUl29C6u1goEDPiQkZBx6/UE27lvJykOhPD3rCuKbME3VHOlFNeSUG5nap2X6bOl/+YW8++4n6MYbifz70y1yzraosjCfJY/dR9chw7nw1jvxC25cMcMXzzxBed5xJs25hx4jxzQ7EbNYyjh06EnKytcREjye3sn/bROFFWeze/t2fvj+B6waNZEhoQwfM5q+ffue1p+xttrMuiWHqCw2ct3fh6P1bFsJUp3VTnZ5LTa7oG9MABm7S/h54QEyPez84mmlSu18f7hzfFf+Nr03QgiWpeaRFO5LUrhvs0fFJalBdivk76Iu3Nkhwd+/PzUVeezYOYOyQx70GvAAAy+42a0hysSuAe5M7GwWC7+t+IId3y5Dq1EYH55FX59slDEPwJTn3BJTQ2wOwedFFVwZEYSXWsUBvZF4Lx3+mlNHXCorK0lLSyMtLY38/HwA7r77biIjI7Faraf1mLNYKqiu3oWnZzR+fsno9QfZkXIpAF5eXQgMGEJAwGBCQyeh0zkXfm84XMIDn+1Gq1bxzo2DGdHVtcndZztySS+s4ZnLWnZk1ZKXT9YVV6CNjaXL55+hauFmyu5mMug5sn0zAy6aDkBlUQFBkee34XZpbjY/L5hPceZRkoaNYtLce/ANal7TZiEE+fmfcDTjBby9Ehg+fFWDVc/uVHPkCJv+9hQZ3bpS5eVFcHAw999/f/1yhez9ZaxbeghLnZ2xVyXRZ3xMmxuJ/DO7zcG+NZmkfJ+JzaHBf2AIFfGe9E0IZGKvCPKrTIz597r646MCPEkK92XO2EQu7BmOxebAaLER6N2x/mbaGuFwUPXllwRcdlnHHanDOaBQVraOgoIvKK/YjJ9vX0TBjez45kus5jr6T57O6Kuuxzsg0K1xysSuAW2hj1153nHWvPcW+ekHiYnyZ9ac69H1n+lsmlh2FOJHuDW+s7ELwZjfDqG3OXiqaxTXRASiUavJzMxk6dKlAERFRZGcnEzv3r0JDf19REQIO4WFy0+MxqViNGYBEBs7m549/oXDYaOs/BcCAoaccyTlWKmBO5buJLfcyL8u7cNNI1t+Fw2LzcEz3x3kk99ymdAjjHdvHoJO0zLr9YTFQvZNs7Fkdrx+dUII0rdsYP3SRdQZ9Nzy8tuExMQ1+XwOu52dq1aw7atP0Gi1XPm3Z4lKav4aOYPhCFZrJUFBI3A4bAhhQ61ufhGMK9Ru20bOHXdimDgR3dw5DBg4EJvVzvtvfUJtthdRIfFMub0PIdHNLzgBKLfYWFdRQ08fT/r7ebfIOU+T+iG13/yTX6M+In2fjfAEf6563Dm6b3cIjlcY69fuZZQYyCgxcO8FSVzcN5Kd2RVc9b/thPrq6B7uS/cI58jelOTIFilkkpyqv/uOgr/8lZjXXsV/2jR3h+MSefmfkpn5GlZrBTpdJFHmSPb8ZCQ7R03XIcMZf+NtzXr9akkysWtAW0jswPmJ6MDGteTu38v0Bx5zLvLe8BLKhuchcQJM+Gv9fH9bsjEnn39mFpKOhq7YmD+4NwO9tezYsYPk5GSCgoKw283U6PdRXb0LlaIhPn6us0Hq1jE4hIWAgMEEBDiLHPz8+qFWn9/6spo6Kw99tpv1h0v55r4xDIwLbLHHV6o3c+8nqaRkV3L3hG78ZWrP89pqqSHW/Hxy58wlbN48/C+e2mLndbfKwnzWvr+A3P17iErqyeQ77iM8oWuLnLuiIJ9fv/6ci+64Dw+dZ/02XC0hK+tNiku+p0+f1/HzbZt7X1Z8+ill89+gy+efoUtMpLy8ggVvLcQmzAQEBDJs2FAGDRp01p0tGlJrt6Og4K1WsSS/jMeP5AEw1N+bObFhzAgLQNtSa4qEgIXjnN/v3kJRdg0Wk4345BDsVgcVhbWExZ99zWx+lYnv9xXUV+xmFBvQm20su3sUQxOCWZtWzMJNx0gK96tP/LqH+xHhr2vzo5lthbBYODb9ElR+fiQuX9ZhGhLb7UaKS34gLHQSHh5BFBZ+TWnZWrT2kST2vALdznfJXfk6zHiN+AlXujvcU8jErgFtJbH7s5rSEr75z78YPySchLxPnPvYdRnjTPC6XuDu8Ni0aRP79u2jrKwMAVT1HsAvkYmUOWDloCSGB/qSe3wxxcXfo9cfQAhnxWdQ0GgGD/oIALO5BK02rEVeYO0OweajpVzQ0zlN+8fF280559TXN5FXaeSlqwZw6YDzmz5sLIfF0qGmX+02G4semIvFZGLc9bfQ/6KLz1gc0RKs5jo+/8fj9J98Mf0nNX8Rc3nFFtLS/oLVWkVS0l+Ji72lTU7PWsvLOXywjsQBofgE6LCYrRzNOEJKSgrZ2dmo1WrmzJlzWuPjs57PIdhYqWdFcSU/llXzr27R3BwTSrXVxjGjmdQaI4vzy8g0mUnw0rJ1RO+WaV5+PAXenwyXvArD5p5y0561uWxdnkHv0VGMvKwb3v4N/40IISiuMRPk44FOo2ZtWjHvbsrkSImeKqO1/rjNf72QuGBvNh0pJb2ohu7hjW++3NlUfPopxc/+H3HvLsR3/Hh3h9MsQgj0+v3kF3xBcfEq7HYDvXq9QEz0tVQW5rPpkw/JSNnOuBtuZfjUi+C1ftDtArhmqbtDP0VbS+za1kreNsykr8Fms7H8m530Gj2XCwZ74bNnAfy6oNUTOyEEhYWFHD9+nBEjnNPCBQUF+Pr6MmzYUBISdNhs6dxc+QXfVXsz1N/ZxmVXTS0RaIiPu42AE2vktNrf10WdXCvXEtQqhQt6hiMcgt0Z5fzl2wPMv2EQvTy1WPINOEy2+i9hshFwSSIq3bmfjmqVwlPTexPur6NPdPOrMf/Imp9PxdKlhM2bh8qzY0wZFWYcJqJrEmqNhmn3PUpwTGyz18E1xGIy4enry9pFb3N42yam3PUggZFNb6odEjyWEcO/51D6kxw9+hzl5RtJ7v1Siz5Xm8ukt7Du8zyy95dTtm4bw2ck4j10KH369KFPnz6UlJSwd+9eIiOdhT27d+8GoG/fvqetbbULwd+P5vNtSRXlVhuBGjVXRgQxyN857RrgoWFwgIbBAT7MjQ1lY4We3DoL6hNtY549VsBFIQGMCvRp2ge0ne+D1hf6X3PaTcljoqmttrDvl+McSy1h2IxE+l0Yi/ocH9gURTllCnZycgSTkyMQQlBea+FosYGMEj0xgc51YusPl7B4a3b98V4eanpE+vH1PaNRqxSOFOvRqlXEnaX5cksTQiCsjvrXKYfR+ZqljfND7a/FWlSL4bdChMkGioImzAuPcG90XQNQebd8YYnDaKTsnQV4Dx2Kz7hxLX7+1mS3m9iZejUGwyFUKk8iwqcTHX0tWlV31n24kL2rf0DtoWXMtbMZdPEM0HnC8Nth86tQegTCerj7IbRZcsTuPNgsFnZ8+xU7vvkKjU7H+Otuov+oYeAXCeXHYMXdMO5R6DEVWnhaweFwkJ+fz6FDh0hLS6OqqgqVSsXDD9+Lr28AoKa4eAVHjj6PzVYNgIdHMIEBQ+jd+98Y8WXI9jTCtBqeTYrhotDGJ0bCIUCAolaw11qx/ikxc5hs+I6KQhPkielQOTVrcn5P2sx2EPCwr4UDZgsf9u1C7O7y30+uVlB5aQh/YBCaAB2GXwtQ+Wjx6huCoijY7A5e+CGdLiHe3DI6oUV/p/WP74/7wH6zwiV7gbYmk76GjR9/wMENa7nozgfoP6l1p5SFEBxYv4YNSxfhsNsZe91sBk2b2axRQiEE+QWfkZHxHwYP+gh///4tGHHT5aaV88uHhzAbbYy8JA7f+ffjaGBP2aVLl5KZmYmnpyeDBg0iuN9AclUeXHmiqv3K3RmEaDVcER7EhSF+6Bo56llQZ2FSymEqbXZ6+ngyJyaUqyKC8Gns+lMhYNU80PrA1OfPelhlUS1bvjpK7sEKug+LYMrclt2asbLWQkaps/Hy0RI9NSYbr1wzAIBbPtjBxiOlpzRfHhQXyJyxiScegjgtoRVCICx252vSicRME+yJJsgTu96CYVvBaR80/SbG4dU7BHNmNaXv7jstxpCbeuPVN5S6I5WUf5aOyksDDoG9ygxA2L0D0MX7YzpcgTG1GI9wbzTh3s7voV4oTdwRx5qfT8ETTxI2bx7egwc16RzuIoSDyspfMdQeJj7uNgDSD/8TX9+eREbMrG+L9c1/nyMzdQf9Jk5h9DU34hP4h9ZAhlJ4vR/0vRIuf9sdD+OM2tqInUzsmqCiII+1771NUHQMF91xv/OH2Vvgm3ugKhci+zunaHte0qzGng6HA4fDgUajYffu3Xz77bfodHV076EiMtKARpOD0ZjOoIFLCAoaSWVVCkWFX9c3AfbySqh/kRPCObXz9JF8MkxmLtB58rTOnwQLOEw2PHuHoI3ywVJgoHpV5qkvdGY7Ibf2watXMKa0csqXpp0aqEZF2Ny+6BIDqMuowrAlH5WXBpWXBuXEd1NSAPeu2EdGThX3DovntolJqH08UDxUv8foEJQs2Iv1uB5tF3+UC2N5aPNRth0r545xiTx1SXKTf5fn8vs+sK+363V1QgjSNq1j40fvYzbWMmTGLEZdeR0eOveMQOorylj73tvUGQxc98x/WmQtkM2mr38DKC7+ntDQiajV7qkKPPxrIWs/PERQlA9T5vYhNNa3UXvKCiHYkZHJ4vRMtggPyvwC0SJIHz8Ab7XqjMlJY5nsDr4pqeSDvDL2G0z4qVV8MbAbg/2bv7ftnx9Dzv5yvAO0hHfxp85gxWyyERDmmn8LIQTCbCc9u5LMvGoyq+vYozeRVaznWkXH9f1jcJisbNhXhJddkB2mw9griN6+nvT9LgfFcer5AqYn4jc+FmupkeJXU095rVJ5afAbF4tnjyDsNRZqdxXX//zklybUC9UZWtc4zHZspUY8IrxRPNTU7iqm5pdc7BV1cPKtVgVRT4xA7a/FnFWNvdrsTPrCvFA8XLNEwp3qzEUUFi6noOAr6uqO4+ERzJjRm+sLooQQHPl1K9E9euEXEkp53nGEw05ofMKZT7h/GUQNbFM7RcnErgHtIbED55PRbrWi0WopzDhMxo7tjLz8KjwOfwubX4aKTIgeBHPXNnqPO3A2Qs3NzSUtLY1Dhw4yblw3+vUbihChpKf/TFX1XwBQKTp8PZLxU/UjxDEV/7hkdF38sRssVH6d8fvUwYmvgIsT8B0djbHQwJvfHODdbjosalixuZbIOkHQld3xGRaJtaiWym8yTnkRUzw1eA8IwyPcG3utFVup8cRtHs7bG9k932Jz8I9vD/B5ynFevnoAVw05fURD2AXG1GLKf85CVWtjo2LDf1oCM8cnNvp3eD46Ur+61e++yf5ffiaqRy8uuuN+ws72wtiKhBBYTCZ03t7UVlVycOMvDLnk8vpdLZqqtvYYv/42FW/vbvTt8xp+fq5J+s/kZOJVV2tl95pchk1PQKP9/Q25oT1lPyss55H04wign7eOQcZKro2LZEhSVyoqKkhLS2Pw4MF4eze96lUIQWqNkU8Ly3m+eyxeahU/lFahVhQmh/ifvh7P4YCStCY3Zd/0+RHSthQw8KI4hlycgIfu9ARFOJzJmcNkA0AT7Hxjr00txmGwnPJhUhvnh9+4WOeyk+d/w1Fr/T0xAnxGRhF0eRLC7iD/qa2gApWXhmqHoFo4WK2x82GtAY2AFyNCmTI4BsVLzYepefgF6gjp4k9ClyC6hvrg5aFGcfG0rrDasZaasJUYsZaa8J8cj6IoVHx1BGNqsfMgBdTBnnhE+hByU2/njEWV2flaq1NTs2YNXv0H4BHRdpYhNKSo6FsOpj0GOAgKHEl09LWEhU2pT+oKjhxiw0fvU3gknRGzrmHsde7tR9dUMrFrQHtJ7P7otxVfsuXzpQSERzBpzj0k9h8IB7+G6uPOqVmAjF+ca/FUaux6Cw6jFUedvf6FTPHV8Ev6ZvLyfkGryyPQvxR//zJUGgvBhdPoGvIYflOiyc1ZgvVzDzxruqCI398c/S6II+DiBBxGKyUL9532CdOrTyi6rgE4LHbMmdWUe8A6m5kbo0NQeWnYXWtioL83KhdXpgkhWJNWzKTeEahVzvYJf14rU6o3M/Wl9dyg0nGN0BJ51wC0MS3TLuKUWKxWMqZORRMY1G771dmsVoTDjofOk+Np+6nIz2uRogVX2PXDt6xf8h5hCV2ZevdDRCR2a9b5Kiq2cjDtMazWSrp1e4z4uDkuLawQQnBwcwFHU4q59KGBqM8xnVbxyScUv/AikUs/Ylt8Il8XV3J9VAiTQ/zJMppZVlzBFRFBdPM+dTT1t99+48cff0StVtO3b1+GDx/e6IKLhszafZTtVbXEenpwa3QoN0SHEOxx4jXk2Dr4aBbc8KVzKcnZfgcOgaizIawO1Cf2lq07Uokx30B2ajHVeQa8PNVE9A4m4eZk537Ti/ZjyTcg6mz1yZmuRxBhc5xJZOGLO7BXm+uXZai8NHglhxAwzflhruqHLJQ/3Kby0jjXskU4RyEdZhuKVn3aKGed1U5WWS0alUL3CD/0dVaueGcbWWW12BzOQBQFHpvSk/suTMJksfPdvgK6t2LzZWFzYCs3YS02OpO+EiPC6iD0Fuf0dumi/ZgzqlD5abBk7kMT5kXw9dPwHhDm8tiawmjMoqDgK4KCRhISMh6TKZ/8gs+IjroKb++E+uOqiovY/OmHHPl1Cz5BwYy59ib6TJjU+OUaZUdh3XNwySvg4/5G5jKxa0B7SOyE1X7qGjOjjbKCHNZ+/y4VBXmM63c9XRL6obarnbfX6NFW/0Rw5I8w7jEKvkvEWmsmzyuT2sAjxBBIZPhlrLL8SnTMq6gUI9q6WHwtvfGx98FfGYh/Ug+8B4Q7t/LaW3rKtEH9yFoTq04zjHWM/y2dAX7ePN8jpsWnbc6msNrE7Pd38I8ZyYzvceoL1fLUPMb1CCVUq6kvqqj8NgO1nxbfsTGotC0zZWHOykLRaNDGtY1+SOcj98A+1i56m65DhnPB7LkN36ENOLpjG2sXvYNJX8Pwy65m5JXXoWnGXrwWSwWH0p+krGwtYaEX0a/fApe0zagzWFn30SGy9pYR1zuIKbf3xdPnzHE7hGBrpYGvMnL5yWynxuYg1EPD37tFc21Uw8UrJSUlpKSksHfvXiwWC/Hx8dx6662n7NPcFFaH4Oeyaj7IK2VbdS06lcITiVHMVXtjW/kSjtICHKOfwmERgELgdGdiVfltBnXpFaesmdWEeRH5qPN9rGThXixZNc6LqBQsQlBuduC4II4Rl3alenU2DpPtlFF+TbAnuq7Odb52vQVFpz5lWYYrWe0OcsprT6zhMzAiMZgRXUPYl1fFpW9trT/uZPPlByZ2Z3hiMHVWO3VWe6s2X647UoklX49+za/YKq2og7ugSwwg7PZ+AM71fyrl1DV8Ed6oz/LcdAW73URJyU8UFH5JVdUOFEVNYuJDJCacfU/p1Qvf4NDWjQybeQVDZ16B1vM8p/BLj8Dbw50DJ5P+3sxH0HwysWtAayR2Z6p0EnYHnif2b6xNLT6tQEDl40Hozc7pnpJ39mDJ1Z9yTo84P0Lu7MPOlcvRbREE+UfhFexfn3RpPfPwLHuO/Y4KikJDwK8SnWctAN66JEYMWoXipUFvOIiXZzweHv4u/R38kUMIlhVX8tyxAkosNq6LDOZvXaMI17n2xSGv0sjtS3ZypFjPY1N7siunijljEhiddPonMOEQlH9yiLqD5aj9tfhP6YL34IgmT6EYd+3Ga9DAdtk7y1hTzaaPP+Dgxl8IiIhk8tx7SRgw2N1hNZrJoGfj0kXOadkZs5qdlAohKCj4HJVKS1RUy/e3ykuvYO3iNEwGK6NmdWPAxLjTnndCCIotNiJ1HjiEYMSvh6i02pgeFsDFBTmMDfDBf+iQ87puXV0d+/btw2AwMHHiRMA5ote9e3eCAgJBpTin6yrqsJYaT1l64Vx+kYiiVtBvyceYWnzKmtkMfzU/XhnHpBB/hv6cSe7hWlJC1EwqsqFVK2gCPYl8zPk+pd+Yh7Wo9pR1aGp/Ld79nR/GbFV1KIqCcmJZhhCQvq2Q2N5B+Id4oa+oQ6NV4eXbtkfET2u+fCLxe/qS3ozoGsLPB4u466PUU5ovdw/3ZXq/KEJ8XbeXtDkri8wZMwm6/noi/vY3RJ0NlbcHQgiqvs7AUlSLrdiIsNgB8B4cTvA1PRFCUP1dJppQLzThXniE+6Dy82jx17wdKZeh1x/Ayyue6KhriYq64rSqdbvNyp6ffyCmVzKR3bpjrK7CYbfjG9yM3Ym+uAkyN8G8A+DZeu+XZyITuwa0RmJX8cVhjLtLTvmZykdD9N9HAVD+URp1x6pOWywbNKs7AMa9pX/4BHriy8ejfs1IVVEhXoGeGIwHyUr/DodSwLCRS9i0cRN5+S8SHJyPovciLPFyuiZNJyCgLyqV+/dcNNjsvJZTzLvHS/HXqEkZlYx3M3vPNaSiwsQ/vj3AqsMl+CkKT4zoyg2X9Tzri485s5qqH7OwHtfjEelD0DU90J5nV/+T6+qiXniBwCtmtcTDaDVZe1L54c2XsZiMDLv0SkZccS0eWte9qbhS1p5UIhK74R0QiL68DE9f3xYp9CgoWEZ1zW56dH8Ktbp5uzM4HIIvntuBwy6YMrfPac15c0xmvi6u5OviSsqtNvaO7ouHSuGQwUSClw5Ph53MSy/DXlVFwldfoY1t+rRqRUk5by54CyEEAQ5vonvGExETSZeaIDy21ZxyrOKhIurJ4ai8PTDsKKTuUMWpo/teGnxHRaOoFGw/vMLC/CL+L+lGQj003BQdws3RIUR7tkwituqtvRRlVjN8ZiJ9x8egcvFriqtkldWyJq2ofqTvWImz+fIvj06gW5gvy1Lz+GrncXpG+tE9wo+eJ74Cmtn2JG/ePAwbN5G0+mc0oWeedhRCYK+2YCtxrn/WxvlhN1goejnVOQV+guKpca63HhmFw2LHklXtHOELaFyDaKu1huLilZSU/sSA/u+jVusoLfsFjdqHwMDhpy2FEEKQsWM7mz5dTFVRIcMuvZLxN97WrN9Hvfxd8N6FMPlfMHZey5yziWRi14DWSOxMB8uwlppOTcy8PerXcZ1vVdrJ36GiKJSWruZY5uvU1h4FHAihYKryws98J30nXUOlvoLELkloDPkQlAAOO3x8JfScBoNvBg/37/uXaTSzR2/kigjnCOaumtoWn54tzzewb30eR34rov/EOHJjPfDJNJKzvoDQOF8GXRRP0pDwM74JCCEw7S9Dvy6X0Dl9UfvrEDZHo1oI1O8DGxdHl88+bTfr6k4+JysK8vjl/QVceOudhMa1/HZt7iCE4LN//AVTdTVT7nqAuD7Na2WSmfUGWVlv4O2dSJ8+r+Hvd/4FAVUlRrz9tWg9NVSXmvD2155SELClUs+LmYWk1hgBGBngwxURQVwTGYznn56z5swssq87d6XsuTjqbOT8sh/brxU4rA4ywysp0+g5bMhEY/Hg4slTGBTXl8KaElZv/YXwiAgiIiMIDw8nIiICX99zfPARAt4ejiOwC5umf8AHeWWsKa9BpcAlYYH8L7lLs9fdVhTUsvnLI+SlVxIc7cO4a7oT28u1/RRbw8nmy2F+OtQqhW9257N0ezZHig0YzL8nUwefmYqPTsP69BJKDWZ6RvjRPcIXb23DBUTCbqfwqafxiI4m7MEHmhSjw2A9ZQ2fV58QPLsHYc6tofSdvQAoWvWJUT1vfMfEoI3xRdgdzkWIClRV7aCg8EtKSn7E4TDj65tMv75vnrJu7s+KMo6w4aNF5KenERIbz4Sb5pAwcEjLjhguvRyKD8LD+9z63ikTuwa0hzV2DocNgyGN6updJ/ZW3UXfPvPR6frwww8vgbKG6uowrJZ4IiNG4sgvInPTL/iFhjFpzj10GzL895MZSuDLWyB3G/hGwJiHYMhtoHXRPpDnaWOFnmv3HuOiEH+eTYoh0bt5o0NZe0vZ+8tx8o9UofFQ0WNEJP0vjCUkxhe71cHhHUXsWZNLZZERv2BPBkyOo/+FsWd8MTiZ7AghKHtvP+oAHf5Tu6AJPPOozyn7wK74ul2sq7NZLPz2zZdUFRVyyYN/cXc4LnP84D5WL3yTquJCBlw0jXE33IauGVWhFRXbSEt7DIu1gm5dHyE+/vZGFVYIITi0rZDNXx6l9+goxl/rbIJaa7PzY1k1/fy86enjybZKA08dzeOKiCBmRQQR28DoVkOVsmficDjYWbyTr3Z9xt1bZrDfN4PSQVZuu/huykxlPL3laXYW7MRD5cGUblOYEjCF7F3ZlJSUUFtbW3+euXPnEhcXR2FhIYWFhYSHhxMeHo725Icas965D3aQ84NCjsnM0oJyKq02Xu3l3Cv557JqxgT64tvEPZmFEGTtLWPrsqPUlNUx6dbe9BrZ9MbVbZkQgoLqOo4U6cmrNDJ7VAIAd320k58PFtcfFxfsxZD4IF6/ztmPrrDaRLCP9oz7XjenBc7ZOCx2rHkGrCW/J33WYiMh1/dE1zWQ2n2lVH11BEt8Hpnd/oYaH0K9Liaux40EhAxo8Py/Lv+c3T+vYsw1N9H3wotQNeI5f95ytjkLf8Y8BLqzb3XnajKxa0BbTOxsNj0OhwWtNgSD4TApO6/E4TABoFJCUam7M2jg4/j59eWDDz4gOjqa5ORk4uLi6hc856UfZO17b1Oel8u1//w3scl/GkXI3gIb/wNZm8A7FG77AcKav6F6c1kcDt7LK+PV7CKsDsFdcWE83CWi8U1PAUudDe2Jnk8/vXuA4uxq+k2IJXlMNJ6+p09TCIcg+0A5u1fnoPXSMOO+Aaed55Tj7Q6qV+dg2JoPgN+YGPwujDutz1Txiy9SsWQpMfPn4z91SqPjd5ecfXtY+/7bVBUV0nvchUy9+0HUGvdP2buK1VzH1i8+JvWHb/ELDuWKJ//VrFFJq7WSQ+l/o7R0NYMHf05Q4LBzHl9Xa2XDJ4c5tquEmJ6BTLilNzsdFr4uruSnshpMDgfzukTweNeoJr3RntwKKuaN+fhPOfvzz15jRr8pn7zsLK73e5hgz2Bui7+ZywddSaBn4CnHZlRm8Pnhz1l5bCUmm4lPp39Kv7B+GAwGSkpKKC4uZtCgQXh6erJ+/Xo2btxYf9+goCAiIiK4/PLL8fT0xGQyodVqUf/pDTjXZGb4r4fwVau4NjKY22JDSfJu2pS5zWpn3/o8+o6LQeuloarYiE+QDo8WKoZqy+wOQW6FkcNFeo4U6zl8YheN164dCMCMNzdzqFBPYqgPPSP8GGIpoXekH6OmjWm1GB0OG+XlGyko/BKtLYyogjlYSmqptG7AK6c3KoeOyL8MRRPihXFPCaa08vrCDeGvkLr5O6J69aL7sFFYLWaE3Y7Wq20MUriSTOwa4O7ETghBXd1xqqpSqT4xGmeoPUKX+DtISnqcmppy9u77B0WFPmRkgNnsTUxMDHfccUeD57bbrBzZvoVeYy9AURSKs44R1iXh1BLvnO2w52OYMd/Z/+74DmeC59myW2idr2KzlecyC/iqqJK+vl6sGdqjwTe2+unWHUVc/cQwgqN9qDNY0XqpG73Oxmqx46FVU11q4vPndtBzRCQDJ8cRGH76i4Wtqo6an3Mw7ilB5aUh9La+aON+/xRn2LgR4549hD/00Pk9+FZm0tewfsl7HNq8nsDIKCbPvY8u/Qe6O6xWU3AknR3ffsUlD/0VD62uWaMVQgiqq1MJDHS+5hqNOXh7n54sluTU8OP/9mOstjDisq70nxzH2JR0sk0WgjRqZoYHckVEEMMDfJo1NVn72w68hw874+PRl1SS9v12oo76okLBo18QWwcc5pKeM9Cpzz1Srrfo+SX3Fy7rdhmKorBgzwIsDgvX9LiGKF/nyJjD4aCyspKSkhJn0nf8GJXZ+7nz1ptQYofwzTffsH//fsLCwupH9SIjI+nWrRu7TuxN+21JFVYhGB/kyws9Ypuc4DnjEXz+fzuw1tkYc1V3ug1umX2q26sf9xdysKCGw8V6jhTV8NCKl4i1Gxi2bQOKRsNNi34jzE9Hjwg/ekb60iPCj5hArxb5nZlMuRQUfEVh4XLMlmI8PEKIi51NYuLv07/1zZejfVFUCobtBei35J/SfNku7OQNyGPMDTdRd9hZSe3y5stCwOEfQK2D7pNdc40GyMSuAa2d2DkcFvSGQ9hsekKCxyKEg02bh2KzVaNW+xIQMAgvz75ERU0hIKA/q1atYufOnQQHB5OcnExycjJRUVHn/cdVW1XJogdvJyQmnovuvP/MPb1sZnitD9gtMPJeGHEXeAWdflwrSq2updxqY0poADaH4LCxjj6+v69tcDgE2fvK2Lf+OPmHq1B7qOg5PIIh0xLwD236Ggh9RR07f8jm8K9F2O0Oug0MY9CULkQknl4NZck3oN+UR9CV3VFp1dgqalEHebebNw1jTTVL//oA/SZOYcTl16BpJ+sAXcFaV8fyF//BkBmz6D5sVLPOpTekk5JyOVFRV9Cj+9OnFFak5lUxf/0xarv7smyE80PL0vwyInUeXBDsh7aF+wLWHTmCo7YW70GDKDOVsXb9d4zclIhAkNGlmAuvuQxNSNP/Xp7a8hSrMlcBcGHchVzX6zpGRI449W/gp7/BjoUwLw38Ijh69ChZWVkUFxdTUlKCXq8nJCSEBx5wvrmvXr2aMqudXYHhbBQefDugK9F+vqTXmgjz8CCkEWvG/qzgaCWbvjhKeZ6B6O6BjLu2B6GxLd+zsr05WeDl89TfiZ99A2abnTuWpnK0WE9hdV39cXeN78qT03tjttn55NfcE4UbvoT5NlwMYbebUam0KIpC+uG/k5//OSEhE4iOvprQkImNKujL3rebDYsXYS8zkZg4iF6DxhE9ayAAZR8epC69wnngiebLui7+BF/jnImyVdSh8vFAdYZm1ufF4YD/jQHhgHu2N2u3p6aSiV0DWiOxq6z8jfKKzVRXp1JTsw+How5v726MGrkagLKydVitfmRnWzl0KJ3c3Fxuv/12YmNjKS8vx2q1EhER0axEQQjB4W2bWL/kPUw1NQyePpPR19x0ej+fgj2w6b+Qvgp0/jD8Thh1H3i7f/Hx0vwyHj+Sxw1RwTyRGEmYTktdrZUlT27F09fjnNOtTVVbbWb/+jwObMrHarFz67/HnLONgsNYR/7f16L21xFyy3B0Ce4d+TybsuM57Pn5eybOuQuVSo3VXOe2rcDakuqSYr595XlKszPpOWocE+fcjbd/0/4NHQ4LmVnzyclZiLd3At7h/+bTdB92hiocrK1DBUwI9uPdPgn4NXEtWWMIIci+6mpsVXbS7p7KM3Xvorap+Jv5HpIuGky/bi2zB2iBoYAvD3/J8qPLqTJXMbfvXB4e8rDzRosRXu0N3SbC1YvPeH+j0YjBYCA83Nm64osvviAzMxOz2Yyz0x306dOHJV0HsN9g4kKdipsjAhkfF4XmPHYWcTgEaVsK+PXbY1iMNi5/ZBDR3d37AdadhN1O1uWXI6w2uq76DuVPv8tqk5WjJ6Zye0X6M6RLEOlFNVz8+ub6Y4K8PegR4ceDk7ozJimUOqsds9VBgLcHekM6BQVfUFT0LQMGvEdgwBDq6gpAUeGpi2xcjCdG0dM2r+e3r79g/E1z6Dr41JHoMzVfVjzUBF/tXLdaPH8X1sJa1IG6+h58usQAvPo0oQXKvi/h6zvguk+h1yXnf/9m6nSJnaIoHwAzgBIhRIPlaa2R2B1Me4zi4pX4+iYTGDCkfm9VnS6CyspKli9fTl5eHgDh4eEkJyczaNAgAgJaPimoqzWw5bMl7F3zI/5h4dzy37fOvCahaL8zwUtbCbd8B4njWjyW81Vjs/P8geN8XFGF1i54omcMc2LDqMozEBLj49K2BpY6G0WZ1cQnO18E1n+STlTXALoPizhlR4CiF/6NfsNRvEfegrAoeCaHEDAtAY+wtrHuw2ox89vXX5CycjlaL2+ue+YlQmLbflFHa7LbbKSsXM6vyz/Dw8ubibfdRa/R45v0warKaqO6aidZBx5ms6MXb6seZoCXJ1fHhnBZeCBhWteuYRRCsHdfChFbHdhzrdiMBXx2+UFuGDqXLv6uqXI22838nP0zycHJJAUlkVaexort/+H6vavoeuO3kDD2vOKvrq6uH9Xz9/dHl9SDD46X8mleCTa1hoiaCi6sKmKsj5a+ffvSq1evUzoHnE1drZUDG/MZfHEXVCqFisJaAiO8Ubl4u6+2puqbbyh84snz2rtaCEGZweJcu1ek52iJ8/tjU3oyOimUdenH+XDNAiZ1+Y1Y32wcQoPVYzwDej9ETFjjq8ZrykrZ+vlSwhK6MnTGLMSJ/cybskWg6VA51sJaZ/FGsXOrNa8+IYRc3wuA4tdTUflqT2m+7BHpjepM7WPsNnhzsHMXitt/cVbztqLOmNiNBwzA0raS2JnNpWg0PqjV3pSXl5OWloaPjw+DBw/GarXy0Ucf0b17d3r37k3oWfoGtbT8w4fIO3SAEZdf7YzRaDxzVWBFJgQlOp+4a/8FdiuMfgD8GvdJqyU47A6y95U7p1uPVFERpGHz+AD2eQpmhAWwqK9r9nU9G4vJxtcv76I834BPoI4BE+PoMy4a87aNzn1gZ88m/C+PY9iaj35DHsJqJ/yegaesv3OH7L27WPv+O1QXF9FnwiTG3zSnyaNRnUF5Xi4/L5iPolZz3b/+3eht00x2B2vKa1hRXMkv5TVcXqbQe1MO0ROW4ZM0gskD7nVx5GB32Nm6cx2W9SX0qozHqrXjl6Ch9I1H8B05pNGVsi1h+ZHlPL/tX1gVGBE5gut7X8+E2AloVE3fv9fhcJBZVMyneSV8bbAytqaUblnp9B82nF5Dh+FnqeOtt96qX7sXEeFsxxIVFYWn5+kj0xaTjY/+vh2fAB3jru1OTI/OM4JX8fEn6FevJn7Jh82eFbJYStHpwskqreDo/onU2oJILRnH9xn9qKzz5ueHx9Mz0o8f9hfy9a78+rV7PSP96Brqi/bEh2Sz0UjKymWkrvoGgWDUldczYtY1LfWQnfE6BMJiR+WpQdgcVH59tL5iV1gcAPiOjyVweiLCaqfq+6zfk74Ib1SHPkL54RG4eSV0ndCisTWk0yV2AIqiJACr2kpiV1paSlpaGmlpaRQXO8vP+/fvzxVXXOHS6zZWYcZhlj33d0ZffSODLp5x9jLx7x6GXUtB7QGDb3GWfAe0zL6S53L410LWfngI32Bd/XSrzkfD6vIaAjVqRgT6UmOzU2m10cWrdZrnCiE4nlbBrtW55B+uxEOnov++BUSEOOjy6Sf1/ersBgu1KcX4TYhFUSmYc2rwiPJpsS3KGstht/Pho86EYvLt9xHft3m92zoLh8NOncGAt38AtVWVZO3eSZ8LJp+1Hc5jh4+zsqQKvd1BhFZDn1wL3ffqmTk+nkFTu6BSgaKoqKjYitVWQ0T4tBaO18GX6V+w5NBSuhZEcF/xdVT0tzNo+gR8fH2de8r+33NE/vMfBF1/fYte+6yEoGLXEr6u2s8Xlfsoqi2iR1APls1c1iLrUB1CYBfgoVL4MK+Uvx3NZ3KgNwOKcwkqPE5pSQkmk7OrwKxZsxgwYAClpaXs2rWrPukLDQ0ld38VW5cfxVBhJmloOKOvSMIvuHMsT2hOwZDFUkZh0TcUFHyJEFZGjfwFRVFRV1eITheJojj36M4pryUu2BsPtYplqXm8u+kYmaW/76OrUSns+sdFlOxP5Yf/vYHVUEPcsLFcNPs2giIiWvLhnpOz+bIZW4kJdYAWjwgfrGUmSt7a86fmy2qCAr7Ae/o0HHGTsOQZ8Ij0Ru3v+vcgmdg1oDUSu88//5z09HTi4uJITk6md+/eBAYGuvSa56O6pJhf3n+HrD2phCd2Y8qdDxDRNenMB5cfgy2vwt7PQVHBzDdgYMu+QZysbg3v4kefcTFYLXaOH6wgoX/IWadbn80o4P38Uu6JC+eBLuH4tNJoBDgrHFOXbqfLjy+Q9MXHlNX54enjQXD0qY1hHWY7hS/uQNGqCLioC95Dmr5FWWMIh4ODm9bRY+QYtJ5eVBUV4hsS2qy9UjuzbV99wvZlnxHfbyBT7nwA/7Bw9hlMpFbXMifWud3VXQez0SkKV4QHMi7En6IjzoKeyK6njozu3XcXZWVriYq6mh7d/45G07yG3EarEeWoiZr1x/lJs5HVcTu4rfdtTIgaj8efet5Vf7cK/6lTUNxQJGNz2NiYt5GKugqu7nE1QgheS32Ni7pcRL+wfs0+//E6C0vyy/i0sJwKq53u3jrmxIQyy09LWWkpERER+Pn5cejQIZYvX47N5nyjVhSF4OBgrph1Ffl76khZfQQUOzc+NYHA8NbZy7q12Q21GHf8hu+FFzYpqaup2Ud2zkLKyn5BCCsBAUOIjrqGyMjLUTVyNNZss5NVVkt6YQ3Hy/Q8cFFv8tIP8uEb77BSN5QSXTg6jYqkcF8GxAXywiznc6TaZMXfU9OqBWpCCBx6K9YS55Zq1hIjPkMj0cb5YUorp3xpmnNqd3ayy2ORid2Zb78TuBMgPj5+SE5OjkvjKSsrQ6vV4u/v3v3lzkUIwZFft7L+w4UYq6sZdukVjLvh1rPfoTLHmeCNvA/CejinbFEguGnTon+ebtV4qBh8cReGXdK48xWaLTx3rJDlxZVE6zz4R7doLgsPbNU/fLtej9rPj69eTKEkR09C/1AGTYknqltAfRzm7Gqqf8jCkqtHE+FNwLREPHsGtXicpbnZrHnvLQqPpDNpzj0MnNr6C3w7GuFwsHftT3yz8hsOJvYha+Bo8lQeeKoU9ozuQ6CHhppyE2s/SCO2VxDDZ3Y967kcDitZWfPJzvkfXl7x9O3zOv7+5z+KmlOVzaa1P5J4IJiEumjUQTp0EyMJGhrX4HPKVlmJtaAArz59zvu6jWaqgtTFzhH+MxRg5dTkcM1312C0Gekb0pfre1/P1ISpDbZbaUid3cG3JVW8n1+Kp0rFysHO7RlLLdb6dY0Oh4OKior69XvFxcXMnDkTHx8fVv+4lm2/bUGj0RAeHk6AbzBxCdEMGzYMjw7ywaj07bcpe/MtEr9ZgWevXo26j8mUj1rtiVYbQknpz6SnP01U5Cyio6/Bx+csgwENKMnOZONH7xMcE8ukOfcAYDTbOFZa62zFcmIdn4daYdEtzt6QV7yzlSPFBrpH+NIzwo8eEX4MiAtkSBc3TKFb63Ac2YzVaziKh6pVltzIxK4B7u5j19aYjbVs+XwpfiFhDL/sqkYtQgacu1kc+g4GXAfjHoWQM7RTOYefFx0gY2fJKdOtTalu3VFl4Omj+ewzmLg/Ppynu0Wf9znOh37dehS1Ct8Jv6+xMBks7N+Qz/71edTVWons6s+Iy7oR29P5oiOEwHSgnJqfsrCV1xH+0GC0US0zKmCtq2P78s9I/f4bdN4+XHDz7fQe17RP5NLplhVVcP+hXBQhiC3IYoa/Jw9Nm0Kgh4ajO4vZ8MlhhBBMuL4nPUc0vA61svI3DqY9isVSyrChX+Pn17gka0/JHj48+CF9f4vk4qoxVPnWEjKxG5EjuqE0sogo9447qTtwoNl7yp7Tr/+Dnx6HOzdC9MAzHmKwGPgu8zs+S/+MrOosgnRBLJq6iB5BPZp9eSEEersDf42aMouNodsPMjzAhzkxYVwU6o/6LH8X5eXl5ObmUlxcTEFeIXm5BQiVnXtvf5iwWH/Wrl1LXl5e/dq9iIgIwsLC0Onaxz7KtspKjk2+CJ/Ro4h9881zHutwmCktXcv/s3fWcXaddf5/P8eu3zuumWQm2iR1N+pKXSiFAkVbXJYfUmAXWJzdxZddoJRSWCqUUlrq7m1Sb+M+7jPXjz+/P86dyUwy8aRNm/t5vZ7Xc1zu955zPs9Xu3v+yvDwk7S1foaZMz+H77uAj6LsnOY3OzzIUzf9mSWPP0Q4Fue4y9633QPQv73QyaudoyXil2M4b3PGgnp++4GA63zqLy9SEzOY2xCQvrl1u15Dd4t4/D/h4e/AJ5+Duu0jyLuKMrHbBsrEbutY+dxTLHnsIU798MdJ1tRtecNMDzz9C3j+D+BZsP+lcML/22I1i6GuHK8+2smR57YRS4XoWjmClXe3am7dXnhScmPPMEdXxJgdDdNrOehC7FTeq63B7uxk3UUXY7S20nrzTZs51zu2x/Kne3j5wXaOPG8m845qwLE9hABNV5Guj7lqhMj8INI2/0IfobYU2i749dz9q/9i2ROPsP/JZ3DCFR8kkth7tcR7O3Klsl639Y1waX0llzRU0Wc53No3wgW1KTKLn6L14MPQjBgP3/ACq1/I0jCzgtM/vJBU7fbnhHOcNN09f2V6y0cQQuD7zhZzeknXp+fpVXxg5dUUYw4fr/sQZ6ROoe7Qth026+9qTdltQkr476MgFIePPbwdm0ue632Of675J9885pvoqs4DGx4grsc5uvHoXR6cpB2X67uG+GP3IN2Ww7SwzpVNNby/qZoKfcvvBt/zWfJEN8/csQLXVDjgxGa82l5WrVlBf38/juMAUFFRwec//3kAXnnlFVRVpa6ujurq6s2qa7zZ6Pvhjxi+4QZm3vEPQrOn1rRJKVmz5sd09/wVxxkhHGqiseldNDVeSji8awPmlc8+yT2//inS8zjk7PM56qLLCMd2Pp/gYM6iaHu0VEVxPJ93/+aZzWrofuKkWXzlrP1wPZ+/v9TFvIYEs+u2r4buVlEYDvK/zj8fLv7Nrh1rO7HPETshxI3ASUAN0Ad8U0r5+y1tXyZ2W8erD93HI3/8LQLBse96L4e+84Kt1+DL9cPTv4TF1wYJjk/71vgq35esf2Vw3Nyq6gpnfnQhbQfV7tF7+Ojr63hiJMeX2xq4sqkGbTf4tUnbZv0V78Nevz6oAztt2ha39b0gwkpRFV64dz2vPNzJgSdPY/8TmgnHSmahokvPDxchXZ/4cU0kT2qZOsx+CuSGhxCKQqyikuHuLgqjI5uXkCtjuyCl5IGhDH/rG+H+wTRFXzItrPOl1kbe3Th1Lsf+9Wn+7+v/j2hS56Iv/z/q2rZsgt0WisUOXnzpCmbP/ir1de8EwHRN/rniDpSX8xyzYQFexmb4GJj9zsOI6ruWRif31FN0XHU18RNOYNqvfrl7I2XXPQF/PBcu+DUccsVOHeKyOy9j2fAy2lJtXD7vcs6fdT5xY9cSCru+5L6hNNd1DvL0aI6nj5pPWzREwfOJbmVQWczZPHfHOpY80UU0YXDFvx+NZiiMjo7S39+P67rsv3/w3P3iF79geDhIlquqKjU1NSxcuJATTjgBgFwuRywWe1M06U5PD2vOPIvkOefQ9IPvT1rnunlGRp+ltuZUAF57/bOApKnxXVRVHYcQO///8H0PK58nkkgy2tfLUzf/ieMvfz+puj2TYWFiDd2VfVkOaE5x7OwaVvfnOO0nQak7IWB6VZQ5dQk+cnwbx8yqxvF8pGQ8Qne7cO/X4Ln/hc++NF4DeU9inyN2O4oysds2MgP9PHTd/7D2xcXUts7kjI99mobZ2zCT5AdBUYPKFSvvw33+L9z42ofIjPi7bG7dUSzPF/nXVV08MZJjv1iY785p5vjKXfOD6P3+9xm54U80//IXJE8/fbv36149ygt3r6d96TBaSGXh8U0cdGoLiaowbtoic/8GCi/2IcIayVOmEz+mEbGFF4zve7zywD08eeMNtB18GOd+/iu7dE/7KnwpWVe0mFUqV3Xq4uX0WA7n1VZwSX0lR6Q2/wD7vqRz2TDTF1YjpeTVhx/hqZt+j5XPc9RFl3HURe/aqTq7xWIHry/5HJnMK1TXnc9zbhsjT/Rwbu87qPASaG0JKk6dQWjW7vMfHYuUrf3CF6i5+qrdckwA/vpBWPMIfHE56DtX1cLyLO5ffz83Lr+R1wZfI6pF+eLhX+Syebsn9UWnaTOtFFzywdfW0me5fHhaDefVVhDeAskb6MjSuybNAScFg7mR3jyVDZO1nY7jMDg4uLGcWl8fTU1NnHLKKfi+z/e///1x/70xU25rayu1tXt2kAtQeP55ur/+dWZcdx16czNSSjKZl+nuvoW+/rvwvDzHHvMIkcj0XYqWnYj1L7/AY3++jkR1DRdf8+3dcBc7j6lq6K7szXLNO/fjlP3qeWr1IFdet4i2mhhzGxLjPnzHzKomFdnCM53ugp8fBIddCef81x6/hzKx2wbKxG77IKVk9aJnePj633Di+z7MfsdtO2/PUFeOrpUjHJh6FO77Os8Nnk3NjEraLroUpeWN/U9KKblnMM03V3fTYdr817wWrmiqZtRxMX1Jja5ttyav+MorrH/35VR+4P00fO1rO3U9g51ZXnqgnVWL+2mZX8l5nzl4fJ3dnSN973qsNaM0fPHwKU2z/evX8sDvfkXv6pVMP+BgTvvoJ6ls2LP+hG83LMsVua1vhNv6Rhh2PF4/biExTWVD0aIpZKBv4f+QHTZ58A9L6V41yqVfOXy8zFwhk+aR63/L8qceo2Z6Kxd+6Rs7pY3wfYcnXvoS9uidDLmCRPuHmOeexLSzFhJuq9iVW94ihm+4geQ556BV70QW/qng+3DTe6FmNpzx3d1yyNcHX+fG5TdyzsxzOLbpWHpyPSwdWsqJLbuWE28Mf+ga5PedA6wuWFTpKu9rrOYDzTXjxG8qdK8a5e//9SJzjqjn2ItnE6/cto+d4zi89NJL44Svv78fy7I4+eSTOfHEE8nn89x+++2TSF9NTc0OVdfYFqTvIxSFbHYJS5Z+kXx+FYoSob7+XJqbLiOZPGS3ELrB9vU89ufrWP/Ki6TqGzjhvR9kzlHH7dU+v2sGcvz9xa7xwI324QJSwp2fPp4DpqV4ZHk/d77SvZH0NSRoSoURd34WBlfDB+/a42XGysRuGygTux2DbRbRQ2GEELz60H2EojHmHr3xQd20dqsWUrnye8cSVvOw6HfwzK/AHIVD3g8X/OoNv/6i53Nt5wBXNFVTpWv8pqOfb67uRgDVukZ9SKPO0Pnl/BnUGBqvZQtsKNrUh3TqDI16QyekCLL33EPitNN2OWVEdtjEsTyqGmNkh00e+8sKDj59Os1zK/CGTLRSvdvRu9cS2a+K0MwKVjzzBHf94j+IJJKc9IGPst9xJ+7VL8q9DU+NZPnGqi6W5U1UASdWJri4vpJzt6KlGcOal/p55E/L8TzJCe+ey37HNGz2269+/jlevOt2LrrmW+jG9jvTvzbwGl7OpnVZFblnu7nvmNuYFX+a+pqTmT//+9s+wG6AdBzszk5Cbbsp6bfv77GP3P+88j/8+uVf0xBr4LK5l3HxnIupjuwaMZVS8sRIjj90DXLfYJovtjbwxbYGfCkRbB5E5lgeL963gZfub0eogsPOmsHBp7Wg7UAB+rHqGpqmEY/HGRgY4NZbb2VgYADfD9w4hBBceumlLFy4kGw2S1dXF1VVVYTDYUKhEIZhbNc7IPPwQ9gLFRQjTFXlMTjOCK+8+nEaGy6ivv4cNG33RXSufO4p/vnTHxGKRjn6kss56Ixz3pKplgq2y+r+HPMaEoQ0lZsWtfOzB1fRm9lYQzce0njyX46mIpl8Q6pQlIndNlAmdjsHKSU3f+urdC1fQtvBh3HqRz5BMRfh/muXkB02t2xuNTOB/12iAQ5+L7gWdL0IM3at4PrOYnm+yHOjefpsh37Lpc926LMd/n7IbGKqyjdXd/GbjoFJ+6Q0ldeOW4ihKNzaO8zruSL1hj5O/hpCOrOjOx4A0bFsmAeuW0Ix61A7PcEhZ0xn1iG1yKJL/y9fwkvbhOdXEXpHDc8//g+OvvQ9ROJvbjWLtwJGHJc7+0fZPxHh0GSMJbkiX17RwcX1lZy/A2W9nrxlFa883EHdjASnf3ghFfXb9m9zTJM7f/oDjrro3TTvt3l+K1/6PNH5BLe9cAvzVjRwdvp4dKkRObCW5OkzIOUghIqmxcjlV6GpsV12XN8aev7138g+9BCtt9yy85GyngvZHqjYs6XqxnLi3bT8Jp7teRZd0Tl35rl8+9hv75aBTodpE1MVqnSNf/aP8qN1PXyouYbLGqqIb1LbNz1Q5Om/rWbtywPUTk/wrmsO3+Vr8DyPoaGhcc3eQQcdRE1NDa+88gp///vfJ20rhOCjH/0ozc3NLFu2jKeeeopQKDShFZgWf4XBnr/iVYNhHEpD/fcnbZNMJlF2kYQ7lkl2aIiqpmasQp5Ft/+Vw8+/5G35nppYQ3f9YJ6vvXP+GzbALhO7baBM7HYevufx5M1/46V7bgEkR5x3GQNds9j/pOm0HVizfdGtL/wR7vwstL4DTvgStJ3whtfd2xpGHZdO06bPdll12+10rlyF8r4P8O8HBXmxrlnZyV96hrD8jf/rKl1l6fFBIs2vr+zktVxxXNtXH9KZETG4oC5IfZJzPaKqglK6Z9fxWPFsLy8/2MFoX4GK+ijnfmoWj9/we1KDKWaFDkLaHrEjGkie2Yoae+uNgLeIwjCYaahs3eX/QMHzeWAoiGh9eCiLIyWfbKnj32bvPCla9nQPo30FjjyvbVJ94K1hqLOd2374LTKDAxxy1rkcf/kHMMKBFvah9of4xYu/oH10A/+3+ofEvSjhQ2qoPKUNvWayT5qUkudfeBeFwmr2m/dd6uvP3en72Bp2S6Ts8rvg5vfBh+6B6Ufv/oucAmvTa7l5+c04vsO/HfNvADzW8RhHNR5FWNv16hGPDmf4wdoeXskWiasKlzVU8aHmGubEJh+7Y+kwxZzN3CMbkL4kPVikom731om2bZu+vj5GR0exLGu8HXHEESQSCVasWMFzzz03vry65mFqa19BCAitNnBmXsnjT+WRcjI5/dKXvkQsFuOxxx5j8eLFmxDDEJdeeimaprFy5Ur6+/snrdN1nUL7Wp666Qb0WIL3/+Cn6G9CAux9BWVitw2Uid2OY1Nza32rQNeeYvXiZ7niez/ZdmDFRNgFePGP8NTPg1F+y9Fw4pdg1ql7FcHLPPAAXZ/5LJXvfz8NX5/sVyelJON69Nku/bZDwfM5oyaoNPCf63p5ejRHv+3QZzlkPZ/94xEePCJIA/POF1byarZArbHR1Ht4KsanW+pY91I/f3v+cUZWPkE0m+aAhSdwyrvehf/8AIXXBmn44mEo4d2bwmWPwinC8DoYWb+xjW6Ad/5noN15+pdw/zegYgbMPQvmnhkUjNd2LDeYlJJ3LFrO6oJFg6FzYX0FF9dXckA8skMjaulLXn6wg3BcZ/6xjTt0DRNhm0WevPEGXrr3TuI1tZzysU/Q2riQFx98gv9K/J4r9/8gJ5pHEG5MolVumYQUi+0sWfIvpDMv0dhwMXPnfhNN27UI0amwy5Gyf7oY+pfC518H9c35f64dXcsF/7iAilAFF8+5mMvmXUZzfNdz9b2YyXNd5yB39I8yLWzw1FH7bfE/tfzZHh65YTkHnDyNI85tIxR5Y36LfH4N3T1/pXXGJ9H1JL29dzC64lGcr91N81XXELnsMrLZ7CRSaFkWBx10EKqqsmzZMlatWjVpnW3bfPzjH0cIwR133MGLL7446ZxCSuLLX6Bh9lz82fuzZkM7qqqOE7+KigquvPJKAJ5++mmGhoY20xYuWBBotAcHB5FSjq/bXjPzvoQysdsGysRux7Di2R6eu3Md2aHNza3969dS1xqkelj+9OO0Hngo4fh2fngcE176Ezz5U4jVBAlN95KHeVK+uv/78y751RU8n5zrURcKNG039wyzpmCOk8I+y2FBPML366Lc8V/f51vHXkguXipHJSUxS3Kip/OTQ9uoaIrzs3W9sLiPpuYk0+fX0BAxqDd0IruYC3Cn4PsBOZ9I3EbWw7GfhsaD4PXb4NYPbdzeSEBVK1z4v9Cwf0D6Vj8Iqx+CtY+CW4RQCv7fiiCq0rVBm/zbSyl5KVvgtr4RFo3muefwuahCcHvfCDWGxjEV8S0mod0a8qMWD16/lM7lI8w7qoHTPrRrZYK6c9386f5fEbm3iyMrT2Wa0obQFWo/eTBGw/ZrxXzfZf36/2bd+l8RCU/jkENuIBLZ/SbPsUjZ6o9fTV0pN9v27bgOfnEwnPhVOPma3X5d2wspJYt7F3Pj8ht5pOMRJJITpp3ANUdeQ1N8103ZA7ZDh2lzaDJG0fM578VVnF9XwXsbq6kp5UUrZGye+8calj7dQySuc/SFs5h/TOMeKSPoeQX6+++hq/sW0unnEULjwAP+l5qak5FSsv6yd+MODjLr3ntQdjGJspQS13WxLIvVLz7P/b//NdHKak591+Xsd8w7WLV6NX19fZOIoa7rnHfeeQDcdtttrFmzBsuyxku61dXV8clPBrWsr732Wjo7O8fPJ4SgtbV1nBjedttt5PP5ScSwoaGBgw8+GICVK1cihJi0PhKJvGWSR28P9jZi9xZSL5QxhqGuHMmaCHpIxTY9ElVhjrt09mbm1jFSlx0e5J5f/YRwPM7JV36MeceesO0Rlx6GIz8Gh34Asr0BqSsMw83vh6M/AfPeuccjjaaCtG26vvAvADT/9Ce7HCwRVZVJubK2lBvNtW30cIj/qlAI7ddKv+2yfqjAig2jiJUZ/nLXItoOq+Uns33sWgl2Gl5JA/Chpmp+MK8F2/d5zytrqTM06kJ6YAo2NA5ORpkVDW9/VZGJMDOBlm0icZt/Psw8Ebqeh99PSP0iFEhNg1wpNcX0Y+DS6wJTa2VbkApn4rmr2oL/wJEfC7R7656AwRUbU2X8+WKwczD3LLpaz+AvfgN/70+ztmhhCMHpNUnSrkeVrnFh/c6XFlr3ygAP37Ac1/E46Yp5LDh+54nA0qGlXP/69Sxa8wyf634vR1SdjTQgcXwLyv4xOnuWMrPhiO0+nqJozJz5OaqqjqOj43pCoT2TA6zqiivwhkdInHbqju34wh9AqEHahzcRQgiObDySIxuPpDffyy0rbuGedfeQMAJfrzWja6iP1u90TrxaQx/3zRx0XCp1le+v7eE/1/VyQX0FH2qu4dBkjJPfP5+FJzTzxM0reeRPy+lYOsyZH9u9OSZte4innzkFz8sRjbYxe9ZXaGi8mJBRA4A3MgJSUvvpT+8yqQMoZtIMd3UybcH+HHjcOxBWgYUnnoZWejfOnTuXuXO3bLW5+OKLx6dd18W2bTzPG1922mmnbaZRjG+iIDBNk3Q6Pb6+ra1tnNj94x//IJ/PT9p+//3359JLLwWCHIObEr+5c+dy6KGHIqWcwj8xRGVlJalUCiklnudtMULZsiyEEBj7mBm6rLF7i2BTc+uJ753H/ic0b3deo761q3ngd/9N39pVtB50KKd+5JNU1O/gR6j75UDDM7wW6vcPKlnMv+ANJXi+ZdH3/R8QO/64HcpXtzNYvfhZFt95G5d87dsY4cgWf+v8qMUrD3ewanEfl33jCHKaYO1LvXS92k+faTMzFeW0i+eTCStc+do6+iyHftuhWPID/PrMRj4zo572osUJi5ZTWyJ89SGdOl3l0pjDYXYn+eF21qWHqG+YR/WCs1CyPfCT+ZMvJpwKklAf/uHAP+71v5WIWyukWkDdfT6A/U/+GrH6QWrXP8zDlUdwxQE/4jglw8XzDuCcmhSprVQP2F4MdeW46TuLqGmJc8ZHFm6Wn2xHIKXkM//4JM8XXuKy2Zdx2TPHkzywgfgxTShhjUdv+B0v3PUP5r/jZE6+8mM7XSXEcUZZvuJfmT3rK0QiW06UvbPwcjmGr/sD4YULCC9YgNaweSQwAL4HP1kALUfAu/+8269jV+FLH0UoSCm57J+X0Z5p57xZ53H5vMuZXblzdU4nYkXe5PquQW7pHSbv+Txw+FwOSAT+dVJKVi7qIxLXmb6wGsf2sIsusdT2Ey3XzVEorCWfX0U+vxohNGbN+iIA69b9korKo6lITR20IaUEKTerjrMjcGyLF+/6B4v+8VeMcISP/uo61N2YgmVXMPFdOTAwgGmak4hhKpVi1qygzOWdd9652fqFCxdy4okn4jgO3/ve9zY7/jve8Q5OPfVUCoUCP/7xjyeZmYUQ1NXVUSgU6Ozs5IILLuCggw7ao/e7t2nsysRuL4fvS155sIPXHuuc0ty6Y8fyePm+u3nq5htQVI2r/vsP6OEddGT23IAsPP4fMLQKaufDRx8MyhTtYeyu5JzbQmZwgIf/8BvWPP8sNdNbOf+LX9uunHS+56OowYfq5u8tRvg+h8+pIJG1qf3IAQhVIB0foSvjNTP7LIeUm6Mu30nfYAf/MwIDegV9kcYgMjgzyPdW/ZxL+x/gueQBXHBIkJJGFVCra9Q5w3w7leeY+gY2RJp5tKBQb+jUhQL/wFpDw9iNxDvretw9EARBPDGS5VPT6/h6g4G76kEG1jxB44zDAlJZHIFbPxL45c09MyCWOwAz74xXAVn70gAz9q9G1XfsPhzP4e51d3Pjshv5+YwfIp4cxRrOk/rC/iRjqc3+T67j8Nzfb2HR7bcQjic49cMfZ+7Rx+/QOSGoN/vKq0Fi4f3mfYeGhvN3+BhbQ/HVV1l/+XsCUzugVlYSXrCA2s98msjBByNdFxQlIA3ZXrDzO1wr+o3GWE68e9fdi+3bHNlwJFcfeDVHNh65y8fOuh73D6a5uL4SIQTfW9MNwAeaa2gp5cRb9M91vPxAO4e/s5WDTmmZ9F9znAz5wirMYte4LJcu/RI9vbeNbyOETip1CIce8uetVoMovvIK+vTpaJU7r8GWvs+ypx7jyRtvIDs0wKzDj+aEKz5IVdPuH0S82RgzM29K/JLJJDU1NZimySOPPEJ/fz/Dw8Nks9nxlDSNjY3MnDmTAw88kPr6+j16nWVitw2UiV2AfNoaHz3e+qPn0XSFA09u2S21W7PDg/SuWcWcI45BSslQxwZqprfu2EF8D5b8PUiNclYpp9eGZ2DaEXvEQdvu6KDrC/9C4/e/R3grZoVdge97vHTPP3nq5j8hpRwv2bajo2Dfl6x8rpcX729npCdPvDLEQcdE2W/GCCO3Q6SlSPLyM4ISZb8+FvqXTD7A/PPh3X8Kpp/8GTJciahqZSgxnWe8JH2uT7/t0mcFqWC+OrORgxJRbu8b4eNLN2x2Pf88dA6Hp2I8OZLl5t7hkgl4I/k7KBHdLh/Azy1r5x/9I5i+ZHrY4OL6Si5tqJw6lUzPq/C3j8DgymC+dr+A4B3xsa2m3QiqRnTy3B1rueDzh4wnG94RZO0st668lf9b+n/M7mvkytELaMnXo1aESJw4jdgRDVusHgJBsun7/vfn9K9bw8lXfoxD33nBDl9DsdjBkqX/Qjr9Ig31FzJv3rd2a04yv1jEWrGC4tKlmKXW+O1vEzngANJ33UXvN79FeP58wgsWBJq9+fMxZs7cvSXK9gBGzBFuW3UbN6+4mU8d/CkumH0BeSdP0S1SE6nZ5eNLKfnMsnZu6xsB4MyaFB9urmF/R+Hp219k/UsWqdoYB5+/Hlu7m3x+NbbdX9pbcNKJr6GqEXp778A0O4nFZhOLzSEcbkHZRlJm37JYc9bZGK0zmPGHP+z0PXQue52bv/VV6mfO5sT3fZiWhQfu9LHeikin06xbt461a9eydu1acrkcAFVVVcycOZOZM2fS2tpKNLp7o5+3hjKx2wb2ZWI30dzauzbDlT84lkjcwLE89NCeeSGvXvws//jP73LAqWfyjvd+cOfzG42sh18cEkRQvuOLcNDlu83s59s2G957BfaGDdusA7srkFJyy79fgx4Kc+qHP0GqbjtHeVIG/ocj62F0PVg5OOxKpC/Z8D9f46UVTXTbCzkl+Vvq9dkUvNMRYYPkKS3ElTsQirfRXFoxA8I7ZwJ0fcmgU8r9Zznj5O8DzdXUGjq39g7zg7U99NsuzoTnftHR85keCXFt5wB/6BykLqRRrQjCZhHVtvhCSw0NDQ38e/sgErikvpLDktHt054OrYFV98PKe2H9U/DJZ4PqB+3PwmgHzD4VooFfYyFj89Afl9K+ZJjWA2s45f37EUnsmG9Mxs5w1t/OImtneXf4fD740lmo1WGSJ7cQPbhuq4RuInzP48V77mDBCacQTaYw8zlC0R2rJer7Lus3/Jp1635JY+MlLJj/wx26l51F8dVXSf/lOsxFj2IOSaRlAzD74YfQm5rIP/scTmcH4QULCM2evct+qnsCnu/h46MrOn9c8kd+9uLPOLP1TN6z33s4sObAXdbcrx5dx7XrV/H3dIq0H+IScScX+9czo/rvPHdbARm7l+ZDFlHfvP84eYvFZhMONyPEzg2sh66/nv4f/ojp1/+B2NE7lnZmuLuT3jWrWPCOkwFY/+pLzNj/oF0y5b5VUCwWWb9+/TiRGxoaAiAajY4Tuba2Nip3QQu6qygTu21gXyR2VsFhyZPdvP5oV5BMuDLEAScFRemNPRyS75gmT9/6F1646/Zdq5wgJay4Bx77EfS8DBXT4fh/CZIe72B6jE3R+73vM/KnHa8Duz2wCgWe+duNHHbOBSSqarCLBfTwFGk4XCsgIiPrIdMJh30wWH7/v8LzfwA7u3FbIwHXdASBCIuvhWwvfc4camY3oda0seQxE+3VIWI5G7UiRN2nD0aNv3EfV19KRhyPfjsgf0clI2SGh7lpbQf3posMOB5poVIIBZq49z73AFHHoqqqiqamJhobG8f78I6Y8q0shEoDhzs+G6TVEQq0HM2G2KU8tGgWtg3HXTKb/U9s3u7/4IrhFSzqXcT75l5B4cV+Fm94jrpT5jC/aj7mihHCcyt3KfLR9z1u+tcvE47HOe1jnyZZs2P1Q0fTLxAJTycUqsVxRlDVxDa1O7uMf34BXv4L8rOvYfelMZcvJ3nuuQgh6P7610n/rWRG1HXCc+YQPuAAGr71TYQQ4+Wt9hasT6/nphU3cfvq28k7eRZUL+A9+72HC2ZdsMX/iJQSy+op+b+tCfrCaubMvoZU6lD6++/ltdc/ha9W8ZJxLgfFdeanGuiKnsk/Bn2O6XA5dl4NtdMTmDkHRRW79C72cjnWnHY64QULmH7d77d7v0ImzTO33sirD95DKBbnY7/6PXpo1/MA7s1wXZeOjo5xItfd3Y2UEl3XmTFjxjiZq6ur2+UEzrsLZWK3DexLxM5zfVRNYbSvwP9961maZldw4CnTtj+Z8G7ExFqn899xMu/89Bd37kBSwqoHAoLX+yp89mVI7Xy+qsz999P12c/tUh3YqS9TsmrR0zzyh9+QGx3hjKs+wwFHHjwhsvS8IPpz8bXwxE8h0wVMeFa+2h4EKrx8I3S/tFHjVtkKlTPA2LKT/6I71/Life1UIpnXFKPh8nk0zEzhDptT1qHd3bBtm+7ubtrb2+no6KCjowPTDMrxRKNRpk+fTktLCy0tLSRTKQb6++np6aG7u5uenh7S6fT4saqqqmhsbJxE9iKR7Sgw7/vB77byXlh5L4tX78ca5yRO/8oFVDfFofd1qJ4dRGdPASklz/Q8wx+X/JHnOxdzXvYkPpa/DJl2MNpS1F51wG7zx5S+z0v3/ZMnbvwjiqJw4vs+wgGnnrnDx5fS58WX3oeUDgsX/GSPpEUBAgL9X/sFJv2L/mfz6/B9nPb2wIS7bBnmkqVI22bGnwPzf/vHrsLt7QnMuKUWmj8fdXtTJe0h5J08/1zzT25cfiO10Vp+d8bvkNKnP70U1e0nn19FRcWRpFKHkE6/zPMvXDK+r65XEYvNYWbb56msPBLXzeN5eQyjdpIcr+8a5N9WdWFLyfEVcT48rQb1ri66l45wzEWzmHdUw04NEgZ++SsG//u/af3rX4kcsO0oXNe2eeneO3nu77dgm0UOPPUsjn3Xe4mmKnb43Hs7fN+nr69vnMht2LAB13URQjBt2rRxjdy0adN2a33e3YkysdsG3u7EbqK5NRTVOfvqoCJCZrBIsmY7Poh79No8Xn3gXqIVFcw96jh8z8P3/Z2rJyglDK6C2pI/3N8+Bk2HBJouY/t9Hzqu/jju8PAu56sDgpQdo+2k177Kww+9zNpXXqG2oZrTG9fS6K0Gp7Bx208+C3Xzg6z9y+6cbCqtbA1KsO0CcShkbF57tJPXHu3EKrgcelwjLcuHCM+uIPXONvT6nY/+3BTZbHYSievp6Rl3MK6pqRknctOnT6eqqmqbhCWfz08iej09PYyOjo6vr6ysnET0Ghsbp/R3GerOYeYcmudW4g934qe70dqOBM+B/5gV9DNPDnzz5pwBySAp8YrhFXzjqW+wfHg5p9rH8pmuywmZGkZrkuQp0wnNqdgjQTajfb088Ntf0P76q7QsPJBzPvslYhU7Zv7p7b2D5Sv+FYB5875NY8OFu/06WXwt3PVF+OhDMG3HvzVDv7+OwqJFmEuX4g4E5fuixxw97hc28te/ojc1BRG5b5D5y/ddisV2hBBEIq0MF7pYs+ST5Aqrkb41vt3MmV+krfWTuG6e3r5/EIvOJhabhWFsf83aQdvlxp4hru8apMtymG8YfPLJAv3rMtS3JXnHu+dS37pj7hLd13wNv1hk2s9+ul3bD3V28McvfYq2gw/jhCs+RPW06Tt0vr0dw8PD40Ru3bp1FItFAGpra8c1cjNmzNgxi8CbiDKx2wbeCGLX96Mfk3vkEZRUEjWZQk0m0erqqP/KlwEoLF6MOzoarEslUZNJ1FQKJbbzH1sz77D0qW5ef6xrPLr1wJNbOOT0vfeBff7O23jt4fs5/WOfZtqCXcj1ZOfhL++G9U9ArBaO/WwQObkdkbTScfAyGbTq7Xgx+z7k+gKNW2VrQAS6X4J7vhosy/UCcH/PbJblWzju8is5dH4NyqJfb6Jxa4Wqmbs1NciWYJsuy57uobo+SmqwSObhdnzLI3pYHRVntqImd8yM7fs+AwMD40Suvb19nHRpmkZzc/M4iZs2bdpuczAuFAqTyF53d/cksldRUTFO9hoaGsisU1l8ZzsVdRHe/fUjJ2tBPBfWPlLS5t0H6Q7yQjB44v9jxknfYGi4j68+/FXOPug8zoqeQv7eDpInTyc0M7Vb7mVrkFLy2sP38dpD93HZt36Ibuy4m0Gx2MmSpV8knX6e+vrz2W/ev+++wAop4X+OA0WFqx/f5aTiTn8/1rJlCMMgdswx+JbFisMOh1IiW62pkfCCBVRceCGJ007buVyMky5/Y6Ty+vW/JptbRj6/mkJhPVLaNDZczIIF/xHI4bVPIPQ6Xhrt5b7uV1mVz1GfaOPy/S7nwtkXEtN3bXDk+pIHhtKkXY9311ex9Nke/nVFJ/utKnLFO2ez8Pgds0RIx0FsZZDctXwpG157iWPfdQUQ+NW9XSJd8/n8pICHsXdDIpGY5CeXTO6cf/GbjTKx2wbeCGI3cvMt5J99Bj+dwcsETQmFmHnnHQC0X301+ccen7SPPn06s++/D4Dur16DtXZtQPiSSZRkgtDMWVR94P0A5BctAl+Ok0IlleL5R/p5/q71NM1588ytO4r1L7/AA9f+msxAH/uffDonXPGhnc7tBcCGp+GxHwcf7UgVvPeWIMfWFBi55RYSp52GVrVJwmArFyTkDSWD6Mp0Z+BPNLIeRtvBDUyKnPfzQDvYvxzu+iLdXiN6VTO1s/enYNThJmaQbG7d+XvZQ3j57nWk799AW0gFTVD7L4cRqd6yJte2bTo7O8dJXGdnJ5YVaDDi8fi4SXX69Ok0NDS8oaaMMbI31rq7uxkdypFIzyVkVePHMtQcbNM8o2Gc9MU2GTz15/v4vxd+wV833MMB4f34ceL75J7qICyeo/qwdUGps5knbfTde4MwRkAc0+S+3/yCYy55D9XTtt+06vsuGzb8Lz29f+fII27ffcTOc2HRb4NE1At2b5qV8VOMjgYm3KVLMZcEEbmV730PVR/4AE5PD+vedRnhBfMnmHIXojc3bUb2crmV5HLLx/3f8vnVRMLTOPjgQDP47HNn4ftWELgQnU0sNptE8gDisTmbXZPt2dy/4X5uXH4jrw++zn2X3EdDrAHLswipu6fCwYq8yTkvrCTn+RwQDfPR6XWcHo6QSoS2WKvY6e3Fz+cJzdpyupmR3m6e+Mv1rHruaeJV1Vz5H/+9/RWC9lLYtk17e/s4kevtDQbVoVCI1tbWcTJXU1PztihPViZ228DeYIp1+vrxhgYD0pfO4GXSCF2n4sILAej/yU8xly7Fy2Tw02m8TIbQnDnMuOGPAKw+5zy601E6mk+ipetRagdfRTvuFCq//SNqpsXp+NSnkcXiJI1h+ID9SZ5xBgCF559HRCKoqWCdEo+/ac7MjmXyzN9u4oV//p1QNMaZn/gcsw47atcO2rEYnv01nP+L4IPc+3rwIYpUgO+RueMWur7679R88hPUfuJjcMdnNvq+5QPTECd8GU75ehCNesP5m5hK26DxQIjXYeZzPHnjDbzy4D3MOuwoLvzSN3bt2vcwpJR0LBtmyd3rcdsz9CgKB5zYzMHzqwjPqSCTy46bVNvb2+nt7R3XktTV1Y2TuJaWFiorK/eql2ZuxOSW7y/GLDg0HaJiJ/vp7e1heHh4fJtkMklTUxOiWvCU8xRPDD5BpZPg8/aHOKRrNsKDyGyNhHYrRvdfwUqDogc1bC/638BE/gaid/VK/vaDb+KYRY659L0cft7FO5Qex/ctFCWE51l0d99Ec/MVez6wYg9gjOjanZ0M/uq/MZctw1q9Gl9zcRskiS9cjj87hp3upbn3VMLzF7Ak/W+MjDyNECqRSCux2CxSqcOYMf2jQEB+d+a36Mh00JIMSPbVD1yN4ztcPu9yTp5+Mrqya1r4nOvx174RruscYFXBIuZKPvWizaXnzmb6ws2tCt1fvYbM/fcz57FHUROTybuZz/HMrTfy8n13oWoaR1xwCYefc9GO5xbdC+B5Ht3d3eOm1Y6ODjzPQ1VVWlpaxolcY2Mj6l6ecmdnUCZ228CeJnajfb30rF5BLFVJrCJoodiOpTHYEsy8w7Knenj1wXXkMh6xqOSQWXmmRYbQ6utInXMOAJ2f/wJOT/ckjWHqnHNo+lGQDmH5gQchbXvjgRWFqve/j/prrkH6Ph0f/ShKYsxEnERJpogefjjRQw9Bui7msuUbtYWJxG7JXTXQvp4Hr/01J1zxIZrnzd/2DttA1s6yNr2W7mwXZ9/9Lcj28I/KaroHM7zjFgNZGyN5yy00pVrQf/MOiNdvDEyobIXGg7eadFVKycpnn+SR639LIZ3mkLPO5bh3vw8j8sblNtpV9K1P8+w/VyGyBQ5NCzJqkUWsY73Wg27oNDc3j5O4adOmbV/QwiawXZeOoWHah0fozGTpzhXoNS36HY8hH0ygTno0qdAS0miNRZlZkaSlqpJEVTVGZDvTnhDI5Om/rWbe0Q3UTNv4kTNNc1yj19XdRV9vH4vsRbxW9Rqt2VauGr2UAwrTyTZJ9KNraZjfQiKRCHzw2p+FVfcFORQ/fF+QQ/HpXwUm+blnQstRe9yknh8d4eHr/peVzz1FXesszvzE58bL+W0venvvYMnSL5BMHsL+C39CJLITLhr5wcB8vfDiHfJj3R0YS+JbyK+lsfFShBCsWPZtOntuGN9GCJ2wXUPF5wcRUuDONgjNmEW8+RDqrvoEWs2u56mbCCkl1y+5npuW30R3vpu6aB2Xzb2MS+Zesss58aSUPDWa40/Lejnu3kGy/UWefUcFvSmFqsowlRVh1EwWed8zfNgT1L3nYu71TNKKJBHTieoqwjZ5+dpfceb0Jo697H2s0cJ4viSkKoQUQUhRiKsKlaUKLm9UgvbtgZSSwcHBcY3c+vXrxy0FDQ0N40Ru+vTp+0Q5rzKx2wb2NLF79aH7eOC3v5y0TNU0oqlKYhUVRCs2Er4x8rdxWcVWQ81v+s5zDHXld9jcKqUE10XoOlJKCosX449rCwONYWT//Umceip+oUD7hz6Ml82Oawyl41DzqU9R+5lP4/T3s/qEEzceXAiUeJy6f/kCle95D05fP33f/e4kbaGaShI9+mhCbW34ponb14dSMjNPJIUTXyyP/un3GOEIR174rq0GV4yaoyRDSRShcO/6e7lt5W2sSa+hvxAk/RQInj3lWqKLf8/3Mys46Pp+6kYlX/mQykCFoCZSwyOXPQLAzctvJm2nmRafxrRE0CpDU2ullj7+MPf890+oa5vFGVd9hvqZu16iaE/DsqzNzKq2bYMP88ItHGbOJGprZHRB4owZTDt+2hZf9DnTZMPgEO0jo3RlcnQXCvSZDgOux5AUjKg6aT1MIRRBTqENjlhFklYRQ/oMh6Lkw5OJgu7YJLMjVOQz1NhF6qVLswItYZ0ZsQj1FRXEKyrx/DgvP5jm1A8upKJuap8n13d5cMOD/GHJH7hkziVcVHUuQw+sYbjJYdQwGWjvZah3kPbR7vF9EonEZgEa4/45d3wWXv4L+E4QuTz7NFhw4R4zTY5h5XNP8dDv/4ealum861+/v8P79/X9k+UrvoGUPvPmfouGhot27EP+5E/hwW/BJ5+Duv12+PzbA9seRtPiKIrB4OAjtHdct0kSXzju2CcJhxsZHHyEbG5pkAcuOodIZDrCk1hr146bcM2lS7GWL2f2o4+gJpMM/u53ZO9/YHJE7tw5u1RT1fM9nuh6ghuX38jT3U/zhcO+wIf3/zC+9BGIXSZLnuPzyiMd/MfQEGuioKcMCKtkB4eJ5gze/2iQCun3pyXprp6sgZwx4vAvyyShqMa/z1fo3uQ2j1RD/Kq6Lgi062pnyPUITyB+Z9Yk+e6cwA/vA6+uxZGSsBKsNxTBsRVxLm8MNIk/Wd+LLgQhRZS2UdgvHuagRBRfSp4dzRMu7RcqHaNS10hoKlJKMpnMpHxy2WxwXxUVFZP85DZ1p9gXUCZ228CeJnaOaZIZGqAwOkJ+dIT86Cj59MiE+aAVMunAEXkTGJEIsYpKIslKFK0Ns9jE3MNM4lUVFHMJUnUpmubWEU1WvCF1+6SUSNMEKVGiUfxikfwzz+ClM/iZ9Dg5TJx2GrGjj8Jau47Oz3wGL5PGT2fGNYONP/wBFRdeSOHFF9nw3ivGj6/E4yjJBI3//h3ixx+HuWIFQzfcwHPDPawb7icZS3D8sScz56JL6DWKPLXmITb0r2Kl28mq7DqGzWHuvuhuWpIt3LryVm5deSuzKmYxMzVzvJ+WmIYiFPp//nOG/ud/if/nd+g/oo3ObCe2b/Ouue8C4Kr7r+KZnmcm3f+hdYfyx7MDE/gNr/0RkTZpbV1AY7iezMurOPjks1D2UtX/6OjoOInr6Oigr69vnDzX1dVNilZNpVIUMhYrb1xOYl0GFbhX9Ric5dNe4zLg+wyjMKrqZIwIZmhz7Z3wfWJWgZRjUek7VAtJraZSHzZoikWYlkgyvSrF9OpqYpt8SPOuy5qRNKuGRlmbzbIhb9LpePT4gn5Vp7iJVixkFjh6eZZjV2n4wmN15QrCxhDNKkwLG1QmkqgVMZ7XV3Nf8Wn6nUGOEYfyWfNKKtbpCE0hdU4b8aM3lnKzLIve3t5JARqDg4Pj6+Px+DjZa65JMs1eTaTjMcSq+6HtRLi0lD9s0e9gxnFB1PNu1oAUc1kcs0iypo786AiZgX4a58zb7v1Ns5slS/6F0fRiWls/zayZX9i+HX0ffnFwUA/4Q3ft3MVvdi09DAw+QD6/utRW4TjDHH7YraRSh9Dffy8bNvymlMB3YhLfaTuUxHdi3rzR2/5O+h//wFy6FL9EHJRkkrnPPoNQFPLPPocwDML7zUPZicCf9en1VIYrSYVS3LnmTv609E+8Z7/3cHbb2YS13WcCLb78MmvfcwXJT3yO6KXvpWv5chbf9WcGetaTaJ7B2V/6BrmiztLHu0hkPayCwwrVI+N6zD+thURTjI51adbd28HsXgeAp/cLUzAEMw6vQ08ZDA4WiCzLcnpaIRTV+OkMSVETaAkdR0DR9ThZi/Cluhr0iMrC5as3u86rW2r59uxmcq7H7Cde22z9lXGVEwc6eLWjk5/NPRLV99B8H0MRRFSVTzdXc9Wc6XSZNp9etmGcVI4Rw8sbqjm2Mk6v5fCn7sHN1h9TEWdGJMSo4/J6rkhkk/W1hk5EVfClRLDzQTl7GmVitw3sDT52EGSeL2YzAckbHSGfHg1e1INp+jZoZIZq8L0IUmaxM39H+oObHSOSSG6i8asklqrYbFk49ub50PmmiZfOoMRiqPEY7uAg+aeemqQt9NMZqj54JaH99qPzoX+S+eb3kdkcw4bOkmm1FEI6cxcehHbpUdz5h2v4zJ1BKg0npOEnosQqa5n+818SmtlGYfFisg89XDIhJ8cDUKJHHolfLJJ7+GEqLr10i9dbdIt057rpzHbSmeskqkW5aM5FdK1Yxu/+84sI2+fvJ3bhqYE28ILZF/Cd474DwPWvX091pJqWRAvTEtOoDle/YS8Kz/Po6+ublHYkk8kAoBsGqaZmtKpqvEiUgqKOJw8e9CQjQmVUC5ENRXB0g6Tpc9Yqk9p2m3jRZ/DAMA/UuQhhUSU9qhWo01QaIiGa4lGmJZO0VlfRXFWBPkW5NyklnuNRHLbID1sURk2KIxbFjIVn+USqw8TroyQao6RqopslapVSMup6tJs27UWb9QMZCv/sJL7OpLte4+9HRhmOTt4nVswTG/xPpFxN2Knni+3v4Xh7LrZvs85aQr+xAaMyRqyiilhlJbGKKuKlPlYZLNONEJZl0dfXtxnZG3uvxWIxGhvqmV5XQe30OTTHfZK/Pza4iNT0jbVsW9+xxZx5O4sHfvsrXnv4fg4790KOfdd7tzuxrJQeGzb8ltra04nFZm+fCW7VA/B/l8Kl18H+l2x92/HzjCXx3Ujc8oXVtM74JDU1JzMysogXX3oPmpaYEMAwh7q6swmHG7frHDsLKSVOZyfm0mV4I8NUXn45AOvedRnma6+BEBhtbYQXLCB2zDFUXHLxDp/j4faH+eVLv2T16GpSoRQXz7mYd897N83x7Y92la6PX3TxTRd8iRI3UKIao3/9K4P/+7803fgXHr7xj6x85gliFZUc9+73s/CkU1GUbQ82HcsjO2xiFVysgjPezzq0jlgqRMfyYV59uHPCumD9u79+JBX1UV5+sJ2nbt1I5iTgqnDpN4/CSBm8vqiXjhf6qTF0tKjKmqSg4Fk4lTm6BwcYGi5Qky7QYGapmtHEkpmziFVWoEWi2FJi+j4X1lVySnWS9qLF55a3Y/kSy/exfEnR8/nXWU1cWF/Ji+k873xx1Wb3+JuFM7igrpLHh7Nc9sqazdb/+cCZnFad5J6BUT70+voS6QuInyEE1+7fxiHJKA8PZfjFhr6AOKqCkBCEfJuvVJhMq2qC+I4lFd9RlIndNrC3ELupkBkscuO/P4dr+5PMrb7nUigRv0lav3RpOj0akMOREVzH3uy4iqoRTaXGiV40tdH0uykJNMJ7PtedL326c92sTa9lzegaDqk7hIPrDubVgVe54u6N2rwaJcUCdRon9cyi97WVXPrdH0FmGOOFZfjZ7CQfwoZ/+1f0+nqG//IX+v/jP5GlvEVjmP3YY+j1dTt8rWYuxxM3Xs+rD95LorqGw694L8qcOjqyHXTmOmlNtnJ229lYnsWR/3ckvvTH9w2rYT524Me46sCrcDyHW1beQnO8mWnxaTQnmoloO/9bm6bJ2g0beGXNWlb0DdBRMMlqOgUjjBmKYBohCppBTg+RC0Xwp9AqhhyblGVS6bhU+z61COqESp2i06gZNCghKgagYnkaVEEHAq8yxKzmOIYAHB/f9fFMD89y8S0f3/GQrg+uBF8ifIkiN1dcRZRHSGk3oIpBPFlD2v0ABe8kHAmuAF9VwFBRwipqTEdPGIQqQoSrQrz8+jBLXx/m8BOaOPAdTYiwxpAGi9JruH31jcxt+QD9XgR3xes8GynSrc/ivA6bGkty8wyDnAaVdpHKfJpkeojYUD/J9DCp7Aip7DDxfA6BJBSNbRwwVVaN9+FEEhOFrGUznMnSPzDAwMDAxiCTsMuhiSFm+aupHn0VxTORF1+LOPBdQTCOa43nzNsVWIUCj//fdbz64L1UNDRy5tWf2+G0QVJKli79IuFwM21tn0XZkvP/Xy6HrhfgC0tAMzY5ho9pdo5XYIgnFlBddTyFwgaeefaU8e2CJL6zmTH9KmpqTsbzLFw3vVkS3zcTTl/fJDOuuXQpkQMPZNovfg7A+iveh1ZdvbFG7oIFW02V5Nseizqf4+ZVN/NI32PMjLTx57m/wS96+KaLLJG2gLx5yPFpF7/ogetvflBVoMR11JgCiRB3PfNL2mYdwsHHnU24OomaMFCTBkrMQKh77nctZGwyg0XM/GTid8jp09EMlaVPdfHa4x3kMkWsgoNvC4RUGWx4kqbmRqKjMxldM/n6jLDKR396AkIIXrxvAz1r0oQiGqFo0KKpEPufEBDj0b4CvicJxYJ1iqZgTyB+pu9TrWvENJVRx2VJrjiJGFq+5ISqOI0hgxV5kzv6RrCcIpZVwLIKmI7JF+Rq2gobeNgM8Ut9AZYvsSVYKJw4tIhvrvsfdOkFmuxT/w0OvGyP/NZlYrcN7E3EbiyZcG7E4sCTpyGlZPE/1zHzkNpJzt/bCykldrE4QQu4CRGcaBpOjyL9zV8aeig8gexVjPsCjs9PmFa1rTuNe75HZ64TgWB6cjpZO8tH7vsI69LrMD1zfLvPHPIZrjrwKgpOgTvW3DFuQq2ObHxhmvkc4Vg8cJC/5c/sd9xJW03/IG17nPR56cCHcGs5nqZCur+Pv3zjixQzGQ595/kce9kVWyW+lmdN0vZ1Zjs5ouEITpx2Iu3pDZz7j/MmbV9jVPO52Z/i7JozGC2O8vjgkzRpDVT41RSLOr1Fi17bot916JYuPcJnQBOMGBq5UIiiHprS1JeyPaotnxpLUmNDjSmptWQwb0lq7GBdxNv+38KXEkUICr5kRdEDRTDNUNClxAN8yaRe0RUUQ0UNqWgRDS2ioUc1jJigonA3yQ0/RkxI/OqLEEPVX2aEU/FyLr7pIC0fxfXRBKhIPARRReBKSd6HlCqQSJZE1nBr9QM8l3gNw9P5j/7/x7zCDKTtozfFEQ0R+qMqXWFBlwFdKnQKn07p0eG59HuTfwgdSa3nUGMXqMxlSGSGiA/2Eu7tIj7cR9gqMvFX13SDSGUVWkU1MhbHVg0Knk/OtFBxaaWTwXAb1U1tHOU/z9z1f8St2x91v3ci5p4VJNbeBY16++uvcv9vf0G6r5ezPvkFFp546vbL1XdYvuIb9PTcSjJ5EAsX/JRodMbkjVwbrjsTf9aJFI/+AFK6xONzkdJj8fMXk8+vxvc3Ps/TWz7CnDlfQ0qPru6bdyqJ796AwDfZx8uYSE/gZYr0/eDfsFevwO3rGt8uduIlxE68Aq9gYy9bjJJsQSpJpOUFA5wSBrQRhrU088xWCorJV6f/jFOyR3GGfTzJUBIR0VDCKkpEQwlrpXkNJaKihDUQYA8XeOWBG1k7uI6zDrsaUQA3Y0JxCgIoQInpG4lewhifVhMT5hMGQt89Fp2RkZFJ+eQKhSApe01NTZAUeHorM2e1EYlEGO0vkB4ISJ+VD4ih5/ocdX4QGPTcnWtZ/+pgaZ2DbXrEK0Nc+YPjALjzl6/QvmRo/NyqrlDbkuCSLx8GwLO3ryE7YhIKCUKaSVgtkAxnaKvrhlw/6f4sarGfkNWBlu9G5PvA21wxgqIHwXXxuqCPVkO2F9Y9Cr67cTs9Auf9Yo+QuzKx2wb2NLGzHQ/P8QlpyhZHoWbBYdkzPbz+eDfZYZPKhijvvuYIlF2oN7mj8H0PM5clPzpa0vyNUsiMUphA/AIt4ShmPjvlMcKxBLGKCiKpVBAIkqrkkfBrdKvD9PiDdFm9ONLh/Nbz+O6x30VKyeef+ALTYs3MTM1iZqqNmcmZpELbn/g1MzjAn77+ORzT5IhzL+bIC961nUlcJdKTSNcPmuMj3eDFHUxvbE7BRBUavuPx9KM3MXf20VRXTNtkX7+kmdp8f+nK8WWUlvlS0mvkWRkbYm14iM7QIP36IFXiWPzQfnRqy+kzfzzhanU8rZZc1QdxwvNRnUGihZWE/RQVbop6O0yjozDdM2iQKrUoNKg69bpBSNdAUxC6gtAmNF0BVeBJsCwPy/Ywix6m6VLMOxQLLvm8Qz5jk886uL7Ek+AjUXCo14vsH7UwRIGXCzk0UWD6bJ3qar/04iyiiyK6zCPsHFgZsHNBCaqxNrH6xlTQo0FAQqnJUIqiG6FznU/RjVDZ0ohlhikUDDIFjVtrbmd1vBfXi3Nh32Wcmj+CqNDwAVcP7lmVoLg+OFN8/ABTgd6IQldU0J3Q6I2pdEeVgAjqkN5E2RmT0CglDZ5LjV2kspglmR0iMtRDuK8Dd2gAq5BHCoEfiuKFo/iRKF44RkXIYr5YzVzW0kIPCpKCkuLZA39C84w2GpqbiVfV7LD/rGOaPPv3mznsnAuJJlM4trVDyY37+u9m+fKvI6XHrNlfo7nxMhRFob39OtKZl0pJfNchpUN19UkcfFDgT7h06ZfQ9IqNfnDR2ej6nk/kvD0YI2Zj2rExTZicoBGbUms2YR5v6u+XtAt46Q78TDtaw0yM1v3x8z2k/xIkoRexJPq02Ritc4ifcAahWbMnEDWNDqeLf3v5W7wy+CoRLcK5M8/l8v0uZ27l3CnP5/k+KxY9y1O//28ymTSNzdM545pvE68KyLL0fLycjZexkTkHL2vjZW38bGk65+BlbPy8Paly4RhEWENN6EGLGyhJAzVeIn0JfSMBNNRJ37ViscD69etZt24d69atY2RkFAj8Udva2mhra6O1dQbJ5K7/J3zPx7X9wFXDd+lf1kGuZxArncHO5rFyJobMcHDzc5Af4JFlJzGQb8byItgyCijUG8s4t+qbgOD+kWuw/SiGyBNWcsT0LLWVo8xszQOSoc4iqixiiCK6zKF5WVQvizJBKbEZUi3whdd3+V43RZnYbQN7ktjd/lIX3/n76wzbLnUIribEGUw2W3TYPq8UPDygWhXMDCk06AJlLzFFbAvtRg9rw120Gz20h3ppD/VQ71TxnY5PA/CJtu9iKhbTrUam2w1MtxqZY86g1WraxpG3H6aX5+WhR9iQX0Jcq+SwmjNoiLTu8nE96bEivYiV6ec5o/mDRCcmdVVEiRyJcaKEpiA1hRHNp0/z6Vc9+lSfAcVjQIMBFYY1wZChMhoysLXNzaG665K0TOJ2kbDTh+r0Ip1epDeIzwgL7SM4tHou2cou/tBz3fh+VeEqpsWn8d3jv0tbqo2OTAftI11UejVErRRW2iU/amIOj2KlR3DSo3i5Ubx8BtXPYyiF4IUlihiiQMQwiRgWYb1ISDExRAGNApqfR3FzCN/Z5u8nUZBaFJQwPiGk1PE9Fc9V8G2BZ0n8okdF/dopYwqkhMzoTNSwQDUkiubhSonr2oSUPCElj2BqcjYGX4ZwlTgmMUw3StGNYvkxLBnD9mN4Io4WSaFFKzCiFeixFEa4AiOcQjOSKFJFmh6+6eEXXaTpkrFdOvHoUqErIuiOKHRHlPFpU5t8MxWOpNmGZlfS6Pg02C61tkVNIU8sN0K6OMygncb0RmjQ1pPU8jwujgbgffJvCN9lvdNMt2hFiTVSVVlJvLLk+1fyCYxXBKbhqXKSWbbJTd/8CrGGWmZeeAam5pJxMmTt7KSWsScvwx2hNdfMo+veSdqqRNUzXDD7bk5ofoGsSGIqVXhaHYSnE4rMJGkkSYaSQT9hOqbHUHYguGFLkLI0QJpAusZkMtFcOXneDeQ35pe2BWI2Dk2Mk62NWrIta80mkjMlrE3SdPm2jblkyQQzbpBrr+W/f0X0He9g+LlFDP/qV7jz9qMwew7p2XN5PV7g6Y7b6V/5GKGizwE1H0YUwc+mGahvYdm8Q0ivGUJ/uYucGifpZjm762n+9NEPTulesS/A8G2Sbo6UkyXpjlLhpkk6WZK+R8rNkbL7SDmjpLwcSTdP0i2Q9ExSnkPSzRGWU2jlJsBBkFF1cCqwvQSOH8cuvUM6E0mWVizi80MdTP3FFvCt0d1+z2Vitw3sKWJ3+0tdXHPbaxSdjWYdXcC7KhMscDWkJsAQOAUPa8SFhIKnCzzPx5MS15O4vsT1fTxf4vm7/rupikBVBJqioCkCTRWoY9OKQFXF+LSmKOPznmIzrPYwqPYwILqxRJEr1A+jKgo/c7/PEvkqAkGD0kiLOo0F+n5cFrsEVQHfs1EcF88ycawidrGIY5rYxSK2VcQpFrDNIrZpTmkKVlQNIxLBCEfQw5HxaSMyNh/GCAXTPb0refLxG3Fsi8uv+A6aPnU+o7u6R/jFyl56TYeGiM7n92/mvFm14+RMaAo9nSt59LbrGO7rZPYhR3HsZR9mSEBnNkNnLkt3oUivZTHgeAz6ghFFI6OHyIWj+FM4Kodsk4RVpMKzqcanRhXUGTqN4RCVuopuWXjpUUa6uxgs1ctUFIWGhgZmtDQzvaGKabUpErrEyY6SGeyht381o5lOCvlebGsQ3xlhP3MWhm2RUzbgGn3EfEnc94n7kqj02Z7Pq1TDoEeRagQpwvgYSD8gZb4j8BzwTYlr+vh5Fzdv42YsPL+K0AEfxFcr6cl7vOJVoGU6mNHxILUDL6FIHxGNoiYSqMlEkBsxkaCx/k40JbfZdbhejK71p+FlMli5Ikuqz6Kv6iAqRlYwff0NPHxgmscPBsXw+eGNkrrK/QhNm4/fcx9qTKDFo6hhFzUkUXWJorkI4YC0EH4R1csj2Lr92ZUGjojjqgmkkYJICiVagZaoRE9VIcIppIgjlRg+cXw/yrAXpcMPs94Ps8EXdPgencKnS5F0axJ3giZeyMAs3lT0aSpImos+DUWPhJnHKI6yv/cXmsSrVIkgWGqAKhbJQ1nlHELEloRtD8OywTZxfRNLsckbFlmjyIiRJ2OY5HSbupEQ0/ojWIbPovnDrGsqMPYl0oRGwkhs1gb6W3nmlTZcb+O/RhcOP9B+x6IDFZZqkoyVIWNn8OSWf0dFKCSMBEk9SbVWSa1STQ1VVIoKKkiS8uPE/RgxL0zECxF2DXRHRbMVFIsdJGbKOOlSIhpinHSpm8yPrd9I2jYlZluDLyU5zyftBpGlaafUu1P3GdOiUCwwikrW82lY8RLz1yxn/9VLCVlFHFWhsmAycyDL1dd8n4vuupbQBP9o21DpnNfAhgM+wLJFabwJv4MuJKefMpP5c/ecaVvKwLrhmy7pkTQjoyOMZtOkzWwQbIMgJkLEpU7M1QijECaFgkKBEQrKMJ7q4KkunmrjYdKk7I/EZth5DctdScjLEHFzhP0iUc9mpllP2Ldw1T40MsSlS8x3iUuPuO9R6WlEpYWBu9VrdxBkFEFWUcZbXoQQVhsFNURntINhrVhap5JXNHy9kmmpIzDDOq/mXsb0TRShBA2VSlFNW3g/JBqrnSVcu/xR6pwpNHdljd2bgz1F7I774cN0jRY3Wx5DcG5OZ+aBtRx8WgtCCISgFFoNMHFejC8PrAg+jidxvaB3PB/H87E9H8eVOL5fWiaxXa/Ul7ZxS8s9D9uT2M7GfW03aEWvQEH2YtEH+YNxXImVuBuSTwffACGRUsG3aii2Xw0oCKMbUJF2NbB1c5GuCEKaQthQCWkqIU3B0BRCukpIFUSlRcwrEHELhNw8ITuPbudQrTyqmUOYWShkkGZ+yuNrkShGPIURiZCoawhMUPkcrQceQqq6mnhlJY90uSy+7498nptoEoN0yxp+Kt9N/PDzaKyGnnwB+fh9pFYvpRBN8OwRp7KsbQGF8NSpDqJmnpRtUuG7VONTqynUhwyaoiFaYiFmxDRaYhoJ4YCVxSuOMtrXQbqvk+xQN8XRPhQnTwibiOKS0CGieISkjeYVUdwcqrSmPPdESClwiOApUTwliqOEKKqCvAJZ4TGqOAwLh9Pz85AW3B3r5MmKNDlF4Lsq0ZxCfFjy0TskQgq6q0D1oToD2gS+rUSjQXRxIjGhT6AmglJ3SrQCL1eP0x9FAu0SXhl1iVcaHHvxLGYfMUWQwKu3wJ2fBWfC87KJf4rn+fzjpy9RM9fg4fhN/LPrXizf5qTwIXx45GzquhqQjgZqHsFLyEzPuE/lWLUWP7cpeZQIVQbaQN1Hi6pQlUCmUshoBBnWQAOhuCjCRqWIToGQkscQgcZQFdtwTNTCyHASz0jghmLYeoSMGmZYCTMgwgwQpV9J0Ksk6dUq6NGqyOgJ0lqcjBbHRaPCNjlwdD2nDT/H0dnnWa4uZLE4jGixm4u9e1hFG+vlLKKyjho/SY2foEYmSMkoru/g+Ca2bzFsdbNk9BkKbppKo4FpVfMxYhGUSAgZD0MiikjGEMk4ajLJZx/qZjC/uWa2WmT5rwuOQbpBMIC0PGzTwi6aOKaNZzv4lotvewhbIhyB6oLmqijbGFrYOJiKhalYFBUbU7FwVBdP8/F0QAd0BSWkooQ0tLCBEQ5hhMOEIxFi4TgxLUpUjxHRwihiai2Wj8T0fPITWsHzyXteqZ+43Juw3qfgB9sBqK5D2CwSsQoovk9/bWCJWLj8RWpHB4laBUJmEc02MesaGT3zXcRUhcTtf4L0MEo0ihaNY2g6FaEI04VO4tJLyXVswH7iceynn8MQkKkyWJswubP+PVhic3/rukSIm686Et838V0TzyuSUkMYUmW0OMy6zHqKdgHLLlJ0ipiuyXytlbgfoaPYyfPF17E8G9uzsHwb23c42dyfuGXwKht4OrISGw9H+HjCxxMeJ3UdRWXOZ218BaubO4jik/A3tnNWtlCJzkDVAMPxwUnrkr5Pix1HJR8MtrYCF0FWUSkIjYJQKSg6pqLTxHRcLUq7VmRAc3G1CI4WwzdiKKEIB6f2wwt5rPa6yJFBE0UUCqgijyozVCmjSOli+cH3VhOgCFDVGIZRSyhUN96HjFoMow4jVEuotEzTKjaaobfjHbY7USZ228CeInZtX72L85Qn+bJ2yziB+LF7GXf4x+/2c70dMFmNvel/pFToGwki6IM2Nu2XlgNCMjYjPInieEhF4Bk6vqpwtvMsP9SvJSo2joYL0uCr7kf5e+oUhJDMGNlAQikiUiqVSo4K0lSSJTXWZI6kLJCgQFRaRKRN2HcJSYew7xDyXUK+izqV88om8AW4ioKrqriqUpoea2ppXpTWCVxV4CkCT4CnBM0XPj4+2+OSKRFIIeiTCt1SYdAXDEnBkC9wEVyVEPhCcH1WstKVKEBKgQpVoUlTOC0RaEGHXZ+IIgiLqXM9hcxKWtaejWGleKX+IXJrTiI58xHiTa/h2yGEVDBCGZSS/BoG88zqzBOyfSxDYUNjlKFUnP51p1PX9ARSKxCVgowPX7IMjlV8LvLDzFz1bYRbgYysQdTchRJ9HRWB4oMig16VwbRwJdIGTIEsSmQRpAm+FfhI+xZ4lsSzwLPAnzhdckVy9DjFcA1mpJpiuAonksKLRfGjYURIw1BNDCVPSOQJiRyGMowuhtHVDLqSRVcLhBSTsLCJ4rGt8B1LaGSVKBklRlqNM6okySgxMiKG78GMXBeO1MjKML1KDe1KPRtoIuPHKHphpNRBqoCKLzVcqVCQLpaUSCWMLdiqzvL88jtsr8OOyESRHgounuaAcEFxEMIF4VKVE0QcH2HkcVIjJEWeFHlSskgSkxlFnUrhYWhpNG2YhLRISouktElIiwrfJSIcNLF1dwhPgilULHTMYGhEXkQx/QryooqcqMCiEkEFmkxgyDghP0bUjxHz46SkgYqCr9i4oTSeMYobGqUQHiUfSmOFRnFCaWRoFNVIo+lZhNj83Vtw4mSdFDknRc5JlqYrxpeN9ba/c2mITnMe42r3/6iXg4jUtHJU7JuJPUXsvvXdb/Jl59ebEYhv2h9FyZ4y/snftJ+8LPjoCekED6jvoOCiShfFd1Gki4KLIh2E9FCkiygtE0KiComtW/SlMhTDRXIhm4Ju4mguJ/S2Ue1G6Y1mWBMbIOWHSMkQSUKkFIOYqqMqAqFJUGWgNVRlcHWKXyJQPkJIpPCBTZrvgXRBeps0HyFL65nQSw8fBSlVfERpWgn8tBClaYFEKf1AStDJgN6J0paK9FHwx+fDdpGYmUfBx9ENjhNLJslkDK5UMIVBFGvsyFtFURrkiJCVEXJEyJX67ITpnIxOms8TnrB9lDwhPKGgCR8dF0246Iw1Bw0HHQe9tFwTHqpw0RQPVXioir+xqT6KIlFViaJKVBUUVaBooKoCRRMomoKm+qjCRyvtp5WOoynB8jGO1uPkGHSLpD2TjGeS9kziisr7YrVo0uHn2V56fY8IUK0IaoVkviI5XXXQpMuI71KFiyY1UFyEU0l07Zex6v/OquFpdHSdQ13DkzROexAjNsqjw4dzU89ZDNoVVBujnF/7NNM6D8dMt7Jk1i10Nz3JJ1Muqh9Gz8zGrnsFFJ/aNZeQr15CsXL5pqOD7UKgCVcxPR3L0zE9naKnU/Q0Cr5O0Sut8zVcx8BzNTxHw3f18V6WGq6O74Vx/QieDGETxpEhbBHCFgaO0HARuFLgCoGLRMciLookRZ4khQl9YUKfn9QnStulyGNsQ2NooZEhRpYoWRElTwSTMI4wEEIHxWAkL4gnkgglhuOHcbwIjhtlqd3PNfoNm73D/t35IHPNGL608KWJ75t4mEjPREoXtuH3SGkLWwthamFMPYSlhbDUEKY+Nh/G1CNBP2EbUwthaga2aiC34YdsuDaaZ4/3mlNE8WxUzySRGSWZTRO2LQzbxnBcdNelq0ZB821qRnzi5ib5ExVwpyXQFB0lZyNciaZpqLqBphloRgjNiCClguuC43q4nsRzfVxP4ns+nhcEbfm+H7z2/OBPqAAKIkgFBEypZ5QSUZfh26HrJ8mkKA1+6FxCtwJxfGLSJYZHtaMQFy6GUiSk5YhhERcmcYrERSHoKWCIrZsyLRn8hzIyOqGPkpGxTfqp13tKCEURqEKgKJT6YF5VQBUSXXUwFAtDtTAUk5BaIKwWCas5wmqOiJohrObRVRdNcdAVB11x0RUXww8RciPEnCgRJ0rESRCxgxZyKsCuwPRTFDSDvK6Q1wR5XQTTuiBXmi9qYpcSiLcP51nSnaXoeDRXRPjSmfO48JDtz1G4IygTu21gTxG7wo/2I1rs2Wy5jwKhVPBESy/I4C5LZGiM9JQoTBngoeCLEtETokTZAq3TWB+o5xRQFIRQEIqKoqiopaagUMxmMQsFqoziFh31R1svINXQiufr2KZCMa9QKCjk8xq5vE62aJAphhix4+S8KAWhYxt5TD2HpeextAKe4uFJBemr6KaCXpSECg6hYhHhWniKi6d6WLrAMjRMXcfUNSxVw1RVLFXFUlRsRcVWFByhUqLz+KhIqYHUSr0KUoPt8pzbPijCRREuKi6qcFFx0ISLhosunHHi6ShecC+Kj6v62MKjUoHDtAgRXed2pwtH2CRUlUojTCv1HNm/P9GiQahCp99Q6FpfRPiQmxbi7mwWe4LfkCrhSBsG6h+kWJfhmIoTmDM4E7HBxvUki+amGfZNipaJ6drYrovrufjSx/clUgqkFCAVZOn3kr6OlBq+r+FLPeh9DTn1Z3S7IfCDD43qTvjglHrVKX2IJi8bm9cUF114aPhoSDQhgx6JJiW672J4LiHPxnAtwo5J2C4SsfKEnSJhzyOsKBiaEZTa0w3SkSpMI8zs3Os0Wt14KAwZFYxqCSyhE/EtUm6OpJsjJLcdBLMpfBREogGJxJfBOMufOC3leB8sk5T4Cz6y1G/7A7pxKFfqJRsHbTIY9CpSIqSPKPUqwcDO98GV6vi5pAzeqjHNRhFgeSq2r5bkR2mgCqrm4ovSQFJu8q4p2QjGmhgbVMpgaDm2TIxvsy3IYFxKiU+MueUIsbEpoIzPgyj2o2wHcZ4IT2o4RLD9KJYfxfTjFIhQUDQKiqCoCExhYMowjlOF59Ti2fVIrwqpR5GhEEpUQ0QMlEgIIgaEVNAV0AW+piA1gVRFYEFQBJ6QmG6BgpWjYOUp2kVM26RoW5iOg+W4WK6H5UocT8XxNRxfn9DrOJ5e+s13HpoAQ1EwAAMR9L7EkMG8DoTGliMI6QohQyUc0giHNUJhjXBUJxLRCcd1wjGDSEInbGiBO5GuENIUnlo9yM8eXIU1Ic9gRFf5wcUH7BFyVyZ228Aei4r9VgVTxZFLoGdaLRIfKXwkHhIfX3ogSnuM92J83geKfmCKyvgKSU1Sp0tyvuCejB68OAFNgaQKC8LQogt8HywPovgIP0gSG2yslD58KtJXwFeRUsX1dbIiQVZJkFOSZEWMvIiRFxHySoSCEqGoGBTUMEXFoKiFMDUNUzMwDS14rYrgdTxGyMZ64YPhCHQXQg4YtsBwgz7kQMgeWw5hRxC2IWxLopZDyLZR/ZKm0ndKbarpoFdFoIFSFFAViapAQc1ywqxbqdAym8llxK3gzrXfxA6lsI0kcgrfHMUdQmpDuKEsVsSiEHLHX8wJqdCgG0xLxmiprqa6tgYtmQqCBMZ80eLxSbVwtxtSIq0cbnEQqzCIlR/ELg5jFYexzBGKhTS5YpaCmSdvFcmXXp4Fx6HouphSoYg+bgox0bBL8zYatgjhYARN6LhSw5EanlSD5qsBWR0nlSr4E6Y3I5s7lh9w1+EHfnCKh6pINFWiqaCrYGgKhibQVQVNUdEUFVWoqEJDEFy75wtcT2J7PpbjY7oeRdujYHu42whaihuC6hhUxQSVEUlFRJIKS5Jhn2RYEjd8YoZHzPCJ6B4RzSWseRiqi8DG8y38UnMdE6sUTOTYRRzbxHNNPM/E922EYiMUF6E6wf2qDkLdsrZF8SUVow41wzY1QzYRyycb0fnzEUcyQB1+McQaow05rHDgsy8ybbib0fpaVi04CF2X/GjVT6b8rErgLw3nbEMmEl2AIQS6MtYrwUd2rAmBrggMEdQL1YWCUZrXFIF0PRzbwrVNXMvGsS1StXUY4QjZ4SF6Vq3AtS08dyM5bTvkSNRQnOGeTka71iNUDSE0UDRARYQqAz9h1wXfR0oNIZVxzT9SKRGzrd+bEB4CL+hLpk1Zar5wgwGe8HCFh6MEzVY8LMXDUXx84SG3MHjXkOgSdAkGoCNKJERwYCG7RZn0qCqqlGiAIiWGlBjhCtR4PQOhGaz1m1lbTLIhq2CXFL31VRVMa5xOQ8MsKhP1eBbYxVJy4aKLXXCwSvN20cUyTTx/GM8fRjVGUSNptPAoWiSNFi61SBotnEEom2uTpR9F+FUoVKMq1ehqzbgfWzhaRzTWQDzRSDRehaoruL7Ecn0sxwt61w8IobOF6W1t65aecdvDslxMyw22t0vrPR/bk1gyaLvKVporIjz11VO2veEOYm8jdnu8mKkQ4izg5wTa7GullD/c0+ecEqlpkO7YbHFB13k8MR3fV/F9pdSryFLvo5FGIoVGjUiB0PkLLzJEDkf1xnX0R+sHcW7sdIQSwkq8SlNoGs3hFiqMCnxVIYPHs77LKB6j0iXte2SkT0b6ZH2fnC/JS0ERFRMdW4RxlQhS2Ub1A2mjenl0P0/IyxHx8sTcQeJujiYzS6VfoMq3qRYedUJSr6o06hHq9QRxvQIZr8TTUrhaAk9N4KlxXBE4/Lu+GpgtbA+36OCaNq7p4FkuruXg2i6e7eHaHp7r4zl+sL0r8VyJ44FXUoJ6vsCTAk8qTBw9L8olOTH1a0ITTBm2NHi9+B5ijdXURAXRuEM0CV7MJ6cWGXay9I0OMTA6CoCqqjQ1NXFwqbZqS0vLtgtRSxnkcMuOgjkKxR3p0wjfYcx3PL7ZwQWEkxCugEipVVVvnN9aH07BdpQbklLiShfbs7E8a7yfatp0TYqOQ96xKNg2Rceh6NgUbAfTdSkWbarWRFEsnburn6VvzUVMreGQXH5kH8c934bZaFNcCNH6CJWROFWRBNXRFNWRJDFjz1VHMR2PdNEhXXTIlPqp2ti6zszGZeYW8uSNIWaopCI6yYhOapOWjOikkhvnE2GNKAK14CFzLoVRi+yASWYoT2Y4R340iy+tgOyVyF8kCZmUZCDmEm61qPDbCXtDHD9ajeqNMm/Z3/CBTLiCkZYYr4cr6N1gMq34IgMnzGDISFJjbz4IGgoleXJ2K3ElR5Q8UfLESn2UAjHyhClu5tLgAcVScy2FfE8cJ6/jFAzcgoZb0Kia4xCvE2S7DdY/unlUe9VBDkZ1jOJIFYWR+Qg1hFAjCBFFETGeXVqPIIbvGUhPx7eDXno6gW5V4ghwVYGvCaQmEIYSJM4Oq4QigYYmGtOJx3USiRCpZIjKVNDCMR09pCK25tAqJXgOuGZQVWST3rFzZMwRslaajJ0OIoudLBknT8bJkXGLZNwCGc8k41tkPJuMdMhIl9vaCzR5mxOmHlXlzOkbNUMRN0JdsS5oI3WEvcBvrGAUyKQyFJIF7JTN6pBGSH2NsKWSciRx1SOueEQTDuGkRRgLQxYxZIGIn0fxC1Nbk0QCQRVCVoI/E9wqpFOJNKtwiynsfBIzk8DKqwFBzLv4Uw6aBkstSDA8VmXCiGgYYYWQoWAYYOig65KE6lOleoG7ighcWHRpofk2imshbQvfspCWjbQ2n/ftCessC9/eOO3ZFq7jY4sothbDiVTihitwwimcUBInlMAJxXGMGNcY6pSvsO4pAijfjtijGjshhAqsBE4HOoHFwHuklEu3tM8e09hNESXjq2H6jvo6oy2n4zgOnufhui73DtzL2sJauu1u+p1+XFxma3N5Z/hyRlyXR+07kITQqEGIOnxRh63EMVUdS9GxNR1LNbA0HUs3cKeozzkRmudiuA4h1yHk2oScsWmHkGcT8l0ivktE+gRJHCApBElVIaZqaIpEEz4aHpp0Ss1G8y0030Rzi2heAc3NBc3OojmZYBo32G+qXtURY8Rke0jJxF6f+uMupcT3ZUACHR/X8VGW3Erome+iFnoh2Yw47Zs48y+iq6uLjo4O2tvb6ezspFgqQxaNRmlpaWF6SwstDdU0pUJobnbLZMxMT73M34ovi1BKSXh34v5DyV2qVPBm49jvPUh3dvPI37HRrpd3UGNvtBZw12G53tSEsOCQLrqbEcOMuXG+YG/ddy6iq5OJYFijStWo8AVxF8K2j2b6iLyLm3WwM84kA4KquCysWkxr5HkavMXofhYpdLoWfAX10HdT39qM9dS1hB77VxRvYkUQg/amDzAQOQTbDrSMrlPAck2KZg4PD6lJXM8i2zuC5zh4rhuUlrN9wtN1ojNUPNNh5KmNz4PQJGrYp+KAIokZJr4lya830GMOeszBiNkYcRs97O60G5TvBS4S0tMCC4W/UfMsSr0yQT+mihCKEkJRwqhKCE2PomlB00MxtFACPZTAiCQIRSowYhXo4QRqaZ8tlmPbBXiv3IRy5+cR7sbviqeFWHbUJ3jdmM9Q1xCZngxW1gIketQjWm9jVBbREnkUNYfq59D8PIYsEqIYkLcpfDU9CVlfkPEEGRdyriDvCAq2oGgJTEtgmQLXBNUB3QXDC3rdBcPduCziqYR9lZCnEPYUdE8Q8kJoMozqRVBkGCHDIMNIQkjC+CKML0J4ShhPCeNq0VLkawRXiyKVrX/nFN8JvkVuofRNMtGljYaNMea7rHjoqoeh+hi6RNcFRghChoIW1hGhEErIQBghRCiECBkoodBm86c/kqdnimof+4rGbk8Tu2OAb0kpzyzNXwMgpfzBlvbZo5UnXr0F78FvoWS6GQ2n+Mv0w/hHLMposQeJTk3zx8l5kO69Dt8dxdMacPUmHL0FJzQbz5ixxUML30KVgYEtLBwiwiOmSOIKJFWFlKJSoapUqQaVqk61GqJKNahWDAwpcF13tzdvipHkjkIVY6TRL5E+NyCN0t46KRSgaTqargdOzHoYLRRGC0XRwjG0UAwtkii1JGo0xeDQCB3dPbT3DtMzUmBsAFkT9pgeLtCijzBd9FBl9yCs0YCcya1oYYS6BfK1HYTNSLylydmu4LYn1vG1u5dhTng3hBXBDy45kIsOm/YmXtmbB9v1JxG9SQSxsHWtYX4KUqhISPiClC+oEQq1ikalVEh6EHM8WlhOa+h51lhH0+/MpSn8OiJ/GwYFTm5cT1hY5KngWe9SViuX4JoOdu+t4OaQfh5kUEFEDR2KHj0JKR2s0V+CiCCUGIgYvhLDCc2hGGrDxkGV/fhGHD+SRI2E0Q2FUFgQNSQRwyeme0R0n6jmEVU9wkowgBReEdct4DgFPLeA65l4vokr7VJAh4OPjS+ccfOoVFxQXFC8oKkeQvURqhc0xUdRvaApHsqYaV/d+Xea9EVgjfHU8X4joSyRSl9DyLGmo2AghIEqDBQlhKqEUJUIqhZBLxHL6pHl1K27G80cwtQTvJhayPJIHMMoEgqZxCMWIaOIUPPBfW8C4aloVhjNDKEWdNSchppTUbMKSkagjvgowz6kXTDHNF1bT+K7PfB0BU9T8XQFV1dwNYGrCRwNbE1gqxJbA1v1sVSJqfqYioel+uPbOCrBtAqupuOrEaQILE1CREFEUIiiyAiKjKDJCJofISRjhLwoIS+K4YbRnTCK3LqlQqo+GB4i5CNCEiUEWligRgR6WMGIqBhRjXBE58URl+tfyU3yE96XfOz2tCm2GZho/+wEjtrD59wyDryML/uV3LHqr4QLzyCd1Xi5ejy9BdeYTqfdgCaL6NWfIKx4RIVHTJUkVEFKU6jQeqgyDGpCEepCURoiMZrCSVqiFcT07S8P9EbB9/1xLeSuEsTNljsOrm1iORZ5xw7mXRfX83A9P0jm7AhwgM2qVLlAutQmQ8OlmV6OpZsWumkRA0SVMKgVYFSUyNdh26c9M+K7FFW1r+Lid7ShxA1+fNcyenIWjckwXz57vz0WUfZWgKEp1MRD1MR3/Dl3PH8zLWHGdDcjh6NFhw2l+Vx+ATI/B036VGg2hwnJOZWS9UMav15x5PixbcNnJJXHElArHXw9gWc0II0ERJKIymaM+hTRuEE88kNSlTFSyRAVCYOKqDGuYYxuUopqb4Dv+/i2jV0o4hTyuMUidqGAVczimBkcK4tt53GdPK4bkEuvRCo938KTNj42EhsfF1kilihuqQ9I5FgvdHucXI4vUzwUxUcSmK6nopUDtbC8VgA1pSWraQUoCtRRUAdBzQiUDKhpFSUdzKtFA80MoxBCNcIljVMIxTDGp0XIQKkJIZonaqc2aqyUUGlbY8L60vz4uqnmdR2xkwNXX/qbuYBM5Qoy5TJ/bFkR20tjeRZZz8ZyLWzbwTODdEbSFPiWQNgq2ArC1lAcHdU20N0QhhkhlI9guBFCXoSQG0WVYlxKKeB0XeOJsEtG9WmuiO7RqNi9DXtaY3cpcJaU8qOl+fcDR0kpP73JdlcBVwFMnz79sA0bNuyxa3pmcD03r32aSl1ndqqVllgVTdEkTZEUUW3qyghl7ByklFOTQtvCLWZw86NBX8zgmlkqEjEaGprQYpUbCZoRK5OzMvZZuJ5P1txoJs6kRyi8+E+K8TaS9dOobaijtqaKVEQnrG+5/nUZOwfPtrFzGczCKHZ+FKuYwTEz2FYO18rhOPmAULpFVAT1iWZi4UZCoVq0cGJqUjVGrMqy2ilsiVgWTJNC3qRYsCnmrVLAicMB82czf+bsPXpNe5vGbt8yxZZRRhlllFFGGWXsRuxtxG5POxEtBuYIIdqEEAZwOXDHHj5nGWWUUUYZZZRRxj6JPepjJ6V0hRCfBu4jSAxynZRyyZ48ZxlllFFGGWWUUca+ij2ex05KeTdw954+TxlllFFGGWWUUca+jn0zn0MZZZRRRhlllFHG2xBlYldGGWWUUUYZZZTxNkGZ2JVRRhlllFFGGWW8TVAmdmWUUUYZZZRRRhlvE5SJXRlllFFGGWWUUcbbBGViV0YZZZRRRhlllPE2QZnYlVFGGWWUUUYZZbxNsEdLiu0MhBADwJ4rFhugBhjcw+coY8dRlsveh7JM9k6U5bL3oSyTvRNvhFxmSClr9/A5tht7HbF7IyCEeH5vqutWRoCyXPY+lGWyd6Isl70PZZnsndgX5VI2xZZRRhlllFFGGWW8TVAmdmWUUUYZZZRRRhlvE+yrxO63b/YFlDElynLZ+1CWyd6Jslz2PpRlsndin5PLPuljV0YZZZRRRhlllPF2xL6qsSujjDLKKKOMMsp426FM7Mooo4wyyiijjDLeJigTu7cohBAhIYRemhZv9vWUAUIIpdSX5bGXQAhhCCHU0nRZLnsJSu+vUGm6LJc3EWO/vxAiIoSoLU2XucFeAiFEXAjRWprermelLLy3GIQQxwshlgAPAV8AkGVHyTcNQoiEEOJLQohXgV+UFpefqzcRQoh6IcQ3hRBPAfcCn4Xyc/JmQwhRJ4T4gRDiYeBh4AtCiFBZLm8upJRSCHEw0A585U2+nDIAIUSVEOI7Qoi7gJeAK2H732Hanry4MnYdpZGTkFJ6QogwcBVwDfA4cJcQYi3wt/LL8Y1DSSaKlNIFVKARuAG4AkBK6b2Jl7dPYuJzArQQyOTzBFVsHhZCvCKlfPhNvMR9Eps8KyFAB74BvAY8DTwPPPjmXeG+hzFtnJTSn7B4PoGyoG2KdWW8AdjkWUkAXwXOkFI+sqPHKmsW9lKMqVyllP4YUZBSmsCRwEtSylHgv4CTgHlv0mXuU9hEJm5pehT4AfATwBJCHDJx2zL2LKZ6ToDVwP+TUi6WUvYDiyh9sMp4Y7CFZ6VDSvn/pJRPSymzwFrAfDOvc1/CJjLZlLhdCtwMmEKIwyZuX8aexRaelQ3AklJDCNG4I8csE7s3GSKAuqlPQ0k93iCEOEkI8XMhxHlCiBTwJLB/abMlgAWUycRuxHbK5GdCiAtKywdKL8rXgDNLm5efrd2IHZDJ+VLKUSllTghhlDYLAWUt6h7Ajshlwj4fEkI4BDU8m97oa367Y0ffXyUz7GrgZaCPQHsH5XfYbsUOyOWS0qrXgWeFEC8AvxJCXLW9vo9lwb3BEEJUCCHOKZE0ZABPSulPJGZCiCsITBXvBE4DPgQUgG42PngDQC/QPHasN+5O3j7YSZmcCnyktHzsOXoMOOGNvfq3J3ZBJh8rLdellLYQ4khgBnBreeCz69hVuZRwD1BdWnbxGMEoY+ewCzL5eGnVXKBbSrkOGAWuFkJcXXYp2TXsglw+Wlr1M+CHwHHAj4ALgYu359xlH7s3HgsIfLEs4EEhxDzgfcBRwBNCiF8RmCeOBT4npbxTCPEgcC0ggOXAWQBSyuHS/ve88bfxtsKWZHIk8ORWZHIdBCr00oP6HPCl0rLyS3HXsKsycUrH+RLwayll7o2+gbcpdkkuAFLK3tLkUiFEJ9AmhFDKfl07jZ39pvy+pNWeC7xfCHEVECf4znS/CffxdsPOPit/AJBSPk/ggwqwSAixFKjfnmelrLHbAyipXLf0264nUHvPLs2fRKB5+xKQB/6N4I9wOPBKSfNwP4Gs5gO3AwcLIc4o7T+9tH8ZW8FOyuTLbJSJzeYyGYsmGxuNrQIKQoifCCE+IoSo31P383bAHpTJmGvCMQQvzueFEBcIId4rhEjsqft5u2BPPysTzqMCc4DlZVK3deyhb4oAZhFEXf4QOA84AlhMYJItu/dsA3voWfGneFY0Al/6VdvzrJSJ3R5A6SO/pR9/AOghGCUB/BF4AfgkgQr2eMAobXfUBM1DFrhASlkAvg18UAgxBLxaamVsBbtBJjrQDxy9iUzeCSCEOFoI8RjBh+oQwCEwa5SxBexBmZxbmv4MwYj5WoJo8gJQ3M238bbDHpTLmQBCiKuFEIsJfLpWE2i6y9gK9uA35SIp5V1Syj9IKdcSEMC7Kfmklt17to49+KycDSCEuFIEPnYvASsIAsG2ibIpdhcwlUq0xN5nAh8EHCnltyeul1I6Qoh24FAhxHQCxn41gX/W9wiiK48BfgdcVrLPC2CQQLULgdbuIRlEZJYxAdshE1tK+e8T128ikxkEL7erCVLKTJTJtQQySZZ2HQIOKk23A5+XUr60R27sLYw3WCbDwH6l6euAX0gpn90jN/YWx5sglwNL0y8Bn5ZSlgndJngTvikHlM4RklJaUso08Ps9eItvSbwJz8oBpenXgE/t6DusrLHbTgghlJLpYBxjghZC7C+CHHMQCOvnBCOeP25yjDG1djuBRqcZOBFISSl/D7gEqvFLpJT/IBD4eQQ5bf6Hkkq35IA5Wjqmuq+qy3dSJjdscoxNZdLERplcy5ZlkiSQyazSebvHSF1JJpOua1/BXiCTX1NK/yOlfHDshTjVde1L2MvksmiM1JXfX2/6N2VO6bzWpte2m27zLYe95FmZWzrvixPeYdv9rJQ1dluAEEJMVENPpW4VQnyVIP9PBnhMCHEDQUb1I4C/SinXT9x+wvF6Su1gAu3bB4QQfyMQ6u0EQodgxPUycBiB6vbHm16D3Iec9Msy2fuwt8tk7Pq2Yi55W+ItJJfyszJ5mzf9/bWla3u7Ym+Xy848K2ViNwET1a0TBS2CmqxnApcR2L9/TGAblwSRRyngVqAC+ClB4s2t/bZDpXYM8Fvg0wSRro9JKZdO2C5cOlcKuAu4c1fv8a2Gskz2PryVZDLx+t7uKMtl78NbSSb7Et5KctmpZ0VKuc82gmz0VwHNU6xrBs4tTZ8BPABcAiwsLTuTwDn+QYIoot+XBB8lUJefv41zzwTatrBOfbN/m7JMyjIpy2TvbmW57H2tLJO9s+1rctknNXYT2HoNgaP1aqBLCHEyEJFS3k3gD/IFIcQKArWpRuDIWCgd5gUCFv8xGSR2nHj8PuAAIcQjUspsyS4u2FjLEhlEIE3cZ6ysiJT7kHliDGWZ7H0oy2TvRFkuex/KMtk7sa/KZZ9wkBz7ISf8oGMJZVcS5OsZqyN5AhtLQj1NoIptIkgAPAR8CvipEGJMTboIuEAE5UBOF0H+sgaCsl+9wLiqV06oZSmEmC6CjPibCnmfME9AWSZ7I8oy2TtRlsveh7JM9k6U5RLgbaexE6VoHrkxikVIKaUohXMLIUIEKtmUlPK7QoheYGbpR38ZOFsIUSel7BdC9BCEHT8tpby0dLwEga38GOATBKHOdxHkrPkHkJNS3rHJNYWBc4BTgEMJwsx/WbrOt/2DV5bJ3oeyTPZOlOWy96Esk70TZblsGW95YrepcOWEiBYhRLWUckgIUUcQyXKslHJECGEDFSXBrSXIr9QMrCEIXT6QwJ7eQVC77WYhRAVBrbaDCWzrz5X+EN8Bvrmp0MTkvDenE1SI+F+CLOsOb2O8hWTSQlkmZZm8iSjLZe/DW0gm+8w3Bd5ScnnTn5W3vClWBmrPMcYeE0KcIoT4tRBiJfAHIcQxUsp+gvIeJ5V2WwOECHL4rCFI6DifQF2bJWDcENjb9wMagfrS9rcB7y8dEymlUxolTMp9M/FPJ6W8U0r5Uynla/vCA/gWksnPyjIpy+TNRFkuex/eQjLZZ74p8JaSy5v+rLyliZ0QIiWC+o9/EUIcQSCY7xNEmswFngE+LoSYDTzCRpv6egKb+BwCu/sgMF9KaRNkqz9YCPE6gRPk54EVUsonpZRXSSn/JqXMbHotcoJdfV9GWSZ7H8oy2TtRlsveh7JM9k6U5bJj2OtMsUKM28knJQ2cYjsF+BaBWvVxAgEqwHKCkhwANxLYxY8BHgXeDyClXC2EOArISilvFkJ0AAcJIZJSypVCiHePsfQpzjmJoe8LKMtk70NZJnsnynLZ+/D/2zu7EKuqKI7/1oipWApa2XcxlgYS4WQRJWVBD0YkRVBWEAoZ9FBRYRBMJD2UMEhG1EMPfUCQRFARUilJiVEig4NRlD1MjRqWipCVWbp6WPvYndtY15xx1j3+f7C5H3P3Ofee33lYs/bea8tJTuRl5EgR2JlZtTz4UCW4ejSzGcAud9/TdANcA8x198sbjjMO2ETMPcDd+82sE/jC3TdabMmxHJhKjKn/ajHZcYCY6NgJbK5EN8ttV8n/BznJh5zkRF7yISc5kZfjw6gEduUiNtZ5caJODBap1FOJlSdvlC5bgMVNUf0eSp0Zi2rRhzxWwvQDS8zsdXfvIyYyVlH9QmBBOd477v5z6b+T2KC3E9hc3VTtLvdokJN8yElO5CUfcpITeRkdjktgZ4NXjfwjGjazyUTdmHHERrj7idowt7r7gJltNbMud+9t6LYb+N3Mrnb3DeU4Vb2a74AeixUy64Dect4+oK/hvNV/BduADyk3RdNNVUvkJB9ykhN5yYec5ERecjCigV252POAN8vrakx9HjCfiNa73X2HmS0AvnT3LjObTYyZn1wOtQ64ysw2+9+p0u1m1gs8WI53HTH+/izwGdDh7k8N8Z2GSgUfADYM/xXIh5zkQ05yIi/5kJOcyEsuhnVVrJVx6gqP8eslwB1mthSYZGbTgbuJaHo1sMLMzgbeB34oMrYBHxH7sQF8DlwKTDSzsWY2v7z/BFH8bwqwAnga+IVYxtxZvpM1fi8PapV2/TfkJB9ykhN5yYec5ERecjOsgV11Ec3sfDOba2ZdxEqWZcCFhISHgB3APmLlyhyibswW4BxgArHh7tfEJEeILT+uIKSOB643s/HufsDd17v7I+6+2qPOzEEi1dpTvtMJKxfkJCNykhN5yYec5ERekuPuLTXAiJoxQ/1tQmmXAR8T4rqBM4BHgZ6Gzz5OjG8/CdwMjCvvn0dIml5e3wSsr84J3AJMPML5O4h0bMu/pw5NTvI1OcnZ5CVfk5OcTV7avx2L/MnlcRLwInAncBewvOlzs4EPgAuIOX03AJ80feba8vgpsKA8nwrMrGQOcePZaF+8bE1O8jU5ydnkJV+Tk5xNXtqv/efiiYZJkDOA24CTiNTqDGJMfVoRvpaI4heVce6dwDfu/q7F9hunuXs/sMbMHjOz54h0axfwNhH9LyL2c8PddxOrYfCm9KoX4ycqcpIPOcmJvORDTnIiL/XBWrluZnYx8AqwhpD6I/AasJgYH/8KmOXu+81sDrHC5UrgHmIvtoXEHmynAy+5+xozu53YYHetuw8M8++qPXKSDznJibzkQ05yIi/1oNVyJ9OBb4FXge3u/puZPQM8DLwHvAVMM7Pv3X0THC4EOBMYC7xApG/3ErVncPdVw/g7TkTkJB9ykhN5yYec5EReakCrGbtTgJeJis0dxDLjFcRWH8uAVe7+gJlNIFK43USkvwp4/kjpVGsqZihaR07yISc5kZd8yElO5KUetBTYDeoQqdrFwC4iOl8JnOnuN5qZEYUI/3D3vUP0HUNsB6Jx82FETvIhJzmRl3zISU7kpX1paSi2SDwLuIQoJDgbuN/d95nZRmCKmY3xqCvzU0OfjvIeAI3PxbEhJ/mQk5zISz7kJCfyUg9aKlBcou5zgXuBP4Gl7r7VzC4C7gN63f1gEXy4j+SOHHKSDznJibzkQ05yIi/14KiHYgd1jtUus4CVHkuWxSgjJ/mQk5zISz7kJCfy0l4cVWBXpVyJIF0TIRMgJ/mQk5zISz7kJCfy0t4cU8ZOCCGEEELkoaU5dkIIIYQQIj8K7IQQQgghaoICOyGEEEKImqDATgghhBCiJiiwE0IIIYSoCQrshBBCCCFqwl/NH4JW4v3sUgAAAABJRU5ErkJggg==\n", + "text/plain": [ + "<Figure size 720x360 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + } + ], + "source": [ + "line_styles = ['-' for i in range(10)] + ['--' for i in range(10)] + ['o-' for i in range(2)]\n", + "df_heatmap.transpose().plot(legend=False, style=line_styles, figsize=(10,5), rot=15)" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "We can also just plot each feature vector itself as a bar plot with one bar for each of our 6 features. We have set the y-axis in the below plots to be fixed such that the differences are more obvious." + ] + }, + { + "cell_type": "code", + "execution_count": 17, + "metadata": { + "scrolled": true + }, + "outputs": [ + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAhEElEQVR4nO3debglVXnv8e8PmkkQiNIigtig4IDIYIuixqBeFUeuQ4yKxim2SSSiRowZTPRqInq9zsGEqCiJRozGGU00Is5iMygCgogIiECDoiDK+N4/Vm3ZbE53n64+p3qf09/P89TTe1fVrlr1VvXe71lr1apUFZIkSVo3m2zoAkiSJC1EJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESVrQkrw+yUs2dDk2Zkken+S4DV0OaWgmURKQ5LAkK5Ncm+R96/jZ9yV53XzsN8ltkhyV5PIkv0jy5RnW2TzJWUkuGpv3u0munpgqyZO75VskeUuSi5P8vNvHZmOfX5bk+G7ZJUnemWTJ2PJ9k5yc5Jru333Hlh2R5HtJrkryoyRHzFDmw7tlv+rKvmc3/6FJTk9yZZIrknwsyc5riN9S4A+Bf56Yv1uSm5K8a4bPHJLktCS/7OL6xSS7rW4fa5Pkf7rYLpmYv7pj3CfJGd2+Xza2/mZJvpXkzj3KcFBXhr+YmL+smz+6Bi6dPNfrsI/bdefjV0l+nOQZo2VV9SlgryT3WdftSguZSZTUXAy8DnjvlO33aOB2wD27f186wzpHAKvGZ1TVV6pqm9EEPA64Gvhct8orgeXAvYE9gf2BvxnbxFHAZcBOwL7A7wF/Ci1pAz4B/BvwO8D7gU908wFCS2x+BzgYOCzJ00YbTvJHwPOBxwKjsl3eLT4TeFRVbQ/cCfgBcKtEaMxzgOOr6tcT8/8Q+DnwB0m2GNv33YBjgT8HtgN2A/4RuHEN+1itJIcCt0pI1nKMrwdeDuwD/HWSO3bzXwZ8tKou7FGUZwM/ox33TLbvroO9gQOBF/XYxz8C1wE7AocC70qy19jyfwdW9NiutHBVlZOTUzfREpr3rcP6K4DraT8uVwOfmqv9AvcAfglsu4bP7QacBTwauGgN6x0DHDP2fiXw+2PvnwFcOPb+LOAxY+//L/DP3etHAj8BMrb8AuDg1ez77cA7utebABcCD59FTLagJRxnrmGdLwLPnJgX4IfAnwCXAk8ZW/YU4LQ5ula2A84BHgAUsGQ2x9jFdovu9TeBA4C7ACcBm/Uox9bAVcDTuutw+diyZeNl6+a9ETi6xz6uA/Ycm/evwJFj7x8E/GguYuvktFAma6Kk9VBVRwMfAN5Yrdbn8QBJPt01Sc00fXqWmz8A+DHwmq7p5/RRc9yYdwB/BUzWxPxWkq1pycP7JxdNvN4lyXbd+7cCT+uaE3emJWmjWqy9gO9W1fgzo77bzZ/cd4DfBc7oZu3STfdOcmHX3PWaJJuMfWbXJFd2x/Ry2o/+6uwNnD0x78HdPj4EfJhWSzNyCnCPrinzoUm2mSjvM9Zw3q5MsuvY6v9AqyW7ZGL/azvG7wGPTLILLcn5IfA24Iiqun4Nx7o6T6Il8P8B/NfE8d5CkjsBj6Ilb6N5s7lW9wRuqKpzxjb3HW55zs8CliXZtscxSAuSSZQ0D6rqcVW1/Wqmx81yM7vQmtt+QWvaOgx4f5J7AiR5IrBpVX1sLdt5Eq0p6cSxeZ8DDk+ytGtOenE3/zbdv1+m/UD+EriIVnP18W7ZNl2Zxv0CuO0M+3417XvmmLFjglabtTfwUODptKYvAKrqgmrNeTvQmhi/v4Zj255WCzPu2cBnq+rnwAeBg5Pcodv2ecBBwM60BOvytD5t23TLP7iG87Z9VV0AkGQ5reblHTOUaW3H+HJaLdknac2zD+qO4UdJPpHkxCS/v4ZjnvRs4LiqurE73qfN0Ofp8i4x/QnwK+AjowWzvFa3oV0L4ybP+eg8bL8OZZcWNJMoaXr9mtZU+Lqquq6qTgROoNVibE2roXnxmjbQeTZw7ETN0d8DpwKnAV+nJUjXA5d2NSafA/6T1oyzA61/0xu6z14NTNY2bMtEMpPkMFofncdW1bVjxwSt5u7Kqjqf1in8MZOFrqqfcXN/qyWTyzs/Z+yHPMlWwO/Tagepqm/QmhrHO0F/s6qeWlVLabVkDwH+ejXbv5UuPkcBh1fVDTOsssZjrKofV9Vjqmp/Wt+y19ISqzcBxwFPAN6c5HazKMudaUnaB7pZnwC2pPXFGrdDl5jeBvgarcZqXczmnI/Ow5XruG1pwTKJktZfTc5I8tnc+u640fTZWW73u2vY1x60pqCvJLmElvDslHYn3bKxctyZVvNy7C02UvXrqjqsqnauqt2BK4CTq+omWgf2XYF3VtW1VXUFrSZplOicAdyna6obuQ83N9mR5Hm0zusPr6qLxtY7m9a3Zjxmt4rfmCXAHbj1D/jId2lNTSNP7NY9qovFJbRapxmbuKrq27TY3bsr96FrOG9Xd81529I65R/Xbf/b3eYuSvK763iMfwv8S1VdSqu1WllVv6DV/t1tdUEZ8yza9/inurKcR0uiVne8vwbeBzwgyQ7dMc/mWj0HWJJkj7HN7cPYOafd/HB+VU3WWEmL14bulOXkNA0T7cd6S1pH5n/tXi+Z5WePBD441/ul3fV1LvCqbr1Rs889uvd3HJueRLvT7460Jr7R9v8K+PIM+92Z1kQYWsfoC4FHji0/j5YELaE1z3xsdIzA5rS+WofTOn8f1r3fvFt+KK2f0D1Xc8zHAp+m1VzsQmuue3637EnA3WmJwVJak9spa4jfyxjrJE2rYXnPRGzuC9xES1IeDLwAuEO3/j1oCcJfr8M5y8T270dLknYei8Fqj3FsO/ei9U3atHt/PPDHtLvfLgfu2M3/EvDq1ZTlbFqT6Xh5ngBcC9yeiY7l3fk6EvgpYzcGzPK4P0S7A2/r7lr8BbDXxLV21Ib+v+zkNOS0wQvg5DQNU/dDVBPTq7tlu9KaM3ZdzWf3oDWLXQl8fK722y3fC/gGrR/LmcATV7Odg5jh7ryZfry7+Q8Bzgeu6X6ID51Yvm/34/3z7gf9w8COY8v3A06mNV2dAuw3tuxHtKbBq8emfxpbvm33g3wVLXn729EPOvBn3ed/RUvEPgTcZQ3x24FWa7MVLYm5Adh7hvWOpzWX3Rv4FO2uvau7GLyBHnfFjW37FonK2o5xbJ0TgPuPvd+nO8eXAy8bm/9D4BEz7PcBwG+ApTMsO4OW3I7KNjoPV9L6xt2vx3Hejtbs+yu6JtKJ5acD+wz9f9fJaUNOoy8uSVqQkvwDcFlVvXVDl2WudXfwfbiqHrihy7ImSR4PPKuqnrqhyyINySRKkiSpBzuWS5Ik9WASJUmS1INJlCRJUg8mUZIkST2sbhTg9bLDDjvUsmXL5mPTkiRJc+rkk0++vNpTDNbJvCRRy5YtY+XKlfOxaUmSpDmV5Md9PmdzniRJUg+zSqKSbJ/kI0m+n+SsJAfOd8EkSZKm2Wyb894GfK6qnpJkc9qTwCVJkjZaa02ikmxHe87WcwCq6jraE8olSZI2WrNpztsNWAUck+TUJO9OsvXkSklWJFmZZOWqVavmvKCSJEnTZDZJ1BJgf+BdVbUf7Qner5xcqaqOrqrlVbV86dJ1vktQkiRpQZlNEnURcFFVfat7/xFaUiVJkrTRWmsSVVWXABcmuXs36+HAmfNaKkmSpCk327vz/gz4QHdn3nnAc+evSJIkSdNvVklUVZ0GLJ/fokiSJC0cjlguSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1MOS2ayU5HzgKuBG4IaqWj6fhZIkSZp2s0qiOg+tqsvnrSSSJEkLiM15kiRJPcw2iSrgv5OcnGTFTCskWZFkZZKVq1atmrsSSpIkTaHZJlEPrqr9gUcDL0rykMkVquroqlpeVcuXLl06p4WUJEmaNrNKoqrqJ92/lwEfAw6Yz0JJkiRNu7UmUUm2TnLb0WvgkcD35rtgkiRJ02w2d+ftCHwsyWj9D1bV5+a1VJIkSVNurUlUVZ0H7DNAWSRJkhYMhziQJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6mHWSVSSTZOcmuTT81kgSZKkhWBdaqIOB86ar4JIkiQtJLNKopLsAjwWePf8FkeSJGlhmG1N1FuBVwA3zV9RJEmSFo61JlFJHgdcVlUnr2W9FUlWJlm5atWqOSugJEnSNJpNTdSDgCckOR/4EPCwJP82uVJVHV1Vy6tq+dKlS+e4mJIkSdNlrUlUVf1lVe1SVcuApwFfrKpnznvJJEmSppjjREmSJPWwZF1WrqovAV+al5JIkiQtINZESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPWw1iQqyZZJTkrynSRnJHnNEAWTJEmaZktmsc61wMOq6uokmwFfTfLZqvrmPJdNkiRpaq01iaqqAq7u3m7WTTWfhZIkSZp2s+oTlWTTJKcBlwGfr6pvzWupJEmSptyskqiqurGq9gV2AQ5Icu/JdZKsSLIyycpVq1bNcTElSZKmyzrdnVdVVwInAAfPsOzoqlpeVcuXLl06R8WTJEmaTrO5O29pku2711sBjwC+P8/lkiRJmmqzuTtvJ+D9STalJV0frqpPz2+xJEmSptts7s77LrDfAGWRJElaMByxXJIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKmHtSZRSe6c5IQkZyY5I8nhQxRMkiRpmi2ZxTo3AH9eVackuS1wcpLPV9WZ81w2SZKkqbXWmqiq+mlVndK9vgo4C9h5vgsmSZI0zdapT1SSZcB+wLfmpTSSJEkLxKyTqCTbAB8FXlJVv5xh+YokK5OsXLVq1VyWUZIkaerMKolKshktgfpAVf3nTOtU1dFVtbyqli9dunQuyyhJkjR1ZnN3XoD3AGdV1Zvnv0iSJEnTbzY1UQ8CngU8LMlp3fSYeS6XJEnSVFvrEAdV9VUgA5RFkiRpwXDEckmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQe1ppEJXlvksuSfG+IAkmSJC0Es6mJeh9w8DyXQ5IkaUFZaxJVVV8GfjZAWSRJkhYM+0RJkiT1MGdJVJIVSVYmWblq1aq52qwkSdJUmrMkqqqOrqrlVbV86dKlc7VZSZKkqWRzniRJUg+zGeLg34FvAHdPclGS589/sSRJkqbbkrWtUFVPH6IgkiRJC4nNeZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPWwZEMXYF0te+VnNnQRejn/yMdu6CJIkqQ5ZE2UJElSDyZRkiRJPcyqOS/JwcDbgE2Bd1fVkfNaKk0Vm1CHZ8y1MfA6H54xn1trrYlKsinwj8CjgXsBT09yr/kumCRJ0jSbTXPeAcC5VXVeVV0HfAg4ZH6LJUmSNN1mk0TtDFw49v6ibp4kSdJGK1W15hWSpwAHV9Ufde+fBdy/qg6bWG8FsKJ7e3fg7Lkv7rzbAbh8QxdiI2PMh2fMh2fMh2fMh7eQY36Xqlq6rh+aTcfynwB3Hnu/SzfvFqrqaODodS3ANEmysqqWb+hybEyM+fCM+fCM+fCM+fA2xpjPpjnv28AeSXZLsjnwNOCT81ssSZKk6bbWmqiquiHJYcB/0YY4eG9VnTHvJZMkSZpisxonqqqOB46f57JMgwXdHLlAGfPhGfPhGfPhGfPhbXQxX2vHckmSJN2aj32RJEnqwSRKkiSpB5OoRSTJFkk2615nQ5dnY5Bkk+5f4z2QJJt3j6My7gPpvlu26F4b83k0im+SrZIs7V77Wz2AJNskWda9ntV17olZBJI8OMkZwP8ALwUoO7vNmyS3TXJEku8Cb+9m+39pHiXZMcnfJfka8DngxeB1Pp+S3CHJ65N8Efgi8NIkWxjz+VVVlWRf4ALgLzZwcRa9JLdL8toknwFOBZ4Ns/9umdXdeZou3V8lqaobk2xJGyn+L4EvA59Jch7wUb/s5k4X802q6gbaUB87AccChwJU1Y0bsHiL0vh1ThvwdyfgJcCPgS8m+U5VfXEDFnHRmbjOtwA2A/4GOB34OrAS+MKGK+HiM6plqqqbxmbfk/ZH8W4zLNN6mrjObwu8EnhkVZ2wrtvyr+cFZFS9WFU3jX60q+o3tIdEn1pVVwL/DziI9ugdraeJmN/Qvb4SeD3wZuDaJPuNr6v1M9N1DpwLvLyqvl1VlwEn0f3AaP2t5jq/sKpeXlVfr6qrgPOA32zIci4mEzGfTJKeAhwH/CbJfcfXV3+ruc5/DJzRTSTZaV22aRI1hdJsOtkO3lXz3jHJQUneluTxSbYDvgrcu1vtDOBawB/2dTDLmL81ySHd/FXdF9/pwKO61f3/tA7WIeZPqKorq+rq7qkJ0GpJrP1bR+sS87HPPDfJ9bTnot1p6DIvdOv63dI15Z0LnAZcSquVAr9fZm0dYv7kbtH3gG8mORl4Z5IVs+2H5kmZAkm2T/LYLiGimhur6qbxJCjJobQq9ccA/wt4LnANcDE3/0dbBVwC7Dza1nBHsnD0jPnDged380f/d04EHjJs6Rem9Yj5C7r5m1XVdUkOAO4CfMQ/EtZsfWPe+Sxw+27ek0Y/9prZesT8j7tFewIXV9WPgCuBFyZ5oV0GVm89Yv5H3aK3AkcCDwLeAPxv4Emz2bd9oqbDvWh9a64FvpDk7sAzgfsDX0nyTlo1+gOBw6vqU0m+ALwbCPB94GCAqvpZ9/nPDn8YC8rqYn4A8NU1xPy90KqDu/+c3wKO6Ob5Jbdm6xvz67vtHAEcVVVXD30AC9B6xRygqi7pXp6Z5CJgtySb2E9ntfp+n7+nq2ndE3hWkhXANrTv+Is3wHEsJH2v82MAqmolrb8fwElJzgR2nM11bk3UQLrqxdXF+3xa9e3duvcH0WqUjgB+Bfwt7eJYDnyn+4v8v2nn757Ax4F9kzyy+/yu3ec3aj1j/gpujvl13DrmoztnRn/t/AC4Jsmbkzw/yY7zdTwLwTzGfNQ8fSDty3BlkkOSPCPJbefreBaC+b7Ox/azKbAH8P2NPYGap+/zAHel3SF2JPB44H7At2nNeht194x5us5vmuE6X0LrU/yD2VznJlED6X5wV3dCVgE/pf0FAvB+4GTgT2nVjQ8GNu/Wu//YX+RXAYdU1TXAa4DnJLkC+G43bdTmIOabAZcBD5iI+WMAkjwgyYm0H5b9gOtp1e8brXmM+eO6139G+4vz3bS7Uq8Bfj3Hh7GgzGPMHwWQ5IVJvk3ro3MurfZ1ozaP3+dPrKrPVNUxVXUeLdk6nq7/38bcPWMer/NHAyR5dlqfqFOBs2k3r6yVzXlzbKbqvy573h14DnB9Vb1mfHlVXZ/kAmD/JLvSMuYX0vrb/D3tLrADgX8Bntq1+wa4nFaNCa026n+q3Tm2UZlFzK+rqv8zvnwi5nehfVm9kDZMxHjM302L+bbdR68A9uleXwC8pKpOnZcDm2IDx/xnwD261+8F3l5V35yXA5tiGyDm9+lenwocVlUbXfK0Ab7P9+72sUVVXVtVvwDeM4+HOHU2wHW+d/f6dOBF6/rdYk3UekiySVfF/Vujk5/k3mljOEE7gW+j/TXx/oltjKpnL6DVZOwM/B6wXVW9B7iBVsX75Kr6BO0ieDxtbIt30VVfdp3oruy2uelirfbtGfNjJ7YxGfM7cXPM383qY74tLeZ37fZ78SiB6mJ+i3ItFlMQ86Pohuyoqi+MvuRmKtdiMWUxP2mUQPndAszv9/ke3X6vnSzbHB3mVJmS63zPbr+njH23zPo6tyZqHSTJeHXqTFWLSV5JG+Pjl8CJSY6ljfZ7P+A/qur88fXHtvfTbtqXVqv0h0k+SjvRH6ddCND+mjkNuC+tmvKNk2WoRdTB2ZgPb9pjPirfGqr2F5wFFHOv84G/W1ZXtoVo2mPe5zo3iVqL8arF8ZOf9oy6RwFPpbWrvpHW5lq0uzC2Az4CbA+8hTZQ3ZrifUU3HQgcDRxGu+PuxKo6c2y9Lbt9bQd8BvjU+h7jtDHmw1tIMR8v30JmzIe3kGK+WCykmPe6zqvKaWyijYK8Ath5hmU7A4/rXj8S+DzwZGCvbt6jaB2Lv0C7o+I93cVwG1q17xPWsu/dgd1Ws2zTDR0bY754JmNuzI25MTfm6z9ZE9UZy5Z3oHViPRf4SZKHAltV1fG0PgIvTXI2rYpwCa0z2jXdZk6mZdEvqDZQ2vj2LwX2TnJCVV3VtbeGm58NRrW7McY/MxqivmoRVaOPGPPhGfPhGfPhGfPhbawxX5Sd1WZjFNyxII8GTzyHNibH6LlcD+Hmx3p8nVbteCfaYJZXAC8C3pJkVCV4EnBI2tDyj0gbP+iOtEezXAL8tlqzxp4NlmTXtJGYJ0/8oqhGB2O+IRjz4Rnz4Rnz4RnzZqOoicrEU7KT1nks3W2kSbagVT9uV1WvS3IJsHt3Ik4DHp3kDlV1WZKf0m6J/HpVPaXb3m1pbbAHAn9Cuw3zM7SxKz4BXF1Vn5wo05bAY4GHAfvTbm99R1fOBf8fzZgPz5gPz5gPz5gPz5iv3qJMoiZPeI3dAZDk9lV1RZI70Hr+P7Cqfp7kOmD77mSeRxsjZWfgh7TbKu9Da6e9kPbMneOSbE97xs6+tDbbb3UXyWuBv5s8kbnl+BePoI0s/k+0EYCvZwFbQDG/M8bcmPdkzIe3gGLu9/lGeJ0vyua8alV8o4x56yQPS3JUknOAY5IcWFWX0YaKP6j72A9pT4bfo3t9He2RKufQqh8f2623La29dydgx279/wSe1W2Tqrq+y9JvMQbG+IVYVZ+qqrdU1ekL/T8cLKiYv9WYG/O+jPnwFlDM/T7fCK/zRZdEJdku7XlaH0xyP9rJ+gdaz/w9gW8Af5zkbsAJ3NxWez6trXUPWnvu5cA9q+o62ijJ+yb5Hq0j20uAs6vqq1W1oqo+WlW/nCxLjbXXLmbGfHjGfHjGfHjGfHjGfN0siOa85Lftr7cYqGuG9TYBXk2rQvwy7aRuAnyfNrw7wL/T2lsPBL4EPAugqs5Ncn/gqqo6LsmFwD5Jtq2qc5L8wShLnmGft8iQFwNjPjxjPjxjPjxjPjxjPn+mNolKMrp18abRSR/9m2RP4PKq+tnERfEQ4MFVdb+x7WwBrKS1V1NV5yfZHfheVZ2UNrz7G4Db09pqr0nrsHYhrbPa7sBpo5M/ecIX6omfiTEfnjEfnjEfnjEfnjEfxtQkUV1gx8d7KNp4EaRVG+5A66n/oe4jpwPPm8iqf0Y33kTaaKg3Vbtz4HxgRZIPVNV3aJ3RRln104FDuu19oqqu6j5/Ke0hhrsDp40utIV+wscZ8+EZ8+EZ8+EZ8+EZ8w1jgyVRmXhS82Rg055s/SJaR7XHA7+hjRHxpKq6MMkPkuxfVaeMfewK4NokD6qqr3XbGY1b8WPgTWl3FJwAnNLt9zvAd8b2O8rKLwL+m+5CmbjQFiRjPjxjPjxjPjxjPjxjPh0GT6K6E3AQ8B/d+1Fb7UHAo2nZ8quq6uIkhwBnVtX+SfajtcVu023qBOCBSU6rm6sFf5LkFODwbnsPpbXrvhX4JrBJVb12hjLNVO15HfC1uY/A8Iz58Iz58Iz58Iz58Iz5dJn3u/PStX+OVGsXXQE8LckrgG2T3BV4Ji2bPR54c5Kdgc8BP+1O0EW0Jznfv9vUt4B9gK2TbJbk0d38v6UNuHU74M3A64Ff0W6x3L0rU8bLVc2iqWI05sMz5sMz5sMz5sMz5tNt3pOoUWCT3CXJg5PsT+v5/xrgbrQT8xLgYuBqWk//5bTxI04HdgG2oj2U8GxaRzVow8cfQDvRWwIPS7JlVV1XVV+pqj+vquOrjTdxI61a8U1dmRb1CTfmwzPmwzPmwzPmwzPmU67W72nNYTVPRqadtK2A+wIn0k7mq4A7Ai8H3jS27l/R2k1fDTwB2KKbvyvtxN21e/844CujfQJPBLZezf43oVU9rtcxTttkzI25MTfmxnxxTMZ84U9zfUFs1/27LfAu4BnAocAbJtbbD/gvYBmtX9YjgC9PrPN73b9fBw7pXt8euPvoBM9wMWZDB3TwE2jMjflGMBlzY74xTMZ84U29OpaPdWTbE3gKsDmtGnFPWlvtjt1F8AVaFv3crv30UuCcqvpk2lDuS6vqfODzSf4iydtpVYv7Ax+nZd/PpT2Hh6q6gnb3ADVRlVjdVbBYGfPhGfPhGfPhGfPhGfPFI33jluQewPuAz9NO9GXAscDzaO2uZwF7VdVvkiyn3RHwAODZtGfoPJ327Jw7AP9SVZ9P8ge0hxB+oaouXI/jWpSM+fCM+fCM+fCM+fCM+eKwPkMc3BU4F3g/8JOq+nWSI4GXAZ8GPgrsmOSCqloJvx186+7AZsBRtKrKK2ljUFBVx61HeTYGxnx4xnx4xnx4xnx4xnwRWJ+aqNsCx9BGJN2Edgvkm2nDxr8GOK6qXpxkK1p15atomfZxwDtXV3WYiQHEdDNjPjxjPjxjPjxjPjxjvjj0TqJusZFWLfk82lObjwLeBuxUVY9JEtrgX9dX1ZUzfHZT2tDytseuA2M+PGM+PGM+PGM+PGO+cPVuzutO7J2AvWmDd+0H/GlVXZ3kJOB2STatNr7EqrHPbNLNA2D8tdbMmA/PmA/PmA/PmA/PmC8OvQfb7LLeOwMvAG4AXlFVP0iyB/BC4JSqurE76b/9jCe8P2M+PGM+PGM+PGM+PGO+OMxJc94tNtjuDtgLeFu12yk1z4z58Iz58Iz58Iz58Iz5wrLeSdSoepGWJNuZbQDGfHjGfHjGfHjGfHjGfGGb85ooSZKkjcG8P4BYkiRpMTKJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerh/wOaZo8FhbaIiAAAAABJRU5ErkJggg==\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAg8UlEQVR4nO3de5RkVX3o8e8PZni/rtIigjiAvETk4YgiRhEVRUCu4k1UVHwkQ66SiIkYkxUTTKKAyyAYg14CKkZUVBQVkUQigi/AGZ7yUkKGh7wacHQQgQF+94+9C2qKnunqM1Onq7q/n7XO6upT57HP75yu+vXe++wTmYkkSZKmZo3pLoAkSdIoMomSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkStLIioi1I+KaiNh8ussym0XEmRGx/3SXQ2qbSZRmvfpFfGpE3BQRSyPi8ql8IUTE5yLinxru+4iIWBgRD0bE5yZ4f72IOCki7o6I30TEhRMss1ZEXBsRt3bN+4OIuK9nyog4pOuYPx4Rt0XEr+s+5natPy8izqnv3RERn4yIOV3v7xYRiyLi/vpzt37KVednRPyuq1yn9LvuBBYAF2bm7T3rH1338/wJtvvPEXFr3ffiiDhhkn08QUT8ICIe6DqG67ve2zwivlVjmxExr2fdo+r5vDoidumav3dEnDXVstR1PxcRD/cmkzUOy7rKeW3nGmiwj5dFxHX1nJ8fEc/oevs4oNHfgDTKTKIkmAPcArwE2Bj4W+ArvV9+A3Ib5cvnMyt4/2TgScBO9ed7J1jmKGC8e0Zm/jAzN+hMwIHAfcC5dZEPAPOBZwPbA3tQjrvjJOAuYHNgN0ps3gUlEQG+CXwB+F/AacA36/yVlqvLrl3l++N+jmkF/hT49+4ZERHAW4F7689uf0057j2BDYF9gEv72M9Ejug6hh265j9KifMTkpWa5LwT2Ab4FHBMnT8H+GfgyKkWIiLWr/v6DfDmCRY5o+s6OBL4QkRsNsV9bAp8Hfgg5TpcCJzReT8zLwE2ioj5Uy2/NMpMojTrZebvMvPozFycmY9m5tnA/wDPnWzdiFgAHAq8v/6n/+0p7vvrmXkWcM8E294ReA2wIDPHM/ORzFzUs8zWlC/OYybZ1WHA1zLzd/X3g4BPZOa9mTkOfAJ4R9fyWwNfycwHMvMOSlKwc31vH0rieUJmPpiZnwAC2LdBuZ6g33UjYitKMnJxz1t/QEn+/hx4Q09y9zzgG5l5WxaLM/PzUy3jymTmnZl5EvCzCd7eCrgsM38LnFfLDyW5+VZmLm6wy0OAJcA/UM7zysr2H8BSYNsp7uN1wNWZ+dXMfAA4Gti1XqMdPwAOmOJ2pZFmEiX1qP+lbw9cPdmymXkycDrw0frf/kF1G2dHxJIVTGf3WZQ9gZuAD9Xmn6smaIr5F+BvgN+v5HjWB15PqTFa7q2e11tGxMb19xMoCch6EbEFsD+P12LtDFyZyz8z6koeT7L6KdeFtZnw6xPU+E16TNUuwI2Z+XDP/MOAbwNfqb8f1PXeRcBfRMS7ImKXWmv1mCmet2PqeflxROwzSVk7bgB2iYhNgJcDV0fE04E3AB/rcxu9DgO+BHwZ2DEiJkz+ozgAWAu4ps7baiXHuyQi3lRX3xm4orOtmoz/N8uf82uBXRsegzSSTKKkLlH6BZ0OnJaZ1zXdTmYemJmbrGA6sM/NbElpbvsN8DTgCOC0iNiplvW1wJqZ+Y1JtvM64G7ggq555wLviYixiHgqpdYGYL3680LKF+RvgVspzTdn1fc2qGXq9htK81g/5XoJMA/YkdKceXZtzprKMQFsQqlVeUxErAf8H+CLmbkM+BrLN+kdQ+m/c2g9pl9FxGO1N1M4b39FqUXagtLk+u2ImLR2JzPvAT4MfJ9Sa/M+4MS6vddGxAUR8c2I2LKP4+/Uxr20Hu+dwH/xxCbMP4yIJZTm3G8BH8nMJbU8N6/keDfJzC/Wbaz0nFdLKedEmjVMoqQqItag9K95iJKwTLffA8uAf8rMhzLzAuB8YL9au/RRHk9+VuYw4PM9NUcfBi4DLgd+QkmQlgF31jicS+kDsz6wKaXv03F13fuAjXr2sRGwtJ9yZeaF9XiWAO+hNB3uNMVjAvg1y3+JA7wWeBg4p/5+OrB/RIzVfT+Smf+amXtTvvA/DHymk5j2KzMvzsyltTnzNODHwKv7XPdLmblHZu5PSZIfpJyLj1Fqzb5K/7VSbwGuzczL6++nA2+KrpsEKM2ym2Tm+pRmvLdGxOF9br9jhee86/cNKc2K0qxhEiXxWGfkU4HNgENqLUa/sndGRHw3nnh3XGf6bp/bvXIl+9qOUpvzw4i4g5LwbF6byOZ1lePplD5My/X7yczfZ+YRmblFZm5D6ZO1KDMfpXQc3gr4ZE0S7gE+y+NJwtXAc3qawp5T5/dVrgmOKRqseyWwdXTdNUhJGDcAbq7b+CowF3hT78o1Bv9KScaeVePV9Lx1jqFvEbEu8BHgL+ux31L7Sv2MEs9+vBXYpsboDuB4StI7YUJX+1x9l9rEWZvzVnS890XEoXXVq+lqqqsJ77Ys3+S9E11NftKskJlOTrN+Aj5N6S+zQYN1j6U0pzTZ7xxgHUoz07/X13Pqe3MpfWg+WJfbm/Kf/47196d2Ta+jNI09ldIc1tn+31CGAOjd7xaUJsIAXkC5O3G/rvdvpNzBN4dSY/ONzjFS+tTcRKlFWptSa3dTnb/SclGaCHerrzeg9L26vh5rX8fUcxxXAi/sOqZHgP16tnMsJUGE0oF7H2Ddur/DKDVB20zhnG0CvLJzrihNg78Dtu9aZh1KLV4COwDrTLCdDwPvra83pySym1HuODy7zp9XtzFvgvX3otS67dJzvKcDZ9Zljga+0LXOlsBVwHFTvE7HKM13h9RjOw64qGeZXwB7TvffspNTm9O0F8DJabon4Bn1i+oBSrNFZzq0vr9V/X2rFay/HaVZbAlw1hT3fXTdd/d0dNf7OwM/rV/S1wCvXcF29gFunWD+dcA7J5j/YmAxcD8liTm05/3dKHdb/ZrSn+orwGZd7+8OLKI0OV4K7N5PuSh38F1fj+cuSjPidlM5pp5l3g18qr7+ADVZ6lnmaZSmymdTxpVaVBOCJcAlwIFTPGdjlNqipXUbFwGv6Fmm95xmz/s71m10J7xH1VhfA+xS5/1BPU9zJyjHp6nJUs/8PSmJ4ZPq9bWs65q+va63XoO/k5fX6+n39dqY1/Xe84BLB/236uQ0bFNkPqElQpJGQkSsTelP9LLsGXBzJoiIvwXGM/P/TXdZViYizgROzcxzJl1YmkFMoiRJkhqwY7kkSVIDJlGSJEkNmERJkiQ1YBIlSZLUwJzJF5m6TTfdNOfNmzeITUuSJK1WixYtujszx6a63kCSqHnz5rFw4cJBbFqSJGm1ioibmqxnc54kSVIDfSVREbFJRHwtIq6LiGsjYq9BF0ySJGmY9ducdyJwbma+PiLWAtYbYJkkSZKG3qRJVERsTHnO1tsAMvMh4KHBFkuSJGm49dOctzUwDnw2Ii6LiFMiYv3ehSJiQUQsjIiF4+Pjq72gkiRJw6SfJGoOsAflSem7U56+/oHehTLz5Mycn5nzx8amfJegJEnSSOkniboVuDUzL66/f42SVEmSJM1akyZRmXkHcEtE7FBnvQy4ZqClkiRJGnL93p33Z8Dp9c68G4G3D65IkiRJw6+vJCozLwfmD7YokiRJo8MRyyVJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIamNPPQhGxGFgKPAI8nJnzB1koSZKkYddXElW9NDPvHlhJJEmSRojNeZIkSQ30m0Ql8J8RsSgiFky0QEQsiIiFEbFwfHx89ZVQkiRpCPWbRL0oM/cA9gfeHREv7l0gM0/OzPmZOX9sbGy1FlKSJGnY9JVEZeav6s+7gG8Aew6yUJIkScNu0iQqItaPiA07r4H9gJ8PumCSJEnDrJ+78zYDvhERneW/mJnnDrRUkiRJQ27SJCozbwR2baEskiRJI8MhDiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIa6DuJiog1I+KyiDh7kAWSJEkaBVOpiXoPcO2gCiJJkjRK+kqiImJL4ADglMEWR5IkaTT0WxN1AvB+4NHBFUWSJGl0TJpERcSBwF2ZuWiS5RZExMKIWDg+Pr7aCihJkjSM+qmJ2ht4TUQsBr4M7BsRX+hdKDNPzsz5mTl/bGxsNRdTkiRpuEyaRGXmX2fmlpk5D3gD8P3MfPPASyZJkjTEHCdKkiSpgTlTWTgzfwD8YCAlkSRJGiHWREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNWASJUmS1IBJlCRJUgMmUZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1MGkSFRHrRMQlEXFFRFwdER9qo2CSJEnDbE4fyzwI7JuZ90XEXOBHEfHdzLxowGWTJEkaWpMmUZmZwH3117l1ykEWSpIkadj11ScqItaMiMuBu4DvZebFAy2VJEnSkOsricrMRzJzN2BLYM+IeHbvMhGxICIWRsTC8fHx1VxMSZKk4TKlu/MycwlwPvCqCd47OTPnZ+b8sbGx1VQ8SZKk4dTP3XljEbFJfb0u8ArgugGXS5Ikaaj1c3fe5sBpEbEmJen6SmaePdhiSZIkDbd+7s67Eti9hbJIkiSNDEcslyRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWpg0iQqIp4eEedHxDURcXVEvKeNgkmSJA2zOX0s8zDwl5l5aURsCCyKiO9l5jUDLpskSdLQmrQmKjNvz8xL6+ulwLXAFoMumCRJ0jCbUp+oiJgH7A5cPJDSSJIkjYi+k6iI2AA4EzgyM387wfsLImJhRCwcHx9fnWWUJEkaOn0lURExl5JAnZ6ZX59omcw8OTPnZ+b8sbGx1VlGSZKkodPP3XkBnApcm5nHD75IkiRJw6+fmqi9gbcA+0bE5XV69YDLJUmSNNQmHeIgM38ERAtlkSRJGhmOWC5JktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNWASJUmS1IBJlCRJUgMmUZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUwKRJVER8JiLuioift1EgSZKkUdBPTdTngFcNuBySJEkjZdIkKjMvBO5toSySJEkjwz5RkiRJDay2JCoiFkTEwohYOD4+vro2K0mSNJRWWxKVmSdn5vzMnD82Nra6NitJkjSUbM6TJElqoJ8hDr4E/BTYISJujYh3Dr5YkiRJw23OZAtk5hvbKIgkSdIosTlPkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqYNIHEEuSpJlh3ge+M91FaGTxsQdMdxEmZE2UJElSAyZRkiRJDZhESZIkNWASJUmS1EBfHcsj4lXAicCawCmZeexAS7USdorTbOB13j5jLmmqJq2Jiog1gX8F9geeBbwxIp416IJJkiQNs35qovYEbsjMGwEi4svAwcA1gyyYJGlms/ZPo66fPlFbALd0/X5rnSdJkjRrRWaufIGI1wOvysw/rr+/BXh+Zh7Rs9wCYEH9dQfg+tVf3IHbFLh7ugsxyxjz9hnz9hnz9hnz9o1yzJ+RmWNTXamf5rxfAU/v+n3LOm85mXkycPJUCzBMImJhZs6f7nLMJsa8fca8fca8fca8fbMx5v005/0M2C4ito6ItYA3AN8abLEkSZKG26Q1UZn5cEQcAfwHZYiDz2Tm1QMvmSRJ0hDra5yozDwHOGfAZRkGI90cOaKMefuMefuMefuMeftmXcwn7VguSZKkJ/KxL5IkSQ2YREmSJDVgEjWDRMTaETG3vo7pLs9sEBFr1J/GuyURsVZ9HJVxb0n9bFm7vjbmA9SJb0SsGxFj9bXf1S2IiA0iYl593dd17omZASLiRRFxNfBfwHsB0s5uAxMRG0bEURFxJfCJOtu/pQGKiM0i4u8j4sfAucCfg9f5IEXEUyLimIj4PvB94L0RsbYxH6zMzIjYDbgZ+KtpLs6MFxFPioh/jIjvAJcBh0H/ny193Z2n4VL/K4nMfCQi1qGMFP/XwIXAdyLiRuBMP+xWnxrzNTLzYcpQH5sDnwcOBcjMR6axeDNS93VOGfB3c+BI4Cbg+xFxRWZ+fxqLOOP0XOdrA3OBvwWuAn4CLATOm74SzjydWqbMfLRr9k6Uf4q3nuA9raKe63xD4APAfpl5/lS35X/PI6RTvZiZj3a+tDPzAcpDoi/LzCXAPwP7UB69o1XUE/OH6+slwDHA8cCDEbF797JaNRNd58ANwPsy82eZeRdwCfULRqtuBdf5LZn5vsz8SWYuBW4EHpjOcs4kPTHvTZJeD5wBPBARz+1eXs2t4Dq/Cbi6TkTE5lPZpknUEIpizd528FrN+9SI2CciToyIgyJiY+BHwLPrYlcDDwJ+sU9BnzE/ISIOrvPH6wffVcAr6+L+PU3BFGL+msxckpn31acmQKklsfZviqYS86513h4RyyjPRXta22UedVP9bKlNeTcAlwN3UmqlwM+Xvk0h5ofUt34OXBQRi4BPRsSCfvuheVKGQERsEhEH1ISILB7JzEe7k6CIOJRSpf5q4OXA24H7gdt4/A9tHLgD2KKzrfaOZHQ0jPnLgHfW+Z2/nQuAF7db+tG0CjH/kzp/bmY+FBF7As8AvuY/CSu3qjGvvgs8uc57XefLXhNbhZj/aX1re+C2zPwfYAlweEQcbpeBFVuFmP9xfesE4Fhgb+A44H8Dr+tn3/aJGg7PovSteRA4LyJ2AN4MPB/4YUR8klKN/kLgPZn57Yg4DzgFCOA64FUAmXlvXf+77R/GSFlRzPcEfrSSmH8GSnVw/eO8GDiqzvNDbuVWNebL6naOAk7KzPvaPoARtEoxB8jMO+rLayLiVmDriFjDfjor1PTz/NRa07o98JaIWABsQPmMv20ajmOUNL3OPwuQmQsp/f0ALomIa4DN+rnOrYlqSa1eXFG8F1Oqb59Zf9+HUqN0FPA74O8oF8d84Ir6H/l/Us7fTsBZwG4RsV9df6u6/qzWMObv5/GYP8QTY965c6bz384vgfsj4viIeGdEbDao4xkFA4x5p3l6L8qH4cKIODgi3hQRGw7qeEbBoK/zrv2sCWwHXDfbE6gBfZ4HsC3lDrFjgYOA5wE/ozTrzeruGQO6zh+d4DqfQ+lT/Mt+rnOTqJbUL9wVnZBx4HbKfyAApwGLgHdRqhtfBKxVl3t+13/kS4GDM/N+4EPA2yLiHuDKOs1qqyHmc4G7gBf0xPzVABHxgoi4gPLFsjuwjFL9PmsNMOYH1td/RvmP8xTKXan3A79fzYcxUgYY81cCRMThEfEzSh+dGyi1r7PaAD/PX5uZ38nMz2bmjZRk6xxq/7/Z3D1jgNf5/gARcViUPlGXAddTbl6ZlM15q9lE1X81e94GeBuwLDM/1P1+Zi6LiJuBPSJiK0rGfDilv82HKXeB7QX8G/CHtd03gLsp1ZhQaqP+K8udY7NKHzF/KDP/ofv9npg/g/JhdThlmIjumJ9CiflGddV7gF3r65uBIzPzsoEc2BBrOeb3AjvW158BPpGZFw3kwIbYNMT8OfX1ZcARmTnrkqdp+Dzfpe5j7cx8MDN/A5w6wEMcOtNwne9SX18FvHuqny3WRK2CiFijVnE/pnPyI+LZUcZwgnICT6T8N3FazzY61bM3U2oytgBeAmycmacCD1OqeA/JzG9SLoKDKGNbfIpafVk70S2p21xzplb7Noz553u20Rvzp/F4zE9hxTHfiBLzbet+b+skUDXmy5VrphiCmJ9EHbIjM8/rfMhNVK6ZYshifkkngfKzBRjs5/l2db8P9pZtNR3mUBmS63z7ut9Luz5b+r7OrYmagoiI7urUiaoWI+IDlDE+fgtcEBGfp4z2+zzgq5m5uHv5ru3dXqfdKLVKb42IMykn+izKhQDlv5nLgedSqik/2luGnEEdnI15+4Y95p3yraRqf+SMUMy9zlv+bFlR2UbRsMe8yXVuEjWJ7qrF7pMf5Rl1rwT+kNKu+lFKm2tS7sLYGPgasAnwccpAdSuL9z112gs4GTiCcsfdBZl5Tddy69R9bQx8B/j2qh7jsDHm7RulmHeXb5QZ8/aNUsxnilGKeaPrPDOduibKKMgLgC0meG8L4MD6ej/ge8AhwM513ispHYvPo9xRcWq9GNajVPu+ZpJ9bwNsvYL31pzu2BjzmTMZc2NuzI25MV/1yZqoqitb3pTSifUG4FcR8VJg3cw8h9JH4L0RcT2linAOpTPa/XUziyhZ9J9kGSite/t3ArtExPmZubS2twaPPxuMLHdjdK/TGaI+cwZVo3cY8/YZ8/YZ8/YZ8/bN1pjPyM5q/egEtyvIncETf0EZk6PzXK4X8/hjPX5CqXZ8GmUwy3uAdwMfj4hOleAlwMFRhpZ/RZTxg55KeTTLHcBj1ZrZ9WywiNgqykjMvSd+RlSjgzGfDsa8fca8fca8fca8mBU1UdHzlOyI0nks6m2kEbE2pfpx48z8p4i4A9imnojLgf0j4imZeVdE3E65JfInmfn6ur0NKW2wewH/l3Ib5ncoY1d8E7gvM7/VU6Z1gAOAfYE9KLe3/kst58j/oRnz9hnz9hnz9hnz9hnzFZuRSVTvCc+uOwAi4smZeU9EPIXS8/+FmfnriHgI2KSezBspY6RsAfw35bbK51DaaW+hPHPnjIjYhPKMnd0obbYX14vkH4G/7z2Rsfz4F6+gjCz+acoIwMsYYSMU86djzI15Q8a8fSMUcz/PZ+F1PiOb87JU8XUy5vUjYt+IOCkifgF8NiL2ysy7KEPF71NX+2/Kk+G3q68fojxS5ReU6scD6nIbUdp7Nwc2q8t/HXhL3SaZuaxm6cuNgdF9IWbmtzPz45l51aj/wcFIxfwEY27MmzLm7RuhmPt5Pguv8xmXREXExlGep/XFiHge5WR9hNIzf3vgp8CfRsQzgfN5vK12MaWtdTtKe+7dwE6Z+RBllOTdIuLnlI5sRwLXZ+aPMnNBZp6Zmb/tLUt2tdfOZMa8fca8fca8fca8fcZ8akaiOS/isfbX5QbqmmC5NYCjKVWIF1JO6hrAdZTh3QG+RGlv3Qv4AfAWgMy8ISKeDyzNzDMi4hZg14jYKDN/ERF/1MmSJ9jnchnyTGDM22fM22fM22fM22fMB2dok6iI6Ny6+GjnpHd+RsT2wN2ZeW/PRfFi4EWZ+byu7awNLKS0V5OZiyNiG+DnmXlJlOHdjwOeTGmrvT9Kh7VbKJ3VtgEu75z83hM+qid+Isa8fca8fca8fca8fca8HUOTRNXAdo/3kJTxIohSbbgppaf+l+sqVwHv6Mmq76WONxFlNNRHs9w5sBhYEBGnZ+YVlM5onaz6jcDBdXvfzMyldf07KQ8x3Aa4vHOhjfoJ72bM22fM22fM22fM22fMp8e0JVHR86Tm3sBGebL1uykd1Q4CHqCMEfG6zLwlIn4ZEXtk5qVdq90DPBgRe2fmj+t2OuNW3AR8LModBecDl9b9XgFc0bXfTlZ+K/Cf1Aul50IbSca8fca8fca8fca8fcZ8OLSeRNUTsA/w1fp7p612H2B/Srb8wcy8LSIOBq7JzD0iYndKW+wGdVPnAy+MiMvz8WrBX0XEpcB76vZeSmnXPQG4CFgjM/9xgjJNVO35EPDj1R+B9hnz9hnz9hnz9hnz9hnz4TLwu/Oitn92ZGkXXQC8ISLeD2wUEdsCb6Zks+cAx0fEFsC5wO31BN1KeZLz8+umLgZ2BdaPiLkRsX+d/3eUAbeeBBwPHAP8jnKL5Ta1TNFdrixmTBWjMW+fMW+fMW+fMW+fMR9uA0+iOoGNiGdExIsiYg9Kz/8PAc+knJgjgduA+yg9/edTxo+4CtgSWJfyUMLrKR3VoAwfvyflRK8D7BsR62TmQ5n5w8z8y8w8J8t4E49QqhU/Vss0o0+4MW+fMW+fMW+fMW+fMR9yuWpPaw5W8GRkyklbF3gucAHlZH4QeCrwPuBjXcv+DaXd9GjgNcDadf5WlBO3bf39QOCHnX0CrwXWX8H+16BUPa7SMQ7bZMyNuTE35sZ8ZkzGfPSn1X1BbFx/bgR8CngTcChwXM9yuwP/Acyj9Mt6BXBhzzIvqT9/AhxcXz8Z2KFzgie4GGO6A9r6CTTmxnwWTMbcmM+GyZiP3tSoY3lXR7btgdcDa1GqEbentNVuVi+C8yhZ9Ntr++mdwC8y81tRhnIfy8zFwPci4q8i4hOUqsU9gLMo2ffbKc/hITPvodw9QPZUJWa9CmYqY94+Y94+Y94+Y94+Yz5zRNO4RcSOwOeA71FO9F3A54F3UNpdrwV2zswHImI+5Y6AFwCHUZ6h80bKs3OeAvxbZn4vIv6I8hDC8zLzllU4rhnJmLfPmLfPmLfPmLfPmM8MqzLEwbbADcBpwK8y8/cRcSzwF8DZwJnAZhFxc2YuhMcG39oBmAucRKmqXEIZg4LMPGMVyjMbGPP2GfP2GfP2GfP2GfMZYFVqojYEPksZkXQNyi2Qx1OGjf8QcEZm/nlErEuprvwgJdM+A/jkiqoOo2cAMT3OmLfPmLfPmLfPmLfPmM8MjZOo5TZSqiXfQXlq80nAicDmmfnqiAjK4F/LMnPJBOuuSRla3vbYKTDm7TPm7TPm7TPm7TPmo6txc149sU8DdqEM3rU78K7MvC8iLgGeFBFrZhlfYrxrnTXqPAC6X2vljHn7jHn7jHn7jHn7jPnM0HiwzZr1Ph34E+Bh4P2Z+cuI2A44HLg0Mx+pJ/2xdTzhzRnz9hnz9hnz9hnz9hnzmWG1NOctt8Fyd8DOwIlZbqfUgBnz9hnz9hnz9hnz9hnz0bLKSVSnepGSJNuZrQXGvH3GvH3GvH3GvH3GfLSt9pooSZKk2WDgDyCWJEmaiUyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhr4/9RWAJIpmMWyAAAAAElFTkSuQmCC\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAhzUlEQVR4nO3deZglZXn38e+PYZVVZUQEFFDAncUR11dR44KKxCVxF9fRKHFLNMZExVcT1MsgGoOG4MYb17graCKCIEGUYV9EJQRllWETEGW93z+eOnJou2e6a6Zrunu+n+uqq8+p9am7qs+5z/NUPZWqQpIkSTOzzpougCRJ0nxkEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUpHktyYFJ3rimy7E2S/LgJCes6XJIQzOJkoAk/57k0iTXJvl5klfOYNlPJ3lvz+3un2RZkhuTfHqS6XdKckiSK5L8Jslxk8yzfpKfJrlobNz/SXL9hKGSPLubvkGSDyW5JMnV3TbWG1t++yRHdtMuS/LRJOtOsu2XdOt95di4A5LcPGHbO45N3yfJWd34E5Lcf2xakrw3ycXd/v4gyQNWEL/FwEuAf50wfocktyX52CTL7JvktO5YX5Hk6CQ7TLWNFWx7xyTfTnJdt54PdOM3SPKJJL/spp2WZO+x5bZLcmKSq5L804R1fifJkh5lWdH+VpLfdvG+Isnnk2zRYxsbJPlkF7fLkrx5NK2qzgCuSbLPTNcrzWcmUVJzILB9VW0GPAN4b5KHDLDdS4D3Ap+cYvqhwF2A+3V/3zTJPG8Blo+PqKofVtUmowF4OnA98N1ulrcBS4AHAjsDewB/P7aKQ4DLga2B3YDHAq8d30aSOwNvB86epExfHN9+VZ3fLbMT8FngNcAWwLeAb44laH8GvBz4P93+/gj4f1PEBuClwJFV9bsJ418CXA08N8kGY2W+D3A48FfA5sAOwL8At65gG38kyfrA94CjgbsD2wL/3k1eF7iQFrPNaXH9UpLtu+l/C3ym2/afjpKmJM8F/reqls2kLJ1J93fMrt15sCNwZ+CAHts4ANgJuBfwOOCtSZ4yNv2zwKt7rFeat0yiJKCqzq6qG0dvu+HeK1suyVLghbQvlOuTfGuG2/1qVX0duHKSdd+XltAtrarlVXVrVZ08YZ4dgBfRksAV2Q/4clX9tnu/D/CRqrqqqpYDH6ElLyM7AF+qqt9X1WW05GtijdCB3XJXTGNXR54M/LCqjq+qW4D3A9vQEo7Rdo+vqvOr6lZaYnL/yVcFwN7AseMjkoSWVPw9cHO3ryO70RKV71dzXVV9pap+NYN9gJa8XVJVB1XVb7s4nQHQvT+gqi6oqtuq6tvA/wKjpHwH4Oiq+g1wErBjks1oie3bZ1iOle3vHVTVtcA3WXFMp7If8J6qurqqfgr8Gy0OIz8AnjBFEictSCZRUqdr0roBOBe4FDhyZctU1aG0X+Af6Gpc9unW9e0k10wxfHuaRdoT+CXw7q4Z5sxRc9yYf6Z98U6siRnfr42B59BqP+4wacLrbZNs3r0/GHheWnPiNrRk5bt/mDnZk1aT9fEpNrtP11x1dpK/WMl2Q6sRA/gCcO8kO3fNi/uNb3cSDwJ+NmHco2k1Q18AvtStY+QU4L5dU+bjkmxyh4IlL1jBcbsmyT27WR8OXNA1v13RNTs+aLICJtmKVts3qrE7C3hi16T2kG78e4CDq+qaFezrVFa0vxPLcmfgT4ETx8YdsoL9PWNsua2B08dWdzpjiXVVXUxL4nbpsQ/SvGQSJXWq6rXAprSmpK8CN654iRWu6+lVtcUUw9OnuZptacnFb4B7APsDn0lyP4AkzwQWVdXXVrKeZ9Fqi8ZrbL4LvCHJ4iR3B17fjb9T9/c42hfktcBFwDLg6912F9Ga+/avqtsm2d6XaM2Pi4FXAe9M8vxu2lHAY5Ps1TWJvR1Yf2y7lwLH0xKj39Ga9yZrwhzZArhuwrj9gO9U1dXA54CnJLkbQNesuBet9utLwBVp17Rt0k3/3AqO2xZjNVbbAs+j1cTdAzgC+Ea3T3/QJYKfBT5TVed2ow+knWPHdnFcH3gw8K0kn0tyXJL9V7DPE025v2NOSXIN7Ty4J2PXkFXVa1ewvw/uZhslm78ZW+dvaP8v466jHRNprWASJY3pmsyOp31JTqxBGdrvaL/s31tVN1XVscAxwJO62qUPcHvysyL7AYfXHZ82/g/AqcBpwAm0BOlm4NdJ1qElWV8FNga2pF1H8/5u2dcCZ1TViUyiqs6pqku6WJ4AfJhWE0aXSOwHfJSWMG0JnENL1ADeCTwU2A7YEHg3cHSSOzG5qxn7Ik+yES3x+my3vR8BvwJeMFa+E6vqz6tqMS2ZeQzwd1Osfyq/ozU7fqeqbgI+CNyVljyOyrIO7Xqum2gJ8Gj7V1XVc6tq1y42/wz8Ja057yzgT4DXjJLlFZnO/nb2qKotaDH9GPDDJBvOYH+v7/5uNjZuM/44gd0UuGYG65XmNZMoaXLrMo1rojo1cUTXzDPx7rjR8J1prveMFWxrJ2B72pfhZbSEZ+vurqntx8qxHa3m5fA7rKTqd1W1f1VtU1U70q7JOrmrWboLrbbio1V1Y1VdCXwKeGq3+BOAZ3bbugx4JPBPST46xX4UY014VfXlqnpgVd0VeFe3Hyd1k3ejXZR+UVXdUlWfpiVwU13DcwatqWzkmbQv90PGyrcNUzRxVdVJtNg9sIvXC1dw3K4fa847g0mO+0h3ndIngK2AZ1fVzVPMuhQ4sarOojVNLuuSsjO79ysz0/29GTiMdl3WaJ8/voL9Pbtb7mpa0rvr2Op2Zeymgq7Zd33+uHlVWriqysFhrR6Au9GaZjYBFtEufv4t8IxpLv8+4HM9t70urXbgQFqtxYbAut209YDzgHd08z2K9sv/vt37u48Nz6Ld6Xd3WhPfaP1vB46bZLvb0JqhQru+50LgSWPTz6fVjKxLa5752mgfu/fj2z4BeDOweTd9X1riE9p1XRcD+42t+yFdnBfTmtQ+NzbtXbTmvK1oP/Je3B2LLaaI35uBQ8fe/ycteRkv30OA22hJyaNpTYx36+a/L/Bz4O9meNx2AW6g1RotojU5/g+wfjf947TrjjZZyXl35mgeWtPegd15+AtgSTf+08Cnp1jHCve3m6eA+3SvF9FqxW4A7jLDfX4frQnyzl3cLgWeMjb9BbQ7Jdf4/7SDw1DDGi+Ag8OaHrov82NpzRDXdl9srxqbfk9ac8Y9p1h+J1qz2DXA12e47QO4/W7A0XDA2PQH0G7z/y2t2euZU6xnL+CiScafC7xikvGPAS7ovkx/BrxwwvTdaHdbXU27juZLwFZTbPsHwCvH3n+eVrN1fbf910+Y/3haMngV7dqcjcembUjrcuDS7licMv5FPcm2t6Q1BW5ESwxvGSUPE+Y7ktbk9kBatwq/7sp3Aa2Zcr0e582zaEnutV0MHtCNv1d3HH/fbWM0TIzx4cCfjb3fDvhxF/ODxsZ/f/x8HBu/0v3tXld3/lzflfUk4Mk99ncDWlcc13bxe/OE6UcwzR8eDg4LZUjVlDXSkjTnJflH4PKqOnhNl2V16y5UPx14cE3dJLjGJXkw8K9V9Yg1XRZpSCZRkiRJPXhhuSRJUg8mUZIkST2YREmSJPVgEiVJktTDuiufZea23HLL2n777Wdj1ZIkSavVySeffEW1pxjMyKwkUdtvvz3Lli2bjVVLkiStVkl+2Wc5m/MkSZJ6mFYSlWSLJF9Ocm6SnyaxQzVJkrRWm25z3oeB71bVc7oedKd6orokSdJaYaVJVJLNac/ZeilAtSeM3zS7xZIkSZrbptOctwOwHPhUklOTHJZk44kzJVmaZFmSZcuXL1/tBZUkSZpLppNErQvsAXysqnanPQ38bRNnqqpDq2pJVS1ZvHjGdwlKkiTNK9NJoi4CLqqqH3fvv0xLqiRJktZaK02iquoy4MIku3SjngCcM6ulkiRJmuOme3feXwKf7e7MOx942ewVSZIkae6bVhJVVacBS2a3KJIkSfOHPZZLkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9bDudGZKcgFwHXArcEtVLZnNQkmSJM1100qiOo+rqitmrSSSJEnziM15kiRJPUw3iSrgv5KcnGTpZDMkWZpkWZJly5cvX30llCRJmoOmm0Q9uqr2APYGXpfkMRNnqKpDq2pJVS1ZvHjxai2kJEnSXDOtJKqqLu7+Xg58DdhzNgslSZI01600iUqycZJNR6+BJwFnzXbBJEmS5rLp3J23FfC1JKP5P1dV353VUkmSJM1xK02iqup8YNcByiJJkjRv2MWBJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg/TTqKSLEpyapJvz2aBJEmS5oOZ1ES9AfjpbBVEkiRpPplWEpVkW+BpwGGzWxxJkqT5Ybo1UQcDbwVum72iSJIkzR8rTaKSPB24vKpOXsl8S5MsS7Js+fLlq62AkiRJc9F0aqIeBTwjyQXAF4DHJ/n3iTNV1aFVtaSqlixevHg1F1OSJGluWWkSVVV/W1XbVtX2wPOAo6vqRbNeMkmSpDnMfqIkSZJ6WHcmM1fVD4AfzEpJJEmS5hFroiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6WGkSlWTDJD9JcnqSs5O8e4iCSZIkzWXrTmOeG4HHV9X1SdYDjk/ynao6cZbLJkmSNGetNImqqgKu796u1w01m4WSJEma66Z1TVSSRUlOAy4HvldVP57VUkmSJM1x00qiqurWqtoN2BbYM8kDJ86TZGmSZUmWLV++fDUXU5IkaW6Z0d15VXUNcAzwlEmmHVpVS6pqyeLFi1dT8SRJkuam6dydtzjJFt3rjYAnAufOcrkkSZLmtOncnbc18Jkki2hJ15eq6tuzWyxJkqS5bTp3550B7D5AWSRJkuYNeyyXJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6mGlSVSS7ZIck+ScJGcnecMQBZMkSZrL1p3GPLcAf1VVpyTZFDg5yfeq6pxZLpskSdKctdKaqKq6tKpO6V5fB/wU2Ga2CyZJkjSXzeiaqCTbA7sDP56V0kiSJM0T006ikmwCfAV4Y1VdO8n0pUmWJVm2fPny1VlGSZKkOWdaSVSS9WgJ1Ger6quTzVNVh1bVkqpasnjx4tVZRkmSpDlnOnfnBfgE8NOqOmj2iyRJkjT3Tacm6lHAi4HHJzmtG546y+WSJEma01baxUFVHQ9kgLJIkiTNG/ZYLkmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktTDSpOoJJ9McnmSs4YokCRJ0nwwnZqoTwNPmeVySJIkzSsrTaKq6jjgqgHKIkmSNG94TZQkSVIPqy2JSrI0ybIky5YvX766VitJkjQnrbYkqqoOraolVbVk8eLFq2u1kiRJc5LNeZIkST1Mp4uDzwM/AnZJclGSV8x+sSRJkua2dVc2Q1U9f4iCSJIkzSc250mSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktTDumu6AJI0F2z/tiPWdBF6ueB9T1vTRZDWWtZESZIk9WASJUmS1MO0mvOSPAX4MLAIOKyq3jerpdKcYjOHJEl/bKU1UUkWAf8C7A3cH3h+kvvPdsEkSZLmsunURO0JnFdV5wMk+QKwL3DObBZMWptZ+6e1gee55rvpXBO1DXDh2PuLunGSJElrrdXWxUGSpcDS7u31SX62utY9oC2BK9Z0IdYysxbzvH821rogGPPhGfPhGfPhzefv0Hv1WWg6SdTFwHZj77ftxt1BVR0KHNqnEHNFkmVVtWRNl2NtYsyHZ8yHZ8yHZ8yHtzbGfDrNeScBOyXZIcn6wPOAb85usSRJkua2ldZEVdUtSfYH/pPWxcEnq+rsWS+ZJEnSHData6Kq6kjgyFkuy1wwr5sj5yljPjxjPjxjPjxjPry1LuapqjVdBkmSpHnHx75IkiT1YBIlSZLUg0nUApJkgyTrda+zpsuzNkiyTvfXeA8kyfrd46iM+0C6z5YNutfGfBaN4ptkoySLu9d+Vw8gySZJtu9eT+s898AsAEkeneRs4PvAmwDKi91mTZJNk7wlyRnAR7rR/i/NoiRbJXlXkv8Gvgu8HjzPZ1OSuyU5MMnRwNHAm5JsYMxnV1VVkt2AXwF/s4aLs+AluUuS9yQ5AjgV2A+m/9my2nos13C6XyWpqluTbEjrKf5vgeOAI5KcD3zFD7vVp4v5OlV1C62rj62Bw4EXAlTVrWuweAvS+HlO6/B3a+CNwC+Bo5OcXlVHr8EiLjgTzvMNgPWAvwfOBE4AlgFHrbkSLjyjWqaqum1s9P1oP4p3mGSaVtGE83xT4G3Ak6rqmJmuy1/P88ioerGqbht9aVfV72kPiT61qq4B/gnYC9hlDRVzQZkQ81u619cABwIHATcm2X18Xq2ayc5z4Dzgr6vqpKq6HPgJ3ReMVt0U5/mFVfXXVXVCVV0HnA/8fk2WcyGZEPOJSdJzgC8Cv0/ykPH51d8U5/kvgbO7gSRbz2SdJlFzUJpFE9vBu2reuyfZK8mHk+yTZHPgeOCB3WxnAzcCfrHPwDRjfnCSfbvxy7sPvjOBJ3ez+/80AzOI+TOq6pqqur57agK0WhJr/2ZoJjEfW+ZlSW6mPRftHkOXeb6b6WdL15R3HnAa8GtarRT4+TJtM4j5s7tJZwEnJjkZ+GiSpdO9Ds2DMgck2SLJ07qEiGpurarbxpOgJC+kVak/FfgT4GXADcAl3P6Pthy4DNhmtK7h9mT+6BnzJwCv6MaP/neOBR4zbOnnp1WI+au68etV1U1J9qQ9LPTL/khYsVWNeec7wF27cc8afdlrcqsQ89d0k3YGLqmq/wWuAV6d5NVeMjC1VYj5K7tJBwPvAx4FvB/4U+BZ09m210TNDfenXVtzI3BUkl2AFwEPA36Y5KO0avRHAm+oqm8lOQo4DAhwLvAUgKq6qlv+O8PvxrwyVcz3BI5fQcw/Ca06uPvn/DHwlm6cH3Irtqoxv7lbz1uAQ6rq+qF3YB5apZgDVNVl3ctzklwE7JBkHa/TmVLfz/NPdDWtOwMvTrIU2IT2GX/JGtiP+aTvef4pgKpaRrveD+AnSc4BtprOeW5N1EC66sWp4n0Brfr2Pt37vWg1Sm8Bfgu8k3ZyLAFO736R/xft+N0P+DqwW5Indcvfs1t+rdYz5m/l9pjfxB/HfHTnzOjXzi+AG5IclOQVSbaarf2ZD2Yx5qPm6UfQPgyXJdk3yQuSbDpb+zMfzPZ5PradRcBOwLlrewI1S5/nAe5Nu0PsfcA+wEOBk2jNemv15RmzdJ7fNsl5vi7tmuJfTOc8N4kaSPeFO9UBWQ5cSvsFAvAZ4GTgtbTqxkcD63fzPWzsF/l1wL5VdQPwbuClSa4EzuiGtdpqiPl6wOXAwyfE/KkASR6e5FjaF8vuwM206ve11izG/Ond67+k/eI8jHZX6g3A71bzbswrsxjzJwMkeXWSk2jX6JxHq31dq83i5/kzq+qIqvpUVZ1PS7aOpLv+b22+PGMWz/O9AZLsl3ZN1KnAz2g3r6yUzXmr2WTVf132vCPwUuDmqnr3+PSqujnJr4A9ktyTljG/mna9zT/Q7gJ7BPBvwJ937b4BrqBVY0Krjfp+tTvH1irTiPlNVfV/x6dPiPm9aB9Wr6Z1EzEe88NoMd+sW/RKYNfu9a+AN1bVqbOyY3PYwDG/Crhv9/qTwEeq6sRZ2bE5bA3E/MHd61OB/atqrUue1sDn+YO6bWxQVTdW1W+AT8ziLs45a+A8f1D3+kzgdTP9bLEmahUkWaer4v6D0cFP8sC0PpygHcAP035NfGbCOkbVs7+i1WRsAzwW2LyqPgHcQqvifXZVfYN2EuxD69viY3TVl91FdNd061y0UKt9e8b88AnrmBjze3B7zA9j6phvRov5vbvtXjJKoLqY36FcC8UciPkhdF12VNVRow+5ycq1UMyxmP9klED52QLM7uf5Tt12b5xYttW0m3PKHDnPd+62e8rYZ8u0z3NromYgScarUyerWkzyNlofH9cCxyY5nNbb70OB/6iqC8bnH1vfpd2wG61W6SVJvkI70F+nnQjQfs2cBjyEVk35gYllqAV0gbMxH95cj/mofCuo2p935lHMPc8H/myZqmzz0VyPeZ/z3CRqJcarFscPftoz6p4M/DmtXfUDtDbXot2FsTnwZWAL4EO0jupWFO8ru+ERwKHA/rQ77o6tqnPG5tuw29bmwBHAt1Z1H+caYz68+RTz8fLNZ8Z8ePMp5gvFfIp5r/O8qhzGBlovyEuBbSaZtg3w9O71k4DvAc8GHtCNezLtwuKjaHdUfKI7Ge5Eq/Z9xkq2vSOwwxTTFq3p2BjzhTMYc2NuzI25MV/1wZqozli2vCXtItbzgIuTPA7YqKqOpF0j8KYkP6NVEa5Luxjthm41J9Oy6FdV6yhtfP2/Bh6U5Jiquq5rbw23PxuMandjjC8z6qK+agFVo48Y8+EZ8+EZ8+EZ8+GtrTFfkBerTccouGNBHnWe+HNanxyj53I9htsf63ECrdrxHrTOLK8EXgd8KMmoSvAnwL5pXcs/Ma3/oLvTHs1yGfCHas0aezZYknum9cQ88cAviGp0MOZrgjEfnjEfnjEfnjFv1oqaqEx4SnbSLh5Ldxtpkg1o1Y+bV9V7k1wG7NgdiNOAvZPcraouT3Ip7ZbIE6rqOd36NqW1wT4C+AvabZhH0Pqu+AZwfVV9c0KZNgSeBjwe2IN2e+s/d+Wc9/9oxnx4xnx4xnx4xnx4xnxqCzKJmnjAa+wOgCR3raork9yNduX/I6vq6iQ3AVt0B/N8Wh8p2wD/Q7ut8sG0dtoLac/c+WKSLWjP2NmN1mb74+4keQ/wrokHMnfs/+KJtJ7FP07rAfhm5rF5FPPtMObGvCdjPrx5FHM/z9fC83xBNudVq+IbZcwbJ3l8kkOS/Bz4VJJHVNXltK7i9+oW+x/ak+F36l7fRHukys9p1Y9P6+bbjNbeuzWwVTf/V4EXd+ukqm7usvQ79IExfiJW1beq6kNVdeZ8/4eDeRXzg425Me/LmA9vHsXcz/O18DxfcElUks3Tnqf1uSQPpR2sf6Rdmb8z8CPgNUnuAxzD7W21F9DaWneitedeAdyvqm6i9ZK8W5KzaBeyvRH4WVUdX1VLq+orVXXtxLLUWHvtQmbMh2fMh2fMh2fMh2fMZ2ZeNOclf2h/vUNHXZPMtw5wAK0K8TjaQV0HOJfWvTvA52ntrY8AfgC8GKCqzkvyMOC6qvpikguBXZNsVlU/T/LcUZY8yTbvkCEvBMZ8eMZ8eMZ8eMZ8eMZ89szZJCrJ6NbF20YHffQ3yc7AFVV11YST4jHAo6vqoWPr2QBYRmuvpqouSLIjcFZV/SSte/f3A3eltdXekHbB2oW0i9V2BE4bHfyJB3y+HvjJGPPhGfPhGfPhGfPhGfNhzJkkqgvseH8PResvgrRqwy1pV+p/oVvkTODlE7Lqq+j6m0jrDfW2ancOXAAsTfLZqjqddjHaKKt+PrBvt75vVNV13fK/pj3EcEfgtNGJNt8P+DhjPjxjPjxjPjxjPjxjvmassSQqE57UPDGwaU+2fh3tQrV9gN/T+oh4VlVdmOQXSfaoqlPGFrsSuDHJo6rqv7v1jPqt+CXwwbQ7Co4BTum2ezpw+th2R1n5RcB/0Z0oE060ecmYD8+YD8+YD8+YD8+Yzw2DJ1HdAdgL+I/u/aitdi9gb1q2/I6quiTJvsA5VbVHkt1pbbGbdKs6BnhkktPq9mrBi5OcAryhW9/jaO26BwMnAutU1XsmKdNk1Z43Af+9+iMwPGM+PGM+PGM+PGM+PGM+t8z63Xnp2j9HqrWLLgWel+StwGZJ7g28iJbNHgkclGQb4LvApd0Buoj2JOeHdav6MbArsHGS9ZLs3Y1/J63DrbsABwEHAr+l3WK5Y1emjJermgVTxWjMh2fMh2fMh2fMh2fM57ZZT6JGgU1yrySPTrIH7cr/dwP3oR2YNwKXANfTrvRfQus/4kxgW2Aj2kMJf0a7UA1a9/F70g70hsDjk2xYVTdV1Q+r6q+q6shq/U3cSqtW/GBXpgV9wI358Iz58Iz58Iz58Iz5HFer9rTmMMWTkWkHbSPgIcCxtIP5DuDuwF8DHxyb9+20dtMDgGcAG3Tj70k7cPfu3j8d+OFom8AzgY2n2P46tKrHVdrHuTYYc2NuzI25MV8YgzGf/8PqPiE27/5uBnwMeAHwQuD9E+bbHfhPYHvadVlPBI6bMM9ju78nAPt2r+8K7DI6wJOcjFnTAR38ABpzY74WDMbcmK8NgzGff0OvC8vHLmTbGXgOsD6tGnFnWlvtVt1JcBQti35Z1376a+DnVfXNtK7cF1fVBcD3kvxNko/Qqhb3AL5Oy75fRnsOD1V1Je3uAWpCVWJ1Z8FCZcyHZ8yHZ8yHZ8yHZ8wXjvSNW5L7Ap8Gvkc70JcDhwMvp7W7/hR4QFX9PskS2h0BDwf2oz1D5/m0Z+fcDfi3qvpekufSHkJ4VFVduAr7tSAZ8+EZ8+EZ8+EZ8+EZ84VhVbo4uDdwHvAZ4OKq+l2S9wFvBr4NfAXYKsmvqmoZ/KHzrV2A9YBDaFWV19D6oKCqvrgK5VkbGPPhGfPhGfPhGfPhGfMFYFVqojYFPkXrkXQd2i2QB9G6jX838MWqen2SjWjVle+gZdpfBD46VdVhJnQgptsZ8+EZ8+EZ8+EZ8+EZ84WhdxJ1h5W0asmX057afAjwYWDrqnpqktA6/7q5qq6ZZNlFtK7lbY+dAWM+PGM+PGM+PGM+PGM+f/VuzusO7D2AB9E679odeG1VXZ/kJ8Bdkiyq1r/E8rFl1unGATD+WitmzIdnzIdnzIdnzIdnzBeG3p1tdlnvdsCrgFuAt1bVL5LsBLwaOKWqbu0O+h+W8YD3Z8yHZ8yHZ8yHZ8yHZ8wXhtXSnHeHFba7Ax4AfLja7ZSaZcZ8eMZ8eMZ8eMZ8eMZ8flnlJGpUvUhLkr2YbQDGfHjGfHjGfHjGfHjGfH5b7TVRkiRJa4NZfwCxJEnSQmQSJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktTD/wdT9z50Z2FX8gAAAABJRU5ErkJggg==\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAhvUlEQVR4nO3deZglVX3/8feHAQFZgwygIA4guKCyOKKoUdzFjV+UGJcgauKYKHGLGhNj3BKXPEbFKCYoKkaNxCWuoBHBBRdw2BcFEZFNZABBRnb4/v44dZ1L0z3TXTP3TnfP+/U89fTtqrpVp75Vfe+3zzl1KlWFJEmSZma9tV0ASZKkucgkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJc1qSdyZ51doux7osydOTHLW2yyGNm0mUNCTJrkluTPKpGbznO0n+suf+3p7kzCS3JnnLJMsXJvlMkmuT/DbJpydZZ6sky5KcMDTv+UmWD03XJ6kkD+6Wb5nkyCRXdNNbJmxzzyTf7/Z7SZI3TVj+uCQ/67Z7fJJ7TVj++CSnJPl99/5nDy1bkOSfk1yW5LokpybZsluWbtml3b6/k2T3lcRvIfAC4D8nzN8pye1JPjzJew5IclqS3yW5MslxSXaaah9T7PeFSW6bEOP9hpZPeV6T7JHk7G7frxmav0GSE5PccyZl6d67X3d+/27C/EXd/EEZf5PksCQb9NjHVkn+tzunv0ryvMGyqvoqsHuSB810u9JcZhIl3dGHgJ+McX/nA68Hvj7F8i8ClwM7AtsA75lknXcDPx2eUVWfrqpNBxPwMuAC4JRulfcBdwUWAfsAByV50dAmPgN8D9gKeDTwsiTPAEiydVeuN3XLlwJ/qIVIcv/u/W8EtgD2AE4e2vZbgYcD+wKbAwcBN3bL/hR4MfDH3bZ/BPzXFLEBeCFwdFXdMGH+C4DfAn+WZMOhst0b+CTwt13ZdqKd89tWso+p/Gg4xlX1naFlKzuv7wReS4vLG5Ns181/DfCFqrq4R1kOBq6mHfdktuyugwfS4v7yHvv4EHAzsC3wfODDExLc/waW9NiuNGeZREmdJM8BrgG+PYP3/AvtC/+D3X/6H5zJPqvqyKo6Brhukm0/Ebgn8LqquraqbqmqUyes83DgAcDHV7Grg4FP1opHFDwd+Nequr6qLgSOoCUvA4uAT1fVbVX1C+AEYPCF+Uzg7Kr6XFXdCLwF2CPJfbvl/wj8Z1UdU1W3VtVV3TZI8kfAq4CXVNWvqjmr2w60pOaEqrqgqm4DPgXcfyXHtT/w3QkxCS2Z+Efglu5YB/YEfllV3+72fV1VfaGqLlpZ8GZqZeeVdozHVdWlwM+BHbuavGfRktsZSbIJcCAtMdo1yeKVlOsK4FusPKZT7eNZwJuqanlVnQB8hZYAD3wHeOrMSi/NbSZREpBkc+BttNqAaauqNwLfBw7paiMO6bZ3RpJrppgOm+bmHwacCxyZ5KokP0ny6KEyLwA+CBwCTPn8pu4L+lG0Gpg7LJrw+gFDv78feEHXxHQfWu3Fsd2y3YHTh2Lwe+AXrEiyHtbt98wkv07yqSRbdcseCNwKHJjk8iTnJRmuFfkssEuS3bomp4OBb0x1bN32zp0w75HADt22/qfbxsApwH2TvC/JY5JseoeAJM9byXm7JsmOQ6vv1TXJnZfkTUnWX0k5h50FPDHJDrRk9RfAobRk+ZZpbmPYM4HlwOeAb0443jtIcg/gScCPh+Z9bSXH+7Vutd2AW6vqvKHNnc6Kcw6tNnRR97ckrRNMoqTm7cARVXXJmthYVT2oqracYnrZNDezA/BE4HhgO+DfgC93zWkArwBOrKqTp3j/wAuA71fVL4fmfQN4Q5LNuiauF9Oa9wa+RqvduAH4GS02g2bOTYFrJ+zjWmCzoXIfRKu52BXYGPj3oWVb0L6Ud+r28ZYkT+iW/5pW63Vut+8/BV69kmPbkjvX9hwMHFNVv6U1Kz45yTYAVXUBsB+wPS3BujLJJwbJVFV9ZiXnbcuhGqvv0ZLObbrjfC7wupWUc9hrgb+m1eS8GnhEdwy/TPLlJN9N8qfT3NbgeI/qau4+Azxnkj5PVya5BrgU+D3w+cGCqnraSo73ad1qmwK/m7DN4XMOK87DljMouzSnmURpnZdkT+Dx9GhKGbEbgAur6oiuKe+zwMXAI7oahVfQ+h2tyguAIyfMe0W3/Z8DX6b1Z7kEWgdiWpL1NmAjWpPik5IMkr/ltL5MwzZnxZfoDcDHq+q8qloOvAN4ytAygLdV1Q1VdQatxmiw/J+Ah3T73IjWf+q4JMMJ3rDfMvRFnmRjWuL1aYCq+hFwETDcCfrHVfXsqlpIa4p9FNOL4x90zY2/rKrbq+pMWqwOnOZ7f1VVT6mqvWmxfzstsXoPrW/ZM4D3DtXeTanrhP4YuuPttrcRd25W27qqtqQlyj+g1VjNxKrOOaw4D9fMcNvSnGUSJbWaiUXARUkup32hPSvJKSt705A7NaV1d18tn2L6j2lu94xJtj34fR/g7sA5XZkPBfbpmsgWDJXjEcA9GKp5AKiqq6vq+VW1XVXtTvssOKlbvDNwW1V9suvTdAl3THTOpnWKHuxjE2CXbv5k5R5+fcYk84Zf70mrVbmk2/cngD9i6j48Z9BqtQb+hPblflgXi8tptU6TNnF1tWtfpGvKzJ3vapw47TjZdrpjyBTLVuafgI9U1W9oTZNLq+paWkJ772m8/yDauftqd6wX0JKoqY73BuATwMMGNZpJjlnJ8R7TvfU8YP0kuw5tbg9WnHOA+9GS/ok1VtL8VVVOTuv0RPvvfLuh6T20pGPhNN//WeAdPfe9Ae1L7zPAP3evF3TLtqLVtBwMLKDVdFwNbA1sOKHMrwROBLabsP3DaR3KJ+53F+Bu3Xb3B64Edu+WbU6rTXge7Qt6O9pdcu/oli+kNeU8qyvvu4EfD237xcAvacnYXWnNZv81tPx7tCEJNqR98V4BPK5b9mZac9623b4PojU/bTlF/F4DHD70+zdpneSHY/Ng4HZakvJI4CXANt3696UlCG+c4XnbH9h2aBtnAW+eznkdWuf+tL5Jg/N9NPBX3bFfOTiXtA7bb5miHOfSOvYPH+8zgJu687uIluCt362/IfAuWrNpZnjMn6XVWG5Ca4K8dnDNdMv/AThsbf89OzmNc1rrBXBymm1T96X0qaHf/xhYvpL19+2+iH8LfGCG+/pE9yU3PL1wwr7PpDWnLAX+eIrtvJB2V9vwvI1oydDjJln/2cBlwPXAacCTJix/LG2oh2tpQyx8BLjr0PLH0/pK3dB9yS+a8P63Asu66b+APxpatj2tuXA5rebkpRPK/KHuS/53tI7gT15J/Lam1dps3G33VuCBk6x3NC05fgDwVeA33f4vpCWBG8zwvL2n28bvu2N42/A2VnVeu3WOBx469PsewDm0BOo1Q/N/ATxhkjI8jDY0xJ2SfVoN0SGsSKKWd9M1tLsZH9Lj72Ir4EvdMV8EPG/C8jOBPdbG36yT09qaUjXlTT2SNOsleQdwRVW9f22XZU3r7uD7n6p6+Nouy8okeTpwUFU9e5UrS/OISZQkSVIPdiyXJEnqwSRKkiSpB5MoSZKkHkyiJEmSepjus55mZOutt65FixaNYtOSJElr1Mknn3xltacYzMhIkqhFixaxdOnSUWxakiRpjUryqz7vszlPkiSph2klUUm2TPL5JD9L8tMk+466YJIkSbPZdJvzDgW+UVUHJrkL7XlYkiRJ66xVJlFJtgAeRXs2F1V1M3DzaIslSZI0u02nOW8n2kNEP57k1CQfTbLJxJWSLEmyNMnSZcuWrfGCSpIkzSbTSaLWB/YGPlxVe9Ge4P2GiStV1eFVtbiqFi9cOOO7BCVJkuaU6SRRlwCXVNWJ3e+fpyVVkiRJ66xVJlFVdTlwcZL7dLMeB5wz0lJJkiTNctO9O+9vgE93d+ZdALxodEWSJEma/aaVRFXVacDi0RZFkiRp7nDEckmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQe1p/OSkkuBK4DbgNurarFoyyUJEnSbDetJKrzmKq6cmQlkSRJmkNszpMkSephuklUAf+X5OQkSyZbIcmSJEuTLF22bNmaK6EkSdIsNN0k6pFVtTewP/DyJI+auEJVHV5Vi6tq8cKFC9doISVJkmabaSVRVXVp9/MK4H+BfUZZKEmSpNlulUlUkk2SbDZ4DTwROGvUBZMkSZrNpnN33rbA/yYZrP+ZqvrGSEslSZI0y60yiaqqC4A9xlAWSZKkOcMhDiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6mHYSlWRBklOTfG2UBZIkSZoLZlIT9Urgp6MqiCRJ0lwyrSQqyQ7AU4GPjrY4kiRJc8N0a6LeD7weuH10RZEkSZo7VplEJXkacEVVnbyK9ZYkWZpk6bJly9ZYASVJkmaj6dREPQJ4RpILgc8Cj03yqYkrVdXhVbW4qhYvXLhwDRdTkiRpdlllElVVf19VO1TVIuA5wHFV9ecjL5kkSdIs5jhRkiRJPaw/k5Wr6jvAd0ZSEkmSpDnEmihJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHlaZRCXZKMlJSU5PcnaSt46jYJIkSbPZ+tNY5ybgsVW1PMkGwAlJjqmqH4+4bJIkSbPWKpOoqipgeffrBt1UoyyUJEnSbDetPlFJFiQ5DbgC+FZVnTjSUkmSJM1y00qiquq2qtoT2AHYJ8kDJq6TZEmSpUmWLlu2bA0XU5IkaXaZ0d15VXUNcDzw5EmWHV5Vi6tq8cKFC9dQ8SRJkman6dydtzDJlt3rjYEnAD8bcbkkSZJmtencnXd34MgkC2hJ1/9U1ddGWyxJkqTZbTp3550B7DWGskiSJM0ZjlguSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1MMqk6gk90xyfJJzkpyd5JXjKJgkSdJstv401rkV+NuqOiXJZsDJSb5VVeeMuGySJEmz1iproqrq11V1Svf6OuCnwPajLpgkSdJsNqM+UUkWAXsBJ46kNJIkSXPEtJOoJJsCXwBeVVW/m2T5kiRLkyxdtmzZmiyjJEnSrDOtJCrJBrQE6tNV9cXJ1qmqw6tqcVUtXrhw4ZosoyRJ0qwznbvzAhwB/LSq3jv6IkmSJM1+06mJegRwEPDYJKd101NGXC5JkqRZbZVDHFTVCUDGUBZJkqQ5wxHLJUmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknpYZRKV5GNJrkhy1jgKJEmSNBdMpybqE8CTR1wOSZKkOWWVSVRVfQ+4egxlkSRJmjPsEyVJktTDGkuikixJsjTJ0mXLlq2pzUqSJM1KayyJqqrDq2pxVS1euHDhmtqsJEnSrGRzniRJUg/TGeLgv4EfAfdJckmSvxh9sSRJkma39Ve1QlU9dxwFkSRJmktszpMkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKmH9dd2ASTd2aI3fH1tF6GXC9/11LVdBEkaG2uiJEmSejCJkiRJ6mFazXlJngwcCiwAPlpV7xppqVbCZg5JkjQbrLImKskC4EPA/sD9gecmuf+oCyZJkjSbTacmah/g/Kq6ACDJZ4EDgHNGWTDNHtb+aV3gda51gdf5mjWdPlHbAxcP/X5JN0+SJGmdlapa+QrJgcCTq+ovu98PAh5aVYdMWG8JsKT79T7AuWu+uCO3NXDl2i7EOsaYj58xHz9jPn7GfPzmcszvVVULZ/qm6TTnXQrcc+j3Hbp5d1BVhwOHz7QAs0mSpVW1eG2XY11izMfPmI+fMR8/Yz5+62LMp9Oc9xNg1yQ7JbkL8BzgK6MtliRJ0uy2ypqoqro1ySHAN2lDHHysqs4eeckkSZJmsWmNE1VVRwNHj7gss8Gcbo6co4z5+Bnz8TPm42fMx2+di/kqO5ZLkiTpznzsiyRJUg8mUZIkST2YRM0jSTZMskH3Omu7POuCJOt1P433mCS5S/c4KuM+Jt1ny4bda2M+QoP4Jtk4ycLutd/VY5Bk0ySLutfTus49MfNAkkcmORv4NvBqgLKz28gk2SzJ65KcAXygm+3f0ggl2TbJm5P8APgG8ArwOh+lJNskeWeS44DjgFcn2dCYj1ZVVZI9gYuAv1vLxZn3kmyV5O1Jvg6cChwM0/9smdbdeZpduv9KUlW3JdmINlL83wPfA76e5ALgC37YrTldzNerqltpQ33cHfgk8HyAqrptLRZvXhq+zmkD/t4deBXwK+C4JKdX1XFrsYjzzoTrfENgA+AfgTOBHwJLgWPXXgnnn0EtU1XdPjT7frR/ineaZJlW04TrfDPgDcATq+r4mW7L/57nkEH1YlXdPvjSrqobaQ+JPrWqrgH+DdiP9ugdraYJMb+1e30N8E7gvcBNSfYaXlerZ7LrHDgfeG1V/aSqrgBOovuC0eqb4jq/uKpeW1U/rKrrgAuAG9dmOeeTCTGfmCQdCBwF3JjkwcPrq78prvNfAWd3E0nuPpNtmkTNQmkWTGwH76p5t0uyX5JDkzw9yRbACcADutXOBm4C/GKfgWnG/P1JDujmL+s++M4EntSt7t/TDMwg5s+oqmuqann31ARotSTW/s3QTGI+9J4XJbmF9ly0e4y7zHPdTD9buqa884HTgN/QaqXAz5dpm0HMn9UtOgv4cZKTgQ8mWTLdfmielFkgyZZJntolRFRzW1XdPpwEJXk+rUr9KcDjgRcB1wOXseIPbRlwObD9YFvjO5K5o2fMHwf8RTd/8LfzXeBR4y393LQaMX9JN3+Dqro5yT7AvYDP+0/Cyq1uzDvHAHfr5j1z8GWvya1GzP+qW7QbcFlV/RK4BnhpkpfaZWBqqxHzv+wWvR94F/AI4N3A/wOeOZ192ydqdrg/rW/NTcCxSe4D/DnwUOD7ST5Iq0Z/OPDKqvpqkmOBjwIBfgY8GaCqru7ef8z4D2NOmSrm+wAnrCTmH4NWHdz9cZ4IvK6b54fcyq1uzG/ptvM64LCqWj7uA5iDVivmAFV1effynCSXADslWc9+OlPq+3l+RFfTuhtwUJIlwKa0z/jL1sJxzCV9r/OPA1TVUlp/P4CTkpwDbDud69yaqDHpqheniveFtOrbe3e/70erUXod8Hvgn2gXx2Lg9O4/8v+jnb/7AV8C9kzyxO79O3bvX6f1jPnrWRHzm7lzzAd3zgz+2/k5cH2S9yb5iyTbjup45oIRxnzQPL0v7cNwaZIDkjwvyWajOp65YNTX+dB+FgC7Aj9b1xOoEX2eB9iFdofYu4CnAw8BfkJr1lunu2eM6Dq/fZLrfH1an+KfT+c6N4kak+4Ld6oTsgz4Ne0/EIAjgZOBl9GqGx8J3KVb76FD/5FfBxxQVdcDbwVemOQq4IxuWqetgZhvAFwBPGxCzJ8CkORhSb5L+2LZC7iFVv2+zhphzJ/Wvf4b2n+cH6XdlXo9cMMaPow5ZYQxfxJAkpcm+Qmtj875tNrXddoIP8//pKq+XlUfr6oLaMnW0XT9/9bl7hkjvM73B0hycFqfqFOBc2k3r6ySzXlr2GTVf132vDPwQuCWqnrr8PKquiXJRcDeSXakZcwvpfW3+RfaXWD7Ah8Bnt21+wa4klaNCa026tvV7hxbp0wj5jdX1duGl0+I+b1oH1YvpQ0TMRzzj9Jivnn31quAPbrXFwGvqqpTR3Jgs9iYY341cN/u9ceAD1TVj0dyYLPYWoj5g7rXpwKHVNU6lzythc/zB3b72LCqbqqqa4EjRniIs85auM4f2L0+E3j5TD9brIlaDUnW66q4/2Bw8pM8IG0MJ2gn8FDafxNHTtjGoHr2IlpNxvbAo4EtquoI4FZaFe+zqurLtIvg6bSxLT5MV33ZdaK7ptvmgvla7dsz5p+csI2JMb8HK2L+UaaO+ea0mO/S7feyQQLVxfwO5ZovZkHMD6MbsqOqjh18yE1WrvlilsX8pEEC5WcLMNrP8127/d40sWxr6DBnlVlyne/W7feUoc+WaV/n1kTNQJIMV6dOVrWY5A20MT5+B3w3ySdpo/0+BPhcVV04vP7Q9n7dTXvSapVekOQLtBP9JdqFAO2/mdOAB9OqKf91YhlqHnVwNubjN9tjPijfSqr255w5FHOv8zF/tkxVtrlotse8z3VuErUKw1WLwyc/7Rl1TwKeTWtX/Vdam2vR7sLYAvg8sCXwPtpAdSuL91XdtC9wOHAI7Y6771bVOUPrbdTtawvg68BXV/cYZxtjPn5zKebD5ZvLjPn4zaWYzxdzKea9rvOqchqaaKMgLwG2n2TZ9sDTutdPBL4FPAvYvZv3JFrH4mNpd1Qc0V0Md6VV+z5jFfveGdhpimUL1nZsjPn8mYy5MTfmxtyYr/5kTVRnKFvemtaJ9Xzg0iSPATauqqNpfQReneRcWhXh+rTOaNd3mzmZlkW/pNpAacPb/w3wwCTHV9V1XXtrWPFsMKrdjTH8nsEQ9VXzqBp9wJiPnzEfP2M+fsZ8/NbVmM/LzmrTMQjuUJAHgyeeRxuTY/Bcrkex4rEeP6RVO96DNpjlVcDLgfclGVQJngQckDa0/BPSxg/ajvZolsuBP1Rr1tCzwZLsmDYS88QTPy+q0cGYrw3GfPyM+fgZ8/Ez5s06UROVCU/JTlrnsXS3kSbZkFb9uEVV/XOSy4GduxNxGrB/km2q6ookv6bdEvnDqjqw295mtDbYfYG/pt2G+XXa2BVfBpZX1VcmlGkj4KnAY4G9abe3/ntXzjn/h2bMx8+Yj58xHz9jPn7GfGrzMomaeMJr6A6AJHerqquSbEPr+f/wqvptkpuBLbuTeQFtjJTtgV/Qbqt8EK2d9mLaM3eOSrIl7Rk7e9LabE/sLpK3A2+eeCJzx/EvnkAbWfw/aCMA38IcNodifk+MuTHvyZiP3xyKuZ/n6+B1Pi+b86pV8Q0y5k2SPDbJYUnOAz6eZN+quoI2VPx+3dt+QXsy/K7d65tpj1Q5j1b9+NRuvc1p7b13B7bt1v8icFC3Tarqli5Lv8MYGMMXYlV9tareV1VnzvU/OJhTMX+/MTfmfRnz8ZtDMffzfB28zuddEpVki7TnaX0myUNoJ+sdtJ75uwE/Av4qyb2B41nRVnshra11V1p77pXA/arqZtooyXsmOYvWke1VwLlVdUJVLamqL1TV7yaWpYbaa+czYz5+xnz8jPn4GfPxM+YzMyea85I/tL/eYaCuSdZbD3gLrQrxe7STuh7wM9rw7gD/TWtv3Rf4DnAQQFWdn+ShwHVVdVSSi4E9kmxeVecl+bNBljzJPu+QIc8Hxnz8jPn4GfPxM+bjZ8xHZ9YmUUkGty7ePjjpg59JdgOurKqrJ1wUjwIeWVUPGdrOhsBSWns1VXVhkp2Bs6rqpLTh3d8N3I3WVnt9Woe1i2md1XYGThuc/IknfK6e+MkY8/Ez5uNnzMfPmI+fMR+PWZNEdYEdHu+haONFkFZtuDWtp/5nu7ecCbx4QlZ9Nd14E2mjod5e7c6BC4ElST5dVafTOqMNsurnAgd02/tyVV3Xvf83tIcY7gycNrjQ5voJH2bMx8+Yj58xHz9jPn7GfO1Ya0lUJjypeWJg055s/XJaR7WnAzfSxoh4ZlVdnOTnSfauqlOG3nYVcFOSR1TVD7rtDMat+BXwnrQ7Co4HTun2ezpw+tB+B1n5JcD/0V0oEy60OcmYj58xHz9jPn7GfPyM+eww9iSqOwH7AZ/rfh+01e4H7E/Llt9UVZclOQA4p6r2TrIXrS12025TxwMPT3JaragWvDTJKcAru+09htau+37gx8B6VfX2Sco0WbXnzcAP1nwExs+Yj58xHz9jPn7GfPyM+ewy8rvz0rV/DlRrF10CPCfJ64HNk+wC/Dktmz0aeG+S7YFvAL/uTtAltCc5P7Tb1InAHsAmSTZIsn83/59oA25tBbwXeCfwe9otljt3ZcpwuaqZN1WMxnz8jPn4GfPxM+bjZ8xnt5EnUYPAJrlXkkcm2ZvW8/+twL1pJ+ZVwGXAclpP/8W08SPOBHYANqY9lPBcWkc1aMPH70M70RsBj02yUVXdXFXfr6q/raqjq403cRutWvE9XZnm9Qk35uNnzMfPmI+fMR8/Yz7L1eo9rTlM8WRk2knbGHgw8F3ayXwTsB3wWuA9Q+v+A63d9C3AM4ANu/k70k7cLt3vTwO+P9gn8CfAJlPsfz1a1eNqHeNsm4y5MTfmxtyYz4/JmM/9aU1fEFt0PzcHPgw8D3g+8O4J6+0FfBNYROuX9QTgexPWeXT384fAAd3ruwH3GZzgSS7GrO2Ajv0EGnNjvg5MxtyYrwuTMZ97U6+O5UMd2XYDDgTuQqtG3I3WVrttdxEcS8uiX9S1n/4GOK+qvpI2lPvCqroQ+FaSv0vyAVrV4t7Al2jZ94toz+Ghqq6i3T1ATahKrO4qmK+M+fgZ8/Ez5uNnzMfPmM8f6Ru3JPcFPgF8i3airwA+CbyY1u76U2D3qroxyWLaHQEPAw6mPUPnubRn52wDfKSqvpXkz2gPITy2qi5ejeOal4z5+Bnz8TPm42fMx8+Yzw+rM8TBLsD5wJHApVV1Q5J3Aa8BvgZ8Adg2yUVVtRT+MPjWfYANgMNoVZXX0MagoKqOWo3yrAuM+fgZ8/Ez5uNnzMfPmM8Dq1MTtRnwcdqIpOvRboF8L23Y+LcCR1XVK5JsTKuufBMt0z4K+OBUVYeZMICYVjDm42fMx8+Yj58xHz9jPj/0TqLusJFWLfli2lObDwMOBe5eVU9JEtrgX7dU1TWTvHcBbWh522NnwJiPnzEfP2M+fsZ8/Iz53NW7Oa87sfcAHkgbvGsv4GVVtTzJScBWSRZUG19i2dB71uvmATD8WitnzMfPmI+fMR8/Yz5+xnx+6D3YZpf13hN4CXAr8Pqq+nmSXYGXAqdU1W3dSf/Dezzh/Rnz8TPm42fMx8+Yj58xnx/WSHPeHTbY7g7YHTi02u2UGjFjPn7GfPyM+fgZ8/Ez5nPLaidRg+pFWpJsZ7YxMObjZ8zHz5iPnzEfP2M+t63xmihJkqR1wcgfQCxJkjQfmURJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9fD/AUT5JcLgab3OAAAAAElFTkSuQmCC\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAhaElEQVR4nO3deZhlVXnv8e+PZlSmi7SIILag4IQKtiiiBmdx4jrEOOOQtF41inHMTUxQ40Aeg0OcLhEVIyoqifMQiTigEWwmEXBA0jJLA6K0KON7/1i75HBS3VW9u8/uqurv53n2U6f22cPa7951zltrrb12qgpJkiStnU02dAEkSZLmI5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiTNW0m2SHJ2kp03dFk2ZkmOS3LQhi6HNDSTKAlI8q0kf0iyqpt+upbr/nnP/b45yZlJbkhy2DTvL07yiSS/SfLrJMdMs8wOSVYmOXFk3rNGjmVVkmuSVJL7du9vn+ToJJd102Ej6+42tu6qbt1Xde8nyd8kOT/Jb5N8Ksm2syzXkm5bo9t+w8j7uyT5fJIrk1yY5MUzhHAZ8J2qumRs34d1+7n/2PzNk/xTt+1VSVYkedcM+5hWkqcnOSfJ75L8IsmDp1nm77pyPGJk3muSXJ7krCR7j8w/IMnnepblo901tPPY/MOSXD8S63OSPKXnPh6e5CfdtXRCkjuOvH048A99tivNZyZR0s1eVlVbd9NeA+3zXOC1wJdX8/6/AZcCuwG3Bd4xzTKHA+eMzqiqY0aOZWvgJcB5wKndIu8EbgUsAfYDnpPk+d2654+tuzdwE3Bct+5zgecABwC3B7YC/nk25Rqx/cg+3jwy/+PAfwM7AY8D3prkoavZBsCLgX8dnZEkXRmv7H6O+mtgaXfM2wAHcnNMZi3JI2nH9/xuOw+hxXd0mT2APwUuGZm3M/BCYHfgA8DbuvmbAv8EHNqjLLcGngL8Bnj2NIscO3IuDwU+nmSntdzHjrRr8Q3ADsBy4Nip96vqZGDbJEvXtvzSfGYSJa2DJG8BHgy8t/tP/71rs35VHV1VXwWunmbbjwLuALymqn5TVddX1WljyzwQuCfwkRl2dQjwsbr5EQVPAP6xqq6pqhXAUcALVrPuc2m1PStG1j2qqi6oqlW0ZOLPktyqR7lGj2VrWlLzlu5YzwA+u7pyJdmNloycNPbWg4GdgZcDT0+y+ch79wP+vaourmZFVX1stmUc8UbgTVX1g6q6qaouqqqLxpZ5H/A64LqRebsBp1XVb4Hju/JDS26+MBLjtfEU4CrgTbTzvFpV9XXatbbHWu7jycBZVfWZqvoDcBhw7yR3HVnmW7TEV9pomERJN3tb18zyvSQHzmaFqvob4LvcXIv1MoAkP0py1Wqm98+yPA8AfgocneSKJD9M8idTbyZZBLwXeBmw2uc3dc0uDwHGk4WMvb7nNOtO1eocPcO6WwB3WYty/bJrUvtIV8sxus0Zy9XZGzivqm4Ym38I8EXg093vTxh57wfAXyV5SZK9u+O7eWfJl9Zw3r40cnxLgcVJzu2O471JthrZzp8C11bVV8bKdi6wd5LtgUcAZyW5A/B0pq9lnI1DgE8CnwLumq7Jdlxrhc3jgM2Bs7t5u63heK9K8sxu9XsAZ0xtq6p+B/yimz/lHODePY9BmpdMoqTmdbRagV2AI4Evds0xvVTVvapq+9VML5nlZnYFHgWcANyO1tzz+ZGk4+XASVV1ygzbeS7w3ar675F5XwNen2SbJHem1fbcapp1H0RrWvvs2Lp/nta/aTta7BhZf03lupxWG3RH4L60prBjAKrqauB7wBuSbJlkX1oty3TlAtiesRq8rjbsT4FPVNX1XblHm/TeRqs5exatSeqiJH+svamqx6/hvD2+W2wnYDPgqbRar/sA+wB/25VhG+CtwCvGC1xVVwBvAb5Jq7V5NfBuWgyflOTbaX3Cdl3NMd9CVxv30O54fwX8J/+zCfNpSa4CVgFfAN5aVVd15Tl/Dce7fVV9otvG1rTmwlG/oZ2/KVfTzom00TCJkoCqOqmqrq6qa6vqaNqX+WM3cLF+D6yoqqO65q1PARcAByS5PS1Z+ZtZbGe6mqSXd9v/OfB5Wk3GhdOsewhwXNdsN+XD3fLfAs6iJXkAF85UrqpaVVXLq+qG7kv/ZcCjusQDWnJzp+44P0DrIzVduQB+zS2/xAGeBNwATNUAHQMclGRxt/8bq+p9VXUA7Qv/LcCHk9xtNfuYzu+7n/9cVZdU1eXAEdx8vRwG/Ovqmuaq6pNVtW9VHUSrZbsWOI1WE/UE4DPMvlbqOcA5VXV69/sxwDOTbDayzKe7hOjWtGa85yZ50Sy3P2UVMH7zwLbcMondhtasKG00TKKk6RW3bFaaadlb6O68Gr/DbWr64Cy3+6Nptj31+360fj9nJ7mUVpuxX5JLu+amqXJMdf7+7C02UnVlVT2rqm5XVfegfRacPHYMW9FqdY4eW/emqvr7qlpSVbvSEqmLumlW5ZrmeDbptv3LrjZocVXdH9hxvFxj8blT1yl7yiG0WpPzu/1/hlZr9Mzxlavq91X1PloydvfumL+6hvP21W69X9MSu9FzM/r64cDLu2O+lNav7dNJXjeyzFR83wq8itYUekHXV+qHwL1Wc8zjngvsPrKvI2gxm/YfgC6x+ypdE2emvxNzdHpWt+pZjDTVpXVm36ObP+VujDT5SRuFqnJy2qgnWo3Eo4EtgU1ptSG/A/ac5fqfojWR9Nn3Zt1+P0G7RXxLYFH33g60L/hDgEW05qMraV+SW9Ca+KamV9A6WN9ubPtH0jqUj+93D+A23XYPojWz3WNsmWcCK4CMzd+hWz+05OPHwLLuvTWWC7g/sBctaboN7Q6vE0a2fTdajcbmtDvNLgcWryF+PwIe2L3eBbiR1gQ6Woa3A6d0yxxK67y+VXeuD6HVBO2+luftTbRk57bA/6L1i3tz995txvZ/AS0Z3XpsG28BXtm93hm4gtZU+GLgS938JbQEbck0ZdifVuu299j+jqHVHkKrFfv4yDq7AmcCh6/l8S6mNd89hXaNHg78YGyZnwH7bei/ZyenIacNXgAnpw09dV8QP6Q1TVxF63z8yJH3HwysWsP6+3dfIL8G3rOW+/5o9yU5Oj1vbN9n0ppTlgMPXs12ngecODZvy+54Hj7N8k8DLgauAU4HHj3NMl+fSgzG5u9J6/B+DfBL4K/WcHy3KBfwDNoQBr+j3fr/MUYSP1qSs7J7/0Rg6Qzxeynwge716+mSpbFlbg9cT2s6Wwac0iUEV9FquR7f45rZDHh/t41LgfcAW65m2RXAI8bm3bW75haNzHsNLWk8G9h75PyvADabZrsfpEuWxubvR0sMd6AlUdd318+qLuYfBG7V45gfAfyE1pz5LUYSO1o/t1PX99+mk9Ncn1K12pt6JGlOS7IFrT/Rw2tswM2FIMnfAiur6v9t6LKsSZLjaMNejN+NKC1oJlGSJEk92LFckiSpB5MoSZKkHkyiJEmSejCJkiRJ6mHTmRdZezvuuGMtWbJkEpuWJElar0455ZTLq2rx2q43kSRqyZIlLF++fBKbliRJWq+S/LLPejbnSZIk9TCrJCrJ9kk+m+QnSc5Jsv+kCyZJkjSXzbY5793A16rqqUk2B241wTJJkiTNeTMmUUm2Ax5CewYWVXUdcN1kiyVJkjS3zaY57060B4J+JMlpST6U5NbjCyVZlmR5kuUrV65c7wWVJEmaS2aTRG0K7Et7Uvo+tKerv358oao6sqqWVtXSxYvX+i5BSZKkeWU2SdSFwIVVdVL3+2dpSZUkSdJGa8YkqqouBS5Islc36+HA2RMtlSRJ0hw327vz/hI4prsz7zzg+ZMrkiRJ0tw3qySqqk4Hlk62KJIkSfOHI5ZLkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9bDpbBZKsgK4GrgRuKGqlk6yUJIkSXPdrJKozkOr6vKJlUSSJGkesTlPkiSph9kmUQX8R5JTkiybboEky5IsT7J85cqV66+EkiRJc9Bsk6gHVdW+wEHAS5M8ZHyBqjqyqpZW1dLFixev10JKkiTNNbNKoqrqou7nZcC/A/tNslCSJElz3YxJVJJbJ9lm6jXwKODHky6YJEnSXDabu/N2Av49ydTyn6iqr020VJIkSXPcjElUVZ0H3HuAskiSJM0bDnEgSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1MOsk6gki5KcluRLkyyQJEnSfLA2NVGvAM6ZVEEkSZLmk1klUUl2BR4HfGiyxZEkSZofZlsT9S7gtcBNkyuKJEnS/DFjEpXk8cBlVXXKDMstS7I8yfKVK1eutwJKkiTNRbOpiToAeGKSFcCngIcl+fj4QlV1ZFUtraqlixcvXs/FlCRJmltmTKKq6q+rateqWgI8HfhmVT174iWTJEmawxwnSpIkqYdN12bhqvoW8K2JlESSJGkesSZKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqYcZk6gkWyY5OckZSc5K8sYhCiZJkjSXbTqLZa4FHlZVq5JsBpyY5KtV9YMJl02SJGnOmjGJqqoCVnW/btZNNclCSZIkzXWz6hOVZFGS04HLgG9U1UkTLZUkSdIcN6skqqpurKr7ALsC+yW55/gySZYlWZ5k+cqVK9dzMSVJkuaWtbo7r6quAk4AHjPNe0dW1dKqWrp48eL1VDxJkqS5aTZ35y1Osn33eivgkcBPJlwuSZKkOW02d+ftDBydZBEt6fp0VX1pssWSJEma22Zzd96PgH0GKIskSdK84YjlkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST3MmEQluUOSE5KcneSsJK8YomCSJElz2aazWOYG4FVVdWqSbYBTknyjqs6ecNkkSZLmrBlroqrqkqo6tXt9NXAOsMukCyZJkjSXrVWfqCRLgH2AkyZSGkmSpHli1klUkq2B44BDq+q307y/LMnyJMtXrly5PssoSZI058wqiUqyGS2BOqaq/m26ZarqyKpaWlVLFy9evD7LKEmSNOfM5u68AEcB51TVEZMvkiRJ0tw3m5qoA4DnAA9Lcno3PXbC5ZIkSZrTZhzioKpOBDJAWSRJkuYNRyyXJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6mHGJCrJh5NcluTHQxRIkiRpPphNTdRHgcdMuBySJEnzyoxJVFV9B7hygLJIkiTNG/aJkiRJ6mG9JVFJliVZnmT5ypUr19dmJUmS5qT1lkRV1ZFVtbSqli5evHh9bVaSJGlOsjlPkiSph9kMcfBJ4L+AvZJcmOSFky+WJEnS3LbpTAtU1TOGKIgkSdJ8YnOeJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUw4wPIJY0vCWv//KGLkIvK97+uA1dBEkajDVRkiRJPZhESZIk9WASJUmS1INJlCRJUg+z6lie5DHAu4FFwIeq6u0TLdUa2OFWkhYGP881381YE5VkEfA+4CDg7sAzktx90gWTJEmay2ZTE7UfcG5VnQeQ5FPAwcDZkyyY5g7/W5Qk6X+aTZ+oXYALRn6/sJsnSZK00Vpvg20mWQYs635dleSn62vbA9oRuHwSG87hk9jqgmDMh2fMhzexmGu1vM6HN5+v8zv2WWk2SdRFwB1Gft+1m3cLVXUkcGSfQswVSZZX1dINXY6NiTEfnjEfnjEfnjEf3sYY89k05/0QuEuSOyXZHHg68IXJFkuSJGlum7EmqqpuSPIy4Ou0IQ4+XFVnTbxkkiRJc9is+kRV1VeAr0y4LHPBvG6OnKeM+fCM+fCM+fCM+fA2upinqjZ0GSRJkuYdH/siSZLUg0mUJElSDyZRC0iSLZJs1r3Ohi7PxiDJJt1P4z2QJJt3j6My7gPpPlu26F4b8wmaim+SrZIs7l77XT2AJFsnWdK9ntV17olZAJI8KMlZwH8CrwQoO7tNTJJtkrwmyY+A93Sz/VuaoCQ7Jfn7JN8Dvga8HLzOJynJbZO8Lck3gW8Cr0yyhTGfrKqqJPcBzgdet4GLs+Al2SHJm5N8GTgNOARm/9my3kYs13C6/0pSVTcm2ZI2UvxfA98BvpzkPOA4P+zWny7mm1TVDbShPnYGPgY8C6CqbtyAxVuQRq9z2oC/OwOHAr8EvpnkjKr65gYs4oIzdp1vAWwG/C1wJvB9YDlw/IYr4cIzVctUVTeNzL4b7Z/iO03zntbR2HW+DfB64FFVdcLabsv/nueRqerFqrpp6ku7qv5Ae0j0aVV1FfBPwIHAXhuomAvKWMxv6F5fBbwNOAK4Nsk+o8tq3Ux3nQPnAq+uqh9W1WXAyXRfMFp3q7nOL6iqV1fV96vqauA84A8bspwLyVjMx5OkpwLHAn9Ict/R5dXfaq7zXwJndRNJdl6bbZpEzUFpFo23g3fVvLdLcmCSdyd5QpLtgBOBe3aLnQVcC/jFvhZmGfN3JTm4m7+y++A7E3h0t7h/T2thLWL+xKq6qqpWdU9NgFZLYu3fWlqbmI+s8/wk19Oei3b7ocs8363tZ0vXlHcucDrwK1qtFPj5MmtrEfOndG/9GPhBklOA9yZZNtt+aJ6UOSDJ9kke1yVEVHNjVd00mgQleRatSv2xwCOA5wPXABdz8x/aSuBSYJepbQ13JPNHz5g/HHhhN3/qb+fbwEOGLf38tA4x/4tu/mZVdV2S/WgPC/2s/ySs2brGvPNV4DbdvCdPfdlreusQ8xd3b+0JXFxV/w1cBbwoyYvsMrB66xDzP+/eehfwduAA4HDgfwNPns2+7RM1N9yd1rfmWuD4JHsBzwbuD3w3yXtp1egPBF5RVV9McjzwISDAT4DHAFTVld36Xx3+MOaV1cV8P+DENcT8w9Cqg7s/zpOA13Tz/JBbs3WN+fXddl4DvL+qVg19APPQOsUcoKou7V6eneRC4E5JNrGfzmr1/Tw/qqtp3RN4TpJlwNa0z/iLN8BxzCd9r/OPAFTVclp/P4CTk5wN7DSb69yaqIF01Yuri/cKWvXtnbvfD6TVKL0G+B3wd7SLYylwRvcf+X/Qzt/dgM8B90nyqG793br1N2o9Y/5abo75dfzPmE/dOTP1387PgWuSHJHkhUl2mtTxzAcTjPlU8/T+tA/D5UkOTvLMJNtM6njmg0lf5yP7WQTcBfjJxp5ATejzPMAetDvE3g48Abgf8ENas95G3T1jQtf5TdNc55vS+hT/fDbXuUnUQLov3NWdkJXAJbT/QACOBk4BXkKrbnwQsHm33P1H/iO/Gji4qq4B3gg8L8kVwI+6aaO2HmK+GXAZ8ICxmD8WIMkDknyb9sWyD3A9rfp9ozXBmD++e/2XtP84P0S7K/Ua4Pfr+TDmlQnG/NEASV6U5Ie0Pjrn0mpfN2oT/Dx/UlV9uao+UlXn0ZKtr9D1/9uYu2dM8Do/CCDJIWl9ok4Dfkq7eWVGNuetZ9NV/3XZ8+7A84Drq+qNo+9X1fVJzgf2TbIbLWN+Ea2/zVtod4HtD/wL8LSu3TfA5bRqTGi1Uf9Z7c6xjcosYn5dVb1p9P2xmN+R9mH1ItowEaMx/xAt5tt2q14B3Lt7fT5waFWdNpEDm8MGjvmVwF271x8G3lNVP5jIgc1hGyDm9+penwa8rKo2uuRpA3ye793tY4uquraqfgMcNcFDnHM2wHW+d/f6TOCla/vZYk3UOkiySVfF/UdTJz/JPdPGcIJ2At9N+2/i6LFtTFXPnk+rydgF+BNgu6o6CriBVsX7lKr6PO0ieAJtbIsP0FVfdp3oruq2uWihVvv2jPnHxrYxHvPbc3PMP8TqY74tLeZ7dPu9eCqB6mJ+i3ItFHMg5u+nG7Kjqo6f+pCbrlwLxRyL+clTCZSfLcBkP8/v0u332vGyrafDnFPmyHW+Z7ffU0c+W2Z9nVsTtRaSZLQ6dbqqxSSvp43x8Vvg20k+Rhvt937AZ6pqxejyI9u7pJvuQ6tVem6S42gn+nO0CwHafzOnA/elVVP+43gZagF1cDbmw5vrMZ8q3xqq9uedeRRzr/OBP1tWV7b5aK7HvM91bhI1g9GqxdGTn/aMukcDT6O1q/4jrc21aHdhbAd8FtgeeCdtoLo1xfuKbtofOBJ4Ge2Ou29X1dkjy23Z7Ws74MvAF9f1GOcaYz68+RTz0fLNZ8Z8ePMp5gvFfIp5r+u8qpxGJtooyMuAXaZ5bxfg8d3rRwHfAJ4C3KOb92hax+LjaXdUHNVdDLeiVfs+cYZ97w7caTXvLdrQsTHmC2cy5sbcmBtzY77ukzVRnZFseUdaJ9ZzgYuSPBTYqqq+Qusj8MokP6VVEW5K64x2TbeZU2hZ9F9UGyhtdPu/AvZOckJVXd21t4abnw1GtbsxRteZGqK+agFVo08x5sMz5sMz5sMz5sPbWGO+IDurzcZUcEeCPDV44s9oY3JMPZfrIdz8WI/v06odb08bzPIK4KXAO5NMVQmeDBycNrT8I9PGD7od7dEslwJ/rNaskWeDJdktbSTm8RO/IKrRwZhvCMZ8eMZ8eMZ8eMa82ShqojL2lOykdR5Ldxtpki1o1Y/bVdU/JLkU2L07EacDByW5bVVdluQS2i2R36+qp3bb24bWBrs/8H9ot2F+mTZ2xeeBVVX1hbEybQk8DngYsC/t9tZ/7so57//QjPnwjPnwjPnwjPnwjPnqLcgkavyE18gdAEluU1VXJLktref/A6vq10muA7bvTuZ5tDFSdgF+Qbut8l60dtoLaM/cOTbJ9rRn7NyH1mZ7UneRvBn4+/ETmVuOf/FI2sjiH6SNAHw989g8ivkdMObGvCdjPrx5FHM/zzfC63xBNudVq+KbyphvneRhSd6f5GfAR5LsX1WX0YaKP7Bb7Re0J8PfpXt9He2RKj+jVT8+rltuW1p7787ATt3y/wY8p9smVXV9l6XfYgyM0Quxqr5YVe+sqjPn+x8czKuYv8uYG/O+jPnw5lHM/TzfCK/zBZdEJdku7Xlan0hyP9rJeiutZ/6ewH8BL05yZ+AEbm6rXUFra70LrT33cuBuVXUdbZTk+yT5Ma0j26HAT6vqxKpaVlXHVdVvx8tSI+21C5kxH54xH54xH54xH54xXzvzojkv+WP76y0G6ppmuU2Aw2hViN+hndRNgJ/QhncH+CStvXV/4FvAcwCq6twk9weurqpjk1wA3DvJtlX1syR/NpUlT7PPW2TIC4ExH54xH54xH54xH54xn5w5m0Qlmbp18aapkz71M8mewOVVdeXYRfEQ4EFVdb+R7WwBLKe1V1NVK5LsDvy4qk5OG979cOA2tLbaa9I6rF1A66y2O3D61MkfP+Hz9cRPx5gPz5gPz5gPz5gPz5gPY84kUV1gR8d7KNp4EaRVG+5I66n/qW6VM4EXjGXVV9KNN5E2GupN1e4cWAEsS3JMVZ1B64w2lVU/Azi4297nq+rqbv1f0R5iuDtw+tSFNt9P+ChjPjxjPjxjPjxjPjxjvmFssCQqY09qHg9s2pOtX0rrqPYE4A+0MSKeXFUXJPl5kn2r6tSR1a4Ark1yQFV9r9vO1LgVvwTekXZHwQnAqd1+zwDOGNnvVFZ+IfAfdBfK2IU2Lxnz4Rnz4Rnz4Rnz4RnzuWHwJKo7AQcCn+l+n2qrPRA4iJYtv6GqLk5yMHB2Ve2bZB9aW+zW3aZOAB6Y5PS6uVrwoiSnAq/otvdQWrvuu4AfAJtU1ZunKdN01Z7XAd9b/xEYnjEfnjEfnjEfnjEfnjGfWyZ+d1669s8p1dpFlwFPT/JaYNskewDPpmWzXwGOSLIL8DXgku4EXUh7kvP9u02dBNwbuHWSzZIc1M3/O9qAWzsARwBvA35Hu8Vy965MGS1XNQumitGYD8+YD8+YD8+YD8+Yz20TT6KmApvkjkkelGRfWs//NwJ3pp2YQ4GLgVW0nv5LaeNHnAnsCmxFeyjhT2kd1aANH78f7URvCTwsyZZVdV1VfbeqXlVVX6k23sSNtGrFd3RlWtAn3JgPz5gPz5gPz5gPz5jPcbVuT2sOq3kyMu2kbQXcF/g27WS+Abgd8GrgHSPL/l9au+lhwBOBLbr5u9FO3B7d748Hvju1T+BJwK1Xs/9NaFWP63SMc20y5sbcmBtzY74wJmM+/6f1fUFs1/3cFvgA8EzgWcDhY8vtA3wdWELrl/VI4Dtjy/xJ9/P7wMHd69sAe02d4GkuxmzogA5+Ao25Md8IJmNuzDeGyZjPv6lXx/KRjmx7Ak8FNqdVI+5Ja6vdqbsIjqdl0c/v2k9/Bfysqr6QNpT74qpaAXwjyeuSvIdWtbgv8Dla9v182nN4qKoraHcPUGNVidVdBQuVMR+eMR+eMR+eMR+eMV840jduSe4KfBT4Bu1EXwZ8DHgBrd31HOAeVfWHJEtpdwQ8ADiE9gydZ9CenXNb4F+q6htJ/oz2EMLjq+qCdTiuBcmYD8+YD8+YD8+YD8+YLwzrMsTBHsC5wNHARVX1+yRvB/4K+BJwHLBTkvOrajn8cfCtvYDNgPfTqiqvoo1BQVUduw7l2RgY8+EZ8+EZ8+EZ8+EZ8wVgXWqitgE+QhuRdBPaLZBH0IaNfyNwbFW9PMlWtOrKN9Ay7WOB966u6jBjA4jpZsZ8eMZ8eMZ8eMZ8eMZ8YeidRN1iI61a8gW0pza/H3g3sHNVPTZJaIN/XV9VV02z7iLa0PK2x64FYz48Yz48Yz48Yz48Yz5/9W7O607s7YG9aYN37QO8pKpWJTkZ2CHJomrjS6wcWWeTbh4Ao6+1ZsZ8eMZ8eMZ8eMZ8eMZ8Yeg92GaX9d4B+AvgBuC1VfXzJHcBXgScWlU3dif9j+t4wvsz5sMz5sMz5sMz5sMz5gvDemnOu8UG290B9wDeXe12Sk2YMR+eMR+eMR+eMR+eMZ9f1jmJmqpepCXJdmYbgDEfnjEfnjEfnjEfnjGf39Z7TZQkSdLGYOIPIJYkSVqITKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSevj/1yc4QpVzGUAAAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAhU0lEQVR4nO3de5wkVXnw8d/DcpWrygoI4oKCElQuWVEEleCVm0TlTVCCiJrFCEZNgjG+MZFoIvgaBOUlhqB4iUaiKFG5JBIRUAK43OUiEoKCgCwgwspdnvxxTkttM7PTWztd0z3z+34+9ZnuquqqU0/V9DxzzqlTkZlIkiRpxawy0wWQJEkaRyZRkiRJLZhESZIktWASJUmS1IJJlCRJUgsmUZIkSS2YREkaaxHx/YjYYabLMZdFxDsj4qiZLofUNZMoqYqI/SPimoj4VUT8d0S8eMDPfTYiPtxyn4dFxOKIeDAiPjvB8idExPERcUdE/DIizp1gndVruW9uzHtxRCztmzIiXl+XrxERH4+IWyLiF3UfqzU+vyAiTq/LbouI4yJi1Qn2/aa63bc15kVEHBURd9bpqIiIxvKsMe6V68TGssMj4ocRcW9E/E9EHD5F/PYB7s3MS/vmv7nu5/cn+Mz767aXRsTNEXHy8vYxyX6v6ovtIxHxzcbyeRHx4RrfeyPi0ojYoC57Wd3/bRGxf+MzG0TEJRGxbovyTHi8EbFbRDzaKOfPIuKIFd1+3daCiDg7Iu6LiGsj4uWNxf8EHBART2mzbWlcmURJQES8AjgKOBhYF3gJcEMHu74F+DDwmUmWnwA8Cdim/nzPBOscDixpzsjM8zJznd4E7A0sBc6sq7wPWAg8B9ga2BH4y8YmjgduBzYBtgdeCryjuY+IeCLwfuCqvvIsAn4X2A54HrAPcEjfOts1yve2xvwA3gQ8EXg1cFgz0ZjA24EvTDD/IOCuuq1mmQ8CDgReXuOyEPjP5Wx/Qpm5bSO26wI3AV9prHIE8CJgZ2C9us8H6rJjKDF5FXB8RMyr8z8CHJmZ965oeZjkeKtbGmXdFXhrRPxui338C3Ap8GTg/wJfjYj5AJn5AHDGJPuXZq/MdHKa8xNwPvDWFp9bBDwMPERJUr7Zcv8fBj7bN+/ZwD3Aesv53BbANcAewM3LWe8k4KTG+8XA/2m8fyNwU+P9NcCejff/D/jHvm1+ipJYfRd4W18sFzXevxW4oPE+gWcOGJdPAJ+cZNnqwP3AZn3znw48CrweeATYuLHsOOCYab52XgrcC6xd3z+xXgvPmGT9GxqvbwOeAuwEnNly/8s73t36rwvgX4H3r+A+tgYeBNZtzDsPeHvj/QHA2dMZWyenUZ+sidKcV2sCFgLzI+L62sRzXESsNdVnM/ME4IvAR7P8t79P3ea3IuLuSaZvDVi0nYCfAEfU5rwre81xDZ+k1Abdv5zjWxvYD/hc/6K+15tFxPr1/THA/rU5cVNKknbmb1aO2IkSs09NsMttgcsb7y+v85rOrc1ZX4uIBZOUO4AX8/iarp6tgEcz8+a++W8CFmfmKZRk8IDGsguAN9Vmw4WNWqDePo9fznm7YpJyHASckpm/qu+fS0lm9qvHeF1EHNpY//aI2C4itqMkP78AjgX+eJLtT2V5x7uMiNgK2IUSh968K5ZzzMfX1balJH/NWrL+83oNpfZRmjNMoiTYCFiNkmi8mNJ8tQPLNm+tkMzcOzM3mGTae8DNbEZpbvsl8FTgMOBzEbENQES8FpiXmV+fYjuvA+4AzmnMOxN4V0TMj4iNeewP+BPqz3MpfyDvAW6m1FydWvc7j9Lcd1hmPjrB/tapZe75JbBOo1/US4EFlJq2W4BvxQT9rYAPUr6jTprkuDag1AD1exPwpfr6SzSamDLzn4F3UprSzqEkNH/eWP6O5Zy35/XvKCKeQLluPtuYvRmwPqX2Zou6/IO1yRhKE+SxlKbaA4E/As4C1oyIf6/9jl46yTFPZNLjrZ5aE6J7gOuAC4HvNY75ecs55l4Tbv85pb5v9t+6tx63NGeYREmP1eJ8MjNvzcw7gKOBPWewTFDK9TDw4cx8KDPPAc4GXllrlz7KYLUXBwGfz8zm08b/ltK/5TJK89updV8/j4hVKEnW14C1gQ0pTVS9u6/eAVyRmRcwsaWUfkA96wFLe/vPzHPr8dwNvIuSaGzT3EBEHEZJBvbKzAcn2c8vWPaPOBGxS93el+usLwHPjYjte+tk5hcz8+WUJOztwIci4lWT7GMqr6P0RWomqL3r6W8y8/7MvKKWZ8+6/8syc7fMfAFwNfAW4O+AEyl9qQ4GvtBIOic1yPFS+kRtkJnrUY75fh5fKzmV/nNKfd9MYtfl8YmWNKuZRGnOy8xfUGpbmklGTrL6hJvonxERZ8Tj747rTWcMuN2Jmo96+9qKUptzXkTcRkl4NqnNRwsa5XgapV/M55fZSPnjflhmbpqZWwJ3AhfXmqUnAZsDx2Xmg5l5J6U2qJdUvgx4bd3XbZQO1H8fEcfV5VexbLPOdkzeJNc7pubde2+hdHx/2QRNdU3Xl9Vj08a8g+q2Lqtlu7Axf9mdZj6cmV+hxPk5dd+fWs55m+gYJkpQe+dtkOvp48BfZub9lGbAxZl5I6VmdP7kh77ixwuQmb+kJFr79ObF4+80bE695tqrgC1j2TsH+8/rNizbjCvNfjPdKcvJaRQm4G+AH1A6+T6R0mn2QwN+9kjgSy33uyqwJuXOrC/U16vWZatREoUP1PV2ofzn/+z6fuPG9DpK09jGlCa+3vbfD5w7wX43pTQRBvBCyt1lr2wsv4GSyKxKqb34eu8Y6/vmvs8H/gRYvy5/O6V/TG8fV1E7IFOaCLcH5lGaiI4BfgSsVpcfQOlsvc2A8fsG8Mb6ek3gbkpH9mb5DgV+Xo/lzcBelFqTVSh9ve4Hdm1x7jaj9H16XAdySnPoPwJrUJKL2ylJYXOdVwCnNt5fTbkjcVtK7da8Ov9G4M0T7GOQ492NRsfyGvMvABe2ON4LgI/V/b627nt+Y/kJwHtn+nfZyanLacYL4OQ0ChMlYTm+/mG4jXJX2Jp12eaU5ozNJ/nsVpRmsbubfxQH3O8HKbUUzemDjeXbAv8F/Kr+kX3tJNtZ5o9lY/61THDXIWUIhxuB+2oSc0Df8u0pd939gtKf6l+BjSbZ93dZ9u68oDQ13lWnjwJRl+1e9/ermlicCmzV+Oz/UJoVlzamTy0nfnsBZ9TX+wO3UhOyxjprUWra9qYkm9+vx3UPcOVECcqA5+4vgPMmWbYppUl0KSUhPaRv+Rr1mnl6Y97L6jm5Fdi/zludmjhPsI9Bjnc3Suf1XizvBE5jwLsj+7a7oJ7r++s5fHlj2ZqU2twJrxEnp9k69b7YJGksRcT3KZ3cL53psky3iNgVODQz3zDTZVmeiHgn8LTMfO9Ml0XqkkmUJElSC3YslyRJasEkSpIkqQWTKEmSpBZMoiRJklqY6FELK23DDTfMBQsWDGPTkiRJ0+riiy++IzMHGeB2GUNJohYsWMDixYuHsWlJkqRpFRE/afM5m/MkSZJaGCiJiogNIuKrEXFtRFwTETsPu2CSJEmjbNDmvGOBMzNzv4hYHXjCEMskSZI08qZMoiJifcpztt4MkJkPAQ8Nt1iSJEmjbZDmvC2AJcBJEXFpRJwYEWv3rxQRiyJicUQsXrJkybQXVJIkaZQMkkStCuwI/ENm7kB5+vr7+lfKzBMyc2FmLpw/f4XvEpQkSRorgyRRNwM3Z+aF9f1XKUmVJEnSnDVlEpWZtwE3RcSz6qyXAVcPtVSSJEkjbtC7894JfLHemXcDcPDwiiRJkjT6BkqiMvMyYOFwiyJJkjQ+HLFckiSpBZMoSZKkFkyiJEmSWjCJkiRJasEkSpIkqQWTKEmSpBZMoiRJklowiZIkSWrBJEqSJKkFkyhJkqQWTKIkSZJaMImSJElqwSRKkiSpBZMoSZKkFkyiJEmSWjCJkiRJasEkSpIkqYVVB1kpIm4E7gV+DTySmQuHWShJkqRRN1ASVf1OZt4xtJJIkiSNEZvzJEmSWhg0iUrgPyLi4ohYNNEKEbEoIhZHxOIlS5ZMXwklSZJG0KBJ1K6ZuSOwB3BoRLykf4XMPCEzF2bmwvnz509rISVJkkbNQElUZv6s/rwd+Dqw0zALJUmSNOqmTKIiYu2IWLf3Gngl8MNhF0ySJGmUDXJ33kbA1yOit/6XMvPMoZZKkiRpxE2ZRGXmDcB2HZRFkiRpbDjEgSRJUgsmUZIkSS2YREmSJLVgEiVJktSCSZQkSVILJlGSJEktmERJkiS1YBIlSZLUgkmUJElSCyZRkiRJLZhESZIktWASJUmS1IJJlCRJUgsmUZIkSS2YREmSJLVgEiVJktSCSZQkSVILAydRETEvIi6NiG8Ns0CSJEnjYEVqot4FXDOsgkiSJI2TgZKoiNgM2As4cbjFkSRJGg+D1kQdA7wXeHR4RZEkSRofUyZREbE3cHtmXjzFeosiYnFELF6yZMm0FVCSJGkUDVITtQvwmoi4EfgysHtE/HP/Spl5QmYuzMyF8+fPn+ZiSpIkjZYpk6jM/IvM3CwzFwD7A9/JzD8YeskkSZJGmONESZIktbDqiqycmd8FvjuUkkiSJI0Ra6IkSZJaMImSJElqwSRKkiSpBZMoSZKkFkyiJEmSWjCJkiRJasEkSpIkqQWTKEmSpBZMoiRJklowiZIkSWrBJEqSJKkFkyhJkqQWTKIkSZJaMImSJElqwSRKkiSpBZMoSZKkFkyiJEmSWpgyiYqINSPiooi4PCKuiogjuiiYJEnSKFt1gHUeBHbPzKURsRrwvYg4IzMvGHLZJEmSRtaUSVRmJrC0vl2tTjnMQkmSJI26gfpERcS8iLgMuB34dmZeONRSSZIkjbiBkqjM/HVmbg9sBuwUEc/pXyciFkXE4ohYvGTJkmkupiRJ0mhZobvzMvNu4Gzg1RMsOyEzF2bmwvnz509T8SRJkkbTIHfnzY+IDerrtYBXANcOuVySJEkjbZC78zYBPhcR8yhJ179m5reGWyxJkqTRNsjdeVcAO3RQFkmSpLHhiOWSJEktmERJkiS1YBIlSZLUgkmUJElSCyZRkiRJLZhESZIktWASJUmS1IJJlCRJUgsmUZIkSS2YREmSJLVgEiVJktSCSZQkSVILJlGSJEktmERJkiS1YBIlSZLUgkmUJElSCyZRkiRJLUyZREXE0yLi7Ii4OiKuioh3dVEwSZKkUbbqAOs8AvxpZl4SEesCF0fEtzPz6iGXTZIkaWRNWROVmbdm5iX19b3ANcCmwy6YJEnSKFuhPlERsQDYAbhwKKWRJEkaEwMnURGxDnAK8O7MvGeC5YsiYnFELF6yZMl0llGSJGnkDJRERcRqlATqi5n5tYnWycwTMnNhZi6cP3/+dJZRkiRp5Axyd14Anwauycyjh18kSZKk0TdITdQuwIHA7hFxWZ32HHK5JEmSRtqUQxxk5veA6KAskiRJY8MRyyVJklowiZIkSWrBJEqSJKkFkyhJkqQWTKIkSZJaMImSJElqwSRKkiSpBZMoSZKkFkyiJEmSWjCJkiRJasEkSpIkqQWTKEmSpBZMoiRJklowiZIkSWrBJEqSJKkFkyhJkqQWTKIkSZJamDKJiojPRMTtEfHDLgokSZI0Dgapifos8Oohl0OSJGmsTJlEZea5wF0dlEWSJGls2CdKkiSphWlLoiJiUUQsjojFS5Ysma7NSpIkjaRpS6Iy84TMXJiZC+fPnz9dm5UkSRpJNudJkiS1MMgQB/8C/BfwrIi4OSLeOvxiSZIkjbZVp1ohM9/QRUEkSZLGic15kiRJLZhESZIktWASJUmS1IJJlCRJUgsmUZIkSS2YREmSJLVgEiVJktSCSZQkSVILJlGSJEktmERJkiS1MOVjX0bNgvedNtNFaOXGI/ea6SJojHidS9LosyZKkiSpBZMoSZKkFkyiJEmSWhi7PlGSJKkd+1tOL2uiJEmSWjCJkiRJamGg5ryIeDVwLDAPODEzjxxqqTRSrP7VXOB13j1jrnE3ZU1URMwD/j+wB/BbwBsi4reGXTBJkqRRNkhz3k7A9Zl5Q2Y+BHwZ2He4xZIkSRptgyRRmwI3Nd7fXOdJkiTNWZGZy18hYj/g1Zn5tvr+QOAFmXlY33qLgEX17bOAH01/cYduQ+COmS7EHGPMu2fMu2fMu2fMuzfOMX96Zs5f0Q8N0rH8Z8DTGu83q/OWkZknACesaAFGSUQszsyFM12OucSYd8+Yd8+Yd8+Yd28uxnyQ5rwfAFtFxBYRsTqwP/CN4RZLkiRptE1ZE5WZj0TEYcC/U4Y4+ExmXjX0kkmSJI2wgcaJyszTgdOHXJZRMNbNkWPKmHfPmHfPmHfPmHdvzsV8yo7lkiRJejwf+yJJktSCSZQkSVILJlGzSESsERGr1dcx0+WZCyJilfrTeHckIlavj6My7h2p3y1r1NfGfIh68Y2ItSJifn3t3+oORMQ6EbGgvh7oOvfEzAIRsWtEXAX8J/AegLSz29BExLoRcXhEXAF8os72d2mIImKjiPjriPg+cCbwx+B1PkwR8ZSI+EhEfAf4DvCeiFjDmA9XZmZEbA/8FPjzGS7OrBcRT4qID0XEacClwEEw+HfLQHfnabTU/0oiM38dEWtSRor/C+Bc4LSIuAE4xS+76VNjvkpmPkIZ6mMT4PPAAQCZ+esZLN6s1LzOKQP+bgK8G/gJ8J2IuDwzvzODRZx1+q7zNYDVgL8ErgTOBxYDZ81cCWefXi1TZj7amL0N5Z/iLSZYppXUd52vC7wPeGVmnr2i2/K/5zHSq17MzEd7f7Qz8wHKQ6Ivzcy7gb8HdqM8ekcrqS/mj9TXdwMfAY4GHoyIHZrrauVMdJ0D1wN/lpk/yMzbgYuof2C08ia5zm/KzD/LzPMz817gBuCBmSznbNIX8/4kaT/gZOCBiPjt5vpqb5Lr/CfAVXUiIjZZkW2aRI2gKOb1t4PXat6NI2K3iDg2IvaJiPWB7wHPqatdBTwI+Id9BQwY82MiYt86f0n94rsSeFVd3d+nFbACMX9NZt6dmUvrUxOg1JJY+7eCViTmjc8cHBEPU56L9tSuyzzuVvS7pTblXQ9cBvycUisFfr8MbAVi/vq66IfABRFxMXBcRCwatB+aJ2UERMQGEbFXTYjI4teZ+WgzCYqIAyhV6nsCLwcOBu4DbuGxX7QlwG3Apr1tdXck46NlzF8GvLXO7/3unAO8pNvSj6eViPkf1vmrZeZDEbET8HTgq/6TsHwrG/PqDODJdd7ren/sNbGViPnb66KtgVsy83+Au4FDIuIQuwxMbiVi/ra66BjgSGAX4Cjgd4HXDbJv+0SNht+i9K15EDgrIp4F/AHwAuC8iDiOUo3+IuBdmfnNiDgLOBEI4Frg1QCZeVf9/BndH8ZYmSzmOwHfW07MPwOlOrj+cl4IHF7n+SW3fCsb84frdg4Hjs/MpV0fwBhaqZgDZOZt9eXVEXEzsEVErGI/nUm1/T7/dK1p3Ro4MCIWAetQvuNvmYHjGCdtr/OTADJzMaW/H8BFEXE1sNEg17k1UR2p1YuTxftGSvXtM+v73Sg1SocDvwL+inJxLAQur/+R/wfl/G0DnApsHxGvrJ/fvH5+TmsZ8/fyWMwf4vEx79050/tv58fAfRFxdES8NSI2GtbxjIMhxrzXPL0z5ctwcUTsGxFvjIh1h3U842DY13ljP/OArYBr53oCNaTv8wCeQblD7EhgH+D5wA8ozXpzunvGkK7zRye4zlel9Cn+8SDXuUlUR+of3MlOyBLgVsp/IACfAy4G3kGpbtwVWL2u94LGf+T3Avtm5n3AEcCbI+JO4Io6zWnTEPPVgNuBF/bFfE+AiHhhRJxD+cOyA/Awpfp9zhpizPeur99J+Y/zRMpdqfcB90/zYYyVIcb8VQARcUhE/IDSR+d6Su3rnDbE7/PXZuZpmXlSZt5ASbZOp/b/m8vdM4Z4ne8BEBEHRekTdSnwI8rNK1OyOW+aTVT9V7PnLYE3Aw9n5hHN5Zn5cET8FNgxIjanZMyHUPrb/C3lLrCdgX8Cfq+2+wZwB6UaE0pt1H9muXNsThkg5g9l5t80l/fF/OmUL6tDKMNENGN+IiXm69WP3glsV1//FHh3Zl46lAMbYR3H/C7g2fX1Z4BPZOYFQzmwETYDMX9efX0pcFhmzrnkaQa+z59b97FGZj6Ymb8EPj3EQxw5M3CdP7e+vhI4dEW/W6yJWgkRsUqt4v6N3smPiOdEGcMJygk8lvLfxOf6ttGrnv0ppSZjU+ClwPqZ+WngEUoV7+sz898oF8E+lLEt/oFafVk70d1dtzlvtlb7toz55/u20R/zp/JYzE9k8pivR4n5M+p+b+klUDXmy5RrthiBmB9PHbIjM8/qfclNVK7ZYsRiflEvgfK7BRju9/lWdb8P9pdtmg5zpIzIdb513e8lje+Wga9za6JWQEREszp1oqrFiHgfZYyPe4BzIuLzlNF+nw98JTNvbK7f2N6tddqeUqv0pog4hXKiT6VcCFD+m7kM+G1KNeVH+8uQs6iDszHv3qjHvFe+5VTtj50xirnXecffLZOVbRyNeszbXOcmUVNoVi02T36UZ9S9Cvg9SrvqRyltrkm5C2N94KvABsDHKQPVLS/ed9ZpZ+AE4DDKHXfnZObVjfXWrPtaHzgN+ObKHuOoMebdG6eYN8s3zox598Yp5rPFOMW81XWemU6NiTIK8iJg0wmWbQrsXV+/Evg28Hpg2zrvVZSOxWdR7qj4dL0YnkCp9n3NFPveEthikmXzZjo2xnz2TMbcmBtzY27MV36yJqpqZMsbUjqxXg/8LCJ+B1grM0+n9BF4T0T8iFJFuCqlM9p9dTMXU7LoP8wyUFpz+z8HnhsRZ2fmvbW9NXjs2WBkuRuj+ZneEPWZs6gavceYd8+Yd8+Yd8+Yd2+uxnxWdlYbRC+4jSD3Bk+8jjImR++5XC/hscd6nE+pdnwqZTDLO4FDgY9HRK9K8CJg3yhDy78iyvhBG1MezXIb8JtqzWw8GywiNo8yEnP/iZ8V1ehgzGeCMe+eMe+eMe+eMS/mRE1U9D0lO6J0Hot6G2lErEGpflw/Mz8cEbcBW9YTcRmwR0Q8JTNvj4hbKbdEnp+Z+9XtrUtpg90Z+CPKbZinUcau+DdgaWZ+o69MawJ7AbsDO1Jub/1kLefY/6IZ8+4Z8+4Z8+4Z8+4Z88nNyiSq/4Rn4w6AiHhyZt4ZEU+h9Px/UWb+IiIeAjaoJ/MGyhgpmwL/Tbmt8nmUdtqbKM/cOTkiNqA8Y2d7SpvthfUi+RDw1/0nMpYd/+IVlJHFP0UZAfhhxtgYxfxpGHNj3pIx794Yxdzv8zl4nc/K5rwsVXy9jHntiNg9Io6PiOuAkyJi58y8nTJU/G71Y/9NeTL8VvX1Q5RHqlxHqX7cq663HqW9dxNgo7r+14AD6zbJzIdrlr7MGBjNCzEzv5mZH8/MK8f9Fw7GKubHGHNj3pYx794Yxdzv8zl4nc+6JCoi1o/yPK0vRcTzKSfr7yg987cG/gt4e0Q8Ezibx9pqb6S0tW5Fac+9A9gmMx+ijJK8fUT8kNKR7d3AjzLze5m5KDNPycx7+suSjfba2cyYd8+Yd8+Yd8+Yd8+Yr5ixaM6L+E376zIDdU2w3irABylViOdSTuoqwLWU4d0B/oXS3roz8F3gQIDMvD4iXgDcm5knR8RNwHYRsV5mXhcRv9/LkifY5zIZ8mxgzLtnzLtnzLtnzLtnzIdnZJOoiOjduvho76T3fkbE1sAdmXlX30XxEmDXzHx+YztrAIsp7dVk5o0RsSXww8y8KMrw7kcBT6a01d4XpcPaTZTOalsCl/VOfv8JH9cTPxFj3j1j3j1j3j1j3j1j3o2RSaJqYJvjPSRlvAiiVBtuSOmp/+X6kSuBt/Rl1XdRx5uIMhrqo1nuHLgRWBQRX8zMyymd0XpZ9RuAfev2/i0z762f/znlIYZbApf1LrRxP+FNxrx7xrx7xrx7xrx7xnxmzFgSFX1Pau4PbJQnWx9K6ai2D/AAZYyI12XmTRHx44jYMTMvaXzsTuDBiNglM79ft9Mbt+InwMei3FFwNnBJ3e/lwOWN/fay8puB/6BeKH0X2lgy5t0z5t0z5t0z5t0z5qOh8ySqnoDdgK/U97222t2APSjZ8gcy85aI2Be4OjN3jIgdKG2x69RNnQ28KCIuy8eqBX8WEZcA76rb+x1Ku+4xwAXAKpn5oQnKNFG150PA96c/At0z5t0z5t0z5t0z5t0z5qNl6HfnRW3/7MnSLroI2D8i3gusFxHPAP6Aks2eDhwdEZsCZwK31hN0M+VJzi+om7oQ2A5YOyJWi4g96vy/ogy49STgaOAjwK8ot1huWcsUzXJlMWuqGI1594x594x594x594z5aBt6EtULbEQ8PSJ2jYgdKT3/jwCeSTkx7wZuAZZSevovpIwfcSWwGbAW5aGEP6J0VIMyfPxOlBO9JrB7RKyZmQ9l5nmZ+aeZeXqW8SZ+TalW/Fgt06w+4ca8e8a8e8a8e8a8e8Z8xOXKPa05mOTJyJSTthbw28A5lJP5AWBj4M+AjzXWfT+l3fSDwGuANer8zSkn7hn1/d7Aeb19Aq8F1p5k/6tQqh5X6hhHbTLmxtyYG3NjPjsmYz7+03RfEOvXn+sB/wC8ETgAOKpvvR2AfwcWUPplvQI4t2+dl9af5wP71tdPBp7VO8ETXIwx0wHt/AQac2M+ByZjbsznwmTMx29q1bG80ZFta2A/YHVKNeLWlLbajepFcBYliz64tp/+HLguM78RZSj3+Zl5I/DtiPjziPgEpWpxR+BUSvZ9MOU5PGTmnZS7B8i+qsSsV8FsZcy7Z8y7Z8y7Z8y7Z8xnj2gbt4h4NvBZ4NuUE3078HngLZR212uAbTPzgYhYSLkj4IXAQZRn6LyB8uycpwD/lJnfjojfpzyE8KzMvGkljmtWMubdM+bdM+bdM+bdM+azw8oMcfAM4Hrgc8DPMvP+iDgS+BPgW8ApwEYR8dPMXAy/GXzrWcBqwPGUqsq7KWNQkJknr0R55gJj3j1j3j1j3j1j3j1jPgusTE3UusBJlBFJV6HcAnk0Zdj4I4CTM/OPI2ItSnXlByiZ9snAcZNVHUbfAGJ6jDHvnjHvnjHvnjHvnjGfHVonUctspFRLvoXy1ObjgWOBTTJzz4gIyuBfD2fm3RN8dh5laHnbY1eAMe+eMe+eMe+eMe+eMR9frZvz6ol9KvBcyuBdOwDvyMylEXER8KSImJdlfIkljc+sUucB0Hyt5TPm3TPm3TPm3TPm3TPms0PrwTZr1vs04A+BR4D3ZuaPI2Ir4BDgksz8dT3pv/mMJ7w9Y949Y949Y949Y949Yz47TEtz3jIbLHcHbAscm+V2Sg2ZMe+eMe+eMe+eMe+eMR8vK51E9aoXKUmyndk6YMy7Z8y7Z8y7Z8y7Z8zH27TXREmSJM0FQ38AsSRJ0mxkEiVJktSCSZQkSVILJlGSJEktmERJkiS1YBIlSZLUwv8CH0DQ6qhEru0AAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAhi0lEQVR4nO3deZxkVXnw8d/DsMoaZNgGcEABN1ZHFEFEjAgK4hZ3xCUOeZUoJmowb4zyauLyGgQ1mCAokBf3XVlUIoKILMO+K0GURaRZBhgRGOB5/zinpKbonqm+03W7quf3/Xzup6vrbuc+93bV0+ece25kJpIkSZqclaa7AJIkSaPIJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpAZMoSSMtIg6OiCOnuxwrsojYPiLOme5ySG0ziZKAiFjUMz0cEZ/tc93jI+KjDfd7SEQsiIgHIuL4ceY/LiKOjojbI+LuiDhrnGVWjYirI+KmrveeO84xZUS8ss5fLSI+HRG3RMRddR+rdK0/NyJOqfNujYjPRcTKdd4GEfGLiLgjIhZGxC8jYreudQ+KiAsj4p6IuCkiPtlZt89j/uuIuK6W+bSI2HQp8VsV+Cfg//a8v1Zd/9Rx1tk9Is6p8byzHsszJ9rHUvY9OyK+XLdzV0ScNM4y60fEWESc3fXe5hFxbt33v/Usf2pEzGtQli0j4pGI+Pw48zIi/ljjcXtEfCUi1muwj9Ui4ov1vN4aEX/XmZeZlwELI2L/yW5XGmUmURKQmWt1JmBj4E/AN1rY9S3AR4EvTjD/GGB94Cn153vGWeZ9wFj3G5n5855j2g9YBJxWFzkMmAc8HdgG2JmSjHQcDdwGbALsCDwPeEedtwh4KzAb+AvgE8APuhKlxwGHAhsAzwJeALy3n2OOiD2BfwUOqMf7G+Ar4xxzxwHANZl5c8/7rwQeAF4YERt3bX8d4IfAZ+v25wCH12Un69vArcAWwIbAp8ZZ5hPA1T3vfQA4AdgSeFknaYqI1wC/ycwFDcryJuAu4DURsdo483eo18FWlHP24Qb7+DCwNfAE4PnA+yNin675JwEHN9iuNLJMoqTHeiUlgfj5shaMiPnAGyhfKIsi4geT2VFmfjszvwvcMc62nwy8FJifmWOZ+XBmXtizzJbAG4GPLWNXBwHfzMw/1t/3Bz6TmXdm5hjwGUpi1LEl8PXMvD8zb6UkX0+rZb4/M6/NzEeAAB6mfDGvX+d/viZxD9bk5iTgzzVVSztmSrL3jcy8MjMfBD4C7BERT5zguPYFzpzgeP8DuIwSn45tahm+UuP5p8z8ca1J6VtE7A1sDrwvM+/OzMWZeXHPMs+hJKlf6ll9S+CnmXk3cAGwVU3uDgP+cTLlqPsJShL1T8BiyrkdV2beA3wfeOpk90OJ6Ucy867MvBr4AvDmrvk/A14wQRInzUgmUdJjHQScmH08Eykzj6EkCZ+stT77A0TED2tT13jTD/ssxy7Ab4HDazPM5Z3muC6fpXzx/mmijUTEmsCrKLUfS8zqeb1ZRKxbfz8SeG1tTpxDSVZOW2LliMuA+ylfysdm5m0TFGEP4MqJyjdekcd5/fQJlt0OuLanXE8A9qScl5MoCUbHr4CHI+KEiNg3Iv6iZ93dl3LeFkbE7nXRZ9f9nlCbNS+IiOd1bWcW8DngEKD3OrqCUkO2HvAMSmw+AhyZmQsnOM6l2R3YDPgq8HXK9TuuerwvA87teu/opRzvZV3rbQJc2rW5S6mJNUBNmBcD2zY4BmkkmURJXeoX8PN4bMIxKZm5X2auN8G0X5+b2YySPNwNbEr5Qj4hIp5Sy/pyYFZmfmcZ23kFcDtL1ticBry79uvZGHhXff9x9edZlC/Ie4CbgAXAd3uOcXtgHeD1wNmMIyLeSmk2HK+pazynAa+O0lF5DeCfKUnI4yZYfj3g3p73DgQuy8yrKInF0yJip1rmeyhJR1JqUsYi4vsRsVGdf/ZSztt6mdk5zs2AvYEzKM2//wZ8LyI2qPPfBZzXW3NYfQx4LuV8HA2sCmxPaRL9ckScFRGH9BkvKEnTqZl5F/BlYJ+I2LBnmYsiYiHlOtgC+M/OjMx8x1KOd/u62Fr1591d27wbWLtnP/dSzom0QjCJkpZ0IHB2Zv5mugtCqV1aDHy0No2dSfnS3rvWLn2SR5OfpRmvZu1fgIuBS4BzKAnSYuAPEbESJZn5NrAmpW9Tp+/TEmrT3leAwyJih+55EfEySsKwb2be3s8BZ+bpwIeAbwE31OleSiI3nrt47Bf5myg1UJ3akTPpqp3JzKsz882Z2UlSN6XUvE3Gn4AbMvO42pT3VeBGYLcoHeHfBfzvCY7xzsx8TWbuABxFqU38W0pz3hXAXwJ/00mWl6Ymmn/Vdby/BH5HSWy77ZyZ6wGrA58Hfh4Rq0/ieBfVn+t0vbcOj01g1wYWTmK70kgziZKW9CYmXwv1mGa/epdV791xnekxd4xNYLx+Op19bQ3MpXwZ3kpJeDapd03N7SrH5pSmrROX2EjpC3RIZs7JzK0o/ZMurP2c1qfUVnwuMx/IzDso/XpevJSyrkLptNzZ7z6Ump79M/PyPo+3U7Z/z8ytM3MjSjK1MiW5GM9l1H5Odb/PocTmAzUWt1I6t7++q+N7976uAY6nNhfG+Hc1dk/P7dpv73nv/L4Lpenrqrr/o4Bdanlm9awzHzg3M6+gNE0uqH3BLq+/L8vLKcnM0V3HO4cJmvQyczFwLKVfVueY/2Mpx3tlXe8u4PdAd6K8A13NtLXZd1V6mlelGS0znZycMgGeA/wRWHuS630c+HLDfa5MqR34GPBf9fXKdd4qwHXAB+tyu1H+839y/X3jrukVlLveNqY08XW2/4/AWePsdw6lBiYo/XtuBPbumn89pWZkZUrzzHc6x1iX353yhbkG8A+1XJvW+XtRkrI9Ghzz6pQv96Akcj8D/nUp8XsF8OOu3/8T+HFPbLas5du/xu7vgc3q8psDvwC+MMnztj6lFuwgYBalz9mdlFq71Xr2/27gPGDjnm1sSEmW1qq/H11jshbwa2Beff944PgJyvEj4Lie/T0DeATYri6TwJPq61mUZuH7gPUbXOdnUmoln0xJqvbpmv964JTp/jt2cmpzmvYCODkNy1S/gP9rnPe3oDRnbDHBeltTmsUWAt+d5D4/XL/kuqcPd81/GvBLSnJ3FfDyCbazJ3DTOO9fA7xtnPf3oDSV3UepOXhDz/wdawJzF6UfzdeBjeq851E6Fd9bE4cz6UqYKE2OD9WYdaZT+zlmSsJ2WT3eW2tSMWsp8VuF0ny1KSUBu4tS+9W73NHANynJ49eBm+s+bq7nfZ0G18tzKUnQIkqfsedOsNybKU3Eve+fCPxV1++bU5Ktu4Ajut7/b+Dt46w/p8Z5u3HmnQJ8qr7OeqyLKH3cLgBe1OB4V6MMS3EP8Afg73rmnwy8tI2/VSenYZkic5k3IEnS0KrDTDw1Mw+d7rJMtSiDiV4KbJ+lKW4oRcT2wH9m5q7TXRapTSZRkiRJDdixXJIkqQGTKEmSpAZMoiRJkhowiZIkSWrgMYPPTYUNNtgg586dO4hNS5IkTakLL7zw9sycPdn1BpJEzZ07lwULFgxi05IkSVMqIn7bZD2b8yRJkhroK4mKiPUi4psRcU1EXB0RDqgmSZJWaP025x0FnJaZr6oj6D5ugGWSJEkaestMoiJiXcpztt4MkOUJ4w8OtliSJEnDrZ/mvC2BMeBLEXFxRBwbEWv2LhQR8yNiQUQsGBsbm/KCSpIkDZN+kqiVgZ2Bz2fmTpSngR/Wu1BmHpOZ8zJz3uzZk75LUJIkaaT0k0TdBNyUmefV379JSaokSZJWWMtMojLzVuDGiNi2vvUC4KqBlkqSJGnI9Xt33t8CJ9U7864H3jK4IkmSJA2/vpKozLwEmDfYokiSJI0ORyyXJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJamDlfhaKiBuAe4GHgYcyc94gCyVJkjTs+kqiqudn5u0DK4kkSdIIsTlPkiSpgX6TqAR+HBEXRsT88RaIiPkRsSAiFoyNjU1dCSVJkoZQv0nU7pm5M7Av8M6I2KN3gcw8JjPnZea82bNnT2khJUmShk1fSVRm3lx/3gZ8B9hlkIWSJEkadstMoiJizYhYu/Ma2Bu4YtAFkyRJGmb93J23EfCdiOgs/+XMPG2gpZIkSRpyy0yiMvN6YIcWyiJJkjQyHOJAkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqYG+k6iImBURF0fEDwdZIEmSpFEwmZqodwNXD6ogkiRJo6SvJCoiNgNeAhw72OJIkiSNhn5roo4E3g88MriiSJIkjY5lJlERsR9wW2ZeuIzl5kfEgohYMDY2NmUFlCRJGkb91ETtBrw0Im4AvgrsFRH/r3ehzDwmM+dl5rzZs2dPcTElSZKGyzKTqMz8QGZulplzgdcCP83MNw68ZJIkSUPMcaIkSZIaWHkyC2fmz4CfDaQkkiRJI8SaKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGlplERcTqEXF+RFwaEVdGxOFtFEySJGmYrdzHMg8Ae2XmoohYBTg7Ik7NzHMHXDZJkqShtcwkKjMTWFR/XaVOOchCSZIkDbu++kRFxKyIuAS4DfhJZp430FJJkiQNub6SqMx8ODN3BDYDdomIp/cuExHzI2JBRCwYGxub4mJKkiQNl0ndnZeZC4EzgH3GmXdMZs7LzHmzZ8+eouJJkiQNp37uzpsdEevV12sALwSuGXC5JEmShlo/d+dtApwQEbMoSdfXM/OHgy2WJEnScOvn7rzLgJ1aKIskSdLIcMRySZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAaWmURFxOYRcUZEXBURV0bEu9somCRJ0jBbuY9lHgL+PjMvioi1gQsj4ieZedWAyyZJkjS0llkTlZm/z8yL6ut7gauBOYMumCRJ0jCbVJ+oiJgL7AScN5DSSJIkjYi+k6iIWAv4FnBoZt4zzvz5EbEgIhaMjY1NZRklSZKGTl9JVESsQkmgTsrMb4+3TGYek5nzMnPe7Nmzp7KMkiRJQ6efu/MCOA64OjOPGHyRJEmShl8/NVG7AQcCe0XEJXV68YDLJUmSNNSWOcRBZp4NRAtlkSRJGhmOWC5JktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNWASJUmS1IBJlCRJUgMmUZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUwDKTqIj4YkTcFhFXtFEgSZKkUdBPTdTxwD4DLockSdJIWWYSlZlnAXe2UBZJkqSRYZ8oSZKkBqYsiYqI+RGxICIWjI2NTdVmJUmShtKUJVGZeUxmzsvMebNnz56qzUqSJA0lm/MkSZIa6GeIg68AvwS2jYibIuJtgy+WJEnScFt5WQtk5uvaKIgkSdIosTlPkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqYJkPIJbUvrmHnTzdRWjkho+/ZLqLoBHida5RZ02UJElSAyNXE+V/Lu0z5pIkPZY1UZIkSQ2YREmSJDXQV3NeROwDHAXMAo7NzI8PtFSS1DKbrSVN1jJroiJiFvDvwL7AU4HXRcRTB10wSZKkYdZPTdQuwHWZeT1ARHwVOAC4apAFkyRJU8sa16nVT5+oOcCNXb/fVN+TJElaYUVmLn2BiFcB+2TmX9ffDwSelZmH9Cw3H5hff90WuHbqiztwGwC3T3chVjDGvH3GvH3GvH3GvH2jHPMnZObsya7UT3PezcDmXb9vVt9bQmYeAxwz2QIMk4hYkJnzprscKxJj3j5j3j5j3j5j3r4VMeb9NOddAGwdEVtGxKrAa4HvD7ZYkiRJw22ZNVGZ+VBEHAL8iDLEwRcz88qBl0ySJGmI9TVOVGaeApwy4LIMg5FujhxRxrx9xrx9xrx9xrx9K1zMl9mxXJIkSY/lY18kSZIaMImSJElqwCRqBomI1SJilfo6prs8K4KIWKn+NN4tiYhV6+OojHtL6mfLavW1MR+gTnwjYo2ImF1f+13dgohYKyLm1td9XeeemBkgInaPiCuB/wbeA5B2dhuYiFg7It4XEZcBn6lv+7c0QBGxUUR8KCJ+AZwGvAu8zgcpIjaMiI9FxE+BnwLviYjVjPlgZWZGxI7A74B/mObizHgRsX5EfCQiTgYuBg6C/j9b+ro7T8Ol/lcSmflwRKxOGSn+A8BZwMkRcT3wLT/spk6N+UqZ+RBlqI9NgBOBNwBk5sPTWLwZqfs6pwz4uwlwKPBb4KcRcWlm/nQaizjj9FznqwGrAP8EXA6cAywATp++Es48nVqmzHyk6+2nUP4p3nKceVpOPdf52sBhwN6ZecZkt+V/zyOkU72YmY90vrQz837KQ6IvzsyFwL8Be1IevaPl1BPzh+rrhcDHgCOAByJip+5ltXzGu86B64D3ZuYFmXkbcD71C0bLb4Lr/MbMfG9mnpOZ9wLXA/dPZzlnkp6Y9yZJrwK+BtwfEc/oXl7NTXCd/xa4sk5ExCaT2aZJ1BCKYlZvO3it5t04IvaMiKMiYv+IWBc4G3h6XexK4AHAL/ZJ6DPmR0bEAfX9sfrBdznworq4f0+TMImYvzQzF2bmovrUBCi1JNb+TdJkYt61zlsiYjHluWibtl3mUTfZz5balHcdcAnwB0qtFPj50rdJxPyVddYVwLkRcSHwuYiY328/NE/KEIiI9SLiJTUhIouHM/OR7iQoIt5AqVJ/MfCXwFuA+4BbePQPbQy4FZjT2VZ7RzI6Gsb8BcDb6vudv50zgT3aLf1oWo6Yv72+v0pmPhgRuwBPAL7pPwlLt7wxr04FHl/fe0Xny17jW46Y/02dtQ1wS2b+BlgIHBwRB9tlYGLLEfO/rrOOBD4O7AZ8AngZ8Ip+9m2fqOHwVErfmgeA0yNiW+CNwLOAn0fE5yjV6M8B3p2ZP4iI04FjgQCuAfYByMw76/qntn8YI2WimO8CnL2UmH8RSnVw/eM8D3hffc8PuaVb3pgvrtt5H3B0Zi5q+wBG0HLFHCAzb60vr4qIm4AtI2Il++lMqOnn+XG1pnUb4MCImA+sRfmMv2UajmOUNL3OvwSQmQso/f0Azo+Iq4CN+rnOrYlqSa1enCjeN1Cqb59Uf9+TUqP0PuCPwD9TLo55wKX1P/IfU87fU4DvAjtGxN51/S3q+iu0hjF/P4/G/EEeG/POnTOd/3Z+DdwXEUdExNsiYqNBHc8oGGDMO83Tu1I+DBdExAER8fqIWHtQxzMKBn2dd+1nFrA1cM2KnkAN6PM8gCdS7hD7OLA/8EzgAkqz3grdPWNA1/kj41znK1P6FP+6n+vcJKol9Qt3ohMyBvye8h8IwAnAhcA7KNWNuwOr1uWe1fUf+b3AAZl5H3A48OaIuAO4rE4rtCmI+SrAbcCze2L+YoCIeHZEnEn5YtkJWEypfl9hDTDm+9XXf0v5j/NYyl2p9wF/muLDGCkDjPmLACLi4Ii4gNJH5zpK7esKbYCf5y/PzJMz80uZeT0l2TqF2v9vRe6eMcDrfF+AiDgoSp+oi4FrKTevLJPNeVNsvOq/mj1vBbwZWJyZh3fPz8zFEfE7YOeI2IKSMR9M6W/zL5S7wHYFvgC8urb7BnA7pRoTSm3Uf2e5c2yF0kfMH8zM/9M9vyfmT6B8WB1MGSaiO+bHUmK+Tl31DmCH+vp3wKGZefFADmyItRzzO4En19dfBD6TmecO5MCG2DTEfPv6+mLgkMxc4ZKnafg8367uY7XMfCAz7waOG+AhDp1puM63q68vB9452c8Wa6KWQ0SsVKu4/6xz8iPi6VHGcIJyAo+i/DdxQs82OtWzv6PUZMwBngesm5nHAQ9RqnhfmZnfo1wE+1PGtvg8tfqydqJbWLc5a6ZW+zaM+Yk92+iN+aY8GvNjmTjm61Bi/sS631s6CVSN+RLlmimGIOZHU4fsyMzTOx9y45VrphiymJ/fSaD8bAEG+3m+dd3vA71lm6LDHCpDcp1vU/d7UddnS9/XuTVRkxAR0V2dOl7VYkQcRhnj4x7gzIg4kTLa7zOBb2TmDd3Ld23v93XakVKr9KaI+BblRH+XciFA+W/mEuAZlGrKT/aWIWdQB2dj3r5hj3mnfEup2h85IxRzr/OWP1smKtsoGvaYN7nOTaKWobtqsfvkR3lG3YuAV1PaVT9JaXNNyl0Y6wLfBNYDPk0ZqG5p8b6jTrsCxwCHUO64OzMzr+pabvW6r3WBk4EfLO8xDhtj3r5Rinl3+UaZMW/fKMV8philmDe6zjPTqWuijII8H5gzzrw5wH719d7AT4BXAk+r772I0rH4dModFcfVi+FxlGrfly5j31sBW04wb9Z0x8aYz5zJmBtzY27MjfnyT9ZEVV3Z8gaUTqzXATdHxPOBNTLzFEofgfdExLWUKsKVKZ3R7qubuZCSRb89y0Bp3dv/A7BdRJyRmffW9tbg0WeDkeVujO51OkPUZ86gavQOY94+Y94+Y94+Y96+FTXmM7KzWj86we0KcmfwxF9RxuToPJdrDx59rMc5lGrHTSmDWd4BvBP4dER0qgTPBw6IMrT8C6OMH7Qx5dEstwJ/rtbMrmeDRcQWUUZi7j3xM6IaHYz5dDDm7TPm7TPm7TPmxQpRExU9T8mOKJ3Hot5GGhGrUaof183Mj0bErcBW9URcAuwbERtm5m0R8XvKLZHnZOar6vbWprTB7gr8L8ptmCdTxq74HrAoM7/fU6bVgZcAewE7U25v/Wwt58j/oRnz9hnz9hnz9hnz9hnzic3IJKr3hGfXHQAR8fjMvCMiNqT0/H9OZt4VEQ8C69WTeT1ljJQ5wP9QbqvcntJOeyPlmTtfi4j1KM/Y2ZHSZntevUg+Anyo90TGkuNfvJAysvh/UEYAXswIG6GYb44xN+YNGfP2jVDM/TxfAa/zGdmcl6WKr5MxrxkRe0XE0RHxK+BLEbFrZt5GGSp+z7ra/1CeDL91ff0g5ZEqv6JUP76kLrcOpb13E2Cjuvy3gQPrNsnMxTVLX2IMjO4LMTN/kJmfzszLR/0PDkYq5kcac2PelDFv3wjF3M/zFfA6n3FJVESsG+V5Wl+OiGdSTta/UnrmbwP8EvibiHgScAaPttXeQGlr3ZrSnns78JTMfJAySvKOEXEFpSPbocC1mXl2Zs7PzG9l5j29Zcmu9tqZzJi3z5i3z5i3z5i3z5hPzkg050X8uf11iYG6xlluJeDDlCrEsygndSXgGsrw7gBfobS37gr8DDgQIDOvi4hnAfdm5tci4kZgh4hYJzN/FRGv6WTJ4+xziQx5JjDm7TPm7TPm7TPm7TPmgzO0SVREdG5dfKRz0js/I2Ib4PbMvLPnotgD2D0zn9m1ndWABZT2ajLzhojYCrgiM8+PMrz7J4DHU9pq74vSYe1GSme1rYBLOie/94SP6okfjzFvnzFvnzFvnzFvnzFvx9AkUTWw3eM9JGW8CKJUG25A6an/1brK5cBbe7LqO6njTUQZDfWRLHcO3ADMj4iTMvNSSme0Tlb9OuCAur3vZea9df0/UB5iuBVwSedCG/UT3s2Yt8+Yt8+Yt8+Yt8+YT49pS6Ki50nNvYGN8mTrd1I6qu0P3E8ZI+IVmXljRPw6InbOzIu6VrsDeCAidsvMX9TtdMat+C3wqSh3FJwBXFT3eylwadd+O1n5TcCPqRdKz4U2kox5+4x5+4x5+4x5+4z5cGg9iaonYE/gG/X3TlvtnsC+lGz5g5l5S0QcAFyVmTtHxE6Utti16qbOAJ4TEZfko9WCN0fERcC76/aeT2nXPRI4F1gpMz8yTpnGq/Z8EPjF1Eegfca8fca8fca8fca8fcZ8uAz87ryo7Z8dWdpF5wOvjYj3A+tExBOBN1Ky2VOAIyJiDnAa8Pt6gm6iPMn5WXVT5wE7AGtGxCoRsW99/58pA26tDxwBfAz4I+UWy61qmaK7XFnMmCpGY94+Y94+Y94+Y94+Yz7cBp5EdQIbEU+IiN0jYmdKz//DgSdRTsyhwC3AIkpP/3mU8SMuBzYD1qA8lPBaSkc1KMPH70I50asDe0XE6pn5YGb+PDP/PjNPyTLexMOUasVP1TLN6BNuzNtnzNtnzNtnzNtnzIdcLt/TmoMJnoxMOWlrAM8AzqSczA8CGwPvBT7Vtew/UtpNPwy8FFitvr8F5cQ9sf6+H/Dzzj6BlwNrTrD/lShVj8t1jMM2GXNjbsyNuTGfGZMxH/1pqi+IdevPdYDPA68H3gB8ome5nYAfAXMp/bJeCJzVs8zz6s9zgAPq68cD23ZO8DgXY0x3QFs/gcbcmK8AkzE35ivCZMxHb2rUsbyrI9s2wKuAVSnViNtQ2mo3qhfB6ZQs+i21/fQPwK8y8/tRhnKfnZk3AD+JiH+IiM9QqhZ3Br5Lyb7fQnkOD5l5B+XuAbKnKjHrVTBTGfP2GfP2GfP2GfP2GfOZI5rGLSKeDBwP/IRyom8DTgTeSml3vRp4WmbeHxHzKHcEPBs4iPIMnddRnp2zIfCFzPxJRLyG8hDC0zPzxuU4rhnJmLfPmLfPmLfPmLfPmM8MyzPEwROB64ATgJsz808R8XHg74AfAt8CNoqI32XmAvjz4FvbAqsAR1OqKhdSxqAgM7+2HOVZERjz9hnz9hnz9hnz9hnzGWB5aqLWBr5EGZF0JcotkEdQho0/HPhaZr4rItagVFd+kJJpfw343ERVh9EzgJgeZczbZ8zbZ8zbZ8zbZ8xnhsZJ1BIbKdWSb6U8tflo4Chgk8x8cUQEZfCvxZm5cJx1Z1GGlrc9dhKMefuMefuMefuMefuM+ehq3JxXT+ymwHaUwbt2At6RmYsi4nxg/YiYlWV8ibGudVaq7wHQ/VpLZ8zbZ8zbZ8zbZ8zbZ8xnhsaDbdasd3Pg7cBDwPsz89cRsTVwMHBRZj5cT/qf1/GEN2fM22fM22fM22fM22fMZ4Ypac5bYoPl7oCnAUdluZ1SA2bM22fM22fM22fM22fMR8tyJ1Gd6kVKkmxnthYY8/YZ8/YZ8/YZ8/YZ89E25TVRkiRJK4KBP4BYkiRpJjKJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrg/wMTADkuftk4LAAAAABJRU5ErkJggg==\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAh2klEQVR4nO3deZhlVXnv8e+PZlQZIjSoIDYgOIECtgOCiiYOqMhVuU6oOMTWOM9RE6NG45B4FYdgLgGnq0ZUjNGIGFEUccJmkkFBQpBZGhClReb3/rF2weFY1V21u8/pGr6f59lPndrjOu/edc5ba629dqoKSZIkzcx667oAkiRJc5FJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGS5pQk703ymnVdDk0tySuTvH9dl0MaNZMoLUhJliQ5Oslvk1yW5GNJ1p/mtu9I8tmex316kh8luTbJ9yZZvijJu5NckuSaJKck2WKS9b6TpCbKnGT7JCuHpkry+m55kvxNkguS/D7JF5JsNrC/M4e2vSnJ1weW75/kjG7Zj5Lcd2DZM5OcneR3SS5P8unBfQ+st3OS6wZjl+SJSU5IcnV3Hg5Psukq4rcYeB7wf4fm75DkliQfn2SbA5Kc2r3vK5J8N8kOUx1jiuPumuRb3fZ/Mrheks8mubQ7xjlJ/nJo+R2SHNpt/7skxw8se3a37flJHjUwf6cu1otmUtZu23d05/8hQ/Ofn+TmgfN8XpK/mun+u30d1p33W5I8f2jxvwIHJdm6z76lucIkSgvVocDlwF2B3YFHAi8bw3GvAg4B3jfF8ncCDwP2AjYDngtcN7hCkoOADQbnVdUFVXWniQnYDbgFOKpb5XndvvYG7gZsAnx0YPv7DWy7KXAh8KXueDsDnwNeCmwBfB342kDS+UNg76raHNgRWB949yTv7Z+Bnw3N27xb927AfYBtgX+aIjYAzweOrqo/Ds1/HvBb4BlJNpqYmeSewGeA13fH2qErx82rOMZkbgS+CLxoiuXvBZZU1WbAk4F3J3ngwPLDgDvT3uOdgdd25Vufdi3sCbyCgXMCfAR4bVXNqKxJQovHVd3PYT8eONdPA/4xyR4zOUbnNNrfzMnDC6rqOuCbUxxfmjdMorRQ7QB8saquq6rLgGOA+61uoySPB95K+7JemeS0mRy0qo6tqi8Cl0yy7z8DXgO8uKp+Xc0Z3RfSxDqbA28H3rSaQz0POL6qzu9+3x84oqourKqVwPu793CHSbZ9BLAVtyVgjwN+UFUnVNVN3bbb0hJPun1eMbD9zcA9h97bM4Grge8MxePzVXVMVV1bVb+l1WDsvYr3tR/w/aF9TyQNf0tLdvYfWLw78D9V9Z0untdU1VFVdcEqjvEnqursqjoCOHOK5WdW1fUTv3bTTl357k1LrJZV1YqqurmqTurW3RK4uKouBY6lJaEkObCb/9OZlLPzcNo/B68Cnplkw1W8r1OAX9CSuxmpqn+uqu8wlOQP+B7wxJnuV5pLTKK0UB1C+4K5Q5JtaV/Ox6xuo6o6BngPcGT33/wDALqmmqunmH4+zTLtBtwEHNg1bZ2T5OVD67wH+Dhw2VQ7GUgqPj28aOj1RsDOk+ziYOCoqvrDKrYNsOvAMfdJ8jvgGlrtxiEDyzYD/h543VRlHvAIpkhUOrsBZw/N2wfYDvgCrbbo4IFlJwP3TvKhJI9KcqfBDbumtKnO29VJtp9GmSf2dWiSa4FfApcCR3eLHgz8Gnhn15x3epKndctWAFsm2Q54DHBm15z5t8BbpnvsIQfTagu/2P2+/1QrJnkQsAuwfGDequLx5hmU4xfAA3qUX5ozTKK0UB1Pq3n6PXAR7Uvkq313VlUvq6otppjuP83dbEdrctqFVlN2IPCOJI8BSLKUVkvz0Sn30OwDbAN8eWDeMcBfpvUF2xz4627+7WqiupqpA4FPDcw+Fnhkkn27Wo23AhsObtvVUm3evYd/As4f2P5dtFqwi1ZV6O59Hgz83SpW24KWqA06GPhmV5P1eeDxE31xquo8YF9azdkXgSuSfGoimepqwqY6b1vMpMaqql5Gawp9OPAVYKJmajtawvk7WrPlK4BPJ7lPVd0C/BXtXL0BeDGtSfejwP2THNf1xdqVaejO3/8GPl9VN3b7HW5Se2iXEF0DnAj8P+BXA+9jVfGYqhl6MtfQrmdp3jKJ0oKTZD1aUvEV4I60pqs/ozVTrUsT/Xz+vqr+WFU/p9WuPKEr86HAq7smtVWZqElaOTDvE8C/0ZpYzgSO6+YPJzZPpfWlubXJrKp+2e3zY7Qalq2AsybZlqq6mBbbLwAk2R34C+BDqypwkofSEqADq+qcVaz6W1qiMrHdJrSk4XPd8X8MXAA8e6BMP6mqp1fVYlqC8wjgb1ZVnr66proTaInTRIftP9KaGd9dVTdU1fdp8X9st813quqhVfVIWjPgUloS+xlaH7B3AYdPswhPodVmTtSCfQ7YL61D/oSfdAnRpsBdaP9MvKfH212dTWmJozRvmURpIbozsD3wsaq6vqquBD4JPGGa2092d9a/5E/vjpuYVtU8NWii2W9w/xOvN6N9uR6Z5DJu66B9UZKHD5RjIqm4XVNeVd1SVW+vqiVVtR0tkbq4mwYdDHymqmpo+y9X1a5VtSWtT9YS/rST+IT16foD0WqBlgAXdOV+A/C0JLd2Ru46NX8NeGHXx2ZVfk6rqZvwFFpsDu2aQC+j1TodPNnGVfUzWvK8a3fsg1Zx3lbOpDlvyGAMJmvOnewaCi1RfRUtUV1UVb+mxXm6tZkHA3fitnh/iXYTwrMnW7mqfkPr+3Zrk99q4vHWaZYDWj+rGfUZlOacqnJyWnATcB7wZtqX3RbAv9OaQKaz7UuBE4D1ehx3EbBxt4/ju9cbDCw/nnb7/ka0L6HLgT+n9UG6y8D0INoX8bbAhgPbP5vWlJah496Z9qUe4L7AGbSOzoPrbEerxdhpknI/sCv7Ylqz2OcHlh0EbN+9vgetFusr3e93GCr3B2hNTIu75bsCvwGeMc34vQ44bOD3bwFHDB3jgbQ7E3ejNW2+GNi6W//ewDnA38zwvKU7V/ft4r4xsFG3bGvgmbTkZRGtI/4fgCd3yzcAzgXe1l1ve9Oauu49dIwXAx/uXq9Pq3W7L/B44IyB9QrYd5Iybkvr1P/YoXi8DzipW+f5wAkD22xJa649sse1vGEXhx92Zd+Ygb8J2h2Jb1rXf+tOTqOc1nkBnJzWxUS7a+t73RfVFV1isM3A8pXAw6fYdktaEvVb4OQZHvf53Hb31sT0qYHl29Kaw1bSEr2XTLGfJd226w/N/xbwrknW34XWIftaWifn102yzltod+FNdrwTui/+q2hJ3h0Hlv0DrWnvD93Pw4Atp9jPO4DPDvz+SVrCs3JgOnMV8duqO8YmXaxuAnabZL2jaQnbrrRO1r/p9n0+rdl2g6mOsZp4D07nd8sW0xLHq2l97E6n3WE5uP39gB93MToLeMok7+sMYLOBeQfRbiA4H3hUN+/u3TH+JL60fwpOmmT+3WjNibt219/NA7G+nNbMu3WPv6HvTRKTfbtlG3fnaZuZ7tfJaS5NqfqTWmVJmrWSvAe4vKoOWddlGbckzwHuV1V979wbiySvBO5eVasbikOa00yiJEmSerBjuSRJUg8mUZIkST2YREmSJPVgEiVJktTD+qtfZea22mqrWrJkySh2LUmStFaddNJJV1R7qsGMjCSJWrJkCcuXL1/9ipIkSetYkl/32c7mPEmSpB6mlUQl2SLJl5P8Mskvkuw16oJJkiTNZtNtzvswcExVHZhkQ9rzsCRJkhas1SZRSTYHHkF75hJVdQNww2iLJUmSNLtNpzlvB2AF8MkkpyQ5PMkdh1dKsizJ8iTLV6xYsdYLKkmSNJtMJ4laH9gT+HhV7UF7Cvmbh1eqqsOqamlVLV28eMZ3CUqSJM0p00miLgIuqqqfdr9/mZZUSZIkLVirTaKq6jLgwiT36mb9OXDWSEslSZI0y0337rxXAp/r7sw7D3jB6IokSZI0+00riaqqU4Gloy2KJEnS3OGI5ZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9rD+dlZKcD1wD3AzcVFVLR1koSZKk2W5aSVTnUVV1xchKIkmSNIfYnCdJktTDdJOoAv4ryUlJlk22QpJlSZYnWb5ixYq1V0JJkqRZaLpJ1D5VtSewH/DyJI8YXqGqDquqpVW1dPHixWu1kJIkSbPNtJKoqrq4+3k58O/Ag0dZKEmSpNlutUlUkjsm2XTiNfBY4IxRF0ySJGk2m87dedsA/55kYv3PV9UxIy2VJEnSLLfaJKqqzgMeMIaySJIkzRkOcSBJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUw7STqCSLkpyS5D9HWSBJkqS5YCY1Ua8GfjGqgkiSJM0l00qikmwHPBE4fLTFkSRJmhumWxN1CPAm4JbRFUWSJGnuWG0SleRJwOVVddJq1luWZHmS5StWrFhrBZQkSZqNplMTtTfw5CTnA18AHp3ks8MrVdVhVbW0qpYuXrx4LRdTkiRpdlltElVVb6mq7apqCfBM4LtV9ZyRl0ySJGkWc5woSZKkHtafycpV9T3geyMpiSRJ0hxiTZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSD6tNopJsnOTEJKclOTPJO8dRMEmSpNls/Wmscz3w6KpamWQD4IQk36yqn4y4bJIkSbPWapOoqipgZffrBt1UoyyUJEnSbDetPlFJFiU5Fbgc+HZV/XSkpZIkSZrlppVEVdXNVbU7sB3w4CS7Dq+TZFmS5UmWr1ixYi0XU5IkaXaZ0d15VXU1cBzw+EmWHVZVS6tq6eLFi9dS8SRJkman6dydtzjJFt3rTYDHAL8ccbkkSZJmtencnXdX4NNJFtGSri9W1X+OtliSJEmz23Tuzvs5sMcYyiJJkjRnOGK5JElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg+rTaKS3D3JcUnOSnJmklePo2CSJEmz2frTWOcm4PVVdXKSTYGTkny7qs4acdkkSZJmrdXWRFXVpVV1cvf6GuAXwLajLpgkSdJsNqM+UUmWAHsAPx1JaSRJkuaIaSdRSe4EHAW8pqp+P8nyZUmWJ1m+YsWKtVlGSZKkWWdaSVSSDWgJ1Oeq6iuTrVNVh1XV0qpaunjx4rVZRkmSpFlnOnfnBTgC+EVVfXD0RZIkSZr9plMTtTfwXODRSU7tpieMuFySJEmz2mqHOKiqE4CMoSySJElzhiOWS5Ik9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPWw2iQqySeSXJ7kjHEUSJIkaS6YTk3Up4DHj7gckiRJc8pqk6iqOh64agxlkSRJmjPsEyVJktTDWkuikixLsjzJ8hUrVqyt3UqSJM1Kay2JqqrDqmppVS1dvHjx2tqtJEnSrGRzniRJUg/TGeLg34AfA/dKclGSF42+WJIkSbPb+qtboaqeNY6CSJIkzSU250mSJPVgEiVJktSDSZQkSVIPq+0TJUmS5oclb/7Gui5CL+e/74nrugiTsiZKkiSpB5MoSZKkHmzOk2Yhq9wlafazJkqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB6mlUQleXySs5Ocm+TNoy6UJEnSbLfaJCrJIuCfgf2A+wLPSnLfURdMkiRpNpvOA4gfDJxbVecBJPkCcABw1igLNhUfzCppFPxskTRT02nO2xa4cOD3i7p5kiRJC9Z0aqKmJckyYFn368okZ6+tfY/RVsAVo9hx3j+Kvc4LI4u5puR1Pn7GfPz8bBm/uXyd36PPRtNJoi4G7j7w+3bdvNupqsOAw/oUYrZIsryqlq7rciwkxnz8jPn4GfPxM+bjtxBjPp3mvJ8BOyfZIcmGwDOBr422WJIkSbPbamuiquqmJK8AvgUsAj5RVWeOvGSSJEmz2LT6RFXV0cDRIy7LbDCnmyPnKGM+fsZ8/Iz5+Bnz8VtwMU9VresySJIkzTk+9kWSJKkHkyhJkqQeTKLmkSQbJdmge511XZ6FIMl63U/jPSZJNuweR2Xcx6T7bNmoe23MR2givkk2SbK4e+139RgkuVOSJd3raV3nnph5IMk+Sc4EvgO8FqDs7DYySTZN8sYkPwc+0s32b2mEkmyT5O1JfggcA7wKvM5HKcnWSd6b5LvAd4HXJtnImI9WVVWS3YELgL9ex8WZ95LcOcm7knwDOAU4GKb/2bLWRizX+HT/laSqbk6yMW2k+LcAxwPfSHIecJQfdmtPF/P1quom2lAfdwU+AxwEUFU3r8PizUuD1zltwN+7Aq8Bfg18N8lpVfXddVjEeWfoOt8I2AD4W+B04EfAcuDYdVfC+WeilqmqbhmYfR/aP8U7TLJMa2joOt8UeDPw2Ko6bqb78r/nOWSierGqbpn40q6q62gPiT6lqq4G/g+wL3CvdVTMeWUo5jd1r68G3gt8ELg+yR6D62rNTHadA+cCb6iqn1XV5cCJdF8wWnNTXOcXVtUbqupHVXUNcB5w3bos53wyFPPhJOlA4EjguiQPHFxf/U1xnf8aOLObSHLXmezTJGoWSrNouB28q+a9S5J9k3w4yf5JNgdOAHbtVjsTuB7wi30GphnzQ5Ic0M1f0X3wnQ48rlvdv6cZmEHMn1xVV1fVyu6pCdBqSaz9m6GZxHxgmxckuZH2XLS7jbvMc91MP1u6prxzgVOB39BqpcDPl2mbQcyf1i06A/hJkpOAjyVZNt1+aJ6UWSDJFkme2CVEVHNzVd0ymAQlOYhWpf4E4C+AFwDXApdw2x/aCuAyYNuJfY3vncwdPWP+58CLuvkTfzvfBx4x3tLPTWsQ8xd38zeoqhuSPJj2sNAv+0/Cqq1pzDvfBLbs5j114stek1uDmL+0W7QLcElV/Q9wNfCSJC+xy8DU1iDmf9ktOgR4H7A38H7gfwFPnc6x7RM1O9yX1rfmeuDYJPcCngM8BPhBko/RqtEfBry6qr6e5FjgcCDAL4HHA1TVVd323xz/25hTpor5g4ETVhHzT0CrDu7+OH8KvLGb54fcqq1pzG/s9vNG4NCqWjnuNzAHrVHMAarqsu7lWUkuAnZIsp79dKbU9/P8iK6mdRfguUmWAXeifcZfsg7ex1zS9zr/JEBVLaf19wM4MclZwDbTuc6tiRqTrnpxqnifT6u+vWf3+760GqU3An8A/o52cSwFTuv+I/8v2vm7D/BVYPckj+22377bfkHrGfM3cVvMb+BPYz5x58zEfzu/Aq5N8sEkL0qyzajez1wwwphPNE/vRfswXJ7kgCTPTrLpqN7PXDDq63zgOIuAnYFfLvQEakSf5wF2ot0h9j5gf+BBwM9ozXoLunvGiK7zWya5zten9Sn+1XSuc5OoMem+cKc6ISuAS2n/gQB8GjgJeBmtunEfYMNuvYcM/Ed+DXBAVV0LvBN4fpIrgZ9304K2FmK+AXA58NChmD8BIMlDk3yf9sWyB3Ajrfp9wRphzJ/UvX4l7T/Ow2l3pV4L/HEtv405ZYQxfxxAkpck+Rmtj865tNrXBW2En+dPqapvVNUnq+o8WrJ1NF3/v4XcPWOE1/l+AEkOTusTdQpwNu3mldWyOW8tm6z6r8uedwSeD9xYVe8cXF5VNya5ANgzyfa0jPkltP42/0C7C2wv4F+Bp3ftvgGuoFVjQquN+k61O8cWlGnE/Iaq+vvB5UMxvwftw+oltGEiBmN+OC3mm3WbXgk8oHt9AfCaqjplJG9sFhtzzK8C7t29/gTwkar6yUje2Cy2DmJ+/+71KcArqmrBJU/r4PN8t+4YG1XV9VX1O+CIEb7FWWcdXOe7da9PB14+088Wa6LWQJL1uiruW02c/CS7po3hBO0Efpj238Snh/YxUT17Aa0mY1vgkcDmVXUEcBOtivdpVfUftItgf9rYFh+nq77sOtFd3e1z0Xyt9u0Z888M7WM45nfjtpgfztQx34wW8526414ykUB1Mb9dueaLWRDzQ+mG7KiqYyc+5CYr13wxy2J+4kQC5WcLMNrP8527414/XLa19DZnlVlyne/SHffkgc+WaV/n1kTNQJIMVqdOVrWY5M20MT5+D3w/yWdoo/0+CPhSVZ0/uP7A/i7tpt1ptUrPS3IU7UR/lXYhQPtv5lTggbRqyn8cLkPNow7Oxnz8ZnvMJ8q3iqr9OWcOxdzrfMyfLVOVbS6a7THvc52bRK3GYNXi4MlPe0bd44Cn09pV/5HW5lq0uzA2B74MbAF8iDZQ3arifWU37QUcBryCdsfd96vqrIH1Nu6OtTnwDeDra/oeZxtjPn5zKeaD5ZvLjPn4zaWYzxdzKea9rvOqchqYaKMgLwO2nWTZtsCTutePBb4NPA24XzfvcbSOxcfS7qg4orsY7kCr9n3yao69I7DDFMsWrevYGPP5MxlzY27MjbkxX/PJmqjOQLa8Fa0T67nAxUkeBWxSVUfT+gi8NsnZtCrC9Wmd0a7tdnMSLYt+cbWB0gb3/xtgtyTHVdU1XXtruO3ZYFS7G2Nwm4kh6qvmUTX6BGM+fsZ8/Iz5+Bnz8VuoMZ+XndWmYyK4A0GeGDzxHNqYHBPP5XoEtz3W40e0ase70QazvBJ4OfChJBNVgicCB6QNLf+YtPGD7kJ7NMtlwK3VmjXwbLAk26eNxDx84udFNToY83XBmI+fMR8/Yz5+xrxZEDVRGXpKdtI6j6W7jTTJRrTqx82r6t1JLgN27E7EqcB+SbauqsuTXEq7JfJHVXVgt79NaW2wewF/RbsN8xu0sSv+A1hZVV8bKtPGwBOBRwN70m5v/WhXzjn/h2bMx8+Yj58xHz9jPn7GfGrzMokaPuE1cAdAki2r6sokW9N6/j+sqn6b5AZgi+5knkcbI2Vb4L9pt1Xen9ZOeyHtmTtHJtmC9oyd3Wlttj/tLpJ3AW8fPpG5/fgXj6GNLP4vtBGAb2QOm0MxvzvG3Jj3ZMzHbw7F3M/zBXidz8vmvGpVfBMZ8x2TPDrJoUnOAT6ZZK+qupw2VPy+3Wb/TXsy/M7d6xtoj1Q5h1b9+MRuvc1o7b13Bbbp1v8K8Nxun1TVjV2WfrsxMAYvxKr6elV9qKpOn+t/cDCnYn6IMTfmfRnz8ZtDMffzfAFe5/MuiUqyedrztD6f5EG0k/UeWs/8XYAfAy9Nck/gOG5rqz2f1ta6M6099wrgPlV1A22U5N2TnEHryPYa4OyqOqGqllXVUVX1++Gy1EB77XxmzMfPmI+fMR8/Yz5+xnxm5kRzXnJr++vtBuqaZL31gHfQqhCPp53U9YBf0oZ3B/g3WnvrXsD3gOcCVNW5SR4CXFNVRya5EHhAks2q6pwkz5jIkic55u0y5PnAmI+fMR8/Yz5+xnz8jPnozNokKsnErYu3TJz0iZ9JdgGuqKqrhi6KRwD7VNWDBvazEbCc1l5NVZ2fZEfgjKo6MW149/cDW9Laaq9N67B2Ia2z2o7AqRMnf/iEz9UTPxljPn7GfPyM+fgZ8/Ez5uMxa5KoLrCD4z0UbbwI0qoNt6L11P9Ct8npwAuHsuqr6MabSBsN9ZZqdw6cDyxL8rmqOo3WGW0iq34WcEC3v/+oqmu67X9De4jhjsCpExfaXD/hg4z5+Bnz8TPm42fMx8+YrxvrLInK0JOahwOb9mTrl9M6qu0PXEcbI+KpVXVhkl8l2bOqTh7Y7Erg+iR7V9UPu/1MjFvxa+ADaXcUHAec3B33NOC0geNOZOUXAf9Fd6EMXWhzkjEfP2M+fsZ8/Iz5+Bnz2WHsSVR3AvYFvtT9PtFWuy+wHy1bfltVXZLkAOCsqtozyR60ttg7dbs6DnhYklPrtmrBi5OcDLy629+jaO26hwA/AdarqndNUqbJqj1vAH649iMwfsZ8/Iz5+Bnz8TPm42fMZ5eR352Xrv1zQrV20WXAM5O8CdgsyU7Ac2jZ7NHAB5NsCxwDXNqdoItoT3J+SLernwIPAO6YZIMk+3Xz/4424NadgQ8C7wX+QLvFcseuTBksVzXzporRmI+fMR8/Yz5+xnz8jPnsNvIkaiKwSe6RZJ8ke9J6/r8TuCftxLwGuARYSevpv5Q2fsTpwHbAJrSHEp5N66gGbfj4B9NO9MbAo5NsXFU3VNUPqur1VXV0tfEmbqZVK36gK9O8PuHGfPyM+fgZ8/Ez5uNnzGe5WrOnNYcpnoxMO2mbAA8Evk87mW8D7gK8AfjAwLpvpbWbvgN4MrBRN3972onbqfv9ScAPJo4JPAW44xTHX49W9bhG73G2TcbcmBtzY27M58dkzOf+tLYviM27n5sBHweeDRwEvH9ovT2AbwFLaP2yHgMcP7TOI7ufPwIO6F5vCdxr4gRPcjFmXQd07CfQmBvzBTAZc2O+ECZjPvemXh3LBzqy7QIcCGxIq0bchdZWu013ERxLy6Jf0LWf/gY4p6q+ljaU++KqOh/4dpK/TvIRWtXinsBXadn3C2jP4aGqrqTdPUANVSVWdxXMV8Z8/Iz5+Bnz8TPm42fM54/0jVuSewOfAr5NO9GXA58BXkhrd/0FcL+qui7JUtodAQ8FDqY9Q+dZtGfnbA38a1V9O8kzaA8hPLaqLlyD9zUvGfPxM+bjZ8zHz5iPnzGfH9ZkiIOdgHOBTwMXV9Ufk7wPeB3wn8BRwDZJLqiq5XDr4Fv3AjYADqVVVV5NG4OCqjpyDcqzEBjz8TPm42fMx8+Yj58xnwfWpCZqU+CTtBFJ16PdAvlB2rDx7wSOrKpXJdmEVl35NlqmfSTwsamqDjM0gJhuY8zHz5iPnzEfP2M+fsZ8fuidRN1uJ61a8oW0pzYfCnwYuGtVPSFJaIN/3VhVV0+y7SLa0PK2x86AMR8/Yz5+xnz8jPn4GfO5q3dzXndi7wbsRhu8aw/gZVW1MsmJwJ2TLKo2vsSKgW3W6+YBMPhaq2bMx8+Yj58xHz9jPn7GfH7oPdhml/XeHXgxcBPwpqr6VZKdgZcAJ1fVzd1Jv3UbT3h/xnz8jPn4GfPxM+bjZ8znh7XSnHe7Hba7A+4HfLja7ZQaMWM+fsZ8/Iz5+Bnz8TPmc8saJ1ET1Yu0JNnObGNgzMfPmI+fMR8/Yz5+xnxuW+s1UZIkSQvByB9ALEmSNB+ZREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT18P8BNPsNR2Mx9YgAAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAhj0lEQVR4nO3debwkVXnw8d8DDIvIEmQEBGQAARGVJSMIoqJGEBGIy2sUg0uMQ14lcTfqq1HURGJ8EWKCbxBBSDTikriCCmFVFBg22RERZREYwFEW2Z/3j3Naivbemb41t+t23/v7fj71ud21nnqqbvfT51SdisxEkiRJU7PSTBdAkiRpHJlESZIktWASJUmS1IJJlCRJUgsmUZIkSS2YREmSJLVgEiVprEXEQRFx+EyXYy6LiH0j4oSZLofUNZMoCYiIbSPi1Ij4TURcExEvncKyn4+Ij7Xc7sERsTgi7ouIz08w/TERcWRE3FbLduYE86waEVdExA2Ncc+OiLv6hoyIl9fpq0XEpyLipoj4dd3GvMby/cs+FBGfbkx/Zd3mnRFxeUT8aWPa6+v8zeX3aEzfISLOqvtzQ0R8sDHtmRFxckTcERFLIuIrEbHRMuK3KvAB4J/6xj+2bvekCZbZPSLOrtu/IyJ+GBHPmGwbyxMRx9TYPqkx7vSIuLex/1c1pm0fEZfVY/qOxvh5EXFORGzaogx71DL8bd/4BXV8rxy39B/rKWxjvYj474i4OyJ+EREH9KZl5reA7SLi6VNdrzTOTKI050XEKsA3gG8D6wGLgP+IiK072PxNwMeAYyaZflQt07b179snmOfdwJLmiMw8KzMf2xuAlwB3Ad+ts7wXWAg8Fdga2ImSjPSWby67IfA74CsAEbEx8B/AO4C16/a/GBGPbxThR811ZObpjWlfBM6s+/Nc4M0RsV+d9kd1nxcAmwF3AsdOEhuA/YErM/PGvvEvB+4DXhgRG/ZGRsTalOP86br9jYFD6rxTFhG7A1tOMvngxv5v0xj/ceBdwPbA/2mU7x3A1zLz+hZFeR1wB/DaSaavW4/l04Bdgbe02Ma/AvcDGwCvAT4TEds1pv8n5X9Hmjsy08FhTg+UROIuIBrjvg98dIBlFwEPUL5c7gK+1bIMHwM+3zfuycBvgbWXsdzmwBXA3sANy5jvWODYxvvFwP9qvD8AuH6SZV8HXNuLD7ALcGvfPEuAXevr1wM/WEZZ7gGe0nj/FeB9k8y7E3DnMtZ1DPCBCcafCvw9cAHwrsb4hcDSaTpvVgEuBJ4OJPCkxrTTgb+cZLkrgNXq6x8DO1MSxnOBeS3KsSYl2XxVPQ8XNqYtqGVbpTHuE8BRLbZxP7B1Y9y/A4c23j8L+Pl0xNbBYVwGa6KkiQUluVqmzDwK+ALwiSw1DvsCRMS3I2LpJMO3ByzDzsAvgENq088lvea4hk8D76fUFE28IxFrAq8AjptgH5uvN4mIdSZYxeuA4zOz94yoxcAVEbFfRKxcm/LuA37SWGbHWuarI+KDtbav53DgtbX5ahtKzcgpkxT/OcBlk+0bpWblquaIiNgM2INyXL7Ao2tnrgYeiojjImLviPijvmV3X8ZxW1prnnreDpyZmc39bvp4jcEPm82ZwKXAnhGxCSXJ+RlwBPDuzHxgGfs6mZdREvivAN+jHK8JRcQTgL0oyVtv3CDn6tbAg5l5dWN1FwPNmqgrgAW1tk+aG2Y6i3NwmOkBmEepaXlPfb0n5Vf39wZc/vPAx1awDBPVRL2fUovwYWBVStPXXcC2dfpLgZPq6z2YpCYKOBD4OY+uafsY8ENgPqW57py6rY36lt0MeAjYvG/8G2tZHqTULO3TmLYFpYZsJUqSczmNmiZgN+CaumwCh0xS7qdTmqievYy4/RR4Ud+4DwAX1dcb1/Lv2Ji+bT1mN9QyfBPYYIrHa9O6D+vU9/01UbsAawGrUZKaO4EtGzE9kVJL9mpgP0qtzhMpzcpn0KglHKAspwCH19evptQKzqvvF9SyLa1DAmezjNrNSbbxbODmvnFvAk7v+z9K4InD+D91cBjFwZoozXlZfv3/KbAPcDPwTuDLlC/ZmfQ7SlPhxzLz/sw8AziNUouxJqVZ5m8GWE9/TRKUpq4LgYsoX6pfr9u6pW/ZAylNcz/vjYiIP6nb3oNHkrujI2IHgMy8NjN/npkPZ+YlwEcoNWFExHqU67I+AqxOSUb2iog3NzdaL9I+CXhrZp61jH37NSVZaXotpQaKLNdKnUGjdiYzr8jM12fmJpTaxidQasem4nDgI5n5m4kmZuY5mXlnZt6XmcdREtYX12m/yMwXZ+ZOlKTpo5RrpD4JnEBJqg6rsVqmehH683r7W9e3OuVcblo/M9cFHlPL8r0p7CuUhLm/hmltSnLY0zsOS6e4bmlsmURJQGb+JDOfm5mPy8y9KLUp5w66eP+IiDgp/vAOt97wB3eMTWKiZqLetrai1DKcFRE3A/8FbBQRN0fEgkY5NqUkO8c/aiWZv8vMgzNz48zcArgdOD8zH+7b3mv5w2bAHSjNWItronQepSbrTybZj+SRpsMtgIcy8/jMfDAzbwC+RE0wapk3o9SufDQz/32Sdfb8hNLU1Ft2N0ps3ldjcTOlVuiAvibFXhyupNRKPbUuP9Fdjc3h2XXRFwD/1NgGwI+ad6wtIwZNfwd8NjNvodTaLa6J2Q3AkyaYv9+BlM/xb9VyXEtJoiZs0svM39X9fWZErF/3eZBz9WpglYjYqrG67Xl0U+u2wHWZ+dsByi3NDjNdFebgMAoDpelodcov9XdRmr9WG3DZQ4EvttzuKnW7H6c06axOvQiY0jxyDfDBOt+zKL/8n1zfb9gYXka5029DYOXG+t9PSXj6t7sxpQYmgGcC1wN79s2zG3A3sFbf+OcCtwE71Pc7UpKwPev7vanNY7WslwIfqu/XptRUHED58t8Q+BHwD41y/YzGxeDLid/LgO833v8b5aaAZmw2r3Hbt5bnncAmdf5NKTUzn53icXt83zayxnENYF3KdUer1+P0mhrHrfvW8RTKtUkr1/cnAn9FufvtNmDDOv504MOTlOMqSnNvsyz7Ua5Rexx9F5ZTmhcPBX5Fo3l3wH3+EuUOvDXrufgbYLu+c+3Imf5fdnDocpjxAjg4jMJA6Wfo15Rmi5N49PUtT6zjJ7zWg1LzcVFNDr4+xe1+uH7JNYcPN6ZvV5OMuynXFr10kvXswQTXRAFXAm+cYPxzgOso1zNdBbxmgnn+Dfj3SbZ3MCXBu5NS+/HOxrRPUpoF767TPkLjrjPg+cB59Uv4ZuCzwGPqtA/VGNzVHJYRv3nALykJ4er1GO47wXxHAl+lJGlfBm6s5bux7ueUrhGaYP2/vyaKcp3ZeTU2SymJ0gsnWOY0YJfG++3rMb4NeEdj/M8mWf6ZwL3A/AmmXVaP0YK+eC6lNG8+o8U+rkdp9r27xvyAvumXANsP8//UwWHUht4ty5I0liJiEaXLhLfNdFmmW72D78uZudtMl2VZImJf4MDMfOVMl0XqkkmUJElSC15YLkmS1IJJlCRJUgsmUZIkSS2YREmSJLXwB53PTYf1118/FyxYMIxVS5IkTavzzz//tsycP9XlhpJELViwgMWLFw9j1ZIkSdMqIn7RZjmb8yRJkloYKImKiHUj4qsRcWVEXBERuw67YJIkSaNs0Oa8I4DvZuYrImJVyvPFJEmS5qzlJlERsQ7lOVuvB8jM+4H7h1ssSZKk0TZIc97mwBLg2Ii4MCKOjog1+2eKiEURsTgiFi9ZsmTaCypJkjRKBkmiVgF2Aj6TmTtSnuD93v6ZMvOozFyYmQvnz5/yXYKSJEljZZAk6gbghsw8p77/KiWpkiRJmrOWm0Rl5s3A9RGxTR31AuDyoZZKkiRpxA16d95fA1+od+ZdC7xheEWSJEkafQMlUZl5EbBwuEWRJEkaH/ZYLkmS1IJJlCRJUgsmUZIkSS2YREmSJLVgEiVJktSCSZQkSVILJlGSJEktmERJkiS1YBIlSZLUgkmUJElSCyZRkiRJLZhESZIktWASJUmS1IJJlCRJUgsmUZIkSS2YREmSJLVgEiVJktTCKoPMFBHXAXcCDwEPZubCYRZKkiRp1A2URFXPy8zbhlYSSZKkMWJzniRJUguDJlEJfD8izo+IRRPNEBGLImJxRCxesmTJ9JVQkiRpBA2aRO2emTsBewNviYjn9M+QmUdl5sLMXDh//vxpLaQkSdKoGSiJyswb699bgf8Gdh5moSRJkkbdcpOoiFgzItbqvQb2BC4ddsEkSZJG2SB3520A/HdE9Ob/YmZ+d6ilkiRJGnHLTaIy81pg+w7KIkmSNDbs4kCSJKkFkyhJkqQWTKIkSZJaMImSJElqwSRKkiSpBZMoSZKkFkyiJEmSWjCJkiRJasEkSpIkqQWTKEmSpBZMoiRJklowiZIkSWrBJEqSJKkFkyhJkqQWTKIkSZJaMImSJElqwSRKkiSphYGTqIhYOSIujIhvD7NAkiRJ42AqNVFvBa4YVkEkSZLGyUBJVERsAuwDHD3c4kiSJI2HQWuiDgfeAzw8vKJIkiSNj+UmURHxEuDWzDx/OfMtiojFEbF4yZIl01ZASZKkUTRITdSzgP0i4jrgS8DzI+I/+mfKzKMyc2FmLpw/f/40F1OSJGm0LDeJysz3ZeYmmbkAeBVwamb++dBLJkmSNMLsJ0qSJKmFVaYyc2aeDpw+lJJIkiSNEWuiJEmSWjCJkiRJasEkSpIkqQWTKEmSpBZMoiRJklowiZIkSWrBJEqSJKkFkyhJkqQWTKIkSZJaMImSJElqwSRKkiSpBZMoSZKkFkyiJEmSWjCJkiRJasEkSpIkqQWTKEmSpBZMoiRJklpYbhIVEatHxLkRcXFEXBYRh3RRMEmSpFG2ygDz3Ac8PzPvioh5wA8i4qTM/PGQyyZJkjSylptEZWYCd9W38+qQwyyUJEnSqBvomqiIWDkiLgJuBU7OzHOGWipJkqQRN1ASlZkPZeYOwCbAzhHx1P55ImJRRCyOiMVLliyZ5mJKkiSNlindnZeZS4HTgBdNMO2ozFyYmQvnz58/TcWTJEkaTYPcnTc/Itatr9cAXghcOeRySZIkjbRB7s7bCDguIlamJF1fzsxvD7dYkiRJo22Qu/N+AuzYQVkkSZLGhj2WS5IktWASJUmS1IJJlCRJUgsmUZIkSS2YREmSJLVgEiVJktSCSZQkSVILJlGSJEktmERJkiS1YBIlSZLUgkmUJElSCyZRkiRJLZhESZIktWASJUmS1IJJlCRJUgsmUZIkSS2YREmSJLWw3CQqIjaNiNMi4vKIuCwi3tpFwSRJkkbZKgPM8yDwzsy8ICLWAs6PiJMz8/Ihl02SJGlkLbcmKjN/lZkX1Nd3AlcAGw+7YJIkSaNsStdERcQCYEfgnKGURpIkaUwMnERFxGOBrwFvy8zfTjB9UUQsjojFS5Ysmc4ySpIkjZyBkqiImEdJoL6Qmf810TyZeVRmLszMhfPnz5/OMkqSJI2cQe7OC+BzwBWZedjwiyRJkjT6BqmJehZwIPD8iLioDi8ecrkkSZJG2nK7OMjMHwDRQVkkSZLGhj2WS5IktWASJUmS1IJJlCRJUgsmUZIkSS2YREmSJLVgEiVJktSCSZQkSVILJlGSJEktmERJkiS1YBIlSZLUgkmUJElSCyZRkiRJLZhESZIktWASJUmS1IJJlCRJUgsmUZIkSS2YREmSJLWw3CQqIo6JiFsj4tIuCiRJkjQOBqmJ+jzwoiGXQ5IkaawsN4nKzDOBOzooiyRJ0tjwmihJkqQWpi2JiohFEbE4IhYvWbJkulYrSZI0kqYticrMozJzYWYunD9//nStVpIkaSTZnCdJktTCIF0c/CfwI2CbiLghIt44/GJJkiSNtlWWN0NmvrqLgkiSJI0Tm/MkSZJaMImSJElqwSRKkiSpBZMoSZKkFkyiJEmSWjCJkiRJasEkSpIkqQWTKEmSpBZMoiRJklowiZIkSWrBJEqSJKkFkyhJkqQWTKIkSZJaMImSJElqYZWZLoAkSerGgvd+Z6aL0Mp1h+4z00WYkDVRkiRJLZhESZIktTBQc15EvAg4AlgZODozDx1qqTRSrP7tnjGXpNG33JqoiFgZ+Fdgb+ApwKsj4inDLpgkSdIoG6Qmamfgmsy8FiAivgTsD1w+zIJNxl/okobBzxZJUzXINVEbA9c33t9Qx0mSJM1ZkZnLniHiFcCLMvMv6/sDgV0y8+C++RYBi+rbbYCrpr+4Q7c+cNtMF2KOMebdM+bdM+bdM+bdG+eYb5aZ86e60CDNeTcCmzbeb1LHPUpmHgUcNdUCjJKIWJyZC2e6HHOJMe+eMe+eMe+eMe/eXIz5IM155wFbRcTmEbEq8Crgm8MtliRJ0mhbbk1UZj4YEQcD36N0cXBMZl429JJJkiSNsIH6icrME4ETh1yWUTDWzZFjyph3z5h3z5h3z5h3b87FfLkXlkuSJOkP+dgXSZKkFkyiJEmSWjCJmkUiYrWImFdfx0yXZy6IiJXqX+PdkYhYtT6Oyrh3pH62rFZfG/Mh6sU3ItaIiPn1td/VHYiIx0bEgvp6oPPcAzMLRMTuEXEZ8D/A2wHSi92GJiLWioh3R8RPgH+uo/1fGqKI2CAiPhQRPwS+C/wNeJ4PU0Q8PiI+HhGnAqcCb4+I1Yz5cGVmRsQOwC+Bv53h4sx6EbFeRHw0Ir4DXAi8Dgb/bBno7jyNlvqrJDLzoYhYndJT/PuAM4HvRMS1wNf8sJs+NeYrZeaDlK4+NgKOB14DkJkPzWDxZqXmeU7p8Hcj4G3AL4BTI+LizDx1Bos46/Sd56sB84APAJcAZwOLgVNmroSzT6+WKTMfbozelvKjePMJpmkF9Z3nawHvBfbMzNOmui5/PY+RXvViZj7c+9LOzHspD4m+MDOXAv8X2IPy6B2toL6YP1hfLwU+DhwG3BcROzbn1YqZ6DwHrgHelZnnZeatwLnULxituEnO8+sz812ZeXZm3glcC9w7k+WcTfpi3p8kvQI4Abg3Iv64Ob/am+Q8/wVwWR2IiI2msk6TqBEUxcr97eC1mnfDiNgjIo6IiH0jYh3gB8BT62yXAfcBfrFPwYAxPzwi9q/jl9QPvkuAvers/j9NwRRivl9mLs3Mu+pTE6DUklj7N0VTiXljmTdExAOU56I9oesyj7upfrbUprxrgIuAWyi1UuDny8CmEPOX10mXAj+OiPOBf4mIRYNeh+ZBGQERsW5E7FMTIrJ4KDMfbiZBEfEaSpX6i4E/Ad4A3APcxCP/aEuAm4GNe+vqbk/GR8uYvwB4Yx3f+985A3hOt6UfTysQ8zfV8fMy8/6I2BnYDPiqPxKWbUVjXp0EPK6Oe1nvy14TW4GY/1WdtDVwU2b+HFgKHBQRB3nJwORWIOZ/WScdDhwKPAv4R+BPgZcNsm2viRoNT6FcW3MfcEpEbAP8ObALcFZE/AulGn034K2Z+a2IOAU4GgjgSuBFAJl5R13+pO53Y6xMFvOdgR8sI+bHQKkOrv+c5wDvruP8kFu2FY35A3U97waOzMy7ut6BMbRCMQfIzJvry8sj4gZg84hYyet0JtX28/xztaZ1a+DAiFgEPJbyGX/TDOzHOGl7nh8LkJmLKdf7AZwbEZcDGwxynlsT1ZFavThZvK+jVN8+qb7fg1Kj9G7gbuDvKCfHQuDi+ov8+5Tjty3wdWCHiNizLv/Euvyc1jLm7+GRmN/PH8a8d+dM79fOT4F7IuKwiHhjRGwwrP0ZB0OMea95elfKh+HiiNg/Ig6IiLWGtT/jYNjneWM7KwNbAVfO9QRqSJ/nAWxJuUPsUGBf4BnAeZRmvTl9ecaQzvOHJzjPV6FcU/zTQc5zk6iO1C/cyQ7IEuBXlF8gAMcB5wNvplQ37g6sWufbpfGL/E5g/8y8BzgEeH1E3A78pA5z2jTEfB5wK/DMvpi/GCAinhkRZ1C+WHYEHqBUv89ZQ4z5S+rrv6b84jyaclfqPcDvpnk3xsoQY74XQEQcFBHnUa7RuYZS+zqnDfHz/KWZ+Z3MPDYzr6UkWydSr/+by5dnDPE83xsgIl4X5ZqoC4GrKDevLJfNedNsouq/mj1vAbweeCAzD2lOz8wHIuKXwE4R8URKxnwQ5Xqbv6fcBbYr8FnglbXdN4DbKNWYUGqj/ifLnWNzygAxvz8zP9Kc3hfzzSgfVgdRuoloxvxoSszXroveDmxfX/8SeFtmXjiUHRthHcf8DuDJ9fUxwD9n5o+HsmMjbAZi/vT6+kLg4Mycc8nTDHyeP61uY7XMvC8zfwN8boi7OHJm4Dx/Wn19CfCWqX62WBO1AiJipVrF/Xu9gx8RT43ShxOUA3gE5dfEcX3r6FXP/pJSk7Ex8Fxgncz8HPAgpYr35Zn5DcpJsC+lb4vPUKsv60V0S+s6V56t1b4tY3583zr6Y/4EHon50Uwe87UpMd+ybvemXgJVY/6ocs0WIxDzI6lddmTmKb0PuYnKNVuMWMzP7SVQfrYAw/0836pu977+sk3Tbo6UETnPt67bvaDx2TLweW5N1BRERDSrUyeqWoyI91L6+PgtcEZEHE/p7fcZwFcy87rm/I31/aoOO1BqlV4bEV+jHOivU04EKL9mLgL+mFJN+Yn+MuQsusDZmHdv1GPeK98yqvbHzhjF3PO848+Wyco2jkY95m3Oc5Oo5WhWLTYPfpRn1O0FvJLSrvoJSptrUu7CWAf4KrAu8ClKR3XLivftddgVOAo4mHLH3RmZeXljvtXrttYBvgN8a0X3cdQY8+6NU8yb5Rtnxrx74xTz2WKcYt7qPM9Mh8ZA6QV5EbDxBNM2Bl5SX+8JnAy8HNiujtuLcmHxKZQ7Kj5XT4bHUKp991vOtrcANp9k2sozHRtjPnsGY27MjbkxN+YrPlgTVTWy5fUpF7FeA9wYEc8D1sjMEynXCLw9Iq6iVBGuQrkY7Z66mvMpWfSbsnSU1lz/LcDTIuK0zLyztrcGjzwbjCx3YzSX6XVRnzmLqtF7jHn3jHn3jHn3jHn35mrMZ+XFaoPoBbcR5F7niVdT+uToPZfrOTzyWI+zKdWOT6B0Znk78BbgUxHRqxI8F9g/StfyL4zSf9CGlEez3Az8vlozG88Gi4gnRumJuf/Az4pqdDDmM8GYd8+Yd8+Yd8+YF3OiJir6npIdUS4ei3obaUSsRql+XCczPxYRNwNb1ANxEbB3RDw+M2+NiF9Rbok8OzNfUde3FqUNdlfgf1Nuw/wOpe+KbwB3ZeY3+8q0OrAP8HxgJ8rtrZ+u5Rz7fzRj3j1j3j1j3j1j3j1jPrlZmUT1H/Bs3AEQEY/LzNsj4vGUK/93y8xfR8T9wLr1YF5L6SNlY+BnlNsqn05pp72e8sydEyJiXcozdnagtNmeU0+SjwIf6j+Q8ej+L15I6Vn8/1F6AH6AMTZGMd8UY27MWzLm3RujmPt5PgfP81nZnJeliq+XMa8ZEc+PiCMj4mrg2IjYNTNvpXQVv0dd7GeUJ8NvVV/fT3mkytWU6sd96nxrU9p7NwI2qPP/F3BgXSeZ+UDN0h/VB0bzRMzMb2XmpzLzknH/h4OxivnhxtyYt2XMuzdGMffzfA6e57MuiYqIdaI8T+uLEfEMysH6B8qV+VsDPwL+KiKeBJzGI22111HaWreitOfeBmybmfdTekneISIupVzI9jbgqsz8QWYuysyvZeZv+8uSjfba2cyYd8+Yd8+Yd8+Yd8+YT81YNOdF/L799VEddU0w30rAhylViGdSDupKwJWU7t0B/pPS3rorcDpwIEBmXhMRuwB3ZuYJEXE9sH1ErJ2ZV0fEn/Wy5Am2+agMeTYw5t0z5t0z5t0z5t0z5sMzsklURPRuXXy4d9B7fyNia+C2zLyj76R4DrB7Zj6jsZ7VgMWU9moy87qI2AK4NDPPjdK9+z8Cj6O01d4T5YK16ykXq20BXNQ7+P0HfFwP/ESMefeMefeMefeMefeMeTdGJomqgW3295CU/iKIUm24PuVK/S/VRS4B/qIvq76D2t9ElN5QH85y58B1wKKI+EJmXky5GK2XVb8a2L+u7xuZeWdd/hbKQwy3AC7qnWjjfsCbjHn3jHn3jHn3jHn3jPnMmLEkKvqe1Nwf2ChPtn4L5UK1fYF7KX1EvCwzr4+In0bETpl5QWOx24H7IuJZmfnDup5evxW/AD4Z5Y6C04AL6nYvBi5ubLeXld8AfJ96ovSdaGPJmHfPmHfPmHfPmHfPmI+GzpOoegD2AL5S3/faavcA9qZkyx/MzJsiYn/g8szcKSJ2pLTFPrau6jRgt4i4KB+pFrwxIi4A3lrX9zxKu+7hwI+BlTLzoxOUaaJqz/uBH05/BLpnzLtnzLtnzLtnzLtnzEfL0O/Oi9r+2ZOlXXQR8KqIeA+wdkRsCfw5JZs9ETgsIjYGvgv8qh6gGyhPct6lruocYHtgzYiYFxF71/F/R+lwaz3gMODjwN2UWyy3qGWKZrmymDVVjMa8e8a8e8a8e8a8e8Z8tA09ieoFNiI2i4jdI2InypX/hwBPohyYtwE3AXdRrvRfSOk/4hJgE2ANykMJr6JcqAal+/idKQd6deD5EbF6Zt6fmWdl5jsz88Qs/U08RKlW/GQt06w+4Ma8e8a8e8a8e8a8e8Z8xOWKPa05mOTJyJSDtgbwx8AZlIP5QWBD4F3AJxvzvp/SbvphYD9gtTr+iZQDt2V9/xLgrN42gZcCa06y/ZUoVY8rtI+jNhhzY27Mjbkxnx2DMR//YbpPiHXq37WBzwAHAK8B/rFvvh2B7wELKNdlvRA4s2+e59a/ZwP719ePA7bpHeAJTsaY6YB2fgCNuTGfA4MxN+ZzYTDm4ze0urC8cSHb1sArgFUp1YhbU9pqN6gnwSmULPoNtf30FuDqzPxmlK7c52fmdcDJEfG3EfHPlKrFnYCvU7LvN1Cew0Nm3k65e4Dsq0rMehbMVsa8e8a8e8a8e8a8e8Z89oi2cYuIJwOfB06mHOhbgeOBv6C0u14BbJeZ90bEQsodAc8EXkd5hs6rKc/OeTzw2cw8OSL+jPIQwlMy8/oV2K9ZyZh3z5h3z5h3z5h3z5jPDivSxcGWwDXAccCNmfm7iDgUeAfwbeBrwAYR8cvMXAy/73xrG2AecCSlqnIppQ8KMvOEFSjPXGDMu2fMu2fMu2fMu2fMZ4EVqYlaCziW0iPpSpRbIA+jdBt/CHBCZv5NRKxBqa78ICXTPgH4l8mqDqOvAzE9wph3z5h3z5h3z5h3z5jPDq2TqEetpFRL/gXlqc1HAkcAG2XmiyMiKJ1/PZCZSydYdmVK1/K2x06BMe+eMe+eMe+eMe+eMR9frZvz6oF9AvA0SuddOwJvzsy7IuJcYL2IWDlL/xJLGsusVMcB0HytZTPm3TPm3TPm3TPm3TPms0PrzjZr1rsp8CbgQeA9mfnTiNgKOAi4IDMfqgf998t4wNsz5t0z5t0z5t0z5t0z5rPDtDTnPWqF5e6A7YAjstxOqSEz5t0z5t0z5t0z5t0z5uNlhZOoXvUiJUn2YrYOGPPuGfPuGfPuGfPuGfPxNu01UZIkSXPB0B9ALEmSNBuZREmSJLVgEiVJktSCSZQkSVILJlGSJEktmERJkiS18P8B/+9LhSrveYYAAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAh1UlEQVR4nO3debgkVX3/8feHGTZZg4zIoo4QcSUCjiCCxl1RlLjEuAFxyWjURDRu+T1xi3FLFJcoGuIexZXEBZdEIqKIiMMiyCIiGQEBGdBRFmX9/v44daGnuTP3Ts1032Xer+ep53ZXVVef+lZ19/eec+pUqgpJkiStnY1mugCSJElzkUmUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZLmjSSbJjknyY4zXZYNWZJjkhw40+WQRs0kShukJC9NsizJ9Uk+PsnyRyY5L8l1SY5PcrdpbndxkkqysEeZdkzylSSXdttYPMk6j0pyWpJrk1yS5OmTrHNo9/oXDMz7RpJrBqYbkpw1sPzBSU5JcnWSM5McMLTNv0nyf0l+18XtgIFlL09yYbfs0iTvHt7/JC/rXn9tknOT7D6wbFGSo5P8Nslvknx6YNnOSb6c5Nfd/r5oijAuBb5bVZcNvf8bu5jsOzR/kyTv6rZ9TZLlSd4zxXtMKskzun27NsnPkzxkknVe35XjUQPzXpXkyiRnJ9ljYP7+Sb7UsywfT3LTcDLZxeHGgfPg3CRP7fkea/qMvAP4pz7bleaUqnJy2uAm4CnAnwEfBD4+tGx74LfAnwObAf8CnDzN7S4GCljYo0w7AC8G9uu2sXho+X2AK4ADgYXAHYHdhtb5I+A84CfAC9bwXt8BXt893g64qtvfBcBzgN8Af9Qt3xe4FngAEOCvgRXAgm75bsC2A9v6NvCKgfd6AXBmV/506283sPx7wBHANsDGwF4Dy44H3tPNvz/wa+Dha9ivs4H9h+YFuLDbxw8MLXsDcAKwU7feYuDQHsfu0cAvgAfR/jndGdh5aJ3dgLOAS4FHdfN27I7X1sBLgWO7+QuBk4fPgWmWZQvg6m5/XzW07I3ApwaePxb4PbDDWr7HlJ8R4GfAklF9hp2cZsM04wVwcprJifbf8seH5i0FThp4vkX3Q3OvaWzvIloCdE037dejTAuZPIk6GnjzFK/9EC0R+w6rSaK6ROHmie0DBwFnD61zPvD87vFfAKcMxaOAHSfZ9h2B44Aju+cbARcDj1xNWR4DLKdLyIaWbdm9z6KBeUcB/7Gabd21O04Lh+Y/tJv/7C6x2GRg2bHA4evhPDppIl5rWOebwOO7/Z1IovYFPtM9vhdwTvf4lcD/61mWQ7uYvwz4ydCyVZKobt4VwIPX8j2m/IwA/w68YV1j6+Q0myeb86Tbuy/w44knVXUt8PNu/lQe2v3dtqq2rKofJDkgyco1TAescYu3eRBAkrOSXJbkU0m2m1iYZB9gCS2RWpNDge9V1fKBeRlaJ8D9usffABYk2TfJAuB5wBnA5QPv/awkvwOupNUY/Vu3aJduul+Si7smvTclmfjueRDwU+ATSa5K8qMkfzpUpsGyDZZr2B7AhVV109D8w4CvAp/vnj9xYNnJwCuSvDjJHklWiUOSY9dw3I7t1llAi/uiJBd0TYPvT7L5wHb+HLi+qr4+VLYLgD2SbAs8Cjg7yV2AZwDvXM1+TuUw4DPAZ4F7JXnAZCuleQKwCXBON++uU5yrz+pePp3PyLm0c0Gat0yipNvbktZUMei3wFZ9NlZVJ1bVtmuYTpzmpnYBDgGeCtwD2Bz4V7j1h/xI4KVVdcsU2zkU+PjA8x8AOyV5ZpKNkxxGa3q6Q7f8auAY4ETgeloT2NKquvXGm1V1dFVtDexOS+J+NVBmaDVOewAPB54JPH9g+WNozXZ3Bt4FfDnJ9lV1NfB94HVJNkuyd7fvE+Uatm1X1lsluQOtyenoqroR+GK3/xPeRuu/82xgGfDLbv8n9uugNRy3g7rVdqA1Nz4NeAiwJ7AX8A9dGbYC3kqrGVpFVV0FvIXWBPoEWg3Ue4HXAE9OckLXJ2yX4ddOJsldaTE+uqp+Bfzv0P4CPD3JSlpN6VeAt1bVyq48F01xrh7dbWM6n5GracdEmrdMoqTbu4bWR2XQ1gz9QM+A3wMfq6rzq+oa2g/z47tlLwbOrKqT17SBrtbrzrRkArj1h/xg4BW05OdxtCa5S7pVng88l1bLsAmtz9SxSXYa3n5V/YzWL+nIgTID/HNVrexqv/5toNy/B5ZX1Ueq6saq+iytKWr/bvmzgbt38z4IfGqgXMN+w+0T3ScDNwETNUCfBg5Msqgr781V9YGq2p/2g/8W4KNJ7r2a95jMxD7+a1VdVlVX0vp4TezjG2lNkMsne3FVfaaq9q6qA2m1bNcDp9Nqop4IfIHp10odApxbVWd0zz8NPCvJxgPrfL5LiLagJcuHJnnhNLc/YTqfka2AlWu5XWlOMYmSbu9sBpohkkz82Jw9jdfW8IwkD8mqV8YNT7e7ims1zhza/uDjR9JqLi5PcjnwYOBdSd4/tI3DgP/skrDbNlR1QlU9sKq2o/0Q3ws4pVu8J63D8/lVdUtVfRO4rHuPySykxQtaU90Nayj38D6tsryqftHVBi2qqn1pHZpPYXJnAnfPqlcGHkarNbmoi8sXaLVGzxp+cVX9vqo+QEvG7gOTXtU4OH2je91vaIndmo7N3w4cm7sAn0/ymsH375r/3gr8Ha2m8eKq+h3wI+BPVrPPww4Fdh14ryNoMXv8ZCt3id036Jo4u+a8NZ2rz+5eOp3PyL0ZaPKT5qWZ7pTl5DQTE+2HfjNac85/dI8XdssW0ZomntrNfwfTvzrvDrRO27v3LNdm3NZx+57AZgPLngf8H7Br9z6fp+tkTatFufPAdBKtZmmbgddv3u3XIyZ5371oycXWtKvhvj+w7DBaR/NdaX2SHg1cR9eJmHb13Z26x/eh/ZAeMfD6T9I6cG9Fa747j9s6rW9HS1oOo10Z+DTaFXjbd8vv3b1uogbsSgY6mk+yH2fSdZKmXSF3M625cDA2bwdO7dY5HHhYF5uFXTmuB3Zdy+P2j7Rk5060KyS/R3cRAK2z/eD7X0xrYtxyaBtvAV7ePd6R1gl+B+BF3HbV3mImueigW7YfrdZtj6H3+zRwTLfOG1n16rxdaFcMvmMt93fKz0h3zuwz0591J6dRTjNeACenmZi6H5Mamt44sPxR3Y/972lXui0eWPYh4ENr2PY/0oYAWAk8aC3LNVymGlr+pm7bK2jJ3x+tZjvfYejqPFpfpF8AmWT9z3Q/ir8FPkeXFHXL0u3TRbTmmnOBQwaWf4zWDHgt7cqzf2HV5G9rWifnq7sE4vWDZaD1IzqL1kS0DHjIwLLDu329ltYna42XzAMvAT7YPX4tXbI0tM5OwI20prOlwKndfq+k1XId1ON82pjWhLmS1uH+fYMxGFp3Od3VeQPz7kVLwhYMzHsVLWk8B9hjIFbLgY0n2e6H6JKlofn70BLD7Wjn/Y3cdvXoZd3r7tBjn9f0GXkgcNqoP8dOTjM9pep2rQ+SNCcl2ZTWn+iRNTTg5nyQ5B+AFVX1b1OuPIOSHAN8pG5/NaI0r5hESZIk9WDHckmSpB5MoiRJknowiZIkSerBJEqSJKmHhVOvsva23377Wrx48Sg2LUmStF6deuqpV1bVorV93UiSqMWLF7Ns2bJRbFqSJGm9SvKLPq+zOU+SJKmHaSVRSbZN8sUk5yU5N8l+oy6YJEnSbDbd5rz3At+sqqcl2YR23y5JkqQN1pRJVJJtgIcCfwlQVTfQ7souSZK0wZpOc97daTcA/ViS05N8OMkWwyslWZpkWZJlK1asWO8FlSRJmk2mk0QtBPam3Rl9L9rd1F87vFJVHVVVS6pqyaJFa32VoCRJ0pwynSTqEuCSqvph9/yLtKRKkiRpgzVlElVVlwMXJ7lnN+uRwDkjLZUkSdIsN92r8/4G+HR3Zd6FwHNHVyRJkqTZb1pJVFWdASwZbVEkSZLmDkcslyRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSeph4XRWSrIcuBq4GbipqpaMslCSJEmz3bSSqM7Dq+rKkZVEkiRpDrE5T5IkqYfpJlEF/E+SU5MsnWyFJEuTLEuybMWKFeuvhJIkSbPQdJOoA6pqb+BA4CVJHjq8QlUdVVVLqmrJokWL1mshJUmSZptpJVFV9cvu7xXAfwH7jLJQkiRJs92USVSSLZJsNfEYeAzwk1EXTJIkaTabztV5OwD/lWRi/aOr6psjLZUkSdIsN2USVVUXAvcfQ1kkSZLmDIc4kCRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSeph2klUkgVJTk9y7CgLJEmSNBesTU3Uy4BzR1UQSZKkuWRaSVSSXYAnAB8ebXEkSZLmhunWRL0HeDVwy+iKIkmSNHdMmUQlOQi4oqpOnWK9pUmWJVm2YsWK9VZASZKk2Wg6NVH7A09Kshz4LPCIJJ8aXqmqjqqqJVW1ZNGiReu5mJIkSbPLlElUVf19Ve1SVYuBZwDfrqrnjLxkkiRJs5jjREmSJPWwcG1WrqrvAN8ZSUkkSZLmEGuiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknqYMolKslmSU5L8OMnZSd40joJJkiTNZgunsc71wCOq6pokGwMnJvlGVZ084rJJkiTNWlMmUVVVwDXd0427qUZZKEmSpNluWn2ikixIcgZwBfCtqvrhSEslSZI0y00riaqqm6tqT2AXYJ8k9xteJ8nSJMuSLFuxYsV6LqYkSdLsslZX51XVSuB44HGTLDuqqpZU1ZJFixatp+JJkiTNTtO5Om9Rkm27x5sDjwbOG3G5JEmSZrXpXJ23I/CJJAtoSdfnq+rY0RZLkiRpdpvO1XlnAnuNoSySJElzhiOWS5Ik9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPUwZRKV5C5Jjk9yTpKzk7xsHAWTJEmazRZOY52bgL+rqtOSbAWcmuRbVXXOiMsmSZI0a01ZE1VVl1XVad3jq4FzgZ1HXTBJkqTZbK36RCVZDOwF/HAkpZEkSZojpp1EJdkSOAY4vKp+N8nypUmWJVm2YsWK9VlGSZKkWWdaSVSSjWkJ1Ker6j8nW6eqjqqqJVW1ZNGiReuzjJIkSbPOdK7OC/AR4NyqOmL0RZIkSZr9plMTtT9wCPCIJGd00+NHXC5JkqRZbcohDqrqRCBjKIskSdKc4YjlkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST1MmUQl+WiSK5L8ZBwFkiRJmgumUxP1ceBxIy6HJEnSnDJlElVV3wV+PYaySJIkzRn2iZIkSephvSVRSZYmWZZk2YoVK9bXZiVJkmal9ZZEVdVRVbWkqpYsWrRofW1WkiRpVrI5T5IkqYfpDHHwGeAHwD2TXJLk+aMvliRJ0uy2cKoVquqZ4yiIJEnSXGJzniRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPUx52xdJ47f4tV+b6SL0svztT5jpIkjS2FgTJUmS1INJlCRJUg8mUZIkST3YJ0qSNCPs+zd+xnz9siZKkiSpB5MoSZKkHqbVnJfkccB7gQXAh6vq7SMtlWYVq38lSbq9KWuikiwAPgAcCNwHeGaS+4y6YJIkSbPZdGqi9gEuqKoLAZJ8FjgYOGeUBZOkcbLGVdLamk6fqJ2BiweeX9LNkyRJ2mClqta8QvI04HFV9YLu+SHAvlX10qH1lgJLu6f3BH66/os7ctsDV850ITYwxnz8jPn4GfPxM+bjN5djfreqWrS2L5pOc94vgbsMPN+lm7eKqjoKOGptCzCbJFlWVUtmuhwbEmM+fsZ8/Iz5+Bnz8dsQYz6d5rwfAfdIcvckmwDPAL4y2mJJkiTNblPWRFXVTUleCvw3bYiDj1bV2SMvmSRJ0iw2rXGiqurrwNdHXJbZYE43R85Rxnz8jPn4GfPxM+bjt8HFfMqO5ZIkSbo9b/siSZLUg0mUJElSDyZR80iSTZNs3D3OTJdnQ5Bko+6v8R6TJJt0t6My7mPSfbds2j025iM0Ed8kmydZ1D32t3oMkmyZZHH3eFrnuQdmHkhyQJKzgf8FXg5QdnYbmSRbJXlVkjOB93Wz/SyNUJIdkrwhyfeBbwJ/C57no5TkTkneluTbwLeBlyfZ1JiPVlVVkj2Bi4DXzHBx5r0k2yV5c5KvAacDh8H0v1umdXWeZpfuv5JU1c1JNqONFP/3wHeBryW5EDjGL7v1p4v5RlV1E22ojx2BTwLPBqiqm2ewePPS4HlOG/B3R+Bw4BfAt5P8uKq+PYNFnHeGzvNNgY2BfwDOAk4ClgHHzVwJ55+JWqaqumVg9r1p/xTffZJlWkdD5/lWwGuBx1TV8Wu7Lf97nkMmqher6paJH+2q+gPtJtGnV9VK4F3Aw2i33tE6Gor5Td3jlcDbgCOA65PsNbiu1s1k5zlwAfDKqvpRVV0BnEL3A6N1t5rz/OKqemVVnVRVVwMXAn+YyXLOJ0MxH06SngZ8DvhDkgcMrq/+VnOe/wI4u5tIsuPabNMkahZKs2C4Hbyr5r1zkocleW+SJybZBjgRuF+32tnA9YA/7GthmjF/T5KDu/krui++s4DHdqv7eVoLaxHzJ1XVyqq6prtrArRaEmv/1tLaxHzgNc9NciPtvmg7jbvMc93afrd0TXkXAGcAv6LVSoHfL9O2FjF/arfoJ8DJSU4F3p9k6XT7oXlQZoEk2yZ5QpcQUc3NVXXLYBKU5Nm0KvXHA48CngtcB1zKbR+0FcDlwM4T2xrfnswdPWP+SOD53fyJz84JwEPHW/q5aR1i/lfd/I2r6oYk+wB3A77oPwlrtq4x73wDuGM37ykTP/aa3DrE/EXdot2BS6vq/4CVwAuTvNAuA6u3DjF/QbfoPcDbgf2BdwB/BjxlOu9tn6jZ4T60vjXXA8cluSfwHGBf4HtJ3k+rRn8w8LKq+mqS44APAwHOAx4HUFW/7l7/jfHvxpyyupjvA5y4hph/FFp1cPfh/CHwqm6eX3Jrtq4xv7HbzquAI6vqmnHvwBy0TjEHqKrLu4fnJLkEuHuSjeyns1p9v88/0tW07g4ckmQpsCXtO/7SGdiPuaTvef4xgKpaRuvvB3BKknOAHaZznlsTNSZd9eLq4r2cVn37x93zh9FqlF4FXAu8nnZyLAF+3P1H/j+043dv4EvAnkke073+rt3rN2g9Y/5qbov5Ddw+5hNXzkz8t/Mz4LokRyR5fpIdRrU/c8EIYz7RPL0f7ctwWZKDkzwryVaj2p+5YNTn+cD7LADuAZy3oSdQI/o+D7Ab7QqxtwNPBB4I/IjWrLdBd88Y0Xl+yyTn+UJan+KfTec8N4kak+4Hd3UHZAVwGe0/EIBPAKcCL6ZVNx4AbNKtt+/Af+RXAwdX1XXAm4C/THIVcGY3bdDWQ8w3Bq4AHjQU88cDJHlQkhNoPyx7ATfSqt83WCOM+UHd47+h/cf5YdpVqdcBv1/PuzGnjDDmjwVI8sIkP6L10bmAVvu6QRvh9/mTq+prVfWxqrqQlmx9na7/34bcPWOE5/mBAEkOS+sTdTrwU9rFK1OyOW89m6z6r8uedwX+Erixqt40uLyqbkxyEbB3krvSMuYX0vrbvIV2Fdh+wL8DT+/afQNcSavGhFYb9b/VrhzboEwj5jdU1T8OLh+K+d1oX1YvpA0TMRjzD9NivnX30quA+3ePLwIOr6rTR7Jjs9iYY/5r4F7d448C76uqk0eyY7PYDMT8T7rHpwMvraoNLnmage/zPbr32LSqrq+q3wIfGeEuzjozcJ7v0T0+C3jJ2n63WBO1DpJs1FVx32ri4Ce5X9oYTtAO4Htp/018YmgbE9WzF9FqMnYG/hTYpqo+AtxEq+J9alV9mXYSPJE2tsUH6aovu050K7ttLpiv1b49Y/7JoW0Mx3wnbov5h1l9zLemxXy37n0vnUigupivUq75YhbE/Ei6ITuq6riJL7nJyjVfzLKYnzKRQPndAoz2+/we3fteP1y29bSbs8osOc937973tIHvlmmf59ZErYUkGaxOnaxqMclraWN8/A44IcknaaP9PhD4QlUtH1x/YHuXddOetFqlQ5McQzvQX6KdCND+mzkDeACtmvKfh8tQ86iDszEfv9ke84nyraFqf86ZQzH3PB/zd8vqyjYXzfaY9znPTaKmMFi1OHjw0+5R91jg6bR21X+mtbkW7SqMbYAvAtsC76YNVLemeF/VTfsBRwEvpV1xd0JVnTOw3mbde20DfA346rru42xjzMdvLsV8sHxzmTEfv7kU8/liLsW813leVU4DE20U5KXAzpMs2xk4qHv8GOBbwFOB+3bzHkvrWHwc7YqKj3Qnwx1o1b5PmuK9dwXuvpplC2Y6NsZ8/kzG3Jgbc2NuzNd9siaqM5Atb0/rxHoB8MskDwc2r6qv0/oIvDzJT2lVhAtpndGu6zZzKi2L/qtqA6UNbv9XwB5Jjq+qq7v21nDbvcGodjXG4GsmhqivmkfV6BOM+fgZ8/Ez5uNnzMdvQ435vOysNh0TwR0I8sTgiefTxuSYuC/XQ7ntth4n0aodd6INZnkV8BLg3UkmqgRPAQ5OG1r+0WnjB92ZdmuWy4FbqzVr4N5gSe6aNhLz8IGfF9XoYMxngjEfP2M+fsZ8/Ix5s0HURGXoLtlJ6zyW7jLSJJvSqh+3qap/SnI5sGt3IM4ADkxyp6q6IslltEsiT6qqp3Xb24rWBrsf8Ne0yzC/Rhu74svANVX1laEybQY8AXgEsDft8tZ/7co55z9oxnz8jPn4GfPxM+bjZ8xXb14mUcMHvAauAEhyx6q6KsmdaD3/H1xVv0lyA7BtdzAvpI2RsjPwc9pllX9Ca6e9mHbPnc8l2ZZ2j509aW22P+xOkjcDbxg+kFl1/ItH00YW/xBtBOAbmcPmUMzvgjE35j0Z8/GbQzH3+3wDPM/nZXNetSq+iYx5iySPSHJkkvOBjyXZr6quoA0V/7DuZT+n3Rn+Ht3jG2i3VDmfVv34hG69rWntvTsCO3Tr/ydwSLdNqurGLktfZQyMwROxqr5aVe+uqrPm+gcO5lTM32PMjXlfxnz85lDM/T7fAM/zeZdEJdkm7X5aRyd5IO1gvZXWM3934AfAi5L8MXA8t7XVLqe1td6D1p57JXDvqrqBNkrynkl+QuvIdjjw06o6saqWVtUxVfW74bLUQHvtfGbMx8+Yj58xHz9jPn7GfO3Miea85Nb211UG6ppkvY2AN9KqEL9LO6gbAefRhncH+AytvXU/4DvAIQBVdUGSfYGrq+pzSS4G7p9k66o6P8lfTGTJk7znKhnyfGDMx8+Yj58xHz9jPn7GfHRmbRKVZOLSxVsmDvrE3yS7A1dW1a+HToqHAgdU1QMHtrMpsIzWXk1VLU+yK/CTqjolbXj3dwB3pLXVXpfWYe1iWme1XYEzJg7+8AGfqwd+MsZ8/Iz5+Bnz8TPm42fMx2PWJFFdYAfHeyjaeBGkVRtuT+up/9nuJWcBzxvKqn9NN95E2miot1S7cmA5sDTJp6vqx7TOaBNZ9TOBg7vtfbmqru5e/yvaTQx3Bc6YONHm+gEfZMzHz5iPnzEfP2M+fsZ8ZsxYEpWhOzUPBzbtztYvoXVUeyLwB9oYEU+pqouT/CzJ3lV12sDLrgKuT7J/VX2/287EuBW/AN6ZdkXB8cBp3fv+GPjxwPtOZOWXAP9Dd6IMnWhzkjEfP2M+fsZ8/Iz5+Bnz2WHsSVR3AB4GfKF7PtFW+zDgQFq2/LqqujTJwcA5VbV3kr1obbFbdps6HnhwkjPqtmrBXyY5DXhZt72H09p13wOcDGxUVW+epEyTVXveAHx//Udg/Iz5+Bnz8TPm42fMx8+Yzy4jvzovXfvnhGrtokuBZyR5NbB1kt2A59Cy2a8DRyTZGfgmcFl3gC6h3cl5325TPwTuD2yRZOMkB3bzX08bcGs74AjgbcC1tEssd+3KlMFyVTNvqhiN+fgZ8/Ez5uNnzMfPmM9uI0+iJgKb5G5JDkiyN63n/5uAP6YdmMOBS4FraD39l9DGjzgL2AXYnHZTwp/SOqpBGz5+H9qB3gx4RJLNquqGqvpeVf1dVX292ngTN9OqFd/ZlWleH3BjPn7GfPyM+fgZ8/Ez5rNcrdvdmsNq7oxMO2ibAw8ATqAdzNcBdwZeCbxzYN3/R2s3fSPwJGDTbv5daQdut+75QcD3Jt4TeDKwxWrefyNa1eM67eNsm4y5MTfmxtyYz4/JmM/9aX2fENt0f7cGPgg8C3g28I6h9fYC/htYTOuX9Wjgu0Pr/Gn39yTg4O7xHYF7ThzgSU7GzHRAx34Ajbkx3wAmY27MN4TJmM+9qVfH8oGObLsDTwM2oVUj7k5rq92hOwmOo2XRz+3aT38FnF9VX0kbyn1RVS0HvpXkNUneR6ta3Bv4Ei37fi7tPjxU1VW0qweooarE6s6C+cqYj58xHz9jPn7GfPyM+fyRvnFLci/g48C3aAf6CuCTwPNo7a7nAvetqj8kWUK7IuBBwGG0e+g8k3bvnDsB/15V30ryF7SbEB5XVRevw37NS8Z8/Iz5+Bnz8TPm42fM54d1GeJgN+AC4BPAL6vq90neDrwCOBY4BtghyUVVtQxuHXzrnsDGwJG0qsqVtDEoqKrPrUN5NgTGfPyM+fgZ8/Ez5uNnzOeBdamJ2gr4GG1E0o1ol0AeQRs2/k3A56rqb5NsTquufB0t0/4c8P7VVR1maAAx3caYj58xHz9jPn7GfPyM+fzQO4laZSOtWvJ5tLs2Hwm8F9ixqh6fJLTBv26sqpWTvHYBbWh522PXgjEfP2M+fsZ8/Iz5+Bnzuat3c153YHcC9qAN3rUX8OKquibJKcB2SRZUG19ixcBrNurmATD4WGtmzMfPmI+fMR8/Yz5+xnx+6D3YZpf13gX4K+Am4NVV9bMk9wBeCJxWVTd3B/3W13jA+zPm42fMx8+Yj58xHz9jPj+sl+a8VTbYrg64L/DeapdTasSM+fgZ8/Ez5uNnzMfPmM8t65xETVQv0pJkO7ONgTEfP2M+fsZ8/Iz5+BnzuW2910RJkiRtCEZ+A2JJkqT5yCRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqYf/D6giMMvkzNqDAAAAAElFTkSuQmCC\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAh/klEQVR4nO3debgkVX3/8feHYVW2CCOyqIiKCyiLI4gr7iIqUYk74hJH474H80Qj0cTlZ9xiTH6IG7+oQcUVxAVFCa4MmwiIEoKAbCOIggvr9/fHqStNOzO3b810T98779fz9HP7dlWfOvWtut3fe86pU6kqJEmSNDfrre0KSJIkzUcmUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJmleSbJTkrCTbru26qJ8kL0vyjrVdD2l1mURpwUry0iTLklyb5GNDyzZM8tkk5yepJPvOsexKcpcedZp1u0n2THJCkmuSXJbkFStY5yHd+9868Np/dO+ZeVyb5OqB5fdI8q0kv0lybpInDpX5lCRnJ7m6S1L+cmDZc5LcOFT+vt2y2yb5VJKLu7K/m2TvobJfluR/k/y2OyYPHFj25iTXD5W90yrCuBQ4oaouGdrGm7uYDG97wyT/kuSiruzzk7x3FeWv0KrOp275w5P8NMnvkxyf5I4DyzZK8pFu/y9N8uqh994qyQeT/KqL4QkDy56R5JKu3g8deP3OSb6XZFGPfVlZrIaP83lJ/mau5XdlHZbknCQ3JXnO0OIPAc9Mcts+ZUvTwiRKC9nFwFuBj6xk+YnAs4BLJ1ajWbabZGvgq8D/BbYC7gJ8fWidDYD3AT8cfL2qXlRVm848gE8Bn+nesz7wReBo4Da0ROQ/k+zcLd8e+E/g1cDmwOuATw59yX1/sPyq+nb3+qbAScB9urI/DhyTZNOu7L2BtwMHAlsAHwY+P/Tlf+RQ2eetIn4vAv7fUEwCPBu4svs56A3AEmAvYDNgX+CUVZS/Mis9n7rj9jngjbQYLAOOHFjlzcBdgTsCDwVen+QxA8sP6953j+7nq7py16fFbk/gpcC/Drzn/cCrqurGuezELLGCgeMMPBl4Z5I95rKNzunAi1lBrKvqj8CxK9m+NG+YRGnBqqrPVdUXgCtWsOy6qnpvVZ0IzPVLaKaV4PTuv/WnzqFOs2331cDXquoTVXVtVV1dVWcPrfMaWmL101XU8da0L8CPdy/dHdgOeE9V3VhV3wK+CxzULd8BuKqqjq3mGOB3wJ1H2KfzqurdVXVJV/ZhwIbA3bpVdgTOrKqTq90i4Qhga2DOrRBJ7gDsxFACCTwI2BZ4OfC0JBsOLLsv8Pmqurjbt/Or6oi5bntV5xPwJNo+fqZLEN4M7Jbk7t3yg4G3VNWvu+P5IeA53T7dHXgCsLSqlncxPLl731bAL7tWt+O6fSfJgd3rw3EYxapiNbzPpwJn05K7Oamqf6uqbwJ/XMkq3wb2n2u50jQxiZLmqKoe3D3drfuP/cgkd0hy1Soezxix+PsBV3bdNJcn+XKXOADQdRE9D/jHWcp5MrAcOGEV6wTYtXu+DDg7yROSLOq68q4Ffjyw/h5dd9PPkryxayX580KT3WlJ1LndS8cCi5Ls3bU+PQ84jVu2xD0+yZVJzpyl++hewHlVdcPQ6wcDXwY+PVPewLIfAK9O8uIk9+paYgbre/QqjtvRq6jLoF1oLS8AVNXvgP8BdknyF7Sk5fSB9U/v3gOthewXwKFdfM9I8uRu2XJgqyQ7AI8EzkyyGfD3tBa2PlYVq1tIcl9gZ9r5MfPaqs7zQ+ZQj7OB3XrUX5oaK/wQlDQ3VXUBsOUaKGoHWtfNI4EzgHfSuuUe0C1/P/DGqrpmKBcYdjBwRN18c8xzgMuB1yV5D61L6SHA8V39b0xyBPBJYGPgOuCvumQAWjK2K+3LfhdaV9UNwNsGN5pkc1pX26FV9Zvu5auBo2jdmAGuAvYbqNunad1ZlwF7A0cluaqqPrWC/dqyK29wm7cC/gp4dlVdn+SztG6io7pV3gb8Gngm8B7giiRvqKqPd/v+uJWHcWSb0hKeQb+hdR9uOvD78DJox3zXrr7bAfvQukPPqqqzu6Tys7Sk9gXAobRuvXsneRPtWL2mqn4yWyVHiBXA/ZJcBSzq6v4B4OczC6tqy9m2M6Krad270rxlS5Q0Xf5A63o6qesWOhS4f5Itkjwe2KyqjlxVAV3L1b60bjMAqup64C9p3SeX0roEPw1c1L3nEbSEbV9aK9JDgMO7VqWZLrv/raqbquoMWkvYgUPb3YTWwvGDqhpMrp4PPJeWfG1IGw92dJLturLP6rrabqyq79HGe92i7AG/5ubkY8YTaQndV7rfPwHsl2RxV/6NXdfSA2hJ2D8BH0ky5y6qVbiGNpZs0Oa0ROGagd+Hl0E75tcDb+26e79DS24f1dX/m1V1v6p6CFC08V0fox3f5wBvAQ4fsZ6rjFXnB1W1ZVVtBtyOdtz+ecTy52IzbplYSvOOSZS0BnTdedes4vHMEYv6Me2Lcsbg84cDS9Ku7roUeCrwyiRfHCrjIOC7w4Ozq+rHVfWQqtqqqh5NG1/zo27x7rQr3pZ1idJJtHFHj1hJPYvWqjSz/xsBX6AlZS8cWnd34Oiq+llX9leBS4D7j1L2kB8DdxrqSjyY1mJyQReXzwAbAH/WhVpVf6iqf6MlY/fs6n7sKo7bsSupx7AzGeia6sak3Zk2TurX3f4Odl3t1r1nZp/+rKrDL3TdkB+gjWXaGlhUVb+gDeq/94j1HDlWAFV1Ga2V6k9dfrOc5383Yj2gjbM6fda1pClmEqUFK8n6STamdUssSrLx4Jdv2mXnG3e/btgtX2Uf2YDL6Ab5QuvOG7q6bPjxiRG3+1HgiUl2T7sK743AiV3X2Btp41N27x5fog1Qfu5Q3Z5Na6kYjse9u23dKslraeN0ZtY7CXjQTMtT2tVYD6L7gk+yX5Jtuud37+ryxe73DWjdTX8ADq6qm4Y2fRKwf5Kd0jyy24+fdO8/IMlfdMv2oiUJw4nhTJwvoo212qt77/a05PJxA3HZDXhHFweSvDLJvkk26c6Jg2mtIKd2Ze63iuO230D8VnU+fR7YNcmTu3XeBPy4qmYG/x8B/H23n3endcvNxP4E4ALgDd02HkDrbv3a0O7/NXBKVZ1GG9y+SZJ7duv+KWHOyqfOmDVWK3jPVrTWq5mEj1nO838eeO+GXSwCbNDFa/A75yG08XLS/FVVPnwsyAftCqkaerx5YPn5K1i+Y7fs74BjV1H2i2itC1cBT5ljvVa63W753wC/pLWWfBm4/UrK+RitC2jwtX1oV9VttoL1/09X5jW0L6+7DC1/KS1BuZr2pfyagWXvoiWOv+uW/SOwQbdsppvp913ZM48HdcvTrX9BV/bZwEEDZX+KlhRcQ7vi8OWzxO8lwL93zw8BTl7BOtvRush2pU3ncDKt6+gqWuvb48ZwPj2iq/8faFeeDR7TjWhTI/y2i+Orh8reBfh+F9+zgCcOLd+alnRuPvDaM2lds+cDD+1eu323ja1WUP9RYvUc2lWjM8fw8u743LZHvL69gnjt2y3bmNZquc0kPxN8+FjTj1T9WauxJE2truvwVODhNTTh5rouybOAXaqq75V7E5HkZbR/Dl6/tusirQ6TKEmSpB4cEyVJktSDSZQkSVIPJlGSJEk9mERJkiT1MJbbvmy99da14447jqNoSZKkNerkk0/+VVUtnn3NWxpLErXjjjuybNmy2VeUJElay5L8os/77M6TJEnqYaQkKsmWST6b5KdJzk6yz7grJkmSNM1G7c57H/DVqjowyYbArcZYJ0mSpKk3axKVZAvgwbR7KlFV1wHXjbdakiRJ022U7rw7AcuBjyY5NcnhSW49vFKSpUmWJVm2fPnyNV5RSZKkaTJKErU+sCftrul70O4yfsjwSlV1WFUtqaolixfP+SpBSZKkeWWUJOoi4KKq+mH3+2dpSZUkSdI6a9YkqqouBS5McrfupYcDZ421VpIkSVNu1KvzXgZ8orsy7zzgueOrkiRJ0vQbKYmqqtOAJeOtiiRJ0vzhjOWSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPaw/ykpJzgeuBm4EbqiqJeOslCRJ0rQbKYnqPLSqfjW2mkiSJM0jdudJkiT1MGoSVcDXk5ycZOmKVkiyNMmyJMuWL1++5mooSZI0hUZNoh5YVXsC+wEvSfLg4RWq6rCqWlJVSxYvXrxGKylJkjRtRkqiquqX3c/Lgc8De42zUpIkSdNu1iQqya2TbDbzHHgU8JNxV0ySJGmajXJ13jbA55PMrP/JqvrqWGslSZI05WZNoqrqPGC3CdRFkiRp3nCKA0mSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeRk6ikixKcmqSo8dZIUmSpPlgLi1RrwDOHldFJEmS5pORkqgkOwD7A4ePtzqSJEnzw6gtUe8FXg/cNL6qSJIkzR+zJlFJHgdcXlUnz7Le0iTLkixbvnz5GqugJEnSNBqlJeoBwBOSnA/8F/CwJP85vFJVHVZVS6pqyeLFi9dwNSVJkqbLrElUVb2hqnaoqh2BpwHfqqpnjb1mkiRJU8x5oiRJknpYfy4rV9W3gW+PpSaSJEnziC1RkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSD3O6AfE02PGQY9Z2FXo5/+37r+0qaB7xPJek6WdLlCRJUg8mUZIkST2YREmSJPVgEiVJktTDrElUko2T/CjJ6UnOTHLoJComSZI0zUa5Ou9a4GFVdU2SDYATkxxbVT8Yc90kSZKm1qxJVFUVcE336wbdo8ZZKUmSpGk30pioJIuSnAZcDnyjqn441lpJkiRNuZGSqKq6sap2B3YA9kqy6/A6SZYmWZZk2fLly9dwNSVJkqbLnK7Oq6qrgOOBx6xg2WFVtaSqlixevHgNVU+SJGk6jXJ13uIkW3bPNwEeCfx0zPWSJEmaaqNcnbct8PEki2hJ16er6ujxVkuSJGm6jXJ13o+BPSZQF0mSpHnDGcslSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSepg1iUpy+yTHJzkryZlJXjGJikmSJE2z9UdY5wbgNVV1SpLNgJOTfKOqzhpz3SRJkqbWrC1RVXVJVZ3SPb8aOBvYftwVkyRJmmZzGhOVZEdgD+CHY6mNJEnSPDFyEpVkU+Ao4JVV9dsVLF+aZFmSZcuXL1+TdZQkSZo6IyVRSTagJVCfqKrPrWidqjqsqpZU1ZLFixevyTpKkiRNnVGuzgvwYeDsqnr3+KskSZI0/UZpiXoAcBDwsCSndY/HjrlekiRJU23WKQ6q6kQgE6iLJEnSvOGM5ZIkST2YREmSJPVgEiVJktTDKLd9kaQFb8dDjlnbVejl/Lfvv7arIK2zbImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHb/uiWXk7DEnj4GeL5jtboiRJknowiZIkSeph1iQqyUeSXJ7kJ5OokCRJ0nwwSkvUx4DHjLkekiRJ88qsSVRVnQBcOYG6SJIkzRuOiZIkSephjSVRSZYmWZZk2fLly9dUsZIkSVNpjSVRVXVYVS2pqiWLFy9eU8VKkiRNJbvzJEmSehhlioNPAd8H7pbkoiTPH3+1JEmSptust32pqqdPoiKSJEnziffOkyRpHeH9Ctcsx0RJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPYyURCV5TJJzkpyb5JBxV0qSJGnazZpEJVkE/BuwH3BP4OlJ7jnuikmSJE2zUVqi9gLOrarzquo64L+AA8ZbLUmSpOk2ShK1PXDhwO8Xda9JkiSts1JVq14hORB4TFX9dff7QcDeVfXSofWWAku7X+8GnLPmqzt2WwO/WtuVWMcY88kz5pNnzCfPmE/efI75Hatq8VzftP4I6/wSuP3A7zt0r91CVR0GHDbXCkyTJMuqasnarse6xJhPnjGfPGM+ecZ88tbFmI/SnXcScNckd0qyIfA04EvjrZYkSdJ0m7UlqqpuSPJS4GvAIuAjVXXm2GsmSZI0xUbpzqOqvgJ8Zcx1mQbzujtynjLmk2fMJ8+YT54xn7x1LuazDiyXJEnSn/O2L5IkST2YREmSJPVgErWAJNkoyQbd86zt+qwLkqzX/TTeE5Jkw+52VMZ9QrrPlo2658Z8jGbim2STJIu7535XT0CSTZPs2D0f6Tz3wCwASR6Y5Ezgm8CrAMrBbmOTZLMkr0vyY+D93cv+LY1Rkm2S/EOS7wJfBV4OnufjlOS2Sd6W5FvAt4BXJdnImI9XVVWS3YELgL9dy9VZ8JLcJslbkhwDnAocDKN/tox0dZ6mS/dfSarqxiQb02aKfwNwAnBMkvOAo/ywW3O6mK9XVTfQpvrYFjgCeCZAVd24Fqu3IA2e57QJf7cFXgn8AvhWktOr6ltrsYoLztB5vhGwAfD3wBnA94BlwHFrr4YLz0wrU1XdNPDyPWj/FN9pBcu0mobO882AQ4BHVdXxcy3L/57nkZnmxaq6aeZLu6r+SLtJ9KlVdRXwL8C+tFvvaDUNxfyG7vlVwNuAdwPXJtljcF2tnhWd58C5wGur6qSquhz4Ed0XjFbfSs7zC6vqtVX1vaq6GjgP+OParOdCMhTz4STpQOBI4I9J7jO4vvpbyXn+C+DM7kGSbedSpknUFEqzaLgfvGvmvV2SfZO8L8njk2wBnAjs2q12JnAt4Bf7HIwY8/cmOaB7fXn3wXcG8Ohudf+e5mAOMX9CVV1VVdd0d02A1kpi698czSXmA+95bpLrafdF227SdZ7v5vrZ0nXlnQucBlxGa5UCP19GNoeYP7lb9BPgB0lOBj6QZOmo49A8KFMgyZZJ9u8SIqq5sapuGkyCkjyT1qT+WOARwHOB3wMXc/Mf2nLgUmD7mbImtyfzR8+YPxx4fvf6zN/Od4AHT7b289NqxPwF3esbVNV1SfYC7gh81n8SVm11Y945Ftiqe+1JM1/2WrHViPmLukU7AxdX1f8CVwEvTPJChwys3GrE/K+7Re8F3g48AHgH8JfAk0bZtmOipsM9aWNrrgWOS3I34FnA3sB/J/kArRn9/sArqurLSY4DDgcC/BR4DEBVXdm9/9jJ78a8srKY7wWcuIqYfwRac3D3x/lD4HXda37Irdrqxvz6rpzXAR+sqmsmvQPz0GrFHKCqLu2enpXkIuBOSdZznM5K9f08/3DX0rozcFCSpcCmtM/4i9fCfswnfc/zjwJU1TLaeD+AHyU5C9hmlPPclqgJ6ZoXVxbv82nNt3fpft+X1qL0OuB3wJtoJ8cS4PTuP/Kv047fPYAvALsneVT3/jt071+n9Yz567k55tfx5zGfuXJm5r+dnwO/T/LuJM9Pss249mc+GGPMZ7qn96F9GC5LckCSZyTZbFz7Mx+M+zwf2M4i4K7AT9f1BGpMn+cB7ky7QuztwOOB+wIn0br11unhGWM6z29awXm+Pm1M8c9HOc9Noiak+8Jd2QFZDlxC+w8E4OPAycCLac2NDwQ27Nbbe+A/8quBA6rq98ChwHOSXAH8uHus09ZAzDcALgfuNxTzxwIkuV+S79C+WPYArqc1v6+zxhjzx3XPX0b7j/Nw2lWpvwf+sIZ3Y14ZY8wfDZDkhUlOoo3ROZfW+rpOG+Pn+ROr6piq+mhVnUdLtr5CN/5vXR6eMcbzfD+AJAenjYk6FTiHdvHKrOzOW8NW1PzXZc87Ac8Brq+qQweXV9X1SS4A9kxyB1rG/ELaeJt/ol0Ftg/wIeApXb9vgF/RmjGhtUZ9s9qVY+uUEWJ+XVX94+DyoZjfkfZh9ULaNBGDMT+cFvPNu7deAezWPb8AeGVVnTqWHZtiE475lcDdu+cfAd5fVT8Yy45NsbUQ83t3z08FXlpV61zytBY+z+/VbWOjqrq2qn4DfHiMuzh11sJ5fq/u+RnAS+b62WJL1GpIsl7XxP0nMwc/ya5pczhBO4Dvo/038fGhMmaaZy+gtWRsDzwE2KKqPgzcQGvifXJVfZF2EjyeNrfFv9M1X3aD6K7qyly0UJt9e8b8iKEyhmO+HTfH/HBWHvPNaTG/c7fdi2cSqC7mt6jXQjEFMf8g3ZQdVXXczIfciuq1UExZzH80k0D52QKM9/P8rt12rx2u2xrazakyJef5zt12Txn4bBn5PLclag6SZLA5dUVNi0kOoc3x8VvgO0mOoM32e1/gM1V1/uD6A+Vd0j12p7UqPTvJUbQD/QXaiQDtv5nTgPvQminfOVyHWkADnI355E17zGfqt4qm/XlnHsXc83zCny0rq9t8NO0x73Oem0TNYrBpcfDgp92j7tHAU2j9qu+k9bkW7SqMLYDPAlsC76FNVLeqeF/RPfYBDgNeSrvi7jtVddbAeht329oCOAb48uru47Qx5pM3n2I+WL/5zJhP3nyK+UIxn2Le6zyvKh8DD9osyEuB7VewbHvgcd3zRwHfAJ4M7NK99mjawOLjaFdUfLg7GW5Fa/Z9wizb3gm400qWLVrbsTHmC+dhzI25MTfmxnz1H7ZEdQay5a1pg1jPBX6Z5KHAJlX1FdoYgVclOYfWRLg+bTDa77tiTqZl0S+oNlHaYPmXAfdKcnxVXd31t4ab7w1GtasxBt8zM0V91QJqRp9hzCfPmE+eMZ88Yz5562rMF+RgtVHMBHcgyDOTJ/6MNifHzH25HszNt/X4Hq3ZcTvaZJZXAC8B3pNkpknwR8ABaVPLPzJt/qDb0W7Ncinwp2bNGrg3WJI7pM3EPHzgF0QzOhjztcGYT54xnzxjPnnGvFknWqIydJfspA0eS3cZaZKNaM2PW1TVW5NcCuzUHYjTgP2S3LaqLk9yCe2SyO9V1YFdeZvR+mD3Af6GdhnmMbS5K74IXFNVXxqq08bA/sDDgD1pl7f+a1fPef+HZswnz5hPnjGfPGM+ecZ85RZkEjV8wGvgCoAkW1XVFUluSxv5f/+q+nWS64Atu4N5Hm2OlO2B/6FdVnlvWj/thbR77hyZZEvaPXZ2p/XZ/rA7Sd4C/MPwgcwt5794JG1m8f+gzQB8PfPYPIr57THmxrwnYz558yjmfp6vg+f5guzOq9bEN5Mx3zrJw5J8MMnPgI8m2aeqLqdNFb9v97b/od0Z/q7d8+tot1T5Ga35cf9uvc1p/b3bAtt0638OOKgrk6q6vsvSbzEHxuCJWFVfrqr3VNUZ8/0PDuZVzN9rzI15X8Z88uZRzP08XwfP8wWXRCXZIu1+Wp9Mcl/awfpn2sj8nYHvAy9KchfgeG7uqz2f1td6V1p/7q+Ae1TVdbRZkndP8hPaQLZXAudU1YlVtbSqjqqq3w7XpQb6axcyYz55xnzyjPnkGfPJM+ZzMy+685I/9b/eYqKuFay3HvBmWhPiCbSDuh7wU9r07gCfovW37gN8GzgIoKrOTbI3cHVVHZnkQmC3JJtX1c+SPHUmS17BNm+RIS8ExnzyjPnkGfPJM+aTZ8zHZ2qTqCQzly7eNHPQZ34m2Rn4VVVdOXRSPBh4YFXdd6CcjYBltP5qqur8JDsBP6mqH6VN7/4OYCtaX+3v0wasXUgbrLYTcNrMwR8+4PP1wK+IMZ88Yz55xnzyjPnkGfPJmJokqgvs4HwPRZsvgrRmw61pI/X/q3vLGcDzhrLqK+nmm0ibDfWmalcOnA8sTfKJqjqdNhhtJqt+OnBAV94Xq+rq7v2X0W5iuBNw2syJNt8P+CBjPnnGfPKM+eQZ88kz5mvHWkuiMnSn5uHApt3Z+iW0gWqPB/5ImyPiSVV1YZKfJ9mzqk4ZeNsVwLVJHlBV3+3KmZm34hfAu9KuKDgeOKXb7unA6QPbncnKLwK+TneiDJ1o85IxnzxjPnnGfPKM+eQZ8+kw8SSqOwD7Ap/pfp/pq90X2I+WLb+xqi5OcgBwVlXtmWQPWl/spl1RxwP3T3Ja3dws+MskpwCv6Mp7KK1f973AD4D1quotK6jTipo9rwO+u+YjMHnGfPKM+eQZ88kz5pNnzKfL2K/OS9f/OaNav+hS4GlJXg9snuTOwLNo2exXgHcn2R74KnBJd4Auot3Jee+uqB8CuwG3TrJBkv26199Em3DrNsC7gbcBv6NdYrlTV6cM1quaBdPEaMwnz5hPnjGfPGM+ecZ8uo09iZoJbJI7Jnlgkj1pI/8PBe5COzCvBC4GrqGN9F9Cmz/iDGAHYBPaTQnPoQ1UgzZ9/F60A70x8LAkG1fVdVX131X1mqr6SrX5Jm6kNSu+q6vTgj7gxnzyjPnkGfPJM+aTZ8ynXK3e3ZrDSu6MTDtomwD3Ab5DO5hvBG4HvBZ418C6f0frN30z8ARgo+71O9AO3J273x8H/PfMNoEnArdeyfbXozU9rtY+TtvDmBtzY27MjfnCeBjz+f9Y0yfEFt3PzYF/B54BPBN4x9B6ewBfA3akjct6JHDC0DoP6X5+Dzige74VcLeZA7yCkzFrO6ATP4DG3JivAw9jbszXhYcxn3+PXgPLBway7QwcCGxIa0bcmdZXu013EhxHy6Kf2/WfXgb8rKq+lDaV++KqOh/4RpK/TfJ+WtPinsAXaNn3c2n34aGqrqBdPUANNSVWdxYsVMZ88oz55BnzyTPmk2fMF470jVuSuwMfA75BO9CXA0cAz6P1u54N7FJVf0yyhHZFwP2Ag2n30Hk67d45twU+VFXfSPJU2k0Ij6uqC1djvxYkYz55xnzyjPnkGfPJM+YLw+pMcXBn4Fzg48Avq+oPSd4OvBo4GjgK2CbJBVW1DP40+dbdgA2AD9KaKq+izUFBVR25GvVZFxjzyTPmk2fMJ8+YT54xXwBWpyVqM+CjtBlJ16NdAvlu2rTxhwJHVtXLk2xCa658Iy3TPhL4wMqaDjM0gZhuZswnz5hPnjGfPGM+ecZ8YeidRN2ikNYs+TzaXZs/CLwP2LaqHpsktMm/rq+qq1bw3kW0qeXtj50DYz55xnzyjPnkGfPJM+bzV+/uvO7AbgfcizZ51x7Ai6vqmiQ/Am6TZFG1+SWWD7xnve41AAafa9WM+eQZ88kz5pNnzCfPmC8MvSfb7LLe2wMvAG4AXl9VP09yV+CFwClVdWN30P/0Hg94f8Z88oz55BnzyTPmk2fMF4Y10p13iwLb1QG7AO+rdjmlxsyYT54xnzxjPnnGfPKM+fyy2knUTPMiLUl2MNsEGPPJM+aTZ8wnz5hPnjGf39Z4S5QkSdK6YOw3IJYkSVqITKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSevj/qdMLq8AScJcAAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAhyUlEQVR4nO3deZhkZXn38e+PAQFlcxkQQTYVYhRZHBdcAI2KiIoLr7uCRgejGE1cQnK9JhpNNHmNUWPQEBc0ihI1ioq4oCiKCgyLoiCKiIIIDCAKElnv94/nNBRl93TPma6a6p7v57rONdV1Tp266z5nqu9+nuc8J1WFJEmSVs96azsASZKkhcgiSpIkqQeLKEmSpB4soiRJknqwiJIkSerBIkqSJKkHiyhJC0qSk5PssbbjUD9JtkpybpIN13Ys0pqyiNKilOSwJCuSXJ/kqKF1D03ylSRXJVmZ5BNJtl6NfVeSe/eI6Q5JPpnkwm4f+06zzZ5JTkpybZLLkrxymm326V7/5oHn3tu9Zmq5Psk1A+vvm+RrSX6T5PwkTx3a5zO6X2zXJDknyVMG1h2S5Oah/e/brdsyyceSXNLt++QkDxna99IkR3frf53kowPr7pLkmCRXJrkiyUeTbLaKHD4JuKaqzhx6/pAuJ8+c5jV/k+RnXdwXJzlmpv2v4n2fkeTbSa5L8vWhdTsnObY7l65K8qUkuwysn+3YrOpcvWeS73b7/ZehdccnWdbjs+yY5JYk75lmXSX5XRfnFd2x3aLHe8yYr6q6DDgRWL66+5UmjUWUFqtLgDcDH5hm3Z2BI4EdgO2Ba4APjimubwHPAy4dXpHkbsAXgf8A7grcG/jy0DYbAO8EThl8vqpeWlWbTC3Ax4BPdK9ZHzgW+DxwF9ovr48k2blbvw3wEeAvgc2A1wJHJ9ly4C2+M7j/qvp69/wmwGnAA7t9fwg4LskmA6/9n+7zbgdsCbxtYN2bacdjR+BewFbAG2bIHcBLgf+a5vmDgauAFww+meRg4PnAY7q8LAO+uor9z+Qq4B3AW6dZtwXwWWAXWvyn0vINrPrYdFZ1rv41Lac7Ak+ZKpq6YvFnVbWix2d5AfBr4JkztAbt1sW5E+3YvKHHe6wqXwAfBQ7tsV9pslSVi8uiXWi/nI6aZZs9aa0bc9nfSUABvwOuBZ7ZM66LgX2HnvtH4L9med3hwD8DRwFvnmGbO9EKw326n+/fxZqBbb4MvKl7/BDg8qF9rAT26h4fAnxrNT7bb4EHdo8fB1wILJlh2+OBlw38/HLgSzNsewfgf4Fth57fHrgFeDpwE3D3gXXvBt4xj+fTi4Gvz7LNXbpz5K6zHZvZztUuP7t0jz8OPINW6J4JbNEj/gA/Bf4MuAw4aGh9Afce+PllwJfnO1/A+sB1wPbzdWxcXNbGYkuUBHsDP5zLhlW1d/dwt2otC8ck2S7J1atYnjPHOB4KXNV1g1ye5HNJtptamWR74EXA38+yn6fTiqCTVrFNaMUVwArg3CRPTrKk68q7Hvj+wPZ7dN07P07y+q516w93muxOK3bOH/hM5wEf6rrsTkuyz8BL/h14YpI7J7lzF/vxM8R8H+CWqrp46PkXACuq6lPAucBzB9Z9F3hBktcmWZZkyVC8R6ziuA1+/tWxN3BpVV05zbq5HJtBPwAe23WpPZB2nr6JVhhe3SO2RwDb0gqy/6a14E2rOx5PoeVw6rl5yVdV3UQ7R3br8RmkiWERpXVakgcAf0vrwuqlqn5RVVusYjl6jrvalvZL7ZW0rq+f0bp+prwLeH1VXTvLfg4GPlxVUzfGPA+4HHhtkg2SPA7YB7hjF//NwIeBo2nF09HAoVX1u+71J9EKri1pRcCzmSZf3Vim/wLeWFW/GfhMj6ONgbk78C/AsV3XJcAZtKLrym65GThihs+1Ba0VZ9gLupjp/r21S6+qPgK8AtgP+AZweZK/Glj/slUctwfMEMeMkmxLKwz/coZNho/NbN4CPLKL/Qharh4AfC5tnNlJSQ5bjRAPBo6vql/TcvX4oW5bgDOSXA1cQTsP/2NqxTzn6xraMZUWLIsorbPSBocfD7yyqr65tuOhdVV9uqpOq6rfA28EHpZk825A9aZVtcpB0V3L1b60ogiAqrqR1qJwAG1s0qtprRAXd695DK2LcF/aL+l9gPd1rUpU1QVV9bOquqWqzqa1hB009L4bA58DvltVbxn6TBdW1fur6saq+jhwEfDwbv1/Az8GNqV1U/2UNj5rOr/utht834fTxgt9vHvqaGDXqdi7+D9aVY+h/cJ+KfCmJPvN8B69JVlK6yY9oqo+Ns36Pzg2s6mqq6rqmVW1G20s3L/RisLDaa1UjwFemuS+c4hvY+D/0MYjUVXfAX4BDLeU7llVWwAbAe8Bvplko7nGvBo2Ba4ewX6lsbGI0jqp6xo7gTYuaLqByquzr+2Grr4aXp47+16A1n022EIx+PhPgGVJLk1yKfBM4FVJjuX2ng+cXFUXDD5ZVd+vqn2q6q5VtR9t0PCp3erdgZOqakVXKJ1GG7j+mBniLFp34NTn3xD4DK0oGx4sPPyZhj/X7sB/VNXvuha29wJPmOF9z29vl20Gnju4i+WsLi+nDDx/+zdtRdwnupju38U+fOXc4DKnLt5uP3emFVCfrap/mGGzaY/NalhOK1J/AOxK68K8ATi7+3k2T6UVqkcMnEfbMEOXXld8v49WpM53vtanXTjxvbm+RppEFlFalJKs3/31vARYkmSjqXE83S/hrwHvrqr39tj9ZbQiBLi1O2+TVSyDl/RvOPBX/R26uKYKkg8CT02ye9pVeK+nDej+Tfd4Z1rRsTvtarD/BF44FNsLaIPOh/PxgO697pjkNcDWA9udBjxyqvUmbQ6mR9KNiUqyf5Ktusd/1MVybPfzBsAnaS1OB1fVLUNv/WngzkkO7sZbHUTr4jt54L1fnGTjrqVkObcfi3WrrmA4gdZSRpfHZ3Sv2X1geQXwnO4cOCTJAUk2TbJekv2B+9EVWzV05dzQcr+B/C3p3m99YL0ulxt06zYDvkQrkA6fLvbOTMdmxnN1YJstaYPu39A99TPgUWlXQS4DLui2OypD0yQMOJh2BeCuA7l6OLBbkj8owtLGj72QdmwvmK98dR5Ma6H8+QyxSgvDXEafu7gstIX2y6aGljd06/6u+/nawWXgtX9DGzcy075fCvyK1hXxjNWM68Jp4tphYP2fAb+kdV19DrjnDPs5iqGr84C9aFcNbjrN9v+v2+e1tC7Mew+tP4zW0nMN7RfmqwfWvY1WOP6uW/f3wAbdun26z3DdUD4fOfD6R9JaS66lDWIfXLdj9zmvpF0W/0XgPqvI3wFTxwZ4VnccNhjaZuNuf08EnkYr2H5Nu2rwbOCQHufTIdMct6O6dQdz+ys2p5bt5nhsZjxXB7b5MPB/Bn6+J60Q/DXw9oHnvwq8ZJr32IZ25eKu06z7AvC27vHg5/gtrcjdbz7z1a3/d+DPx/Fd4OIyyiVVcx3fKElrX5KTgcNqaMLNdV2SO9C6xx5QrStuInWtat8A9qg29k9asCyiJEmSenBMlCRJUg8WUZIkST1YREmSJPVgESVJktTDtPe/WlN3u9vdaocddhjFriVJi8TZv/zN7BtNoF232Xxth6B5dvrpp19RVUtX93UjKaJ22GEHVqxYMYpdS5IWiR0OP25th9DLircesLZD0DxL0mviV7vzJEmSephTEZVkiySfTPKjJOcm2WvUgUmSJE2yuXbnvRP4YlUd1M2Ke8cRxiRJkjTxZi2ikmwO7E27FxLVbgJ6w2jDkiRJmmxz6c7bEVgJfDDJmUnel+ROwxslWZ5kRZIVK1eunPdAJUmSJslciqj1gT2B91TVHrQ7fB8+vFFVHVlVy6pq2dKlq32VoCRJ0oIylyLqYuDiqjql+/mTtKJKkiRpnTVrEVVVlwIXJdmle+pPgHNGGpUkSdKEm+vVea8APtpdmXcB8MLRhSRJkjT55lREVdVZwLLRhiJJkrRwOGO5JElSDxZRkiRJPVhESZIk9WARJUmS1INFlCRJUg8WUZIkST1YREmSJPVgESVJktSDRZQkSVIPFlGSJEk9WERJkiT1YBElSZLUg0WUJElSDxZRkiRJPVhESZIk9WARJUmS1INFlCRJUg/rz2WjJBcC1wA3AzdV1bJRBiVJkjTp5lREdR5VVVeMLBJJkqQFxO48SZKkHuZaRBXw5SSnJ1k+3QZJlidZkWTFypUr5y9CSZKkCTTXIuoRVbUnsD/w8iR7D29QVUdW1bKqWrZ06dJ5DVKSJGnSzKmIqqpfdv9eDnwaePAog5IkSZp0sxZRSe6UZNOpx8DjgB+MOjBJkqRJNper87YCPp1kavujq+qLI41KkiRpws1aRFXVBcBuY4hFkiRpwXCKA0mSpB4soiRJknqwiJIkSerBIkqSJKkHiyhJkqQeLKIkSZJ6sIiSJEnqwSJKkiSpB4soSZKkHiyiJEmSerCIkiRJ6sEiSpIkqQeLKEmSpB4soiRJknqwiJIkSerBIkqSJKkHiyhJkqQe5lxEJVmS5Mwknx9lQJIkSQvB6rREvRI4d1SBSJIkLSRzKqKSbAscALxvtOFIkiQtDHNtiXoH8DrgltGFIkmStHDMWkQleSJweVWdPst2y5OsSLJi5cqV8xagJEnSJJpLS9TDgScnuRD4OPDoJB8Z3qiqjqyqZVW1bOnSpfMcpiRJ0mSZtYiqqr+uqm2ragfgWcDXqup5I49MkiRpgjlPlCRJUg/rr87GVfV14OsjiUSSJGkBsSVKkiSpB4soSZKkHiyiJEmSerCIkiRJ6sEiSpIkqQeLKEmSpB4soiRJknqwiJIkSerBIkqSJKkHiyhJkqQeLKIkSZJ6sIiSJEnqwSJKkiSpB4soSZKkHiyiJEmSerCIkiRJ6sEiSpIkqYdZi6gkGyU5Ncn3kvwwyRvHEZgkSdIkW38O21wPPLqqrk2yAfCtJMdX1XdHHJskSdLEmrWIqqoCru1+3KBbapRBSZIkTbo5jYlKsiTJWcDlwFeq6pSRRiVJkjTh5lREVdXNVbU7sC3w4CT3H94myfIkK5KsWLly5TyHKUmSNFlW6+q8qroaOBF4/DTrjqyqZVW1bOnSpfMUniRJ0mSay9V5S5Ns0T3eGHgs8KMRxyVJkjTR5nJ13tbAh5IsoRVd/11Vnx9tWJIkSZNtLlfnfR/YYwyxSJIkLRjOWC5JktSDRZQkSVIPFlGSJEk9WERJkiT1YBElSZLUg0WUJElSDxZRkiRJPVhESZIk9WARJUmS1INFlCRJUg8WUZIkST1YREmSJPVgESVJktSDRZQkSVIPFlGSJEk9WERJkiT1YBElSZLUw6xFVJJ7JjkxyTlJfpjkleMITJIkaZKtP4dtbgJeXVVnJNkUOD3JV6rqnBHHJkmSNLFmbYmqql9V1Rnd42uAc4FtRh2YJEnSJFutMVFJdgD2AE4ZSTSSJEkLxJyLqCSbAJ8CXlVVv51m/fIkK5KsWLly5XzGKEmSNHHmVEQl2YBWQH20qv5num2q6siqWlZVy5YuXTqfMUqSJE2cuVydF+D9wLlV9fbRhyRJkjT55tIS9XDg+cCjk5zVLU8YcVySJEkTbdYpDqrqW0DGEIskSdKC4YzlkiRJPVhESZIk9WARJUmS1MNcbvsyUXY4/Li1HUIvF771gLUdgiRJmke2REmSJPVgESVJktSDRZQkSVIPFlGSJEk9WERJkiT1YBElSZLUg0WUJElSDxZRkiRJPVhESZIk9WARJUmS1INFlCRJUg8WUZIkST1YREmSJPUwaxGV5ANJLk/yg3EEJEmStBDMpSXqKODxI45DkiRpQZm1iKqqk4CrxhCLJEnSguGYKEmSpB7mrYhKsjzJiiQrVq5cOV+7lSRJmkjzVkRV1ZFVtayqli1dunS+ditJkjSR7M6TJEnqYS5THHwM+A6wS5KLk/zp6MOSJEmabOvPtkFVPXscgUiSpNHa4fDj1nYIvVz41gPWdgjTsjtPkiSph1lboiSNn38tStLksyVKkiSpB4soSZKkHiyiJEmSerCIkiRJ6sEiSpIkqQeLKEmSpB4soiRJknqwiJIkSerByTY1Kyd+lCTpD9kSJUmS1INFlCRJUg8WUZIkST1YREmSJPVgESVJktSDRZQkSVIPcyqikjw+yXlJzk9y+KiDkiRJmnSzFlFJlgD/DuwP/DHw7CR/POrAJEmSJtlcWqIeDJxfVRdU1Q3Ax4EDRxuWJEnSZJtLEbUNcNHAzxd3z0mSJK2zUlWr3iA5CHh8Vb24+/n5wEOq6rCh7ZYDy7sfdwHOm/9wR+5uwBVrO4h1jDkfP3M+fuZ8/Mz5+C3knG9fVUtX90VzuXfeL4F7Dvy8bffc7VTVkcCRqxvAJEmyoqqWre041iXmfPzM+fiZ8/Ez5+O3LuZ8Lt15pwH3SbJjkjsAzwI+O9qwJEmSJtusLVFVdVOSw4AvAUuAD1TVD0cemSRJ0gSbS3ceVfUF4AsjjmUSLOjuyAXKnI+fOR8/cz5+5nz81rmczzqwXJIkSX/I275IkiT1YBElSZLUg0XUIpJkwyQbdI+ztuNZFyRZr/vXfI9Jkjt0t6My72PSfbds2D025yM0ld8kGydZ2j32d/UYJNkkyQ7d4zmd5x6YRSDJI5L8EPgq8BcA5WC3kUmyaZLXJvk+8K7uaf8vjVCSrZL8XZKTgS8Cfw6e56OUZMskb0nyNeBrwF8k2dCcj1ZVVZLdgV8Af7WWw1n0ktwlyZuSHAecCRwMc/9umdPVeZos3V8lqaqbk2xEmyn+r4GTgOOSXAB8yi+7+dPlfL2quok21cfWwIeB5wJU1c1rMbxFafA8p034uzXwKuDnwNeSfK+qvrYWQ1x0hs7zDYENgP8LnA18G1gBnLD2Ilx8plqZquqWgafvS/ujeMdp1mkNDZ3nmwKHA4+rqhNXd1/+9byATDUvVtUtU7+0q+r3tJtEn1lVVwP/AuxLu/WO1tBQzm/qHl8NvAV4O3B9kj0Gt9Wame48B84HXlNVp1XV5cCpdL9gtOZmOM8vqqrXVNW3q+oa4ALg92szzsVkKOfDRdJBwDHA75M8cHB79TfDef5z4IfdQpKtV2efFlETKM2S4X7wrpn37kn2TfLOJE9KsjnwLeD+3WY/BK4H/MW+GuaY83ckObB7fmX3xXc2sF+3uf+fVsNq5PzJVXV1VV3b3TUBWiuJrX+raXVyPvCaFya5kXZftHuMO+aFbnW/W7quvPOBs4DLaK1S4PfLnK1Gzp/erfoB8N0kpwPvTrJ8ruPQPCgTIMkWSQ7oCiKqubmqbhksgpI8l9ak/gTgMcALgeuAS7jtP9pK4FJgm6l9je+TLBw9c/4nwJ92z0/93/kGsPd4o1+Y1iDnL+me36CqbkjyYGB74JP+kbBqa5rzzvHAXbvnnjb1y17TW4Ocv7RbtTNwSVX9DLgaODTJoQ4ZmNka5PzF3ap3AG8FHg78E/AU4GlzeW/HRE2GP6aNrbkeOCHJLsDzgIcA30zybloz+sOAV1bV55KcALwPCPAj4PEAVXVV9/rjx/8xFpSZcv5g4FuryPkHoDUHd/85TwFe2z3nl9yqrWnOb+z281rgiKq6dtwfYAFao5wDVNWl3cNzklwM7JhkPcfpzKjv9/n7u5bWnYHnJ1kObEL7jr9kLXyOhaTvef5BgKpaQRvvB3BqknOAreZyntsSNSZd8+JM+b6Q1nx77+7nfWktSq8Ffgf8Le3kWAZ8r/uL/Mu043df4DPA7kke171+u+7167SeOX8dt+X8Bv4w51NXzkz9tfMT4Lokb0/yp0m2GtXnWQhGmPOp7um9aF+GK5IcmOQ5STYd1edZCEZ9ng+8zxLgPsCP1vUCakTf5wHuRbtC7K3Ak4AHAafRuvXW6eEZIzrPb5nmPF+fNqb4J3M5zy2ixqT7hTvTAVkJ/Ir2FwjAh4DTgZfRmhsfAdyh2+4hA3+RXwMcWFXXAW8EDklyJfD9blmnzUPONwAuBx46lPMnACR5aJJv0H6x7AHcSGt+X2eNMOdP7B6/gvYX5/toV6VeB/zvPH+MBWWEOd8PIMmhSU6jjdE5n9b6uk4b4ff5U6vquKr6YFVdQCu2vkA3/m9dHp4xwvN8f4AkB6eNiToTOI928cqs7M6bZ9M1/3XV807AIcCNVfXGwfVVdWOSXwB7JtmOVjEfShtv8w+0q8D2Av4TeEbX7xvgClozJrTWqK9Wu3JsnTKHnN9QVX8/uH4o59vTvqwOpU0TMZjz99Fyvln30iuB3brHvwBeVVVnjuSDTbAx5/wq4I+6xx8A3lVV3x3JB5tgayHnD+genwkcVlXrXPG0Fr7Pd+3eY8Oqur6qfgO8f4QfceKshfN81+7x2cDLV/e7xZaoNZBkva6J+1ZTBz/J/dPmcIJ2AN9J+2viQ0P7mGqe/QWtJWMbYB9g86p6P3ATrYn36VV1LO0keBJtbov30DVfdoPoru72uWSxNvv2zPmHh/YxnPN7cFvO38fMOd+MlvN7de97yVQB1eX8dnEtFhOQ8yPopuyoqhOmvuSmi2uxmLCcnzpVQPndAoz2+/w+3ftePxzbPH3MiTIh5/nO3fueMfDdMufz3Jao1ZAkg82p0zUtJjmcNsfHb4FvJPkwbbbfBwGfqKoLB7cf2N+vumV3WqvSC5J8inagP0M7EaD9NXMW8EBaM+U/D8dQi2iAszkfv0nP+VR8q2jaX3AWUM49z8f83TJTbAvRpOe8z3luETWLwabFwYOfdo+6/YBn0PpV/5nW51q0qzA2Bz4JbAH8K22iulXl+8pu2Qs4EjiMdsXdN6rqnIHtNurea3PgOOBza/oZJ405H7+FlPPB+BYycz5+Cynni8VCynmv87yqXAYW2izIy4Ftplm3DfDE7vHjgK8ATwfu1z23H21g8Qm0Kyre350Md6Q1+z55lvfeCdhxhnVL1nZuzPniWcy5OTfn5tycr/liS1RnoFq+G20Q6/nAL5M8Cti4qr5AGyPwF0nOozURrk8bjHZdt5vTaVX0S6pNlDa4/8uAXZOcWFXXdP2t4bZ7g1HtaozB10xNUV+1iJrRp5jz8TPn42fOx8+cj9+6mvNFOVhtLqaSO5DkqckTf0ybk2Pqvlx7c9ttPb5Na3a8B20yyyuBlwP/mmSqSfBU4MC0qeUfmzZ/0N1pt2a5FLi1WbMG7g2WZLu0mZiHD/yiaEYHc742mPPxM+fjZ87Hz5w360RLVIbukp20wWPpLiNNsiGt+XHzqnpzkkuBnboDcRawf5Itq+ryJL+iXRL57ao6qNvfprQ+2L2AP6Ndhnkcbe6KY4Frq+qzQzFtBBwAPBrYk3Z56791cS74/2jmfPzM+fiZ8/Ez5+Nnzme2KIuo4QNeA1cAJLlrVV2ZZEvayP+HVdWvk9wAbNEdzAtoc6RsA/yUdlnlA2j9tBfR7rlzTJItaPfY2Z3WZ3tKd5K8Cfi74QOZ289/8VjazOLvpc0AfCML2ALK+T0x5+a8J3M+fgso536fr4Pn+aLszqvWxDdVMd8pyaOTHJHkx8AHk+xVVZfTporft3vZT2l3hr9P9/gG2i1Vfkxrfjyg224zWn/v1sBW3fb/Azy/2ydVdWNXpd9uDozBE7GqPldV/1pVZy/0/3CwoHL+DnNuzvsy5+O3gHLu9/k6eJ4vuiIqyeZp99M6OsmDaAfrH2kj83cGvgO8NMm9gRO5ra/2Qlpf631o/blXAPetqhtosyTvnuQHtIFsrwLOq6pvVdXyqvpUVf12OJYa6K9dzMz5+Jnz8TPn42fOx8+cr54F0Z2X3Nr/eruJuqbZbj3gDbQmxJNoB3U94Ee06d0BPkbrb90L+DrwfICqOj/JQ4BrquqYJBcBuyXZrKp+nOSZU1XyNO95uwp5MTDn42fOx8+cj585Hz9zPjoTW0Qlmbp08Zapgz71b5KdgSuq6qqhk2Jv4BFV9aCB/WwIrKD1V1NVFybZCfhBVZ2aNr37PwF3pfXVXpc2YO0i2mC1nYCzpg7+8AFfqAd+OuZ8/Mz5+Jnz8TPn42fOx2NiiqgusYPzPRRtvgjSmg3vRhup//HuJWcDLxqqqq+im28ibTbUW6pdOXAhsDzJR6vqe7TBaFNV9bOBA7v9HVtV13Svv4x2E8OdgLOmTrSFfsAHmfPxM+fjZ87Hz5yPnzlfO9ZaEZWhOzUPJzbtztYvpw1UexLwe9ocEU+rqouS/CTJnlV1xsDLrgSuT/Lwqjq528/UvBU/B96WdkXBicAZ3ft+D/jewPtOVeUXA1+mO1GGTrQFyZyPnzkfP3M+fuZ8/Mz5ZBh7EdUdgH2BT3Q/T/XV7gvsT6uWX19VlyQ5EDinqvZMsgetL3aTblcnAg9Lclbd1iz4yyRnAK/s9vcoWr/uO4DvAutV1ZumiWm6Zs8bgJPnPwPjZ87Hz5yPnzkfP3M+fuZ8soz86rx0/Z9TqvWLLgeeleR1wGZJ7gU8j1bNfgF4e5JtgC8Cv+oO0MW0Ozk/pNvVKcBuwJ2SbJBk/+75v6VNuHUX4O3AW4Df0S6x3KmLKYNxVbNomhjN+fiZ8/Ez5+NnzsfPnE+2kRdRU4lNsn2SRyTZkzby/43AvWkH5lXAJcC1tJH+y2jzR5wNbAtsTLsp4Xm0gWrQpo9/MO1AbwQ8OslGVXVDVX2zql5dVV+oNt/EzbRmxbd1MS3qA27Ox8+cj585Hz9zPn7mfMLVmt2tOcxwZ2TaQdsYeCDwDdrBfD1wd+A1wNsGtv0bWr/pG4AnAxt2z29HO3D36n5+IvDNqfcEngrcaYb3X4/W9LhGn3HSFnNuzs25OTfni2Mx5wt/me8TYvPu382A9wDPAZ4L/NPQdnsAXwJ2oI3Leixw0tA2+3T/fhs4sHt8V2CXqQM8zcmYtZ3QsR9Ac27O14HFnJvzdWEx5wtv6TWwfGAg287AQcAdaM2IO9P6arfqToITaFX0C7v+08uAH1fVZ9Omcl9aVRcCX0nyV0neRWta3BP4DK36fiHtPjxU1ZW0qweooabE6s6Cxcqcj585Hz9zPn7mfPzM+eKRvnlL8kfAUcBXaAf6cuDDwIto/a7nAverqt8nWUa7IuChwMG0e+g8m3bvnC2B/6yqryR5Ju0mhCdU1UVr8LkWJXM+fuZ8/Mz5+Jnz8TPni8OaTHFwL+B84EPAL6vqf5O8FfhL4PPAp4CtkvyiqlbArZNv7QJsABxBa6q8mjYHBVV1zBrEsy4w5+NnzsfPnI+fOR8/c74IrElL1KbAB2kzkq5HuwTy7bRp498IHFNVf55kY1pz5etplfYxwLtnajrM0ARiuo05Hz9zPn7mfPzM+fiZ88WhdxF1u520ZskX0e7afATwTmDrqnpCktAm/7qxqq6e5rVLaFPL2x+7Gsz5+Jnz8TPn42fOx8+cL1y9u/O6A3sPYFfa5F17AC+rqmuTnArcJcmSavNLrBx4zXrdcwAMPtaqmfPxM+fjZ87Hz5yPnzlfHHpPttlVvfcEXgLcBLyuqn6S5D7AocAZVXVzd9BvfY0HvD9zPn7mfPzM+fiZ8/Ez54vDvHTn3W6H7eqA+wHvrHY5pUbMnI+fOR8/cz5+5nz8zPnCssZF1FTzIq1IdjDbGJjz8TPn42fOx8+cj585X9jmvSVKkiRpXTDyGxBLkiQtRhZRkiRJPVhESZIk9WARJUmS1INFlCRJUg8WUZIkST38f9oDrtHoc2OTAAAAAElFTkSuQmCC\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAh4klEQVR4nO3deZxkVX338c+XHZXlUUZEUAEV3AUcUdQI4oqiRsV9wSWOJqLiGpInJhpN1DwGl7gkBFSMqLhvgAsRRDQCw74pEjICAjKAGEDZf88f57YUZc9M952pmuruz/v1uq+urnvr1Lm/e7vq1+ece26qCkmSJM3OOmu7ApIkSXORSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkuasJBsmOSfJVmu7LlqxJCcmeeDaroe0pplEaUFIsl+SpUluSPLpoXUP6Nb9pluOTvKAWZRdSe7To04bJPlykmVdGXtMs80uSY5Lcm2SXyd54zTb7N69/j0Dz/1r95qp5YYk1wysv3+SHyT5bZLzkzxrqMznJTk3yTVdkvKnA+tenuSWofL3GFj/7iRnJrk5yTuHyn1ct+7qJFcm+VqSrYe2eUKSU5Jcl+TiJM9bSRiXAMdV1aVDZbyzi8kjhp7fIMk/d+Ve28X+Qysp/490idshSX7Zxee0JHsNrF/p+dTF4Jgu9suGyl4vyRe6+HwnyaYD6/46yZtnU9fudUlyQZJzpll3bJLru1j8tjvXHtzjPR6U5LtJrkgy3eSDHwD+frblSpPOJEoLxSXAe4BPrmDdPsCdgS2AbwJfGFO9jgdeAlw2vCLJFsB3gH8D7gLcB/je0DbrAx8GThh8vqpeW1V3mlqAzwNf6l6zHvAN4Nu0fV4CfDbJDt36rYHPAm8GNgXeBnwuyV0H3uK/BsuvqmMH1p0PvB04Ypr9PQd4clVtDtwd+AXwiYH9eQDwOeD/ApsBDwVOnqacKa8F/mMoJgFeBlzV/Rz0V8BiYFdgE2AP4JSVlD+d9YCLgN27Ov4N8MUk23brV3U+XUc7D982TdnPBqp73W9px4Yk2wHPAD4yy7oCPBa4K7B9kodPs36/7hy5M3AsQ/GcoZuALwKvWsH6bwKPS3K3HmVLE8skSgtCVX21qr4OXDnNuquralm16fsD3EJLWFYpyXHdw9O7/+afP4s63VhVH6qq47v3HPZm4LtVdVhV3VBV11TVuUPbvIWWWP1sJXW8I/Ac4NDuqfvREpgPVtUtVfUD4MfAS7v12wBXV9VR1RxB++K/9wz369CqOgq4Zpp1v66qSwaeGo713wD/1r33zVV1ZVX99wr2657A9gwlkMCfAFsBbwBekGSDgXUPB75WVZd0+7asqj4zk/0a2Ifrquqd3WtvrapvA/8DPKxbv9LzqapOrKr/AC6YpvjtgGOr6mbgmG7/oCVPb+men619aUnzkd3jFe3XLbRkb8atsAOv/XlVHQKcvYL119OS4SfPtmxpkplESZ0kVwPXA/8C/ONMXlNVj+0ePrRrkTk8yT277pgVLS+aYZUeCVyV5CdJLk/yrS5xmKrvvYBXsupukucAy4HjVrJNgAd1j5cC5yZ5RpJ1u668G4AzBrbfueu6OS/JO7rWrRmZig/we+CtwD8NrH5kt82ZSS5N8tkkd15BUQ8GLpgmsdgX+BatZQTg6QPrfgq8OclfJHlw12o1WLdvr+S4fXsF+7MlsANDCUSf8wk4C9gzyYbA44Cz07par6iqH8+wjME63IHWKnZYtwwnlYPbbgC8mBajqedetIpz+Z7TlbUC59JaFqV5Y8YffNJ8V1Wbd602+wK/XI1yLgQ2XwNV2gbYBXgicCYt2fg88Ohu/UeAd1TVtUO5wLB9gc/UbTfK/DlwOfC2JB+kfVnvTmv5oKpuSfIZWrfaRsCNwHOr6rru9cfREq5fAg8EDgduBt47k52aik+XHL2a27eibUNrEXsSrVvsUFoS8uJpitqcodauLml4LvCyqropyZdpXXpf6TZ5L/CbrrwPAlcm+auqOrSr294z2YeB91uflpwcWlW3aw3seT4dSWtJO4mWzHwB+E/giUn+oVt3FrB/Vd04g/KeTUuAv0f7vF8feBrwtYFtPpLkA8DGtKTv2QP78DnaebAmXENrIZTmDVuipAFdovCvwGeGxgCtDb+ndT2d1HWHvAt4VJLNkjwd2KSqDl9ZAV1LwR7AH7qsquom4E9pX6aX0boEvwhc3L3mCbSEbQ9gA1qCdXCSnbrXX1BV/9N1ZZ1JawnbZ7Y7V1VX0ZKkbwy0ZP0e+FRVnVdV19JacJ66giJ+QxvXNOhZtITuyO73w4C9kizq3vOWqvpYVT2aloT9A/DJJPefbf2TrEMbP3QjsN8K9nFW51PXxXhAVT2kqpYAB3SvfzhtLNfutGPyyhlWc1/gi13X6PW0ZHK4S+8N3Ri1jYG9gS8necgMy5+NTYCrR1CutNaYREl/bB3gDsDWq9pwOl131bUrWaZrVZnOGbRBxlMGHz8eWJzksiSXAc8H9k/yjaEyXgr8uKpuN/6mqs6oqt2r6i5V9WTa2JsTu9U70a54W9olSifRxh09YQX1nBr708d6tEHPU1ehrWyfh50BbDfUlbgvcCfgwi4uX6K1vvxRF2pV/b6qPkZLxh4AkOSolRy3o6Ze23UDHgJsCTynS0xXpNf5lHaV3KOAg2hdlyd3rYknAatMcpJsA+wJvGTgPNkHeGraRQu30x3rH9EuDHhSV8aLV3Euz6Y77/7A6bPYXpp4JlFaENIuHd8IWBdYN8lGU1++SZ6YZOdu/M+mwIG0L9bhQdwr8mtuGwBMVV04dOXa8HLYQL027OoFsEFXr6mE5FPAs5Ls1HUbvQM4vqp+2z3egZbw7ES7+unfgVcM1e1lwKenicdDuve6Q5K30rpZprY7CfiTqZanJDvTupHO6H7fqxsHRJL7dXX5xkDZ63f7tA6wXvc+63brnp1kxyTrdK1DBwKndq1SU/v8iiTbd11zB9CuIvwjVXUx7Qt/167srWnJ5d4DcXko8P4uDiTZP8keSTbuzol9aS0kp3Zl7rWS47bXwNt/gpYUPL2qfj8U25WeT92+b0RL7tLFZ4OhMgJ8lNZKdCtt4Ppjuu12pxuUnjbdxLLp4kNLoM8DdhyIxw60FscXTveCJLvREsqzu3gctopz+cKp+nb7tEH3+0Zp47qmyt2INvD++yuoqzQ3VZWLy7xfgHfSWjUGl3d2655LG5dzLW0A9hHAQwZe+9fAUSsp+7XApbSuiufNsl7LpqnXtgPr/xz4Fe1L+FvAPVZQzqeB9ww9txvtqrpNptn+/3VlXgscBdxnaP1+tATlGtoX9lsG1n2Aljhe1637e2D9oboM79PLu3WvpyUE19G6Er8A3Gvovd/VHYfltO6y/7OS+L0O+ET3+ABaa83wNnenXYL/INqUASfTpg+4mtb6tvcsj9m9un26vovf1PLiGZ5Pe0wTn2OH3uOVwMcGfl+vi9Vvge8Cm3bPvwM4bAX1/Bnw+mmefzuwtHt87NB+nA+8qcff17bT7NOygfXPBb46zr95F5dxLKlaWWu5JE2urrXjVODxNTTh5kKQ5HvAG+uPp76YKElOAF5VVWet7bpIa5JJlCRJUg+OiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6GMltX7bYYovadtttR1G0JEnSGnXyySdfUVWLZvu6kSRR2267LUuXLh1F0ZIkSWtUkl73S7U7T5IkqYcZJVFJNk/y5SQ/S3Jud2sASZKkBWum3XkfBr5TVft09266wwjrJEmSNPFWmUQl2Qx4LPBygKq6EbhxtNWSJEmabDPpztuOdhPNTyU5NcnBSe44vFGSJUmWJlm6fPnyNV5RSZKkSTKTJGo9YBfandJ3pt19/YDhjarqoKpaXFWLFy2a9VWCkiRJc8pMkqiLgYur6oTu9y/TkipJkqQFa5VJVFVdBlyUZMfuqccD54y0VpIkSRNuplfnvR44rLsy7wLgFaOrkiRJ0uSbURJVVacBi0dbFUmSpLnDGcslSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSelhvJhslWQZcA9wC3FxVi0dZKUmSpEk3oySq87iqumJkNZEkSZpD7M6TJEnqYaZJVAHfS3JykiXTbZBkSZKlSZYuX758zdVQkiRpAs00iXpMVe0C7AW8LsljhzeoqoOqanFVLV60aNEaraQkSdKkmVESVVW/6n5eDnwN2HWUlZIkSZp0q0yiktwxySZTj4EnAWeNumKSJEmTbCZX520JfC3J1Pafq6rvjLRWkiRJE26VSVRVXQA8dAx1kSRJmjOc4kCSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSphxknUUnWTXJqkm+PskKSJElzwWxaot4InDuqikiSJM0lM0qikmwDPA04eLTVkSRJmhtm2hL1IeDtwK2jq4okSdLcscokKsnewOVVdfIqtluSZGmSpcuXL19jFZQkSZpEM2mJejTwjCTLgC8Aeyb57PBGVXVQVS2uqsWLFi1aw9WUJEmaLKtMoqrqr6pqm6raFngB8IOqesnIayZJkjTBnCdKkiSph/Vms3FVHQscO5KaSJIkzSG2REmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1sMokKslGSU5McnqSs5O8axwVkyRJmmTrzWCbG4A9q+raJOsDxyc5qqp+OuK6SZIkTaxVJlFVVcC13a/rd0uNslKSJEmTbkZjopKsm+Q04HLg+1V1wkhrJUmSNOFmlERV1S1VtROwDbBrkgcNb5NkSZKlSZYuX758DVdTkiRpsszq6ryquho4BnjKNOsOqqrFVbV40aJFa6h6kiRJk2kmV+ctSrJ593hj4InAz0ZcL0mSpIk2k6vztgIOTbIuLen6YlV9e7TVkiRJmmwzuTrvDGDnMdRFkiRpznDGckmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeVplEJblHkmOSnJPk7CRvHEfFJEmSJtl6M9jmZuAtVXVKkk2Ak5N8v6rOGXHdJEmSJtYqW6Kq6tKqOqV7fA1wLrD1qCsmSZI0yWY1JirJtsDOwAkjqY0kSdIcMeMkKsmdgK8A+1fV/06zfkmSpUmWLl++fE3WUZIkaeLMKIlKsj4tgTqsqr463TZVdVBVLa6qxYsWLVqTdZQkSZo4M7k6L8AhwLlVdeDoqyRJkjT5ZtIS9WjgpcCeSU7rlqeOuF6SJEkTbZVTHFTV8UDGUBdJkqQ5wxnLJUmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6mG9tV0BSZoE2x5wxNquQi/L3ve0tV0FacGyJUqSJKkHkyhJkqQeVplEJflkksuTnDWOCkmSJM0FM2mJ+jTwlBHXQ5IkaU5ZZRJVVccBV42hLpIkSXOGY6IkSZJ6WGNJVJIlSZYmWbp8+fI1VawkSdJEWmNJVFUdVFWLq2rxokWL1lSxkiRJE8nuPEmSpB5mMsXB54H/AnZMcnGSV42+WpIkSZNtlbd9qaoXjqMikiRJc4ndeZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9bDK275I2x5wxNquQi/L3ve0tV0FSdI8ZkuUJElSDyZRkiRJPZhESZIk9eCYKEmSFgjHuK5ZtkRJkiT1YBIlSZLUw4y685I8BfgwsC5wcFW9b6S1kiTNe3Ytaa5bZUtUknWBjwF7AQ8AXpjkAaOumCRJ0iSbSUvUrsD5VXUBQJIvAM8EzhllxaSFzP/QJWnyzWRM1NbARQO/X9w9J0mStGClqla+QbIP8JSq+rPu95cCj6iq/Ya2WwIs6X7dEfj5mq/uyG0BXLG2K7HAGPPxM+bjZ8zHz5iP31yO+b2qatFsXzST7rxfAfcY+H2b7rnbqaqDgINmW4FJkmRpVS1e2/VYSIz5+Bnz8TPm42fMx28hxnwm3XknAfdNsl2SDYAXAN8cbbUkSZIm2ypboqrq5iT7Ad+lTXHwyao6e+Q1kyRJmmAzmieqqo4EjhxxXSbBnO6OnKOM+fgZ8/Ez5uNnzMdvwcV8lQPLJUmS9Me87YskSVIPJlGSJEk9mETNI0k2TLJ+9zhruz4LQZJ1up/Ge0ySbNDdjsq4j0n32bJh99iYj9BUfJNsnGRR99jv6jFIcqck23aPZ3See2DmgSSPSXI28J/AmwDKwW4jk2STJG9Lcgbwke5p/5ZGKMmWSf4uyY+B7wBvAM/zUUpy1yTvTfID4AfAm5JsaMxHq6oqyU7AhcBfruXqzHtJ7pzk3UmOAE4F9oWZf7bM6Oo8TZbuv5JU1S1JNqLNFP9XwHHAEUkuAL7ih92a08V8naq6mTbVx1bAZ4AXA1TVLWuxevPS4HlOm/B3K2B/4JfAD5KcXlU/WItVnHeGzvMNgfWBvwHOBH4CLAWOXns1nH+mWpmq6taBp+9P+6d4u2nWaTUNneebAAcAT6qqY2Zblv89zyFTzYtVdevUl3ZVXU+7SfSpVXU18M/AHrRb72g1DcX85u7x1cB7gQOBG5LsPLitVs905zlwPvDWqjqpqi4HTqT7gtHqW8F5flFVvbWqflJV1wAXANevzXrOJ0MxH06S9gEOB65P8rDB7dXfCs7zXwJndwtJtppNmSZREyjNusP94F0z792S7JHkw0menmQz4HjgQd1mZwM3AH6xz8IMY/6hJM/snl/effCdCTy529y/p1mYRcyfUVVXV9W13V0ToLWS2Po3S7OJ+cBrXpHkJtp90e4+7jrPdbP9bOm68s4HTgN+TWuVAj9fZmwWMX9Ot+os4KdJTgY+mmTJTMeheVAmQJLNkzytS4io5paqunUwCUryYlqT+lOBJwCvAH4HXMJtf2jLgcuArafKGt+ezB09Y/544FXd81N/Oz8EHjve2s9NqxHzV3fPr19VNybZFbgX8GX/SVi51Y155yjgLt1zz576stf0ViPmr+1W7QBcUlX/A1wNvCbJaxwysGKrEfM/61Z9CHgf8Gjg/cCfAs+eyXs7JmoyPIA2tuYG4OgkOwIvAR4B/CjJR2nN6I8C3lhV30pyNHAwEOBnwFMAquqq7vVHjX835pQVxXxX4PiVxPyT0JqDuz/OE4C3dc/5Ibdyqxvzm7py3gZ8vKquHfcOzEGrFXOAqrqse3hOkouB7ZKs4zidFer7eX5I19K6A/DSJEuAO9E+4y9ZC/sxl/Q9zz8FUFVLaeP9AE5Mcg6w5UzOc1uixqRrXlxRvJfRmm/v0/2+B61F6W3AdcDf0k6OxcDp3X/k36Mdv/sDXwd2SvKk7vX37F6/oPWM+du5LeY38scxn7pyZuq/nV8Av0tyYJJXJdlyVPszF4ww5lPd07vRPgyXJnlmkhcl2WRU+zMXjPo8H3ifdYH7Aj9b6AnUiD7PA9ybdoXY+4CnAw8HTqJ16y3o4RkjOs9vneY8X482pvgXMznPTaLGpPvCXdEBWQ5cSvsPBOBQ4GTgL2jNjY8BNui2e8TAf+TXAM+sqt8B7wJenuRK4IxuWdDWQMzXBy4HHjkU86cCJHlkkh/Svlh2Bm6iNb8vWCOM+d7d49fT/uM8mHZV6u+A36/h3ZhTRhjzJwMkeU2Sk2hjdM6ntb4uaCP8PH9WVR1RVZ+qqgtoydaRdOP/FvLwjBGe53sBJNk3bUzUqcDPaRevrJLdeWvYdM1/Xfa8PfBy4Kaqetfg+qq6KcmFwC5J7knLmF9DG2/zD7SrwHYD/h14XtfvG+AKWjMmtNao/6x25diCMoOY31hVfz+4fijm96J9WL2GNk3EYMwPpsV80+6lVwIP7R5fCOxfVaeOZMcm2JhjfhVwv+7xJ4GPVNVPR7JjE2wtxPwh3eNTgf2qasElT2vh8/zB3XtsWFU3VNVvgUNGuIsTZy2c5w/uHp8JvG62ny22RK2GJOt0Tdx/MHXwkzwobQ4naAfww7T/Jg4dKmOqefZCWkvG1sDuwGZVdQhwM62J9zlV9Q3aSfB02twWn6BrvuwG0V3dlbnufG327RnzzwyVMRzzu3NbzA9mxTHflBbze3fve8lUAtXF/Hb1mi8mIOYfp5uyo6qOnvqQm65e88WExfzEqQTKzxZgtJ/n9+3e94bhuq2h3ZwoE3Ke79C97ykDny0zPs9tiZqFJBlsTp2uaTHJAbQ5Pv4X+GGSz9Bm+3048KWqWja4/UB5l3bLTrRWpZcl+QrtQH+ddiJA+2/mNOBhtGbKfxquQ82jAc7GfPwmPeZT9VtJ0/6cM4di7nk+5s+WFdVtLpr0mPc5z02iVmGwaXHw4Kfdo+7JwPNo/ar/ROtzLdpVGJsBXwY2Bz5Im6huZfG+slt2Aw4C9qNdcffDqjpnYLuNuvfaDDgC+Nbq7uOkMebjN5diPli/ucyYj99civl8MZdi3us8ryqXgYU2C/ISYOtp1m0N7N09fhLwfeA5wAO7555MG1h8NO2KikO6k+EOtGbfZ6zivbcHtlvBunXXdmyM+fxZjLkxN+bG3Jiv/mJLVGcgW96CNoj1fOBXSR4HbFxVR9LGCLwpyc9pTYTr0Qaj/a4r5mRaFv3qahOlDZb/a+DBSY6pqmu6/tZw273BqHY1xuBrpqaor5pHzehTjPn4GfPxM+bjZ8zHb6HGfF4OVpuJqeAOBHlq8sTzaHNyTN2X67HcdluPn9CaHe9Om8zySuB1wAeTTDUJngg8M21q+SemzR90N9qtWS4D/tCsWQP3Bktyz7SZmIcP/LxoRgdjvjYY8/Ez5uNnzMfPmDcLoiUqQ3fJTtrgsXSXkSbZkNb8uFlVvSfJZcD23YE4DdgryV2r6vIkl9IuifxJVe3TlbcJrQ92N+DPaZdhHkGbu+IbwLVV9c2hOm0EPA3YE9iFdnnrv3T1nPN/aMZ8/Iz5+Bnz8TPm42fMV2xeJlHDB7wGrgBIcpequjLJXWkj/x9VVb9JciOweXcwL6DNkbI18N+0yyofQuunvYh2z53Dk2xOu8fOTrQ+2xO6k+TdwN8NH8jcfv6LJ9JmFv9X2gzANzGHzaGY3wNjbsx7MubjN4di7uf5AjzP52V3XrUmvqmM+Y5J9kzy8STnAZ9KsltVXU6bKn6P7mX/Tbsz/H27xzfSbqlyHq358WnddpvS+nu3Arbstv8q8NKuTKrqpi5Lv90cGIMnYlV9q6o+WFVnzvU/OJhTMf+QMTfmfRnz8ZtDMffzfAGe5/MuiUqyWdr9tD6X5OG0g/WPtJH5OwD/Bbw2yX2AY7itr3YZra/1vrT+3CuA+1fVjbRZkndKchZtINv+wM+r6viqWlJVX6mq/x2uSw30185nxnz8jPn4GfPxM+bjZ8xnZ0505yV/6H+93URd02y3DvBOWhPicbSDug7wM9r07gCfp/W37gYcC7wUoKrOT/II4JqqOjzJRcBDk2xaVeclef5UljzNe94uQ54PjPn4GfPxM+bjZ8zHz5iPzsQmUUmmLl28deqgT/1MsgNwRVVdNXRSPBZ4TFU9fKCcDYGltP5qqmpZku2Bs6rqxLTp3d8P3IXWV/u7tAFrF9EGq20PnDZ18IcP+Fw98NMx5uNnzMfPmI+fMR8/Yz4eE5NEdYEdnO+haPNFkNZsuAVtpP4XupecCbxyKKu+im6+ibTZUG+tduXAMmBJksOq6nTaYLSprPqFwDO78r5RVdd0r/817SaG2wOnTZ1oc/2ADzLm42fMx8+Yj58xHz9jvnastSQqQ3dqHg5s2p2tX0cbqPZ04HraHBHPrqqLkvwiyS5VdcrAy64Ebkjy6Kr6cVfO1LwVvwQ+kHZFwTHAKd37ng6cPvC+U1n5xcD36E6UoRNtTjLm42fMx8+Yj58xHz9jPhnGnkR1B2AP4Evd71N9tXsAe9Gy5XdU1SVJngmcU1W7JNmZ1hd7p66oY4BHJTmtbmsW/FWSU4A3duU9jtav+yHgp8A6VfXuaeo0XbPnjcCP13wExs+Yj58xHz9jPn7GfPyM+WQZ+dV56fo/p1TrF10CvCDJ24FNk9wbeAktmz0SODDJ1sB3gEu7A3Qx7U7Oj+iKOgF4KHDHJOsn2at7/m9pE27dGTgQeC9wHe0Sy+27OmWwXtXMmyZGYz5+xnz8jPn4GfPxM+aTbeRJ1FRgk9wryWOS7EIb+f8u4D60A7M/cAlwLW2k/2La/BFnAtsAG9NuSvhz2kA1aNPH70o70BsBeybZqKpurKofVdVbqurIavNN3EJrVvxAV6d5fcCN+fgZ8/Ez5uNnzMfPmE+4Wr27NYcV3BmZdtA2Bh4G/JB2MN8B3A14K/CBgW3/mtZv+k7gGcCG3fP3pB24e3e/7w38aOo9gWcBd1zB+69Da3pcrX2ctMWYG3NjbsyN+fxYjPncX9b0CbFZ93NT4BPAi4AXA+8f2m5n4LvAtrRxWU8EjhvaZvfu50+AZ3aP7wLsOHWApzkZs7YDOvYDaMyN+QJYjLkxXwiLMZ97S6+B5QMD2XYA9gE2oDUj7kDrq92yOwmOpmXRr+j6T38NnFdV30ybyn1RVS0Dvp/kL5N8hNa0uAvwdVr2/QrafXioqitpVw9QQ02J1Z0F85UxHz9jPn7GfPyM+fgZ8/kjfeOW5H7Ap4Hv0w705cBngFfS+l3PBR5YVdcnWUy7IuCRwL60e+i8kHbvnLsC/15V30/yfNpNCI+uqotWY7/mJWM+fsZ8/Iz5+Bnz8TPm88PqTHFwb+B84FDgV1X1+yTvA94MfBv4CrBlkgurain8YfKtHYH1gY/Tmiqvps1BQVUdvhr1WQiM+fgZ8/Ez5uNnzMfPmM8Dq9MStQnwKdqMpOvQLoE8kDZt/LuAw6vqDUk2pjVXvoOWaR8OfHRFTYcZmkBMtzHm42fMx8+Yj58xHz9jPj/0TqJuV0hrlnwl7a7NHwc+DGxVVU9NEtrkXzdV1dXTvHZd2tTy9sfOgjEfP2M+fsZ8/Iz5+Bnzuat3d153YO8OPJg2edfOwF9U1bVJTgTunGTdavNLLB94zTrdcwAMPtbKGfPxM+bjZ8zHz5iPnzGfH3pPttllvfcAXg3cDLy9qn6R5L7Aa4BTquqW7qD/4TUe8P6M+fgZ8/Ez5uNnzMfPmM8Pa6Q773YFtqsDHgh8uNrllBoxYz5+xnz8jPn4GfPxM+Zzy2onUVPNi7Qk2cFsY2DMx8+Yj58xHz9jPn7GfG5b4y1RkiRJC8HIb0AsSZI0H5lESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPXw/wEEgfeKcoeqpgAAAABJRU5ErkJggg==\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAiPklEQVR4nO3deZhlVXnv8e+PGRmDtIggtig4IArYgiAq4oioJGqME+CIiRqH60S8MdGYRPQ6oHEkTqioqDgjDiiOqNAMioAgklaQqQFRkMj43j/WLjkcqrtP7e5zuqr6+3me/dSpPZ21373rnLfWWnvtVBWSJEmambVWdwEkSZLmIpMoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiTNKUnunWRxkqzusqifJG9L8g+ruxzSyjKJ0ryV5MXdl+11ST66nPX+JUklecSI+13Yrb9OjzJtneTLSS7q9rFwmnUekeTUJH9KcmGSp0yzzkHd9s8bmHdckmsGpuuTnDGwfK8kJyW5OsnPk+w9tM9/TPI/Sf7YxW3vgWWvT3LD0P63H1i+S5JTklzb/dxlaN+7Jfl+t92lSV46armm8UbgrTU0yF2S7yb5fZL1h+Zvm+SYJJcn+UOSXyR51gre4zaSHJHknCQ3D2+f5ODuuP/YnbO3DF4fSbZI8oXunP4mydOHtl+Q5JNd+X6f5KiBZa/qyn5mkp0H5j8oyRdnehzdth9NcmOSrYfmD5/ns5M8qcf+10vyuSRLuut0n6FV3gq8Nsl6fcovzRYmUZrPLgL+HfjwslZIcjfgb4GLJ1Smm4GvA9N+MSW5N/BJ4P8CmwH3A04ZWuevgNcCZw7Or6r9qmrjqQk4Efhst80WwFeA/wdsDrwF+Eq3L5LsARwGPLl73w8BX0iy9sBbHD24/6o6v9t2PeBLwCeAvwKOBL409QWZZMvumD8A3B64O/DNUco1TXy2Bh4GfHFo/kLgwUABTxja7OPABcBduvc/ELh0uv2vwM+AFwKnTrPsdsDLgC2BPYCHA68cWP4e4HpgK+AZwPuS7DSw/PPAJcB2wB1oScbU8T4X2B54H/Cmbv46wNu695yRJBvRrr8/AM+cZpWjB66hlwGfSLLVTN8H+GG3/0uGF1TVxcAvue25kuYUkyjNW1X1+ar6InDFclZ7D/Aa2hfcqL7f/byq+299zxmU6dKqei9w8jJW+WfgA1V1XFXdWFVXVNWvh9Z5E/Au4PJlvc9AUvGxbtZewCVV9dmquqmqPgEsBZ7YLV8InFlVp3Q1PB+jJQR3GOGw9gHWAQ6vquuq6l1AgH275f8H+EZVHdUtv7qqzh6xXMMeCZxaVX8emn8Q8BPgo8DBQ8seAHy0qv7UxfS0qjpuhOO6lap6T1V9Gxh+b6rqfVX1g6q6vqp+BxwFPAhulbS8rqquqaofAl+mJXMkeRRwZ+BVVfWHqrqhqk7rdr0dcFpV/RE4npZMQUtuvlxVS2Z6HF1ZrgL+jdvGavi4vgFcDdxtJm/QxeHw7lhvWsZq3wX2n8l+pdnGJEprrCR/C1xXVV+b4aYP6X5u3v3H/uMkeye5ajnTipqopjywK9sZSS5O8omutmaqzLsDi4D3r2A/BwE/GPqSHe5DFOA+3evjgLWT7NHVPj0HOJ1b1yI8PsmVXbPSYH+WnYCfDzWv/bybP3VMVyY5McllSb6SZLsRyzVsZ+CcaeYfREtcjgIePVRz8hPgPUmeOvS+7c2Wf94OXUY5VuQh3FJTuCNwY1WdO7D8Z9w6PucARya5IsnJSR7aLTsP2DnJ5sAjgDOT3Bl4Kl1tVQ8HA58CPg3cM8n9p1spzf7AesBZ3bztVhCvp0+3r2U4m1bTKs1ZM+7TIc0HSTYB/pNWs7HSuv+4N18Fu9qWVkPxKFpz5JHAfwHP6JKb9wIvrqqbs/x+1QfRmjKn/Bi4U5KnAZ8Dnk6rXbhdt/xq4BhaE0xoNRX7DSRGnwGOoDWD7QEck+SqqvoUsDGtaWjQH4BNBo5pN1qsz6A12X2KVlOzonIN25yhmsUuQb0L8JmqujzJr7v9vKNb5W9ptY2voyUNZwDPr6qTAapq82W8Vy9JnkNLdKf6q20M/HFoteH4PKpb/9m0mqIvJbl7dzz/AXyHFvu/B97ZHc/fJHkh7Vy9qKouHKFs29GaQ19RVZcm+TbtWhlsMn5KkscB6wIbAP9UVVcBVNVvWTXXObRrblXtS1otrInSmur1wMd7NoeM0/8CH6mqc6vqGlqi99hu2QtpNT4/Wd4OuqTijrSkBICqugI4gNa0dinwGFrz0NQX73NpX+A70Woengl8Ncmduu3PqqqLuia3E2lf5E/utr0G2HSoGJvSviSnjukLVXVy1wz3BmCvJJuNUK5hv+eW5GPKwcA3q2qqefOTDDRTVdXvq+rQqtqJ1ifpdOCLWUEW2keSv6Y1t+43UJ5R4rOkqj7UNeV9mtaH60Fd+T9VVbtV1X60GrrrgNNoNVGPp/V7G7VW6kDg7Ko6vfv9KODpSdYdWOczVbV5VW1ES2gPSvKCEfc/E5vQEkBpzjKJ0prq4cBLklyS5BJan5TPJHnNCNvW8IwkD86t71wbnh48Yrl+PrT/wdcPp9U+TJV5L+BtSd49tI+Dgc93SdgtO6r6XlU9oKq2oH2Z3hM4qVu8C/DVLnm7uaq+Tutsv9cyylnc0gx3JnDfoaTkvtzSnLW8Y1pRuYb9nNY8BkCSDYGnAA8diMvLgfsluU1TUZfYvBW4E7BFt4/lnbfXLqMct5HkMcB/A4+vqjMGFp0LrJNkh4F592PZ8WGa36eO9T+BVwA7ABd0faVOpsV7FAcB2w/E6u20vm+PnW7l7p+M42jJ2lRz3vLi9YwRywFwL1qzpjR3VZWT07ycaM3VG9BqBj7evV6nW3Z7Wm3N1HQBrdln4xH2eztaZ9kde5ZrA2Aj2hflPYANBpY9B/gfWgfi29Ga0T7eLdt8qMwn0mpwNhvYfkNaU9G+07zvrrQmmk2Bw4EfDSw7mPZlvz0tOXokcC1wz275AbQ77wLsDvwOOLhbth7wG+ClwPrAi7vf1+uW70urQdqle/930PprrbBc0xzDVrTmvA26358GXEnrgD0Ym+8Db+vWeTOtBmcdWu3He4Bf9Thv63Xn7kfA87vXaw0c4xXAQ5ax7adpTZgb0WqY/gDs1C3boovPwcDatBq+K4Eth/bxH8DLu9dbd++3Fa2J76vd/IXddbVwmjLsCdxI61c2GKujgGO6dV4PfGJgm21pTbBv7hGv9bsYXUhrrtwAyMDybwJPWd2fE05OKzOt9gI4OY1r6r4Qamh6/TLWXQI8YuD39wPvX86+/412F9lVwANnWK7hMtXQ8jd0+15KS/7+ahn7+S7wvKF5T6MlMJlm/U91X95/AI4G7jCwLN0x/ZbWzHQ2cODQtlfQmqZ+CbxkaN+70vrV/C9tCIBdh5b/Ay3x+j1tSIM7j1KuZRz3Z4G/615/nS5ZGlrnKbRO8evQ+pT9qiv7UuCrwL16XE/fnebc7dMtO4GWoFwzMB03sO0WtGEZ/tTF+OlD+34wLVm5BlgMPHho+T1pNU5rD8x7Fe0OzbOAnQf2swRYd5ryv58uWRqavzutiXAL2t/MDQPHcHG33e16xGvJNPFa2C3bmpZcrbcq/+adnCY9peo2tcaSNGuljaV1JLB7+QF2K0n+GVhaVR9Y3WVZniRvA35dbbgPac4yiZIkSerBjuWSJEk9mERJkiT1YBIlSZLUg0mUJElSD2N57MuWW25ZCxcuHMeuJUmSVqlTTjnl8qpaMNPtxpJELVy4kMWLF49j15IkSatUkt/02c7mPEmSpB5GSqKSbJ7kc0l+meTsJHuOu2CSJEmz2ajNee8Evl5VT06yHu2ZXpIkSWusFSZRSTYDHgI8C6CqrgeuH2+xJEmSZrdRmvPuSnto50eSnJbkg0k2Gl4pySFJFidZvHTp0lVeUEmSpNlklCRqHWA34H1VtSvtKeSHDq9UVUdU1aKqWrRgwYzvEpQkSZpTRkmiLgQurKqfdr9/jpZUSZIkrbFWmERV1SXABUnu0c16OHDWWEslSZI0y416d94/Akd1d+adDzx7fEWSJEma/UZKoqrqdGDReIsiSZI0dzhiuSRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIP64yyUpIlwNXATcCNVbVonIWSJEma7UZKojoPq6rLx1YSSZKkOcTmPEmSpB5GrYkq4JtJCvhAVR0xvEKSQ4BDALbbbrtVV0JJkrRKLDz02NVdhF6WHLb/6i7CtEatidq7qnYD9gNelOQhwytU1RFVtaiqFi1YsGCVFlKSJGm2GSmJqqrfdT8vA74A7D7OQkmSJM12K0yikmyUZJOp18CjgF+Mu2CSJEmz2Sh9orYCvpBkav1PVtXXx1oqSZKkWW6FSVRVnQ/cbwJlkSRJmjMc4kCSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSph5GTqCRrJzktyVfHWSBJkqS5YCY1US8Fzh5XQSRJkuaSkZKoJNsC+wMfHG9xJEmS5oZRa6IOB14N3Dy+okiSJM0dK0yikjwOuKyqTlnBeockWZxk8dKlS1dZASVJkmajUWqiHgQ8IckS4NPAvkk+MbxSVR1RVYuqatGCBQtWcTElSZJmlxUmUVX1T1W1bVUtBJ4KfKeqnjn2kkmSJM1ijhMlSZLUwzozWbmqvgt8dywlkSRJmkOsiZIkSephRjVRkiZj4aHHru4i9LLksP1XdxEkaWKsiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeVphEJdkgyUlJfpbkzCRvmETBJEmSZrN1RljnOmDfqromybrAD5McV1U/GXPZJEmSZq0VJlFVVcA13a/rdlONs1CSJEmz3Uh9opKsneR04DLgW1X107GWSpIkaZYbKYmqqpuqahdgW2D3JPcZXifJIUkWJ1m8dOnSVVxMSZKk2WVGd+dV1VXACcBjpll2RFUtqqpFCxYsWEXFkyRJmp1GuTtvQZLNu9cbAo8EfjnmckmSJM1qo9ydtzVwZJK1aUnXZ6rqq+MtliRJ0uw2yt15Pwd2nUBZJEmS5gxHLJckSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqYYVJVJI7JzkhyVlJzkzy0kkUTJIkaTZbZ4R1bgReUVWnJtkEOCXJt6rqrDGXTZIkadZaYU1UVV1cVad2r68Gzga2GXfBJEmSZrMZ9YlKshDYFfjpWEojSZI0R4ycRCXZGDgGeFlV/XGa5YckWZxk8dKlS1dlGSVJkmadkZKoJOvSEqijqurz061TVUdU1aKqWrRgwYJVWUZJkqRZZ5S78wJ8CDi7qt4+/iJJkiTNfqPURD0IOBDYN8np3fTYMZdLkiRpVlvhEAdV9UMgEyiLJEnSnOGI5ZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9rDCJSvLhJJcl+cUkCiRJkjQXjFIT9VHgMWMuhyRJ0pyywiSqqr4PXDmBskiSJM0Z9omSJEnqYZUlUUkOSbI4yeKlS5euqt1KkiTNSqssiaqqI6pqUVUtWrBgwararSRJ0qxkc54kSVIPowxx8Cngx8A9klyY5LnjL5YkSdLsts6KVqiqp02iIJIkSXOJzXmSJEk9mERJkiT1YBIlSZLUwwr7REnSmmDhoceu7iL0suSw/Vd3EaQ1ljVRkiRJPZhESZIk9WASJUmS1INJlCRJUg9zrmO5nT8lSdJsYE2UJElSDyZRkiRJPZhESZIk9TDn+kRp8uyHJknSbVkTJUmS1INJlCRJUg8mUZIkST2YREmSJPUwUsfyJI8B3gmsDXywqg4ba6kkSfOeN61orlthTVSStYH3APsB9waeluTe4y6YJEnSbDZKc97uwHlVdX5VXQ98GjhgvMWSJEma3UZJorYBLhj4/cJuniRJ0horVbX8FZInA4+pqud1vx8I7FFVLx5a7xDgkO7XewDnrPrijt2WwOWruxBrGGM+ecZ88oz55BnzyZvLMb9LVS2Y6UajdCz/HXDngd+37ebdSlUdARwx0wLMJkkWV9Wi1V2ONYkxnzxjPnnGfPKM+eStiTEfpTnvZGCHJHdNsh7wVODL4y2WJEnS7LbCmqiqujHJi4Fv0IY4+HBVnTn2kkmSJM1iI40TVVVfA7425rLMBnO6OXKOMuaTZ8wnz5hPnjGfvDUu5ivsWC5JkqTb8rEvkiRJPZhESZIk9WASNY8kWT/Jut3rrO7yrAmSrNX9NN4TkmS97nFUxn1Cus+W9bvXxnyMpuKbZMMkC7rXfldPQJKNkyzsXo90nXti5oEkeyc5E/g28HKAsrPb2CTZJMmrkvwceFc327+lMUqyVZJ/TfIj4OvAS8DrfJyS3CHJm5J8B/gO8PIk6xvz8aqqSrIL8FvgNau5OPNeki2SvDHJscBpwMEw+mfLSHfnaXbp/itJVd2UZAPaSPH/BHwfODbJ+cAxftitOl3M16qqG2lDfWwNfAx4BkBV3bQaizcvDV7ntAF/twZeBvwG+E6Sn1XVd1ZjEeedoet8fWBd4J+BM4ATgcXA8auvhPPPVC1TVd08MPtetH+K7zrNMq2koet8E+BQ4FFVdcJM9+V/z3PIVPViVd089aVdVX+mPST6tKq6CngbsA/t0TtaSUMxv7F7fRXwJuDtwHVJdh1cVytnuuscOA94ZVWdXFWXASfRfcFo5S3jOr+gql5ZVSdW1dXA+cCfV2c555OhmA8nSU8Gjgb+nOT+g+urv2Vc578Bzuwmkmw9k32aRM1CadYebgfvqnnvmGSfJO9M8vgkmwE/BO7TrXYmcB3gF/sMjBjzw5Mc0M1f2n3wnQE8ulvdv6cZmEHMn1BVV1XVNd1TE6DVklj7N0MzifnANs9OcgPtuWh3mnSZ57qZfrZ0TXnnAacDl9JqpcDPl5HNIOZP6hb9AvhJklOAdyc5ZNR+aJ6UWSDJ5kn27xIiqrmpqm4eTIKSPINWpf5Y4BHAs4FrgYu45Q9tKXAJsM3UviZ3JHNHz5g/HHhuN3/qb+d7wEMmW/q5aSVi/vxu/rpVdX2S3YG7AJ/zn4TlW9mYd44Dbt/Ne+LUl72mtxIx//tu0Y7ARVX1P8BVwAuSvMAuA8u2EjF/XrfocOAw4EHAm4G/Bp44ynvbJ2p2uDetb811wPFJ7gE8E9gD+EGSd9Oq0fcCXlpVX0lyPPBBIMAvgccAVNWV3fbHTf4w5pRlxXx34IfLifmHoVUHd3+cPwVe1c3zQ275VjbmN3T7eRXw3qq6ZtIHMAetVMwBquqS7uVZSS4E7ppkLfvpLFPfz/MPdTWtOwIHJjkE2Jj2GX/RajiOuaTvdf4RgKpaTOvvB3BSkrOArUa5zq2JmpCuenFZ8V5Cq769e/f7PrQapVcBfwL+hXZxLAJ+1v1H/k3a+bsX8EVglySP6rbfrtt+jdYz5q/mlphfz21jPnXnzNR/O78Crk3y9iTPTbLVuI5nLhhjzKeap/ekfRguTnJAkqcn2WRcxzMXjPs6H3iftYEdgF+u6QnUmD7PA9yNdofYYcDjgQcAJ9Oa9dbo7hljus5vnuY6X4fWp/hXo1znJlET0n3hLuuELAUupv0HAnAkcArwQlp1497Aet16ewz8R341cEBVXQu8AXhWkiuAn3fTGm0VxHxd4DLggUMxfyxAkgcm+R7ti2VX4AZa9fsaa4wxf1z3+h9p/3F+kHZX6rXA/67iw5hTxhjzRwMkeUGSk2l9dM6j1b6u0cb4ef43VXVsVX2kqs6nJVtfo+v/tyZ3zxjjdb4fQJKD0/pEnQacQ7t5ZYVszlvFpqv+67Ln7YFnATdU1RsGl1fVDUl+C+yWZDtaxvwCWn+b/6DdBbYn8N/AU7p23wCX06oxodVGfbvanWNrlBFifn1V/dvg8qGY34X2YfUC2jARgzH/IC3mm3abXgHcr3v9W+BlVXXaWA5sFptwzK8E7tm9/jDwrqr6yVgObBZbDTG/b/f6NODFVbXGJU+r4fN85+491q+q66rqD8CHxniIs85quM537l6fAbxopp8t1kSthCRrdVXcfzF18pPcJ20MJ2gn8J20/yaOHNrHVPXsb2k1GdsADwU2q6oPATfSqnifVFVfol0Ej6eNbfE+uurLrhPdVd0+156v1b49Y/6xoX0Mx/xO3BLzD7LsmG9Ki/nduve9aCqB6mJ+q3LNF7Mg5u+lG7Kjqo6f+pCbrlzzxSyL+UlTCZSfLcB4P8936N73uuGyraLDnFVmyXW+Y/e+pw58tox8nVsTNQNJMlidOl3VYpJDaWN8/BH4XpKP0Ub7fQDw2apaMrj+wP4u7qZdaLVKByU5hnaiv0i7EKD9N3M6cH9aNeVbhstQ86iDszGfvNke86nyLadqf86ZQzH3Op/wZ8uyyjYXzfaY97nOTaJWYLBqcfDkpz2j7tHAU2jtqm+htbkW7S6MzYDPAZsD76ANVLe8eF/RTXsCRwAvpt1x972qOmtgvQ2699oMOBb4ysoe42xjzCdvLsV8sHxzmTGfvLkU8/liLsW813VeVU4DE20U5EOAbaZZtg3wuO71o4BvAU8CdurmPZrWsfh42h0VH+ouhtvRqn2fsIL33h646zKWrb26Y2PM589kzI25MTfmxnzlJ2uiOgPZ8pa0TqznAb9L8jBgw6r6Gq2PwMuTnEOrIlyH1hnt2m43p9Cy6OdXGyhtcP+XAjsnOaGqru7aW8Mtzwaj2t0Yg9tMDVFfNY+q0acY88kz5pNnzCfPmE/emhrzedlZbRRTwR0I8tTgiefSxuSYei7XQ7jlsR4n0qod70QbzPIK4EXAO5JMVQmeBByQNrT8I9PGD7oj7dEslwB/qdasgWeDJdkubSTm4RM/L6rRwZivDsZ88oz55BnzyTPmzRpRE5Whp2QnrfNYuttIk6xPq37crKr+PcklwPbdiTgd2C/JHarqsiQX026JPLGqntztbxNaG+yewD/QbsM8ljZ2xZeAa6rqy0Nl2gDYH9gX2I12e+t/deWc839oxnzyjPnkGfPJM+aTZ8yXbV4mUcMnvAbuAEhy+6q6IskdaD3/96qq3ye5Hti8O5nn08ZI2Qb4Ne22yvvS2mkvoD1z5+gkm9OesbMLrc32p91F8kbgX4dPZG49/sUjaSOLv582AvANzGFzKOZ3xpgb856M+eTNoZj7eb4GXufzsjmvWhXfVMa8UZJ9k7w3ybnAR5LsWVWX0YaK36fb7Ne0J8Pv0L2+nvZIlXNp1Y/7d+ttSmvv3RrYqlv/88CB3T6pqhu6LP1WY2AMXohV9ZWqekdVnTHX/+BgTsX8cGNuzPsy5pM3h2Lu5/kaeJ3PuyQqyWZpz9P6ZJIH0E7Wf9J65u8I/Bj4+yR3B07glrbaJbS21h1o7bmXA/eqqutpoyTvkuQXtI5sLwPOqaofVtUhVXVMVf1xuCw10F47nxnzyTPmk2fMJ8+YT54xn5k50ZyX/KX99VYDdU2z3lrA62lViN+nndS1gF/ShncH+BStvXVP4LvAgQBVdV6SPYCrq+roJBcA90uyaVWdm+TvprLkad7zVhnyfGDMJ8+YT54xnzxjPnnGfHxmbRKVZOrWxZunTvrUzyQ7ApdX1ZVDF8VDgL2r6gED+1kfWExrr6aqliTZHvhFVZ2UNrz7m4Hb09pqr03rsHYBrbPa9sDpUyd/+ITP1RM/HWM+ecZ88oz55BnzyTPmkzFrkqgusIPjPRRtvAjSqg23pPXU/3S3yRnAc4ay6ivpxptIGw315mp3DiwBDklyVFX9jNYZbSqrfhpwQLe/L1XV1d32l9IeYrg9cPrUhTbXT/ggYz55xnzyjPnkGfPJM+arx2pLojL0pObhwKY92fpFtI5qjwf+TBsj4olVdUGSXyXZrapOHdjsCuC6JA+qqh91+5kat+I3wFvT7ig4ATi1e9+fAT8beN+prPxC4Jt0F8rQhTYnGfPJM+aTZ8wnz5hPnjGfHSaeRHUnYB/gs93vU221+wD70bLl11XVRUkOAM6qqt2S7Epri92429UJwF5JTq9bqgV/l+RU4KXd/h5Ga9c9HPgJsFZVvXGaMk1X7Xk98KNVH4HJM+aTZ8wnz5hPnjGfPGM+u4z97rx07Z9TqrWLHgI8NcmrgU2T3A14Ji2b/Rrw9iTbAF8HLu5O0IW0Jznv0e3qp8D9gI2SrJtkv27+v9AG3NoCeDvwJuBPtFsst+/KlMFyVTNvqhiN+eQZ88kz5pNnzCfPmM9uY0+ipgKb5C5J9k6yG63n/xuAu9NOzMuAi4BraD39F9HGjzgD2BbYkPZQwnNoHdWgDR+/O+1EbwDsm2SDqrq+qn5QVa+oqq9VG2/iJlq14lu7Ms3rE27MJ8+YT54xnzxjPnnGfJarlXtac1jGk5FpJ21D4P7A92gn83XAHYFXAm8dWPe1tHbT1wNPANbv5m9HO3F3635/HPCDqfcE/gbYaBnvvxat6nGljnG2TcbcmBtzY27M58dkzOf+tKoviM26n5sC7wOeDjwDePPQersC3wAW0vplPRL4/tA6D+1+nggc0L2+PXCPqRM8zcWY1R3QiZ9AY27M14DJmBvzNWEy5nNv6tWxfKAj247Ak4H1aNWIO9LaarfqLoLjaVn0s7v200uBc6vqy2lDuS+oqiXAt5K8Jsm7aFWLuwFfpGXfz6Y9h4equoJ29wA1VJVY3VUwXxnzyTPmk2fMJ8+YT54xnz/SN25J7gl8FPgW7URfBnwMeA6t3fVsYKeq+nOSRbQ7Ah4IHEx7hs7TaM/OuQPw31X1rSR/R3sI4fFVdcFKHNe8ZMwnz5hPnjGfPGM+ecZ8fliZIQ7uBpwHHAn8rqr+N8lhwP8BvgocA2yV5LdVtRj+MvjWPYB1gffSqiqvoo1BQVUdvRLlWRMY88kz5pNnzCfPmE+eMZ8HVqYmahPgI7QRSdei3QL5dtqw8W8Ajq6qlyTZkFZd+Tpapn008O5lVR1maAAx3cKYT54xnzxjPnnGfPKM+fzQO4m61U5ateRzaE9tfi/wTmDrqnpsktAG/7qhqq6aZtu1aUPL2x47A8Z88oz55BnzyTPmk2fM567ezXndib0TsDNt8K5dgRdW1TVJTgK2SLJ2tfEllg5ss1Y3D4DB11o+Yz55xnzyjPnkGfPJM+bzQ+/BNrus987A84EbgVdX1a+S7AC8ADi1qm7qTvpftvGE92fMJ8+YT54xnzxjPnnGfH5YJc15t9phuztgJ+Cd1W6n1JgZ88kz5pNnzCfPmE+eMZ9bVjqJmqpepCXJdmabAGM+ecZ88oz55BnzyTPmc9sqr4mSJElaE4z9AcSSJEnzkUmUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg//H2GwAkQ5VtWiAAAAAElFTkSuQmCC\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAhyklEQVR4nO3debgkVX3/8feHRUDZVEZEUEYUcFdgBFGCinFBRdyicSVuo3GJJlFD8ouJW5QY4xaDhoAicUPFuOOC4oqAAyK7SBAFERhAFERZv78/Tl1p2jszfWume/reeb+ep57pW+upb9X0/d5zTp1KVSFJkqS5WW9tF0CSJGk+MomSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkStK8lWRRkrOTbLK2y6LZJdk6yVlJNlrbZZHWNJMorROSvDzJsiTXJjl8aNniJJXk6oHpdSPud2bbDXqUaZskn0tyUbePxbOs86dJTk7y2yQXJnnaLOs8t9v+hQPzjh46n+uSnDaw/MFJTkxyVZJTk+w1tM9XJPlpkt90cdtrYNnrk1w/tP8dumU7JflskuVJrkjylSQ7D2x7n27eZUn+aJC6lV2nFTgQOLyqfje0n8OT3JBkm6H5Wyb5QJKLu3M/J8mBIxxnVkke2sX+zQPzDkhyUhe7C5O8beb+SLJRksOS/Kw7/ilJ9h3Y9s5Jju9i9+9Dxzo6yZIeZbxrkpuSvG+WZdXdW1d31+RjSbbscYynJTkuyTVJvjm4rKouAY4Fls51v9K0M4nSuuIi4M3AB1ayzpZVtWk3vWkCZboJ+DLwlNkWJrkX8FHg/wFbAPcHThpa57bAPwBnDM6vqn0HzmVT4Djgk902twM+D/wbsCXwNuDz3b5IsgdwEPDU7riHAf+bZP2BQxw5uP+qOq+bvyXwOWBnYGvgROCzA9tdD3wCeMEKYjLKdZo5942AA4APD82/DS2mvwaePbTZO4FNgXt25/YE4NxVHWsFx98QeDdwwtCiWwOvArYC9gAeAby6W7YBcAHw0O74/wh8YiCB/nvgQ8BdgSfOJE1Jng78tKqW9Sjqc4FfAU9fQW3Q/bt7ZAfgtsDrexzjCuBdtPtmNh8BXtxjv9JUM4nSOqGqPl1VnwEuX8O7/nb375XdX/N7zqFMl1TVwcAPVrDKPwL/VVVHV9UNVXV5Vf3f0DpvBd4DXLai43S/oP8EOKKb9WDg4qr6ZFXdWFUfBpYDT+6WLwbOqKqTqr3S4AhaQnCHEc7pxKo6rKquqKrraUnLzklu3y3/cVUdxlDSN7D9XK7THsCVVXXh0PynAFcCb6QlWYMeCHy0qn5VVTdV1dlV9akRjjWbvwW+Cpw9OLOq3ldV36mq66rqF7QE4iHdst9W1eur6vzu+F8Afgrs1m1+V+AbVfVr2n2xQ5LNaTVu/zDXAiYJLYn6R1oCu9+K1q2q39AS4HvN9ThVdUxVfYKWBM/mBNq5bD/XfUvTzCRKutnPuuaXDybZasRt9u7+nanF+n6SvZJcuZJpr5Xu8WYPAkhyWpJfJvlwV4tEN393YAnw/lXs57nAd6rq/IF5GVonwH26z0cD6yfZo6t9ej5wCnDxwPr7dU1OZyT5y5Uce29awramk1eA+wI/nmX+AcDHgI8D90iy28Cy44F/SfK8JDsOb9g1ba7ouh08sN72tLi8cYRy7s0KksYkWwM7DSw/HXhk16S2Wzf/TcC7qurKEY41bC9gO1osPsEfJ5WDZbkt8ERajGbmHbySeJw6aiGq6gZajd/9e5yDNLVMoqRWi/NAYHvaL67NaLUHvVTVd6tqy5VM3x1xV9sBz6HVrOwIbAL8B0CX3BwMvLyqblrFfp4LHD7w8/eBOyV5RpINkxwA3I3WDAVwFXAU8F3gWuCfgaV184s2P0FrDlsEvAj4pyTPGD5oku2A/wT+ZsTznastu7IOHvMuwMNptU2XAF+nnf+MV9Cu7cuBM5OcO9gnqarut5Lr9tKB/bwHeF1VXb2yAiZ5Pi3RffssyzbsyvKhqpqpzXorrdbwW7TreyvgfrTm1o8m+XaSl68iLoMOAI6uql/RmoYfk2S4RvHkJFfS/h/cBfivmQVV9dKVxON+cygHtGu15Ry3kaaaSZTWeVV1dVUt65rMLqH9gn1Uks3WctF+B3ywqs7pflm/BXhst+ylwKlVdfwKtwa6Wq87An9osupqhfanJTeXAI8BjgFmmsVeADwPuDftl/izgS8kuVO3/ZlVdVHXFHgcrV/QU4eOu4jW1HVwVX2s5/mvyq9oCe+g5wBnVdUp3c8fAZ7ZJSxU1e+q6i1VtRtwe1pC+MnBGr5VSbIfsFlVHbmK9Z5IS4r2rarLhpatB/wPcB3tfqMr3xVV9fSquj8trv9BS/wOpNVS/SnwkiT3HKGcmwB/RvcHQVV9H/g58MyhVXetqi2BjYH3Ad9JsvGq9t/DZrRmVmnBMImS/thMjcso/z9me8LsT3LLJ9eGpz8ZsRynDu1/8PMjgCelPWV2Ma2f078nee/QPg4APj1cY1JV36qqB1bV7WiJxz1oncABHgB8oUvebqqqLwO/7I4xm2KgebBrFvoq8Lmq+pcRz7WPU2lNYYOeS+t7MxOXd9D6cz12eOOuD9BbgNvQ+iLRNU+u6LrNNJs+AlgycIynA69K8ocO9EkeA/w3sF9VnTZ43K6f0mG0jvdP6fqOzWYpcHxVnU5rulxWVdcBp3U/r8qTgM2BgwfKui0raNLrynFoF4v7dGV9/0riMWsT5WzSnk68O/CjUbeR5oWqcnJa8BPtqaiNaTUD/9N93qBbtgftabL1aLUTRwLHjrjfWwM3Ajv1LNfGtF/i1ZVh44Flz6d1Ot6hO84ngP/plm1Jq2GamY6j1SxtMbD9JrQn1PaZ5bi7ABvSfsm+C/jewLIDgHO64wZ4JHANcI9u+f60p7gC7A78AjigW7Y5LRl77wrON90536s7542BjUa5TrPs61a0DvHbdj/vCdxASzAGY/MR4KhundfRmm5v1e37/9FqtDadwzXbbGj/R9I60N+uW74PrWP83ivY/v20fkcrPCatE/9pM+vQmvbeSnuy8CfAkm7+4bQhHmbbx1doydpgWXejPRV6326dAu7efV6fVit2zcy5zCEm63fxfAntYYuNgQ0Hlj8YOHNtfgc4OY1jWusFcHKaxER7bLuGptd3y55BS1Z+S6txOQK448C27wfev5J9v7H7ZX4l8KA5lmu4TDW0/A3dvpd3ScVtV7CfbwIvHJr3DOBnQGZZ/2O0BOvXXRJwh4Fl6c7p57R+LGcBzxna9nLgatqTaX81sOyA7jx+2y2fme7SLV88yzmfP8p1WsF5/xvwdwPX6ahZ1tmd1rfrdrSn1E4HfkN7LP+bwINX8946HHjzwM/H0pK5wfM/ulu2fXdOvx9a/qyhfR4B/NnAz3emPeH2K+AdA/O/DrxoljJt25XhvrMs+xLw9oH7b+Za/Yb2ROCje8TgL2a5bocPLP/PwfvEyWmhTKn6o9YISZoXur5X3wF2qaEBNxe6JLeiNY/dr1bcJLjWdR3Zv0W7Rr9f2+WR1iSTKEmSpB7sWC5JktSDSZQkSVIPJlGSJEk9mERJkiT1sME4drrVVlvV4sWLx7FrSZKkNeqkk066rKoWzXW7sSRRixcvZtmyZePYtSRJ0hqV5Gd9trM5T5IkqYeRkqgkWyb5VJKzk5yVZM9xF0ySJGmajdqc927gy1X11G6U3FuPsUySJElTb5VJVJItgL1p70ai2lvErxtvsSRJkqbbKM15d6W9/PSDSX6Y5NAktxleKcnSJMuSLFu+fPkaL6gkSdI0GSWJ2gDYFXhfVe1Ce+P3gcMrVdUhVbWkqpYsWjTnpwQlSZLmlVGSqAuBC6vqhO7nT9GSKkmSpHXWKpOoqroYuCDJzt2sRwBnjrVUkiRJU27Up/NeAXykezLvPOB54yuSJEnS9BspiaqqU4Al4y2KJEnS/OGI5ZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9bDDKSknOB64CbgRuqKol4yyUJEnStBspieo8vKouG1tJJEmS5hGb8yRJknoYNYkq4KtJTkqydLYVkixNsizJsuXLl6+5EkqSJE2hUZOovapqV2Bf4GVJ9h5eoaoOqaolVbVk0aJFa7SQkiRJ02akJKqqftH9eynwv8Du4yyUJEnStFtlEpXkNkk2m/kMPAo4fdwFkyRJmmajPJ23NfC/SWbW/2hVfXmspZIkSZpyq0yiquo84P4TKIskSdK84RAHkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2MnEQlWT/JD5N8YZwFkiRJmg/mUhP1SuCscRVEkiRpPhkpiUqyHfA44NDxFkeSJGl+GLUm6l3Aa4GbxlcUSZKk+WOVSVSSxwOXVtVJq1hvaZJlSZYtX758jRVQkiRpGo1SE/UQ4AlJzgc+DuyT5MPDK1XVIVW1pKqWLFq0aA0XU5IkabqsMomqqr+vqu2qajHw58A3qurZYy+ZJEnSFHOcKEmSpB42mMvKVfVN4JtjKYkkSdI8Yk2UJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg+rTKKSbJzkxCQ/SnJGkjdMomCSJEnTbIMR1rkW2Keqrk6yIfDdJEdX1fFjLpskSdLUWmUSVVUFXN39uGE31TgLJUmSNO1G6hOVZP0kpwCXAl+rqhPGWipJkqQpN1ISVVU3VtUDgO2A3ZPcZ3idJEuTLEuybPny5Wu4mJIkSdNlTk/nVdWVwLHAY2ZZdkhVLamqJYsWLVpDxZMkSZpOozydtyjJlt3nTYBHAmePuVySJElTbZSn87YBPpRkfVrS9Ymq+sJ4iyVJkjTdRnk671RglwmURZIkad5wxHJJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHlaZRCW5c5Jjk5yZ5Iwkr5xEwSRJkqbZBiOscwPwt1V1cpLNgJOSfK2qzhxz2SRJkqbWKmuiquqXVXVy9/kq4Cxg23EXTJIkaZrNqU9UksXALsAJYymNJEnSPDFyEpVkU+Ao4FVV9ZtZli9NsizJsuXLl6/JMkqSJE2dkZKoJBvSEqiPVNWnZ1unqg6pqiVVtWTRokVrsoySJElTZ5Udy5MEOAw4q6reMf4iSdLkLT7wi2u7CL2cf9Dj1nYRpHXWKDVRDwGeA+yT5JRueuyYyyVJkjTVVlkTVVXfBTKBskiSJM0bjlguSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDxus7QJo+i0+8Itruwi9nH/Q49Z2ESRJC5g1UZIkST2YREmSJPWwyiQqyQeSXJrk9EkUSJIkaT4YpSbqcOAxYy6HJEnSvLLKJKqqvg1cMYGySJIkzRv2iZIkSephjSVRSZYmWZZk2fLly9fUbiVJkqbSGkuiquqQqlpSVUsWLVq0pnYrSZI0lWzOkyRJ6mGUIQ4+Bnwf2DnJhUleMP5iSZIkTbdVvvalqp4xiYJIkiTNJzbnSZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUwypf+yJJ0jgsPvCLa7sIvZx/0OPWdhE0JayJkiRJ6sEkSpIkqQeTKEmSpB7sEyVJ0jrCfmhrljVRkiRJPZhESZIk9TBSc16SxwDvBtYHDq2qg8ZaqpWwKlKSJE2DVdZEJVkf+E9gX+BewDOS3GvcBZMkSZpmo9RE7Q6cW1XnAST5OLA/cOY4Cyaty6xxlaTpN0qfqG2BCwZ+vrCbJ0mStM5KVa18heSpwGOq6oXdz88B9qiqlw+ttxRY2v24M/DjNV/csdsKuGxtF2IdY8wnz5hPnjGfPGM+efM55ttX1aK5bjRKc94vgDsP/LxdN+8WquoQ4JC5FmCaJFlWVUvWdjnWJcZ88oz55BnzyTPmk7cuxnyU5rwfADsmuWuSWwF/DnxuvMWSJEmabqusiaqqG5K8HPgKbYiDD1TVGWMvmSRJ0hQbaZyoqvoS8KUxl2UazOvmyHnKmE+eMZ88Yz55xnzy1rmYr7JjuSRJkv6Yr32RJEnqwSRKkiSpB5OoBSTJRkk27D5nbZdnXZBkve5f4z0hSW7VvY7KuE9I992yUffZmI/RTHyTbJJkUffZ39UTkGTTJIu7zyPd516YBSDJXknOAL4O/DVA2dltbJJsluQ1SU4F3tPN9v/SGCXZOsk/J/ke8GXgr8D7fJyS3CHJW5N8A/gG8NdJNjLm41VVleQBwM+Bv1vLxVnwktwuyZuSfBH4IXAAjP7dMtLTeZou3V8lqaobk2xMGyn+74FvA19Mch5wlF92a04X8/Wq6gbaUB/bAEcAzwKoqhvXYvEWpMH7nDbg7zbAq4CfAd9I8qOq+sZaLOKCM3SfbwRsCPwjcBpwHLAMOGbtlXDhmallqqqbBmbfk/ZH8V1nWabVNHSfbwYcCDyqqo6d677863kemalerKqbZn5pV9XvaS+J/mFVXQn8O/Aw2qt3tJqGYn5D9/lK4K3AO4Brk+wyuK5Wz2z3OXAu8Oqq+kFVXQqcSPcLRqtvBff5BVX16qo6rqquAs4Dfr82y7mQDMV8OEl6KnAk8Pskuw2ur/5WcJ//DDijm0iyzVz2aRI1hdKsP9wO3lXz3jHJw5K8O8l+SbYAvgvcp1vtDOBawF/sczBizN+VZP9u/vLui+804NHd6v5/moM5xPwJVXVlVV3dvTUBWi2JtX9zNJeYD2zzvCTX096LdqdJl3m+m+t3S9eUdy5wCnAJrVYK/H4Z2Rxi/pRu0enA8UlOAt6bZOmo/dC8KFMgyZZJHtclRFRzY1XdNJgEJXkWrUr9scCfAs8DrgEu4ub/aMuBi4FtZ/Y1uTOZP3rG/BHAC7r5M/93vgXsPdnSz0+rEfMXdfM3rKrrkuwObA98yj8SVm51Y945Grh9N+/JM7/sNbvViPlLukU7ARdV1U+BK4EXJ3mxXQZWbDVi/sJu0buAg4CHAP8KPBF48ijHtk/UdLgXrW/NtcAxSXYGng3sAXwnyXtp1egPBl5ZVZ9PcgxwKBDgbOAxAFV1Rbf90ZM/jXllRTHfHfjuSmL+AWjVwd1/zhOA13Tz/JJbudWN+fXdfl4DHFxVV0/6BOah1Yo5QFVd3H08M8mFwF2TrGc/nRXq+31+WFfTuhPwnCRLgU1p3/EXrYXzmE/63ucfBKiqZbT+fgAnJjkT2HqU+9yaqAnpqhdXFO/zadW3d+9+fhitRuk1wG+Bf6LdHEuAH3V/kX+Vdv3uCXwGeECSR3Xb36Xbfp3WM+av5eaYX8cfx3zmyZmZv3Z+AlyT5B1JXpBk63Gdz3wwxpjPNE/vSfsyXJZk/yTPTLLZuM5nPhj3fT5wnPWBHYGz1/UEakzf5wHuRntC7CBgP+CBwA9ozXrrdPeMMd3nN81yn29A61P8k1Huc5OoCel+4a7ogiwHfkn7CwTgQ8BJwEtp1Y17Abfq1ttj4C/yq4D9q+oa4A3AXyS5HDi1m9ZpayDmGwKXAg8aivljAZI8KMm3aL9YdgGup1W/r7PGGPPHd59fQfuL81DaU6nXAL9bw6cxr4wx5o8GSPLiJD+g9dE5l1b7uk4b4/f5k6rqi1X1wao6j5ZsfYmu/9+63D1jjPf5vgBJDkjrE/VD4Me0h1dWyea8NWy26r8ue94B+Avg+qp6w+Dyqro+yc+BXZPchZYxv5jW3+ZfaE+B7Qn8N/C0rt03wGW0akxotVFfr/bk2DplhJhfV1VvHFw+FPPtaV9WL6YNEzEY80NpMd+82/Ry4P7d558Dr6qqH47lxKbYhGN+BXCP7vMHgPdU1fFjObEpthZifr/u8w+Bl1fVOpc8rYXv8/t2x9ioqq6tql8Dh43xFKfOWrjP79t9Pg142Vy/W6yJWg1J1uuquP9g5uInuU/aGE7QLuC7aX9NfGhoHzPVsz+n1WRsCzwU2KKqDgNuoFXxPqWqPku7CfajjW3xPrrqy64T3ZXdPtdfqNW+PWN+xNA+hmN+J26O+aGsOOab02J+t+64F80kUF3Mb1GuhWIKYn4w3ZAdVXXMzJfcbOVaKKYs5ifOJFB+twDj/T7fsTvutcNlW0OnOVWm5D7fqTvuyQPfLSPf59ZEzUGSDFanzla1mORA2hgfvwG+leQI2mi/DwQ+WVXnD64/sL9fdtMDaLVKz01yFO1Cf4Z2I0D7a+YUYDdaNeXbhstQC6iDszGfvGmP+Uz5VlK1P+/Mo5h7n0/4u2VFZZuPpj3mfe5zk6hVGKxaHLz4ae+oezTwNFq76ttoba5FewpjC+BTwJbAO2kD1a0s3pd3057AIcDLaU/cfauqzhxYb+PuWFsAXwQ+v7rnOG2M+eTNp5gPlm8+M+aTN59ivlDMp5j3us+rymlgoo2CvBTYdpZl2wKP7z4/Cvga8BTg3t28R9M6Fh9De6LisO5muDWt2vcJqzj2DsBdV7Bs/bUdG2O+cCZjbsyNuTE35qs/WRPVGciWt6J1Yj0X+EWShwObVNWXaH0E/jrJj2lVhBvQOqNd0+3mJFoW/aJqA6UN7v8S4L5Jjq2qq7r21nDzu8Go9jTG4DYzQ9RXLaBq9BnGfPKM+eQZ88kz5pO3rsZ8QXZWG8VMcAeCPDN44jm0MTlm3su1Nze/1uM4WrXjnWiDWV4OvAx4Z5KZKsETgf3ThpZ/ZNr4QXekvZrlYuAP1Zo18G6wJHdJG4l5+MIviGp0MOZrgzGfPGM+ecZ88ox5s07URGXoLdlJ6zyW7jHSJBvRqh+3qKo3J7kY2KG7EKcA+ya5Q1VdmuSXtEcij6uqp3b724zWBrsn8Je0xzC/SBu74rPA1VX1uaEybQw8DtgH2JX2eOt/dOWc9//RjPnkGfPJM+aTZ8wnz5iv2IJMooYveA08AZDk9lV1eZI70Hr+P7iqfpXkOmDL7mKeRxsjZVvg/2iPVd6P1k57Ae2dO0cm2ZL2jp0H0NpsT+hukjcB/zx8IXPL8S8eSRtZ/P20EYCvZx6bRzG/M8bcmPdkzCdvHsXc7/N18D5fkM151ar4ZjLm2yTZJ8nBSc4BPphkz6q6lDZU/MO6zf6P9mb4HbvP19FeqXIOrfrxcd16m9Pae7cBtu7W/zTwnG6fVNX1XZZ+izEwBm/Eqvp8Vb2zqk6b7//hYF7F/F3G3Jj3Zcwnbx7F3O/zdfA+X3BJVJIt0t6n9dEkD6RdrLfQeubvBHwfeEmSuwPHcnNb7fm0ttYdae25lwH3rKrraKMkPyDJ6bSObK8CflxV362qpVV1VFX9ZrgsNdBeu5AZ88kz5pNnzCfPmE+eMZ+bedGcl/yh/fUWA3XNst56wOtpVYjfpl3U9YCzacO7A3yM1t66J/BN4DkAVXVukj2Aq6rqyCQXAPdPsnlVnZPk6TNZ8izHvEWGvBAY88kz5pNnzCfPmE+eMR+fqU2iksw8unjTzEWf+TfJTsBlVXXF0E2xN7BXVT1wYD8bActo7dVU1flJdgBOr6oT04Z3/1fg9rS22mvSOqxdQOustgNwyszFH77g8/XCz8aYT54xnzxjPnnGfPKM+WRMTRLVBXZwvIeijRdBWrXhVrSe+h/vNjkNeP5QVn0F3XgTaaOh3lTtyYHzgaVJPlJVP6J1RpvJqp8B7N/t77NVdVW3/SW0lxjuAJwyc6PN9ws+yJhPnjGfPGM+ecZ88oz52rHWkqgMval5OLBpb7Z+Ga2j2n7A72ljRDy5qi5I8pMku1bVyQObXQ5cm+QhVfW9bj8z41b8DHh72hMFxwInd8f9EfCjgePOZOUXAl+lu1GGbrR5yZhPnjGfPGM+ecZ88oz5dJh4EtVdgIcBn+x+nmmrfRiwLy1bfl1VXZRkf+DMqto1yS60tthNu10dCzw4ySl1c7XgL5KcDLyy29/Dae267wKOB9arqjfNUqbZqj2vA7635iMwecZ88oz55BnzyTPmk2fMp8vYn85L1/45o1q76FLgz5O8Ftg8yd2AZ9Oy2S8B70iyLfBl4JfdBbqQ9ibnPbpdnQDcH7hNkg2T7NvN/yfagFu3A94BvBX4Le0Ryx26MmWwXNUsmCpGYz55xnzyjPnkGfPJM+bTbexJ1Exgk2yfZK8ku9J6/r8BuDvtwrwKuAi4mtbTfwlt/IjTgO2ATWgvJfwxraMatOHjd6dd6I2BfZJsXFXXVdV3qupvq+pL1cabuJFWrfj2rkwL+oIb88kz5pNnzCfPmE+eMZ9ytXpvaw4reDMy7aJtAuwGfIt2MV8H3BF4NfD2gXX/gdZu+nrgCcBG3fy70C7c3bqfHw98Z+aYwJOA26zg+OvRqh5X6xynbTLmxtyYG3NjvjAmYz7/pzV9Q2zR/bs58D7gmcCzgH8dWm8X4CvAYlq/rEcC3x5a56Hdv8cB+3efbw/sPHOBZ7kZs7YDOvELaMyN+TowGXNjvi5Mxnz+Tb06lg90ZNsJeCpwK1o14k60ttqtu5vgGFoW/byu/fQS4Jyq+lzaUO6Lqup84GtJ/i7Je2hVi7sCn6Fl38+jvYeHqrqc9vQANVSVWN1dsFAZ88kz5pNnzCfPmE+eMV840jduSe4BHA58jXahLwWOAJ5Pa3c9C7h3Vf0+yRLaEwEPAg6gvUPnGbR359wB+O+q+lqSp9NeQnhMVV2wGue1IBnzyTPmk2fMJ8+YT54xXxhWZ4iDuwHnAh8CflFVv0tyEPA3wBeAo4Ctk/y8qpbBHwbf2hnYEDiYVlV5JW0MCqrqyNUoz7rAmE+eMZ88Yz55xnzyjPkCsDo1UZsBH6SNSLoe7RHId9CGjX8DcGRV/VWSTWjVla+jZdpHAu9dUdVhhgYQ082M+eQZ88kz5pNnzCfPmC8MvZOoW+ykVUs+n/bW5oOBdwPbVNVjk4Q2+Nf1VXXlLNuuTxta3vbYOTDmk2fMJ8+YT54xnzxjPn/1bs7rLuydgPvSBu/aBXhpVV2d5ETgdknWrza+xPKBbdbr5gEw+FkrZ8wnz5hPnjGfPGM+ecZ8Yeg92GaX9d4ZeBFwA/DaqvpJkh2BFwMnV9WN3UX/wzZe8P6M+eQZ88kz5pNnzCfPmC8Ma6Q57xY7bE8H3Bt4d7XHKTVmxnzyjPnkGfPJM+aTZ8znl9VOomaqF2lJsp3ZJsCYT54xnzxjPnnGfPKM+fy2xmuiJEmS1gVjfwGxJEnSQmQSJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktTD/wc6BSF24WiakgAAAABJRU5ErkJggg==\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAh3UlEQVR4nO3deZxkVXnw8d8zAwzI+ioDsqgDyKaigCMIGEAUFBER5XVDgksymEgUFwz6iQkYE9HXIJoElYCKCRoiGhFZVGQTlGXYZZWQUXYGEAWBYXveP85pKYru6eo7Xberun/fz+d+uqruUuc+93bVU+ece25kJpIkSZqYWVNdAEmSpGFkEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUgEmUpKEVEXMi4pqIWGeqy6LR1WN0XUTMneqySJPNJEozQkQcGBELI2JJRHxjlPnPiIijIuLuiPhdRJw7gW1nRDy/QZlWiIgTI2JR3cbOoyyzdUScGxEPRMSdEfHBUZbZqa7/6Y7XvlLXGZmWRMT9HfM3j4gz677eGBF7d23zLRFxbUTcX5OUN3bMe1dEPN61/Z3rvLUi4tsRcVvd9vkRsW3Hup/oWu+hiHgiItas8z8XETdHxO8j4tcR8YlxwrgAODczb+8q/6E1Jtt2vb5CRPxTRNxS339RRBw5zns8TUScHREPd+zH9R3z9oiI8yLivoi4IyKOiYhVO+aPuY8RsXpE/Kiue3xEzO6Yd3REvKlBWVepZTxtlHmL6jF4ICJ+GxGnRMRzGrzHKyPirHrMF3XOy8wlwNeAQya6XWnQmURpprgN+DTlw3w0RwPPBDavfz/UUrnOA94J3NE9oyYWpwNfBZ4FPB/4cdcyywNfBC7sfD0z35eZq4xMwLeB79R1lgNOAn5I2dcFwH9ExCZ1/nrAfwAfBlYDDga+FRFrdbzFLzq3n5ln19dXAS4GXlq3fRxwSkSsUsv1j13l+ixwdmbeXdc/FtgsM1cDtgf2HSdxeB/w710xCeBPgXvr304fB+YD2wCrAjsDly5l+0tzYMe+bNrx+uqUc21dyvm0HvD/OuYvbR8PAC4D1gbmAXvXfdoOWDczv9egnG8GlgC7RsSzR5m/Zz0W6wB3Av/c4D3+QPnfOniM+d8C9o+IOQ22LQ0skyjNCJn5vcz8PnBP97yI2Ax4A7AgMxdn5uOZeUkv2+2osbqi/pp/6wTK9EhmHpmZ5wGPj7LIh4EfZebxmbkkM+/PzGu7lvkIJbG6billXJnyRXpcfWkzyhf8F+q+ngmcD+xX568P3JeZp2VxCuVLcqMe9ummzDwiM2+v2z4aWAHYtHvZjmTnuI71r8/MP3Qs9gQleRxtv54LbEhXAgn8CSUh+ADwtohYoWPey4D/zszb6r4tysxvjrdfE5GZ38rM0zPzwcz8LfBvwA4d85e2jxsAZ9Xam58BG9baqC/U/Wlif+ArwJWUhH2scj8MnAi8YKJvkJkXZea/AzeNMf8W4LfAyye6bWmQmURJpVbi18BhUZrzroqIN/eyYmbuWB++pNZInBARz63NMWNN7+ixXC8H7o2In0fEXRFxck0cAIiI5wHvAT41znbeDCwGltZEGcCL6uOFwLUR8YaImF2b8pZQvoRHbFVjdUNEfLLWbj19oxFbUpKoG0eZ/SfAWsB3u9Y5JCIeAG4BVqbUYoxmC+CmzHys6/X9gZOB/6rP9+yYdwHw4Yj4y4jYoiZyne/9w6Uctx92vc9nagzOj1GaYjvsCFzd4z7+Enh1RKxEic/VlOTptMwcNUFZmnqO7AwcX6fumrnOZZ8BvJUSo85yjnkuT7A41wIvmeg+SAMtM52cZsxEaWb5RtdrnwASOJTyhb8T8ACweY/bTOD5y1iuW4Cdu167AbiPUnuyIvAl4PyO+ScBb62PvwF8eoxt/xQ4tOP58pQag4/Vx7sBj1BqvUaWeW+NwWPAg8AeHfM2pNSYzKIkMtcAHx/lfVcDrhptXp1/bPex6JgXwFbAYcCqYyyzL3BB12vPAH4PvLE+/ypwUsf82cD7KTVvSyjNvPs3OF7bUpoD51CStvuBjUZZbldKDcwmvexjPc5HUxLWwym1gpdSmgi/QkmERz3OY5Tzb4DL6+P1KDWeW3XMX1SP833AozUeWyzDefxqYNEY844H/nZZ/k+cnAZtsiZKgocoXyCfztLEdg5wFiW5mEoPUZqeLs7S1HIYsH3tfLwn5Yv3hKVtoNZc7Qz8sckqMx8F3gjsQemL9RFKrc0tdZ1XA5+r640klcfUWiWyNNn9b2Y+kZlXUWrC9ul635UotUEXZOZnRinXM4D/S0dTXqcsLqsxOGyM3fstJZHptDcl8Tu1Pj8e2D3qlWFZmhj/NTN3ANYA/gH4WkRsPsZ7jCozL8zSvLokM4+jJGWv69rHl1NqmPbJzBt62cfMfDgzF2TmizPzEEoz3icoCeMsyrHYNiJe22NR/7TGgMy8FTiHkvR1emNmrkFJ4A4Ezhmj79SyWpWSrEnThkmU9NRmqhHZdGO1Oe+BpUz7TqBcneXofPwqYH6Uq7/uoDTDHBQRJ3VtYz9K7dVTmoIy88rM3Ckzn5WZr6HULl1UZ29JueJtYU2ULqb0O3r1GOVMSq3KyP7PAb5PScoOGGOdvSkdv88eY/6I5Ri7L9aVwAZdTYn7Uzq3/6bG5TuU2ranNaFm5kOZ+a+UZOwFteynLeW4Pe3qts7N8dQYbAX8AHhPZv60yT7WRCky83RKjd/CzExKc+uLx9kmEbE9sDHw8Y7zZFvgHaM1v9YE83uU2qpX1G10X035lGm8MnTZHLhigutIg22qq8KcnNqYKF9UKwKfoVzNtSKwXJ23PKXPzifrcjtQmmc263HbdwC7NSzXnFqWWyg1XytSvjgBdqF8wW9Zy/gF4Gd13qrAszumE+r8Z3Zt/3rKF3n3+764vtczgI8C/wvMqfN2Au4GtqzPt6J0yN+tPt8dWLs+3ozSj+fvOmJ5MiWJWm4p+/1j4FNdr82iJF3/h5KQbAPcDnxgKdu5Eti+Ph5prtqtKzaHA5fUZQ6i1LCtVI/1/pRmvQ0ncMzWAF4zcg5Raon+QG2yo/Qtu5Pa1NpkH+u2LwfWr88/RqnVWoHSpLdPff1QytWNo5XzqzXOnbHYgHJu71mXWQS8uj4OYC9KTd4LJ3gez6pl3p3Sv3BFYIWO+evVc2jOVH8WODlN5jTlBXByamOqXzbZNR3aMf+FwC/ql+E1wN4d8z5B6dg71rbfV78I7wPeMsFyLRqlXPM65v8FcCslmToZeM4Y2/kGXX1lgO3q/jytTxHlkvvfUvrDnEZXny5Ks86N9Qv3JuAjHfM+X5OEP9R5nwKWr/N2qvvwYN32yPQnHeuvV7+ou99zFmVIh3vrOjfU2MdS4vd+4Mv18SHUZKlrmXUpzbUvogzncAnwu3q8LgJeP8FjNpcyjMP9dRsXALt2zP865Yq7zv2/eiL7WGN6cMfz1SkJ0e8oydTs+vqxwD+MUsYV6/Hdc5R5RwEndpx/D9Wy3E9JiPdt8P+18yjn8dkd8w8Gjmj7/97Jqd/TyC9eSRo6tenwMuBV2TXg5kwQEZdT9v1pQ3cMinqMrgB2zMy7pro80mQyiZIkSWrAjuWSJEkNmERJkiQ1YBIlSZLUgEmUJElSA6Pe72pZrbnmmjlv3rx+bFqSJGlSXXLJJXdn5tyJrteXJGrevHksXLiwH5uWJEmaVBHx6ybr2ZwnSZLUQE9JVESsEREnRsR1EXFtRGzX74JJkiQNsl6b874InJ6Z+0TECpT7bUmSJM1Y4yZREbE6sCPwLoDMfAR4pL/FkiRJGmy9NOdtACwGvh4Rl0XEMRGxcvdCEbEgIhZGxMLFixdPekElSZIGSS9J1HLA1pQ7pW9FuXP7Id0LZebRmTk/M+fPnTvhqwQlSZKGSi9J1C3ALZl5YX1+IiWpkiRJmrHGTaIy8w7g5ojYtL70KuCavpZKkiRpwPV6dd5fAcfXK/NuAt7dvyJJkiQNvp6SqMy8HJjf36JIkiQND0cslyRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWpguV4WiohFwP3A48BjmTm/n4WSJEkadD0lUdUrM/PuvpVEkiRpiNicJ0mS1ECvSVQCP46ISyJiwWgLRMSCiFgYEQsXL148eSWUJEkaQL0mUa/IzK2B3YH3R8SO3Qtk5tGZOT8z58+dO3dSCylJkjRoekqiMvPW+vcu4L+BbfpZKEmSpEE3bhIVEStHxKojj4HdgF/2u2CSJEmDrJer89YG/jsiRpb/Vmae3tdSSZIkDbhxk6jMvAl4SQtlkSRJGhoOcSBJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNWASJUmS1IBJlCRJUgMmUZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUQM9JVETMjojLIuKH/SyQJEnSMJhITdQHgWv7VRBJkqRh0lMSFRHrA3sAx/S3OJIkScOh15qoI4GPAU/0ryiSJEnDY9wkKiJeD9yVmZeMs9yCiFgYEQsXL148aQWUJEkaRL3URO0AvCEiFgH/CewSEf/RvVBmHp2Z8zNz/ty5cye5mJIkSYNl3CQqMz+emetn5jzgbcCZmfnOvpdMkiRpgDlOlCRJUgPLTWThzDwbOLsvJZEkSRoi1kRJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNWASJUmS1IBJlCRJUgMmUZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNTBuEhURK0bERRFxRURcHRGHtVEwSZKkQbZcD8ssAXbJzAciYnngvIg4LTMv6HPZJEmSBta4SVRmJvBAfbp8nbKfhZIkSRp0PfWJiojZEXE5cBfwk8y8sK+lkiRJGnA9JVGZ+XhmbgmsD2wTES/qXiYiFkTEwohYuHjx4kkupiRJ0mCZ0NV5mXkfcBbw2lHmHZ2Z8zNz/ty5cyepeJIkSYOpl6vz5kbEGvXxSsCuwHV9LpckSdJA6+XqvHWA4yJiNiXp+q/M/GF/iyVJkjTYerk670pgqxbKIkmSNDQcsVySJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpgXGTqIh4TkScFRHXRMTVEfHBNgomSZI0yJbrYZnHgI9k5qURsSpwSUT8JDOv6XPZJEmSBta4NVGZeXtmXlof3w9cC6zX74JJkiQNsgn1iYqIecBWwIV9KY0kSdKQ6DmJiohVgO8CB2Xm70eZvyAiFkbEwsWLF09mGSVJkgZOT0lURCxPSaCOz8zvjbZMZh6dmfMzc/7cuXMns4ySJEkDp5er8wI4Frg2M4/of5EkSZIGXy81UTsA+wG7RMTldXpdn8slSZI00MYd4iAzzwOihbJIkiQNDUcslyRJasAkSpIkqQGTKEmSpAZ6ue3LQJl3yClTXYRGFh2+x1QXQUPE81xSP/jZMrmsiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWpg3CQqIr4WEXdFxC/bKJAkSdIw6KUm6hvAa/tcDkmSpKEybhKVmecC97ZQFkmSpKFhnyhJkqQGJi2JiogFEbEwIhYuXrx4sjYrSZI0kCYticrMozNzfmbOnzt37mRtVpIkaSDZnCdJktRAL0McfBv4BbBpRNwSEe/tf7EkSZIG23LjLZCZb2+jIJIkScPE5jxJkqQGTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaWG6qCyBJmpnmHXLKVBehkUWH7zHVRdCAsCZKkiSpAZMoSZKkBnpKoiLitRFxfUTcGBGH9LtQkiRJg27cJCoiZgP/CuwOvAB4e0S8oN8FkyRJGmS9dCzfBrgxM28CiIj/BPYCrulnwTQ47PwpSdLT9dKctx5wc8fzW+prkiRJM1Zk5tIXiNgHeG1m/ll9vh+wbWYe2LXcAmBBfbopcP3kF7fv1gTunupCzDDGvH3GvH3GvH3GvH3DHPPnZebcia7US3PercBzOp6vX197isw8Gjh6ogUYJBGxMDPnT3U5ZhJj3j5j3j5j3j5j3r6ZGPNemvMuBjaOiA0iYgXgbcAP+lssSZKkwTZuTVRmPhYRBwI/AmYDX8vMq/teMkmSpAHW021fMvNU4NQ+l2UQDHVz5JAy5u0z5u0z5u0z5u2bcTEft2O5JEmSns7bvkiSJDVgEiVJktSASdQ0EhFzImL5+jimujwzQUTMqn+Nd0siYoV6Oyrj3pL62TKnPjbmfTQS34hYKSLm1sd+V7cgIlaJiHn1cU/nuQdmGoiIV0TE1cBPgQ8BpJ3d+iYiVo2IgyPiSuBL9WX/l/ooItaOiL+LiPOB04EPgOd5P0XEWhHxmYg4EzgT+FBEzDHm/ZWZGRFbAr8B/nqKizPtRcQzI+LvI+IU4DJgf+j9s6Wnq/M0WOqvksjMxyNiRcpI8R8HzgVOiYibgO/6YTd5asxnZeZjlKE+1gG+CewLkJmPT2HxpqXO85wy4O86wEHAr4EzI+KKzDxzCos47XSd53OA5YG/Aa4Cfg4sBM6YuhJOPyO1TJn5RMfLm1N+FG8wyjwto67zfFXgEGC3zDxrotvy1/MQGalezMwnRr60M/Nhyk2iL8vM+4B/Anam3HpHy6gr5o/Vx/cBnwGOAJZExFady2rZjHaeAzcCH83MizPzLuAi6heMlt0Y5/nNmfnRzPx5Zt4P3AQ8PJXlnE66Yt6dJO0DnAA8HBEv7VxezY1xnv8auLpORMQ6E9mmSdQAimJ2dzt4reZ9dkTsHBFfjIg9I2J14DzgRXWxq4ElgF/sE9BjzI+MiL3q64vrB99VwGvq4v4/TcAEYv6GzLwvMx+od02AUkti7d8ETSTmHeu8OyIepdwXbd22yzzsJvrZUpvybgQuB+6k1EqBny89m0DM31xn/RK4ICIuAf4lIhb02g/NgzIAImKNiNijJkRk8XhmPtGZBEXEvpQq9dcBrwbeDTwI3MaT/2iLgTuA9Ua21d6eDI+GMX8V8N76+sj/zjnAju2WfjgtQ8z/vL6+fGY+EhHbAM8DTvRHwtIta8yr04Bn1dfeNPJlr9EtQ8zfV2dtAtyWmf8L3AccEBEH2GVgbMsQ8z+rs44EDgd2AD4LvBF4Uy/vbZ+owfACSt+aJcAZEbEp8E5gW+BnEfEvlGr07YEPZubJEXEGcAwQwHXAawEy8966/mnt78ZQGSvm2wDnLSXmX4NSHVz/OS8EDq6v+SG3dMsa80frdg4GjsrMB9regSG0TDEHyMw76sNrIuIWYIOImGU/nTE1/Tw/tta0bgLsFxELgFUon/G3TcF+DJOm5/nXATJzIaW/H8BFEXENsHYv57k1US2p1YtjxXsRpfr2+fX5zpQapYOBPwB/Szk55gNX1F/kP6Ycv82B7wNbRsRudf3n1vVntIYx/xhPxvwRnh7zkStnRn7t/Ap4MCKOiIj3RsTa/dqfYdDHmI80T29H+TBcGBF7RcQ7ImLVfu3PMOj3ed7xPrOBjYHrZnoC1afP8wA2olwhdjiwJ/Ay4GJKs96M7p7Rp/P8iVHO8+UofYp/1ct5bhLVkvqFO9YBWQzcTvkFAnAccAnwl5TqxlcAK9Tltu34RX4/sFdmPggcBrwrIu4BrqzTjDYJMV8euAt4eVfMXwcQES+PiHMoXyxbAY9Sqt9nrD7G/PX18V9RfnEeQ7kq9UHgoUnejaHSx5i/BiAiDoiIiyl9dG6k1L7OaH38PN87M0/JzK9n5k2UZOtUav+/mdw9o4/n+e4AEbF/lD5RlwHXUy5eGZfNeZNstOq/mj1vCLwLeDQzD+ucn5mPRsRvgK0j4rmUjPkASn+bf6BcBbYd8G/AW2q7bwB3U6oxodRG/TTLlWMzSg8xfyQzP9U5vyvmz6N8WB1AGSaiM+bHUGK+Wl31HuAl9fFvgIMy87K+7NgAaznm9wKb1cdfA76UmRf0ZccG2BTE/MX18WXAgZk545KnKfg836K+x5zMXJKZvwOO7eMuDpwpOM+3qI+vAt4/0c8Wa6KWQUTMqlXcfzRy8CPiRVHGcIJyAL9I+TVxXNc2Rqpnf0OpyVgP2AlYPTOPBR6jVPG+OTNPopwEe1LGtvgytfqydqK7r25z9nSt9m0Y8292baM75uvyZMyPYeyYr0aJ+Ub1fW8bSaBqzJ9SruliAGJ+FHXIjsw8Y+RDbrRyTRcDFvOLRhIoP1uA/n6eb1zfd0l32SZpNwfKgJznm9T3vbTjs6Xn89yaqAmIiOisTh2tajEiDqGM8fF74JyI+CZltN+XAd/JzEWdy3ds7/Y6bUmpVfrTiPgu5UB/n3IiQPk1cznwUko15ee6y5DTqIOzMW/foMd8pHxLqdofOkMUc8/zlj9bxirbMBr0mDc5z02ixtFZtdh58KPco+41wFso7aqfo7S5JuUqjNWBE4E1gC9QBqpbWrzvqdN2wNHAgZQr7s7JzGs6lluxvtfqwCnAycu6j4PGmLdvmGLeWb5hZszbN0wxny6GKeaNzvPMdOqYKKMgLwDWG2XeesDr6+PdgJ8AbwZeWF97DaVj8RmUKyqOrSfDMyjVvm8Y5703BDYYY97sqY6NMZ8+kzE35sbcmBvzZZ+siao6suU1KZ1YbwRujYhXAitl5qmUPgIfiojrKVWEy1E6oz1YN3MJJYv+8ywDpXVu/05gi4g4KzPvr+2twZP3BiPL1Rid64wMUZ85jarRRxjz9hnz9hnz9hnz9s3UmE/Lzmq9GAluR5BHBk+8gTImx8h9uXbkydt6/JxS7bguZTDLe4D3A1+IiJEqwYuAvaIMLb9rlPGDnk25NcsdwB+rNbPj3mAR8dwoIzF3H/hpUY0OxnwqGPP2GfP2GfP2GfNiRtRERdddsiNK57Gol5FGxBxK9ePqmfnpiLgD2LAeiMuB3SNircy8KyJup1wS+fPM3Kdub1VKG+x2wF9QLsM8hTJ2xUnAA5n5g64yrQjsAewCbE25vPWfazmH/h/NmLfPmLfPmLfPmLfPmI9tWiZR3Qc8O64AiIhnZeY9EbEWpef/9pn524h4BFijHsybKGOkrAf8D+WyyhdT2mlvptxz54SIWINyj50tKW22F9aT5O+Bv+s+kPHU8S92pYws/hXKCMCPMsSGKObPwZgb84aMefuGKOZ+ns/A83xaNudlqeIbyZhXjohdIuKoiLgB+HpEbJeZd1GGit+5rvY/lDvDb1wfP0K5pcoNlOrHPepyq1Hae9cB1q7Lfw/Yr26TzHy0ZulPGQOj80TMzJMz8wuZedWw/8PBUMX8SGNuzJsy5u0bopj7eT4Dz/Npl0RFxOpR7qf1rYh4GeVg/SOlZ/4mwC+A90XE84GzeLKtdhGlrXVjSnvu3cDmmfkIZZTkLSPil5SObAcB12fmeZm5IDO/m5m/7y5LdrTXTmfGvH3GvH3GvH3GvH3GfGKGojkv4o/tr08ZqGuU5WYBh1KqEM+lHNRZwHWU4d0Bvk1pb90OOBvYDyAzb4yIbYH7M/OEiLgZeElErJaZN0TEW0ey5FHe8ykZ8nRgzNtnzNtnzNtnzNtnzPtnYJOoiBi5dPGJkYM+8jciNgHuzsx7u06KHYFXZObLOrYzB1hIaa8mMxdFxIbALzPzoijDu38WeBalrfbBKB3WbqZ0VtsQuHzk4Hcf8GE98KMx5u0z5u0z5u0z5u0z5u0YmCSqBrZzvIekjBdBlGrDNSk99f+zrnIV8J6urPpe6ngTUUZDfSLLlQOLgAURcXxmXkHpjDaSVb8d2Ktu76TMvL+ufyflJoYbApePnGjDfsA7GfP2GfP2GfP2GfP2GfOpMWVJVHTdqbk7sFHubP1+Ske1PYGHKWNEvCkzb46IX0XE1pl5acdq9wBLImKHzDy/bmdk3IpfA5+PckXBWcCl9X2vAK7oeN+RrPwW4MfUE6XrRBtKxrx9xrx9xrx9xrx9xnwwtJ5E1QOwM/Cd+nykrXZnYHdKtvzJzLwtIvYCrsnMrSNiK0pb7Cp1U2cB20fE5flkteCtEXEp8MG6vVdS2nWPBC4AZmXm349SptGqPR8Bzp/8CLTPmLfPmLfPmLfPmLfPmA+Wvl+dF7X9c0SWdtEFwNsi4mPAahGxEfBOSjZ7KnBERKwHnA7cXg/QLZQ7OW9bN3Uh8BJg5YhYPiJ2r6//LWXArWcCRwCfAf5AucRyw1qm6CxXFtOmitGYt8+Yt8+Yt8+Yt8+YD7a+J1EjgY2I50XEKyJia0rP/8OA51MOzEHAbcADlJ7+8ynjR1wFrA+sRLkp4fWUjmpQho/fhnKgVwR2iYgVM/ORzPxZZn4kM0/NMt7E45Rqxc/XMk3rA27M22fM22fM22fM22fMB1wu292agzHujEw5aCsBLwXOoRzMTwLPBj4KfL5j2U9Q2k0PBd4AzKmvP5dy4Daqz18P/GzkPYG9gZXHeP9ZlKrHZdrHQZuMuTE35sbcmE+PyZgP/zTZJ8Tq9e9qwJeBdwD7Ap/tWm4r4EfAPEq/rF2Bc7uW2an+/TmwV338LGDTkQM8yskYUx3Q1g+gMTfmM2Ay5sZ8JkzGfPimRh3LOzqybQLsA6xAqUbchNJWu3Y9Cc6gZNHvru2ndwI3ZOYPogzlPjczFwE/iYi/jogvUaoWtwa+T8m+3025Dw+ZeQ/l6gGyqyox61kwXRnz9hnz9hnz9hnz9hnz6SOaxi0iNgO+AfyEcqDvAr4JvIfS7not8MLMfDgi5lOuCHg5sD/lHjpvp9w7Zy3g3zLzJxHxVspNCM/IzJuXYb+mJWPePmPePmPePmPePmM+PSzLEAcbATcCxwG3ZuZDEXE48GHgh8B3gbUj4jeZuRD+OPjWpsDywFGUqsr7KGNQkJknLEN5ZgJj3j5j3j5j3j5j3j5jPg0sS03UqsDXKSOSzqJcAnkEZdj4w4ATMvMDEbESpbryk5RM+wTgX8aqOoyuAcT0JGPePmPePmPePmPePmM+PTROop6ykVIt+R7KXZuPAr4IrJOZr4uIoAz+9Whm3jfKurMpQ8vbHjsBxrx9xrx9xrx9xrx9xnx4NW7Oqwd2XWALyuBdWwF/mZkPRMRFwDMjYnaW8SUWd6wzq74GQOdjLZ0xb58xb58xb58xb58xnx4aD7ZZs97nAH8OPAZ8LDN/FREbAwcAl2bm4/Wg/3EdD3hzxrx9xrx9xrx9xrx9xnx6mJTmvKdssFwd8ELgi1kup1SfGfP2GfP2GfP2GfP2GfPhssxJ1Ej1IiVJtjNbC4x5+4x5+4x5+4x5+4z5cJv0mihJkqSZoO83IJYkSZqOTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGvj/lT2mSgfsahAAAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAiSUlEQVR4nO3debgkVX3/8feHYVURooyIKCIq7go4gohBXFAREbe4IeKSjGuUqBjME/NzS0R/xi3G+CPiQoIGBTc2t4giGsFhF3AhiICKDCA6iOzf3x+nrjTtnZmemumevnfer+fp5/btqjp96lt1u7/3nFOnUlVIkiRp1ay3tisgSZI0F5lESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVpzkqyUZLzkmy1tuui2XXH6EdJFq7tukhrmkmU1glJXpNkSZLrk3xyaNl+Sa4ZeFybpJI8fMSyK8l9etRpwyRHJbmoK2OPWdbZKclJXb1+neR1s6zzmG77dw689tGhfbo+ybKB5Q9I8s0kv01yQZJnDJX5nCTnJ1nWJSlPH1j24iQ3D5W/x8DydyQ5J8lNSd46S33/OsnPkvyuOyaPHlj21iQ3DpW93QrCuBg4qap+NfQeb+1issvQ6xsm+eckl3ZlX5TkAysof1ZJvpXkuoE6/nho+QuS/DzJ75N8McmdBpZtm+T4JL9JclmSDydZv1u2WZKvJrk6yRFJFgxsd2iSZ/ao6x26Op4wy7KLkvyhW/6bJMcluUeP93hskhO78+miwWVVdT3wceDgVS1XmnYmUVpX/BJ4J+3D/Daq6oiqusPMA3gVcCFw+gTqdTLwQuCy4QVJtgC+Avw/4M7AfYCvDa2zAfBB4JTB16vqFUP79Bngc9026wNfAo4F7kRLRP4zyfbd8q2B/wReD9wROAj4dJK7DLzF/wyWX1XfGlh2AfAm4LhZ9mkX4BDg2cBmwGHAFwaTBeDIobIvnD10ALwC+I+h9wjwIuCq7uegNwOLgJ2BTYE96H+cXzNQx/sNvP+DaMdsf2BL4FrgIwPbfQS4HNgK2AF4DO2cA3g5cEa33bbAM7oydwXuVlWf71HPZwHXA3smuessy/fpzpGtgF8D/9LjPX5P+9s6aDnLPw0ckGSjHmVLU8skSuuEqvp8VX0RuHKE1Q8ADq8RpvNPclL39Kzuv/nnrkKdbqiqD1TVycDNs6zyeuCrXZJ3fVUtq6rzh9Z5Ay2x+tEK6nh72hfpp7qX7g/cDXh/Vd1cVd8Evkv70ge4O3B1VZ1QzXG0L8l7j7hfn6qqE4BlsyzeFji3qk7r4ns4sAVwl1nWXaEk2wDbMZRAAn9OSwheCzwvyYYDyx4BfKGqftnt20VVdfiqvvdK7AccU1UnVdU1wFuAZybZtFt+L+CzVXVdVV1GS5QfNLDsxK715jvAdl2C+f5uf/o4APgocDYtYZ9VVV0HHAU8cFXfoKpOrar/oP3zMdvyS4HfAI9c1bKlaWYSJQ1Ick9gd9qX+0pV1e7d04d1LRJHJtmm645Z3uMFI1bnkcBVSb6X5PIkx3SJw2BdXwq8fSXlPAtYCpy0gnUCPLh7vgQ4P8nTkizouvKup30Jz9gxyRVJfpLkLTPdUSM4AViQZJcuOXgpcCa3bYnbJ8lVSc5N8soVlPUQ4MKqumno9QOAY4DPzpQ3sOz7wOuTvCrJQ7pWqz9KcuwKjtuxQ+/zri4G381tu2IfBJw180tV/S9wA7B999IHaMnd7bpWv71oiRTAD4EnJNmElgyeS0ueTlhJi9ysunNkD+CI7jHcMje47u2A59JiNPPawSs6l1exOucDD1vVfZCm2agffNK64kXAd6rqZ30LqKqLgc3XQF3uDuwE7AmcA7yH1i23W7f8Q8BbquqaoVxg2HDL2o9p3UkHJXk/8Fhal9KJXf1vTnI4rQtmY1oC8BdV9ftu+5NoCdfPaQnDkcBNwLtG2KdlwNG0bswAVwN7DdTts8ChtG6lXYCjk1xdVZ+ZpazNGWrt6hKBvwBeVFU3JjmKdkyP7lZ5F61FZD9a686VSd5cVZ/q9v2pI+wDwN8C59Fi8zzgmCQ7dAnTHYDfDq3/W1r3IbT4LQZ+ByygtRB+sVt2GO24ngIcT0vG3gE8NslHaa1EJ1XV349Yz/2Bs6vqvCS/Bd6TZMeqOmNgnS8muQm4PS3ZftLMgqo6hNb9uiYsY838XUhTw5Yo6bZexK3dXmvbH2hdTz/oulreBjyqG3y8D7BpVR25ogK6lqs9GGhZq6obgacDe9NagN5AS14u7bZ5Ai1h2wPYkJZgfSzJDt32F1bVz6rqlqo6h9YS9uwR9+llwEtoydeGtO6lY5PcrSv7vK6r7eaq+h5tvNfyyv4NtyYmM55BS+iO734/Atgr3ZVhXbn/WlW70b7Q/xH4eJIHjFh/unJO6bpXr+8SsO8CT+kWX0MbSzbojsCyJOvRWp0+T0tatgD+DHh3V+51VbW4qh5aVQfTEr2/oyV969GOxS5JnjxiVV/UxYCq+gXwbVpSPejpVbU5LWF+DfDt5YydWl2b0pJmad4wiZI6SXajjRU6ajXL2Sa3vbps+LHfiEWdDQyOyxp8/nhgUdrVXZfRumEOTPKloTL2B7473BVUVWdX1WOq6s5V9STa2KJTu8U70Fo7lnSJ0g9oLSNPWE49i9aqNIodgGOr6idd2V8BfgU8qkfZZwP3GupKPIDWEnRxF5fPARsAf9KFWlV/qKp/pSVjDwRIcsIKjtufXN22nHqey0C3VdrVhRsBP6EN5N8G+HCXgF0JfIJbEzAGtnsykC5GDwGWdC12S4CHrqAuM9s/Crgv8OaB82QX4AWzdb92CebnaePzHt2V8XcrOpdXVochD2Cgm1OaD0yitE5Isn6SjWndJwuSbDzLF8kBwNFVNduA6BX5NS0JAVp33tDVZcOPIwbqtVFXL4ANu3rNfBl/AnhGkh3SrsJ7C3ByVf22e749LSnZAfgy8O+0Vp5BLwI+OUs8Htq91+2SvJE2EHtmvR8Afz7T8pRkR9r4nLO73/dKsmX3/P5dXb40UPYG3T6tB6zfvc+CgbL3TrJdmj27/fhht+2+Sf6sW7YzbTzQcGI4E+dLaVcC7txtuzUtuXzqQFweRmvleVG3zoFJ9kiySXdOHEBrITmjK3OvFRy3vboyNk/ypJlzqEuKd+fWcU1H0MZ1/XnaoP63A5/vWq6uAH4GvLLbdnPaeTc43owufocAB3Yv/QzYI22Q/G50A7jTpnL41mzx6cr9Oi1BnInHg4FNaOOwbqOL+b60lrHzu3j804rO5YFt1+vqvEFX1MYZGNDfHZs7MTDeSpoXqsqHj3n/AN5Kay0YfLx1YPnGtK6Gx8+y7d/RBvYur+xX0FpTrgaes4r1umiWem07sPyVwC9orSXHAPdYTjmfBN459NqutKvqNp1l/f/blXkNbbD3fYaWv4aWoCyjfWG/YWDZe2mJ4++7ZW8HNhiqy/A+vbhblm79i7uyzwf2H9j2M7QrKK+hXXH42pXE79XAv3XPDwZOm2WduwE30hKIxcBptDFKV9Na3566isdsIS0ZXNaV8X1gz6F1XtDt4+9pSeCdBpbtAHyri/8VtK7ULYe2fztw0MDvm9Guwvwtbazagu71w4B/nKWOG3fl7zPLso8ARw2cf3/o4r2Mlszu1+Pva49Zjvm3BpYfBLxv3H/nPnxM+pGqlV7FLUlTKW3eoTNoye+vVrb+fJPkTNq+jzJ1x1rRHaOzgN2r6vK1XR9pTTKJkiRJ6sExUZIkST2YREmSJPVgEiVJktSDSZQkSVIPY7ntyxZbbFHbbrvtOIqWJElao0477bQrqmrhqm43liRq2223ZcmSJeMoWpIkaY1K8vM+29mdJ0mS1MNISVR3m4OjkvwoyflJdh13xSRJkqbZqN15HwS+UlXP7u6HdLsx1kmSJGnqrTSJSrIZ7eaaLwaoqhuAG8ZbLUmSpOk2SnfevYClwCeSnJHkY92dyW8jyeIkS5IsWbp06RqvqCRJ0jQZJYlaH9iJdqf0HWl3JT94eKWqOrSqFlXVooULV/kqQUmSpDlllCTqUuDSqjql+/0oWlIlSZK0zlppElVVlwGXJLlf99LjgfPGWitJkqQpN+rVeX8NHNFdmXch8JLxVUmSJGn6jZREVdWZwKLxVkWSJGnucMZySZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB7WH2WlJBcBy4CbgZuqatE4KyVJkjTtRkqiOo+tqivGVhNJkqQ5xO48SZKkHkZNogr4WpLTkiyebYUki5MsSbJk6dKla66GkiRJU2jUJOrRVbUTsBfw6iS7D69QVYdW1aKqWrRw4cI1WklJkqRpM1ISVVW/6H5eDnwB2HmclZIkSZp2K02iktw+yaYzz4EnAj8cd8UkSZKm2ShX520JfCHJzPqfrqqvjLVWkiRJU26lSVRVXQg8bAJ1kSRJmjOc4kCSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSph5GTqCQLkpyR5NhxVkiSJGkuWJWWqNcB54+rIpIkSXPJSElUkrsDewMfG291JEmS5oZRW6I+ALwJuGV8VZEkSZo7VppEJXkqcHlVnbaS9RYnWZJkydKlS9dYBSVJkqbRKC1RuwFPS3IR8F/A45L85/BKVXVoVS2qqkULFy5cw9WUJEmaLitNoqrqzVV196raFnge8M2qeuHYayZJkjTFnCdKkiSph/VXZeWq+hbwrbHURJIkaQ6xJUqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSph5UmUUk2TnJqkrOSnJvkbZOomCRJ0jRbf4R1rgceV1XXJNkAODnJCVX1/THXTZIkaWqtNImqqgKu6X7doHvUOCslSZI07UYaE5VkQZIzgcuBr1fVKWOtlSRJ0pQbKYmqqpuragfg7sDOSR48vE6SxUmWJFmydOnSNVxNSZKk6bJKV+dV1dXAicCTZ1l2aFUtqqpFCxcuXEPVkyRJmk6jXJ23MMnm3fNNgD2BH425XpIkSVNtlKvztgI+lWQBLen6bFUdO95qSZIkTbdRrs47G9hxAnWRJEmaM5yxXJIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKmHlSZRSe6R5MQk5yU5N8nrJlExSZKkabb+COvcBLyhqk5PsilwWpKvV9V5Y66bJEnS1FppS1RV/aqqTu+eLwPOB7Yed8UkSZKm2SqNiUqyLbAjcMpYaiNJkjRHjJxEJbkDcDRwYFX9bpbli5MsSbJk6dKla7KOkiRJU2ekJCrJBrQE6oiq+vxs61TVoVW1qKoWLVy4cE3WUZIkaeqMcnVegMOA86vqfeOvkiRJ0vQbpSVqN2B/4HFJzuweTxlzvSRJkqbaSqc4qKqTgUygLpIkSXOGM5ZLkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktTDSm/7Im178HFruwq9XHTI3mu7CpJWwM8WzXW2REmSJPVgEiVJktSDSZQkSVIPc25MlH3oksbBzxZJq8qWKEmSpB5MoiRJknpYaRKV5ONJLk/yw0lUSJIkaS4YpSXqk8CTx1wPSZKkOWWlSVRVnQRcNYG6SJIkzRmOiZIkSephjU1xkGQxsBhgm222WVPFSpKkNcSpPNasNdYSVVWHVtWiqlq0cOHCNVWsJEnSVLI7T5IkqYdRpjj4DPA/wP2SXJrkZeOvliRJ0nRb6Zioqnr+JCoiSZI0l9idJ0mS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktTDSElUkicn+XGSC5IcPO5KSZIkTbuVJlFJFgD/CuwFPBB4fpIHjrtikiRJ02yUlqidgQuq6sKqugH4L2Df8VZLkiRpuq0/wjpbA5cM/H4psMt4qiMJYNuDj1vbVejlokP2XttVkKSJSVWteIXk2cCTq+ovu9/3B3apqtcMrbcYWNz9ej/gx2u+umO3BXDF2q7EOsaYT54xnzxjPnnGfPLmcszvWVULV3WjUVqifgHcY+D3u3ev3UZVHQocuqoVmCZJllTVorVdj3WJMZ88Yz55xnzyjPnkrYsxH2VM1A+A+ya5V5INgecBXx5vtSRJkqbbSluiquqmJK8BvgosAD5eVeeOvWaSJElTbJTuPKrqeOD4MddlGszp7sg5yphPnjGfPGM+ecZ88ta5mK90YLkkSZL+lLd9kSRJ6sEkSpIkqQeTqHkkyUZJNuieZ23XZ12QZL3up/GekCQbdrejMu4T0n22bNQ9N+ZjNBPfJJskWdg997t6ApLcIcm23fORznMPzDyQ5NFJzgX+G/gbgHKw29gk2TTJQUnOBj7Uvezf0hgl2TLJ/0nyXeArwGvB83ycktwlybuSfBP4JvA3STYy5uNVVZVkB+Bi4G/XcnXmvSR3SvKOJMcBZwAHwOifLSNdnafp0v1Xkqq6OcnGtJni3wycBByX5ELgaD/s1pwu5utV1U20qT62Ag4H9gOoqpvXYvXmpcHznDbh71bAgcDPgW8mOauqvrkWqzjvDJ3nGwEbAH8PnAN8D1gCfGPt1XD+mWllqqpbBl5+AO2f4nvNskyraeg83xQ4GHhiVZ24qmX53/McMtO8WFW3zHxpV9V1tJtEn1FVVwP/DOxBu/WOVtNQzG/qnl8NvAt4H3B9kh0H19Xqme08By4A3lhVP6iqy4FT6b5gtPqWc55fUlVvrKrvVdUy4ELgurVZz/lkKObDSdKzgSOB65I8fHB99bec8/znwLndgyRbrUqZJlFTKM2C4X7wrpn3rkn2SPLBJPsk2Qw4GXhwt9q5wPWAX+yrYMSYfyDJvt3rS7sPvnOAJ3Wr+/e0ClYh5k+rqqur6prurgnQWkls/VtFqxLzgW1ekuRG2n3R7jbpOs91q/rZ0nXlXQCcCfya1ioFfr6MbBVi/qxu0Q+B7yc5DfhwksWjjkPzoEyBJJsn2btLiKjm5qq6ZTAJSrIfrUn9KcATgJcA1wK/5NY/tKXAZcDWM2VNbk/mjp4xfzzwsu71mb+dbwO7T7b2c9NqxPyvutc3qKobkuwM3BM4yn8SVmx1Y945Abhz99ozZ77sNbvViPkrukXbA7+sqp8BVwMvT/Jyhwws32rE/C+7RR8ADgF2A94NPB145ijv7Zio6fBA2tia64FvJLkf8EJgF+A7ST5Ma0Z/FPC6qjomyTeAjwEBfgQ8GaCqruq2P2HyuzGnLC/mOwMnryDmH4fWHNz9cZ4CHNS95ofciq1uzG/syjkI+EhVXTPpHZiDVivmAFV1Wff0vCSXAvdKsp7jdJar7+f5YV1L6/bA/kkWA3egfcb/ci3sx1zS9zz/BEBVLaGN9wM4Ncl5wJajnOe2RE1I17y4vHhfRGu+vU/3+x60FqWDgN8D/0A7ORYBZ3X/kX+NdvweAHwR2CHJE7vtt+m2X6f1jPmbuDXmN/CnMZ+5cmbmv52fAtcmeV+SlyXZclz7MxeMMeYz3dO70j4MlyTZN8kLkmw6rv2ZC8Z9ng+8zwLgvsCP1vUEakyf5wHuTbtC7BBgH+ARwA9o3Xrr9PCMMZ3nt8xynq9PG1P801HOc5OoCem+cJd3QJYCv6L9BwLwKeA04FW05sZHAxt26+0y8B/5MmDfqroWeBvw4iRXAmd3j3XaGoj5BsDlwCOHYv4UgCSPTPJt2hfLjsCNtOb3ddYYY/7U7vlf0/7j/BjtqtRrgT+s4d2YU8YY8ycBJHl5kh/QxuhcQGt9XaeN8fP8GVV1XFV9oqoupCVbx9ON/1uXh2eM8TzfCyDJAWljos4Afky7eGWl7M5bw2Zr/uuy5+2AFwM3VtXbBpdX1Y1JLgZ2SrINLWN+OW28zT/SrgLbFfh34Dldv2+AK2jNmNBao/672pVj65QRYn5DVb19cPlQzO9J+7B6OW2aiMGYf4wW8zt2m14JPKx7fjFwYFWdMZYdm2ITjvlVwP275x8HPlRV3x/Ljk2xtRDzh3bPzwBeU1XrXPK0Fj7PH9K9x0ZVdX1V/RY4bIy7OHXWwnn+kO75OcCrV/WzxZao1ZBkva6J+49mDn6SB6fN4QTtAH6Q9t/Ep4bKmGmevZjWkrE18Bhgs6o6DLiJ1sT7rKr6Eu0k2Ic2t8W/0TVfdoPoru7KXDBfm317xvzwoTKGY343bo35x1h+zO9Ii/m9u/f95UwC1cX8NvWaL6Yg5h+hm7Kjqr4x8yE3W73miymL+akzCZSfLcB4P8/v273v9cN1W0O7OVWm5Dzfvnvf0wc+W0Y+z22JWgVJMticOlvTYpKDaXN8/A74dpLDabP9PgL4XFVdNLj+QHm/6h470FqVXpTkaNqB/iLtRID238yZwMNpzZTvGa5DzaMBzsZ88qY95jP1W0HT/pwzh2LueT7hz5bl1W0umvaY9znPTaJWYrBpcfDgp92j7knAc2j9qu+h9bkW7SqMzYCjgM2B99MmqltRvK/sHrsChwKvoV1x9+2qOm9gvY2799oMOA44ZnX3cdoY88mbSzEfrN9cZswnby7FfL6YSzHvdZ5XlY+BB20W5MXA1rMs2xp4avf8icDXgWcBD+peexJtYPE3aFdUHNadDLejNfs+bSXvvR1wr+UsW7C2Y2PM58/DmBtzY27MjfnqP2yJ6gxky1vQBrFeAPwiyWOBTarqeNoYgb9J8mNaE+H6tMFo13bFnEbLov+q2kRpg+X/GnhIkhOralnX3xpuvTcY1a7GGNxmZor6qnnUjD7DmE+eMZ88Yz55xnzy1tWYz8vBaqOYCe5AkGcmT/wJbU6Omfty7c6tt/X4Hq3Z8W60ySyvBF4NvD/JTJPgqcC+aVPL75k2f9BdabdmuQz4Y7NmDdwbLMk2aTMxDx/4edGMDsZ8bTDmk2fMJ8+YT54xb9aJlqgM3SU7aYPH0l1GmmQjWvPjZlX1ziSXAdt1B+JMYK8kd6mqy5P8inZJ5Peq6tldeZvS+mB3BV5JuwzzONrcFV8CrqmqLw/VaWNgb+BxwE60y1v/pavnnP9DM+aTZ8wnz5hPnjGfPGO+fPMyiRo+4DVwBUCSO1fVlUnuQhv5/6iq+k2SG4DNu4N5IW2OlK2B/6VdVvlQWj/tJbR77hyZZHPaPXZ2oPXZntKdJO8A/s/wgcxt57/Ykzaz+EdpMwDfyBw2h2J+D4y5Me/JmE/eHIq5n+fr4Hk+L7vzqjXxzWTMt0/yuCQfSfIT4BNJdq2qy2lTxe/Rbfa/tDvD37d7fgPtlio/oTU/7t2td0daf+9WwJbd+p8H9u/KpKpu7LL028yBMXgiVtUxVfX+qjpnrv/BwZyK+QeMuTHvy5hP3hyKuZ/n6+B5Pu+SqCSbpd1P69NJHkE7WP9EG5m/PfA/wCuS3Ac4kVv7ai+i9bXel9afewXwgKq6gTZL8g5JfkgbyHYg8OOqOrmqFlfV0VX1u+G61EB/7XxmzCfPmE+eMZ88Yz55xnzVzInuvOSP/a+3mahrlvXWA95Ka0I8iXZQ1wN+RJveHeAztP7WXYFvAfsDVNUFSXYBllXVkUkuAR6W5I5V9ZMkz53Jkmd5z9tkyPOBMZ88Yz55xnzyjPnkGfPxmdokKsnMpYu3zBz0mZ9JtgeuqKqrhk6K3YFHV9UjBsrZCFhC66+mqi5Ksh3ww6o6NW1693cDd6b11V6bNmDtEtpgte2AM2cO/vABn6sHfjbGfPKM+eQZ88kz5pNnzCdjapKoLrCD8z0Ubb4I0poNt6CN1P+vbpNzgJcOZdVX0c03kTYb6i3Vrhy4CFic5IiqOos2GG0mq34+sG9X3peqalm3/a9pNzHcDjhz5kSb6wd8kDGfPGM+ecZ88oz55BnztWOtJVEZulPzcGDT7mz9atpAtX2A62hzRDyzqi5J8tMkO1XV6QObXQlcn2S3qvpuV87MvBU/B96bdkXBicDp3fueBZw18L4zWfmlwNfoTpShE21OMuaTZ8wnz5hPnjGfPGM+HSaeRHUHYA/gc93vM321ewB70bLlt1TVL5PsC5xXVTsl2ZHWF3uHrqgTgUclObNubRb8RZLTgdd15T2W1q/7AeD7wHpV9Y5Z6jRbs+cNwHfXfAQmz5hPnjGfPGM+ecZ88oz5dBn71Xnp+j9nVOsXXQw8L8mbgDsmuTfwQlo2ezzwviRbA18BftUdoEtpd3LepSvqFOBhwO2TbJBkr+71f6BNuHUn4H3Au4Df0y6x3K6rUwbrVc28aWI05pNnzCfPmE+eMZ88Yz7dxp5EzQQ2yT2TPDrJTrSR/28D7kM7MAcCvwSuoY30X0SbP+Ic4O7AJrSbEv6YNlAN2vTxO9MO9MbA45JsXFU3VNV3quoNVXV8tfkmbqY1K763q9O8PuDGfPKM+eQZ88kz5pNnzKdcrd7dmsNy7oxMO2ibAA8Hvk07mG8B7gq8EXjvwLp/R+s3fSvwNGCj7vVtaAfu3t3vTwW+M/OewDOA2y/n/dejNT2u1j5O28OYG3NjbsyN+fx4GPO5/1jTJ8Rm3c87Av8GvADYD3j30Ho7Al8FtqWNy9oTOGloncd0P78H7Ns9vzNwv5kDPMvJmLUd0IkfQGNuzNeBhzE35uvCw5jPvUevgeUDA9m2B54NbEhrRtye1le7ZXcSfIOWRb+k6z/9NfCTqvpy2lTuC6vqIuDrSf42yYdoTYs7AV+kZd8vod2Hh6q6knb1ADXUlFjdWTBfGfPJM+aTZ8wnz5hPnjGfP9I3bknuD3wS+DrtQF8OHA68lNbvej7woKq6Lski2hUBjwQOoN1D5/m0e+fcBfj3qvp6kufSbkL4jaq6ZDX2a14y5pNnzCfPmE+eMZ88Yz4/rM4UB/cGLgA+Bfyiqv6Q5BDg9cCxwNHAlkkurqol8MfJt+4HbAB8hNZUeTVtDgqq6sjVqM+6wJhPnjGfPGM+ecZ88oz5PLA6LVGbAp+gzUi6Hu0SyPfRpo1/G3BkVb02ySa05sq30DLtI4EPL6/pMEMTiOlWxnzyjPnkGfPJM+aTZ8znh95J1G0Kac2SL6XdtfkjwAeBrarqKUlCm/zrxqq6epZtF9Cmlrc/dhUY88kz5pNnzCfPmE+eMZ+7enfndQf2bsBDaJN37Qi8qqquSXIqcKckC6rNL7F0YJv1utcAGHyuFTPmk2fMJ8+YT54xnzxjPj/0nmyzy3rvAfwVcBPwpqr6aZL7Ai8HTq+qm7uD/sdtPOD9GfPJM+aTZ8wnz5hPnjGfH9ZId95tCmxXBzwI+GC1yyk1ZsZ88oz55BnzyTPmk2fM55bVTqJmmhdpSbKD2SbAmE+eMZ88Yz55xnzyjPnctsZboiRJktYFY78BsSRJ0nxkEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUw/8H4OIhbh/3V9QAAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAibUlEQVR4nO3deZglZXn38e+PYRVZIoyILCKbGyrgiOKKxA1Rictr3HCNQ6Im4gIar5hIFrcooolLiLgFF+IuAi4IaHABhk0FBJGMgAgMEBRU9vv946mGw6Fnprtm+szp7u/nuurq06fq1Lnrrupz7n6ep6pSVUiSJGl61lrTAUiSJM1GFlGSJEk9WERJkiT1YBElSZLUg0WUJElSDxZRkiRJPVhESZrVknwuyZ+t6Ti0fEnel+Sv1nQc0upmEaV5IclrkyxJcmOST04y/3lJzktyXZJzp/OlnGRpkif2jOvwJOcnuS3JyyaZv32Sb3RxXZXkPZMss1OSG5IcOfDcW5NcPzD9sXuPzbv5WyX5WpJrklya5C+H1rl3kjOS/C7JRUkWLyf+jyepJDsOPPeAJCck+W2SC5M8a2Deukm+2OWskuw1tL71knw0yRVdbEcn2WoF+XsI8FDga0PP79Wt/82TvOaVSX7e5fSKJMcm2Wh577GC9949yfe7/F6R5HUD805MsqzL39lJ9ht67cIkn+1y9H9JPjMw76BuX5+T5MEDzz86yVenG2f32k8muSXJlkPPvz3JzQPHyXlJntNj/Svcr8B7gbcmWbdP/NK4sojSfHEZ8M/Ax4dndF/SRwJvADYGDgI+m+SeI4jrbODVwBmTxLUu8B3gBOBewNZdnMM+BJw2+ERVvaOq7j4xAe8GTqqqq7pFjgT+F9gC2Bd4R5IndO+7DvAV4D+ATYA/Bw5N8tCh+B4D7DD03Nq0guYbwD2AxcCRSXYeWOxk4MXA5ZNsy+uAPYGHAPcG/g/4t0mWm3AA8Jm661WDXwpcA7xkKL7HA+8AXlBVGwEPAI5awfon1RWj36TlaDNgR+DbQ9uxZVVtzB05GCxgvkzb/m2Be9KKDLplXglsD3wEeGf3/NrA+4ADe8S6IfAc4Le0vA87auA4ObCLdYvpvg8r2K9V9Rvg58Aze6xXGlsWUZoXqurLVfVV4OpJZm8NXFtVx1VzDPB7hgqEyST5L9oX4dHdf/IHTzOuD1XVd4EbJpn9MuCyqjq0qn5fVTdU1U+G3v/5wLXAd1cQY2jFxKe63+8O7AX8S1XdXFVnA18EXtG95B60YvK/unycBpwHPHBgnWvTipu/Hnq7+9OKn/dX1a1VdQLwA2D/bntvqqrDqupk4NZJwr0v8K2quqKqbqAVOA9a3rYB+wDfG9reDYHnAq8BdkqyaGD2w4EfVdWZXTzXVNWnquq6FbzHZN7QxfmZqrqxqq6rqvMmZlbVT6rqlolfgXWAbbr4ntw9PqiqftvtgzO7ZbcFzqyq3wHH04opaMXN16tq6TTjhFZAXQv8I624XK6q+hZwHVM49odet7L9CnASrWCX5gyLKAmWAOcleWaSBWldeTcCP1nxy6Cq9gcuBp7R/Tf/HoAk165gessU43oksDTJcV33zklD3Tsb074Y37CS9TyW1trxpYmXDv2ceLxLt01XAJ8DXt7lY0/gPrSWhgmvB74/XNQtx+3rnoIjgEcnuXeSuwEvAo6bdKWtWLovcP7QrGcD1wNfAL7FnQuHU4CnJDmk6x5bb2idb1nRvhtY9JHANUl+mOTKrttx26F1fSPJDd17nkQ7ziZeez7wqSRXJzmtayEDuBB4cJJNgScC5yTZBng+XWtVDy+l7c/PA/dP8rDJFkqzL7AucG733LYrOZZfOI04zqN1vUpzR1U5Oc2bidal98lJnn8l7Yv3FuAPwL7TWOdS4ImrGNfJwMuGnvs2cDOttWVdWjfjRcC63fwPAG/uHr8dOHI56z5ieJu79/s3YH1gd1rX1/kD858BXNHl4xbgVQPztqF92W/S/V7Ajt3jdboYD+4ePxm4idZqMxzXpcBeQ89tQvuyr+59zwTusZzt2qpbbv2h548HDusevwBYBqwzMH8f4Gha68z1wKHAgmnurwu61z+8y+EHgR9Mstw63fu9YeC5w7u4X9nNn2hN3Hwg5jNoxeN9aF1/f0rrVv0erbt06ynGuS1wG7Br9/u3gA8MzH97t3+upbW+3gocvIrH8l32a/f8k4CLVmXdTk7jNtkSpXkvbVD4e2hdXOsCjwc+lmTXNRgWwB+Bk6t1M95Ea4nYDHhAF9sTgfevaAVda87/o+vKG/AiWivOJbSxN0fSvvxIcn9aIfMSWj4eBBzctVIAHAb8Y1X9dvj9qupm4M9o3TaXA28E/nti3VPwIWC9bjs3pBUQk7ZE0b74AW4fFN612jwBmBio/TVakXN7N1KXz2fQui33o3Wb/sUU45vwR+ArVXVatW7HQ4BHJdlkcKFqXXXHAU9O8syB1y6tqiO6+Z+n7YdHd6/5XFXtXlX70FrwbqQVk++lFbdfYOqtUvsD51XVWd3vnwFe2I17m/DfVbVpVW1I68Z7SZIDppGLqdqIO/aZNCdYREmwK61raklV3VZtDNAptCJlKoYHNZM7nxk3PL11iuv9yWTr7uwFbAdcnORy4E3Ac5IMD1B/Fq2V6aQ7BVz1q6p6elUtrKpHAJsDp3azdwEuqKpvdfk4HziG1qICrVXkX5Nc3r03wI8munaqjQd6fFVtVlVPoY3rOZWp2ZXWanZNVd1Iay3boxvIfSdV9Xvgl8DgoPX9aZ9rR3exXUQrou4yFqjbtu/SBu7vApOe1XinaeDlw/tmeftpwtrcMc5osv062TG0AW0Q/BuBnYBLqo2VOo028H4qXgJsP7CvDqXt66dNtnC1MVfH0Yq1ie68FR3LL5piHNAG8Z89jeWlsWcRpXkhydpJ1gcWAAuSrN8Njob2pfTYiZanJLvRxhFNZbwPtG6v7QefqIEz4yaZ3jEQ17pdXAHW6eKa+Ls8EnhkkicmWUAbXHwVbWzJ4bQv5V276aO0QucpQ7G9FPh0Vd3pSzrtMgQbde//Ylq326Hd7DNpA7L37sbJ7AA8fSAfO9PGtky8N7Qv3a90635Itx13S/ImYEvgkwPvvV63zQDrdstOjM86jdYSsknXWvJq2uD6ibMKhx1Lazkc3N5DBmLblTaw+mlJNkuyX5LnJ/mTbtv26F7/Y7jrWY3D08D7fAJ4VpJduzjfRms1/G2S+yfZJ8kGSdbp8vs47hgA/xXgT5K8NG3M2XNpJzf8YGjb/o5WUF5GG3d3v7Sz5p5AKw5Jsl3aJQW2G05M2li2HYA9BnKxC/BZhs5aHHjN1sBTgXO6fFy8kmN58NIMK9qvdHleXquiNDut6f5EJ6dRTLSxHzU0vX1g/mtp43yuo31BvXFg3ouAc1aw7v1oX3LXAm+aZlwnTRLXXgPzn93F9btu2QetYPuOHHpuK9q4oh0nWf5A2lih39PGRy0amv884GddPi6lXSJhreW8dw2+B/CvtEsTXE/70txxaPmlk2zzdt28zWhdTld2+TwZ2GMF+duF9oUf2oDtG4CFkyx3TrePH0c7k/GqbtsuoOcYIOCvgF9323o0sE33/ANoLZnXddtwGvCsodc+Fvhpl6MlwGOH5t+/e92CgecO6uI+F3jwwHqWMjDma2D5jwJfmuT5PWhdhPfojpubuziuB37Tve5uPfKxov26ZXccrTuKv3cnp1FNqVpZK7Qkja8kn6WN6/nqmo5l1JL8HbCsqv5jTceyIkneB/yyqj68pmORVieLKEmSpB4cEyVJktSDRZQkSVIPFlGSJEk9WERJkiT1sPbKF5m+zTffvLbbbruZWLUkSdJqdfrpp19VVQun+7oZKaK22247lixZsvIFJUmS1rAkv+rzOrvzJEmSephSEZVk0yRfTPLzJOd1txOQJEmat6banfcB4JtV9dwk6wJ3m8GYJEmSxt5Ki6gkm9DuN/UygKq6CbhpZsOSJEkab1Ppzrsv7Ualn0hyZpKPJdlweKEki5MsSbJk2bJlqz1QSZKkcTKVImptYHfgI1W1G+2u728ZXqiqDq+qRVW1aOHCaZ8lKEmSNKtMpYi6FLi0qk7pfv8iraiSJEmat1ZaRFXV5cAlSe7XPfWnwLkzGpUkSdKYm+rZeX8NfKY7M+8i4OUzF5IkSdL4m1IRVVVnAYtmNhRJkqTZwyuWS5Ik9WARJUmS1INFlCRJUg8WUZIkST1YREmSJPVgESVJktSDRZQkSVIPFlGSJEk9WERJkiT1YBElSZLUg0WUJElSDxZRkiRJPVhESZIk9WARJUmS1INFlCRJUg8WUZIkST1YREmSJPWw9lQWSrIUuA64FbilqhbNZFCSJEnjbkpFVOcJVXXVjEUiSZI0i9idJ0mS1MNUi6gCvp3k9CSLJ1sgyeIkS5IsWbZs2eqLUJIkaQxNtYh6TFXtDuwDvCbJ44YXqKrDq2pRVS1auHDhag1SkiRp3EypiKqqX3c/rwS+Auwxk0FJkiSNu5UWUUk2TLLRxGPgycDPZjowSZKkcTaVs/O2AL6SZGL5z1bVN2c0KkmSpDG30iKqqi4CHjqCWCRJkmYNL3EgSZLUg0WUJElSDxZRkiRJPVhESZIk9WARJUmS1INFlCRJUg8WUZIkST1YREmSJPVgESVJktSDRZQkSVIPFlGSJEk9WERJkiT1YBElSZLUg0WUJElSDxZRkiRJPVhESZIk9WARJUmS1MOUi6gkC5KcmeQbMxmQJEnSbDCdlqjXAefNVCCSJEmzyZSKqCRbA/sCH5vZcCRJkmaHqbZEHQYcDNw2c6FIkiTNHistopI8Hbiyqk5fyXKLkyxJsmTZsmWrLUBJkqRxNJWWqEcDz0yyFPg8sHeSI4cXqqrDq2pRVS1auHDhag5TkiRpvKy0iKqqv62qratqO+D5wAlV9eIZj0ySJGmMeZ0oSZKkHtaezsJVdRJw0oxEIkmSNIvYEiVJktSDRZQkSVIPFlGSJEk9WERJkiT1YBElSZLUg0WUJElSDxZRkiRJPVhESZIk9WARJUmS1INFlCRJUg8WUZIkST1YREmSJPVgESVJktSDRZQkSVIPFlGSJEk9WERJkiT1YBElSZLUw0qLqCTrJzk1ydlJzklyyCgCkyRJGmdrT2GZG4G9q+r6JOsAJyc5rqp+PMOxSZIkja2VFlFVVcD13a/rdFPNZFCSJEnjbkpjopIsSHIWcCXwnao6ZUajkiRJGnNTKqKq6taq2hXYGtgjyS7DyyRZnGRJkiXLli1bzWFKkiSNl2mdnVdV1wInAk+dZN7hVbWoqhYtXLhwNYUnSZI0nqZydt7CJJt2jzcAngT8fIbjkiRJGmtTOTtvS+BTSRbQiq7/rqpvzGxYkiRJ420qZ+f9BNhtBLFIkiTNGl6xXJIkqQeLKEmSpB4soiRJknqwiJIkSerBIkqSJKkHiyhJkqQeLKIkSZJ6sIiSJEnqwSJKkiSpB4soSZKkHiyiJEmSerCIkiRJ6mGlNyCWNHrbveWYNR1CL0vfte+aDkGSRsaWKEmSpB4soiRJknqwiJIkSerBIkqSJKmHlRZRSbZJcmKSc5Ock+R1owhMkiRpnE3l7LxbgDdW1RlJNgJOT/Kdqjp3hmOTJEkaWyttiaqq31TVGd3j64DzgK1mOjBJkqRxNq0xUUm2A3YDTpmRaCRJkmaJKRdRSe4OfAk4sKp+N8n8xUmWJFmybNmy1RmjJEnS2JlSEZVkHVoB9Zmq+vJky1TV4VW1qKoWLVy4cHXGKEmSNHamcnZegCOA86rq0JkPSZIkafxNpSXq0cD+wN5Jzuqmp81wXJIkSWNtpZc4qKqTgYwgFo0pb4YrSdJdecVySZKkHiyiJEmSerCIkiRJ6sEiSpIkqQeLKEmSpB4soiRJknqwiJIkSerBIkqSJKkHiyhJkqQeLKIkSZJ6sIiSJEnqwSJKkiSpB4soSZKkHiyiJEmSelh7TQcgSeNgu7ccs6ZD6GXpu/Zd0yFI85YtUZIkST1YREmSJPWw0iIqyceTXJnkZ6MISJIkaTaYSkvUJ4GnznAckiRJs8pKi6iq+j5wzQhikSRJmjUcEyVJktTDarvEQZLFwGKAbbfddnWt9i48DVmSJI2D1dYSVVWHV9Wiqlq0cOHC1bVaSZKksWR3niRJUg9TucTB54AfAfdLcmmSV858WJIkSeNtpWOiquoFowhEkiRpNvHeeZKkNcIThTTbOSZKkiSpB4soSZKkHuzOkyRpnrALdfWyJUqSJKkHiyhJkqQeLKIkSZJ6sIiSJEnqwSJKkiSpB4soSZKkHiyiJEmSerCIkiRJ6sEiSpIkqQeLKEmSpB4soiRJknqwiJIkSerBIkqSJKmHKRVRSZ6a5PwkFyZ5y0wHJUmSNO5WWkQlWQB8CNgHeCDwgiQPnOnAJEmSxtlUWqL2AC6sqouq6ibg88B+MxuWJEnSeJtKEbUVcMnA75d2z0mSJM1bqaoVL5A8F3hqVf1F9/v+wCOq6rVDyy0GFne/3g84f/WHO+M2B65a00HMM+Z89Mz56Jnz0TPnozebc36fqlo43RetPYVlfg1sM/D71t1zd1JVhwOHTzeAcZJkSVUtWtNxzCfmfPTM+eiZ89Ez56M3H3M+le6804Cdktw3ybrA84Gvz2xYkiRJ422lLVFVdUuS1wLfAhYAH6+qc2Y8MkmSpDE2le48qupY4NgZjmUczOruyFnKnI+eOR89cz565nz05l3OVzqwXJIkSXflbV8kSZJ6sIiSJEnqwSJqDkmyXpJ1usdZ0/HMB0nW6n6a7xFJsm53OyrzPiLdZ8t63WNzPoMm8ptkgyQLu8d+V49Akrsn2a57PKXj3B0zByR5TJJzgO8CrwcoB7vNmCQbJTkoyU+AD3ZP+7c0g5JskeQfkvwA+CbwN+BxPpOS3DPJO5OcAJwAvD7JeuZ8ZlVVJdkVuBh48xoOZ85Lco8k/5TkGOBM4KUw9c+WKZ2dp/HS/VeSqro1yfq0K8X/LfB94JgkFwFf8sNu9elyvlZV3UK71MeWwKeBFwFU1a1rMLw5afA4p13wd0vgQOBXwAlJzq6qE9ZgiHPO0HG+HrAO8HfAT4EfAkuA49dchHPPRCtTVd028PQDaP8U33eSeVpFQ8f5RsBbgCdX1YnTXZf/Pc8iE82LVXXbxJd2Vd1Au0n0mVV1LfA+YC/arXe0ioZyfkv3+FrgncChwI1JdhtcVqtmsuMcuBB4U1WdVlVXAqfSfcFo1S3nOL+kqt5UVT+squuAi4Ab1mScc8lQzoeLpOcCRwE3JHnY4PLqbznH+a+Ac7qJJFtOZ50WUWMozYLhfvCumfdeSfZK8oEkz0iyCXAysEu32DnAjYBf7NMwxZwflmS/7vll3QffT4GndIv79zQN08j5M6vq2qq6vrtrArRWElv/pmk6OR94zcuT3Ey7L9q9Rx3zbDfdz5auK+9C4CzgClqrFPj5MmXTyPlzulk/A36c5HTg35Msnuo4NHfKGEiyaZJ9u4KIam6tqtsGi6AkL6I1qT8NeCLwcuAPwGXc8Ye2DLgc2GpiXaPbktmjZ87/FHhl9/zE3873gMeNNvrZaRVy/qru+XWq6qYkewD3Ab7oPwkrtqo57xwHbNY99+yJL3tNbhVy/pfdrJ2By6rqf4FrgQOSHOCQgeVbhZz/RTfrMOBdwKOBdwN/Bjx7Ku/tmKjx8EDa2JobgeOT3A94MfAI4H+S/DutGf1RwOuq6ugkxwMfAwL8HHgqQFVd073+uNFvxqyyvJzvAZy8gpx/HFpzcPfHeQpwUPecH3Irtqo5v7lbz0HAh6vq+lFvwCy0SjkHqKrLu4fnJrkUuG+StRyns1x9P8+P6Fpadwb2T7IYuDvtM/6yNbAds0nf4/wTAFW1hDbeD+DUJOcCW0zlOLclakS65sXl5Xsprfl2x+73vWgtSgcBvwf+nnZwLALO7v4j/zZt/z0A+Cqwa5Ind6/ftnv9vNYz5wdzR85v4q45nzhzZuK/nV8Af0hyaJJXJtliprZnNpjBnE90T+9J+zBckmS/JC9MstFMbc9sMNPH+cD7LAB2An4+3wuoGfo8D7AD7QyxdwHPAB4OnEbr1pvXwzNm6Di/bZLjfG3amOJfTOU4t4gake4Ld3k7ZBnwG9p/IACfAk4HXk1rbnwMsG633CMG/iO/Dtivqv4AHAK8LMnVwE+6aV5bDTlfB7gSeORQzp8GkOSRSb5H+2LZDbiZ1vw+b81gzp/ePf5r2n+cH6OdlfoH4I+reTNmlRnM+VMAkhyQ5DTaGJ0Laa2v89oMfp4/q6qOqapPVNVFtGLrWLrxf/N5eMYMHuf7ACR5adqYqDOB82knr6yU3Xmr2WTNf131vD3wMuDmqjpkcH5V3ZzkYmD3JNvSKuYDaONt/oV2FtiewH8Cz+v6fQNcRWvGhNYa9d1qZ47NK1PI+U1V9Y+D84dyfh/ah9UBtMtEDOb8Y7Scb9y99Grgod3ji4EDq+rMGdmwMTbinF8D3L97/HHgg1X14xnZsDG2BnL+kO7xmcBrq2reFU9r4PP8wd17rFdVN1bVb4EjZnATx84aOM4f3D3+KfCa6X622BK1CpKs1TVx325i5yfZJe0aTtB24Ado/018amgdE82zF9NaMrYCHg9sUlVHALfQmnifU1Vfox0Ez6Bd2+IjdM2X3SC6a7t1Lpirzb49c/7poXUM5/ze3JHzj7H8nG9My/kO3fteNlFAdTm/U1xzxRjk/MN0l+yoquMnPuQmi2uuGLOcnzpRQPnZAszs5/lO3fveOBzbatrMsTImx/nO3fueMfDZMuXj3JaoaUiSwebUyZoWk7yFdo2P3wHfS/Jp2tV+Hw58oaqWDi4/sL7fdNOutFallyT5Em1Hf5V2IED7b+Ys4GG0Zsr3DMdQc2iAszkfvXHP+UR8K2jan3VmUc49zkf82bK82Gajcc95n+PcImolBpsWB3d+2j3qngI8j9av+h5an2vRzsLYBPgisCnwftqF6laU76u7aU/gcOC1tDPuvldV5w4st373XpsAxwBHr+o2jhtzPnqzKeeD8c1m5nz0ZlPO54rZlPNex3lVOQ1MtKsgLwa2mmTeVsDTu8dPBr4DPAd4UPfcU2gDi4+nnVFxRHcw3I3W7PvMlbz39sB9lzNvwZrOjTmfO5M5N+fm3Jyb81WfbInqDFTLm9MGsV4I/DrJE4ANqupY2hiB1yc5n9ZEuDZtMNofutWcTquiX1XtQmmD678CeHCSE6vquq6/NdxxbzCqnY0x+JqJS9RXzaFm9AnmfPTM+eiZ89Ez56M3X3M+JwerTcVEcgeSPHHxxAto1+SYuC/X47jjth4/pDU73pt2McurgdcA708y0SR4KrBf2qXln5R2/aB70W7Ncjlwe7NmDdwbLMm2aVdiHt7xc6IZHcz5mmDOR8+cj545Hz1z3syLlqgM3SU7aYPH0p1GmmQ9WvPjJlX1z0kuB7bvdsRZwD5J7llVVyb5De2UyB9W1XO79W1E64PdE/gr2mmYx9CuXfE14Pqq+vpQTOsD+wJ7A7vTTm/9ty7OWf+HZs5Hz5yPnjkfPXM+euZ8+eZkETW8w2vgDIAkm1XV1UnuSRv5/6iq+r8kNwGbdjvzIto1UrYCfkk7rfIhtH7aS2j33Dkqyaa0e+zsSuuzPaU7SP4J+IfhHZk7X//iSbQri3+UdgXgm5nFZlHOt8Gcm/OezPnozaKc+3k+D4/zOdmdV62Jb6Ji3jDJ3kk+nOQC4BNJ9qyqK2mXit+re9kvaXeG36l7fBPtlioX0Jof9+2W25jW37slsEW3/JeB/bt1UlU3d1X6na6BMXggVtXRVfX+qvrpbP+Dg1mV88PMuTnvy5yP3izKuZ/n8/A4n3NFVJJN0u6n9dkkD6ftrHfQRubvDPwI+MskOwInckdf7VJaX+tOtP7cq4AHVNVNtKsk75rkZ7SBbAcC51fVyVW1uKq+VFW/G46lBvpr5zJzPnrmfPTM+eiZ89Ez59MzK7rzktv7X+90oa5JllsLeDutCfH7tJ26FvBz2uXdAT5H62/dEzgJ2B+gqi5M8gjguqo6KsklwEOTbFxVFyT584kqeZL3vFOFPBeY89Ez56NnzkfPnI+eOZ85Y1tEJZk4dfG2iZ0+8TPJzsBVVXXN0EHxOOAxVfXwgfWsByyh9VdTVUuTbA/8rKpOTbu8+7uBzWh9tX9IG7B2CW2w2vbAWRM7f3iHz9YdPxlzPnrmfPTM+eiZ89Ez56MxNkVUl9jB6z0U7XoRpDUbbk4bqf/57iU/BV4xVFVfQ3e9ibSrod5W7cyBpcDiJJ+pqrNpg9EmquoXAPt16/taVV3Xvf4K2k0MtwfOmjjQZvsOH2TOR8+cj545Hz1zPnrmfM1YY0VUhu7UPJzYtDtbv4Y2UO0ZwA20a0Q8u6ouSfKLJLtX1RkDL7sauDHJo6vqB916Jq5b8SvgvWlnFJwInNG979nA2QPvO1GVXwp8m+5AGTrQZiVzPnrmfPTM+eiZ89Ez5+Nh5EVUtwP2Ar7Q/T7RV7sXsA+tWn5bVV2WZD/g3KraPclutL7Yu3erOhF4VJKz6o5mwV8nOQN4Xbe+J9D6dQ8DfgysVVX/NElMkzV73gT8YPVnYPTM+eiZ89Ez56NnzkfPnI+XGT87L13/54Rq/aKLgecnORjYOMkOwItp1eyxwKFJtgK+Cfym20GX0u7k/IhuVacADwU2TLJOkn265/+edsGtewCHAu8Efk87xXL7LqYMxlXNnGliNOejZ85Hz5yPnjkfPXM+3ma8iJpIbJL7JHlMkt1pI/8PAXak7ZgDgcuA62kj/RfRrh/xU2BrYAPaTQnPpw1Ug3b5+D1oO3p9YO8k61fVTVX1P1X1xqo6ttr1Jm6lNSu+t4tpTu9wcz565nz0zPnomfPRM+djrlbtbs1hOXdGpu20DYCHAd+j7cy3AfcC3gS8d2DZt9L6Td8OPBNYr3t+W9qO26H7/enA/0y8J/AsYMPlvP9atKbHVdrGcZvMuTk35+bcnM+NyZzP/ml1HxCbdD83Bj4CvBB4EfDuoeV2A74FbEcbl/Uk4PtDyzy++/lDYL/u8WbA/SZ28CQHY9Z0Qke+A825OZ8Hkzk35/NhMuezb+o1sHxgINvOwHOBdWnNiDvT+mq36A6C42lV9Mu7/tMrgAuq6utpl3JfWFVLge8keXOSD9KaFncHvkqrvl9Ouw8PVXU17ewBaqgpsbqjYK4y56NnzkfPnI+eOR89cz53pG/ektwf+CTwHdqOvhL4NPAKWr/recCDquqGJItoZwQ8Engp7R46L6DdO+eewH9W1XeS/DntJoTHV9Ulq7Bdc5I5Hz1zPnrmfPTM+eiZ87lhVS5xsANwIfAp4NdV9cck7wLeAHwD+BKwRZKLq2oJ3H7xrfsB6wAfpjVVXku7BgVVddQqxDMfmPPRM+ejZ85Hz5yPnjmfA1alJWoj4BO0K5KuRTsF8lDaZeMPAY6qqr9JsgGtufJttEr7KODfl9d0mKELiOkO5nz0zPnomfPRM+ejZ87nht5F1J1W0polX0G7a/OHgQ8AW1bV05KEdvGvm6vq2kleu4B2aXn7Y6fBnI+eOR89cz565nz0zPns1bs7r9ux9wYeTLt4127Aq6vq+iSnAvdIsqDa9SWWDbxmre45AAYfa8XM+eiZ89Ez56NnzkfPnM8NvS+22VW92wCvAm4BDq6qXyTZCTgAOKOqbu12+u2vcYf3Z85Hz5yPnjkfPXM+euZ8blgt3Xl3WmE7O+BBwAeqnU6pGWbOR8+cj545Hz1zPnrmfHZZ5SJqonmRViQ7mG0EzPnomfPRM+ejZ85Hz5zPbqu9JUqSJGk+mPEbEEuSJM1FFlGSJEk9WERJkiT1YBElSZLUg0WUJElSDxZRkiRJPfx/oyt56Bp064wAAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAiZElEQVR4nO3deZhkVXn48e/LAAOyBhmQRRxAUFyBjCBIABEQBESFnxsS4pLBRBKIikETo0RFTAyiUUwI4BJFiWg0skUJm0pYhn1HJCMMiwwgyL6+vz/OKaYou2eq73Tdru7+fp7nPl11tzr3vber3z7n3HMjM5EkSdLYLDPRBZAkSZqMTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkjRpRcTMiLg2ItaZ6LJoZPUcXR8Rsya6LNJ4M4nStBARB0XEvIh4LCK+PsLy90XETRHxYEScERHrjmHfGREvbFCm5SPi5IiYX/ex4wjrbBkR59Vy/SYiDh5hnR3q9p/umvcvdZvO9FhEPNC1fLOIOCsi7q/H/eaefb41Iq6LiAdqkvKmUY7hf+pnL9s1b9uIuKhue2VEbNe1LCLibyLiloj4XUR8NyJW7dnnzhFxaUQ8FBELIuKtiwnjXOC8zLyjZx+frOXaumf+8hHxT3W/D9bYH72Y/Y8qIt5eY/RQRPwqIv6oa9nrauLwcEScHREv6Fq2XkT8KCLureV4f9ey1SLivyPivoj4dkTM6Fp2bES8pUE5V67HevoIy+ZHxCN1+W8j4tSIeH6Dz3htPc77I2J+97LMfAw4AThsrPuVhp1JlKaL24FPU77Mn6UmL0cAewNrAP8HfKelcv0ceBdw5wjlWhM4A/hX4LnAC4Gf9KyzHPBF4MLu+Zn5/sxcuTNRjud7dZtlgR8Bp1COdy7wrYjYtC5fD/gW8EFgVeBQ4MSIWKvns/cDluuZtwbwY+AfgdWBfwB+HBF/UFf5Y2B/4DXAusCKwD93bf8S4ETgb4DVgFcCl4wSO4D3A//eU4aon3Nv/dnto8AcYCtgFWBH4NLF7H9EEbEL8Dng3XU/2wM312VrAj8APk6J7zzgpK7Nv0W5xtYG9gCOiIjX1mUHApfVZbOBN9d9bgOsm5k/GGtZgX2Ax4BdIuJ5Iyzfq14j6wC/oet8jMFDlN+tQ0dZfiJwQETMbLBvaXhlppPTtJkoidTXe+Z9HvhK1/t1gQQ27mN/59V1HwIeBN7WsFwLgB175h0B/PsStjuMkqh8Hfj0KOusBDwA7FDfv6yWNbrW+Qnwqfp6a+Cunn0sBLbper8acCPw6nr8y9b5ewLX9Gx7I/De+vpk4NCuZdsCjwLPqe9P7JSjj5htADzS+eyu+dvX+fsB9wDLdy07BThkHK6j8zvHNMKyucD5PfF/BHgxsHKN16yu5cd2zjPwVeD19fWRwEeAGcAFwEYNy3oW8BlKsvjhnmXzgZ273r8BuHEp4rIzMH+UZb/sXINOTlNlsiZKKmKE1y9b0kaZuX19+costT4nRcQGtTlmtOmdfZbp1cC9EXF+RNwVET+OiA2eKWRpInoP8PdL2M8+lCTovMWsEyw63nnAdRHxxoiYUZvyHgOu7Fr/CMof/N+rQePZsezdd+/yAGYCm9T3rwaIiKsi4o6I+Fat3RrJy4GbM/PJnvkHUGrD/qO+36tr2QXAByPizyPi5bXWalFhIk5ZzHk7pa4zg1KbNStKU+iCiPhyRKxYd/NS4IrOPjPzIeBXdX7n83pj0InP1cDOdV9/BFwD/CVwembePEocRlWvkR2Bb9ept2aue93nAG+jxKgz77DFXctjLM51lJpFacowiZJKk9lbI+IV9Y/X31FqC57TZGeZeUtmrr6Y6cQ+d7U+JSE4mFLr0tvM+CXg45n54BL2cwDwzczsPCjzBuAu4NCIWC4idgV2oB5vZj4FfJNSK/RY/XlgTQaIiDmU5riRmn3+F1g3It5R930AsDGLYnkG8L6ImB0RqwF/Xed3lq9Pae7bh5JYPau5r8fqlBq2Z9RE4P8BJ2bmE5Sar+7E4bOUZrj9KMnibbWM1GPfczHnbc+62tqUZsx9KYnO5sAWwN/W5SsD9/eU9X5glcx8APgF8PGIWCEitqzH2jn+4ym1fBcCP6MkY/sDR0fp53ZedPV968P+wJWZeS3wXeClEbFFzzo/rAnR/cAulKbYTjyOXNy1PIZyQDlXY91GGmomUZr2MvNM4BPA9ynNG/MpX/gLJq5UQGkC+s/MvDgzHwUOB7atnY/3ovxRPmlxO6g1VztSkiIAanLxJkp/nDuBD1FqbRbUbXamNBHuCCxPSbCOi4jNI2IZ4Bjg4BFqgMjMeyh9yz5I6V+zG3Ami2J5AiURPIdSy3J2nd9Z/gjwtcy8sSaHR1CamEbyW0p/pG5vBp4ETqvvvw3sHvXOsMx8KjO/kpmvofxB/wxwQkRsNspnjOSR+vOfM/OOzLwbOKqrnA9S+pJ1W5VFCd9+wIbArZTavG9Rjz8zH83MuZn5isw8DPgC8LG6zTKUc7F1ROzWZ1n/mBIDMvM24FxKUt3tTTUhWgE4CDh3lL5TS2sV4L4B7FeaMCZRElD/sG6SmWtTkqllKU0rY1ab8x5czLRfn7u6klIj9kwxu16/DpgTEXdGxJ2UZphDIuJHPfvYH/hFb1NQZl6ZmTtk5nMz8/XARsBFdfHmlDve5mXm05l5MaVmZGdKMjAHOKl+7sV1mwVR707LzHMz81WZuUb9/Bd39l3394nMnJ2Z61MSqdvqtKRjHik+G0bXnYGUBGFl4JZavu9Rao1+rwk1Mx/JzK9QkrGXAETE6Ys5b6fX7X5LSXpGK+c1dDVbRcRKlNq4a+r2v641XrMyc2tgTRbFnq7tdqP0WzuD0nQ5r9YmzgNesZi4dLbfllKb99Gu62Rr4J09MevE46ksHdefArar+/jY4q7lJZWhx2Z0NXNKU8JEd8pycmpjoiRFK1Cac/69vu50hl6B0iclKM1m5wBHjGHfdwK7NizXzPr5C4Bd6+uoy3ai/IHfnJIIfAH4WV22CvC8rumkunyNnv3fALxnhM99Rf2s5wAfpjQVzqzLdgDuBjav77egdNDetcao+3NfRUkg1qN24K7rL0dJuI6mJHGdz12DklAEJXG5Gpjbtfw9tSwb1bL9B4vpXE9JpLatr9ejJAC79pTxSOCSus4hlBq2Fes1cQClyXJMnbYp/dAuBtYC/oDS9NbpmD+L0jS2T43x54ALurbdrJ6/5Sl3Zt5NV0fzrmvycmD9+v4jlGbV5Sl92/at8z8JnDNKGf+VcsNAdyw2pNSI7VXXmU/tWF7Pyd6UmryXjjEey9Qy7w78ur7u7tC/Xr2GZk70d4GT03hOE14AJ6c2pvrHJnumT9Zlq9c/xg9REqLPAjO6tv0YpWPvaPt+P3AHpanirWMs1/wRyjW7a/mfUWppfkvpLP38UfbzdXruzgO2qce0ygjr/2Pd54PA6cALe5YfBNxU/+DeDHxolM+dTdfdeXXed2oScT8luVura9mmlMTu4frH9oMj7PNwSkf4hZSE9w8WE78PAF+trw+jJks966wLPEFJlOdShky4v56vi4A9G1xPy1GaNe+r18yXgBW6lu8MXE9p+jun55weUo/tIcoQF3NG2P/f8+y7GFejJET3U5KpGXX+8cBnRth+hXp+9xph2THAyV3X3yP1OniAktTu1yAeO45wHZ/TtfxQ4KhB/G47OU3k1PmPV5ImnTru0GXA67JnwM3pICIupxz7PRNdltHUc3QFsH1m3jXR5ZHGk0mUJElSA3YslyRJasAkSpIkqQGTKEmSpAZMoiRJkhr4vQHXxsOaa66Zs2fPHsSuJUmSxtUll1xyd2bOGut2A0miZs+ezbx58waxa0mSpHEVEb9usp3NeZIkSQ30lURFxOoRcXJEXB8R10XENoMumCRJ0jDrtznvi8AZmblvRCxPeaaVJEnStLXEJCoiVgO2B/4EIDMfBx4fbLEkSZKGWz/NeRtSHpb5tYi4LCKOi4iVeleKiLkRMS8i5i1cuHDcCypJkjRM+kmilgW2pDwpfQvKk8cP610pM4/NzDmZOWfWrDHfJShJkjSp9JNELQAWZOaF9f3JlKRKkiRp2lpiEpWZdwK3RsSL6qzXAdcOtFSSJElDrt+78/4C+Ha9M+9m4N2DK5IkSdLw6yuJyszLgTmDLYokSdLk4YjlkiRJDZhESZIkNWASJUmS1IBJlCRJUgMmUZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNWASJUmS1IBJlCRJUgMmUZIkSQ0s289KETEfeAB4CngyM+cMslCSJEnDrq8kqnptZt49sJJIkiRNIjbnSZIkNdBvEpXATyLikoiYO9IKETE3IuZFxLyFCxeOXwklSZKGUL9J1HaZuSWwO/CBiNi+d4XMPDYz52TmnFmzZo1rISVJkoZNX0lUZt5Wf94F/Cew1SALJUmSNOyWmERFxEoRsUrnNbArcPWgCyZJkjTM+rk7b23gPyOis/6JmXnGQEslSZI05JaYRGXmzcArWyiLJEnSpOEQB5IkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNWASJUmS1IBJlCRJUgMmUZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkN9J1ERcSMiLgsIk4ZZIEkSZImg7HURB0MXDeogkiSJE0mfSVREbE+sAdw3GCLI0mSNDn0WxN1NPAR4OnBFUWSJGnyWGISFRF7Andl5iVLWG9uRMyLiHkLFy4ctwJKkiQNo35qol4DvDEi5gPfBXaKiG/1rpSZx2bmnMycM2vWrHEupiRJ0nBZYhKVmR/NzPUzczbwduCszHzXwEsmSZI0xBwnSpIkqYFlx7JyZp4DnDOQkkiSJE0i1kRJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNWASJUmS1IBJlCRJUgMmUZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNbDEJCoiVoiIiyLiioi4JiIOb6NgkiRJw2zZPtZ5DNgpMx+MiOWAn0fE6Zl5wYDLJkmSNLSWmERlZgIP1rfL1SkHWShJkqRh11efqIiYERGXA3cBP83MCwdaKkmSpCHXVxKVmU9l5ubA+sBWEfGy3nUiYm5EzIuIeQsXLhznYkqSJA2XMd2dl5n3AWcDu42w7NjMnJOZc2bNmjVOxZMkSRpO/dydNysiVq+vVwR2Aa4fcLkkSZKGWj93560DfCMiZlCSrv/IzFMGWyxJkqTh1s/deVcCW7RQFkmSpEnDEcslSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGlhiEhURz4+IsyPi2oi4JiIObqNgkiRJw2zZPtZ5EvhQZl4aEasAl0TETzPz2gGXTZIkaWgtMYnKzDuAO+rrByLiOmA9wCRKGpDZh5060UVoZP6Re0x0ESSpNWPqExURs4EtgAsHUhpJkqRJou8kKiJWBr4PHJKZvxth+dyImBcR8xYuXDieZZQkSRo6fSVREbEcJYH6dmb+YKR1MvPYzJyTmXNmzZo1nmWUJEkaOv3cnRfA8cB1mXnU4IskSZI0/PqpiXoNsD+wU0RcXqc3DLhckiRJQ62fu/N+DkQLZZEkSZo0HLFckiSpAZMoSZKkBkyiJEmSGujnsS+a5hw9W5KmBr/Px5c1UZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNWASJUmS1IBJlCRJUgMmUZIkSQ0sMYmKiBMi4q6IuLqNAkmSJE0G/dREfR3YbcDlkCRJmlSWXdIKmXleRMxuoSx9mX3YqRNdhEbmH7nHRBdBkiSNI/tESZIkNTBuSVREzI2IeRExb+HCheO1W0mSpKE0bklUZh6bmXMyc86sWbPGa7eSJElDyeY8SZKkBvoZ4uA7wP8CL4qIBRHx3sEXS5Ikabj1c3feO9ooiCRJ0mRic54kSVIDJlGSJEkNmERJkiQ1sMQ+UZIkDYJPoNBkZ02UJElSAyZRkiRJDZhESZIkNWASJUmS1IBJlCRJUgMmUZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkN+NgXScJHkEgaO2uiJEmSGjCJkiRJaqCvJCoidouIGyLipog4bNCFkiRJGnZLTKIiYgbwFWB34CXAOyLiJYMumCRJ0jDrpyZqK+CmzLw5Mx8HvgvsPdhiSZIkDbd+kqj1gFu73i+o8yRJkqatyMzFrxCxL7BbZr6vvt8f2DozD+pZby4wt759EXDD+Bd34NYE7p7oQkwzxrx9xrx9xrx9xrx9kznmL8jMWWPdqJ9xom4Dnt/1fv0671ky81jg2LEWYJhExLzMnDPR5ZhOjHn7jHn7jHn7jHn7pmPM+2nOuxjYJCI2jIjlgbcD/zXYYkmSJA23JdZEZeaTEXEQ8N/ADOCEzLxm4CWTJEkaYn099iUzTwNOG3BZhsGkbo6cpIx5+4x5+4x5+4x5+6ZdzJfYsVySJEm/z8e+SJIkNWASJUmS1IBJ1BQSETMjYrn6Oia6PNNBRCxTfxrvlkTE8vVxVMa9JfW7ZWZ9bcwHqBPfiFgxImbV1/6tbkFErBwRs+vrvq5zT8wUEBHbRcQ1wP8AfwWQdnYbmIhYJSIOjYgrgS/V2f4uDVBErB0Rn4iIXwBnAH8JXueDFBFrRcRnI+Is4CzgryJipjEfrMzMiNgcuAX46wkuzpQXEWtExKci4lTgMuAA6P+7pa+78zRc6n8lkZlPRcQKlJHiPwqcB5waETcD3/fLbvzUmC+TmU9ShvpYB/gmsB9AZj41gcWbkrqvc8qAv+sAhwC/Bs6KiCsy86wJLOKU03OdzwSWA/4WuAo4H5gHnDlxJZx6OrVMmfl01+zNKP8UbzjCMi2lnut8FeAwYNfMPHus+/K/50mkU72YmU93/mhn5qOUh0Rflpn3Af8E7Eh59I6WUk/Mn6yv7wM+CxwFPBYRW3Svq6Uz0nUO3AR8ODMvzsy7gIuof2C09Ea5zm/NzA9n5vmZ+QBwM/DoRJZzKumJeW+StC9wEvBoRPxh9/pqbpTr/NfANXUiItYZyz5NooZQFDN628FrNe/zImLHiPhiROwVEasBPwdeVle7BngM8A/7GPQZ86MjYu86f2H94rsKeH1d3d+nMRhDzN+Ymfdl5oP1qQlQakms/RujscS8a5t3R8QTlOeirdt2mSe7sX631Ka8m4DLgd9QaqXA75e+jSHm+9RFVwMXRMQlwJcjYm6//dA8KUMgIlaPiD1qQkQWT2Xm091JUETsR6lSfwOwM/Bu4GHgdhb9oi0E7gTW6+yrvSOZPBrG/HXAe+v8zu/OucD27ZZ+clqKmP9pnb9cZj4eEVsBLwBO9p+ExVvamFenA8+t897S+WOvkS1FzN9fF20K3J6Z/wfcBxwYEQfaZWB0SxHz99VFRwNHAq8BPge8CXhLP59tn6jh8BJK35rHgDMj4kXAu4CtgZ9FxJcp1ejbAgdn5o8j4kzgOCCA64HdADLz3rr96e0fxqQyWsy3An6+mJifAKU6uP5yXggcWuf5Jbd4SxvzJ+p+DgWOycwH2z6ASWipYg6QmXfWl9dGxAJgw4hYxn46o2r6fX58rWndFNg/IuYCK1O+42+fgOOYTJpe518DyMx5lP5+ABdFxLXA2v1c59ZEtaRWL44W7/mU6tsX1vc7UmqUDgUeAv6OcnHMAa6o/5H/hHL+NgN+CGweEbvW7Teo209rDWP+ERbF/HF+P+adO2c6/+38Eng4Io6KiPdGxNqDOp7JYIAx7zRPb0P5MpwXEXtHxDsjYpVBHc9kMOjrvOtzZgCbANdP9wRqQN/nAWxMuUPsSGAv4FXAxZRmvWndPWNA1/nTI1zny1L6FP+yn+vcJKol9Q/uaCdkIXAH5T8QgG8AlwB/Tqlu3A5Yvq63ddd/5A8Ae2fmw8DhwJ9ExD3AlXWa1sYh5ssBdwGv7on5GwAi4tURcS7lD8sWwBOU6vdpa4Ax37O+/gvKf5zHUe5KfRh4ZJwPY1IZYMxfDxARB0bExZQ+OjdRal+ntQF+n785M0/NzK9l5s2UZOs0av+/6dw9Y4DX+e4AEXFAlD5RlwE3UG5eWSKb88bZSNV/NXveCPgT4InMPLx7eWY+ERG3AFtGxAaUjPlASn+bz1DuAtsG+DfgrbXdN4C7KdWYUGqj/ifLnWPTSh8xfzwz/757eU/MX0D5sjqQMkxEd8yPo8R81brpPcAr6+tbgEMy87KBHNgQaznm9wIvrq9PAL6UmRcM5MCG2ATE/BX19WXAQZk57ZKnCfg+f3n9jJmZ+Vhm3g8cP8BDHDoTcJ2/vL6+CvjAWL9brIlaChGxTK3ifkbn5EfEy6KM4QTlBH6R8t/EN3r20amevYVSk7EesAOwWmYeDzxJqeLdJzN/RLkI9qKMbfFVavVl7UR3X93njKla7dsw5t/s2UdvzNdlUcyPY/SYr0qJ+cb1c2/vJFA15s8q11QxBDE/hjpkR2ae2fmSG6lcU8WQxfyiTgLldwsw2O/zTernPtZbtnE6zKEyJNf5pvVzL+36bun7OrcmagwiIrqrU0eqWoyIwyhjfPwOODcivkkZ7fdVwPcyc373+l37u6NOm1Nqlf44Ir5POdE/pFwIUP6buRz4Q0o15T/0liGnUAdnY96+YY95p3yLqdqfdCZRzL3OW/5uGa1sk9Gwx7zJdW4StQTdVYvdJz/KM+peD7yV0q76D5Q216TchbEacDKwOvAFykB1i4v3PXXaBjgWOIhyx925mXlt13or1M9aDTgV+PHSHuOwMebtm0wx7y7fZGbM2zeZYj5VTKaYN7rOM9Opa6KMgjwXWG+EZesBe9bXuwI/BfYBXlrnvZ7SsfhMyh0Vx9eL4TmUat83LuGzNwI2HGXZjImOjTGfOpMxN+bG3Jgb86WfrImqurLlNSmdWG8CbouI1wIrZuZplD4CfxURN1CqCJeldEZ7uO7mEkoW/adZBkrr3v9vgJdHxNmZ+UBtbw0WPRuMLHdjdG/TGaI+cwpVo3cY8/YZ8/YZ8/YZ8/ZN15hPyc5q/egEtyvIncETb6SMydF5Ltf2LHqsx/mUasd1KYNZ3gN8APhCRHSqBC8C9o4ytPwuUcYPeh7l0Sx3As9Ua2bXs8EiYoMoIzH3nvgpUY0OxnwiGPP2GfP2GfP2GfNiWtRERc9TsiNK57Got5FGxExK9eNqmfnpiLgT2KieiMuB3SNircy8KyLuoNwSeX5m7lv3twqlDXYb4M8ot2GeShm74kfAg5n5Xz1lWgHYA9gJ2JJye+s/13JO+l80Y94+Y94+Y94+Y94+Yz66KZlE9Z7w7LoDICKem5n3RMRalJ7/22bmbyPicWD1ejJvpoyRsh7wK8ptla+gtNPeSnnmzkkRsTrlGTubU9psL6wXyaeAT/SeyHj2+Be7UEYW/xfKCMBPMIlNopg/H2NuzBsy5u2bRDH3+3waXudTsjkvSxVfJ2NeKSJ2iohjIuJG4GsRsU1m3kUZKn7HutmvKE+G36S+fpzySJUbKdWPe9T1VqW0964DrF3X/wGwf90nmflEzdKfNQZG94WYmT/OzC9k5lWT/RcOJlXMjzbmxrwpY96+SRRzv8+n4XU+5ZKoiFgtyvO0ToyIV1FO1hGUnvmbAv8LvD8iXgiczaK22vmUttZNKO25dwObZebjlFGSN4+Iqykd2Q4BbsjMn2fm3Mz8fmb+rrcs2dVeO5UZ8/YZ8/YZ8/YZ8/YZ87GZFM15Ec+0vz5roK4R1lsG+CSlCvE8ykldBrieMrw7wHco7a3bAOcA+wNk5k0RsTXwQGaeFBG3Aq+MiFUz88aIeFsnSx7hM5+VIU8Fxrx9xrx9xrx9xrx9xnxwhjaJiojOrYtPd05652dEbArcnZn39lwU2wPbZearuvYzE5hHaa8mM+dHxEbA1Zl5UZTh3T8HPJfSVvtwlA5rt1I6q20EXN45+b0nfLKe+JEY8/YZ8/YZ8/YZ8/YZ83YMTRJVA9s93kNSxosgSrXhmpSe+t+tm1wFvKcnq76XOt5ElNFQn85y58B8YG5EfDszr6B0Rutk1e8A9q77+1FmPlC3/w3lIYYbAZd3LrTJfsK7GfP2GfP2GfP2GfP2GfOJMWFJVPQ8qbk3sFGebP0BSke1vYBHKWNEvCUzb42IX0bElpl5addm9wCPRcRrMvMXdT+dcSt+DXw+yh0FZwOX1s+9Arii63M7WfkC4CfUC6XnQpuUjHn7jHn7jHn7jHn7jPlwaD2JqidgR+B79X2nrXZHYHdKtvzxzLw9IvYGrs3MLSNiC0pb7Mp1V2cD20bE5bmoWvC2iLgUOLju77WUdt2jgQuAZTLzUyOUaaRqz8eBX4x/BNpnzNtnzNtnzNtnzNtnzIfLwO/Oi9r+2ZGlXXQu8PaI+AiwakRsDLyLks2eBhwVEesBZwB31BO0gPIk563rri4EXgmsFBHLRcTudf7fUQbcWgM4Cvgs8BDlFsuNapmiu1xZTJkqRmPePmPePmPePmPePmM+3AaeRHUCGxEviIjtImJLSs//w4EXUk7MIcDtwIOUnv5zKONHXAWsD6xIeSjhDZSOalCGj9+KcqJXAHaKiBUy8/HM/FlmfigzT8sy3sRTlGrFz9cyTekTbszbZ8zbZ8zbZ8zbZ8yHXC7d05qDUZ6MTDlpKwJ/CJxLOZkfB54HfBj4fNe6H6O0m34SeCMws87fgHLiNq7v9wR+1vlM4M3ASqN8/jKUqselOsZhm4y5MTfmxtyYT43JmE/+abwviNXqz1WBrwLvBPYDPtez3hbAfwOzKf2ydgHO61lnh/rzfGDv+vq5wIs6J3iEizEmOqCtn0BjbsynwWTMjfl0mIz55JsadSzv6si2KbAvsDylGnFTSlvt2vUiOJOSRb+7tp/+BrgxM/8rylDuszJzPvDTiPjriPgSpWpxS+CHlOz73ZTn8JCZ91DuHiB7qhKzXgVTlTFvnzFvnzFvnzFvnzGfOqJp3CLixcDXgZ9STvRdwDeB91DaXa8DXpqZj0bEHModAa8GDqA8Q+cdlGfnrAX8W2b+NCLeRnkI4ZmZeetSHNeUZMzbZ8zbZ8zbZ8zbZ8ynhqUZ4mBj4CbgG8BtmflIRBwJfBA4Bfg+sHZE3JKZ8+CZwbdeBCwHHEOpqryPMgYFmXnSUpRnOjDm7TPm7TPm7TPm7TPmU8DS1EStAnyNMiLpMpRbII+iDBt/OHBSZv5lRKxIqa78OCXTPgn48mhVh9EzgJgWMebtM+btM+btM+btM+ZTQ+Mk6lk7KdWS76E8tfkY4IvAOpn5hogIyuBfT2TmfSNsO4MytLztsWNgzNtnzNtnzNtnzNtnzCevxs159cSuC7ycMnjXFsCfZ+aDEXERsEZEzMgyvsTCrm2WqfMA6H6txTPm7TPm7TPm7TPm7TPmU0PjwTZr1vt84E+BJ4GPZOYvI2IT4EDg0sx8qp70Z7bxhDdnzNtnzNtnzNtnzNtnzKeGcWnOe9YOy90BLwW+mOV2Sg2YMW+fMW+fMW+fMW+fMZ9cljqJ6lQvUpJkO7O1wJi3z5i3z5i3z5i3z5hPbuNeEyVJkjQdDPwBxJIkSVORSZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUgEmUJElSA/8f+oKb5AMbupYAAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAiBElEQVR4nO3deZxkVXnw8d/DsIZtAoys6oiyuCCLw6ZoEFf2V+FNREXEZUgU4xIXsqgYk4DG4BKDvkQUjRhRMS4sKsiigIDDviPgIDsDZBREGJbn/eOcgpqye7r6Ttft6u7f9/O5n66uu5373NtVT59z7rmRmUiSJGl8VpjsAkiSJE1FJlGSJEkNmERJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZqyImJORFwbEatNdlk0soh4fkScN9nlkAbBJErTXkSsEhHHRsTNEXF/RFwaEbv3LPOy+mX8YEScGRFP73PbcyMiI2LFBuXaMCJ+EBG3123MHWGZl0fExRHx+4i4NSL+fIRl3lTXf1vXe6dGxANd05KIuKJr/gsj4sIaj8sjYpeebb4rIn4dEb+LiAXd8yPi8Ih4pGf7m3bNPyYirouIxyPizSOUd9OIOKnu+56I+GTXvEPr/h6OiOP6CONhwHGZ+YeefRwXEY9GxIY978+OiC9HxJ11/9dHxGF97Kf3GBZGxB+6jv8noyz3097ro15fi2psL4uIfbvmbR0RV9W4vK/r/ZUi4oKIeGqDsu5ay/Chnvc7127nGO6KiKMjYqUG+xj1vGXm5cDiiNh7vNuVhp1JlGaCFYFbgD8D1gb+AfhWJ2mJiPWA7wIfBtYBFgAntFCux4EfAfuNNDMingN8A/h7Srm3Bi7qWeZPgb8Drup+PzN3z8w1OhNwHvDtus46wA+BfwVmA58Efli3RUTsCBwJ7F/3eyzwPxExq2sXJ3RvPzNv6pp3GfAO4OIRjmll4DTgDGADYBPg612L3A78E/DlkWLSs61VgIN61iciVqfE9LfAG3tW+zSwBvDsemz7ADeMta9R7N11/K8coXxvAEZKSN4NbJiZawHzga93JXtHAO+nnOu/j4gN6vvvA07MzFsalPMg4D7gTaPMn12vka2AnYF3NtjHWOfteOCQBtuVhppJlKa9zPx9Zh6emQsz8/HMPAn4NfCCushrgasy89uZ+RBwOLB1RGzZx+Z/Vn8urv/N7zyOct2VmUcDvxxlkX8A/l9mnpqZj2bmvZl5Y88yRwCfA+4ZbT81WXwx8LX61guBO+vxPpaZXwcWUeIAMJcSj4uyPNLga8B6wFP6PK7/yMyfAg+NMPvNwO2ZeVQ9Lw/VmorOut/NzO8B9/axqx2BxZl5a8/7+wGLgX+kJBDdtge+kZn/W6+FazPzO/0c13hExNrAR4EP9s7LzMsz89HOr5REq1PD9AzgjMy8DfgV8LRaK7ofJQEcbzlWpyTD7wQ2i4h5oy2bmXdTEtznjHc/fZy3s4CX1cRXmjZMojTjRMT6wOY8WXvzXErtCVCSLuDG+v5YXlJ/zq41Er+IiF0iYvEypl2WucUn7VTLe0VE3BERX6+1SJ3j2AGYB3xxjO28Cfh5Zi7sei96lgngefX1qcCsiNix1j69BbgUuLNr+b0j4r7a9PRXfR5P55gW1ubGeyLirIjYahzrd9sKuG6E9w8C/hv4JrBlRLyga975wD9HxMERsVnvirVpc7TzdnTP4sfXZrmfRMTWPfP+BfgCS8esez8nRcRDwAWUBGNBnXUl8MqI2ISSzN4IfBb4QGY+MlogluG1wAOUWsgf88dJZXeZNgJeRYlRdzlHi8dJ/RaiJoWPAFs0OAZpaJlEaUap/T2OB76amdfWt9egNP10+y2wZpN9ZOY5mTl7GdM5fW5qE+BASi3EZsBqwL/X45gFHA0cmpmPj7GdNwHHdf3+C2CjiDig9rU5CHgm8Cd1/v3AicA5wMOUGpX5+eSDNr9FaQ6bA7wd+EhEHDCOY3odpfZsI+Bk4Pu1mW+8ZteyPiEinga8lFLbdBfwU5ZuxnoX5fwfClwdETdEV/+4zHz+Ms7bO7q28wZKkvN04EzgxxExu5ZhHvAi6rkaSWbuRbm+9gB+0nUO3w/8FfAD4L11O/cDv46I70fE2RHxf/uOUEmaTsjMxyhNw68boc/TPRGxGLgN+D3wRM1cZu61jHjsNY5yUI9j9jjXkYaaSZRmjIhYAfgvYAnlS7TjAWCtnsXXoucLehL8AfhKZl6fmQ9Qajf2qPPeAVyemeePujZQa702YOkvxnuBfSn9bO4CXg2cDnSaxd4KHEypiVuZ0q/opFpTQWZenZm316bA8yg1JfuP45jOqU2US4BPAetSkrLx+l/+ONE9ELgmMy+tvx8PvL6TOGTmHzLzXzLzBXW/3wK+3V3D14/MPLdu68HMPILSfPjieo0dDby7q8lutG08kpmnUmqe9qnv3ZyZe2TmdsD3gY9TEqtPUfrp7QMc1U95ayf0l9YYULe3KrBnz6LrZeZsShJ9LqXGahDWpMRJmjZMojQjRERQOkivD+zX0zRyFaUjb2fZ1Sk1M0t11h5F9r4RES+Ope9c651e3GexL+/ZfvfrlwGviXKX2Z2Ufk7/FhGf79nGQcB3axL25IYyz87M7TNzHUrisSVwYZ29DXBSTd4ez8wfAXfUfYwk+ePmwX6PaXlcTmmW7fYmYNOuuBxF6c+1R+/Kmfk7SmK6OqUvErV5crTztqxm004M1qI0sZ5Q99/p73brMs77ipTrrddHgP+sNWpbAQsy87eUZPdZyyhLx4GUz/gf1rLcREmiRmzSy3KH43HATlFuthjpLs/u6dQ+ykDdzsaUhHyk5ldp6spMJ6dpP1H6DZ0PrDHCvDmU5rv9KF8ynwDO73O7fwI8BmzesFyrUr7Ek9JfZNWueW+hdIDftO7nW8B/1XmzKTVMnek8Ss3S2l3rr1aPa7cR9rstpUPzWsBngHO75h0EXF/3G8ArgAeBLev8fYE/rfN2oDQDHdS1/sr1uM6lNPetCqxQ521Rt/VyYBalyepGYOU6f8W6/BGUWsNVgRVHid3KlA7xG9ffdwYepSQc3bE5nnJnG5Q7MLfvKuPfU2q0/ui6WMY5exqlma2zjQ/UcqxbY9K97+3rue0kEVsCu9dzsxKllm8JsF3PPp5DuV5n1d9PAf6S8k/APcAG9f2zgMNHKed1lJskusuzD6WJdl1Kc2R24gusQrkr8w4gxnkdL/O8Aa8HTpnszwEnp4meJr0ATk6Dnij9VpJyt9gDXdMbupZ5OXAtpbnpLGBu17wvAl9cxvb/sX6JLgZ2GmfZsnfqmf+xuu1F9cvpT0fZzlnA23reOwC4eaQvRErH69/W6QTgKV3zoh7TbyhNmtcAB/ase2+N4bXAX49Qlt7j2rVr/mspwwr8ri773K55h4+w7uHLiN+/Ah/qOk8njrDMDjVxWIdyx+OVdd/31f2/cJzn7LmUWrDf1zj8FJg3yrJzWTpReTalM/n99Xr5JfCaEdY7E9ix6/etgaspCdT7ut6/EXjFCOvvRLne54ww7ypKc3anbJ2/h8XA2cD2Df7GlnneKH3f9hnU37iT02RNkTlRNeuS1K6ImAP8HNg2ewbcnO7qHXzfyszRmlmHQkQ8nzJUR9/Df0hThUmUJElSA3YslyRJasAkSpIkqQGTKEmSpAZMoiRJkhpYcRAbXW+99XLu3LmD2LQkSdKEuuiii+7JzDnjXW8gSdTcuXNZsGDB2AtKkiRNsoi4ucl6NudJkiQ10FcSFRGzI+I7EXFtRFwTEQ6aJkmSZrR+m/M+C/woM/ePiJUpz/GSJEmascZMoiJibeAlwJsBMnMJ5YGZkiRJM1Y/zXnPoDz89CsRcUlEfCkiVu9dKCLmR8SCiFiwaNGiCS+oJEnSMOkniVoR2A74QmZuS3ly+WG9C2XmMZk5LzPnzZkz7rsEJUmSppR+kqhbgVsz84L6+3coSZUkSdKMNWYSlZl3ArdExBb1rZcBVw+0VJIkSUOu37vz3gUcX+/Muwk4eHBFkiRJGn59JVGZeSkwb7BFkSRJmjocsVySJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpAZMoSZKkBkyiJEmSGjCJkiRJasAkSpIkqQGTKEmSpAZMoiRJkhowiZIkSWrAJEqSJKkBkyhJkqQGTKIkSZIaMImSJElqwCRKkiSpgRX7WSgiFgL3A48Bj2bmvEEWSpIkadj1lURVL83MewZWEkmSpCnE5jxJkqQG+k2iEvhJRFwUEfNHWiAi5kfEgohYsGjRookroSRJ0hDqN4naJTO3A3YH3hkRL+ldIDOPycx5mTlvzpw5E1pISZKkYdNXEpWZt9WfdwP/A+wwyEJJkiQNuzGTqIhYPSLW7LwGXglcOeiCSZIkDbN+7s5bH/ifiOgs/43M/NFASyVJkjTkxkyiMvMmYOsWyiJJkjRlOMSBJElSAyZRkiRJDZhESZIkNWASJUmS1IBJlCRJUgMmUZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNWASJUmS1IBJlCRJUgN9J1ERMSsiLomIkwZZIEmSpKlgPDVR7wauGVRBJEmSppK+kqiI2ATYE/jSYIsjSZI0NfRbE/UZ4IPA44MriiRJ0tQxZhIVEXsBd2fmRWMsNz8iFkTEgkWLFk1YASVJkoZRPzVRLwL2iYiFwDeB3SLi670LZeYxmTkvM+fNmTNngospSZI0XMZMojLzbzNzk8ycC7wOOCMz3zjwkkmSJA0xx4mSJElqYMXxLJyZZwFnDaQkkiRJU4g1UZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNWASJUmS1IBJlCRJUgMmUZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkNjJlERcSqEXFhRFwWEVdFxMfaKJgkSdIwW7GPZR4GdsvMByJiJeCciDg1M88fcNkkSZKG1phJVGYm8ED9daU65SALJUmSNOz66hMVEbMi4lLgbuC0zLxgoKWSJEkacn0lUZn5WGZuA2wC7BARz+tdJiLmR8SCiFiwaNGiCS6mJEnScBnX3XmZuRg4E3j1CPOOycx5mTlvzpw5E1Q8SZKk4dTP3XlzImJ2fb0a8Arg2gGXS5Ikaaj1c3fehsBXI2IWJen6VmaeNNhiSZIkDbd+7s67HNi2hbJIkiRNGY5YLkmS1IBJlCRJUgMmUZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNTDmA4iHzdzDTp7sIjSy8Mg9J7sIkiRpAlkTJUmS1IBJlCRJUgMmUZIkSQ2YREmSJDUwZhIVEU+NiDMj4uqIuCoi3t1GwSRJkoZZP3fnPQr8TWZeHBFrAhdFxGmZefWAyyZJkjS0xqyJysw7MvPi+vp+4Bpg40EXTJIkaZiNq09URMwFtgUuGEhpJEmSpoi+k6iIWAM4EXhPZv5uhPnzI2JBRCxYtGjRRJZRkiRp6PSVREXESpQE6vjM/O5Iy2TmMZk5LzPnzZkzZyLLKEmSNHT6uTsvgGOBazLzqMEXSZIkafj1UxP1IuBAYLeIuLROewy4XJIkSUNtzCEOMvMcIFooiyRJ0pThiOWSJEkNmERJkiQ1YBIlSZLUgEmUJElSAyZRkiRJDZhESZIkNWASJUmS1IBJlCRJUgNjDrYpSTPB3MNOnuwiNLLwyD0nuwjSjGVNlCRJUgMmUZIkSQ2YREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ1YBIlSZLUwJhJVER8OSLujogr2yiQJEnSVNBPTdRxwKsHXA5JkqQpZcwkKjN/BtzXQlkkSZKmDPtESZIkNTBhSVREzI+IBRGxYNGiRRO1WUmSpKE0YUlUZh6TmfMyc96cOXMmarOSJElDyeY8SZKkBvoZ4uC/gV8AW0TErRHx1sEXS5IkabitONYCmXlAGwXR8Jp72MmTXYRGFh6552QXQZI0jdmcJ0mS1IBJlCRJUgMmUZIkSQ2YREmSJDVgEiVJktSASZQkSVIDYw5xIKl9DishScPPmihJkqQGTKIkSZIaMImSJElqwD5RkqRJYd8/TXXWREmSJDVgTZQkSTOEtX8Ty5ooSZKkBkyiJEmSGjCJkiRJasAkSpIkqYG+kqiIeHVEXBcRN0TEYYMulCRJ0rAbM4mKiFnAfwC7A88BDoiI5wy6YJIkScOsn5qoHYAbMvOmzFwCfBPYd7DFkiRJGm79JFEbA7d0/X5rfU+SJGnGisxc9gIR+wOvzsy31d8PBHbMzEN7lpsPzK+/bgFcN/HFHbj1gHsmuxAzjDFvnzFvnzFvnzFv31SO+dMzc854V+pnxPLbgKd2/b5JfW8pmXkMcMx4CzBMImJBZs6b7HLMJMa8fca8fca8fca8fTMx5v005/0S2CwinhERKwOvA34w2GJJkiQNtzFrojLz0Yg4FPgxMAv4cmZeNfCSSZIkDbG+HkCcmacApwy4LMNgSjdHTlHGvH3GvH3GvH3GvH0zLuZjdiyXJEnSH/OxL5IkSQ2YREmSJDVgEjWNRMQqEbFSfR2TXZ6ZICJWqD+Nd0siYuX6OCrj3pL62bJKfW3MB6gT34hYLSLm1Nd+V7cgItaIiLn1dV/XuSdmGoiIXSLiKuCnwHsB0s5uAxMRa0bEByLicuBz9W3/lgYoItaPiI9GxLnAj4C/Bq/zQYqIp0TEERFxBnAG8N6IWMWYD1ZmZkRsA/wG+NAkF2fai4h1IuLjEXEycAlwEPT/2dLX3XkaLvW/ksjMxyJiVcpI8X8L/Aw4OSJuAk70w27i1JivkJmPUob62BD4GvAGgMx8bBKLNy11X+eUAX83BN4D3AycERGXZeYZk1jEaafnOl8FWAn4B+AK4DxgAXD65JVw+unUMmXm411vP5vyT/EzRpin5dRzna8JHAa8MjPPHO+2/O95CulUL2bm450v7cx8iPKQ6EsyczHwb8CulEfvaDn1xPzR+noxcARwFPBwRGzbvayWz0jXOXAD8P7M/GVm3g1cSP2C0fIb5Tq/JTPfn5nnZeb9wE3AQ5NZzumkJ+a9SdL+wAnAQxHxgu7l1dwo1/nNwFV1IiI2HM82TaKGUBSzetvBazXvBhGxa0R8NiL2joi1gXOA59XFrgIeBvxiH4c+Y/6ZiNi3vr+ofvBdAbyqLu7f0ziMI+b7ZObizHygPjUBSi2JtX/jNJ6Yd61zcEQ8Qnku2kZtl3mqG+9nS23KuwG4FLiLUisFfr70bRwx36/OuhI4PyIuAj4fEfP77YfmSRkCETE7IvasCRFZPJaZj3cnQRHxBkqV+h7Ay4GDgQeB23nyD20RcCewcWdb7R3J1NEw5i8D3lrf7/ztnA28pN3ST03LEfO31/dXyswlEbED8HTgO/6TsGzLG/PqVGDd+t5rO1/2GtlyxPwv66zNgdsz89fAYuCQiDjELgOjW46Yv63O+gxwJPAi4BPA/wFe28++7RM1HJ5D6VvzMHB6RGwBvBHYEfh5RHyeUo3+QuDdmfnDiDgd+BIQwLXAqwEy8766/qntH8aUMlrMdwDOWUbMvwylOrj+cV4AfKC+54fcsi1vzB+p2/kAcHRmPtD2AUxByxVzgMy8s768OiJuBZ4RESvYT2dUTT/Pj601rZsDB0bEfGANymf87ZNwHFNJ0+v8KwCZuYDS3w/gwoi4Gli/n+vcmqiW1OrF0eK9kFJ9+6z6+66UGqUPAL8HPkK5OOYBl9X/yH9COX/PBr4HbBMRr6zrP62uP6M1jPkHeTLmS/jjmHfunOn8t/Mr4MGIOCoi3hoR6w/qeKaCAca80zy9M+XDcEFE7BsRr4+INQd1PFPBoK/zrv3MAjYDrp3pCdSAPs8DeCblDrEjgb2B7YFfUpr1ZnT3jAFd54+PcJ2vSOlT/Kt+rnOTqJbUL9zRTsgi4A7KfyAAXwUuAt5BqW7cBVi5Lrdj13/k9wP7ZuaDwMeAN0fEvcDldZrRJiDmKwF3Azv1xHwPgIjYKSLOpnyxbAs8Qql+n7EGGPO96ut3Uf7j/BLlrtQHgT9M8GFMKQOM+asAIuKQiPglpY/ODZTa1xltgJ/nr8nMkzPzK5l5EyXZOoXa/28md88Y4HW+O0BEHBSlT9QlwHWUm1fGZHPeBBup+q9mz5sCbwYeycyPdc/PzEci4jfAdhHxNErGfAilv80/U+4C2xn4T+DPa7tvAPdQqjGh1Eb9NMudYzNKHzFfkpn/2D2/J+ZPp3xYHUIZJqI75l+ixHytuuq9wNb19W+A92TmJQM5sCHWcszvA7asr78MfC4zzx/IgQ2xSYj58+vrS4BDM3PGJU+T8Hm+Vd3HKpn5cGb+Fjh2gIc4dCbhOt+qvr4CeOd4P1usiVoOEbFCreJ+QufkR8TzoozhBOUEfpby38RXe7bRqZ79DaUmY2Pgz4C1M/NY4FFKFe9+mfl9ykWwN2Vsiy9Qqy9rJ7rFdZuzpmu1b8OYf61nG70x34gnY/4lRo/5WpSYP7Pu9/ZOAlVjvlS5poshiPnR1CE7MvP0zofcSOWaLoYs5hd2Eig/W4DBfp5vVvf7cG/ZJugwh8qQXOeb1/1e3PXZ0vd1bk3UOEREdFenjlS1GBGHUcb4+B1wdkR8jTLa7/bAtzNzYffyXdu7o07bUGqV3hQRJ1JO9PcoFwKU/2YuBV5Aqab8ZG8Zchp1cDbm7Rv2mHfKt4yq/SlnCsXc67zlz5bRyjYVDXvMm1znJlFj6K5a7D75UZ5R9yrgzyntqp+ktLkm5S6MtYHvALOBT1MGqltWvO+t087AMcChlDvuzs7Mq7uWW7Xua23gZOCHy3uMw8aYt28qxby7fFOZMW/fVIr5dDGVYt7oOs9Mp66JMgryfGDjEeZtDOxVX78SOA3YD3hufe9VlI7Fp1PuqDi2Xgx/Qqn23WeMfW8KPGOUebMmOzbGfPpMxtyYG3NjbsyXf7ImqurKltejdGK9AbgtIl4KrJaZp1D6CLw3Iq6jVBGuSOmM9mDdzEWULPrtWQZK697+XcBWEXFmZt5f21uDJ58NRpa7MbrX6QxRnzmNqtE7jHn7jHn7jHn7jHn7ZmrMp2VntX50gtsV5M7giddTxuToPJfrJTz5WI/zKNWOG1EGs7wXeCfw6YjoVAleCOwbZWj5V0QZP2gDyqNZ7gSeqNbMrmeDRcTToozE3Hvip0U1OhjzyWDM22fM22fM22fMixlRExU9T8mOKJ3Hot5GGhGrUKof187Mf4qIO4FN64m4FNg9Ip6SmXdHxB2UWyLPy8z96/bWpLTB7gz8FeU2zJMpY1d8H3ggM3/QU6ZVgT2B3YDtKLe3/nst55T/QzPm7TPm7TPm7TPm7TPmo5uWSVTvCc+uOwAiYt3MvDcinkLp+f/CzPzfiFgCzK4n8ybKGCkbAzdSbqt8PqWd9hbKM3dOiIjZlGfsbENps72gXiQfBz7aeyJj6fEvXkEZWfyLlBGAH2EKm0IxfyrG3Jg3ZMzbN4Vi7uf5DLzOp2VzXpYqvk7GvHpE7BYRR0fE9cBXImLnzLybMlT8rnW1GylPht+svl5CeaTK9ZTqxz3rcmtR2ns3BNavy38XOLBuk8x8pGbpS42B0X0hZuYPM/PTmXnFVP+DgykV888Yc2PelDFv3xSKuZ/nM/A6n3ZJVESsHeV5Wt+IiO0pJ+tfKD3zNwd+AfxlRDwLOJMn22oXUtpaN6O0594DPDszl1BGSd4mIq6kdGR7D3BdZp6TmfMz88TM/F1vWbKrvXY6M+btM+btM+btM+btM+bjMyWa8yKeaH9daqCuEZZbATicUoX4M8pJXQG4ljK8O8B/U9pbdwbOAg4EyMwbImJH4P7MPCEibgG2joi1MvP6iPiLTpY8wj6XypCnA2PePmPePmPePmPePmM+OEObREVE59bFxzsnvfMzIjYH7snM+3ouipcAu2Tm9l3bWQVYQGmvJjMXRsSmwJWZeWGU4d0/AaxLaat9MEqHtVsondU2BS7tnPzeEz5VT/xIjHn7jHn7jHn7jHn7jHk7hiaJqoHtHu8hKeNFEKXacD1KT/1v1lWuAN7Sk1XfRx1vIspoqI9nuXNgITA/Io7PzMsondE6WfUBwL51e9/PzPvr+ndRHmK4KXBp50Kb6ie8mzFvnzFvnzFvnzFvnzGfHJOWREXPk5p7AxvlydbvpHRU2xt4iDJGxGsz85aI+FVEbJeZF3etdi/wcES8KDPPrdvpjFtxM/CpKHcUnAlcXPd7GXBZ1347WfmtwE+oF0rPhTYlGfP2GfP2GfP2GfP2GfPh0HoSVU/ArsC36++dttpdgd0p2fKHM/P2iNgXuDozt4uIbSltsWvUTZ0JvDAiLs0nqwVvi4iLgXfX7b2U0q77GeB8YIXM/PgIZRqp2nMJcO7ER6B9xrx9xrx9xrx9xrx9xny4DPzuvKjtnx1Z2kXnA6+LiA8Ca0XEM4E3UrLZU4CjImJj4EfAHfUE3Up5kvOOdVMXAFsDq0fEShGxe33/I5QBt9YBjgKOAH5PucVy01qm6C5XFtOmitGYt8+Yt8+Yt8+Yt8+YD7eBJ1GdwEbE0yNil4jYjtLz/2PAsygn5j3A7cADlJ7+8yjjR1wBbAKsRnko4XWUjmpQho/fgXKiVwV2i4hVM3NJZv48M/8mM0/JMt7EY5RqxU/VMk3rE27M22fM22fM22fM22fMh1wu39Oag1GejEw5aasBLwDOppzMDwMbAO8HPtW17N9R2k0PB/YBVqnvP41y4p5Zf98L+Hlnn8BrgNVH2f8KlKrH5TrGYZuMuTE35sbcmE+PyZhP/WmiL4i168+1gC8ArwfeAHyiZ7ltgR8Dcyn9sl4B/KxnmT+rP88D9q2v1wW26JzgES7GmOyAtn4CjbkxnwGTMTfmM2Ey5lNvatSxvKsj2+bA/sDKlGrEzSlttevXi+B0ShZ9cG0/vQu4PjN/EGUo9zmZuRA4LSI+FBGfo1Qtbgd8j5J9H0x5Dg+ZeS/l7gGypyox61UwXRnz9hnz9hnz9hnz9hnz6SOaxi0itgSOA06jnOi7ga8Bb6G0u14DPDczH4qIeZQ7AnYCDqI8Q+cAyrNzngL8Z2aeFhF/QXkI4emZectyHNe0ZMzbZ8zbZ8zbZ8zbZ8ynh+UZ4uCZwA3AV4HbMvMPEXEk8D7gJOBEYP2I+E1mLoAnBt/aAlgJOJpSVbmYMgYFmXnCcpRnJjDm7TPm7TPm7TPm7TPm08Dy1EStCXyFMiLpCpRbII+iDBv/MeCEzPzriFiNUl35YUqmfQLw+dGqDqNnADE9yZi3z5i3z5i3z5i3z5hPD42TqKU2Uqol30J5avPRwGeBDTNzj4gIyuBfj2Tm4hHWnUUZWt722HEw5u0z5u0z5u0z5u0z5lNX4+a8emI3AraiDN61LfCOzHwgIi4E1omIWVnGl1jUtc4K9T0Aul9r2Yx5+4x5+4x5+4x5+4z59NB4sM2a9T4VeDvwKPDBzPxVRGwGHAJcnJmP1ZP+xDqe8OaMefuMefuMefuMefuM+fQwIc15S22w3B3wXOCzWW6n1IAZ8/YZ8/YZ8/YZ8/YZ86lluZOoTvUiJUm2M1sLjHn7jHn7jHn7jHn7jPnUNuE1UZIkSTPBwB9ALEmSNB2ZREmSJDVgEiVJktSASZQkSVIDJlGSJEkNmERJkiQ18P8B5ocO3ncVlTcAAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAhDElEQVR4nO3deZgtVXnv8e+PGWWKckQFEVBwVsDjgCIiXlSciMpjVDTgdMyNxiFGo7kx0auJxmsUjUOCoOINKkYTRzSigopG4TDKpCI5MghyAJlE5jd/rGrYNN2nu+ucXae7z/fzPPV0dVXt2qveqt777bVWrUpVIUmSpLlZb20XQJIkaSEyiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRK0mpLcm2SnaZZd3CS49fge70qySFran+auyQbJzknyZK1XRZpbTKJkibpviAOT/KrJNckOTXJfiPrN0ryhSQrklSSvee4/0py/zVd7r6SHJfkFauzj6rarKrO6/n+uyY5Kcl13c9dV7HtRsBfA/9v0vLNukTuG1O8Zs8kP0pyVZIrkvwwyaPmWMZnJDk+yZVJLklyWJLNR9bfLclRSS5PclmSI5Ns0a3bIMnnutd+c2J5t+6vkvz5XMrSvS5Jzkty1hTrjktyfRePq5J8P8nD5voe3b7e0B3v1Uk+kWRjgKq6AfgE8JY++5UWC5Mo6c42AC4AnghsSfvS/nySHUa2OR54MXDJ4KUbWJINxrjvjYAvA/8K/AFwBPDlbvlU9gfOqaqLJi1/HnADsG+Se47sfwvga8A/AXcDtgXe0W07F1sC7wLuDTyo289oIveurvw7AvcDtgHe3q17LlDA1sBVwLKubDsCzwY+NMeyAOwF3APYaZqE8DVVtRntmI8D/v9c3yDJU2lJ0pOB+wI70WI34TPAQROJlbQuMomSJqmq31XV26tqRVXdWlVfA/4beGS3/saqOqSqjgdumcu+k3y/mz2tqyn4ozm+fv+uZuzqJL9M8rRu+ZZd7dnFSS5K8q4k63frDu5qUd6X5LdJ/nuiZi3J3wFPAD7clefD3fJK8uokvwB+0S17ZZJzu9qcryS590i5bqtdS3L3bv3VSU6gJRXT2ZuWtB5SVTdU1YeAAPtMs/1+wPemWH4Q8M/A6bTkdsIuAFX12aq6pap+X1XfqqrTV1GmO6mqz1TVN6vquqr6LfBx4PEjm+wIfKmqrq6qq4D/AB4ysu64qroZOJaWjEBLnt7YLZ+rg2jJ59Hd/HTlvgX4HPDgnu9xeFWd2R3zO4GDR/Z9IfBb4LE99i0tCiZR0gySbEP7Mj5zdfdVVXt1s4/omsCOSrJ919Qz3fSirhyPBj4NvAnYilYbsaLb36eAm4H7A7sBTwFGm+geA/yMVhvyXuDwJKmq/wP8gK7moqpeM/KaP+xe9+Ak+wDvBp4P3Av4Fe3LeSofAa7vtntZN03nIcDpdcfnT53O7QnIZA/rjuM2Se5LS8aO7KY/Hln9c+CWJEck2S/JH0x67Z4zxH7PacqxF3e8Hj4CPDPJH3Tv8TxgomnxDGCfrsbmScCZSZ4DXFZVP5xm/9NKchfggJHjfcF0NXfd8gOBH48se9EMx7x9t+lDgNNGdncasE2Su48sOxt4xFyPQVosxlZNLy0GSTakfVEdUVXnjOM9qup8WlI0k5cDn6iqY7rfL+rKuA3wdGCrqvo98LskH6A1G/1Lt+2vqurj3fZHAB+lNTmtqjny3VV1RfeaA7v3Prn7/a3Ab5PsUFUrJl7Q1X49D3hYVf0OOKN7v73utPdmM1oT16irgM2n2BZanK6ZtOwltETsrCRXAe9NsltVnVJVV3eJ0F/Sao/umeRo4JVV9ZuuNnGrVcTgTpLsS6uleczI4pOBjYDLu9+/Q4sxtNqiJwAn0pKZz3Xr9x2pCTwDeH1V3TiLIjyX1hz5Ldpn+IbAM2i1XxM+lOR9wKa0hPa5Eyuq6jO0priZTD43E/ObjxznNcwxftJiYk2UNI0k69H6ktwIvGaGzYdwH+CXUyy/L+2L9OKJ2gRa8nSPkW1uS5aq6rpudrMZ3u+Ckfl702qfJvZxLe2LdNtJr1nC7X3KJvyK6V0LbDFp2RbcOVGa8FvunGD9MS3Rpesr9T1Gmriq6uyqOriqtgMe2h3LIaso07SSPJaWgBxQVT8fWfV5Wq3X5l35f0nr50U1b6mqh1fVMlo/o38GHgUspfW924hV19iNOgj4fFXdXFXXA1/kzk16r62qrWhJ1DOBLyR5+BwPd/K5mZgfPTebA1fOcb/SomESJU0hSYDDabU1z6uqm8b4Xtt3/ZGmmw7sNr2AqfsXXUCrmdi6qrbqpi2qaromsclqFst/TUvWJsp8V+DudLVhI1bSmhXvM7Jse6Z3JvDwLt4THs70Taen0/Vz6srxOGBn4K1pd5FdQqshelGm6BDf1SZ+ipZMkeQJM8T+CSPvtRvwFeBlVfWdSbveFfiXrj/dtbQk6emT3z/tLrnHAYfSmiZP6poyT+yOe5WSbEfrL/bikeM9AHh6kq2nON5bq+oHwLm0Jl6SHDjDMU+crzO5Y1PdI4DfVNXlI8sexB2b/KR1ikmUNLWP0b4gntU1kd1B2jAIm3S/bpRkk0mJwKr8hts7F1NV53f9kaabjuw2PRx4aZInJ1kvybZJHlhVF9Oadv4xyRbduvsleWKf8kzjs91779r17fl74CejTXndsdwC/Dvw9iR3SfJgVtHxmXbn2C3Aa7uYTtT4fXea7Y+m1dxMOAg4htZxetdueiitBma/JA9M8sYu+SDJfYAX0vURqqofzBD7H3SveyjwTeDPquqrU5TrROAVSTZNsimtKfUOnde76+PDtFqiW2k3K+zZ9Vt6InBet93BSVZMc/wvodV4PWDkeHcBLuyO606S7NHF58zumI+c4ZjP7176aeDlSR6cZCvaXaqfGtnvtrS7/36MtK6qKicnp5GJVuNStL4k145MB45ss6LbZnTaoVv3V8A3VrH/PwEupjWDPH+OZXsO7cv5GlrtwlO75VvSEr8LaX1XTgFe0K07GDh+0n4KuH83vwfti/m3wIcmr59U7l8CV9CGDdhumv0t6dZfDZxAu6vr+FUc027AScDvaX2LdlvFthsC59Oa5DbpyvysKbb7KPAFWnPj52k1Zr/rfv4LsMUc4/5J4NZJ18OZI+t3BL5Ka+K8gpZw7TxpHy8DPjLy+wa0/lFXAf85USbgbcCR05TjHFoiN3n5m4Hl3fxxk67dc4E39Pxb+HNakn11F4ONR9a9CXj/2v57dXJam1OqpqvJl6T5J8ky4MFV9fq1XZZxSPIt4HVVdfbaLst0utrI04C9qurStV0eaW0xiZIkSerBPlGSJEk9mERJkiT1YBIlSZLUg0mUJElSD2N57MvWW29dO+ywwzh2LUmStEaddNJJl1XVkrm+bixJ1A477MDy5cvHsWtJkqQ1KsmqHk81LZvzJEmSephVEpVkqyRfSHJOkrO7xwhIkiSts2bbnPdB4JtVdUD3nKe7jLFMkiRJ896MSVSSLYG9aM/foqpuBG4cb7EkSZLmt9k05+0IrAQ+meSUJIcluevkjZIsS7I8yfKVK1eu8YJKkiTNJ7NJojYAdgc+VlW70Z6E/pbJG1XVoVW1tKqWLlky57sEJUmSFpTZJFEXAhdW1U+6379AS6okSZLWWTMmUVV1CXBBkgd0i54MnDXWUkmSJM1zs70778+AI7s7884DXjq+IkmSJM1/s0qiqupUYOl4iyJJkrRwOGK5JElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8bzGajJCuAa4BbgJurauk4CyVJkjTfzSqJ6jypqi4bW0kkSZIWEJvzJEmSephtElXAt5KclGTZVBskWZZkeZLlK1euXHMllCRJmodmm0TtWVW7A/sBr06y1+QNqurQqlpaVUuXLFmyRgspSZI038wqiaqqi7qflwL/ATx6nIWSJEma72ZMopLcNcnmE/PAU4Azxl0wSZKk+Ww2d+dtA/xHkontP1NV3xxrqSRJkua5GZOoqjoPeMQAZZEkSVowHOJAkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqYdZJ1FJ1k9ySpKvjbNAkiRJC8FcaqJeB5w9roJIkiQtJLNKopJsBzwDOGy8xZEkSVoYZlsTdQjwZuDW8RVFkiRp4ZgxiUryTODSqjpphu2WJVmeZPnKlSvXWAElSZLmo9nURD0eeHaSFcDngH2S/Ovkjarq0KpaWlVLlyxZsoaLKUmSNL/MmERV1Vuraruq2gF4AfDdqnrx2EsmSZI0jzlOlCRJUg8bzGXjqjoOOG4sJZEkSVpArImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6mHGJCrJJklOSHJakjOTvGOIgkmSJM1nG8ximxuAfarq2iQbAscn+UZV/XjMZZMkSZq3ZkyiqqqAa7tfN+ymGmehJEmS5rtZ9YlKsn6SU4FLgWOq6idjLZUkSdI8N6skqqpuqapdge2ARyd56ORtkixLsjzJ8pUrV67hYkqSJM0vc7o7r6quBI4FnjbFukOramlVLV2yZMkaKp4kSdL8NJu785Yk2aqb3xTYFzhnzOWSJEma12Zzd969gCOSrE9Luj5fVV8bb7EkSZLmt9ncnXc6sNsAZZEkSVowHLFckiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqYcZk6gk90lybJKzkpyZ5HVDFEySJGk+22AW29wMvLGqTk6yOXBSkmOq6qwxl02SJGnemrEmqqourqqTu/lrgLOBbcddMEmSpPlsTn2ikuwA7Ab8ZCylkSRJWiBmnUQl2Qz4IvD6qrp6ivXLkixPsnzlypVrsoySJEnzzqySqCQb0hKoI6vq36fapqoOraqlVbV0yZIla7KMkiRJ885s7s4LcDhwdlW9f/xFkiRJmv9mUxP1eOAlwD5JTu2mp4+5XJIkSfPajEMcVNXxQAYoiyRJ0oLhiOWSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPcyYRCX5RJJLk5wxRIEkSZIWgtnURH0KeNqYyyFJkrSgzJhEVdX3gSsGKIskSdKCYZ8oSZKkHtZYEpVkWZLlSZavXLlyTe1WkiRpXlpjSVRVHVpVS6tq6ZIlS9bUbiVJkuYlm/MkSZJ6mM0QB58F/gt4QJILk7x8/MWSJEma3zaYaYOqeuEQBZEkSVpIbM6TJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSethgbRdgrnZ4y9fXdhF6WfGeZ6ztIkhaBT9bhmfMtdDNKolK8jTgg8D6wGFV9Z6xlkrzih90kiTd2YxJVJL1gY8A+wIXAicm+UpVnTXuwknrKhNXSePgZ8uaNZs+UY8Gzq2q86rqRuBzwP7jLZYkSdL8NpskalvggpHfL+yWSZIkrbNSVaveIDkAeFpVvaL7/SXAY6rqNZO2WwYs6359APCzNV/csdsauGxtF2IdY8yHZ8yHZ8yHZ8yHt5Bjft+qWjLXF82mY/lFwH1Gft+uW3YHVXUocOhcCzCfJFleVUvXdjnWJcZ8eMZ8eMZ8eMZ8eOtizGfTnHcisHOSHZNsBLwA+Mp4iyVJkjS/zVgTVVU3J3kN8J+0IQ4+UVVnjr1kkiRJ89isxomqqqOBo8dclvlgQTdHLlDGfHjGfHjGfHjGfHjrXMxn7FguSZKkO/PZeZIkST2YREmSJPVgErWIJNk4yYbdfNZ2edYFSdbrfhrvgSTZqHsclXEfSPfZsnE3b8zHaCK+STZNsqSb97t6AEk2S7JDNz+r69wTswgk2TPJmcB3gDcAlJ3dxibJ5knelOR04EPdYv+WxijJNkn+NskPgW8CrwWv83FKco8k707yXeC7wBuSbGzMx6uqKsmuwPnAX67l4ix6Se6W5J1Jvg6cAhwEs/9smdXdeZpfuv9KUlW3JNmENlL8W4HvA19Pch7wRT/s1pwu5utV1c20oT7uBXwaOBCgqm5Zi8VblEavc9qAv/cCXg/8CvhuktOq6rtrsYiLzqTrfGNgQ+CvgZ8CPwKWA99eeyVcfCZqmarq1pHFD6L9U7zjFOu0miZd55sDbwGeUlXHznVf/ve8gExUL1bVrRNf2lV1Pe0h0adU1ZXAPwJ70x69o9U0KeY3d/NXAu8G3g/ckGS30W21eqa6zoFzgb+oqhOr6lLgBLovGK2+aa7zC6rqL6rqR1V1DXAecP3aLOdiMinmk5OkA4CjgOuTPHJ0e/U3zXX+K+DMbiLJveayT5OoeSjN+pPbwbtq3nsm2TvJB5M8K8mWwPHAQ7vNzgRuAPxin4NZxvyQJPt3y1d2H3w/BZ7abe7f0xzMIebPrqorq+ra7qkJ0GpJrP2bo7nEfOQ1L01yE+25aPceuswL3Vw/W7qmvHOBU4Hf0GqlwM+XWZtDzJ/XrToD+HGSk4APJ1k2235onpR5IMlWSZ7RJURUc0tV3TqaBCU5kFal/nTgfwEvBa4Dfs3tf2grgUuAbSf2NdyRLBw9Y/5k4OXd8om/ne8Bew1b+oVpNWL+ym75hlV1Y5JHA/cFvuA/Cau2ujHvfAO4e7fsuRNf9praasT8T7pVuwC/rqr/Bq4EXpXkVXYZmN5qxPwV3apDgPcAjwf+AfhD4LmzeW/7RM0PD6b1rbkB+HaSBwAvBh4D/CDJh2nV6I8DXldVX03ybeAwIMA5wNMAquqK7vXfGP4wFpTpYv5o4PhVxPwT0KqDuz/OnwBv6pb5Ibdqqxvzm7r9vAn4aFVdO/QBLECrFXOAqrqkmz0ryYXAjknWs5/OtPp+nh/e1bTuArwkyTJgM9pn/K/XwnEsJH2v808CVNVyWn8/gBOSnAVsM5vr3JqogXTVi9PFewWt+vb+3e9702qU3gT8Dvgb2sWxFDit+4/8W7Tz9yDgS8CuSZ7SvX777vXrtJ4xfzO3x/xG7hzziTtnJv7b+QVwXZL3J3l5km3GdTwLwRhjPtE8vQftw3B5kv2TvCjJ5uM6noVg3Nf5yPusD+wMnLOuJ1Bj+jwPcD/aHWLvAZ4FPAo4kdast053zxjTdX7rFNf5BrQ+xb+YzXVuEjWQ7gt3uhOyEriY9h8IwBHAScCf0qob9wQ26rZ7zMh/5NcA+1fVdcA7gIOTXA6c3k3rtDUQ8w2BS4HHTor50wGSPDbJ92hfLLsBN9Gq39dZY4z5M7v5P6P9x3kY7a7U64Dfr+HDWFDGGPOnAiR5VZITaX10zqXVvq7Txvh5/pyq+npVfbKqzqMlW0fT9f9bl7tnjPE63w8gyUFpfaJOAX5Gu3llRjbnrWFTVf912fNOwMHATVX1jtH1VXVTkvOB3ZNsT8uYX0Xrb/N3tLvA9gA+Djy/a/cNcBmtGhNabdR3qt05tk6ZRcxvrKr/O7p+UszvS/uwehVtmIjRmB9Gi/kW3UsvBx7RzZ8PvL6qThnLgc1jA8f8CuCB3fwngA9V1Y/HcmDz2FqI+cO7+VOA11TVOpc8rYXP84d177FxVd1QVVcBh4/xEOedtXCdP6yb/ynw6rl+tlgTtRqSrNdVcd9m4uQneWjaGE7QTuAHaf9NHDFpHxPVs+fTajK2BZ4IbFlVhwM306p4n1dVX6ZdBM+ijW3xMbrqy64T3ZXdPtdfrNW+PWP+6Un7mBzze3N7zA9j+phvQYv5/br3/fVEAtXF/A7lWizmQcw/SjdkR1V9e+JDbqpyLRbzLOYnTCRQfrYA4/0837l73xsml20NHea8Mk+u81269z155LNl1te5NVFzkCSj1alTVS0meQttjI+rge8l+TRttN9HAf9WVStGtx/Z38XdtCutVumPk3yRdqK/RLsQoP03cyrwSFo15Xsnl6EWUQdnYz68+R7zifKtomp/wVlAMfc6H/izZbqyLUTzPeZ9rnOTqBmMVi2Onvy0Z9Q9FXg+rV31vbQ216LdhbEl8AVgK+ADtIHqVhXvy7tpD+BQ4DW0O+6+V1VnjWy3SfdeWwJfB766usc43xjz4S2kmI+WbyEz5sNbSDFfLBZSzHtd51XlNDLRRkFeBmw7xbptgWd2808BjgGeBzykW/ZUWsfib9PuqDi8uxjuQqv2ffYM770TsOM069Zf27Ex5otnMubG3Jgbc2O++pM1UZ2RbHlrWifWc4GLkjwJ2LSqjqb1EXhDkp/Rqgg3oHVGu67bzUm0LPqV1QZKG93/b4CHJTm2qq7p2lvD7c8Go9rdGKOvmRiivmoRVaNPMObDM+bDM+bDM+bDW1djvig7q83GRHBHgjwxeOLPaWNyTDyXay9uf6zHj2jVjvemDWZ5OfBq4ANJJqoETwD2Txtaft+08YPuSXs0yyXAbdWaNfJssCTbp43EPPnEL4pqdDDma4MxH54xH54xH54xb9aJmqhMekp20jqPpbuNNMnGtOrHLavqXUkuAXbqTsSpwH5J7lFVlya5mHZL5I+q6oBuf5vT2mD3AP437TbMr9PGrvgycG1VfWVSmTYBngHsA+xOu731n7pyLvg/NGM+PGM+PGM+PGM+PGM+vUWZRE0+4TVyB0CSu1fV5UnuQev5/7iq+m2SG4GtupN5Hm2MlG2BX9Juq3w4rZ32Atozd45KshXtGTu70tpsf9JdJO8E/nbyicwdx7/Ylzay+D/TRgC+iQVsAcX8PhhzY96TMR/eAoq5n+fr4HW+KJvzqlXxTWTMd02yT5KPJvk58Mkke1TVpbSh4vfuXvZL2pPhd+7mb6Q9UuXntOrHZ3TbbUFr770XsE23/b8DL+n2SVXd1GXpdxgDY/RCrKqvVtUHquqnC/0PDhZUzA8x5sa8L2M+vAUUcz/P18HrfNElUUm2THue1meSPIp2sv6e1jN/F+C/gD9Jcn/gWG5vq11Ba2vdmdaeexnwoKq6kTZK8q5JzqB1ZHs98LOqOr6qllXVF6vq6sllqZH22sXMmA/PmA/PmA/PmA/PmM/NgmjOS25rf73DQF1TbLce8HZaFeL3aSd1PeAc2vDuAJ+ltbfuARwHvASgqs5N8hjgmqo6KskFwCOSbFFVP0/yRxNZ8hTveYcMeTEw5sMz5sMz5sMz5sMz5uMzb5OoJBO3Lt46cdInfibZBbisqq6YdFHsBexZVY8a2c/GwHJaezVVtSLJTsAZVXVC2vDu/wDcndZWe11ah7ULaJ3VdgJOnTj5k0/4Qj3xUzHmwzPmwzPmwzPmwzPmw5g3SVQX2NHxHoo2XgRp1YZb03rqf657yU+Bl03Kqq+gG28ibTTUW6vdObACWJbkyKo6jdYZbSKrfiGwf7e/L1fVNd3rf0N7iOFOwKkTF9pCP+GjjPnwjPnwjPnwjPnwjPnasdaSqEx6UvPkwKY92frVtI5qzwKup40R8dyquiDJL5LsXlUnj7zscuCGJI+vqh92+5kYt+JXwPvS7ig4Fji5e9/TgNNG3nciK78Q+BbdhTLpQluQjPnwjPnwjPnwjPnwjPn8MHgS1Z2AvYF/636faKvdG9iPli2/rap+nWR/4Kyq2j3JbrS22M26XR0LPC7JqXV7teBFSU4GXtft70m0dt1DgB8D61XVO6co01TVnjcCP1zzERieMR+eMR+eMR+eMR+eMZ9fxn53Xrr2zwnV2kWXAS9I8mZgiyT3A15My2aPBt6fZFvgm8DF3Qm6kPYk58d0u/oJ8Ajgrkk2TLJft/xvaANu3Q14P/Bu4He0Wyx36sqU0XJVs2iqGI358Iz58Iz58Iz58Iz5/Db2JGoisEnum2TPJLvTev6/A7g/7cS8Hvg1cC2tp/9S2vgRPwW2AzalPZTwZ7SOatCGj3807URvAuyTZJOqurGqflBVb6yqo6uNN3ELrVrxfV2ZFvUJN+bDM+bDM+bDM+bDM+bzXK3e05rDNE9Gpp20TYFHAt+jncy3AfcE/gJ438i2f0VrN3078Gxg42759rQTd7/u92cCP5h4T+A5wF2nef/1aFWPq3WM820y5sbcmBtzY744JmO+8Kc1fUFs2f3cAvgY8CLgQOAfJm23G/CfwA60fln7At+ftM0Tu58/Avbv5u8OPGDiBE9xMWZtB3TwE2jMjfk6MBlzY74uTMZ84U29OpaPdGTbBTgA2IhWjbgLra12m+4i+DYti35p1376G+DnVfWVtKHcl1TVCuCYJH+Z5EO0qsXdgS/Rsu+X0p7DQ1VdTrt7gJpUlVjdVbBYGfPhGfPhGfPhGfPhGfPFI33jluSBwKeAY2gn+lLg08DLaO2uZwMPqarrkyyl3RHwWOAg2jN0Xkh7ds49gI9X1TFJ/oj2EMJvV9UFq3Fci5IxH54xH54xH54xH54xXxxWZ4iD+wHnAkcAF1XV75O8B/hz4GvAF4FtkpxfVcvhtsG3HgBsCHyUVlV5JW0MCqrqqNUoz7rAmA/PmA/PmA/PmA/PmC8Cq1MTtTnwSdqIpOvRboF8P23Y+HcAR1XVa5NsSquufBst0z4K+PB0VYeZNICYbmfMh2fMh2fMh2fMh2fMF4feSdQddtKqJV9Ge2rzR4EPAveqqqcnCW3wr5uq6sopXrs+bWh522PnwJgPz5gPz5gPz5gPz5gvXL2b87oTe2/gYbTBu3YD/rSqrk1yAnC3JOtXG19i5chr1uuWATA6r1Uz5sMz5sMz5sMz5sMz5otD78E2u6z3PsArgZuBN1fVL5LsDLwKOLmqbulO+m2v8YT3Z8yHZ8yHZ8yHZ8yHZ8wXhzXSnHeHHba7Ax4CfLDa7ZQaM2M+PGM+PGM+PGM+PGO+sKx2EjVRvUhLku3MNgBjPjxjPjxjPjxjPjxjvrCt8ZooSZKkdcHYH0AsSZK0GJlESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPXwP3VijXkjkF5XAAAAAElFTkSuQmCC\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAlEAAADvCAYAAADSI4HyAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAgpklEQVR4nO3dd7xlVX338c+XIqi0KCMCFpqgolIcUSIi4qPYMepjw24c8yixPFFj8sREY4zGKJZY8iDYEgu2WLGAHQ1laAqIgoh0GEBCC/2XP9a+cLjcmTl3z5w99975vF+v/brnnt3W/u19z/ndtdZeO1WFJEmSZmedNV0ASZKk+cgkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJqyzJ1Um2W868lyQ5ajXua78kX11d21M/SY5NsvOaLoe0JplESdMk2SDJoUl+n+SqJCcleeLI/EckOSLJ5UmWJfliki1nsf1KssNkSj97SX6U5E9XZRtVtVFVndVz/wcn+XWSW5K8ZIxV3gG8a9o2kuSsJKfNsP2dk3yvO19XJDk+yZNmWcYVnvPumvnXJBd3y3wjydYj89+f5A9J/jPJvUbef36SD86mLCPr/qjb5gbT3v9kkhu6xPaq7ngf3XMfz+/+Dq5J8tUkdxuZ/R7g7/tsV1ooTKKkO1oPOBd4NLAp8DfAF5Js083/I+BgYBvgvsBVwCcGL+VAkqw34V2cDLwKOGGMsjwM2LSqjp42a2/gHsB23TKjvgEcAdyzW+Y1wJWzLOPKzvlrgT2BhwBbAX8A/qUr8x7AQ7v9HwW8uXt/U+CNtOtrVrpr8VFAAU+bYZF3V9VGwCbAR4GvJFl3lvvYGfj/wAuBLYBrgY+MLPJ14DFJ7jnb8ksLhUmUNE1VXVNVb62qs6vqlqr6JvA72hchVfXtqvpiVV1ZVdcCHwIeOc62k/yke3lyV1PwnNmULcn+Xc3YlUl+m+QJ3fubdrVnFyY5P8k/TH1pTjWnJXlPV3Pxu6matSTvoH0Zf6grz4e69yvJq5OcAZzRvfeKJGd2NS1fT7LVSLlurV1Lcvdu/pVJjgW2X9ExVdWHq+r7wHVjhOCJwI9neP/FwNeAw7vXU+XaHNgW+FhV3dBNP6uqWTUvjnHOtwW+W1UXV9V1wGHAziPzjqqq64HvA1PNnu8A/rmqZpvQAbwIOBr4JCPHO0O5C/gscDdaIjQbBwDfqKqfVNXVwFuAZyTZuNv2dcDxwH6zLr20QJhESSuRZAtgR+DU5Syy9wrm3U5V7d293KVrAjssyX26ZqblTc/vyrEH8Gla7cVm3X7P7rb3SeAmYAdgN+DxwGgT3cOBXwObA+8GDk2Sqvp/wE+BA7vyHDiyztO79R6YZF/gncCzgS2B3wOfX85hfpiWEG0JvKybVpcHd8dxqyR3AZ4FfKabnpvkTt3sy4AzgX9P8vTuXI6uO1bsZzD9nB8KPDLJVl15DgC+3c07FXhUkjsDjwVOTbIY2KmqPtszDi8aOd79ph/XyPGt2y37O+Di7r29VnLMe3Wr70yrJQSgqn4L3ED7W5jyK2CXnscgzXuTrqaX5rUk69O+qD5VVafPMP8hwN8C+/fdR1WdQ0uKVublwMer6oju9/O7MmwBPAnYrKr+G7gmyfuAJbTmGIDfV9XHuuU/RWuW2QK4aAX7e2dVXd6tc0C37xO63/8K+EOSbarq7KkVui/tZwIPrqprgFO6/e19h633sxmtKW3UM4Drge/RPtPWB54M/EdVVZLH0JrQ3gtsm9bJ/eVVdcYsYn+r5ZzzM2hNwOcDNwO/BA4EqKpTknyZVnN0evf+14CXJ3kNLQE8F3h1VV0xxv73ojUpfqGqLk3yW+D5wPtGFntDkgOBDYB0x3tzV56jxjzmjYD/mvbefwEbj/x+FS1ZltZK1kRJy5FkHeDfaP99HzjD/B1otQ2vraqfDlCkewO/neH9+9IShwunahNoydM9Rpa5NVnqmqOgfUmuyLkjr7ei1T5NbeNqWi3P1tPWWcRtfcqm/J7V5w/c/kscWnPWF6rqpq6J6cuMNHFV1XlVdWBVbU+L1TW0Gr1ZW8E5/zAtYbk7cFfgK9xWE0VVva+qdqmq59Bq835C+/xdQqud+hVdX6kxvBj4XlVd2v3+We7YpPeeqtoMuAuwGPjnjNwcMaaraX2qRm3C7ZPYjYErZrldacEwiZJmkCS0JpotgGdW1Y3T5t8XOBJ4e1X92yru6z5df6TlTQd0i57LzP2LzqXVxGxeVZt10yZVNe7t5zXG+xfQEpCpMt+VljCcP22dZbRmxXuPvHefMcsxjl8w0pyUdqfbvsALklyU5CJazc6Tuv5Qt1NV59ISngd1648b+5Wd812BT1bV5V3fp38B9phehq7WcAntrrYHAb/orq3jaJ3SV6hrEnw28OiR4309sEuSOzSrVXMK8DNa7RxJHrWSY35Ut/qpjDTVpQ1hsQHwm5FdPICRJj9pbWMSJc3so7QviKd2TWS3Srt1/QfAh6rqX3ts+2Ju61xMVZ3T9Uda3vSZbtFDgZcmeWySdZJsneT+VXUhrSnrvUk26eZtn/Fva79deZbjc92+d027pf4fgWNGm/K6Y7mZVgvz1iR3SfJAVtDxGSDJnZJsSGt2Wj/Jhl0t4EwOp901OeWFtC/1nWiJzK60JOs84HlJ/ijJ25Ls0MVlc1ofraO78o4V+zHO+XHAi9I6+K9Pu9vwgpHaoikHAW/tagN/BzwsyUbAPsBZ3b72SbK8xPbptObCB44c7wNo/dpeNNMKSe4P7EXXh6uqfrqSY56qYfsM8NQu6borLfH7SlVd1W13Q9rNFkfcca/SWqKqnJycRiZajUvROkdfPTId0M3/u27+6LyrR9b/a+DbK9j+nwEX0ppBnj3Lsv0JrTbmKlqH6f269zelJX7n0fqtnAg8t5v3EtrdYaPbKWCH7vWetETkD8AHp8+fVu7fApcD3wTutZztLermXwkcC7x9+v6nbfdH3fqj0z4rWP444OHd69OBP59hmTcBS2lNa5+idcC/mtas+Tlg61nGfWXn/O60pOOS7rweBewxbRv7At+a9t77u7gfPRVPWmL4s+WU4zvAe2d4/9ndsa1Hu8nghq6M1wDn0JLedXr8LTy/W/8aWj+uu43M+9+0pGqN/806Oa2pKVXL+4dHkuaeJI8HXlVVT1/TZZmEJIcAX6yq767psqxIkmNoHdZPWdNlkdYUkyhJkqQe7BMlSZLUg0mUJElSDyZRkiRJPZhESZIk9TCRx75svvnmtc0220xi05IkSavV8ccff2lVLZrtehNJorbZZhuWLl06iU1LkiStVkl6PZ7K5jxJkqQexkqikmyW5EtJTk/yqyR7TrpgkiRJc9m4zXkfAL5TVc9Kcifak8ElSZLWWitNopJsCuxNe/4WVXUD7blMkiRJa61xmvO2BZYBn0hyYpJDuid6306SJUmWJlm6bNmy1V5QSZKkuWScJGo9YHfgo1W1G+1p3m+evlBVHVxVi6tq8aJFs75LUJIkaV4ZJ4k6Dzivqo7pfv8SLamSJElaa600iaqqi4Bzk+zUvfVY4LSJlkqSJGmOG/fuvD8HPtPdmXcW8NLJFUmSJGnuGyuJqqqTgMWTLYokSdL84YjlkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2sN85CSc4GrgJuBm6qqsWTLJQkSdJcN1YS1XlMVV06sZJIkiTNIzbnSZIk9TBuElXA95Icn2TJTAskWZJkaZKly5YtW30llCRJmoPGTaL2qqrdgScCr06y9/QFqurgqlpcVYsXLVq0WgspSZI014yVRFXV+d3PS4D/APaYZKEkSZLmupUmUUnummTjqdfA44FTJl0wSZKkuWycu/O2AP4jydTyn62q70y0VJIkSXPcSpOoqjoL2GWAskiSJM0bDnEgSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1MPYSVSSdZOcmOSbkyyQJEnSfDCbmqjXAr+aVEEkSZLmk7GSqCT3Ap4MHDLZ4kiSJM0P49ZEvR94E3DL5IoiSZI0f6w0iUryFOCSqjp+JcstSbI0ydJly5attgJKkiTNRePURD0SeFqSs4HPA/sm+ffpC1XVwVW1uKoWL1q0aDUXU5IkaW5ZaRJVVX9VVfeqqm2A5wI/qKoXTLxkkiRJc5jjREmSJPWw3mwWrqofAT+aSEkkSZLmEWuiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknpYaRKVZMMkxyY5OcmpSd42RMEkSZLmsvXGWOZ6YN+qujrJ+sBRSb5dVUdPuGySJElz1kqTqKoq4Oru1/W7qSZZKEmSpLlurD5RSdZNchJwCXBEVR0z0VJJkiTNcWMlUVV1c1XtCtwL2CPJg6Yvk2RJkqVJli5btmw1F1OSJGlumdXdeVV1BfBD4AkzzDu4qhZX1eJFixatpuJJkiTNTePcnbcoyWbd6zsDjwNOn3C5JEmS5rRx7s7bEvhUknVpSdcXquqbky2WJEnS3DbO3Xm/AHYboCySJEnzhiOWS5Ik9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPWw0iQqyb2T/DDJaUlOTfLaIQomSZI0l603xjI3AX9RVSck2Rg4PskRVXXahMsmSZI0Z620JqqqLqyqE7rXVwG/AraedMEkSZLmsln1iUqyDbAbcMxESiNJkjRPjJ1EJdkI+DLwuqq6cob5S5IsTbJ02bJlq7OMkiRJc85YSVSS9WkJ1Geq6iszLVNVB1fV4qpavGjRotVZRkmSpDlnnLvzAhwK/KqqDpp8kSRJkua+cWqiHgm8ENg3yUnd9KQJl0uSJGlOW+kQB1V1FJAByiJJkjRvOGK5JElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8mUZIkST2YREmSJPVgEiVJktSDSZQkSVIPJlGSJEk9mERJkiT1YBIlSZLUg0mUJElSDyZRkiRJPZhESZIk9WASJUmS1INJlCRJUg8rTaKSfDzJJUlOGaJAkiRJ88E4NVGfBJ4w4XJIkiTNKytNoqrqJ8DlA5RFkiRp3rBPlCRJUg+rLYlKsiTJ0iRLly1btro2K0mSNCettiSqqg6uqsVVtXjRokWra7OSJElzks15kiRJPYwzxMHngP8EdkpyXpKXT75YkiRJc9t6K1ugqp43REEkSZLmE5vzJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknowiZIkSerBJEqSJKkHkyhJkqQeTKIkSZJ6MImSJEnqwSRKkiSpB5MoSZKkHkyiJEmSejCJkiRJ6mG9NV0ASXe0zZu/taaL0MvZ73rymi6CpBXws2X1siZKkiSpB5MoSZKkHsZqzkvyBOADwLrAIVX1romWSnOK1b+SJN3RSpOoJOsCHwYeB5wHHJfk61V12qQLNxO/0CVNgp8twzPmmu/Gac7bAzizqs6qqhuAzwP7T7ZYkiRJc9s4SdTWwLkjv5/XvSdJkrTWSlWteIHkWcATqupPu99fCDy8qg6cttwSYEn3607Ar1d/cSduc+DSNV2ItYwxH54xH54xH54xH958jvl9q2rRbFcap2P5+cC9R36/V/fe7VTVwcDBsy3AXJJkaVUtXtPlWJsY8+EZ8+EZ8+EZ8+GtjTEfpznvOOB+SbZNcifgucDXJ1ssSZKkuW2lNVFVdVOSA4Hv0oY4+HhVnTrxkkmSJM1hY40TVVWHA4dPuCxzwbxujpynjPnwjPnwjPnwjPnw1rqYr7RjuSRJku7Ix75IkiT1YBIlSZLUg0nUApJkgyTrd6+zpsuzNkiyTvfTeA8kyZ26x1EZ94F0ny0bdK+N+QRNxTfJnZMs6l77XT2AJBsl2aZ7PdZ17olZAJLsleRU4PvA6wHKzm4Tk2TjJG9M8gvgg93b/i1NUJItkvxdkp8B3wFeA17nk5TkHknemeQHwA+A1yfZwJhPVlVVkl2Bc4C/XMPFWfCS3C3J25N8CzgReDGM/9ky1t15mlu6/0pSVTcn2ZA2UvxfAT8BvpXkLODLftitPl3M16mqm2hDfWwJfBo4AKCqbl6DxVuQRq9z2oC/WwKvA34P/CDJyVX1gzVYxAVn2nW+AbA+8DfAL4GfA0uBI9dcCReeqVqmqrpl5O0H0P4p3naGeVpF067zjYE3A4+vqh/Odlv+9zyPTFUvVtUtU1/aVXUd7SHRJ1bVFcB7gX1oj97RKpoW85u611cA7wQOAq5Pstvoslo1M13nwJnAG6rquKq6BDiW7gtGq2451/m5VfWGqvp5VV0FnAVctybLuZBMi/n0JOlZwGHAdUkeOrq8+lvOdf574NRuIsmWs9mmSdQclGbd6e3gXTXvPZPsk+QDSZ6aZFPgKOBB3WKnAtcDfrHPwpgxf3+S/bv3l3UffL8E9usW9+9pFmYR86dV1RVVdXX31ARotSTW/s3SbGI+ss5Lk9xIey7aVkOXeb6b7WdL15R3JnAScDGtVgr8fBnbLGL+zG7WKcDRSY4HPpRkybj90Dwpc0CSzZI8uUuIqObmqrplNAlKcgCtSv1JwP8CXgpcC1zAbX9oy4CLgK2ntjXckcwfPWP+WODl3ftTfzs/BvYetvTz0yrE/BXd++tX1Q1J9gDuC3zJfxJWbFVj3vk2cPfuvWdMfdlrZqsQ8z/rZu0IXFBVvwOuAF6Z5JV2GVi+VYj5n3az3g+8C3gk8E/A04FnjLNv+0TNDQ+k9a25HjgyyU7AC4CHAz9N8iFaNfofA6+tqm8kORI4BAhwOvAEgKq6vFv/28MfxryyvJjvARy1gph/HFp1cPfHeQzwxu49P+RWbFVjfmO3nTcCH6mqq4c+gHlolWIOUFUXdS9PS3IesG2Sdeyns1x9P88P7WpadwRemGQJsBHtM/6CNXAc80nf6/wTAFW1lNbfD+DYJKcBW4xznVsTNZCuenF58T6bVn27Q/f7PrQapTcC1wB/S7s4FgMnd/+Rf492/h4AfBXYNcnju/Xv062/VusZ8zdxW8xv4I4xn7pzZuq/nTOAa5MclOTlSbaY1PHMBxOM+VTz9J60D8OlSfZP8vwkG0/qeOaDSV/nI/tZF7gfcPrankBN6PM8wPa0O8TeBTwVeBhwHK1Zb63unjGh6/yWGa7z9Wh9is8Y5zo3iRpI94W7vBOyDLiQ9h8IwKeA44FX0aob9wLu1C338JH/yK8C9q+qa4G3AS9Jchnwi25aq62GmK8PXAI8YlrMnwSQ5BFJfkz7YtkNuJFW/b7WmmDMn9K9/nPaf5yH0O5KvRb479V8GPPKBGO+H0CSVyY5jtZH50xa7etabYKf539SVd+qqk9U1Vm0ZOtwuv5/a3P3jAle508ESPLitD5RJwK/pt28slI2561mM1X/ddnzdsBLgBur6m2j86vqxiTnALsnuQ8tY34lrb/NO2h3ge0JfAx4dtfuG+BSWjUmtNqo71e7c2ytMkbMb6iqvx+dPy3m96V9WL2SNkzEaMwPocV8k27Vy4BdutfnAK+rqhMncmBz2MAxvxy4f/f648AHq+roiRzYHLYGYv6Q7vWJwIFVtdYlT2vg8/zB3T42qKrrq+q/gEMneIhzzhq4zh/cvf4l8OrZfrZYE7UKkqzTVXHfaurkJ3lQ2hhO0E7gB2j/TXxq2jamqmfPodVkbA08Gti0qg4FbqJV8T6zqr5GuwieShvb4qN01ZddJ7orum2uu1CrfXvG/NPTtjE95ltxW8wPYfkx34QW8+27/V4wlUB1Mb9duRaKORDzj9AN2VFVR059yM1UroVijsX82KkEys8WYLKf5/fr9nv99LKtpsOcU+bIdb5jt98TRj5bxr7OrYmahSQZrU6dqWoxyZtpY3xcCfw4yadpo/0+DPhiVZ09uvzI9i7spl1ptUovSvJl2on+Ku1CgPbfzEnAQ2nVlO+eXoZaQB2cjfnw5nrMp8q3gqr9eWcexdzrfODPluWVbT6a6zHvc52bRK3EaNXi6MlPe0bdfsCzae2q76a1uRbtLoxNgS8BmwHvow1Ut6J4X9ZNewIHAwfS7rj7cVWdNrLcht2+NgW+BXxjVY9xrjHmw5tPMR8t33xmzIc3n2K+UMynmPe6zqvKaWSijYK8BNh6hnlbA0/pXj8eOAJ4JrBz995+tI7FR9LuqDi0uxjuQqv2fdpK9r0dsO1y5q27pmNjzBfOZMyNuTE35sZ81Sdrojoj2fLmtE6sZwLnJ3kMcOeqOpzWR+D1SX5NqyJcj9YZ7dpuM8fTsuhXVBsobXT7FwMPTvLDqrqqa28Ntz0bjGp3Y4yuMzVEfdUCqkafYsyHZ8yHZ8yHZ8yHt7bGfEF2VhvHVHBHgjw1eOJvaGNyTD2Xa29ue6zHz2nVjlvRBrO8DHg18L4kU1WCxwL7pw0t/7i08YPuSXs0y0XArdWaNfJssCT3SRuJefqJXxDV6GDM1wRjPjxjPjxjPjxj3qwVNVGZ9pTspHUeS3cbaZINaNWPm1bVPyS5CNiuOxEnAU9Mco+quiTJhbRbIn9eVc/qtrcxrQ12T+D/0G7D/BZt7IqvAVdX1denlWlD4MnAvsDutNtb/6Ur57z/QzPmwzPmwzPmwzPmwzPmy7cgk6jpJ7xG7gBIcvequizJPWg9//+4qv6Q5AZgs+5knkUbI2Vr4Le02yofQmunPZf2zJ3DkmxGe8bOrrQ222O6i+TtwN9NP5G5/fgXj6ONLP6vtBGAb2Qem0cxvzfG3Jj3ZMyHN49i7uf5WnidL8jmvGpVfFMZ812T7JvkI0l+A3wiyZ5VdQltqPh9utV+S3sy/P261zfQHqnyG1r145O75TahtfduCWzRLf8V4IXdNqmqG7ss/XZjYIxeiFX1jap6X1X9cr7/wcG8ivn7jbkx78uYD28exdzP87XwOl9wSVSSTdOep/XZJA+jnax/pPXM3xH4T+DPkuwA/JDb2mrPprW13o/Wnnsp8ICquoE2SvKuSU6hdWR7HfDrqjqqqpZU1Zer6srpZamR9tqFzJgPz5gPz5gPz5gPz5jPzrxozktubX+93UBdMyy3DvBWWhXiT2gndR3gdNrw7gCfo7W37gn8CHghQFWdmeThwFVVdViSc4FdkmxSVb9J8pypLHmGfd4uQ14IjPnwjPnwjPnwjPnwjPnkzNkkKsnUrYu3TJ30qZ9JdgQurarLp10UewN7VdXDRrazAbCU1l5NVZ2dZDvglKo6Nm14938C7k5rq702rcPaubTOatsBJ02d/OknfL6e+JkY8+EZ8+EZ8+EZ8+EZ82HMmSSqC+zoeA9FGy+CtGrDzWk99T/frfJL4GXTsurL6cabSBsN9ZZqdw6cDSxJ8pmqOpnWGW0qq34esH+3va9V1VXd+hfTHmK4HXDS1IU230/4KGM+PGM+PGM+PGM+PGO+ZqyxJCrTntQ8PbBpT7Z+Na2j2lOB62hjRDyjqs5NckaS3avqhJHVLgOuT/LIqvpZt52pcSt+D7wn7Y6CHwIndPs9GTh5ZL9TWfl5wPfoLpRpF9q8ZMyHZ8yHZ8yHZ8yHZ8znhsGTqO4E7AN8sft9qq12H+CJtGz5LVV1QZL9gdOqavcku9HaYjfqNvVD4I+TnFS3VQuen+QE4LXd9h5Da9d9P3A0sE5VvX2GMs1U7XkD8LPVH4HhGfPhGfPhGfPhGfPhGfO5ZeJ356Vr/5xSrV10CfDcJG8CNkmyPfACWjZ7OHBQkq2B7wAXdifoPNqTnB/ebeoYYBfgrknWT/LE7v2/pQ24dTfgIOCdwDW0Wyy368qU0XJVs2CqGI358Iz58Iz58Iz58Iz53DbxJGoqsEnum2SvJLvTev6/DdiBdmJeB1wAXE3r6b+YNn7EL4F7AXemPZTw17SOatCGj9+DdqI3BPZNsmFV3VBVP62qv6iqw6uNN3EzrVrxPV2ZFvQJN+bDM+bDM+bDM+bDM+ZzXK3a05rDcp6MTDtpdwYeCvyYdjLfAtwTeAPwnpFl/5rWbvpW4GnABt3796GduO27358C/HRqn8CfAHddzv7XoVU9rtIxzrXJmBtzY27MjfnCmIz5/J9W9wWxafdzE+CjwPOBA4B/mrbcbsB3gW1o/bIeB/xk2jKP7n7+HNi/e313YKepEzzDxZg1HdDBT6AxN+ZrwWTMjfnaMBnz+Tf16lg+0pFtR+BZwJ1o1Yg70tpqt+gugiNpWfRLu/bTi4HfVNXX04ZyX1RVZwNHJPnLJB+kVS3uDnyVln2/lPYcHqrqMtrdA9S0qsTqroKFypgPz5gPz5gPz5gPz5gvHOkbtyT3Bz4JHEE70ZcAnwZeRmt3/RWwc1Vdl2Qx7Y6ARwAvpj1D53m0Z+fcA/hYVR2R5Dm0hxAeWVXnrsJxLUjGfHjGfHjGfHjGfHjGfGFYlSEOtgfOBD4FnF9V/53kXcD/Bb4JfBnYIsk5VbUUbh18aydgfeAjtKrKK2hjUFBVh61CedYGxnx4xnx4xnx4xnx4xnwBWJWaqI2BT9BGJF2HdgvkQbRh498GHFZVr0lyZ1p15VtomfZhwIeWV3WYaQOI6TbGfHjGfHjGfHjGfHjGfGHonUTdbiOtWvJltKc2fwT4ALBlVT0pSWiDf91YVVfMsO66tKHlbY+dBWM+PGM+PGM+PGM+PGM+f/VuzutO7FbAg2mDd+0GvKqqrk5yLHC3JOtWG19i2cg663TvATD6WitmzIdnzIdnzIdnzIdnzBeG3oNtdlnvvYFXADcBb6qqM5LcD3glcEJV3dyd9FvX8YT3Z8yHZ8yHZ8yHZ8yHZ8wXhtXSnHe7Dba7A3YGPlDtdkpNmDEfnjEfnjEfnjEfnjGfX1Y5iZqqXqQlyXZmG4AxH54xH54xH54xH54xn99We02UJEnS2mDiDyCWJElaiEyiJEmSejCJkiRJ6sEkSpIkqQeTKEmSpB5MoiRJknr4H+QNmJ3YD5xkAAAAAElFTkSuQmCC\n", + "text/plain": [ + "<Figure size 720x216 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + } + ], + "source": [ + "for i,row in df_heatmap.iterrows():\n", + " ax = row.plot(kind='bar', figsize=(10,3),title=f'{i}', rot=15)\n", + " ax.set_ylim(np.min(df_heatmap.values),np.max(df_heatmap.values))\n", + " plt.show()" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "Lastly, an alternative way to visualize the distances between the three groups of points from the heatmap would be a series of scatter plots, one for each pair of features. \n", + "\n", + "This should give a good intuition for the distance measures (in 6 dimensional feature space, lastest preprocessed observation plus the 5 lagged values) that underpin the raw anomaly score.\n", + "\n", + "Generally we would expect to see the blue 'normal' points group closer together and 'near' the green cluster centroids, meanwhile the anomalous orange points should tend to be further away from the other two groups." + ] + }, + { + "cell_type": "code", + "execution_count": 18, + "metadata": {}, + "outputs": [ + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAX8AAAEHCAYAAABGNUbLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAewElEQVR4nO3deZwdZZ3v8c83nU46CVkgacISQtguiwxLaBAUHQGJCIp6BwFFRxDIOOMCiPtlRvTiS1REMY5yM6AgICqbE1nCHvYlnbAGZA+TQIAGJYR0kk53/+4fVU06nV5OdZ86S873/Xr1i1N1qk59z6HzO9VPPfU8igjMzKy2DCt3ADMzKz0XfzOzGuTib2ZWg1z8zcxqkIu/mVkNGl7uAN1NmjQppk2bVu4YZmZVZcGCBa9HRGOWfSqq+E+bNo3m5uZyxzAzqyqSXsy6j5t9zMxqkIu/mVkNcvE3M6tBLv5mZjXIxd/MrAZVVG8fs4oUAa/cAquWwcR9Yfyu5U5kNmQu/mb9iYC7joJXbkqXO2D/i2Dbo8say2yo3Oxj1p9XbkkKf/vbyU/HKrj/hORLwayKufib9WfVsg3Xda5JvgTMqpiLv1l/Ju6bNPW8YxiM2R6Gjy5bJLNicPE368/4XWH/30LdKFAdbLIDHDy33KnMhswXfM0Gsu0xMPWTSVPP8DHlTmNWFD7zNyuEhrnw20Yl9+IvaYKkKyX9VdKTkg7I+5hmZta/UjT7nAfMjYijJI0AfKXMzKzMci3+ksYD7weOB4iINqAtz2OamdnA8m722Q5oAX4r6SFJF0har+FU0kxJzZKaW1paco5jZmaQf/EfDkwHfh0RewMrgW913yAiZkdEU0Q0NTZmmoXMzMwGKe/ivxRYGhEPpMtXknwZmJlZGeVa/CPiFWCJpJ3TVYcAT+R5TDMzG1gpevt8Gbgs7enzPHBCCY5pZmb9yL34R8TDQFPexzEzs8L5Dl8zsxrk4m9mVoNc/M3MapCLv5lZDXLxNzOrQS7+ZmY1yMXfzKwGufibmdUgF38zsxrk4m9mVoNc/M3MapCLv5lZDXLxNzOrQS7+ZmY1yMXfzKwGufibmdUgF38zsxrk4m9mVoNc/M3MapCLv5lZDXLxNzOrQS7+ZmY1yMXfzKwGDc/7AJIWAyuADqA9IpryPqaZmfUv9+KfOigiXi/RsczMbABu9jEzq0GlKP4B3CRpgaSZPZ+UNFNSs6TmlpaWEsQxM7NSFP8DI2I68GHgi5Le3/3JiJgdEU0R0dTY2FiCOGZmlnvxj4iX0v++BlwD7Jf3Mc3MrH+5Fn9JYySN7XoMzAAez/OYZmY2sLx7+0wGrpHUdazfR8TcnI9pZmYDyLX4R8TzwJ55HsPMzLJzV08zsxrk4m9mVoMGVfwl/a7YQczMrHQGbPOXNKfnKuAgSRMAIuLIHHKZmVmOCrngOwV4AriA5G5dAU3AT3PMZWZmOSqk2acJWAD8H2B5RMwDVkXEHRFxR57hzMwsHwOe+UdEJ/AzSVek/321kP3MzKxyFVzEI2Ip8ElJRwBv5RfJzMzyVnDxl7RZ+vA+4L50eUVErM0lmZmZ5SZLV8+FQAvwNPBM+nixpIWS9skjnJmZ5SNL8b8ZODwiJkXERJIhmq8F/g34VR7hzMwsH1mK//4RcWPXQkTcBBwQEfcDI4uezMzMcpOl184ySd8E/pAuHwO8KqkO6Cx6MjMzy02WM/9Pk9zw9ef0Z2q6rg44utjBzMwsP1m6er4OfLmPp58tThwzMyuFLF09G4FvAO8CGrrWR8TBOeQyM7McZWn2uQz4K7Ad8D1gMTA/h0xmZpazLMV/YkRcCKxNx/X5POCzfjOzKpSlt0/XnbzL0iEeXgY262d7MzOrUFmK/1mSxgOnA7OAccBpuaQyM7NcZentc236cDlwUD5xzMysFAqZyWsWySQuvYqIrxQ1kZmZ5a6QM//moR4kvQu4GXgpIj4y1NczM7OhKWQyl4sLeSFJsyKir5vATgGeJLlOYGZmZZalq+dA3tvbSklTgCNI5gA2M7MKUMzi35efk9wZ3Ovgb5JmSmqW1NzS0lKCOGZmlmvxl/QR4LWIWNDXNhExOyKaIqKpsbExzzhmZpYqZvFXL+veCxwpaTHJUNAHS7q0iMc0M7NBKKj4S6qTdM4Am53Xc0VEfDsipkTENOBY4LaI+Ez2mGZmVkwFFf+I6AAOHGCbi4oRyMzM8pdleIeHJM0BrgBWdq2MiKsL2Tki5gHzsoQzM7N8ZCn+DcAbrD+SZwAFFX8zM6scWcb2OSHPIGZmVjoF9/aR9L8k3Srp8XR5D0ln5BfNzMzykqWr538B3yYd1z8iHiXpwWNmZlUmS/EfHREP9ljXXswwZmZWGlmK/+uSdiAd3lnSUcCyXFKZmVmusvT2+SIwG9hF0kvAC4Bv2DIzq0JZevs8D3xQ0hhgWESsyC+WmZnlKUtvn1MkjQNagZ9JWihpRn7RzMwsL1na/D8fEW8BM4CJwGeBs3NJZWZmucpS/LtG7Twc+F1ELKL3kTzNzKzCZSn+CyTdRFL8b5Q0lj4maDEzs8qWpbfPicBewPMR0SppIuAhH8zMqlCW4t81pPMeklt7zMyqWZbi//VujxuA/YAFrD/Kp5mZVYEs/fw/2n1Z0jYkk7ObmVmVGcocvkuBXYsVxMzMSqfgM39Js0jH9SH50tgLWJhDJjMzy1mWNv/mbo/bgcsj4p4i5zEzsxLI0uZ/cZ5BzMysdAYs/pK+y7rmnv7Mi4g7hx7JzMzyVsiZ/+ICX+vNwccwM7NSGrD4u7nHzGzjk6W3z3/0tj4ivt/PPg3AncDI9FhXRsR3s4Y0M7PiytLbZ2W3xw3AR4AnB9hnDXBwRLwtqR64W9INEXF/xpxmZlZEWXr7/LT7sqRzgBsH2CeAt9PF+vSnkIvHZmaWo6Hc4TsamDLQRpLqJD0MvAbcHBEP9Hh+pqRmSc0tLS1DiGNmZoXKMo3jY5IeTX8WAU9RwNg+EdEREXuRfFHsJ2n3Hs/PjoimiGhqbGzMlt7MzAYlS5v/R7o9bgdejYj2QneOiDcl3Q4cBjye4bhmZlZkBZ/5R8SLJHP3fgz438A/DLSPpEZJE9LHo4BDgb8OKqmZmRVNlmaf/wAuJvkCmARcJOmMAXbbErhd0qPAfJI2/2sHG9bMzIojS7PPccCeEbEaQNLZwMPAWX3tEBGPAnsPJaCZmRVflt4+L5P07+8yEnipuHHMzKwUspz5LwcWSbqZpK/+ocCDkn4BEBFfySGfmZnlIEvxvyb96TKvuFHMzKxUshT/K4HVEdEByc1bwMiIaM0lmZmZ5SZLm/+twKhuy6OAW4obx8zMSiFL8W+IiK5xekgfjy5+JDMzy1uW4r9S0vSuBUn7AKuKH8nMzPKWpc3/VOAKSS8DArYAjskjlJmZ5SvLkM7zJe0C7Jyueioi1uYTy8zM8pTlzJ+02L8zKJukLSLilaKnMjOzXA1lPH+AC4uSwszMSmpIxT8ijihWEDMzK51MzT6SNgW26b5fRCwsdigzM8tXwcVf0v8FjgeeY908vAEcXPxYZmaWpyxn/kcDO0REW15hzMysNLK0+T8OTMgph5mZlVCWM/8fAg9JehxY07UyIo4seiozM8tVluJ/MfAj4DGgM584ZmZWClmKf2tE/CK3JGZmVjJZiv9dkn4IzGH9Zh939TQzqzJZin/XROz7d1vnrp5mZlUoy8BuB+UZxMzMSqfgrp6SJku6UNIN6fJukk7ML5qZmeUlSz//i4Abga3S5adJxvjvk6RtJN0u6QlJiySdMqiUZmZWVFmK/6SI+BNpN8+IaAc6BtinHTg9InYjuVbwRUm7DSqpmZkVTdZpHCeSjusjaX9geX87RMSyrt5AEbECeBLYepBZzcysSLL09vkqSTfPHSTdAzQCnyx0Z0nTSHoMPdBj/UxgJsDUqVMzxDEzs8HKUvwXAf9IMo2jgKco8C8HSZsAVwGnRsRb3Z+LiNnAbICmpqboZXczMyuyLM0+90VEe0QsiojH0ykd7xtoJ0n1JIX/soi4erBBzcyseAY885e0BUk7/ShJe5Oc9QOMA0YPsK9Ipnp8MiLOHWJWMzMrkkKafT5EMonLFOCnrCv+K4DvDLDve4HPAo9Jejhd952IuD5zUjMzK5oBi39EXAxcLOmfIuKqLC8eEXez7svCzMwqRJY2/ymSxilxgaSFkmbklszMzHKTpfh/Pu2pMwOYSNKcc3YuqczMLFdZin9X883hwO8iYhFu0jEzq0pZiv8CSTeRFP8bJY3FM3qZmVWlLDd5nQjsBTwfEa3pUA8n5JLKzMxyleXM/wpgS+AtgIh4IyIezSWVmZnlKkvx/zXwaeAZSWdL2jmnTGZmlrOCi39E3BIRxwHTgcXALZLulXRCOoSDmZlViSxn/qTt/McDJwEPAeeRfBncXPRkZmaWmyzTOF4D3EUyns9HI+LIiPhjRHwZ2CSvgFZDXvg9XL0F/Gkc3PtZaF9V7kRmG60svX0uB+ZGxFuSzpA0HTgrIhZGRFNO+axWvHYnPHgydLQmy0uugmH1sP9vypvLbCOVpdnnjLTwHwh8kGS0zl/nE8tqzkvXrSv8AB2r4KW/lC+P2UYuS/Hvmq/3CGB2RFwHjCh+JKtJIyfCsB6/TvXjy5PFrAZkKf4vSfp/wDHA9ZJGZtzfrG87ngwNk6GuAVQHdaNgn1+UO5XZRitLm//RwGHAORHxpqQtga/nE8tqzohN4fBH4YVLoH0FbPlh2Gzvcqcyy9/bL8BzF0LnWpj2adh0z5IcVhGVM21uU1NTNDc3lzuGmVlpvPU0zG2C9lagA+pGw0E3wuYHZnoZSQuydrxxs42ZWbk8cTa0r+SdS6odrfDIt0tyaBd/M7NyWbucDQZHXruiJId28TczK5dpn0maerrUjU7WlYCLv5lZuWzziaRX2+htYdTWsNu3YNfTS3LoLL19zMys2HY8MfkpMZ/5m5nVoFyLv6TfSHpN0uN5HsfMzLLJ+8z/IpIbw8zMrILkWvwj4k7gb3kew8zMsit7m7+kmZKaJTW3tLSUO46ZWU0oe/GPiNkR0RQRTY2NjeWOY2ZWE8pe/M3MrPTcz9+ye/MxWPEsjNsVxu9S7jRmNgh5d/W8HLgP2FnSUkmlv5PBiuvxs+DG/eH+42HudHjm/HInMrNByPXMPyI+lefrW4m9/Tws+gF0rF43r9uC02Dq0TBys7JGM7Ns3OZvhVu5BIaNXH/dsHpYtaw8ecxs0Fz8rXDjd01mG1qPYJNp5UhjZkPg4m+Fa9gc3ncl1I1J5tqtnwAfuA6Gj0meX/s23H0sXDkR5uwEr9xW1rhm1jf39rFstvowfPLvsLol+TIY1u1X6N5PwbKboXMNtP0N7vgoHLbAPYLMKpDP/C27YfUweqv1Cz/Ay3OTwt8lOuGVW0qbzcwK4uJvxVM3av3lYXVQP7Y8WcysXy7+Vjx7/2TdlHR1DTBqK5h6VHkzmVmv3OZvxbPTv8DYHeGVm6FhMuxw8rqLwWZWUVz8rbi2OCT5MbOK5mYfgIhyJzCrPP53sVGr7eL/wiVwxQT4Qz3cegi0/b3ciczKb8mfk3s1/lAPN70HVr1a7kSWg9ot/q/fDw/+C6xdDtEBLXfD3R6KyGrcm4vg3uOS+zSiA96YD3ceWe5UloPaLf6vzlt/qILONmi5c4PNVq6E556DNWs2eMps49NyN9CtuSfa4Y1m6OzocxerTrVb/BsaYdiI9dfVj19v8dJLYdIk2HNPmDwZ7r23hPnMyqGhEdSjLAwfndyzYRuV2i3+046DsTvB8E1gWENyg9K7/+udp194AWbOhNWrk7P/5cvhiCOgra2Mmc3ytvWRsOle6/+72NdzNmyMqr6rZwT8/vdwww2wzTbw9a/DZoUMLV/XAB96AP7nyqR9c/JBMGH3d55etAhGjIBVq9bt0tYGy5bBttsW/31YBWtbDk/+GFa+CJM/CNt/DqRyp8rHsOFwyDxYchWsfhUaD4TNppc7leWg6ov/mWfCOedAayvU18Pll8Njj8HYQkYVqBsJ2x3X61PbbbfhWX4EbL75kCNbNWlvhblN0Po/yXWhJdfA8kUw/SflTpafYcNh22PKncJyVtXNPhFw9tnQ2hpsOuZvROda3ngD5szJ9jrLVy/n8scu55JHLuG1la8B8K53wTe+AaNGwbhxMHo0XHxxslyoFSuSL6U+dayGtW9lC2ultWwurH4lKfwAHa3w1M+hs72sscyGqqrP/Ds7YZtNX+DGb36QKZstBeD0y2exZs3MgvZ/5BH4yrdf47499kaj3qK+PhhRN4IHTnqAnSbuxPTpyRdMayuMHw877lhYrlWr4Kij4KabkuXjjoMLL4S6rmtmEbDwq/D0LwHBpP3gH6+DEeP7ekkrl47VvayMpBtkdf/zsRpX1Wf+dXVw+5lHMG3SYkbWtzGyvo0fH3MaRxywoM99rn/mer5/x/c555aLee/72rlTZ7K2voU23mbl2pUsX7OcU+eeypIl8KlPJRd829vhjTdgxozk8UC++U247bZk2/Z2uOIK+PnPu22w+FJ4dnbSjS7WJn2pH/zCkD8Py8HkQ0B1QNrGP6wBtjg0aTI0q2LVferS2cGUcX9F3folNzTA6OHNwD4bbP7vt/07595/LqvWrqKe0az9xGWwth6Gr+vv3xmdLH1rKY8+CsN7fDqtrfDyyzB1av+x7rgj+dLovt/tt8Ppp6crXp2XNB+8c9A2eP3uwt6zldaoyTDj3uTLuXUpTD4Yms4rdyqzIavu4j+sjo5hExjeuW5Yhrb2YTSMnrLBpm+3vc2P7vkRa9Mbu9pYCVvfBwtOgrZ5MCIpxiM0ihk7zmDK5hue5Xd0JP3+B7LddklvoY70vpgRI2D77bttsMkOyRlkZ9c3hGD0NgW+aSu58bvBoRveAGhWzaq62Qfg+NmXsXLNaJa3jmXF6jHMfXgGtz91+AbbrVizgrqeN6rEMFh8ECw8ETqGQ2cdIxcfyQ8O/gF77gknn5xc6B07NrnQ+6tfJcsDOe88mDgx2W/sWJgyJemV9I5dTknvMRib/NSPh3dfMKTPwcwsC0XOI/dJOgw4D6gDLoiIs/vatqmpKZqbmwt+7Y6OpHvntpNeYN/t5/Pq8snMf/H9nHuu+ELahH799fCtb8HSlzpZdeJutI15lk6SU/L6znGs/ekzsHJzUAco2HrL4Sxduu4YDz6Y3PC1xx6w666Fv+8334R585LrEocc0suXRkcbvHordKyCxvcld1aamQ2CpAUR0ZRln1ybfSTVAf8JHAosBeZLmhMRTxTj9evqkrPqxUu2Y3HLdgCMGZN00wS49lr4xCe6mm+Gwfm3oqOPZfS0h5kyYSs+PfIyzlyZdtyPOgjYeef1j7HffslPVhMmwMc/3l/4Eclk6GZmZZB3s89+wLMR8XxEtAF/AD5WzAPMmZPc0TtuXHKx97TT4H3vS547++we7fYrtiYuvIsTX1vBU196iref3vCL8vnni5nOzKwy5X3Bd2tgSbflpcC7u28gaSYwE2DqQN1oerHXXrBkCTzzDDQ2wlZbDbxPfy1dnr/CzGpB2S/4RsTsiGiKiKbGxsG1e48enYy82bPwf+1ryTWB7hoa4KSTksef+1zSTNT9db761UFFMDOrKnkX/5eA7n0Yp6TrSuLjH09usNpll6QNft99k4uwe+6ZPL/77sny4YfDgQfCrFnw5S+XKp2ZWfnk2ttH0nDgaeAQkqI/H/h0RCzqbfusvX3MzKwCe/tERLukLwE3knT1/E1fhd/MzEon9zt8I+J64Pq8j2NmZoUr+wVfMzMrPRd/M7Ma5OJvZlaDXPzNzGpQ7gO7ZSGpBXhxCC8xCXi9SHFKpRozQ3XmdubSqcbc1ZgZktxjIiLTXbIVVfyHSlJz1r6u5VaNmaE6cztz6VRj7mrMDIPP7WYfM7Ma5OJvZlaDNrbiP7vcAQahGjNDdeZ25tKpxtzVmBkGmXujavM3M7PCbGxn/mZmVgAXfzOzGlR1xV/SYZKekvSspG/18vxISX9Mn39A0rQyxNxAAbmPl9Qi6eH056Ry5OyR6TeSXpP0eB/PS9Iv0vf0qKTppc7YS6aBMn9A0vJun/N/lDpjL5m2kXS7pCckLZJ0Si/bVOJnXUjuivq8JTVIelDSI2nm7/WyTUXVkAIzZ68fEVE1PyTDQj8HbA+MAB4Bduuxzb8B56ePjwX+WCW5jwd+We6sPTK9H5gOPN7H84cDNwAC9gceqILMHwCuLXfOHpm2BKanj8eSzIHR8/ejEj/rQnJX1Oedfn6bpI/rgQeA/XtsU1E1pMDMmetHtZ35FzIh/MeAi9PHVwKHSFIJM/Ym94ns8xARdwJ/62eTjwG/i8T9wARJW5YmXe8KyFxxImJZRCxMH68AniSZ/7q7SvysC8ldUdLP7+10sT796dnrpaJqSIGZM6u24t/bhPA9f9ne2SYi2oHlwMSSpOtbIbkB/in9k/5KSdv08nylKfR9VZoD0j+hb5D0rnKH6S5tYtib5Oyuu4r+rPvJDRX2eUuqk/Qw8Bpwc0T0+VlXSg0pIDNkrB/VVvw3Zn8BpkXEHsDNrDvzsOJaCGwbEXsCs4A/lzfOOpI2Aa4CTo2It8qdp1AD5K64zzsiOiJiL5I5xfeTtHuZIw2ogMyZ60e1Ff9CJoR/Z5t0DuHxwBslSde3AXNHxBsRsSZdvADYp0TZhqKQ/x8VJSLe6voTOpJZ5uolTSpzLCTVkxTQyyLi6l42qcjPeqDclfp5A0TEm8DtwGE9nqrEGgL0nXkw9aPaiv98YCdJ20kaQXIxZk6PbeYAn0sfHwXcFukVkTIaMHeP9tsjSdpPK90c4J/Tnij7A8sjYlm5Q/VH0hZd7beS9iP5N1DWf9hpnguBJyPi3D42q7jPupDclfZ5S2qUNCF9PAo4FPhrj80qqoYUknkw9SP3OXyLKfqYEF7S94HmiJhD8st4iaRnSS78HVu+xIkCc39F0pFAO0nu48sWOCXpcpLeGpMkLQW+S3KxiYg4n2Ru5sOBZ4FW4ITyJF2ngMxHAf8qqR1YBRxbAScH7wU+CzyWtusCfAeYCpX7WVNY7kr7vLcELpZUR/JF9KeIuLbCa0ghmTPXDw/vYGZWg6qt2cfMzIrAxd/MrAa5+JuZ1SAXfzOzGuTib2ZWg1z8zcxqkIu/VZx0eNqtyp2jP2nGM8t03F8OYf9+hxa32uHib5XoeKCii3/e0mEFiv2adcB/Ah8GdgM+JWm3Yh/HqoOLvxWdpDGSrktHcnxc0jGS/tzt+UMlXZOOVHhRus1jkk6TdBTQBFyWTkoxStI+ku6QtEDSjV23skuaJ+lnkpolPSlpX0lXS3pG0ll9ZNtX0r1ptgcljU3Ppv87fb1nJH033Xaauk0KI+lrvZ3t9zwbl3StkklMNnh/6fM7SJqbvp+7JO2Srr9I0vmSHgB+XMDn/FElk408JOkWSZPT9Y2SblYy8ccFkl5UMp5OVQ4tbvmoquEdrGocBrwcEUcASBoPfE9SY0S0kAxN8BtgL2DriNg93W5CRLyZDoXxtYhoVjJw2CzgYxHRIukY4AfA59NjtUVEk5JZpP6bZECrvwHPSfpZRLwzjoyScZX+CBwTEfMljSMZcgCSwrg7ydAJ8yVdB7w+xM9hg/eXrp8NfCEinpH0buBXwMHpc1OA90RERwGvfzfJpB6hZOambwCnkwxpcVtE/FDSYcCJ6fa9DQv97sG+OatuLv6Wh8eAn0r6EcksTndJugT4jKTfAgcA/0wy+9P2kmYB1wE39fJaO5MU5ZuVjA9WB3Qf0KxrgLzHgEVdg51Jep5kZMbug4jtDCyLiPmQjDiZbgvJGOlvpMtXAwcy9OGHn+/5/pQMf/we4Aqtmx9kZLd9riiw8EPyRfHH9C+hEcAL6foDgU8ARMRcSX8f2tuwjZGLvxVdRDytZI7Zw4GzJN1KMszsX4DVJAWuHfi7pD2BDwFfAI5m3Rl9F5EU9QP6OFzXMLad3R53LWf5/e45yFWQDJLVvWm0oY99e90uInp7f6cCb6Zjs/dmZYbMs4BzI2KOpA8AZw6wfUUOC23l4TZ/K7q0p05rRFwK/IRknteXgZeBM4DfpttNAoZFxFXp+q5JyVeQ/FUA8BTQKOmAdJ96DX42qKeALSXtm77W2G4XVg+VtJmSIXM/DtwDvApsLmmipJHAR/p43cXAXpKGKZlBab++3l/618YLkj6ZbqP0C2IwxrOueH+u2/p7SL5okDQD2DRdX8iQ6FYjfOZvefgH4CeSOoG1wL+m6y8DGiOia6zxrYHfSuo6Cfl2+t+LgPMlrSJpIjoK+EV67WA48HNgUaFhJF0PnBQRL6fXDGalRX4V8MF0swdJJiWZAlwaEc3pvt9Pn3uJDcd973IPSZPLEyTjqC8c4P0dB/xa0hkkw03/AXik0PfTzZkkzUd/B24DtkvXfw+4XNJngfuAV4AVfQ0tPojj2kbAQzpbyaQ9Yh6KiAvLnaU7SccDTRHxpYz7TIuIM3OKNWjpXykdabE/APh1P81MVqN85m8lIWkBSXv26eXOUgOmAn9K/+JoA04ucx6rQD7zNxsESXsBEyJiXk6vfwJwSo/V90TEF/M4ntUeF38zsxrk3j5mZjXIxd/MrAa5+JuZ1SAXfzOzGvT/AVyWXjaADwNgAAAAAElFTkSuQmCC\n", + "text/plain": [ + "<Figure size 432x288 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAX8AAAEHCAYAAABGNUbLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAeVElEQVR4nO3deZgcZb328e89k5DJxpaMEAgQ9HhAUWQZIlEERBYBo54XBGTRCB6ugyBy8Ljg61ER3yNugCDLyQFkEQHZVwkgIoJskwRN2BHjIRBIQCDLZJuZ3/tH1TCTIZPpmunq6p6+P9c1V6qqq7ru7iS/rnn6qedRRGBmZvWloegAZmZWeS7+ZmZ1yMXfzKwOufibmdUhF38zszo0rOgAPY0fPz4mTZpUdAwzs5oyc+bMVyOiOcsxVVX8J02aRGtra9ExzMxqiqS/Zz3GzT5mZnXIxd/MrA65+JuZ1SEXfzOzOuTib2ZWh3Lv7SNpHrAE6ADaI6Il73PWhPblsOAOaG+DTfeCkROKTmRmdaRSXT0/GhGvVuhc1W/1EpgxGdrmJ+tqgL3/CBttX2wuM6sbbvYpwlNnwdK/QfvS5Gf1Ynjk2KJTmVkdqUTxD+BOSTMlucIBLPs7dK5cc9vyF4vJYmZ1qRLFf7eI2AnYHzhe0u49H5R0rKRWSa2LFi2qQJwqsOnHoHFU93rDCHjHHsXlMbO6k3vxj4gX0z8XAjcAk3s9Pj0iWiKipbk509AUtWurw2CbE0HDQI3QvBvscn7RqcysjuT6ha+k0UBDRCxJl/cFvp/nOWuCBDv8ELY/DTpXw7CRRScyszqTd2+fTYAbJHWd69cRcUfO56wdDcOSHzOzCsu18kTE88AH8jyHmZll566eZmZ1yMXfzKwOufibmdUhF38zszrk4m9mVodc/M3M6pCLv5lZHXLxNzOrQy7+ZmZ1yMXfzKwOufibmdUhF38zszrk4m9mVodc/M3M6pCLv5lZHXLxNzOrQy7+ZmZ1yMXfzKwOufibmdUhF38zszrk4m9mVodc/M3M6pCLv5lZHXLxNzOrQy7+ZmZ1yMXfzKwOufibmdUhF38zszrk4m9mVodc/M3M6pCLv5lZHapI8ZfUKGm2pFsrcT4zM1u3Sl35fwV4skLnMjOzfuRe/CVNBA4ELsz7XGZmVppKXPmfBXwd6Fzbg5KOldQqqXXRokUViGNmZrkWf0mfABZGxMy+9omI6RHREhEtzc3NecYxM7NU3lf+HwY+KWkecBWwl6Rf5XxOMzPrR67FPyJOiYiJETEJOAy4JyKOzPOcZmbWP/fzNzOrQ8MqdaKIuBe4t1LnMzOzvvnK38ysDrn4m5nVoczNPpJ2AyYDcyPizvJHMjOzvPV75S/pkR7L/wr8AhgLfFfSN3PMZmZmOSml2Wd4j+VjgX0i4lRgX+CIXFKZmVmuSmn2aZC0EckHhSJiEUBELJPUnms6MzPLRSnFfwNgJiAgJE2IiAWSxqTbzMysxvRb/NO7c9emE/iXsqYxM7OKKLm3j6SN17J5fhmzmJlZhWTp5z8LWAQ8AzybLs+TNEvSznmEMzOzfGQp/ncBB0TE+IgYB+wP3Ap8CTgvj3BmZpaPLMV/14iY0bWS3uA1JSIeAkaUPZmZmeUmyx2+CyR9g2RcfoBDgVckNdLHLF1mZladslz5Hw5MBG5Mf7ZMtzUCh5Q7mJmZ5afkK/+IeBX4ch8PP1eeOGZmVglZuno2k0zEvh3Q1LU9IvbKIZeZmeUoS7PPFcBTwNbAqcA84NEcMpmZWc6yFP9xEXERsDoi/hARRwO+6jczq0FZevusTv9cIOlA4CVgbXf9mplZlctS/H8gaQPgq8A5wPrAv+eSyszMcpWlt8+t6eKbwEfziWNmZpXQb/GXdA4QfT0eESeWNZGZmeWulCv/1txTmJlZRZUynv+lpTyRpHMioq+bwMzMrIpk6erZnw+X8bnMzCxH5Sz+ZmZWI1z8zczqUDmLvydzNzOrESUVf0mNkn7az24/L0MeMzOrgJKKf0R0ALv1s88l5QhkZmb5yzK8w2xJNwPXAMu6NkbE9X0dIKkJuI9kmsdhwLUR8d0BZjUzszLJUvybgNdYcyTPAPos/sBKYK+IWCppOHC/pN+m8/6amVlBsozt84WsTx4RASxNV4enP30OFWFmZpVRcm8fSf8s6XeS5qbr20v6dgnHNUp6DFgI3BURDw84rZmZlUWWrp7/A5xCOq5/RPwFOKy/gyKiIyJ2IJn8fbKk9/V8XNKxkloltS5atChDHDMzG6gsxX9URDzSa1t7qQdHxBvA74GP99o+PSJaIqKlubk5QxwzMxuoLMX/VUnvIm2zl3QwsGBdB0hqlrRhujwS2IdkHmAzMytQlt4+xwPTgW0lvQj8DTiyn2MmAJdKaiT5oPlNj0lhzMysIFl6+zwP7C1pNNAQEUtKOOYvwI6DyGdmZjnI0tvnK5LWB9qAMyXNkrRvftHMzCwvWdr8j46IxcC+wDjgKOD0XFKZmVmushT/rlE7DwAui4jH8UieZmY1KUvxnynpTpLiP0PSWKAzn1hmZpanLL19jgF2AJ6PiDZJ44DMQz6YmVnxshT/riGdt5fc2mNmVsuyFP+v9VhuAiYDM1lzlE8zM6sBWfr5T+25LmkL4KxyBzIzs/wNZg7f+cB7yhXEzMwqp+Qrf0nn0D0WfwPJl7+zcshkZmY5y9Lm39pjuR24MiIeKHMeMzOrgCxt/pfmGcTMzCqn3+Iv6buUNvXivRFx3+AjmZlZ3kq58p9X4nO9MfAYZmZWSf0Wfzf3mJkNPVl6+3xnbdsj4vvli2NmZpWQpbfPsh7LTcAngCfLG8fMzCohS2+fn/Vcl/RTYEbZE5mZWe4Gc4fvKGBiuYKYmVnlZGnzn0N3l89GoBlwe7+ZWQ3K0ub/iR7L7cArEdFe5jxmZlYBWdr8/y5pJ5Jx/QO4H5idVzAzM8tPyW3+aVfPS0kmbx8PXCLp23kFMzOz/GRp9jkC+EBErACQdDrwGPCDHHKZmVmOsvT2eYmkf3+XEcCL5Y1jZmaVkOXK/03gcUl3kbT57wM8IulsgIg4MYd8ZmaWgyzF/4b0p8u95Y1iZmaVkqX4XwusiIgOAEmNwIiIaMslmZmZ5SZLm//vgJE91kcCd5c3jpmZVUKW4t8UEUu7VtLlUeWPZGZmectS/JelN3kBIGlnYHn5I5mZWd6ytPmfBFwj6SVAwKbAoes6QNIWwGXAJiQ9hKZHxM8HFtXMzMoly/AOj0raFtgm3fR0RKzu57B24KsRMUvSWGCmpLsi4okB5jUzszLIcuVPWuzndq1L2jQiXl7H/guABenyEklPApsDLv5mZgUazHj+ABeVuqOkScCOwMO9th8rqVVS66JFiwYZx8zMSjGo4h8RB5ayn6QxwHXASRGxuNdzTI+IlohoaW5uHkwcMzMrUaZmH0kbAVv0PC4iZvVzzHCSwn9FRFw/kJBmZlZeWWbyOg2YBvyV7hm9AthrHceIpGnoyYg4Y+AxzcysnLJc+R8CvCsiVmU45sPAUcAcSY+l274VEbdneA4zMyuzLMV/LrAhsLDUAyLifpJ7AszMrIpkKf4/BGZLmgus7NoYEZ8seyozM8tVluJ/KfAjYA7QmU8cMzOrhCzFvy0izs4tiZmZVUyW4v9HST8EbmbNZp91dvU0GzIiQP4Ky4aGLMV/x/TPXXtsW2dXT6tDL1wPL94KTRPgPSfDiHFFJxq8F2+Hhz4HK1+HjXeE3W+CUZsXncpsULIM7PbRPIPYEPDET2DO96CjDTQc5l0GB8yF9TYoOtnALXkO7v9M8poA/vEY/H5/OPAvhcYyG6ySh3eQtImkiyT9Nl1/r6Rj8otmNWfOqd1FMlbDyn/AC9cVm2mwFv0J1PO/SQcsfgLaPXup1bYsY/tcAswANkvXnyEZ498s0dnr/r/ohI4an++naS3jTWkYNDZVPotZGWUp/uMj4jek3Twjoh3oyCWV1aYtDoLGHtM8NzTCZvsXl6ccJuwH43eFYaOhYQQ0joKW83r9NmBWe7J84btM0jjScX0k7Qq8mUsqq01TfgkzT4aXbk+umFvOhTHvLDrV4KgB9rwD5t8Ay1+C8VNg3C5FpzIbtCzF/2SSbp7vkvQA0Ax8JpdUVpsam2DyeUWnKL+GRtjy4KJTmJVVluL/OLAHyTSOAp5m8JPBmJlZAbIU7wcjoj0iHo+IuemUjg/mFczMzPLT75W/pE1J5t0dKWlHukfpXB8YlWM2MzPLSSnNPvuRTOIyEfgZ3cV/CfCtfGKZmVme+i3+EXEpcKmkgyKixu/YMTMzyNbmP1HS+kpcKGmWpH1zS2ZmZrnJUvyPjojFwL7AOJLpGU/PJZWZmeUqS/Hvaus/ALgsIh7HUzSamdWkLMV/pqQ7SYr/DElj8YxeZmY1KctNXscAOwDPR0RbOtTDF3JJZWZmucpy5X8NMAFYDBARr0WEBzU3M6tBWYr/+cDhwLOSTpe0TU6ZzMwsZyUX/4i4OyKOAHYC5gF3S/qTpC9IGp5XQDMzK79MA7Ol7fzTgC8Cs4Gfk3wY3FX2ZGZmlpuSv/CVdAPJiJ6XA1MjYkH60NWSWvMIZ2Zm+chy5X8lsGtE/BA4RtL1knYCiIiWXNKZmVkushT/b0fEYkm7AXsDF5F8CWxmZjUmS/Hvmq/3QGB6RNwGrFf+SGZmlrcsxf9FSf8NHArcLmlExuPNzKxKZCnehwAzgP0i4g1gY+Br6zpA0sWSFkqaO/CIVjdWLIQ5p8Gsr8LC+4tOYzakldzbJyLagOt7rC8AFvR9BACXAL8ALhtIOKsjKxbCbe+HVa9DrIZnz4cpl3nidLOc5NpsExH3Af/I8xw2RDx3YXfhB+hYDrPX+YulmQ2C2+ytOrQv6S78b21bVkwWszpQePGXdKykVkmtixYtKjqOFWXip6FxZPd640jY8jOFxTEb6gov/hExPSJaIqKlubm56DhWlPEfhA9fDWP+CZo2hXcdAzufVXQqsyEry3j+ZvmaODX5MbPc5XrlL+lK4EFgG0nzJR2T5/nMcvH6n+GOyXDDRHjgCFi9pOhENtR0rIKOFRU9Za5X/hHx2Tyf3yx3yxfA3bvD6sXJ+gvXwYpX4GN3F5vLhobohEe/BH+9CAjY7ADY7TfQ2JT7qQtv8zerai/fk/wH7dK5EhbeW/GrNBuinjkX/nY5RDtEB7x8F8z+ekVO7eJvti7DRq1lo8DzF1k5vPw76GjrXu9YAa/8viKndvE3W5fN9odRE6FhRLLeOAre+3VoaCw2lw0NYyZBQ48LCTXA6C0rcmr39jFbl8Ym2O9ReOYcWDYPNtkLtjyk6FQ2VLzvOzD/Jlj5WrLesB7sfHZFTj3ki/9TT8Gvfw3DhsFRR8HWWxedaAhob4MVL8PIzSryxVThho+B7U4pOoUNRSM2hgPnwoIZ0NkOm34MRoyryKmHdPGfORP22AOWLwcJfvpTeOQR2HbbopPVsBduhD8dQdLu3QC73wib7lVwKLMaNmw0bPF/Kn7aId3mf8opsGwZdHZCRwcsXQqnnVZ0qhq2/OWk8He0QceyZDye+z4Nq5cWnczMMhrSxf/NN9dcj4DXXy8my5Cw+Ok1v5zqsmxexaOY2eAM6eJ/+OEwenT3+qhRyTYboNFbJf3ce+pcDaM2LyaPmQ3YkC7+J54I3/gGbLIJTJgA//VfcOSRRaeqYWMmwfanJSNuDt8g+XOX82C9jYpOZmYZKSKKzvCWlpaWaG1tLTqG9Wfxs7D0r7D+tskHgpkVStLMiGjJcsyQ7u1jOVn/3cmPmdWsId3sY2Zma+fib2ZWh1z8zczqkIu/mVkdcvE3M6tDLv5m9nbty6BtPnR2FJ3EclL3xb+1FQ44AD7yEbj44mQICLO69tRZcO3GcMs/w01bweJnik5kOajrfv5z58KeeyaDvwHMnp0M/nbiiYXGMivOq4/An/8vdK5K1pe/BH/4BEz1B8BQU1dX/m2r2/jyb7/MTv+9E4dccwjnXvbSW4Ufkg+BM84oLp9Z4V6fCfT89TdgyXNu/hmChsSV/8PX3cSKeXfS2TSRlsNPYOxGY9d4/MEH4cqrgls2/BQLht/Pyo4VzHllDiNH3s83D5rGZqMXc+vsqdw5Zz+k8mR67DG4/PJkEpkvfhHe7RtirRaMnpTM09DTiHGetnIIqvmxfe4970fsMvL7jB7RxorVI3h58Za84/OPMWr9ZOLt22+Hgw+G5XoVTt4chq1669ixDeKK5gamrt/BspWj+MbVZ/Keqcdy/PGDex0PPAD77gttbckkMqNHJ5PIvOc9g3tes9xFwJ+Ogvk3QsMwiHbY/WZP2FPlBjK2T00X/+gMVl4+kqbh3cMML10xhr80TedDh38WgO22gyeeAJpeh69tAo2r39p3rOC6CbBPOuzzytiYEUe8NujXsccecN993etSMproZZcN+qnN8hcBrz0KK16BjXeGUZsVncj6UXcDu3V2dDKssX2NbVInHSu7G/Lb2tKFFRvB01Phn+6A9dpYr6GRTRs7+MjI7mNHDFuxxnNFwIwZMG8e7LgjfPCDpeVa2mtiqwhYvLjEF2VWNAnGTy46heWspr/wbRzeyOwF+7Fi1Yi3tkWIrafs/db6EUckk7gAcO1VDHvoFFo22pdj338ID08aSVPXO9A4co15NCNg2rSkyejkk2GvveDMM0vL9fnP9zgnyfLnPjew12hmloeabvYBWPrGUh77n+N499i7eWP5JrTvPJ3tdu++aunogO98By69FEaOhNNPh4MOSh985V5oPR5Wvg6bT4WWn0NjE9A9+XvP3kDrrQevvQZjxqw7UwT8+Mdw7rnQ2Aj/+Z9w9NGZXpaZWcnqrs2/XGYtmMUZD57B6s7VHNdyHHtO2pPbbkumfOzZXDNqFDz5JGy5ZcUjmpn1qe7a/MvhZ1fO5GtP7E40toHglqdv4bpDrmOnnfZn9eo19x07Fjb3dLVmNgTUdJv/YN1/P3zjhp8Rw5LCD7C8fTmn3XcaI0fC8OFr7r/BBpTtPgAzsyLVdfG/5hro0Mq3bV/dsZqHHnr7/v/7v7BgQQWCmZnlLPfiL+njkp6W9Jykb5b7+Ts6ki9X99gj6Uv/wgulH7tqFdB6HKzq7pqj9lEcP/l4Ro+Gzs63n6tnLx4zs1qVa5u/pEbgXGAfYD7wqKSbI+KJcp3jhBOSm6fa2pKeNTNmwFNPwbhx6z5u/nz49a+BxXvDtVfB7qdBYzsnTP4y03aYRkcHbL99Mtjb8uXJXbpHHgkbbVSu5GZmxcn7C9/JwHMR8TyApKuATwFlKf6dnXDhhdCe3ufV0ZEU6ltvTfrar8u118LKrhafZ6bCM1MZNQrOviDZ1NgI99wD558PzzwDU6Ykxd/MbCjIu/hvDvRsiJkPrHGfrKRjgWMBtixTH8pSeq9GvH2/xl5jV40YASedVJZIZmZVpfAvfCNiekS0RERLc3NzpmMbGpK7cLva4RsboakJDjyw/2MPPjjZt6v3zqhR8KUvZctuZlar8r7yfxHYosf6xHRb2VxwAWy1VTJ658SJyZe/pXyGbLEFPPwwnHIKLFyY3PXrq3wzqxe53uEraRjwDPAxkqL/KHB4RDy+tv2LusPXzKyWVd0dvhHRLukEYAbQCFzcV+E3M7PKyX14h4i4Hbg97/OYmVnpCv/C18zMKs/F38ysDrn4m5nVIRd/M7M6VFWTuUhaBPx9EE8xHni1THEqpRYzQ23mdubKqcXctZgZktyjIyLTXbJVVfwHS1Jr1r6uRavFzFCbuZ25cmoxdy1mhoHndrOPmVkdcvE3M6tDQ634Ty86wADUYmaozdzOXDm1mLsWM8MAcw+pNn8zMyvNULvyNzOzErj4m5nVoZor/v1NCC9phKSr08cfljSpgJhvU0LuaZIWSXos/fliETl7ZbpY0kJJc/t4XJLOTl/TXyTtVOmMa8nUX+Y9Jb3Z433+TqUzriXTFpJ+L+kJSY9L+spa9qnG97qU3FX1fktqkvSIpD+nmU9dyz5VVUNKzJy9fkREzfyQDAv9V+CdwHrAn4H39trnS8AF6fJhwNU1knsa8Iuis/bKtDuwEzC3j8cPAH4LCNgVeLgGMu8J3Fp0zl6ZJgA7pctjSebA6P3voxrf61JyV9X7nb5/Y9Ll4cDDwK699qmqGlJi5sz1o9au/N+aED4iVgFdE8L39Cng0nT5WuBjUtdkjYUpJXfViYj7gH+sY5dPAZdF4iFgQ0kTKpNu7UrIXHUiYkFEzEqXlwBPksx/3VM1vtel5K4q6fu3NF0dnv707vVSVTWkxMyZ1VrxX9uE8L3/sb21T0S0A28C4yqSrm+l5AY4KP2V/lpJW6zl8WpT6uuqNlPSX6F/K2m7osP0lDYx7EhydddTVb/X68gNVfZ+S2qU9BiwELgrIvp8r6ulhpSQGTLWj1or/kPZLcCkiNgeuIvuKw8rr1nAVhHxAeAc4MZi43STNAa4DjgpIhYXnadU/eSuuvc7IjoiYgeSOcUnS3pfwZH6VULmzPWj1op/KRPCv7VPOofwBsBrFUnXt35zR8RrEbEyXb0Q2LlC2QajlL+PqhIRi7t+hY5klrnhksYXHAtJw0kK6BURcf1adqnK97q/3NX6fgNExBvA74GP93qoGmsI0HfmgdSPWiv+jwLvlrS1pPVIvoy5udc+NwOfT5cPBu6J9BuRAvWbu1f77SdJ2k+r3c3A59KeKLsCb0bEgqJDrYukTbvabyVNJvk/UOh/7DTPRcCTEXFGH7tV3XtdSu5qe78lNUvaMF0eCewDPNVrt6qqIaVkHkj9yH0O33KKPiaEl/R9oDUibib5x3i5pOdIvvg7rLjEiRJznyjpk0A7Se5phQVOSbqSpLfGeEnzge+SfNlERFxAMjfzAcBzQBvwhWKSdish88HAcZLageXAYVVwcfBh4ChgTtquC/AtYEuo3vea0nJX2/s9AbhUUiPJB9FvIuLWKq8hpWTOXD88vIOZWR2qtWYfMzMrAxd/M7M65OJvZlaHXPzNzOqQi7+ZWR1y8Tczq0Mu/lZ10uFpNys6x7qkGb9X0Hl/MYjj1zm0uNUPF3+rRtOAqi7+eUuHFSj3czYC5wL7A+8FPivpveU+j9UGF38rO0mjJd2WjuQ4V9Khkm7s8fg+km5IRyq8JN1njqR/l3Qw0AJckU5KMVLSzpL+IGmmpBldt7JLulfSmZJaJT0paRdJ10t6VtIP+si2i6Q/pdkekTQ2vZq+KX2+ZyV9N913knpMCiPpP9Z2td/7alzSrUomMXnb60sff5ekO9LX80dJ26bbL5F0gaSHgR+X8D5PVTLZyGxJd0vaJN3eLOkuJRN/XCjp70rG06nJocUtHzU1vIPVjI8DL0XEgQCSNgBOldQcEYtIhia4GNgB2Dwi3pfut2FEvJEOhfEfEdGqZOCwc4BPRcQiSYcC/w84Oj3XqohoUTKL1E0kA1r9A/irpDMj4q1xZJSMq3Q1cGhEPCppfZIhByApjO8jGTrhUUm3Aa8O8n142+tLt08H/i0inpX0QeA8YK/0sYnAhyKio4Tnv59kUo9QMnPT14GvkgxpcU9E/FDSx4Fj0v3XNiz0Bwf64qy2ufhbHuYAP5P0I5JZnP4o6XLgSEm/BKYAnyOZ/emdks4BbgPuXMtzbUNSlO9SMj5YI9BzQLOuAfLmAI93DXYm6XmSkRl7DiK2DbAgIh6FZMTJdF9Ixkh/LV2/HtiNwQ8//Hzv16dk+OMPAdeoe36QET2OuabEwg/JB8XV6W9C6wF/S7fvBvwLQETcIen1wb0MG4pc/K3sIuIZJXPMHgD8QNLvSIaZvQVYQVLg2oHXJX0A2A/4N+AQuq/ou4ikqE/p43Rdw9h29ljuWs/y77v3IFdBMkhWz6bRpj6OXet+EbG213cS8EY6NvvaLMuQ+RzgjIi4WdKewPf62b8qh4W2YrjN38ou7anTFhG/An5CMs/rS8BLwLeBX6b7jQcaIuK6dHvXpORLSH4rAHgaaJY0JT1muAY+G9TTwARJu6TPNbbHF6v7SNpYyZC5nwYeAF4B3iFpnKQRwCf6eN55wA6SGpTMoDS5r9eX/rbxN0mfSfdR+gExEBvQXbw/32P7AyQfNEjaF9go3V7KkOhWJ3zlb3l4P/ATSZ3AauC4dPsVQHNEdI01vjnwS0ldFyGnpH9eAlwgaTlJE9HBwNnpdwfDgLOAx0sNI+l24IsR8VL6ncE5aZFfDuyd7vYIyaQkE4FfRURreuz308de5O3jvnd5gKTJ5QmScdRn9fP6jgDOl/RtkuGmrwL+XOrr6eF7JM1HrwP3AFun208FrpR0FPAg8DKwpK+hxQdwXhsCPKSzVUzaI2Z2RFxUdJaeJE0DWiLihIzHTIqI7+UUa8DS31I60mI/BTh/Hc1MVqd85W8VIWkmSXv2V4vOUge2BH6T/saxCvjXgvNYFfKVv9kASNoB2DAi7s3p+b8AfKXX5gci4vg8zmf1x8XfzKwOubePmVkdcvE3M6tDLv5mZnXIxd/MrA79f4IDSAyftcurAAAAAElFTkSuQmCC\n", + "text/plain": [ + "<Figure size 432x288 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYkAAAEHCAYAAABbZ7oVAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAiyElEQVR4nO3deZRcdZ338fcnnc5KQkzSQgyBsDMEIYQmsg1G1rBIHImCjrKpHJVFfHBmlIeDwuAI44IKKuYRB1AOBgExYhgIyA6SdEJYwhqQJRClCSEQsjTd/X3+uLfpStOVrtup21Xd/XmdUyd190+VUt/+3eX3U0RgZmbWmQGVDmBmZtXLRcLMzIpykTAzs6JcJMzMrCgXCTMzK2pgpQN0x9ixY2PixImVjmFm1qssXLjw9Yioy7JNrywSEydOpKGhodIxzMx6FUkvZt3Gp5vMzKwoFwkzMyvKRcLMzIpykTAzs6JcJMzMrKheeXdTv7L6eWi8HwaNhnHTYUBNpROZWT/iIlHN/n473D0DlDb4PjAFDr4DBvh/NjPrGT7dVM0eOAFa1kDz6uS1ciG8OLvSqcysH3GRqGZNKzacbmmCta9WJouZ9UsuEtVsdD2o4NTSgFqo269yecys33GRqGb/fAOM2g1UAwMGwZ7fh7r9K53KzPoRXwGtZkO3hCMehuY1UDOk/QK2mVkPcZHoDQYOq3QCM+un/KepmZkV5SJhZmZFuUiYmVlRLhJmZlaUi4SZmRWVa5GQNETSfEmPSFoi6fxO1jlJUqOkxenri3lmMjOz0uV9C+x64KCIWC2pFrhP0i0R8dcO682OiNNzzmJmZhnlWiQiIoDV6WRt+oo8j2lmZuWT+zUJSTWSFgOvAfMi4qFOVjtW0qOSrpc0Ie9MZmZWmtyLRES0RMRkYCtgqqTdOqzyJ2BiROwOzAOu6mw/kk6V1CCpobGxMdfMZmaW6LG7myLiTeBOYHqH+SsiYn06+StgryLbz4qI+oior6uryzWrmZkl8r67qU7SqPT9UOBQ4KkO64wrmDwGeDLPTGZmVrq8724aB1wlqYakIF0XETdLugBoiIg5wJmSjgGagTeAk3LOZGZmJVJyA1LvUl9fHw0NDZWOYWbWq0haGBH1WbbxE9dmZr1BawusWQbN7/ToYT2ehJlZtVv1FPzlYGhaCdECe/4Adj6jRw7tloSZWbW7+2hYuxxa1kJrEyz+JqzomVPuLhJmZtWspQlWP8/7OqtYubhHDu8iYWZWzWoGwaBRG86TYPg2PXJ4Fwkzs2p3wHVQMxxqRyb/TpgJWx7SI4f2hWszs2q35SHw8afhjUUwdEsYXZ+0JnqAi4SZWW8wbHzy6mE+3WRmZkW5SJiZWVEuEmZmVpSLhJmZFeUiYWZmRblImJlZUS4SZmZWlIuEmZkV5SJhZmZFuUiYmVlRuRYJSUMkzZf0iKQlks7vZJ3BkmZLWirpIUkT88xkZmaly7slsR44KCL2ACYD0yXt02GdLwArI2IH4BLg4pwzmZlZiXItEpFYnU7Wpq8OI2cwA7gqfX89cLDUQ90bmpnZRuV+TUJSjaTFwGvAvIh4qMMq44GXASKiGVgFjOlkP6dKapDU0NjYmHNqMzODHigSEdESEZOBrYCpknbr5n5mRUR9RNTX1dWVNaOZmXWux+5uiog3gTuB6R0WvQJMAJA0ENgcWNFTuczMrLi8726qkzQqfT8UOBR4qsNqc4AT0/czgb9ERMfrFmZmVgF5j0w3DrhKUg1JQbouIm6WdAHQEBFzgCuA30haCrwBHJ9zJjMzK1GuRSIiHgX27GT+eQXv1wGfyjOHmZl1j5+4NjOzolwkzMysqJKKhKRdJB0sabMO8zveqWRmZn1Il0VC0pnAH4EzgMclzShY/F95BTMzs8or5cL1l4C9ImJ12vne9ZImRsRPAHefYWbWh5VSJAa09b8UES9ImkZSKLbBRcLMrE8r5ZrEPyRNbptIC8bRwFjgwznlMjOzKlBKkTgB+HvhjIhojogTgANzSWVmZlWhy9NNEbEMQNLoThbPL3siMzOrGlmek1gENALPAM+m71+QtEjSXnmEMzOzyspSJOYBR0bE2IgYAxwB/Bn4KvDzPMKZmVllZSkS+0TErW0TEXFbOu+vwOCyJzMzs4rL0sHfckn/AfwunT6O5M6nGqC17MnMzKzisrQkPksyutxN6WvrdF4N8OlyBzMzs8oruSUREa+TdM3RmaXliWNmZtWk5CIhqQ74d2ASMKRtfkQclEMuMzOrAllON11DMvTotsD5wAvAghwymZlZlchSJMZExBXAuxFxd0ScAmy0FSFpgqQ7JT0haYmkr3WyzjRJqyQtTl/ndbYvMzPreVnubno3/Xe5pKOAV4HOnsIu1AycHRGLJI0AFkqaFxFPdFjv3og4OkMWMzPrAVmKxIWSNgfOBi4FRgJf39gGEbEcWJ6+f1vSk8B4oGORMDOzKpTl7qab07ergI9lPVA6FsWewEOdLN5X0iMkrZNvRMSSrPs3M7Py67JISLoUiGLLI+LMEvaxGXADcFZEvNVh8SJgm3RQoyNJnsHYsZN9nAqcCrD11lt3dUgzMyuDUloSDZtyAEm1JAXimoi4sePywqIREXMl/VzS2PS5jML1ZgGzAOrr64sWLTMzK59Sugq/qpQdSbo0Is7oME/AFcCTEfGjItttCfwjIkLSVJI7rlaUckwzM8tXlgvXXdm/yLzPA49JWpzOO4ekSw8i4nJgJvAVSc3AWuD4iHBLwcysCpSzSLxPRNxHF+NgR8RlwGV55jAzs+7J8jCdWTbrV8Da5eCGoVmvVc6WxEZbDNaPtLbAgyfAy9cDA+ADk+GgW6F2ZKWTmVlGJbUkJNVI+kEXq/2kDHmsL3jmZ7DsJmhtgtZ1sPJhWHB6pVOZWTeUVCQiogU4oIt1rixHIOsDGu+DljXt063r4fUHK5fHzLoty+mmhyXNAX4PvNM2s7NnH6yfG7kzDBicFAcA1cCI7Subycy6JUuRGELy/EJhz68BuEjYhiZ9E175E6x+DhgAA4fC1F9WOpWZdUOWvptOzjOI9SEDh8P0BdB4P7Ssh7r9oHZEpVOZWTeUfAuspJ0k3SHp8XR6d0nn5hfNerUBtbDFNPjQ4S4QZr1Yluck/h/wLdJxJSLiUeD4PEKZmVl1yFIkhkXE/A7zmssZxszMqkuWIvG6pO1Juw2XNJN0QCEzM+ubstzddBpJV927SHoF+BvwuVxSmZlZVchyd9PzwCGShgMDIuLt/GKZmVk1yHJ309ckjQTWAJdIWiTpsPyimZlZpWW5JnFKOorcYcAYknEiLsollfVtbzwMc/eEGz4I93wCmlZWOpGZFZGlSLT18nokcHVELME9v1pWa5fDHdPgzcWwvhFevQXuOqrSqcysiCxFYqGk20iKxK2SRgCt+cSyPuu1ezccX6K1CVYsgHdXVy6TmRWV5e6mLwCTgecjYo2kMYC76rBsBg4nvYt6QzWDezyKmXUtS0viAGAzYHdJBwKTgFEb20DSBEl3SnpC0hJJX+tkHUn6qaSlkh6VNCXLB7BeZstDYcROUDMkma4ZBrv+R9KNh5lVnSwtiX8reD8EmAosZMNeYTtqBs6OiEXp6amFkuZFxBMF6xwB7Ji+PgL8Iv3X+qKaQXDofbD0l/DOi/DBf4YJn6x0KjMrIstzEh8vnJY0AfhxF9ssJ30qOyLelvQkMB4oLBIzSC6EB/BXSaMkjUu3tb5o4FDY5axKpzCzEmQ53dTRMuCfSl1Z0kRgT+ChDovGAy932O/4TrY/VVKDpIbGxsbsac3MLLOSWxKSLqX9iuMAkovYi0rcdjPgBuCs9FmLzCJiFkm3INTX13dy5dPMzMotyzWJhoL3zcC1EXF/VxtJqiUpENcUGer0FWBCwfRW6TwzM6uwLNckrsq6c0kCrgCejIgfFVltDnC6pN+RXLBe5esRZmbVocsiIenbdHpj+/vcFRH3dJi3P0n3HY9JWpzOOwfYGiAiLgfmkjygt5SkXyg/e2FmViVKaUm8UOK+3uw4IyLuo4uuO9K7mk4r8RhmZtaDuiwS3TnNZGZmfUOWu5vO62x+RFxQvjhmZlZNstzd9E7B+yHA0cCT5Y1jZmbVJMvdTT8snJb0A+DWsicyM7OqsSlPXA8jeabBzMz6qCzXJB6j/VbYGqAO8PUIM7M+LMs1iaML3jcD/4iI5jLnMTOzKpLlmsSL6VgPB5C0KO4DHs4rmJmZVV7J1yTSW2CvAsYAY4ErJZ2bVzCzXufvt8Pdn4B7joXGByudxqwsspxu+ldgj4hYByDpImAxcGEOucx6l1fmwn2fgpY1yfTyW+CgO6Bu38rmMttEWe5uepXk+Yg2g3FvrWaJJ/6rvUAAtKyFp35YfH2zXiJLS2IVsETSPJJrEocC8yX9FCAizswhn1nv0NrSyTzf12G9X5Yi8Yf01eau8kYx68V2OQv+ekp7a6JmKOx8RkUjmZVDliJxPbAuIloAJNUAgyNizcY3M+sHtjku+fepH8OAgTDpHNjy4IpGMiuHLEXiDuAQYHU6PRS4Ddiv3KHMeqVtjmsvFmZ9RJYL10Mioq1AkL4fVv5IZmZWLbIUiXfSh+kAkLQXsLb8kczMrFpkOd10FvB7Sa+SjDa3JbDRtrWkX5N05/FaROzWyfJpwB+Bv6WzbvT4FGZm1SNLtxwLJO0C7JzOejoi3u1isyuBy4CrN7LOvRFx9EaWm5lZhWRpSZAWhcfbpiVtGRF/38j690ia2P14ZmZWSZsyngTAFWXIsK+kRyTdImlSGfZnZmZlkqkl0VFEHLWJx18EbBMRqyUdCdwE7NjZipJOBU4F2HrrrTfxsGZmVopMLQlJH5C0u6Qpba9NOXhEvNV2W21EzAVqJY0tsu6siKiPiPq6urpNOayZmZUoy8h0/wmcBDxH+wh1ARzU3YNL2pJk8KKQNJWkaK3o7v7MzKy8spxu+jSwfUQ0lbqBpGuBacBYScuAbwO1ABFxOTAT+IqkZpJnLo6PiCiyOzMz62FZisTjwCjgtVI3iIjPdLH8MpJbZM3MrAplKRLfAx6W9Diwvm1mRBxT9lRmZlYVshSJq4CLgceA1nzimJlZNclSJNZExE9zS2JmZlUnS5G4V9L3gDlseLppUdlTmZlZVchSJPZM/92nYN4m3QJrZmbVLUsHfx/LM4iZmVWfkp+4lrSFpCsk3ZJO7yrpC/lFMzOzSsvSLceVwK3Ah9LpZ0jGmDAzsz4qS5EYGxHXkd7+GhHNQEsuqczMrCpkHb50DGm/TZL2AVblksrMzKpClrub/g/J7a/bS7ofqAM+lUsqMzOrClmKxBLgoyTDlwp4mk0ftMjMzKpYlh/5ByOiOSKWRMTj6VCmD+YVzMzMKq/LlkQ65sN4YKikPUlaEQAjgWE5ZjMzswor5XTT4SSDDW0F/JD2IvE2cE4+sczMrBp0WSQi4irgKknHRsQNPZDJzMyqRJZrEltJGqnEryQtknRYbsnMzKzishSJUyLiLeAwYAzweeCiXFKZmVlVyFIk2q5FHAlcHRFLCuZ1voH0a0mvpaPZdbZckn4qaamkRyVNyZDHzMxylqVILJR0G0mRuFXSCLoeoe5KYPpGlh8B7Ji+TgV+kSGPmZnlLMvDdF8AJgPPR8SatIuOkze2QUTcI2niRlaZQdIqCeCvkkZJGhcRyzPkMjOznGRpSfweGAe8BRARKyLi0U08/njg5YLpZem895F0qqQGSQ2NjY2beFgzMytFliLxC+CzwLOSLpK0c06ZOhURsyKiPiLq6+rqevLQZmb9VslFIiJuj4h/BaYALwC3S3pA0smSart5/FeACQXTW6XzzMysCmTqoC+9DnES8EXgYeAnJEVjXjePPwc4Ib3LaR9gla9HmJlVj5IvXEv6A0kPsL8BPl7wYz5bUkORba4FpgFjJS0Dvg3UAkTE5cBckrullgJr6OJCuJmZ9awsdzddC/xvRLwl6dz0mYYLI2JRRNR3tkFEfGZjO0zvajotQwYzM+tBWU43nZsWiAOAQ4Ar8HMNZmZ9WpYi0Tae9VHArIj4MzCo/JHMzKxaZCkSr0j6JXAcMFfS4Izbm5lZL5PlR/7TwK3A4RHxJjAa+Lc8QpmZWXXI8pzEmoi4MSKeTaeXR8Rt+UUz60WiFRafA9ePhhvq4InvQ0SlU5ltsix3N5lZMU/+EJ7+CbSsSaYf+w4M+SBsd2JFY5ltKl9TMCuHl2a3FwhI3r90XeXymJWJi4RZOQwa3WHGABg0piJRzMrJRcKsHCZfDAOHg2pAtVA7Aj787UqnMttkviZhVg6j94QjFsOL18GAgbDNZ2D4hC43M6t2LhJm5TJiB9jtnEqnMCsrn24yM7OiXCTMzKwoFwng1Vfhox+FzTeHSZNg8eJKJzKrcq0tsOjf4PoxcMMW8MzPKp3IctLvr0m0tsJBB8HSpdDSAk88AdOmJdNjx1Y6nVmVWnIhPPvz9mdDHv53GLIFbD2zsrms7Pp9S2L5cnjppaRAtImA+fMrl8ms6r143fsfHnzRDw/2Rf2+SIwYAc3NG85rbU1OPZlZEYNGdZgxAAb74cG+KPciIWm6pKclLZX0zU6WnySpUdLi9PXFvDMVGjkSzjoLhg9PpocNg332gX337ckUZr3Mnj+AmuFA+vDgoM1h0vv+87Y+INdrEpJqgJ8BhwLLgAWS5kTEEx1WnR0Rp+eZZWMuvhj22w8aGmDbbeHEE2FAv29jmW1E3b4wfT68dD3UDIaJn4Nh4yudynKQ94XrqcDSiHgeQNLvgBlAxyJRURJ84hPJy8xKtPmu8OHzKp3Ccpb338vjgZcLppel8zo6VtKjkq6X5L4MzMyqRDWcVPkTMDEidgfmAVd1tpKkUyU1SGpobGzs0YBmZv1V3kXiFaCwZbBVOu89EbEiItank78C9upsRxExKyLqI6K+rq4uc5AHHoCdd4bRo+HjH4eVKzPvouxeeSV5JuMDH4DJk+HxxyudyMxsQ3kXiQXAjpK2lTQIOB6YU7iCpHEFk8cAT5Y7xIsvwuGHwzPPJMXhtttgxoxyHyWblhb42MfgvvvgzTfh0UfhwAOro3iZmbXJtUhERDNwOnAryY//dRGxRNIFko5JVztT0hJJjwBnAieVO8ddd2043HBTE9x/P6xfX3ST3C1blrQk2h7ii0jeL1xYuUxmZh3l3i1HRMwF5naYd17B+28B38ozw8iRyR1MhQYOhNraPI+6cZ09xNfSksw3M6sW1XDhOndHHQU77ABDhybTw4bBd79b+rMQf/hDcnvs5z+f9O3UmddeS7r4KGyxbMzo0fDlL2/4EN/++8Pee5e2vZlZT1CU+qtWRerr66OhoSHTNuvWwRVXJKd4DjwQpk8vbbsrr4TTToM1a5LWyPDhySmhnXZKljc1wbHHwrx5yfKpU2Hu3PYf/42JgBtvTB7i22GH5CG+gf2+y0Uzy4ukhRFRn2mb/lIkumuHHeC559qnJTj7bPj+95PpCy6Aiy6CtWuT6SFD4JRT4GfuOdnMqkx3ioT/bu3EO03v8NtHf8vKdSt5Z/NDKbwrNwLefbd93fvuay8QkLRYHnyw57KameXJRaKDd5reYcqsKSxbtYymliZ0zAUMavktTY98EkiuHZx4Yvv6//RPcPfdyWknSC6Gt52KMjPr7frFhessfvPob3h51cusaV5DczTzLmsZ/MnTGD06uV6w+ebwj3+0r3/BBbDddsldSSNGwIc+BD/+ccXim5mVlVsSHaxcu5KmlqYN5q1peYvaNcktq8uXJxeqH3gA9tgjKRqLFyenmFpaki7Ghw2rTHYzs3JzS6KDQ7Y7hEE1g96bHlwzGJYezrp17es0NcGtt7ZPDx6cdK9x8MEuEGbWt7hIdLD3+L25+l+uZovhWzCsdhhH7HAEm9+5YZ+DtbWw2WYVCmhm1oN8uim1bh1873uwaBFMmTKTF741kyFDkmVXN8GXvpS0IAYMSB6E+9zn2rddsAAuuSQ5HXXaafDRj1bmM5iZlZuLBMmY1ocdljzUtnYt3H473Hln0ufTgAHJdYi2bj0i4J13kofrRo6E+fOTjvrWpGPC33wz3HRTsj8zs97Op5uAp55KWhBtzzusW5dMP/VUMn3RRe2dAUYk682enUz/93+3FwhIll14Yc9lNzPLk4sEycNxHTsAlNofmmvrqbVNa2t753yFD9YV7s/MrC/oN0WitRX++Ef45S/hkUc2XLbrrjBhAgxKb2qqrU2md901mT75ZBg6phFOOAj+7zCaz5jABz9yBwBf/Wp7x4GQ3N10xhk98IHMzHpAvygSra3w9RMeYqdnJ3Esdbxw9SeZ/dtV7y2vrYV774WZM2HSpOTfe+9NuxJvbeaSz32dSd/4EAO3uxNq1xIjl/Hle47huTee4/DD4dprk95bp0yByy+Hz362cp/VzKyc+sWF67vmvsR3DzqEzYasBuDw3f/MQ898gog73zvNNGYMXHNNJxsv/ibvLv0li9Y301owW4h7X7qX7Udvz4wZlR/pzswsD/2iJTFwxV0U9nU7pLaJ/Xe8l/Vrm4pu856XZlPbupba912zEKOGjCpnTDOzqtMvisR2O73/ybdWahgytISG1MDNGCD40VgYJqgBhtXUMqluEkfteFT5w9rGRcCzs+D2g+CeY2FV2YdEN7MCuRcJSdMlPS1pqaRvdrJ8sKTZ6fKHJE0sd4atph5F69BtWduUPB23tmkYa7Y/H1TCx9/zh1AzjK+OglvG13DBB4dx2WEXc8/J91BbU8HxT/urJy6CRV+H1+6EZX+AWz8Cq/9W6VRmfVaugw5JqgGeAQ4FlgELgM9ExBMF63wV2D0ivizpeOBfIuK4je23W4MONa+BpbNoXb2MAeOmwfijS9/29fnw8o1Quxls/wUYOi7bsa18bqiD9a+3T2sgfPh82O2cymUy6yWqcdChqcDSiHgeQNLvgBlA4UjRM4DvpO+vBy6TpCh39Ro4DHY5q3tNp7FTk5dVoUhfZpaHvE83jQdeLphels7rdJ2IaAZWAWM67kjSqZIaJDU0NjbmFNeq3k5nQk3bAOKCmqGwzfEVjWTWl/WaW2AjYhYwC5LTTRWOY5Wy27kweDS8eC0MGg17fBdGbF/pVGZ9Vt5F4hVgQsH0Vum8ztZZJmkgsDmwIudc1ltJsNNpycvMcpf36aYFwI6StpU0CDgemNNhnTlA26jRM4G/lP16hJmZdUuuLYmIaJZ0OnArySMGv46IJZIuABoiYg5wBfAbSUuBN0gKiZmZVYHcr0lExFxgbod55xW8Xwd8Ku8cZmaWXb944trMzLrHRcLMzIpykTAzs6Jy7ZYjL5IagRe7uflY4PUu16o+vTF3b8wMvTO3M/ec3pi7LfM2EVGXZcNeWSQ2haSGrH2XVIPemLs3ZobemduZe05vzL0pmX26yczMinKRMDOzovpjkZhV6QDd1Btz98bM0DtzO3PP6Y25u525312TMDOz0vXHloSZmZXIRcLMzIrqs0WiGsbWzqqEzCdJapS0OH19sRI5O2T6taTXJD1eZLkk/TT9TI9KmtLTGTtTQu5pklYVfNfndbZeT5I0QdKdkp6QtETS1zpZp6q+7xIzV+N3PUTSfEmPpLnP72SdqvoNKTFz9t+QiOhzL5IeZ58DtgMGAY8Au3ZY56vA5en744HZvSDzScBllf5+O2Q6EJgCPF5k+ZHALYCAfYCHKp25xNzTgJsrnbNDpnHAlPT9CJLx4zv+f6Sqvu8SM1fjdy1gs/R9LfAQsE+HdartN6SUzJl/Q/pqS+K9sbUjogloG1u70AzgqvT99cDBktSDGTsqJXPViYh7SLp4L2YGcHUk/gqMkjSuZ9IVV0LuqhMRyyNiUfr+beBJ3j8ccFV93yVmrjrp97c6naxNXx3v8qmq35ASM2fWV4tE2cbW7kGlZAY4Nj2NcL2kCZ0srzalfq5qtG/adL9F0qRKhymUntrYk+SvxUJV+31vJDNU4XctqUbSYuA1YF5EFP2uq+Q3pJTMkPE3pK8Wib7qT8DEiNgdmEf7XzFWfotI+rnZA7gUuKmycdpJ2gy4ATgrIt6qdJ5SdJG5Kr/riGiJiMkkwy5PlbRbhSN1qYTMmX9D+mqRyDK2NqqOsbW7zBwRKyJifTr5K2CvHsq2KUr536LqRMRbbU33SAbOqpU0tsKxkFRL8mN7TUTc2MkqVfd9d5W5Wr/rNhHxJnAnML3Domr7DXlPsczd+Q3pq0WiN46t3WXmDueWjyE5v1vt5gAnpHfd7AOsiojllQ7VFUlbtp1fljSV5L+Viv4ApHmuAJ6MiB8VWa2qvu9SMlfpd10naVT6fihwKPBUh9Wq6jeklMzd+Q3JffjSSoheOLZ2iZnPlHQM0EyS+aSKBU5Jupbk7pSxkpYB3ya5YEZEXE4ydO2RwFJgDXByZZJuqITcM4GvSGoG1gLHV/iPCID9gc8Dj6XnnQHOAbaGqv2+S8lcjd/1OOAqSTUkReu6iLi5mn9DKC1z5t8Qd8thZmZF9dXTTWZmVgYuEmZmVpSLhJmZFeUiYWZmRblImJlZUS4SZmZWlIuE9Uppl8cfqnSOjUkzfqdCx71sE7bfaJf11r+4SFhvdRJQ1UUib2lXEOXeZw3wM+AIYFfgM5J2LfdxrPdwkbCKkDRc0p/Tnj8fl3ScpJsKlh8q6Q9pr5ZXpus8JunrkmYC9cA16cApQyXtJeluSQsl3drW/YCkuyRdIqlB0pOS9pZ0o6RnJV1YJNvekh5Is82XNCL96/yP6f6elfTtdN2JKhi4SNI3Oms9dPzrXtLNSgbbed/nS5dvL+l/089zr6Rd0vlXSrpc0kPAf5fwPX9cyYA4D0u6XdIW6fw6SfOUDE7zK0kvKukvqVd2WW/56ZPdclivMB14NSKOApC0OXC+pLqIaCTpTuLXwGRgfETslq43KiLeTLsw+UZENCjpQO5SYEZENEo6DvgucEp6rKaIqFcyKtofSTo1ewN4TtIlEfFeP0FK+s2aDRwXEQskjSTpKgKSH9DdSLq7WCDpz8Drm/g9vO/zpfNnAV+OiGclfQT4OXBQumwrYL+IaClh//eRDDwTSkYh+3fgbJJuSP4SEd+TNB34Qrp+Z12Nf6S7H856PxcJq5THgB9KuphkVLJ7Jf0G+Jyk/wH2BU4gGc1sO0mXAn8GbutkXzuT/HjPU9JPXA1Q2KldW0eJjwFL2jq8k/Q8SS+ehZ3J7Qwsj4gFkPRQmq4LSf/8K9LpG4ED2PRurZ/v+PmUdKu9H/B7tY9hM7hgm9+XWCAgKSiz05bVIOBv6fwDgH8BiIj/lbRy0z6G9VUuElYREfGMkvGXjwQulHQHSdfFfwLWkfwQNgMrJe0BHA58Gfg07S2ENiL58d+3yOHaukZuLXjfNp3lv4GOHZ0FSUdphadthxTZttP1IqKzz3cW8GY6LkBn3smQ+VLgRxExR9I04DtdrF91XY1bZfmahFVEemfSmoj4LfB9knGQXwVeBc4F/iddbywwICJuSOdPSXfxNkkrA+BpoE7Svuk2ter+6GZPA+Mk7Z3ua0TBBeJDJY1W0g3zJ4D7gX8AH5Q0RtJg4Ogi+30BmCxpgJLRwKYW+3xp6+Vvkj6VrqO0kHTH5rT/yJ9YMP9+koKEpMOAD6TzS+lm3/oRtySsUj4MfF9SK/Au8JV0/jVAXUS09XM/HvgfSW1/0Hwr/fdK4HJJa0lOTc0Efppe2xgI/BhYUmoYSXOBL0bEq+k1jUvTYrAWOCRdbT7J4DlbAb+NiIZ02wvSZa/w/jEH2txPcqrnCZI+/Bd18fn+FfiFpHNJujD/HfBIqZ+nwHdITlutBP4CbJvOPx+4VtLngQeBvwNvF+uyvhvHtT7CXYVbVUnvAHo4Iq6odJZCkk4C6iPi9IzbTIyI7+QUq9vSVk9LWhT2BX6xkdNb1o+5JWFVQ9JCkvPtZ1c6Sz+wNXBd2oJpAr5U4TxWpdySMMuJpMnAqIi4K6f9nwx8rcPs+yPitDyOZ/2Ti4SZmRXlu5vMzKwoFwkzMyvKRcLMzIpykTAzs6L+P4EwGYW7EwU/AAAAAElFTkSuQmCC\n", + "text/plain": [ + "<Figure size 432x288 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAY8AAAEHCAYAAABWecpSAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAkhklEQVR4nO3deZwcdZ3/8dc7k2NyE5IhQBIIIKKRI+AQYclKkCsEJfgDISAKgvJbF3S9F1zWKCiy6ioLi2CEcCn3oZHDgCCCsEAmnAlsIAaRhEgCIQm5SGby2T+qhvRM5uia6Z7unnk/H49+pOtbVd3vbkJ/UvWt+n4VEZiZmWXRq9QBzMys8rh4mJlZZi4eZmaWmYuHmZll5uJhZmaZ9S51gEIaMWJEjB07ttQxzMwqyty5c9+MiJos+3Sr4jF27Fjq6upKHcPMrKJIejXrPj5tZWZmmbl4mJlZZi4eZmaWmYuHmZll5uJhZmaZdaurraxCLH8M3nkZhn4IhteWOo2ZdYCLh3Wtp78FL/0cJIjNsNd0GPetUqcys4x82sq6zuqX4aX/hoa1UL8GGtbBc9+BDctLnczMMnLxsK6zYSn06tu0rVdf2LCsNHnMrMNcPKzrDBkH0dC0rVdvGLRrafKYWYe5eFjXqR4BB98FfYaBqqB6JBxyH/TuX+pkZpaRO8yta408GI5/C+rXQu+BSce5mVUcFw/rehL0GVTqFGbWCT5tZWZmmbl4mJlZZi4eZmaWWVH7PCTNBD4OLIuIPVtY/03g0zlZPgjURMQKSX8F3gEagPqI8DgWZmZlothHHtcAk1tbGRE/jojxETEeOBf4U0SsyNnkkHS9C4eZWRkpavGIiIeBFe1umDgJuLGIcczMrEDKos9D0gCSI5Tbc5oDuE/SXElntrHvmZLqJNUtX+4xkszMukJZFA/gE8CjzU5ZTYyI/YCjgLMkfbSlHSNiRkTURkRtTU1NV2Q1M+vxyqV4TKPZKauIWJL+uQy4E5hQglxmZtaCkhcPSUOBg4Hf5rQNlDS48TlwBDCvNAnNzKy5Yl+qeyMwCRghaTEwHegDEBFXpJt9ErgvItbm7DoSuFPJuEe9gRsi4vfFzGplon4trHoR+o2AQWNLncbMWlHU4hERJ+WxzTUkl/Tmti0C9ilOKitbbz8HDxwCUQ+bN8JuX4DaS0qdysxaUPLTVmbveeSTsHEFbFoNDRtg0Ux4fXapU5lZC1w8rHysfbXp8uZNsPrF0mQxsza5eFj5GLhz0+VefWDIB0uTxcza5OJh5eMf74C+20KfIVBVDbueDjscUepUZtYCTwZl5WPYPjD1VVj9v9BvOAzapdSJzKwVLh5WXvoMguEeB9Os3Pm0lZmZZebiYWZmmbl4mJlZZi4eZmaWmYuHmZll5uJhZmaZuXiYmVlmLh5mZpaZi4eZmWXm4mFmZpm5eJiZWWZFLR6SZkpaJqnF+cclTZK0StIz6eM7OesmS1ogaaGkc4qZ08zMsin2kcc1wOR2tnkkIsanj/MBJFUBlwFHAeOAkySNK2pSMzPLW1GLR0Q8DKzowK4TgIURsSgiNgI3AVMLGs7MzDqsHPo8DpT0rKR7JX0obRsFvJazzeK0zczMykCp5/N4Ctg5ItZImgL8Btg9ywtIOhM4E2CnnXYqeEAzM9taSY88ImJ1RKxJn98D9JE0AlgCjMnZdHTa1tJrzIiI2oiorampKXpmMzMrcfGQtL0kpc8npHneAuYAu0vaRVJfYBowq3RJzcwsV1FPW0m6EZgEjJC0GJgO9AGIiCuA44EvSqoH1gPTIiKAeklnA7OBKmBmRMwvZlYzM8ufkt/q7qG2tjbq6upKHcNKZeNKeOU62LQadjwatt231InMKoKkuRFRm2WfUneYmxXGxrfhnr1hw5uweRPMvxAm3gajppQ6mVm3VA6X6pp13sJfwoZlsHkD0AAN62Hul0udyqzbcvGw7uHdt2DzxqZtm1aVJotZD+DiYd3DqKOhqv+W5apqGPWJ0uUx6+ZcPKx72O6jMOFKqB4JfYbAmE/B/j8vdSqzbqtTHeaSPhcRVxcqjFmn7HJy8jCzouvskcf3CpLCzMwqSrtHHpKea20VMLKwcczMrBLkc9pqJHAk8HazdgGPFTyRmZmVvXyKx13AoIh4pvkKSQ8VOpCZmZW/dotHRJzRxjr3TpqZ9UB5X20ladsWmt+JiE0FzGNmZhUgy9VWTwHLgZeAl9Pnf5X0lKQPFyOcmZmVpyzF435gSkSMiIjhwFEk/SH/DPhuLDOzHiRL8TggImY3LkTEfcCBEfE40K/gyczMrGxlucN8qaR/BW5Kl08E3pBUBWwueDIzMytbWY48TiaZS/w36WOntK0KOKHQwczMrHzlfeQREW8CX2pl9cLCxKkwsRmW/SmZiGj4ATBgx1InMrOepn49LHsomQRtu4Oh79Auedssl+rWAN8CPgRUN7ZHxMfa2Gcm8HFgWUTs2cL6TwP/SnK3+jvAFyPi2XTdX9O2BqA+6xSJRbe5AR6aAm8+RnIAtxkO+T3UHFTqZGbWU2xcCbMnwPq/J8tV/WHykzBw56K/dZbTVr8G/hfYhWRAxL8Cc9rZ5xpgchvrXwEOjoi9gAuAGc3WHxIR48uucAC8ehMsfxTq10D96uTPxz5d6lRm1pPMuwDWvgr17ySPjW9BXWsniAorS/EYHhFXAZsi4k8RcTrQ6lEHQEQ8DKxoY/1jEdE4ZtbjJH0qlWHd39IpT3M0Vn8zs67wzsKmM2hGA6xZ1CVvnaV4NN5JvlTS0ZL2BVq667yjzgDuzVkO4D5JcyWd2dpOks6UVCepbvny5QWM047hE6BX7hXKVTBs3657fzOzkZOgasCW5apqqPlol7x1luLxfUlDga8D3wCuBL5aiBCSDiEpHv+a0zwxIvYjuRnxLEktfiMRMSMiaiOitqamphBx8rP9obDnv4P6QK++MGR3+Mfbuu79zcze/2UYcxyod/JbVDMR9vtJl7y1IqK4byCNBe5qqcM8Xb83cCdwVES81Mo23wXWRESb30ptbW3U1dV1LnBWDRtg0xroNxykrn1vMzNIfoOiHvpu06HdJc3N2recz2RQl5KcQmpRRHw5yxs2e+2dgDuAz+QWDkkDgV4R8U76/Ajg/I6+T1FVVScPM7NS6TOoy98yn0t1O/xPeUk3ApOAEZIWA9OBPgARcQXwHWA48HMl/2pvvCR3JHBn2tYbuCEift/RHGZmVlgFO20l6dKI6JprxFpRktNWZmYVriOnrbJ0mLfHd8eZmfUQhSweZmbWQ7h4mJlZZoUsHr5O1cysh8ireEiqktTenSf/VYA8ZmZWAfIqHhHRAExsZ5trChHIzMzKX5aZBJ+WNAu4FVjb2BgRdxQ8lZmZlbUsxaMaeIumI+kGyR3iZmbWg2SZSfBzxQxiZmaVI++rrSS9X9IDkualy3tLOq940czMrFxluVT3l8C5pPN6RMRzwLRihDIzs/KWpXgMiIgnm7XVFzKMmZlVhizF401Ju5EOzy7peGBpUVKZmVlZy3K11VnADOADkpYArwCnFCWVmZmVtSxXWy0CDsudqKl4sczMrJxludrqXyQNAdYBP5P0lKQjihfNzMzKVZY+j9MjYjXJlLDDgc8AFxUllZmZlbUsxaNx1NwpwHURMR+PpGtm1iNlKR5zJd1HUjxmSxoMbG5rB0kzJS1rvLGwhfWSdImkhZKek7RfzrpTJb2cPk7NkNPMzIosS/E4AzgH2D8i1gF9gfaGLLkGmNzG+qOA3dPHmcDlAJK2BaYDHwEmANMlDcuQ1czMiijLpbqNQ7LvLeV3tioiHpY0to1NppKcAgvgcUnbSNoBmATcHxErACTdT1KEbsyQ18zMiiRL8fhmzvNqkiOCuTQdZTerUcBrOcuL07bW2rci6UySoxZ22mmnTkQxM7N8ZbnP4xO5y5LGABcXOlBWETGD5OZFamtro8RxzMx6hM7MYb4Y+GAn338JMCZneXTa1lq7mZmVgbyPPCRdSjquFUnRGQ881cn3nwWcLekmks7xVRGxVNJs4MKcTvIjSEb0NTOzMpClz6Mu53k9cGNEPNrWDpJuJOn8HiFpMckVVH0AIuIK4B6SS38Xkty5/rl03QpJFwBz0pc6v7Hz3MzMSk/JhU7dQ21tbdTV1bW/oZmZvUfS3IiozbJPu0cekqaz5XRVWx6KiIezvLmZmVWmfE5b/TXP11rZ8RhmZlZJ2i0eEXFtVwQxM7PKkeVqq++01B4R5xcujpmZVYIsV1utzXleDXwceLGwcczMrBJkucP8P3OXJf0EmF3wRGZmVvY6c4f5AJI7v83MrIfJ0ufxPFsu2a0CagD3d5iZ9UBZ+jw+nvO8HngjIuoLnMfMKt3mTfDqzbDhDaj5RxgxodSJrAiy9Hm8ms70N5HkCOTPwNPFCmZmFWjzJrj/o7DyeYhNoN6w/89hV08G2t3k3eeRXqp7LTAcGAFcI+m8YgUzswq0+Lewah40rIXNG6FhHdSdBd1oGCRLZDlt9Wlgn4jYACDpIuAZ4PtFyGVmlejdtyA2N22rX5+0qao0mawoslxt9TrJ/R2N+uE5Nsws13YfpclQeOoDwydALxeO7iZL8VgFzJd0jaSrgXnASkmXSLqkOPHMrKIM/SBMvAX6bZcUjhEHwMGzSp3KiiDLaas700ejhwobxcy6hVEfh+PeKHUKK7IsxeM2YENENABIqgL6RcS6oiQzM7OyleW01QNA/5zl/sAfChvHzMwqQZbiUR0RaxoX0ucDCh/JzMzKXZbisTa9SRAASR8G1re3k6TJkhZIWijpnBbW/0zSM+njJUkrc9Y15Kxzr5uZWZnI0ufxFeBWSa8DArYHTmxrh7Rf5DLgcGAxMEfSrIh4oXGbiPhqzvZfAvbNeYn1ETE+Q0YzM+sCWYYnmSPpA8AeadOCiNjUzm4TgIURsQhA0k3AVOCFVrY/CZiebyYzMyuNTEOyR8SmiJiXPjZJ2r6dXUYBr+UsL07btiJpZ2AX4MGc5mpJdZIel3RsK/udmW5Tt3z58vw/jJmZdVhn5vMAuKogKRLTgNsaLwVO7RwRtcDJwMWSdmu+U0TMiIjaiKitqakpYBwzM2tNp4pHRBzdziZLgDE5y6NpfUiTacCNzV5/SfrnIpKbEvfdejczM+tqWTrMkTSMpBi8t19EPNXGLnOA3SXtQlI0ppEcRTR/3Q8Aw4D/afZe6yLiXUkjgIOAH2XJa2ZmxZFlJsELgNOAv7Bl5LMAPtbaPhFRL+lskrnOq4CZETFf0vlAXUQ0Xn47Dbgposm4zR8EfiFpM8kR0kW5V2mZmVnpKPIcZ1/SAmCviNhY3EgdV1tbG3V1daWOYWZWUSTNTfuX85alz2MesE2mRGZm1i1l6fP4IfC0pHnAu42NEXFMwVOZmVlZy1I8rgX+A3ge2NzOtmZm1o1lKR7rIsKTPpmZWabi8YikHwKzaHraqq1Ldc3MrBvKUjwab9A7IKetzUt1zcyse8oyMOIhxQxiZmaVI+9LdSWNlHSVpHvT5XGSziheNDMzK1dZ7vO4huRO8R3T5ZdI5vgwM7MeJkvxGBERt5BephsR9UBD27uYmVl3lHUa2uGk41pJOgBYVZRUZmZW1rJcbfU1kst0d5P0KFADfKooqczMrKxlKR7zgYNJpqEVsIDOTyZlZmYVKMuP//9ERH1EzG+chpac+TfMzKznaPfII52nfBTQX9K+JEcdAEOAAUXMZmZmZSqf01ZHkkwCNRr4T7YUj3eAbxcnlpmZlbN2i0dEXAtcK+m4iLi9CzKZmVmZy9LnMVrSECWulPSUpCPa20nSZEkLJC2UdE4L60+TtFzSM+nj8znrTpX0cvo4NUNWMzMroizF4/SIWA0cAQwHPgNc1NYOkqqAy4CjgHHASZLGtbDpzRExPn1cme67LTAd+AgwAZguaViGvGZmViRZikdjX8cU4LqImJ/T1poJwMKIWJTOfX4TMDXP9zsSuD8iVkTE28D9wOQMec3MrEiyFI+5ku4jKR6zJQ2m/RkFRwGv5SwvTtuaO07Sc5JukzQm475mZtbFshSPM4BzgP0jYh3QF/hcATL8DhgbEXuTHF1cm2VnSWdKqpNUt3z58gLEMTOz9mQpHrcCOwCrASLirYh4rp19lgBjcpZHp23vSV+ncWbCK4EP57tvuv+MiKiNiNqampp8P4uZmXVCluJxOXAy8LKkiyTtkcc+c4DdJe0iqS8wjWR8rPdI2iFn8RjgxfT5bOAIScPSjvIj0jYzMyuxLDMJ/gH4g6ShwEnp89eAXwK/Socrab5PvaSzSX70q4CZETFf0vlAXUTMAr4s6RigHlhBckMiEbFC0gUkBQjg/IhY0dEPamZmhaOIyH/jZEj2U0gu030d+DUwEdgrIiYVI2AWtbW1UVdXV+oYZmYVRdLciKjNsk/eRx6S7iQZUfd64BMRsTRddbOkyv7Ffu0OWDob+o+GPb4MfYeWOpF1J5vWwIL/gnV/g5Efg51OALV3lbtZecsyJPuNwO8jYrWk8yTtB3w/Ip7KWrHKyrwfwPwLoWEd9OoLr1wLU56F3gNLncy6g4YNMHt/WPMKbH4XXvkVrHwO9vlBqZOZdUqWDvPz0sIxETgMuIqkE71yRcC8C5LCAbB5I2x4Axb/trS5rPt4/V5YtzgpHJD8XXvhR7DZMzhbZctSPBr/th8NzIiIu0nu9ahcsRmifuu2hvWlyWPdT/26FhoDtr6+xKyiZCkeSyT9AjgRuEdSv4z7l59eVbDjFOhVvaVNvWD7w0uXybqX7T+W/J1q1KsfbDcJqqpb3cWsEmT58T+B5JLbIyNiJbAt8M1ihOpSB90IO09LOsuHfRgO/SMM3KnUqay76L8DHPYwDJ8A/UfBmOPgo3eWOpVZp2W6VLfc+VJdM7PsOnKpbmWfdjIzs5Jw8TAzs8xcPMzMLDMXj0q14BK4dRu4qT88dgo0vNvuLmZmhZLlDnMrF4tnwTPnbrm58bU7oPcQmPDz0uYysx7DRx6VaMldWwoHJDc1vn5X6fKYWY/j4lGJqrcD9Wna1m94abKYWY/k4lGJ9vhKUkCq+id3LFcNhNrLSp3KzHoQ93lUouoRcPQ8ePXm5JTVjlNgyPtLncrMehAXj0rVdxvY/f+XOoWZ9VA+bWVmZpkVvXhImixpgaSFks5pYf3XJL0g6TlJD0jaOWddg6Rn0sesYmcttAi49164/HJ4/PFSpzEzK5yinraSVAVcBhwOLAbmSJoVES/kbPY0UBsR6yR9EfgRybDvAOsjYnwxMxZLBHz2s3DnnbB5czLr6AUXwNe+VupkZmadV+wjjwnAwohYFBEbgZuAqbkbRMQfI6LxpoXHgdFFztQl5s5NCsfatbB+PaxbB+eeC2vWlDqZmVnnFbt4jAJey1lenLa15gzg3pzlakl1kh6XdGxLO0g6M92mbvny5Z0OXChvvAFVVU3beveGFStKk8fMrJDK5morSacAtcDBOc07R8QSSbsCD0p6PiL+krtfRMwAZkAyn0eXBW7Hfvslp6saSTBsGIxqq3SamVWIYh95LAHG5CyPTtuakHQY8G/AMRHx3gh/EbEk/XMR8BCwbzHDFtIOO8CsWVBTkxSO970PHnhg66MRM7NKVOwjjznA7pJ2ISka04CTczeQtC/wC2ByRCzLaR8GrIuIdyWNAA4i6UyvGIccAsuWQUODi4aZdS9FLR4RUS/pbJK5z6uAmRExX9L5QF1EzAJ+DAwCbpUE8LeIOAb4IPALSZtJjpAuanaVVsVw4TCz7sZzmJuZ9XCew7wD/v53GDsWevWC6mq48sqm6xsa4JxzYMcdYbfd4JZbtn6NK5+6krEXj2X0T0fzg0d+QGNBfvFF+MhHYORImDIlOYWVjwj44Q9h9GjYeWf45S879xnNzAqtxx951NTAm282bXvkEZg4MXn+b/8GF1+c3KcB0L8/3H130p8BcPsLt/PZ33yWdZuSDQb2GcgFH7uA0/b4Ku97H7z9dlIM+vSBPfaAZ59NClVbLr4YzjsvuUcEYMAAuO46OO64TB/NzCwvPvLIaOPGrQsHNP2X/g03bCkckNzwd/PNW5avf+769woHwNpNa7n+2et54gmor08KB8CmTfCXv8DSpe3nuv76LYUDkve//vo8P5SZWRfo0cWjdyuXCwwZsuX5wIE5K3rVo4kXcV/N0Xx19ldZuWElQ6uHItRk/8F9BzNoUNP7PCApJgMGtJ9r8OCmy1LTTGZmpdaji0evXklfRK4+fWD69C3LP/5xzg/+cZ8mDr6AV3rfw+VzLueAKw/g6wd8nUF9B9Er/SoH9BnAhYdeyIEHwvjxyWkuSF7jC19IbhRsz4UXbnnPXr1g0CD49rc79VHNzAqqx/d5APz7vyc39O24I1x9NWy/fdP1TzwB193yNlcMHslmbXqvfXDfwdx+wu3sOmxXrnr6KjZt3sQpe53CPtvvAySnxX7xC3jpJTjgADj55OQoIh/PPZecqurdGz7/+aSz3sysGDrS5+Hikac3173JqJ+OYmPDxvfaBvcdzC2fuoXJ75tclPc0M+sK7jAvouH9h3PQmIOo7l0NQJWqGNxvMBN3mljiZGZmXc/FI0+SuOvkuzh9/OnsPXJvpn5gKk9+/kmqew3iwQfhd7/ziLlm1nOUzai6lWBAnwFcdvRl7y2vXw/77ptcgtu7d/L4859h3LgShrTytPpl2LAUhoyD6hGlTmPWaS4eHRQBBx0E8+Y1bT/9dE85a808/U146TLo1ReiAQ6+C0Ye3P5+ZmXMp6066Pbb4fnnt27/29+6PouVseWPwUuXQ8N62LQK6tfAI5/ccveoWYVy8eigl1/e+iZAgAkTuj6LlbF3Xt66bdNqaFi3dbtZBXHx6KC99tpyA2Cj/v3hqqtKk8fK1NAPAc2OMvqNgN4DW9zcrFK4eHTQ0Ucnd4z365cMYTJyJDzzDAwfXupkVlaG18Je06FXP+g9GPpuC5PuLnUqs07zTYKdtHQprFyZ3AHet2+XvrVVkg1vwoY3YNCu0Lt/+9ubdaGO3CToq606aYcdkodZm6pH+BJd61Z82srMzDIrevGQNFnSAkkLJZ3Twvp+km5O1z8haWzOunPT9gWSjix21pbccw8ceWQy+u6f/rT1+meegWOPhUMPhV/9qqvTmZmVRlFPW0mqAi4DDgcWA3MkzYqIF3I2OwN4OyLeJ2ka8B/AiZLGAdOADwE7An+Q9P6IaChm5lx33QUnnJDcSQ7w0ENw771wcHp/14svJjMONk7c9PjjsGoVnHVWVyU0MyuNYh95TAAWRsSiiNgI3ARMbbbNVODa9PltwKGSlLbfFBHvRsQrwML09brMRRdtKRyQPP/Zz7Ysz5zZdJbBdevgJz/punxmZqVS7OIxCngtZ3lx2tbiNhFRD6wChue5L5LOlFQnqW758uUFjN6y5hentbdsZtYdVXyHeUTMiIjaiKitqakp6Gt/4xtNp43t3x++8pUty6ee2nSa2gED4GtfK2gEM7OyVOzisQQYk7M8Om1rcRtJvYGhwFt57ltUxx4LN9wAkybBYYclsw0ecsiW9XvumfSDTJmS9H1ceil86UtdmdDMrDSKepNgWgxeAg4l+eGfA5wcEfNztjkL2Csi/intMP9/EXGCpA8BN5D0c+wIPADs3laHeSluEjQzq3Rld5NgRNRLOhuYDVQBMyNivqTzgbqImAVcBVwvaSGwguQKK9LtbgFeAOqBs7rySiszM2udhycxM+vhPIe5mZl1CRcPMzPLzMXDzMwyc/EwM7PMulWHuaTlwKudeIkRwJsFitNVKjEzVGZuZ+46lZi7EjNDkntgRGS6y7pbFY/OklSX9YqDUqvEzFCZuZ2561Ri7krMDB3P7dNWZmaWmYuHmZll5uLR1IxSB+iASswMlZnbmbtOJeauxMzQwdzu8zAzs8x85GFmZpm5eJiZWWY9rnhImixpgaSFks5pYX0/STen65+QNLYEMbeSR+7TJC2X9Ez6+HwpcjbLNFPSMknzWlkvSZekn+k5Sft1dcYWMrWXeZKkVTnf83e6OmMLmcZI+qOkFyTNl/QvLWxTjt91PrnL6vuWVC3pSUnPppm/18I2ZfUbkmfm7L8fEdFjHiTDwv8F2BXoCzwLjGu2zT8DV6TPpwE3V0ju04D/LnXWZpk+CuwHzGtl/RTgXkDAAcATFZB5EnBXqXM2y7QDsF/6fDDJHDrN/36U43edT+6y+r7T729Q+rwP8ARwQLNtyuo3JM/MmX8/etqRxwRgYUQsioiNwE3A1GbbTAWuTZ/fBhwqSV2YsSX55C47EfEwyRwtrZkKXBeJx4FtJO3QNelalkfmshMRSyPiqfT5O8CLwKhmm5Xjd51P7rKSfn9r0sU+6aP5VUdl9RuSZ+bMelrxGAW8lrO8mK3/sr63TUTUA6uA4V2SrnX55AY4Lj0lcZukMS2sLzf5fq5yc2B6CuDedMbLspGeItmX5F+Xucr6u24jN5TZ9y2pStIzwDLg/oho9bsul9+QPDJDxt+PnlY8urPfAWMjYm/gfrb8y8cK6ylg54jYB7gU+E1p42whaRBwO/CViFhd6jz5aid32X3fEdEQEeOB0cAESXuWOFK78sic+fejpxWPJUBuRR2dtrW4jZI52IcCb3VJuta1mzsi3oqId9PFK4EPd1G2zsjnv0dZiYjVjacAIuIeoI+kESWOhaQ+JD/Av46IO1rYpCy/6/Zyl+v3DRARK4E/ApObrSrH3xCg9cwd+f3oacVjDrC7pF0k9SXpzJrVbJtZwKnp8+OBByPtUSqhdnM3O399DMn543I3C/hseiXQAcCqiFha6lBtkbR94/lrSRNI/h8q6Q9Dmucq4MWI+Gkrm5Xdd51P7nL7viXVSNomfd4fOBz432abldVvSD6ZO/L70buAGcteRNRLOhuYTXIF08yImC/pfKAuImaR/GW+XtJCko7TaaVLnMgz95clHQPUk+Q+rWSBU5JuJLlaZoSkxcB0ks46IuIK4B6Sq4AWAuuAz5Um6RZ5ZD4e+KKkemA9MK0M/nFxEPAZ4Pn0vDbAt4GdoHy/a/LLXW7f9w7AtZKqSArZLRFxV5n/huSTOfPvh4cnMTOzzHraaSszMysAFw8zM8vMxcPMzDJz8TAzs8xcPMzMLDMXDzMzy8zFw7qddHjpHUudoy1pxu+W6H3/uxP7tzk1gPUcLh7WHZ0GlHXxKLZ0WIxCv2YVcBlwFDAOOEnSuEK/j1UGFw8rO5IGSro7HUl1nqQTJf0mZ/3hku5MRwq9Jt3meUlflXQ8UAv8Op3Upr+kD0v6k6S5kmY3DsUg6SFJP5NUJ+lFSftLukPSy5K+30q2/SU9lmZ7UtLg9F/zv01f72VJ09NtxypnUilJ32jpaKP50YCku5RMgrTV50vX7ybp9+nneUTSB9L2ayRdIekJ4Ed5fM+fUDJZ0dOS/iBpZNpeI+l+JRMHXSnpVSXjSVXk1ABWHD1qeBKrGJOB1yPiaABJQ4HvSaqJiOUkQ2vMBMYDoyJiz3S7bSJiZTqUyzciok7JwHuXAlMjYrmkE4EfAKen77UxImqVzGL3W5IB4VYAf5H0s4h4bxwlJeOK3QycGBFzJA0hGTIDkh/WPUmG/pgj6W7gzU5+D1t9vrR9BvBPEfGypI8APwc+lq4bDfxDRDTk8fp/JpkUKJTMHPct4OskQ7I8GBE/lDQZOCPdvqVh3T/S0Q9nlc3Fw8rR88B/SvoPklnkHpF0PXCKpKuBA4HPksw+t6ukS4G7gftaeK09SH7U71cyvl4VkDsgYOMAk88D8xsHC5S0iGRk1NxB+PYAlkbEHEhGfE23hWSOhLfS5TuAiXR++PBFzT+fkuHL/wG4VVvmF+qXs8+teRYOSArNzemRWF/glbR9IvBJgIj4vaS3O/cxrDty8bCyExEvKZljewrwfUkPkAwT/TtgA8kPZD3wtqR9gCOBfwJOYMsRRSORFIUDW3m7xmGoN+c8b1zO8v9H80HigmSQudxTw9Wt7NvidhHR0uf7CrAynZuhJWszZL4U+GlEzJI0CfhuO9uX5bDuVhru87Cyk14ptS4ifgX8mGSe69eB14HzgKvT7UYAvSLi9rR9v/Ql3iE5KgFYANRIOjDdp486PhvdAmAHSfunrzU4p2P6cEnbKhny+ljgUeANYDtJwyX1Az7eyuv+FRgvqZeSGdwmtPb50qOdVyR9Kt1GaYHpiKFs+fE/Naf9UZJChaQjgGFpez5TGlgP4SMPK0d7AT+WtBnYBHwxbf81UBMRjXMNjAKultT4j6Bz0z+vAa6QtJ7kFNfxwCVp30lv4GJgfr5hJN0DfD4iXk/7TC5Ni8R64LB0sydJJjUaDfwqIurSfc9P1y1h63kfGj1KcsroBZJ5FJ5q5/N9Grhc0nkkw8XfBDyb7+fJ8V2S019vAw8Cu6Tt3wNulPQZ4H+AvwPvtDY1QAfe17oBD8luFSO9IunpiLiq1FlySToNqI2IszPuMzYivlukWB2WHiU1pMXiQODyNk6TWQ/lIw+rCJLmkpzP/3qps/QAOwG3pEc8G4EvlDiPlSEfeZiVgKTxwDYR8VCRXv9zwL80a340Is4qxvtZz+PiYWZmmflqKzMzy8zFw8zMMnPxMDOzzFw8zMwss/8DMZ/sf7RmFRwAAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 432x288 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + }, + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAYkAAAEKCAYAAADn+anLAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjUuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/YYfK9AAAACXBIWXMAAAsTAAALEwEAmpwYAAAm9klEQVR4nO3de5xVdb3/8deb4eYAKcLkhYtomeYVdbxbYinhlTp2CstS0+PJ1LLbSatfdkyPdjwdS7soR4lS09LSqDTAe5okg3hDRJE0QVQUBBEEZvj8/lhrYjPMntl7Zq9Zm5n38/HYj1nru9Z37c9ebOYza32/6/tVRGBmZtaaXnkHYGZm1ctJwszMinKSMDOzopwkzMysKCcJMzMryknCzMyKyjRJSBoh6V5JT0uaI+lLrewjSVdKmi/pCUn7Fmw7RdJz6euULGM1M7NNKcvnJCRtB2wXEY9KGgTMAj4aEU8X7HMMcC5wDHAg8KOIOFDS1kADUA9EWne/iFiWWcBmZraR3lkePCIWA4vT5bckzQWGAU8X7DYe+GUk2WqGpK3S5DIGmB4RSwEkTQfGATcVe7+hQ4fGqFGjsvgoZmbd1qxZs16PiLrWtmWaJApJGgXsA/ytxaZhwEsF6wvTsmLlRY0aNYqGhoZOx2pm1pNIerHYti5puJY0EPgtcF5ErKjwsc+U1CCpYcmSJZU8tJlZj5d5kpDUhyRB3BgRv2tll0XAiIL14WlZsfKNRMTEiKiPiPq6ulavlszMrIOy7t0k4DpgbkT8b5HdpgCfTXs5HQQsT9sypgJjJQ2WNBgYm5aZmVkXybpN4lDgM8CTkh5Ly74JjASIiKuBO0h6Ns0HVgGnpduWSvoeMDOtd1FzI7aZmXWNrHs3PQionX0COLvItknApAxCMzOzEnRZ7yYz64bWvgmLpwKC7cZC361yDsgqzUnCzDpm1UL4cz00rgICeg+EcbOgdvu8I7MK8thNZtYxs78Ba16HxregcWWy/Nj5eUdlFeYkYWYd8/aLEE0b1qMR3n4ht3AsG04SZtYx2x4JNbUb1mtqYduj8ovHMuEkYWYds8e3YcTHQDXJa8SJsPsFeUdlFeaGazPrmF694ZAb4MDrAEFN37wjsgw4SZhZ59T0yzsCy5BvN5mZWVFOEmZmVpSThJmZFeUkYWZmRTlJmJlZUU4SZmZWlJOEmZkV5SRhZmZFOUmYmVlRmT5xLWkScBzwWkTs0cr2rwOfLojl/UBdOnXpC8BbQBPQGBH1WcZqZmabyvpKYjIwrtjGiLg8IkZHxGjgAuD+FvNYH5Fud4IwM8tBpkkiIh4Alra7Y+Ik4KYMwzEzszJVRZuEpFqSK47fFhQHME3SLEln5hOZmVnPVi2jwB4PPNTiVtNhEbFI0ruB6ZKeSa9MNpImkDMBRo4c2TXRmpn1EFVxJQFMoMWtpohYlP58DbgNOKC1ihExMSLqI6K+rq4u80DNzHqS3JOEpC2Bw4HfF5QNkDSoeRkYCzyVT4RmZj1X1l1gbwLGAEMlLQQuBPoARMTV6W4fA6ZFxNsFVbcBbpPUHOOvIuLPWcZqZmabyjRJRMRJJewzmaSrbGHZAmDvbKIys4p57QGYdyUg2OVL8O7D8o7IKqxaGq7NbHPz6r1w33HQtCpZf/lPMOZO2ObwfOOyisq9TcLMNlNzLtuQIACaVsPT388vHsuEk4SZdUw0tlK2ruvjsEw5SZhZx+zyRaip3bBeU5u0S1i34iRhZh0zfDwccj0MORCGHASH3AjDjss7KqswN1ybWceN+JfkZd2WryTMzKwoJwkzMyvKScLMzIpykjAzs6KcJMzMrCgnCTMzK8pJwszMinKSMDOzopwkzMysKCcJMzMryknCzMyKyjRJSJok6TVJrc5PLWmMpOWSHktf3ynYNk7SPEnzJZ2fZZxmJYmAVQvhnSV5R2LWZbIe4G8y8GPgl23s85eI2GjoSEk1wE+Ao4CFwExJUyLi6awCNWvT2mVw95GwYi5EE4z8Vzj4lyBfjFv3luk3PCIeAJZ2oOoBwPyIWBARa4GbgfEVDc6sHI+cBcufSmZfW78WXroNnvtZ3lGZZa4a/gw6WNLjku6UtHtaNgx4qWCfhWmZWT7eeCRJDs2aVsGSv+YXj1kXyTtJPArsEBF7A1cBt5d7AElnSmqQ1LBkie8VW0YGvRdUs2G9V3/Y8v35xWPWRXJNEhGxIiJWpst3AH0kDQUWASMKdh2elrV2jIkRUR8R9XV1dZnHbD3UAROh31Do8y7oPRC22gN2/WreUZllLteZ6SRtC7waESHpAJKk9QbwJrCzpB1JksME4FO5BWo2cBQc/1xy26lXPxh6EPTyxI7W/ZX0LU9/gUdEzJS0GzAOeCb967+tejcBY4ChkhYCFwJ9SA52NfBx4CxJjcBqYEJEBNAo6RxgKlADTIqIOR35gGYV02cQbPvhvKMw61JKfie3sYN0IXA0SUKZDhwI3EvSPXVqRFySdZClqq+vj4aGhrzDMDPbrEiaFRH1rW0r5Uri48BooB/wCjA8IlZI+h/gb0DVJAkzM6usUhquGyOiKSJWAc9HxAqAiFgNrM80OjMzy1UpSWKtpNp0eb/mQklb4iRhZtatlXK76YMRsQYgIgqTQh/glEyiMjOzqtBukmhOEJK2brFpPfBMFkGZmVl1KOdhukeBJcCzwHPp8guSHpW0X5s1zcxss1ROkpgOHBMRQyNiCEm32D8CXwB+mkVwZmaWr3KSxEERMbV5JSKmAQdHxAyS7rFmZtbNlDOuwGJJ3yAZthvgk8Cr6dwP7uVkZtYNlXMl8SmSgfZuT18j07Ia4BOVDszMzPJX8pVERLwOnFtk8/zKhGNmZtWk5CQhqQ74D2B3oH9zeUR8KIO4zMysCpRzu+lGkucidgT+E3gBmJlBTGZmViXKSRJDIuI6YF1E3B8RnwN8FWFm1o2V07tpXfpzsaRjgZeBlk9hm5lZN1JOkrg4HdTvqyTzUb8L+HImUZmZWVUop3fTH9PF5cARpdSRNAk4DngtIvZoZfungW8AAt4CzoqIx9NtL6RlTSTDlbc6IYaZ9SCrX4FFfwDVwPDx0G9I3hHlb+0yeOl2iHWw/XFQu31FD99ukpB0FVB0+rqI+GIb1ScDPwZ+WWT734HDI2KZpKOBiSQz3zU7Iu16a11t5QJ49X7o8y4YdjzU9M07IuvpVjwLUw+E9WuT9ccugKMfhdph+caVp9WvwJ37wLoVyfrsr8PYh2HL3Sr2FqVcSXR4PtCIeEDSqDa2/7VgdQbJw3qWt9cegHuPSZYlGLQzjP0r1PRvu55ZlmZ/Nf1lmA7wsH4NPPEdOOi6XMPK1VMXw5rXIRqT9SbBrPPgQ9Mq9halDBX+i1IOJOmqiCj2sF0pTgfuLHxrYJqkAK6JiImdOLaVY8Zp0PT2hvUVz8CCybDz53MLyYzVi9loBKBogtUv5xZOVVi1cEOCACDS81Q55XSBbc+hHa0o6QiSJPGNguLDImJfktFmz5b0wSJ1z5TUIKlhyZIlHQ3BCq1pcYev6R3/Z7T8bX8s1NRuWK+pTcp6su2PhZoBG9ZrtoDtj6noW1QySXSIpL2Aa4HxEfFGc3lELEp/vgbcBhzQWv2ImBgR9RFRX1dX1xUhd391h0GvgjaImi3g3YfnF48ZwB7/D3aYAOqTfD93/jy87+y8o8rXe8+AXc5Nzod6w4iPw94XV/QtyukCW3GSRgK/Az4TEc8WlA8AekXEW+nyWOCinMLseQ6+Hh74KLz+UPIfcu//gm0/nHdU1tP16p20Pxx4bbIu5RtPNZBg9KXJ/1ECVPm/+yuZJDb5F5N0EzAGGCppIXAhydzYRMTVwHeAIcBPlfyDN3d13Qa4LS3rDfwqIv5cwVitLf22hqMegKa10KuP/zNadfH3cVMSrfwKroiSkkQ6Z8T3I+Jrbez2o5YFEXFSW8eNiDOAM1opXwDsXUpsliF3ezXr8Uq6NomIJuCwdvaZXImAzMysepRzu2m2pCnALcA/+0dGxO8qHpWZmVWFcpJEf+ANNh75NUgans3MrBsqZ+ym07IMxMzMqk/J/aUkvU/S3ZKeStf3kvTt7EIzM7O8ldOp9v+AC0jnlYiIJ4AJWQRlZmbVoZwkURsRj7Qoa2x1TzMz6xbKSRKvS3oP6bDhkj4OVHYkKTMzqyrl9G46m2S+h10lLSKZC+LkTKIyM7OqUE7vpgXAkYXjKmUXlpmZVYNyejd9SdK7gFXAFZIelTQ2u9DMzCxv5bRJfC4iVpCMyDoE+AxwWSZRmZlZVSgnSTQPMXgM8MuImENWww6amVlVKCdJzJI0jSRJTJU0iI3mEjQzs+6mnN5NpwOjgQURsUrSEMBDdZiZdWPlJInmocL3kif9MDPrEcpJEl8vWO5PMuf0LDYeFdbMzLqRktskIuL4gtdRwB7AsrbqSJok6bXmQQFb2S5JV0qaL+kJSfsWbDtF0nPp65RS4zQzs8rpzKzZC4H3t7PPZGBcG9uPBnZOX2cCPwOQtDXJfNgHklyxXChpcCdiNTOzDij5dpOkq0jHbSJJLqOBR9uqExEPSBrVxi7jSbrTBjBD0laStgPGANMjYmn63tNJks1NpcZrZmadV06bREPBciNwU0Q81Mn3Hwa8VLC+MC0rVm5mZl2onLGbfpFlIB0l6UySW1WMHDky52jMzLqXdpOEpAvZcJupLfdFxANlvv8iYETB+vC0bBHJLafC8vtaO0BETCQZnZb6+vpS4jQzsxKVciXxQonHerMD7z8FOEfSzSSN1MsjYrGkqcB/FTRWjyWZFc/MzLpQu0miM7eZJN1EckUwVNJCkh5LfdLjXg3cQTLMx3yS0WVPS7ctlfQ9YGZ6qIuaG7HNzKzrlNO76TutlUfERcXqRMRJbR0z7dV0dpFtk4BJpcZnZmaVV07vprcLlvsDxwFzKxuOmZlVk3J6N/2gcF3S/wBTKx6RmZlVjc48cV1L0uvIzMy6qXLaJJ5kQ1fYGqAOKNoeYWZmm79y2iSOK1huBF6NiMYKx2NmZlWknDaJF9NRWg8juaJ4EJidVWBmZpa/ktsk0i6wvwCGAEOByZK+nVVgZmaWv3JuN30a2Dsi3gGQdBnwGHBxBnGZmVkVKKd308skz0c060cyxpKZmXVT5VxJLAfmpHM7BHAU8IikKwEi4osZxGdmZjkqJ0nclr6a3VfZUMzMrNqUkyRuBd6JiCYASTVAv4hYlUlkZmaWu3LaJO4GtihY3wK4q7LhmJlZNSknSfSPiJXNK+lybeVDMjOzalFOkng7fZgOAEn7AasrH5KZmVWLctokzgNukfQyIGBb4JNZBGVmZtWhnGE5ZkraFdglLZoXEeuyCcvMzKpBWUOFR8S6iHgqfa2TtG17dSSNkzRP0nxJ57ey/QpJj6WvZyW9WbCtqWDblHJiNTOzzivndlNrrgOOLbYx7Sb7E5IH7xYCMyVNiYinm/eJiC8X7H8usE/BIVZHxOhOxmhmZh3UmUmHiIiiCSJ1ADA/IhZExFrgZmB8G/ufBNzUmZjMzKxyyrqSkDQYGFFYLyIebaPKMOClgvWFwIFFjr0DsCNwT0Fxf0kNJPNXXBYRt5cTr5mZdU45M9N9DzgVeJ4NM9QF8KEKxTIBuLX5ie7UDhGxSNJOwD2SnoyI51vEdSZwJsDIkSMrFIqZmUF5VxKfAN6T3jYq1SKSK49mwyk+cuwE4OzCgohYlP5cIOk+kvaK51vsMxGYCFBfXx+YmVnFlNMm8RSwVZnHnwnsLGlHSX1JEsEmvZTSrrWDgYcLygZL6pcuDwUOBZ5uWdfMzLJTzpXEpcBsSU8Ba5oLI+KEYhUiolHSOcBUoAaYFBFzJF0ENEREc8KYANwcEYVXAu8HrpG0niSZXVbYK8rMzLKnjX8vt7GjNAe4BngSWN9cHhH3ZxNa+err66OhoSHvMMzMNiuSZkVEfWvbyrmSWBURV1YoJusKr94Lz/wQEOz6Zdjm8LwjMrPNTDlJ4i+SLiVpUyi83dRWF1jLyyt3wf3joSmd7uOV6TDmT7DNmFzDMrPNSzlJovlJ6IMKyirZBdYqac73NyQISJaf/m8nCTMrSzkD/B2RZSBWaU2bFkUrZWZmbSi5C6ykbSRdJ+nOdH03SadnF5p1yi5fhpqCOaFqtoBdz8stHDPbPJXznMRkkq6s26frz5LMMWHVaPjxcOivoO5QqPsAHPYb2P7ovKMys81MOW0SQyPiN5IugH8+A+H7F9Vs+PjkZWbWQeVOXzqEdNwmSQcByzOJyszMqkI5VxJfIen++h5JDwF1wL9mEpWZmVWFcpLEHOBwkulLBcyjk/NRmJlZdSvnl/zDEdEYEXOapy+lYEA+MzPrftq9kkjnsR4GbCFpH5KrCIB3AbVFK5qZ2WavlNtNHyGZbGg48AM2JIm3gG9mE5aZmVWDdpNERPwC+IWkEyPit10Qk5mZVYly2iSGS3qXEtdKelTS2MwiMzOz3JWTJD4XESuAscAQ4DPAZZlEZWZmVaGcJNHcFnEM8MuImFNQZmZm3VA5SWKWpGkkSWKqpEEUzFBXjKRxkuZJmi/p/Fa2nyppiaTH0tcZBdtOkfRc+jqljFjNzKwCynmY7nRgNLAgIlalQ3Sc1lYFSTXAT4CjgIXATElTWpmr+tcRcU6LulsDFwL1JEOBzErrLisjZjMz64RyriRuAbYDVgBExBsR8UQ7dQ4A5kfEgohYC9wMlDri3EeA6RGxNE0M04FxZcRrZmadVE6S+BnwKeA5SZdJ2qWEOsOAlwrWF6ZlLZ0o6QlJt0oaUWZdMzPLSMlJIiLuiohPA/sCLwB3SfqrpNMk9elEDH8ARkXEXiRXC78op7KkMyU1SGpYsmRJJ8IwM7OWyhqgL22HOBU4A5gN/IgkaUwvUmURMKJgfXha9k/pbas16eq1wH6l1k3rT4yI+oior6urK+fjmJlZO8qZvvQ24C8k4zUdHxEnRMSvI+JcYGCRajOBnSXtKKkvMIFkuPHC425XsHoCMDddngqMlTRY0mCS5zOmlhqvmZl1Xjm9m24C/hwRKyR9W9K+wMUR8WhE1LdWIZ297hySX+41wKSImCPpIqAhIqYAX5R0AtAILCW5UiEilkr6HkmiAbgoIpZ25EOamVnHKCJK21F6IiL2knQYcDFwOfCdiDgwywDLUV9fHw0NDXmHYWa2WZE0q9gf++W0STTPZ30sMDEi/gT07WxwZmZWvcpJEoskXQN8ErhDUr8y65uZ2WamnF/ynyBpW/hIRLwJbA18PYugzMysOpTccB0Rq4DfFawvBhZnEZSZmVUH3y4yM7OinCTMzKwoJwkzMyvKScLMzIpykjAzs6KcJMzMrCgnCTMzK8pJwszMinKSMDOzopwkzMysKCcJMzMryknCzMyKyjxJSBonaZ6k+ZLOb2X7VyQ9LekJSXdL2qFgW5Okx9LXlJZ1zcwsW+VMX1o2STXAT4CjgIXATElTIuLpgt1mA/URsUrSWcB/k8xZAbA6IkZnGWMeHnkEHn4YttsOTjwRamryjsjMKmbtMvjHb2H9Gtj+WBg4Ku+IOiXTJAEcAMyPiAUAkm4GxgP/TBIRcW/B/jOAkzOOKVfXXQdf/CI0NUHv3nDNNTBtmhOFWbfwzmtwx2hYtxxYD4+dD0c+AFvvk3dkHZb17aZhwEsF6wvTsmJOB+4sWO8vqUHSDEkfzSC+LrV+PZxzDqxaBWvWwNtvJ1cVU6fmHZmZVcTT34c1r0PTKmh6BxpXQsO5eUfVKVlfSZRM0slAPXB4QfEOEbFI0k7APZKejIjnW9Q7EzgTYOTIkV0Wb0esWQPr1m1a/vrrXR+LmWVg9WKIFv/J17yWTywVkvWVxCJgRMH68LRsI5KOBL4FnBARa5rLI2JR+nMBcB+wyTVbREyMiPqIqK+rq6ts9BW2xRaw++4b31pavx4OOSS/mMysgoYdDzW1G9ZrtkjaJTZjWSeJmcDOknaU1BeYAGzUS0nSPsA1JAnitYLywZL6pctDgUMpaMvYXN15J+y7b5Iohg6FW2+F974376jMrCJ2mAC7X5Akh159YMS/wOjL8o6qUxQR2b6BdAzwQ6AGmBQRl0i6CGiIiCmS7gL2ZMN82f+IiBMkHUKSPNaTJLMfRsR1bb1XfX19NDQ0ZPVRKioCpLyjMLPMbEb/ySXNioj6VrdlnSS60uaSJJatXsbc1+ey7cBt2WnwTnmHY2Y9XFtJomoarvO0ciU8+yy8+90wfHi27/XgPx7k6BuPgfW9WBdr+PJB53HpkZe2W2/NGnjmGRg4EHbaabP5A8XMNnM9fliORx+FkSPhiCNg553hgguye6+I4LgbPsrKtW+xsnE5a5re4QcPXcnDLz3cZr0XX0zaLT7wAdhzTzjppKTB28wsaz0+SYwfD8uWwYoV8M47cNVV8MAD2bzXqnWrWb7mzY3K1q0Vdzwyr816J58MixfDW2/B6tXwhz/A9ddnE6OZWaEenSSammBRiw6569fD01n1oVq3BawasnGZAr2+W5vV5s5NYm22ahU8/ngG8ZmZtdCjk0RNTTJ+UqFevWDXXbN5v9paseUdf4TVg+GdQdDYj94Pf5Nj9j6gzXq77JLEteE4yW0nM7Os9fiG69//Ho46KumttmYNnHUWjBlT2fdYuXYlW/TegppeNdzxf/sz7viXWL/VfBqXb8N/fGFbDjqo7fo33ACHHZY0sDc2wrhxcMoplY3RzKw1PT5J1NcnDcPPPJP0bho1qnLHXrRiEeNuGMczbzxDL/XiR+N+xOcP+TwvLRjAvHl7s+22SaN5e3bcEebPT26DDRwI73ufezeZWdfwcxIZ2v//9mf24tk0RdKgUNunlrs/ezcHDW/n0sHMrAu19ZxEj26TyFphggBoWt/EjIUzcozIzKw8ThIZGlK7cU+m3r16s/aN7Rk0KLldVFMDl7b/HJ2ZWW56fJJYuhTGjoUBA2DECJg+vfS68+bBXntt6G00d+7G26//2PXU9qllUN9BDOw7kENGHMKFnziRlSuT7evXwze/CffcU7nPY2ZWST2+TeKDH4QZMzbM81BbC7NnJ43DbVm9OmnkXrJkwzheQ4fC3/+eJJxmC5Yt4OGXHmZo7VD2G3wUdUM3zcv/9m8wcWJZYZuZVYzHbiqiqQkeemjTIS7uv7/9JDF3bpIomnNscxfauXOTHlPNdhq80z8H8WtsbP1Y22/fwQ9gZpaxHn27qVcv6N9/07Kttmq/7uDBm84yt25d23V794ZPfWrjsi23TG45mZlVox6dJCS44orkFlNNTfJzl12S8Zzas+OOyZhKAwYkiWXAAJgwof0JhG68Ea65Bo47Dr7wBXjlFejbtzKfx8ys0np8mwTAgw8mg/pts03yi79fv9LqRcDttycPub3//fCxj/khNzPb/HjSITMzKyrXh+kkjZM0T9J8See3sr2fpF+n2/8maVTBtgvS8nmSPpJ1rKWKgOuug0MPTcZReuSRvCMyM8tGpklCUg3wE+BoYDfgJEktx8U+HVgWEe8FrgC+n9bdDZgA7A6MA36aHi93V10FD954AxeN+TCf3+2jnPfZ2TzxRGl1Gxvhkkvg8MPhs5+Fl1/ONtYOiYDnroG7PgQPnAjL57Zfx8y6pay7wB4AzI+IBQCSbgbGA4UzNowHvpsu3wr8WJLS8psjYg3wd0nz0+O1PY1bF3j1oZ/x45O/xoD+q1i/Ho7c4y5+cvMj7LVX2/NCAJxxBtxySzInRO/eMG1aMrhgKT2qusycS2HOJdC0ChC8Mh2OeQIGjso7MjPrYlnfbhoGvFSwvjAta3WfiGgElgNDSqybi3//wOUM6L8KSHo21fZ7mwOHXtduvXXrkmG/VyVVaWyEt9+GqVOzjLYD5l2RJgiAgKbV8OJNuYZkZvnY7LvASjpTUoOkhiVLlnTJew7eatPG/j337HgHgKrrO9BaQFUXpJl1hayTxCJgRMH68LSs1X0k9Qa2BN4osS4RMTEi6iOivq6uroKhFzdo/6/QSO2GGHoNYMj+n2u3Xp8+ybMUtWnV5mczPlI1TfKp950LNc2fT1DTH0ZNyDUkM8tH1m0SM4GdJe1I8gt+AtDimWOmAKeQtDV8HLgnIkLSFOBXkv4X2B7YGaiOfkTvO4fevQfCgp9Dn0HU7Pld2GqPkqpOnpw8cDdtWjLh0OWXJ09vV5U9vwP9hsA/boa+Q2DvS2DgTnlHZWY5yPw5CUnHAD8EaoBJEXGJpIuAhoiYIqk/cD2wD7AUmFDQ0P0t4HNAI3BeRNzZ1nv5OQkzs/L5YTozMyvKM9OZmVmHOEmYmVlRThJmZlaUk4SZmRXlJGFmZkV1q95NkpYAL3biEEOB1ysUTlYcY2U4xspwjJWTZ5w7RESrTyN3qyTRWZIainUDqxaOsTIcY2U4xsqp1jh9u8nMzIpykjAzs6KcJDY2Me8ASuAYK8MxVoZjrJyqjNNtEmZmVpSvJMzMrKgekSQkjZM0T9J8See3sr2fpF+n2/8maVTBtgvS8nmSMpv5oYQYvyLpaUlPSLpb0g4F25okPZa+pmQVY4lxnippSUE8ZxRsO0XSc+nrlBxjvKIgvmclvVmwLfNzKWmSpNckPVVkuyRdmcb/hKR9C7Z11TlsL8ZPp7E9KemvkvYu2PZCWv6YpMxG3CwhxjGSlhf8e36nYFub35EujvPrBTE+lX4Ht063dcm5bFNEdOsXyRDlzwM7AX2Bx4HdWuzzBeDqdHkC8Ot0ebd0/37AjulxanKK8QigNl0+qznGdH1lFZ3LU4Eft1J3a2BB+nNwujw4jxhb7H8uyRD2XXYugQ8C+wJPFdl+DHAnIOAg4G9deQ5LjPGQ5vcGjm6OMV1/ARhaBedxDPDHzn5Hso6zxb7Hk8yp06Xnsq1XT7iSOACYHxELImItcDMwvsU+44FfpMu3Ah+WpLT85ohYExF/B+anx+vyGCPi3ohonnh6BslMfV2tlHNZzEeA6RGxNCKWAdOBcVUQ40lAl07gHREPkMydUsx44JeRmAFsJWk7uu4cthtjRPw1jQFy+j6WcB6L6cz3uGxlxtnl38f29IQkMQx4qWB9YVrW6j4R0QgsB4aUWLerYix0Oslfms36K5nne4akj2YQX7NS4zwxvRVxq6TmKWir7lymt+x2BO4pKO6qc9mWYp+hq85huVp+HwOYJmmWpDNziqnZwZIel3SnpN3Tsqo8j5JqSZL+bwuKcz+XWU9fahUm6WSgHji8oHiHiFgkaSfgHklPRsTz+UTIH4CbImKNpH8nuUL7UE6xtGcCcGtENBWUVdO5rHqSjiBJEocVFB+WnsN3A9MlPZP+Nd3VHiX591ypZIbM20mmQa5WxwMPRUThVUfu57InXEksAkYUrA9Py1rdR1JvYEvgjRLrdlWMSDoS+BZwQkSsaS6PiEXpzwXAfSRTwWah3Tgj4o2C2K4F9iu1blfFWGACLS7tu/BctqXYZ+iqc1gSSXuR/BuPj4g3mssLzuFrwG1kc4u2XRGxIiJWpst3AH0kDaXKzmOBtr6P+Z3LPBtEuuJFcrW0gOS2QnMj1e4t9jmbjRuuf5Mu787GDdcLyKbhupQY9yFpbNu5RflgoF+6PBR4jowa4UqMc7uC5Y8BM9LlrYG/p/EOTpe3ziPGdL9dSRoFldO5HEXxBtdj2bjh+pGuPIclxjiSpI3ukBblA4BBBct/BcblFOO2zf++JL9c/5Ge05K+I10VZ7p9S5J2iwF5ncuisXX1G+bxIukt8mz6S/ZbadlFJH+RA/QHbkm/9I8AOxXU/VZabx5wdI4x3gW8CjyWvqak5YcAT6Zf9CeB03M+l5cCc9J47gV2Laj7ufQczwdOyyvGdP27wGUt6nXJuST5a3ExsI7kfvjpwOeBz6fbBfwkjf9JoD6Hc9hejNcCywq+jw1p+U7p+Xs8/R58K8cYzyn4Ls6gIKG19h3JK850n1NJOskU1uuyc9nWy09cm5lZUT2hTcLMzDrIScLMzIpykjAzs6KcJMzMrCgnCTMzK8pJwszMinKSsG4nHa58+7zjaEsa43dzet8fd6J+m8NeW/fjJGHd0alAVSeJrKXDy2RhMhmNPGvVyUnCqo6kAZL+lI7e+ZSkT0q6vWD7UZJuk1QjaXK6z5OSvizp4yQDIN6YTtSyhaT9JN2fjqQ5NR12G0n3KZmAqEHSXEn7S/pdOqHPxUVi2z+dZOdxSY9IGpT+df779HjPSbow3XdU4V/ckr7W2tVDy7/uJf0xnTBnk8+Xbn+PpD+nn+cvknZNyydLulrS34D/LuE8H69kkq3Zku6StE1aXidpuqQ5kq6V9GI65hHR8eG5bTPlUWCtGo0DXo6IYwEkbQn8p6S6iFgCnAZMAkYDwyJij3S/rSLiTUnnAF+LiAZJfYCrSAahWyLpk8AlJMNbAKyNiHpJXwJ+TzIg4VLgeUlXRMHAdZL6Ar8GPhkRMyW9C1idbj4A2ANYBcyU9Cfg9U6eh00+X1o+kWRIh+ckHQj8lA0j7Q4nGX6iifY9CBwUEaFkBsH/AL4KXEgy8c2lksaRDCNhPZSThFWjJ4EfSPo+ycxif5F0PXCypJ8DBwOfBQYBO0m6CvgTMK2VY+1C8st7uiRIZiVbXLC9eYrSJ4E5EbEYQNICkpFC3yjYdxdgcUTMhGSU0XRfSCYDeiNd/x3J0Nm3d+IcQDII3UafT9JAkjGmbknfF5IBKJvdUmKCgCSh/Dq9supLMmAgaewfA4iIP0taVqS+9QBOElZ1IuJZJfM6HwNcLOlukgHl/gC8Q/KLsBFYpmRu5Y+QDJj2CTZcITQTyS//g4u8XfOw5usLlpvXy/n/0XIQtAAa2fiWbv8idVvdLyJa+3znAW9GxOgix3q7jJivAv43IqZIGkMy6KHZRtwmYVUn7Zm0KiJuAC4H9o2Il4GXgW8DP0/3Gwr0iojfpuX7pod4i+QqA5LRe+skHZzW6aMNM5SVax6wnaT902MNKmggPkrS1pK2AD4KPEQyau+7JQ2R1A84rshxXwBGS+qlZCa/A4p9vvTq5e+S/jXdR2ki6Ygt2TCPwikF5Q+RJCQkjSUZltx6KF9JWDXaE7hc0nqS4ZXPSstvBOoiYm66Pgz4uaTmP3YuSH9OBq6WtJrk1tTHgSvTto3ewA9Jhl4uiaQ7gDMi4uW0TeOqNBmsBo5Md3uEZNrJ4cANEdGQ1r0o3bYIeKbIWzxEcqvnaWAuyYxqbX2+TwM/k/RtoA/JHM2Pl/p5CnyX5LbVMpIpXHdMy/8TuEnSZ4CHgVdIEi+SbgLGAEMlLQQujIjrOvDetpnwUOG22Uh7AM2utl9Kkk4lmfPhnDLrjIqI72YUVoelVz1NEdGYXoH9rI3bW9bN+UrCNguSZpHcb/9q3rH0ACOB36RXMGuBf8s5HsuRryTMciBpNLBVRNyX0fFPA77UovihiDg7i/ez7stJwszMinLvJjMzK8pJwszMinKSMDOzopwkzMysKCcJMzMr6v8Dn1LqrOxHXscAAAAASUVORK5CYII=\n", + "text/plain": [ + "<Figure size 432x288 with 1 Axes>" + ] + }, + "metadata": { + "needs_background": "light" + }, + "output_type": "display_data" + } + ], + "source": [ + "# get list of feature pair combinations\n", + "feature_pairs = list(itertools.combinations(df_heatmap.columns, 2))\n", + "feature_pairs_sample = random.sample(feature_pairs,5) # just sample 5 pairs\n", + "\n", + "# define colors of points\n", + "point_colors = ['blue' for i in range(10)] + ['orange' for i in range(10)] + ['green' for i in range(2)]\n", + "\n", + "# plot each pair of features\n", + "for feature_pair in feature_pairs_sample:\n", + " df_heatmap.plot.scatter(x=feature_pair[0], y=feature_pair[1], color=point_colors, subplots=True)" + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "..." + ] + }, + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "You made it! Congratualtions to getting all the way to the end (its ok if you just skipped here too), as a reward [here](https://youtube.com/playlist?list=PL6Zhl9mK2r0Ja7SKX72rD4dfBNnaQbbwR) is a playlist of interesting data science and machine learning youtube videos that you might like considering you just read a jupyter notebook about using kmeans to do unsupervised anomaly detection :)" + ] + } + ], + "metadata": { + "colab": { + "collapsed_sections": [], + "name": "Netdata Anomaly Detection Deepdive.ipynb", + "provenance": [] + }, + "kernelspec": { + "display_name": "Python 3 (ipykernel)", + "language": "python", + "name": "python3" + }, + "language_info": { + "codemirror_mode": { + "name": "ipython", + "version": 3 + }, + "file_extension": ".py", + "mimetype": "text/x-python", + "name": "python", + "nbconvert_exporter": "python", + "pygments_lexer": "ipython3", + "version": "3.8.1" + } + }, + "nbformat": 4, + "nbformat_minor": 1 +}
\ No newline at end of file |
